О. О. Метешкін, д-р техн наук, проф. Харківського військового університету; > Н. А. Кизим, д-р екон. наук, проф. Харківського

Вид материала

Документы

Содержание ЗАВДАННЯ ДЛЯ САМОСТІЙНОЇ РОБОТИ ДО рОзДІЛУ 2

Подобный материал:

• А. В. Ковалевська Рецензенти: доцент, канд екон наук, доцент Харківського національного, 739.76kb.
• А. А. Гвоздев руководительтемы; доктора техн наук, 3579.39kb.
• Інформаційні технології в журналістиці: вітчизняний І світовий досвід Київ 2002, 8272.38kb.
• Дипломных проектов по специальностям, 283.96kb.
• Конкурс-захист проходив на базі Харківського національного університету ім. В. Н. Каразіна,, 342.15kb.
• «Сторінки історії Харківського університету за архівними документами», 72.28kb.
• Міжнародна журналістика – 2002 київ 2002, 2743.9kb.
• Приглашение и программа разнообразие почв и биоты северной и центральной азии, 521.14kb.
• Строительные нормы и правила бетонные и железобетонные конструкции, 3448.03kb.
• Надійності та безпеки в будівництві, 692.13kb.

ЗАВДАННЯ ДЛЯ САМОСТІЙНОЇ РОБОТИ

ДО рОзДІЛУ 2

Варіант 1

Завдання 1. Розв’язати рівняння за допомогою функції root( ) на інтервалі [0, 3] із заданою точністю :



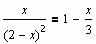
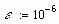
Завдання 2. Розв’язати рівняння g(x)=0: а) числово за допомогою функції polyroots(); б) символьно, де g(x) має вигляд:


x⁴ – 2x³ + x² – 12x + 20.


Завдання 3. Розв’язати систему рівнянь за допомогою функції find або minerr із заданою точністю 10^-8:




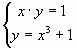
Варіант 2.

Завдання 1. Розв’язати рівняння за допомогою функції root() на інтервалі [1, 5] із заданою точністю :



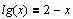
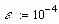
Завдання 2. Розв’язати рівняння g(x)=0: а) числово за допомогою функції polyroots(); б) символьно, де g(x) має вигляд:


x⁴ + 6x³ + x² – 4x – 60.


Завдання 3. Розв’язати систему рівнянь за допомогою функції find або minerr із заданою точністю 10^-8:


.


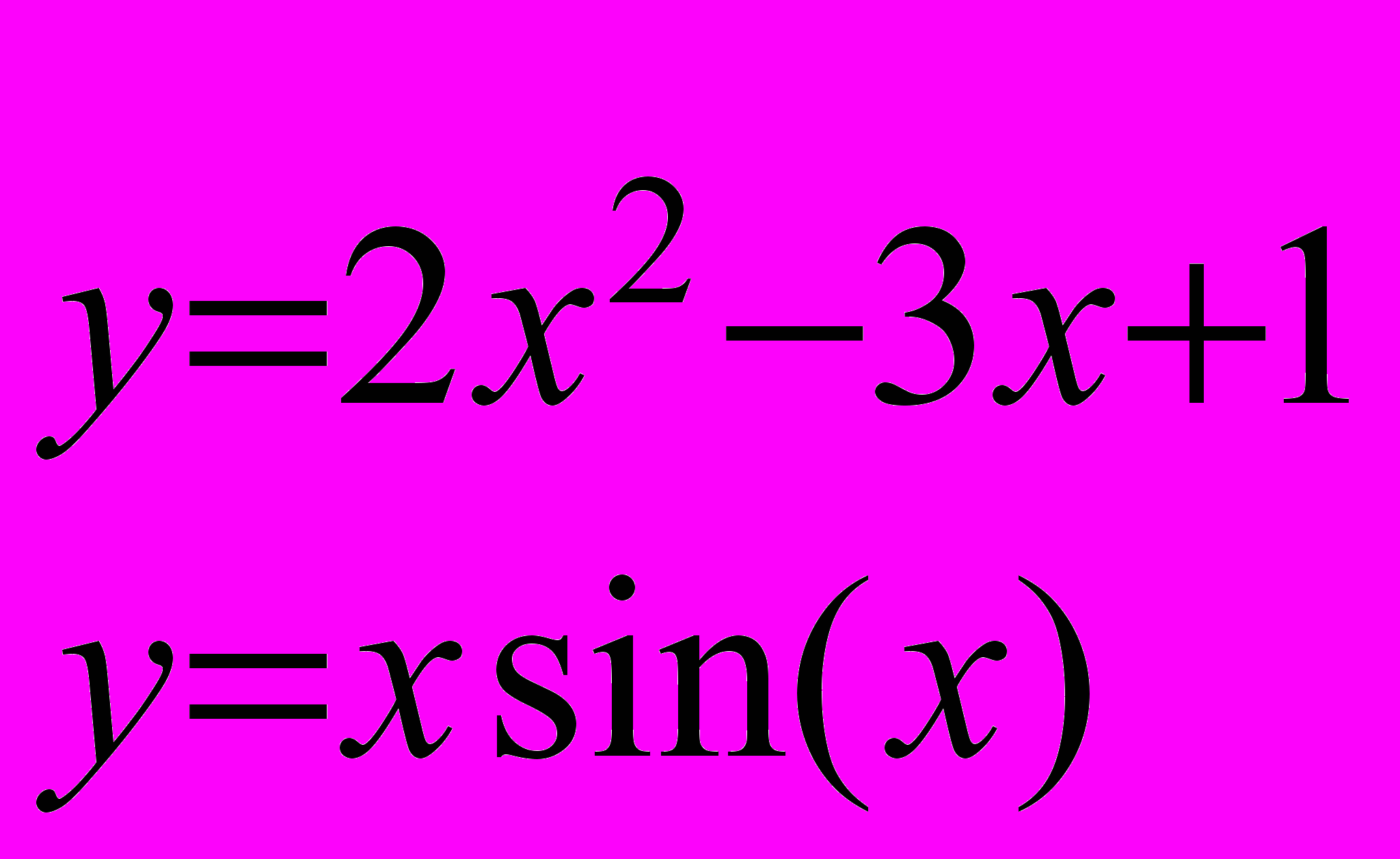
Варіант 3.

Завдання 1. Розв’язати рівняння f(x)=0 за допомогою функції root() із заданою точністю , де f(x) має вигляд:

e^x-1-x³-x, де х[0, 1]



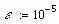
Завдання 2. Розв’язати рівняння g(x)=0: а) числово за допомогою функції polyroots(); б) символьно, де g(x) має вигляд:


x⁴ – 14x² – 40x – 75.


Завдання 3. Розв’язати систему рівнянь за допомогою функції find або minerr із заданою точністю 10^-8:


.


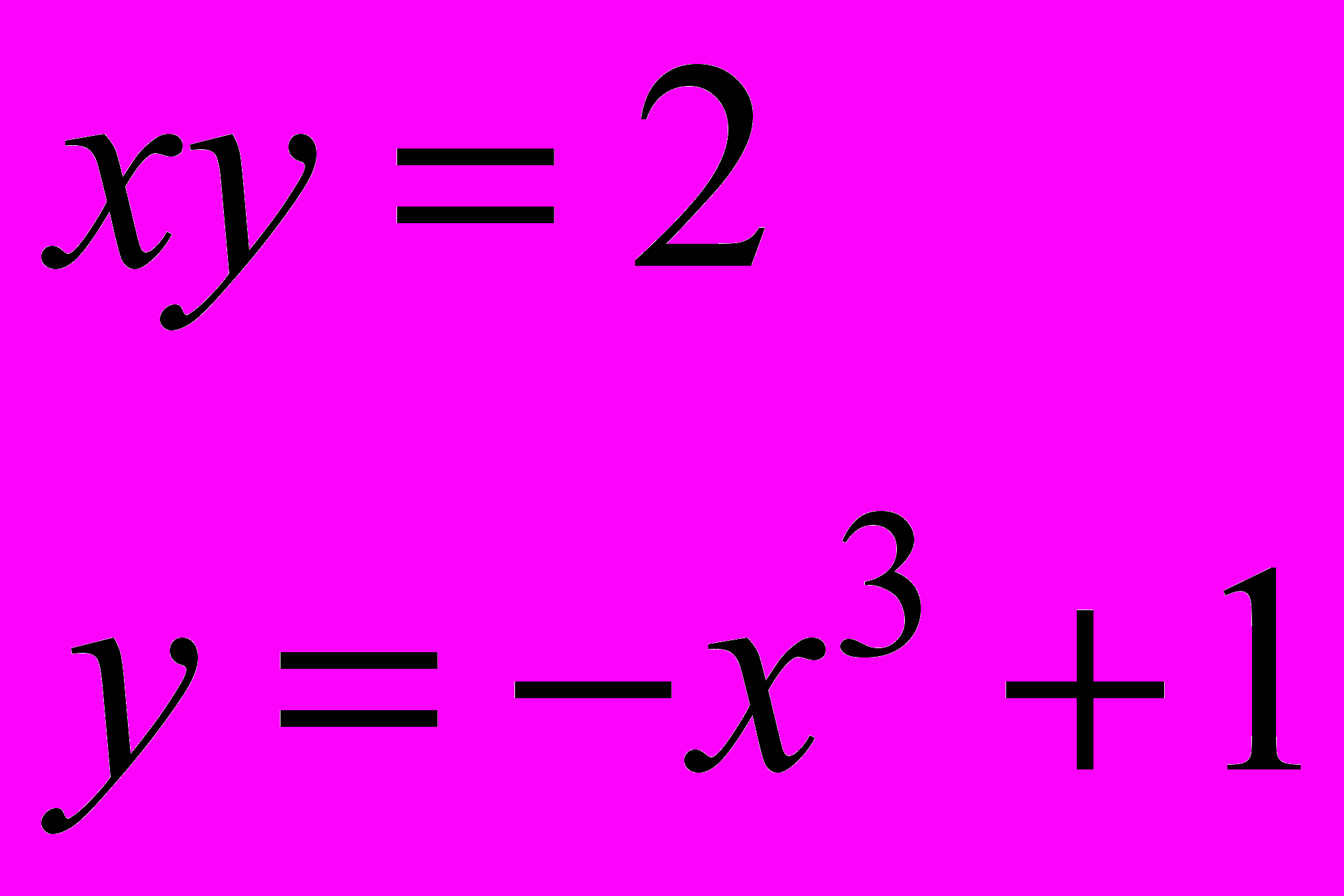
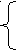Варіант 4

Завдання 1. Розв’язати рівняння f(x)=0 за допомогою функції root() із заданою точністю , де f(x) має вигляд:





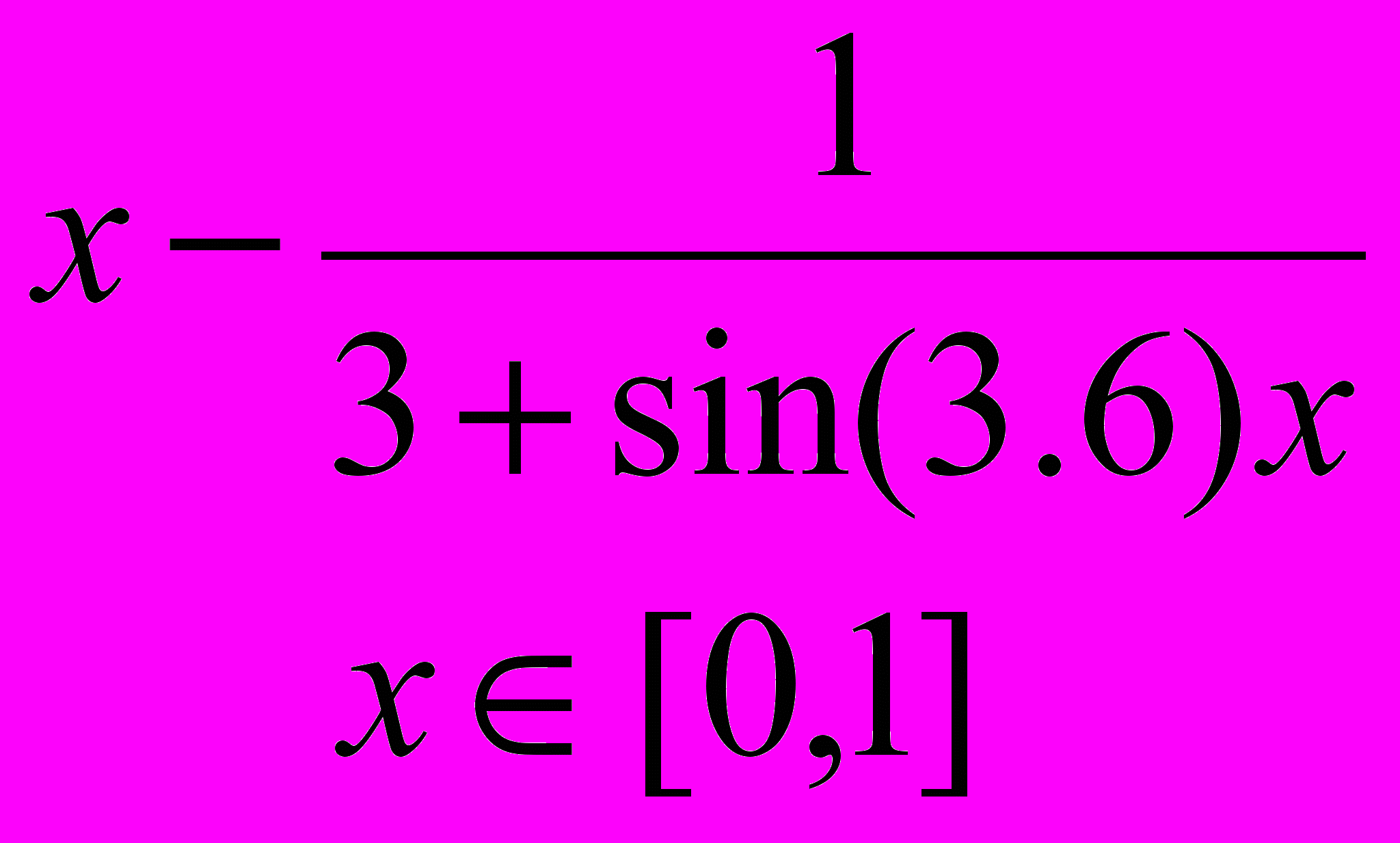
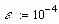
Завдання 2. Розв’язати рівняння g(x)=0: а) числово за допомогою функції polyroots(); б) символьно, де g(x) має вигляд:


x⁴ – x³ + x² – 11x + 10.


Завдання 3. Розв’язати систему рівнянь за допомогою функції find або minerr із заданою точністю 10^-8:

.


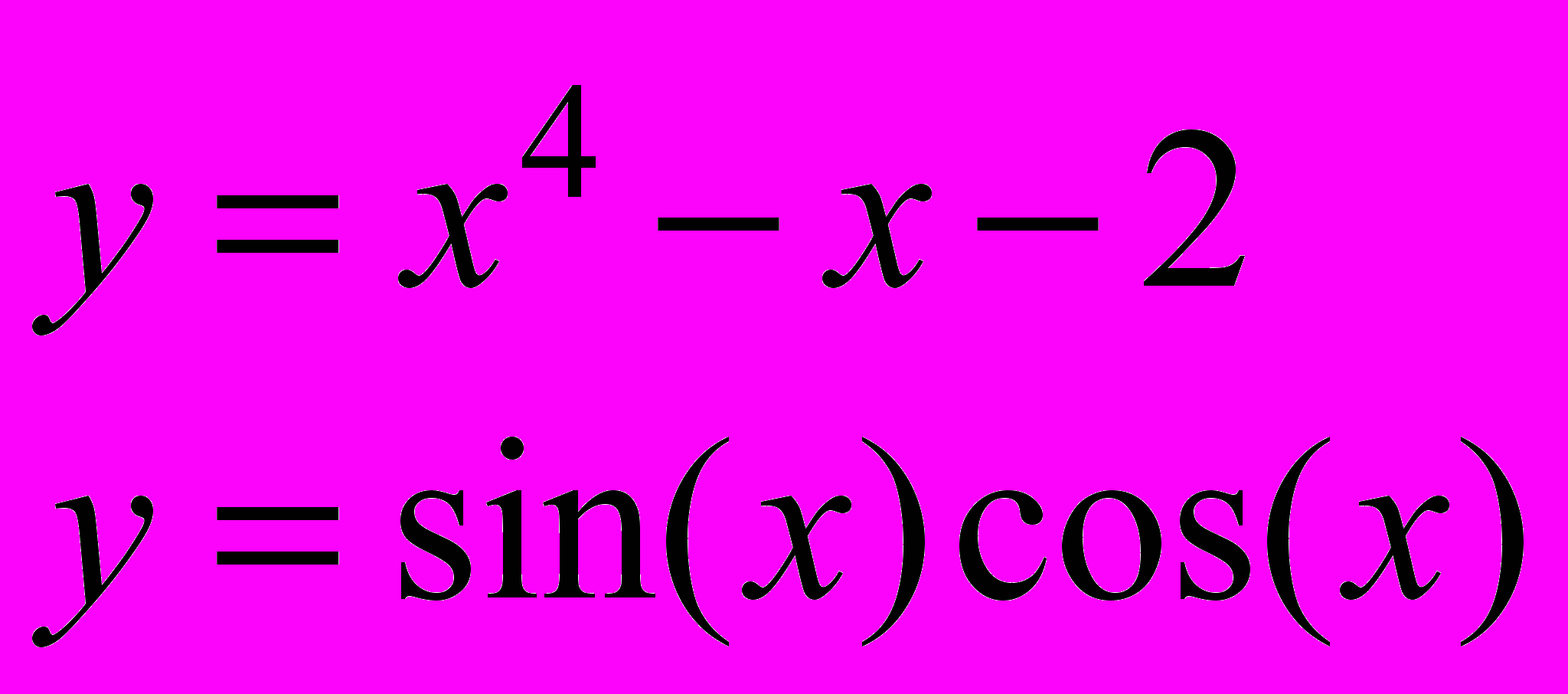
Варіант 5.

Завдання 1. Розв’язати рівняння f(x)=0 за допомогою функції root() із заданою точністю , де f(x) має вигляд:



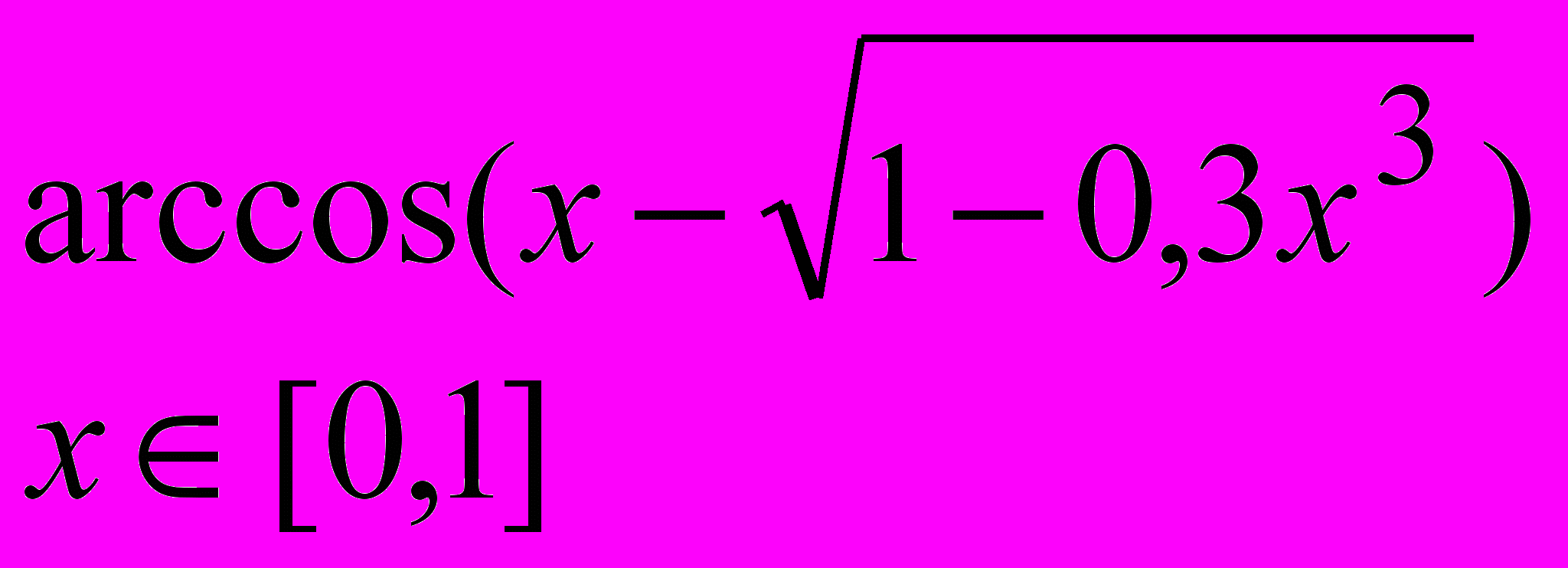
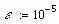
Завдання 2. Розв’язати рівняння g(x)=0: а) числово за допомогою функції polyroots(); б) символьно, де g(x) має вигляд:

x⁴ – x³ – 29x² – 71x – 140.

Завдання 3. Розв’язати систему рівнянь за допомогою функції find або minerr із заданою точністю 10^-8:

.


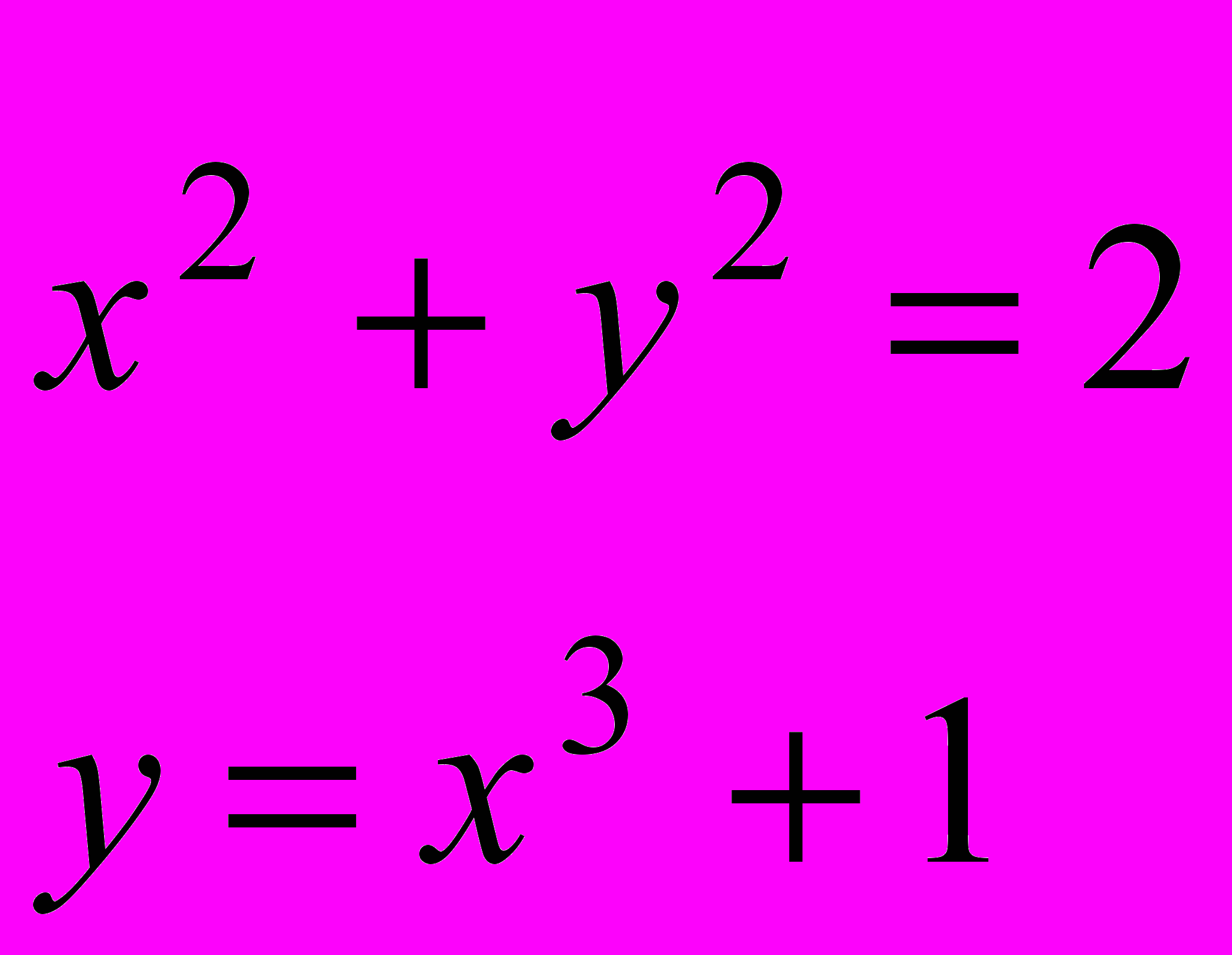
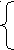Варіант 6.

Завдання 1. Розв’язати рівняння f(x)=0 за допомогою функції root() із заданою точністю , де f(x) має вигляд:



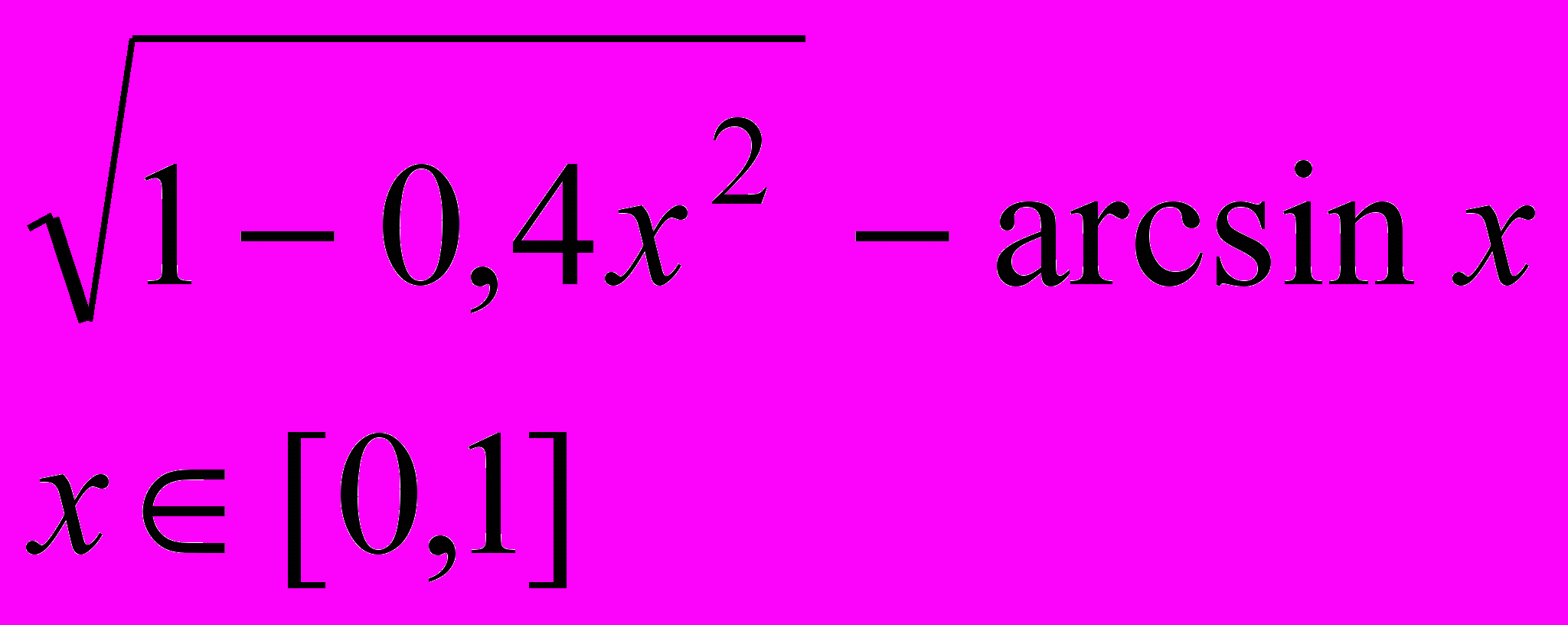
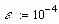
Завдання 2. Розв’язати рівняння g(x)=0: а) числово за допомогою функції polyroots(); б) символьно, де g(x) має вигляд:


x⁴ + 7x³ + 9x² + 13x – 30.


Завдання 3. Розв’язати систему рівнянь за допомогою функції find або minerr із заданою точністю 10^-8:

.


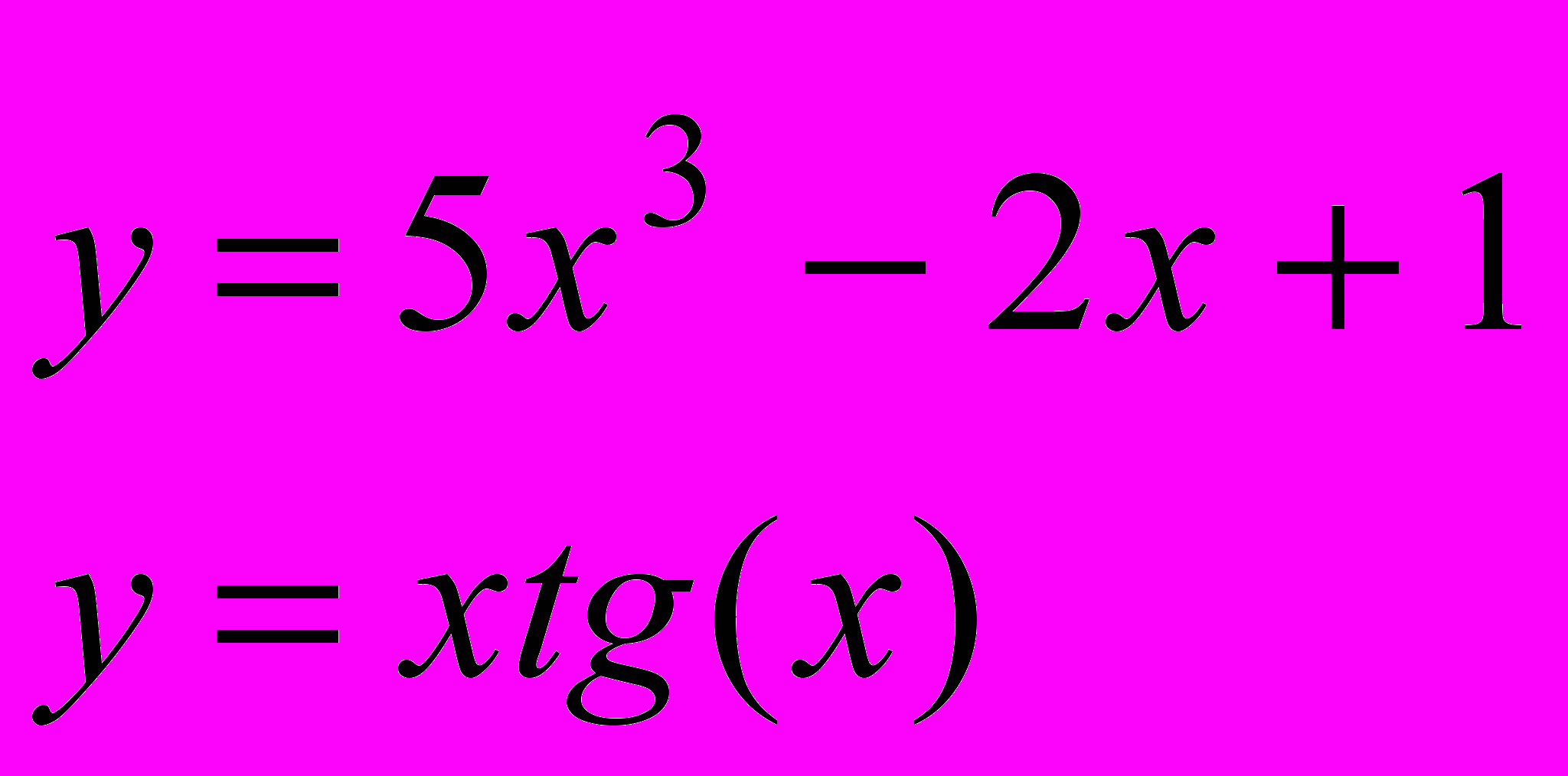
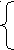Варіант 7.

Завдання 1. Розв’язати рівняння f(x)=0 за допомогою функції root() із заданою точністю , де f(x) має вигляд:



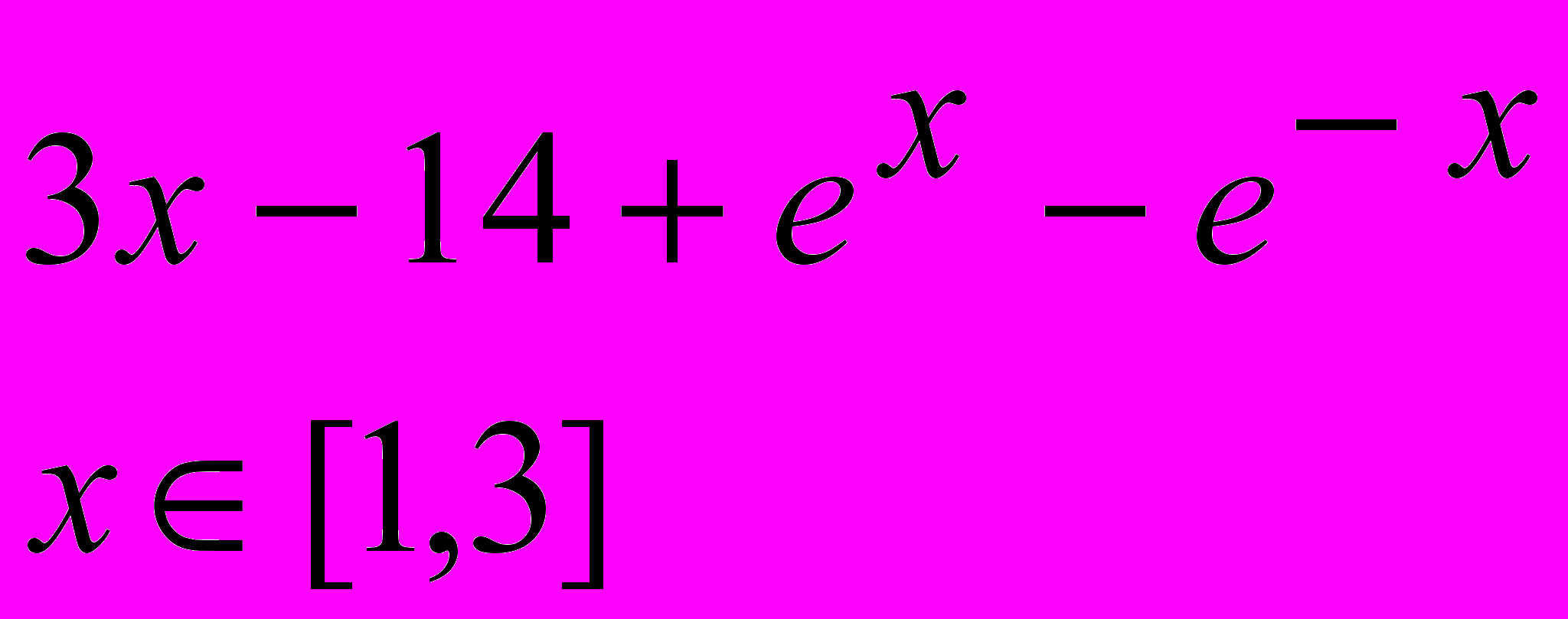
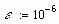
Завдання 2. Розв’язати рівняння g(x)=0: а) числово за допомогою функції polyroots(); б) символьно, де g(x) має вигляд:


x⁴ + 3x³ – 23x² – 55x – 150.

Завдання 3. Розв’язати систему рівнянь за допомогою функції find або minerr із заданою точністю 10^-8:

.


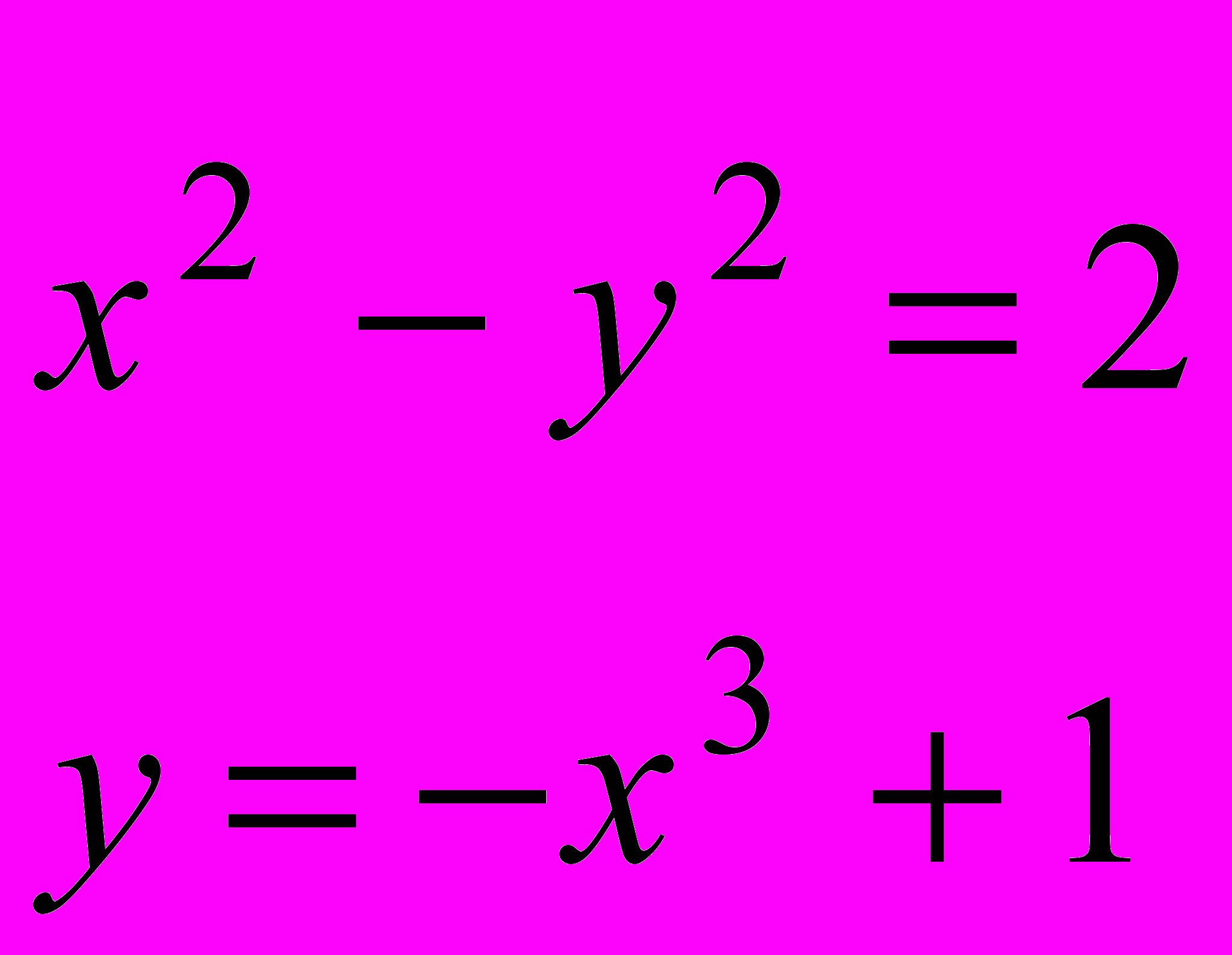
Варіант 8.

Завдання 1. Розв’язати рівняння f(x)=0 за допомогою функції root() із заданою точністю , де f(x) має вигляд:



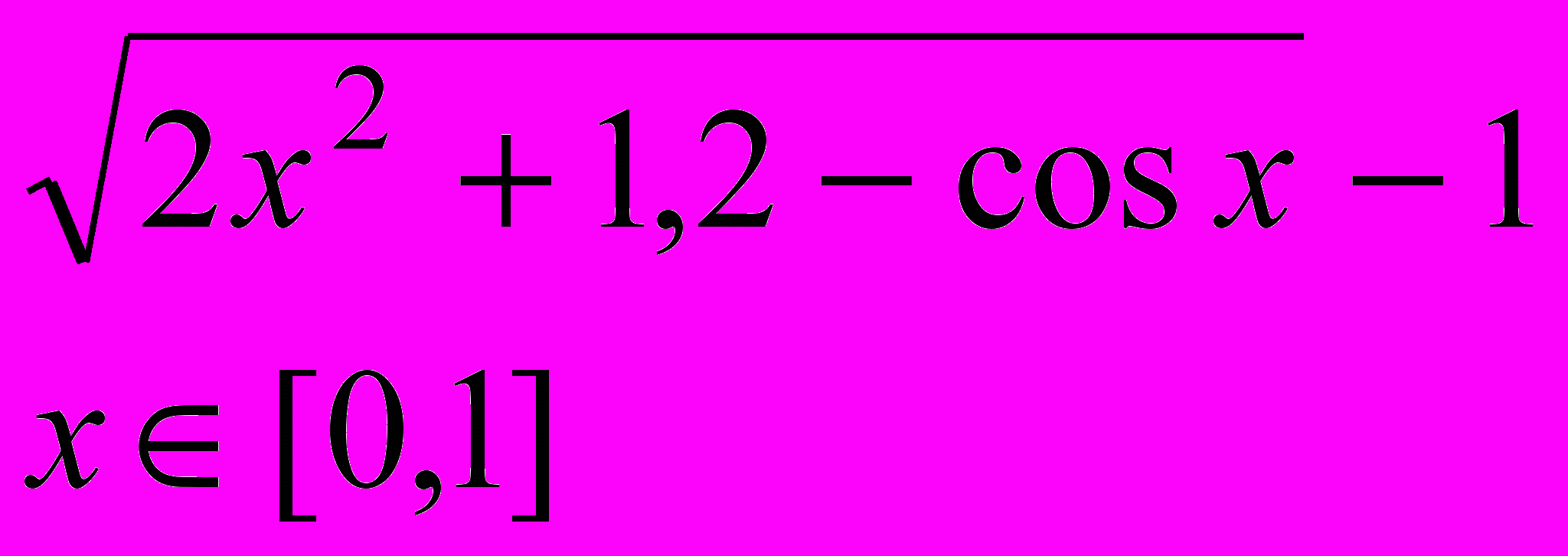
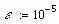
Завдання 2. Розв’язати рівняння g(x)=0: а) числово за допомогою функції polyroots(); б) символьно, де g(x) має вигляд:


x⁴ – 6x³ + 4x² + 10x + 75.


Завдання 3. Розв’язати систему рівнянь за допомогою функції find або minerr із заданою точністю 10^-8:

.


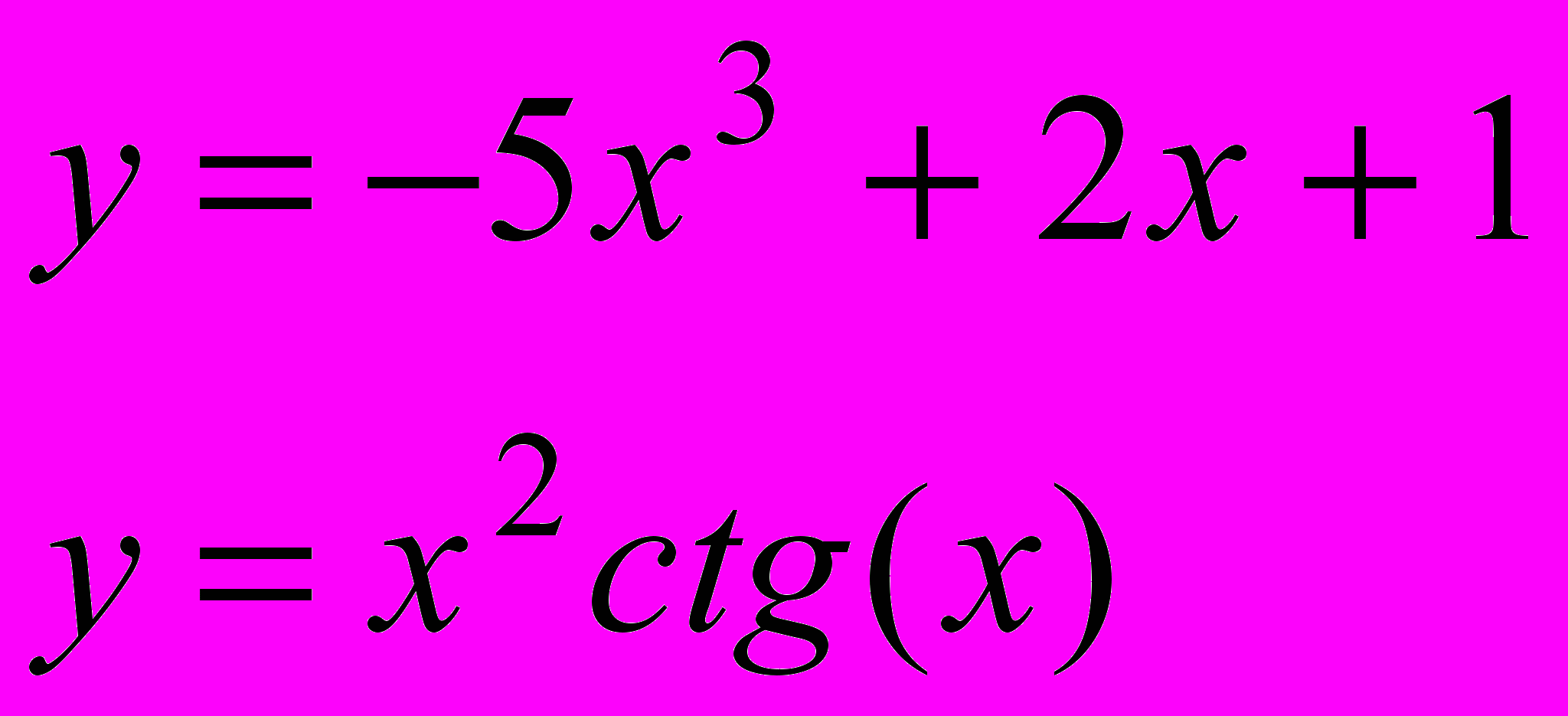
Варіант 9.

Завдання 1. Розв’язати рівняння f(x)=0 за допомогою функції root() із заданою точністю , де f(x) має вигляд:



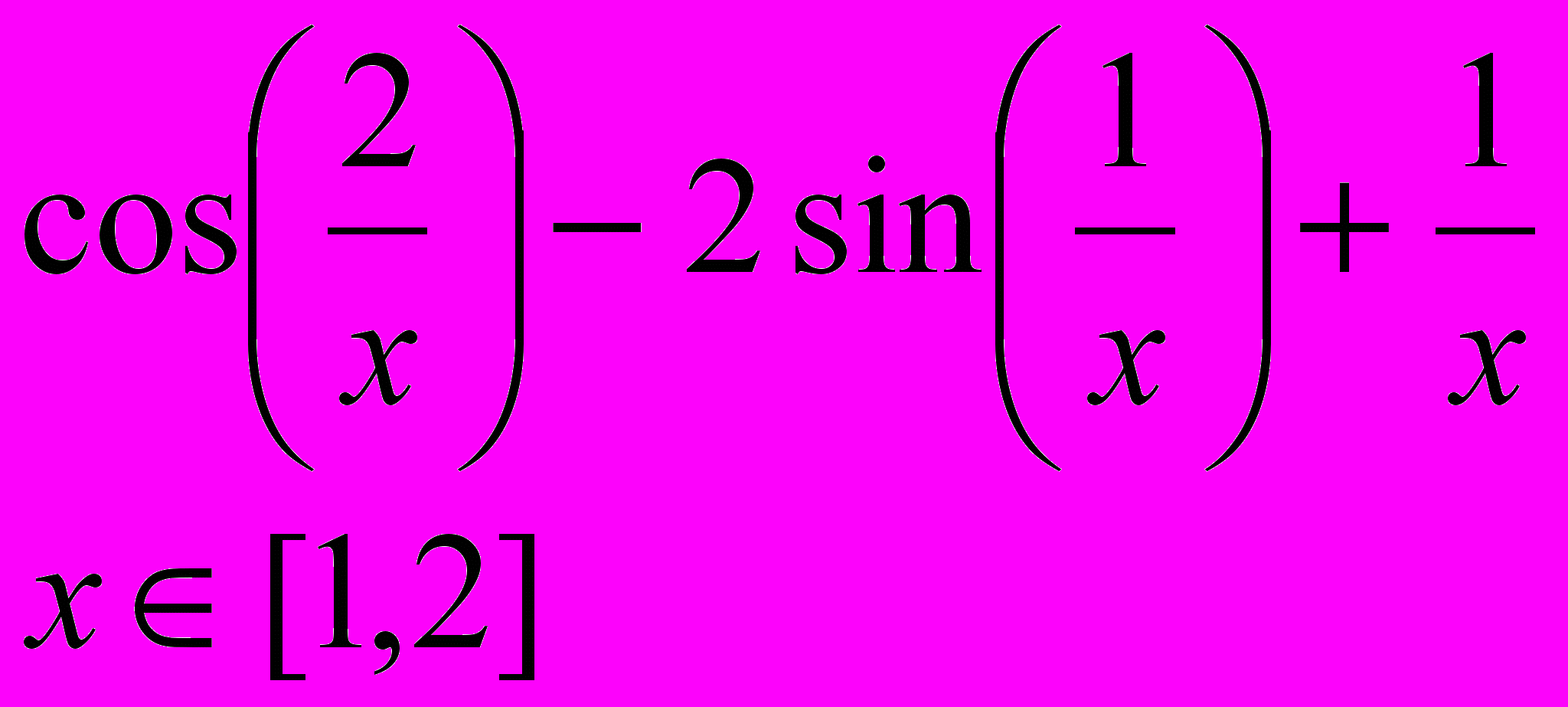
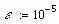
Завдання 2. Розв’язати рівняння g(x)=0: а) числово за допомогою функції polyroots(); б) символьно, де g(x) має вигляд:


x⁴ + x³ – 17x² – 45x – 100.


Завдання 3. Розв’язати систему рівнянь за допомогою функції find або minerr із заданою точністю 10^-8:

.


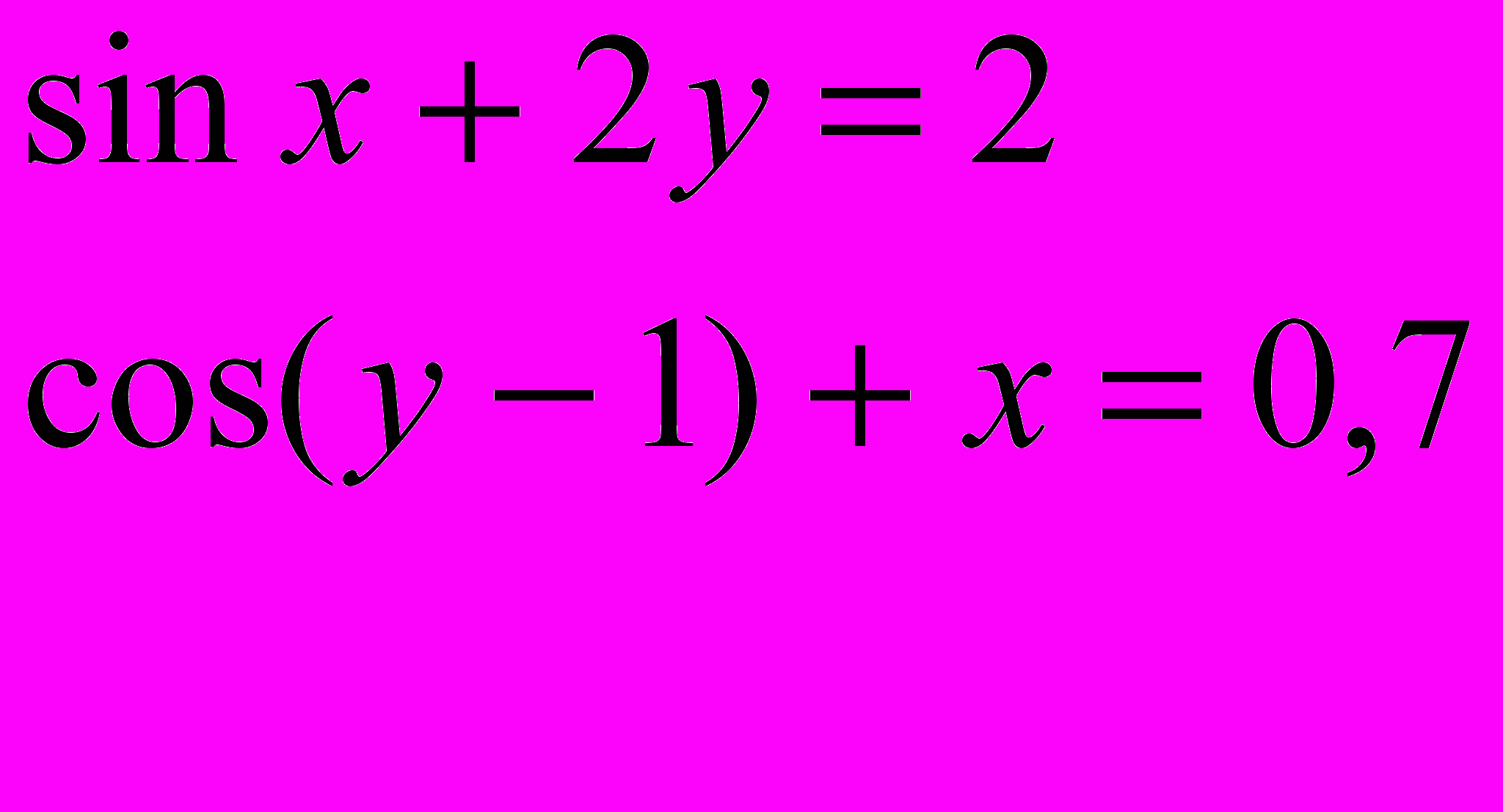
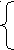Варіант 10

Завдання 1. Розв’язати рівняння f(x)=0 за допомогою функції root() із заданою точністю , де f(x) має вигляд:



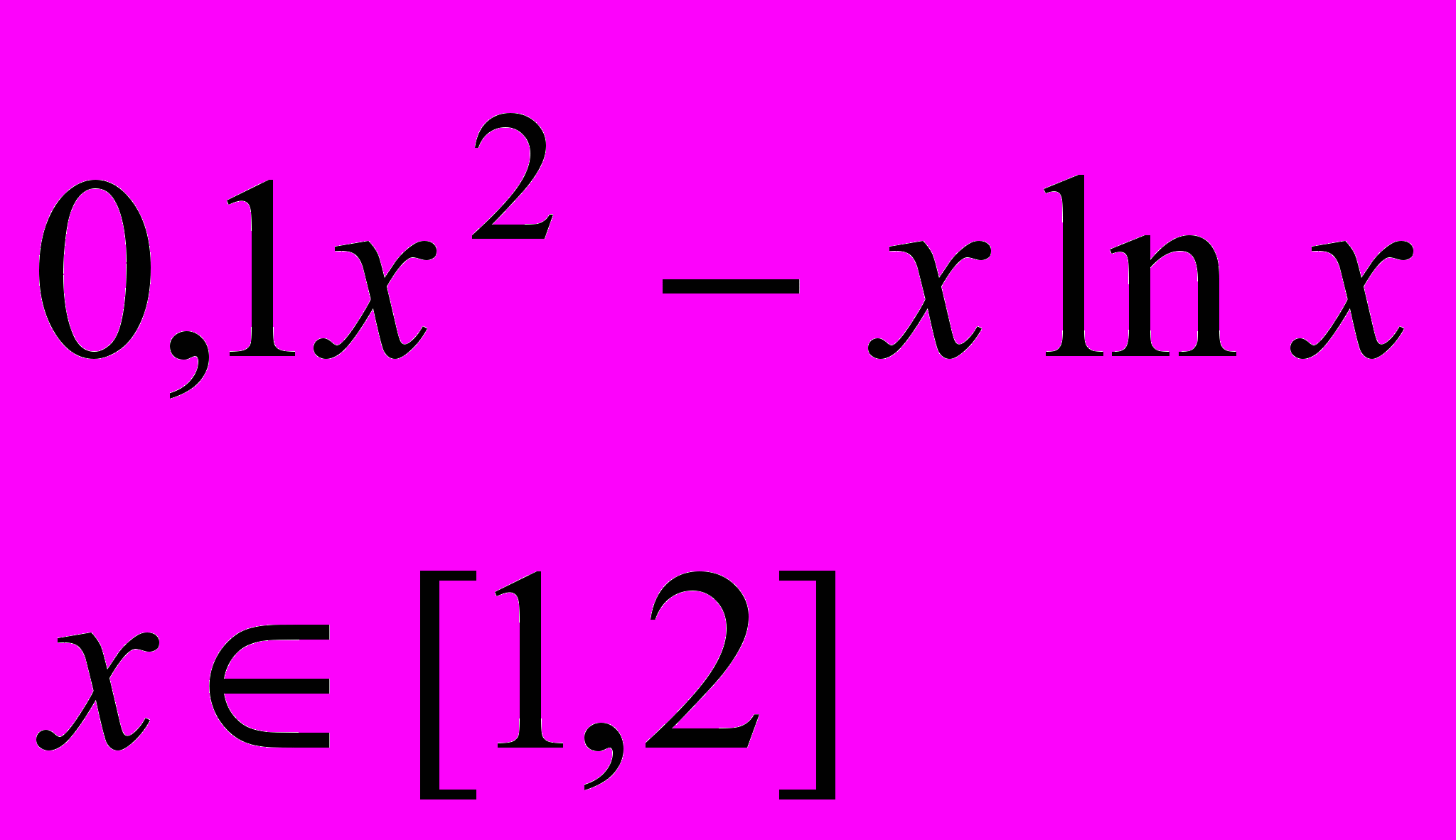
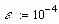
Завдання 2. Розв’язати рівняння g(x)=0: а) числово за допомогою функції polyroots(); б) символьно, де g(x) має вигляд:


x⁴ – 5x³ + x² – 15x + 5.


Завдання 3. Розв’язати систему рівнянь за допомогою функції find або minerr із заданою точністю 10^-8:

.


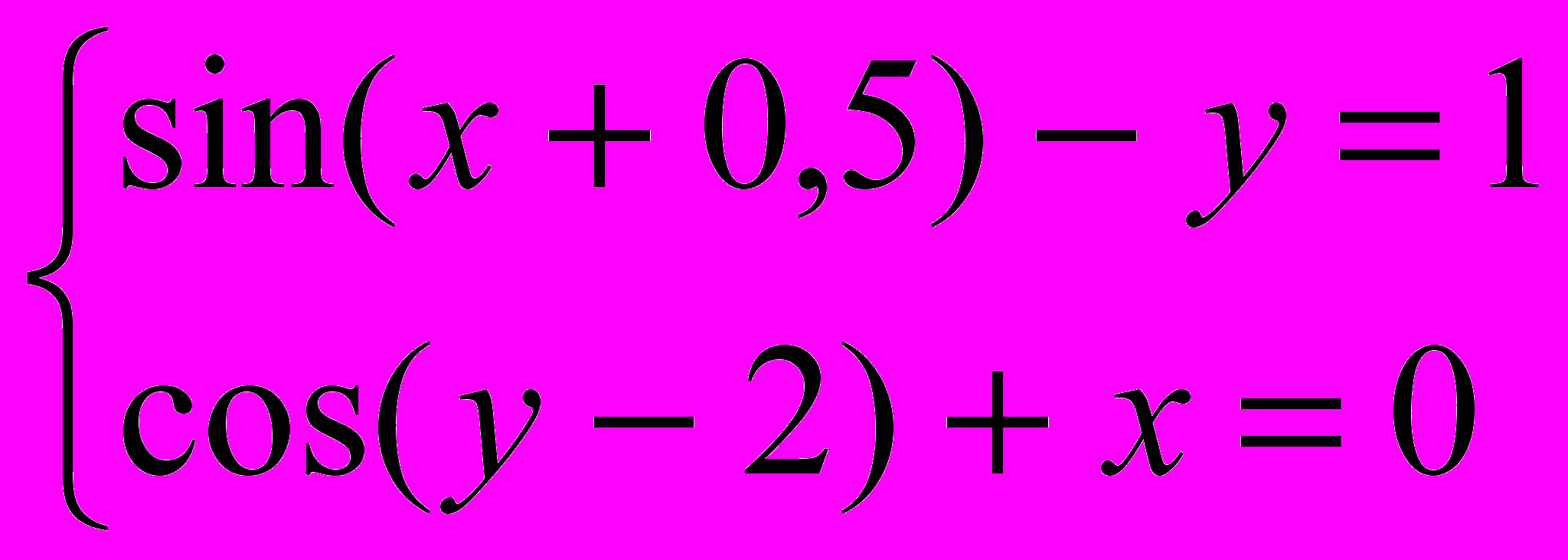Варіант 11.

Завдання 1. Розв’язати рівняння за допомогою функції root() на інтервалі [-10, -6] із заданою точністю :



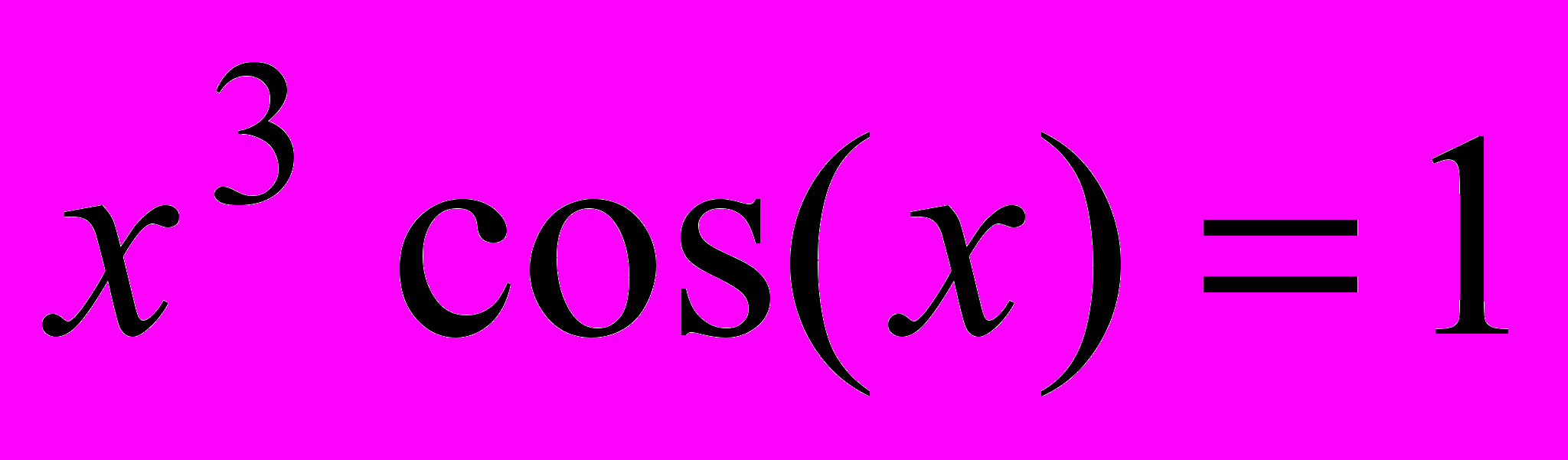
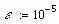
Завдання 2. Розв’язати рівняння g(x)=0: а) числово за допомогою функції polyroots(); б) символьно, де g(x) має вигляд:


x⁴ – 4x³ – 2x² – 20x + 25.


Завдання 3. Розв’язати систему рівнянь за допомогою функції find або minerr із заданою точністю 10^-8:

.


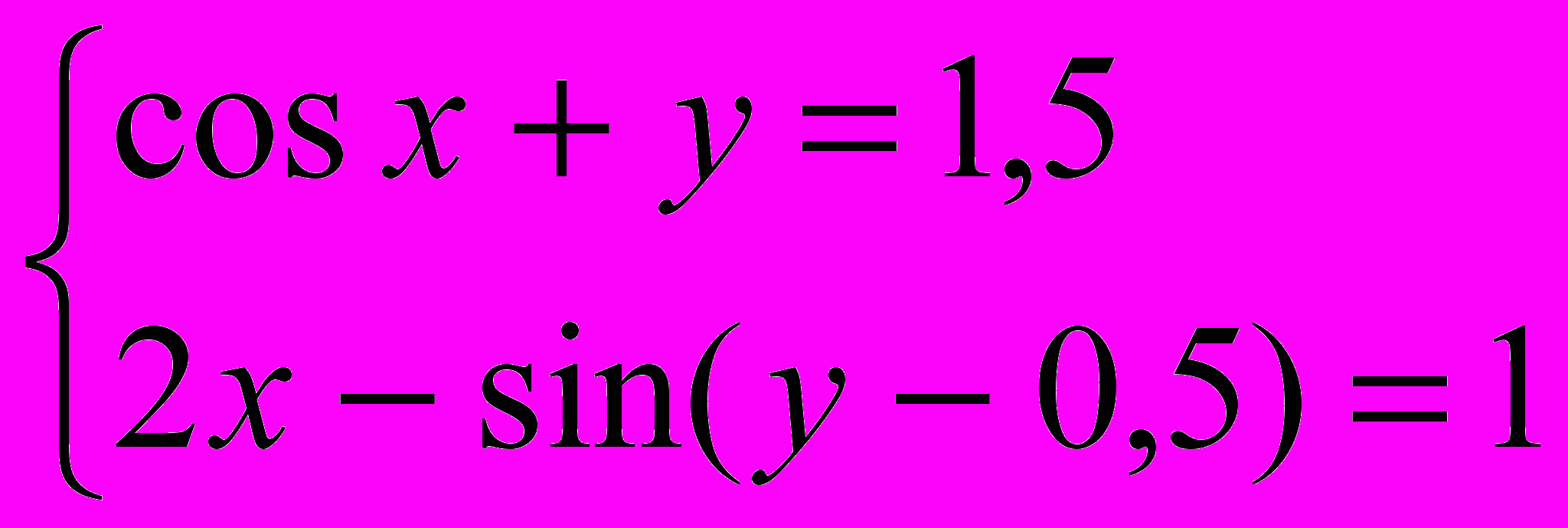Варіант 12.

Завдання 1. Розв’язати рівняння за допомогою функції root() на інтервалі [–8, –1] із заданою точністю :



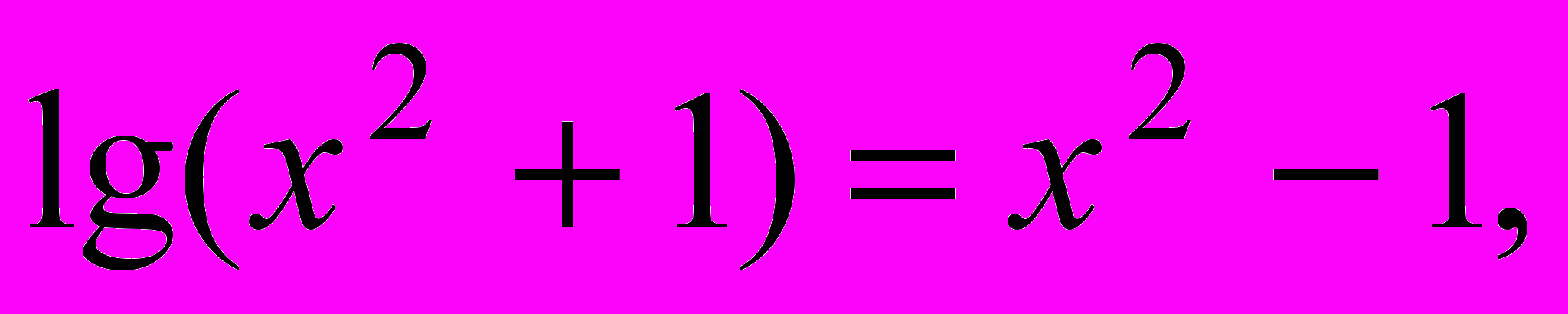
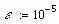
Завдання 2. Розв’язати рівняння g(x)=0: а) числово за допомогою функції polyroots(); б) символьно, де g(x) має вигляд:


x⁴ + 5x³ + 7x² + 7x – 20.


Завдання 3. Розв’язати систему рівнянь за допомогою функції find або minerr із заданою точністю 10^-8:

.

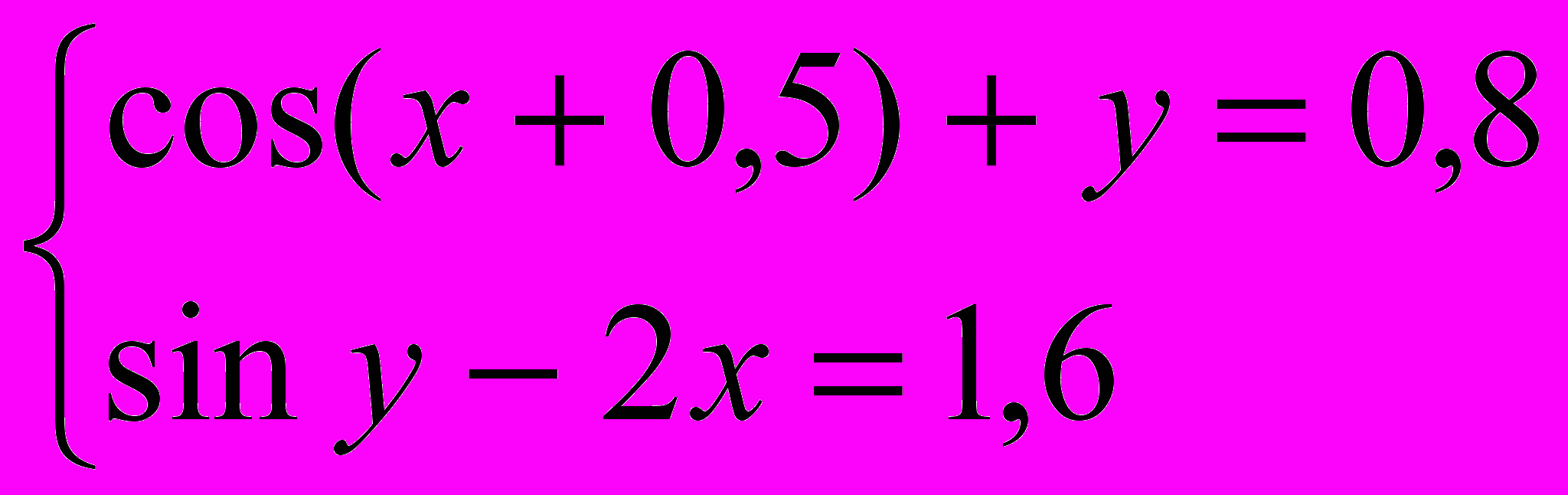Варіант 13.

Завдання 1. Розв’язати рівняння f(x)=0 за допомогою функції root() із заданою точністю , де f(x) має вигляд:

.

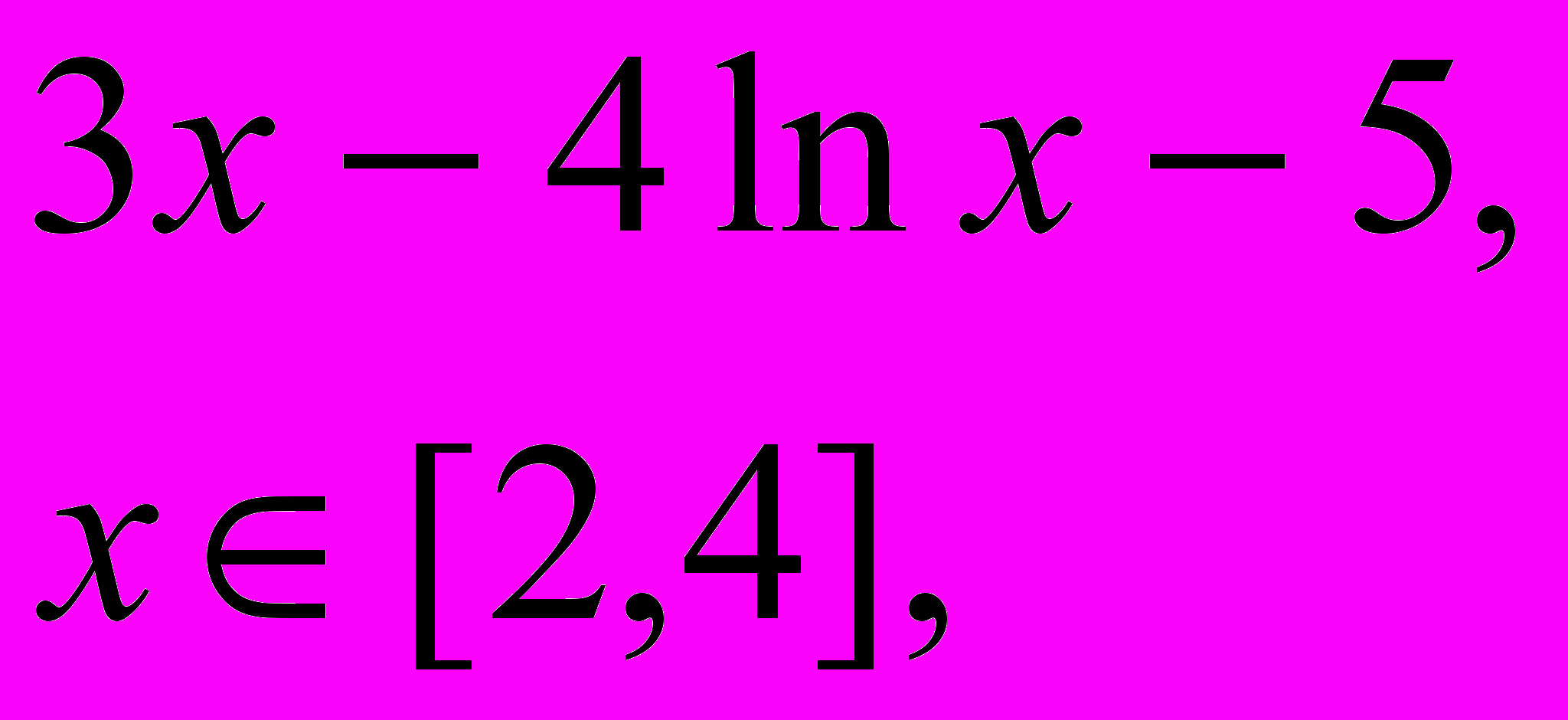
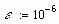Завдання 2. Розв’язати рівняння g(x)=0: а) числово за допомогою функції polyroots(); б) символьно, де g(x) має вигляд:

x⁴ – 7x³ + 7x² – 5x + 100.

Завдання 3. Розв’язати систему рівнянь за допомогою функції find або minerr із заданою точністю 10^-8:

.


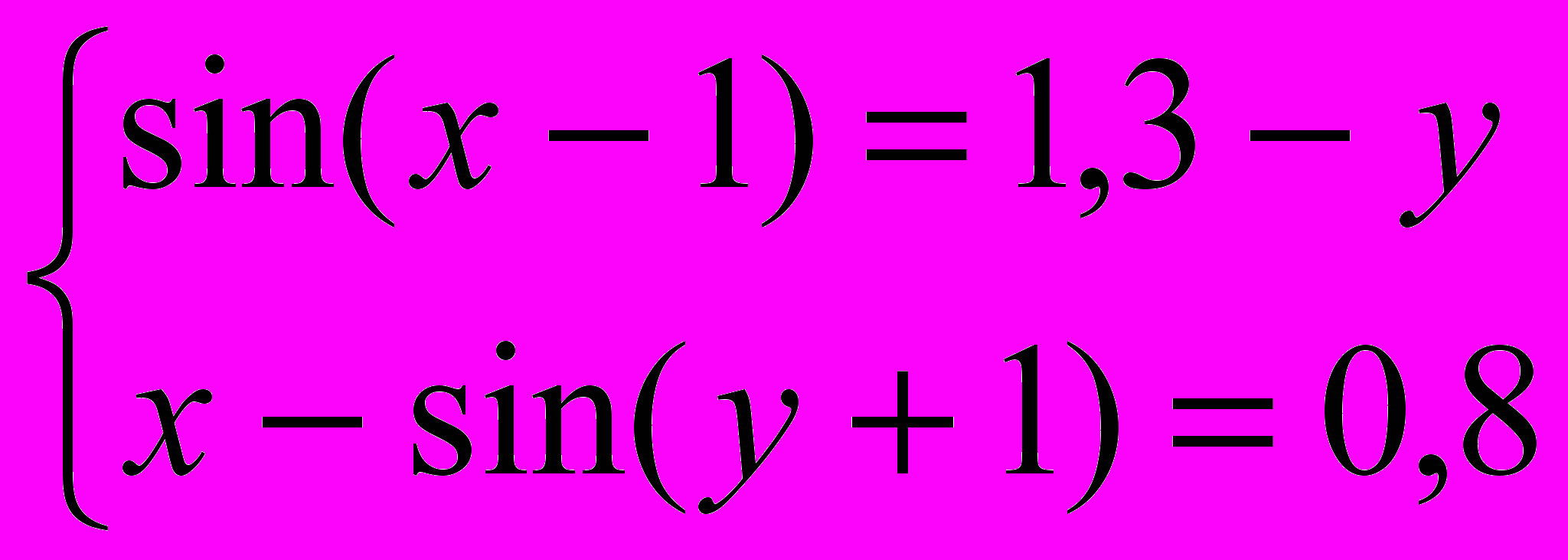Варіант 14.

Завдання 1. Розв’язати рівняння f(x)=0 за допомогою функції root() із заданою точністю , де f(x) має вигляд:



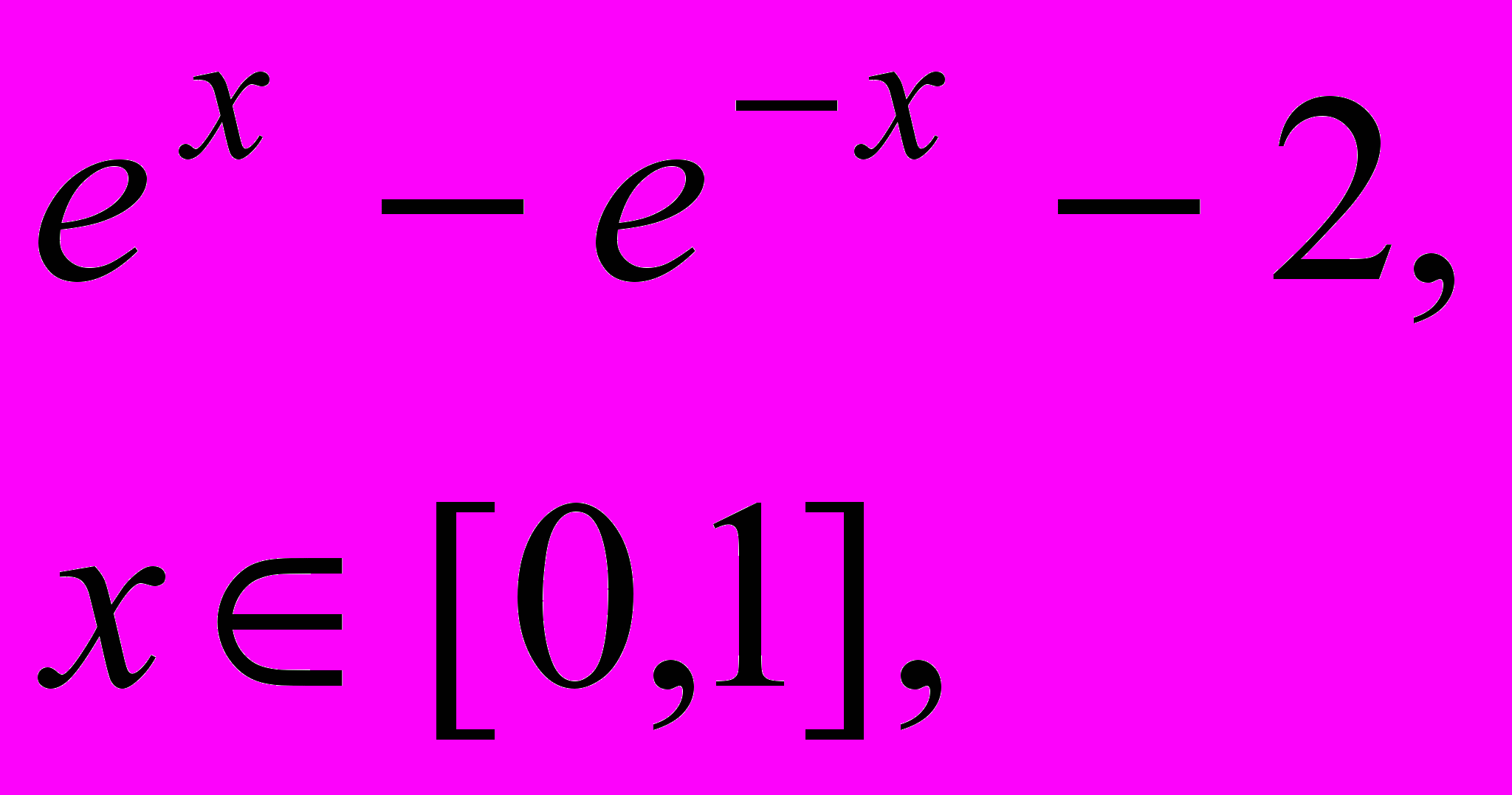
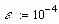
Завдання 2. Розв’язати рівняння g(x)=0: а) числово за допомогою функції polyroots(); б) символьно, де g(x) має вигляд:


x⁴ + 10x³ +36x² +70x+ 75.


Завдання 3. Розв’язати систему рівнянь за допомогою функції find або minerr із заданою точністю 10^-8:

.


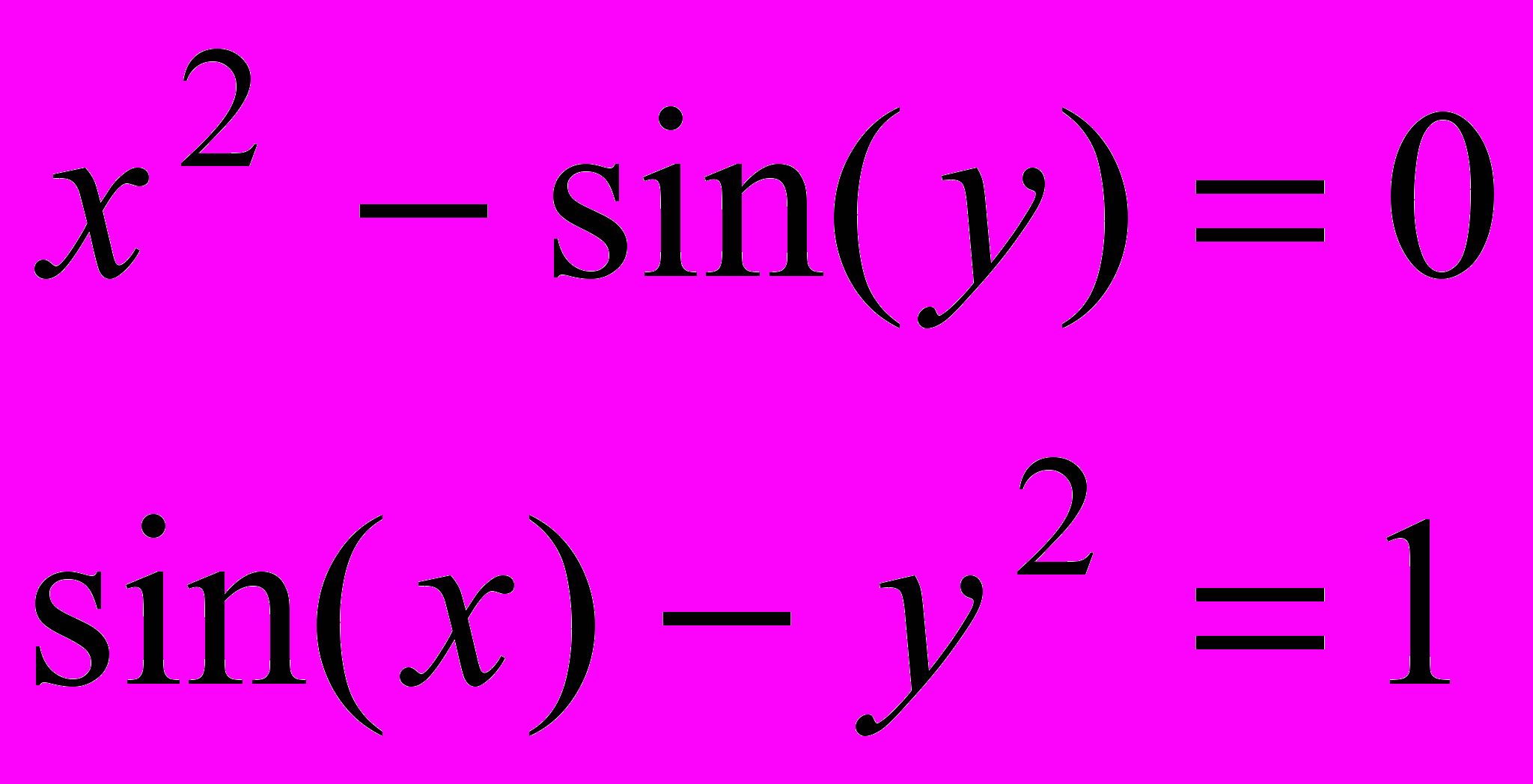
Варіант 15.

Завдання 1. Розв’язати рівняння f(x)=0 за допомогою функції root() із заданою точністю , де f(x) має вигляд:



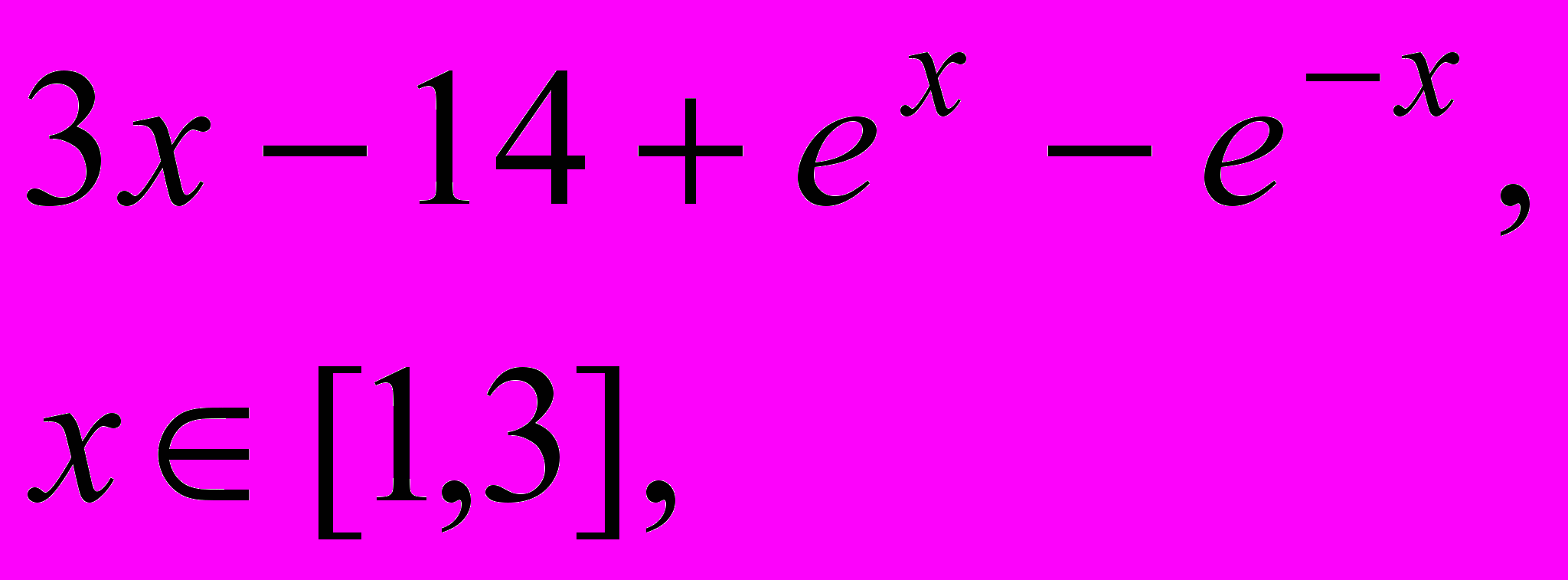
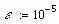
Завдання 2. Розв’язати рівняння g(x)=0: а) числово за допомогою функції polyroots(); б) символьно, де g(x) має вигляд:


x⁴ + 9x³ + 31x² + 59x+ 60.


Завдання 3. Розв’язати систему рівнянь за допомогою функції find або minerr із заданою точністю 10^-8:

.


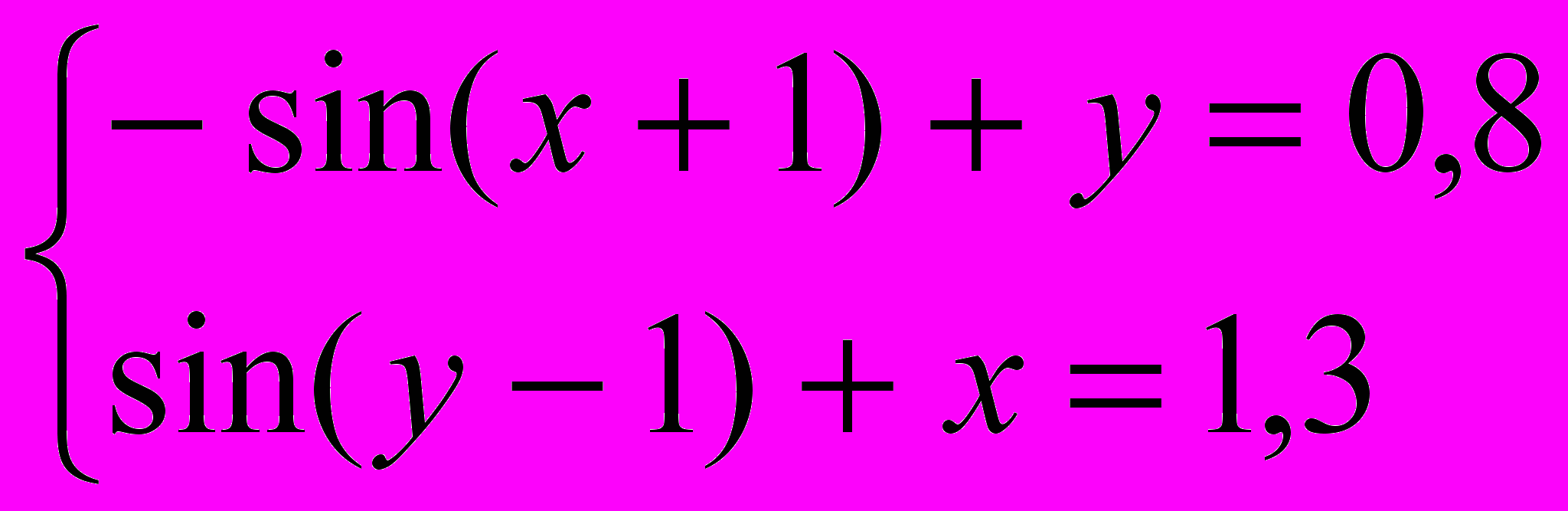Варіант 16.

Завдання 1. Розв’язати рівняння f(x)=0 за допомогою функції root() із заданою точністю , де f(x) має вигляд:



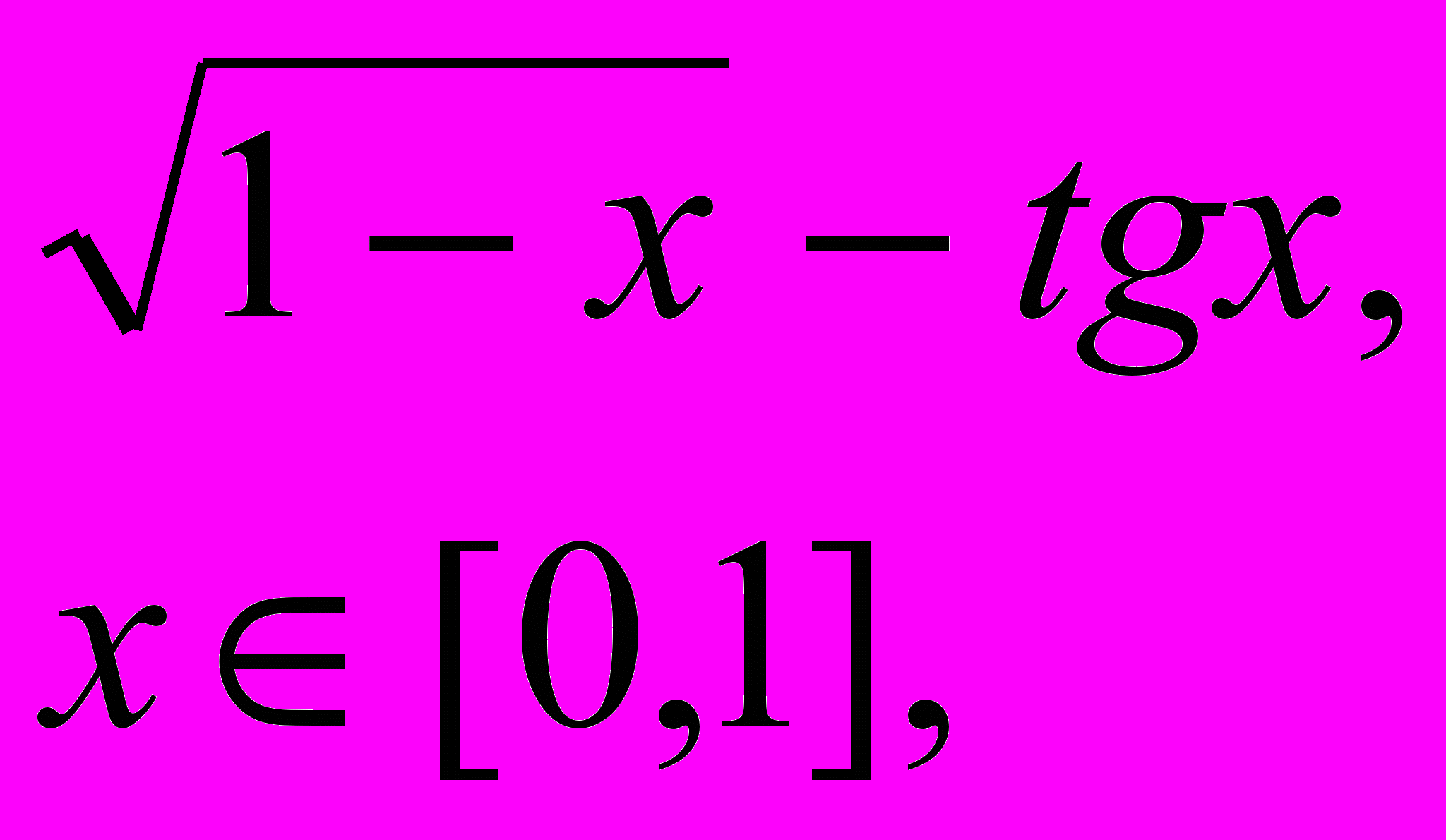
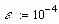
Завдання 2. Розв’язати рівняння g(x)=0: а) числово за допомогою функції polyroots(); б) символьно, де g(x) має вигляд:


x⁴ + 7x³ + 9x² + 13x – 30.


Завдання 3. Розв’язати систему рівнянь за допомогою функції find або minerr із заданою точністю 10^-8:

.


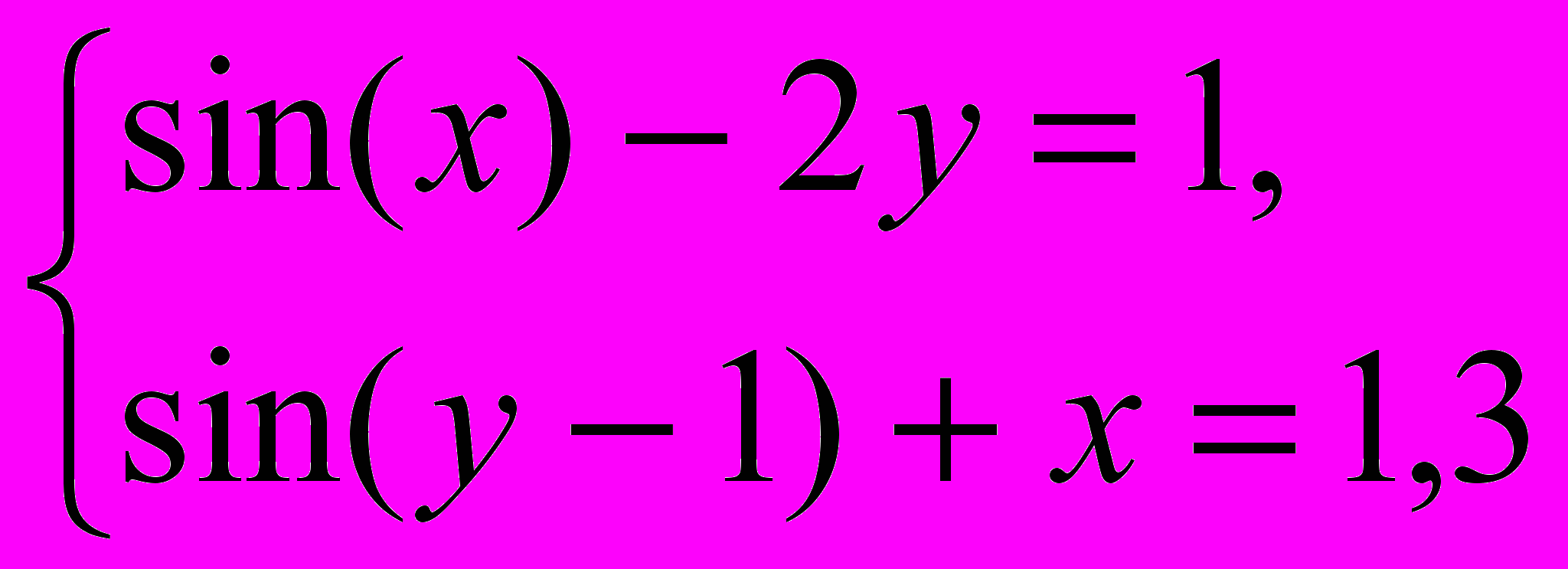Варіант 17.

Завдання 1. Розв’язати рівняння f(x)=0 за допомогою функції root() із заданою точністю , де f(x) має вигляд:

.

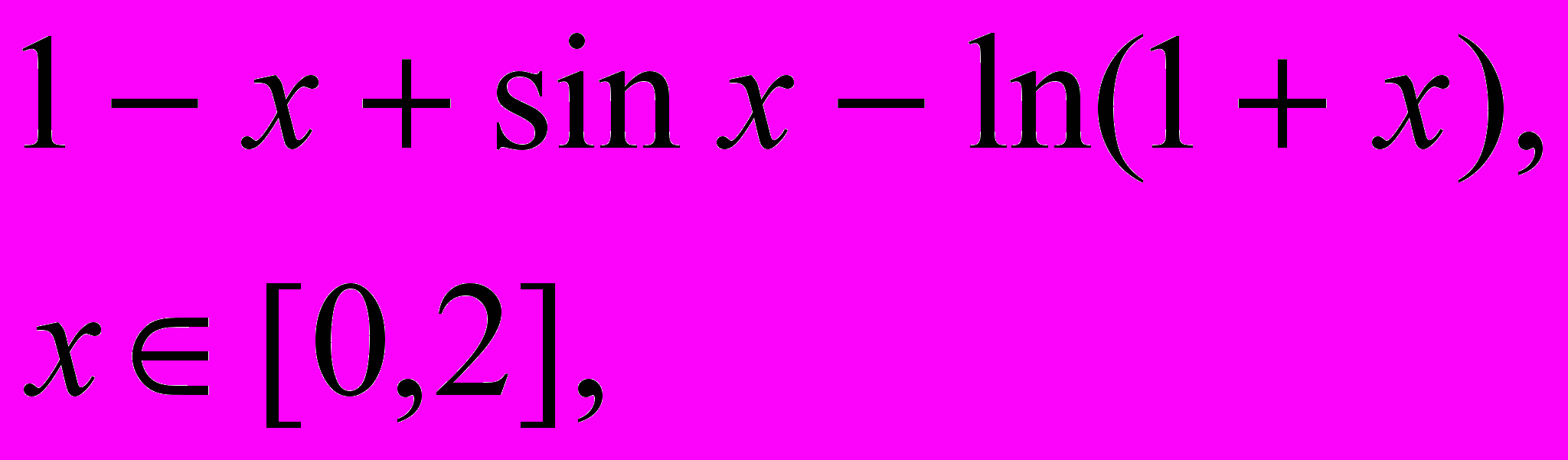
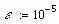Завдання 2. Розв’язати рівняння g(x)=0: а) числово за допомогою функції polyroots(); б) символьно, де g(x) має вигляд:


x⁴ – 4x³ – 2x² – 20x + 25.


Завдання 3. Розв’язати систему рівнянь за допомогою функції find або minerr із заданою точністю 10^-8:

.
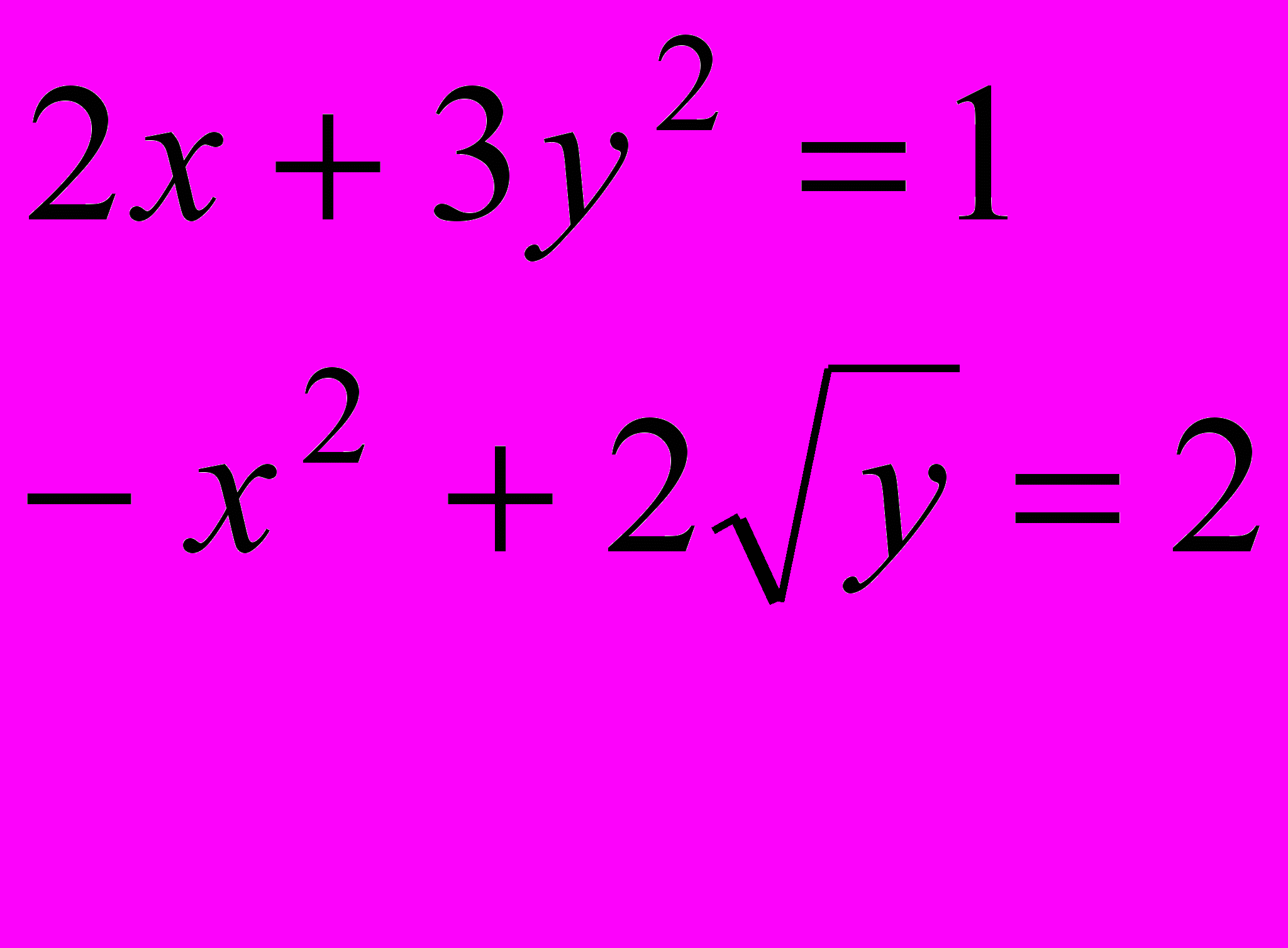