Geum.ru

Посвящен 75-летию развития системы образования Ленинградской области

Вид материалаДокументы
Реализация идей проблемного обучения на уроках математики
Первое задание
Подобный материал:
1   ...   9   10   11   12   13   14   15   16   ...   31

Реализация идей проблемного обучения
на уроках математики


Идеи развивающего обучения все чаще привлекают внимание тех, кто ищет пути кардинальной перестройки школы, возможности принципиальных изменений в ней.

Новая стратегия модернизации содержания общего образования вызвала необходимость пересмотра не только целей и задач современной школы, но и самого содержания обучения, методов, форм организации деятельности и общения детей, т.е. поиск эффективных способов достижения нового качества образования.

Как известно, учебная деятельность – это деятельность, имеющая своим содержанием овладение учащимися обобщенными способами действий в сфере научных понятий. Поэтому такая деятельность должна побуждаться адекватными мотивами. Ими являются только те мотивы, которые непосредственно связаны с ее содержанием, то есть мотивы приобретения обобщенных способов действий, или, проще говоря, мотивы собственного роста, собственного совершенствования. Такие мотивы деятельности психологи называют учебно-познавательными. Они направлены на усвоение обобщенных способов действий в конкретной области изучаемого учебного предмета.

Психологические исследования учебной деятельности показали: для того, чтобы у учащихся выработалось правильное отношение к ней, содержательная ее мотивация, нужно учебную деятельность строить особым образом. Одним из распространенных методов активизации деятельности учащихся является постановка проблем во время урока.

Так, например, перед изучением темы «Квадратные уравнения» (8 кл., алгебра) учащимся предлагается решить текстовую задачу, которая сводится к квадратному уравнению, тем самым демонстрируя необходимость изучить метод решения квадратных уравнений и научиться им пользоваться.

Работа над проблемой проходит успешно тогда, когда возникает проблемная ситуация, то есть такое психическое состояние учащегося, испытывающего интеллектуальное затруднение, которое направляет его мысленную деятельность на решение проблемы. Так, при изучении теоремы Виета (8 кл., алгебра) предлагается двум учащимся на доске решить несколько квадратных уравнений, представленных на карточках.

1 учащемуся
2 учащемуся

1)х2–5х+6=0
1)х2–20х+100=0

2)х2+х–30=0
2)2х2+9х–5=0

Задача учащихся состоит в том, чтобы для каждого из уравнений вычислить суммы и произведения найденных корней, сравнить полученные числа с коэффициентами уравнений, подметить закономерности.

На основе выполнения этого задания силами учащихся класса сформулировать свойство корней квадратного уравнения, которое составляет теорему Виета.

Средняя общеобразовательная школа не может дать человеку знания на всю жизнь. Ее основная задача – дать опорные знания и умения, развить познавательные интересы и способности учащихся, научить применять знания в нестандартных условиях. Именно на умение находить решения в нестандартных ситуациях обращается внимание при составлении заданий. Например, в 6 классе задание «Вычисли произведение…» может быть выполнено чисто расчетным путем. С другой стороны, если заметить, что сомножители можно сгруппировать в пары взаимно обратных чисел, ответ можно получить и без всяких вычислений. С учетом «нестандартного» построения работы детям предлагается на свое усмотрение выбрать задания для решения.

«Выбери те задания, которые можешь решить. Реши их».

Задание 1. Вычисли выражение: –5,4·(4,2–6)-2·(–3,9+9,3).

Задание рассчитано на выявление навыков действий с рациональными числами. Наиболее удачное решение состоит в том, чтобы после выполнения действий в скобках заметить, что выражение превращается в разность одинаковых чисел и, следовательно, равно нулю. При таком ходе решения вычислять значение произведений не требуется.

Задание 2. Реши уравнение:

1,5х=(2–1):0,5х(2,3–3,05).

Для выполнения задания требуется владеть навыками действий с рациональными числами и решения уравнений.

Задание 3. В треугольнике две стороны одинаковые, а третья отличается от них на 9 см. Найди стороны треугольника, если известно, что его периметр равен 60 см.

Задача интересна тем, что имеет два решения. Первому из них отвечает уравнение: 2х+(х+9) = 60, второму 2х+(х–9) = 60.

Дети должны владеть понятием периметра, уметь составлять и решать уравнения.

Задание 4. Реши уравнение. Если не можешь решить некоторые из них, объясни, чем это вызвано:

а) 5х–16–2х=4+2х; в) 5х–16=2х+4–2х;

б) 5х–16–2х =4–2х; г) 5х–16=2х+4+2х.

Задание рассчитано на обоснованный отказ от решения уравнения г), поскольку решать кубические уравнения учащиеся не умеют. В то же время уравнение б) вполне доступно учащимся, так как члены, содержащие х, взаимно уничтожаются.

Одним из главных направлений в процессе изучения математики является развитие у детей подвижности и гибкости мышления при помощи, дидактических игр.

Например, при изучении темы «Произведение суммы и разности двух одночленов» (алгебра, 7 кл.) проводится дидактическая игра «Математический «поединок». Игровой замысел состоит в том, чтобы на основе созданной проблемной ситуации и соревнования команд активизировать мышление учащихся, превратить обучение в процесс активной поисковой деятельности и самостоятельных открытий. Этапы игры совпадают с этапами урока.

В 5 классе игра «Волшебное число» проводится после изучения арифметических действий с натуральными числами для отработки навыков решения линейных уравнений. Сценарий игры основан на сказке об Иване-царевиче и Кащее Бессмертном и вызывает большой интерес у учащихся.

После изучения раздела «Основные свойства простейших фигур» (7 кл„ геометрия) возникает необходимость повторить все аксиомы, проверить, как их усвоили учащиеся. Обыкновенный опрос не вызывает должного интереса. Поэтому, целесообразно использовать игровую форму занятий «Конкурс геометров».

Первое задание:

Для 1 команды
Для 2 команды
Для 3 команды




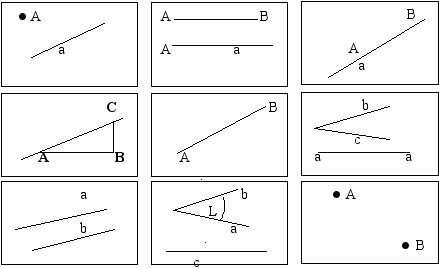
Из числа учащихся класса создаются три команды. Целевая установка учащимся: необходимо следить за изображениями на доске. Будут предлагаться рисунки к аксиомам одновременно для трех команд (рядов) учащихся класса.

Задание состоит в том, чтобы установить, к какой аксиоме является иллюстрацией каждый рисунок, а также заметить, каких элементов (фигур) на каждом из них недостает (например, точки, отрезка и т.д.)

Такая разнообразная работа позволяет поддерживать интерес к предмету, развивать умения учебной деятельности и логическое и аналитическое мышление.


Е.Н. Епишина, М.Ю. Ершова