Утверждено Советом Факультета Председатель 20 г. Санкт-Петербург 2010 пояснительная записка

Вид материала

Пояснительная записка

Содержание 1. Пояснительная записка Цели и задачи освоения дисциплины 2. Содержание дисциплины Теорема Фишера Основы принятия решений в условиях неопределенности Оптимизация портфеля Теория арбитража Временная структура процентных ставок Модели оценки финансовых активов Теория структуры капитала Теория ценообразования опционов Измерение риска: Value at Risk 3. Тематика заданий текущего контроля Финансовый актив 3.2 Примеры письменного домашнего задания 3.3 Вопросы для подготовки к зачету 4. Учебно-методическое обеспечение курса 5. Тематическое распределение часов Наименование разделов и тем

Подобный материал:

• Утверждено Советом Факультета Председатель 200 г. Санкт Петербург 2010 содержание пояснительная, 206.17kb.
• Утверждено Советом Факультета Председатель 200 г Санкт Петербург 2010 содержание пояснительная, 191.69kb.
• Утверждено Советом Факультета Председатель 200 г. Санкт Петербург 2010 содержание пояснительная, 553.18kb.
• Утверждено Советом Факультета Председатель Протокол № от 201 0 г. Санкт-Петербург 2010, 251.78kb.
• Утверждено Советом Факультета Председатель 200 г. Санкт Петербург 2010 содержание пояснительная, 453.72kb.
• Утверждено Советом Факультета Председатель 200 г. Санкт Петербург 2010 оглавление пояснительная, 105.7kb.
• Утверждено Советом Факультета Председатель Совета Факультета 2010г. Санкт Петербург, 247.31kb.
• Утверждено Советом Факультета Председатель /А. В. Бутуханов/ 200 г. Санкт Петербург, 75.3kb.
• Утверждено Советом Факультета Председатель 200 г. Санкт-Петербург 2010 Раздел пояснительная, 108.09kb.
• Утверждено Советом Факультета Председатель 2010 г. Санкт-Петербург 2010 I. пояснительная, 452.49kb.

Правительство Российской Федерации


Государственное образовательное бюджетное учреждение

Высшего профессионального образования

«Государственный университет – Высшая школа экономики»


Санкт-Петербургский филиал

Государственного университета – Высшей школы экономики


Кафедра финансовых рынков и финансового менеджмента


ПРОГРАММА ДИСЦИПЛИНЫ

Математические модели финансовых рынков


Для направления 080100.62 «Экономика» подготовки бакалавра


Курс четвертый

Автор Косенко А.В.

Согласовано УМО ________________________ __________/_____________/ «___» ____________ 20__г.	Одобрено на заседании кафедры Зав. кафедрой _______________ «___» ____________ 20__г.
	Утверждено Советом Факультета ____________________________ Председатель __________________ «___» ____________ 20__г.

Санкт-Петербург

2010

1. Пояснительная записка


Аннотация курса

Современная деятельность на финансовых рынках практически невозможна без развитых математических моделей и алгоритмов. Среди сфер деятельности, где они активно применяются можно назвать торговый процесс, управление портфелем и риск менеджмент, контроль и отчетность. Математические методы используются для решения таких задач как оценка финансовых активов, формирование оптимального портфеля, измерение риска отдельных активов и портфеля в целом, хеджирование, оценка премии за риск, построение кривой временной структуры процентных ставок и другие.

В основе прикладных методов лежат математические модели, развитые в теории финансовых рынков. Они с помощью математического языка выражают концепции и идеи финансовой теории. Математические модели могут иметь дескриптивную форму, но при этом они позволяют лучше понимать функционирование рынка, анализировать возможности и скрытые затраты, совершенствовать структуру рынка и регулятивный механизм.

Многие математические методы из разных областей финансовой деятельности имеют в основе общие корни, одни и те же идеи и допущения. С другой стороны, в рамках отдельных дисциплин специальности финансы и кредит, обычно рассматриваются только практические следствия моделей, без анализа предпосылок, ограничений, эмпирической выполнимости положений, недостатков и направлений развития. Поэтому изложение основных моделей, составляющих ядро теории финансовых рынков, целесообразно в рамках одной дисциплины, с соблюдением необходимой степени математической строгости.

В соответствии с учебным планом по данной дисциплине предусмотрено 48 часов аудиторных занятий, из них 24 часа отводится под лекционные занятия и столько же под семинары.


Рассматриваемые в курсе модели финансовых рынков используют математический аппарат, однако математические модели в курсе являются лишь инструментом для анализа представлений теории финансовых рынков или для решения практически ориентированных задач.

Цели и задачи освоения дисциплины

Дисциплина «Математические модели финансовых рынков» читается в 7-м семестре студентам направления «Экономика». Перед изучением курса студенты должны прослушать следующие дисциплины: финансовый менеджмент, микроэкономика, теория вероятностей, эконометрика, базовые математические дисциплины.

Целью изучения дисциплины «Математические модели финансовых рынков» является формирование у студентов-бакалавров компетенций в области современных теоретических концепций, моделей и подходов, находящих приложение в профессиональной деятельности на финансовых рынках, в частности, инвестиционной деятельности, риск-менеджменте, торговле рыночными и структурными продуктами.

В результате изучения данного курса студенты должны:

• знать основные положения современной теории финансовых рынков; основные модели финансовых рынков, изучаемые в данном курсе, предположения и выводы моделей;
  
• уметь объяснять выводы моделей и роль, которую играют те или иные предпосылки в справедливости сделанных заключений;
  
• получить навыки анализа экономических проблем, решения ряда прикладных задач, связанных с профессиональной деятельностью на финансовых рынках;
  
• иметь представление о практических задачах в области деятельности на финансовых рынках, применяемых для их решения математических методах, направлениях развития теории финансовых рынков.
  

Формы работы студентов


При изучении данной дисциплины предусматривается:

• Проведение лекционных занятий в соответствии с сеткой часов, приведенной далее по тексту;
  
• Проведение семинарских занятий;
  
• Самостоятельное изучение литературы, освоение теоретического материала;
  
• Выполнение домашних заданий в качестве закрепления пройденного на семинарах материала и подготовки к следующему семинарскому занятию;
  
• Проведение двух промежуточных контрольных работ;
  
• Выполнение домашнего задания в форме моделирования в Эксель в рамках текущего контроля;
  
• Проведение итоговой работы.
  

Методика формирования результирующей оценки


Аудиторная работа студентов оценивается на основании правильности решения задач, активности студента во время семинарских занятий при коллективном обсуждении выполняемого задания, участие в дискуссиях, ответы на вопросы преподавателя, решение задач у доски. Самостоятельная работа студентов оценивается с учетом правильности и регулярности выполнение текущих домашних заданий (задания, выдаваемые на семинарских занятиях), выполнения письменного домашнего задания в рамках текущего контроля. Результирующая оценка по 10-ти балльной шкале за работу на семинарских занятиях (с учетом текущих домашних заданий) определяется перед промежуточным или итоговым контролем О_{семинары}. Результирующая оценка по 10-ти балльной шкале за самостоятельную работу (письменное домашнее задание) определяется перед промежуточным или итоговым контролем – О_дз.

Текущий контроль включает также две контрольные работы. Работы оцениваются по 10-бальной шкале. Вес работ одинаков. Результирующая оценка по каждой из контрольных работ – О_{текущий}, О_{текущий2} выставляются в рабочую ведомость.


Результирующая оценка за итоговый контроль в форме зачета выставляется по следующей формуле, где О_зачет – оценка за работу непосредственно на зачете:

О_{итоговый} = k₁·О_зачет + k₂·О_{текущий} + k₃·О_{текущий2} + k₄·О_дз + k₅·О_{семинары}

где k₁ = 0,4; k₂ = 0,15; k₃= 0,15; k₄=0,1, k₅ = 0,2.

Результирующая оценка за текущий контроль учитывает результаты студента по текущему контролю следующим образом:

О_{текущий} =(k₂·О_{текущий} + k₃·О_{текущий2} + k₄·О_дз + k₅·О_{семинары})/(k₂+ k₃+ k₄+ k₅·).


2. Содержание дисциплины


Обзор моделей финансовых рынков


Основные направления развития современной теории финансовых рынков. Нормативные и дескриптивные модели финансовых рынков. Сферы практической деятельности на финансовых рынках, использующие математические (количественные) методы и алгоритмы.


Теорема Фишера


Межвременной выбор потребителя. Линия трансформации. Карта безразличия. Линия инвестиционных возможностей индивидуума. Потребительский оптимум индивидуума. Теорема Фишера о разделении финансовых и инвестиционных решений. Критерий NPV и оптимум инвестора.


Основы принятия решений в условиях неопределенности

Принятие решений на основе математического ожидания и дисперсии. Предпосылки использования дисперсии как меры риска, недостатки. Использование моментов более высоких порядков. Коэффициент асимметрии и эксцесс. Функции полезности, основанные на моментах распределения. Значение нормального распределения.

Теория полезности в условиях неопределенности. Матрицы результатов и лотерея. Принцип Бернулли. Достаточные аксиомы. Существование кардиналистской функции полезности. Виды отношений к риску. Нерасположенность к риску, нейтральность к риску и расположенность к риску. Интенсивность не расположенности к риску. Избранные функции полезности и их оценка. Стохастическое доминирование. Стохастическое доминирование первого порядка. Стохастическое доминирование второго порядка. Выбор в пространстве риск-доходность и следствие нормальности распределения доходностей.

Оптимизация портфеля

Модель Марковица. Оптимизация портфеля из двух активов. Значение коэффициента корреляции. Эффективная граница. Постановка задачи квадратичного программирования. Построение эффективной границы.

Теория арбитража

Допущения. Воможности арбитража на финансовых рынках. Теорема доминирования и теорема аддитивности стоимости. Условия арбитража. Примитивные и рыночные ценные бумаги. Лемма Минковского-Фаркаша. Однозначность системы цен. Полнота рынка капитала.


Временная структура процентных ставок


Кривая доходности и временная структура процента. Использование кривой доходности для определения цены облигации. Доходность к погашению. Теории, объясняющие временную структуру процентных ставок. Построение теоретической кривой доходности. Форвардная ставка. Имплицитная форвардная ставка. Соотношение между спот ставкой процента и форвардной ставкой процента.


Модели оценки финансовых активов

Представления CAPM и их варианты. Анализ равновесия. Диверсификация. Взаимный фонд и теорема о разделении Тобина. Рыночный портфель. Альтернативное доказательство CAPM Дженсена. Портфель, состоящий из безрискового и рисковых финансовых активов. Линия рынка капитала. Линия рынка ценных бумаг. CAPM при отсутствии безрисковой процентной ставки. Эмпирическая проверка CAPM. Критика CAPM.

Факторные модели. Трехфакторная модель Фамы и Френча. Теория абитражного ценообразования.

Теория структуры капитала

Теорема Модильяни — Миллера. Основные допущения. CAPM и теорема иррелевантности. Теория арбитража и теорема иррелевантности. Требования собственников к доходности. Средневзвешенная стоимость капитала. Структура капитала и налоги. Налоговая система 1 (налог на прибыль юридических лиц). Налоговая система 2 (налог на прибыль юридических лиц и подоходный налог с физических лиц). Налоговая система 3 (налог на прибыль юридических лиц, подоходный налог с физических лиц и налог на доход с промысла). Структура капитала и издержки банкротства.

Теория ценообразования опционов

Простейшая модель оценки опционов по безарбитражному принципу: “два момента времени — две ситуации”. Оценка европейского опциона колл. Риск-нейтральные вероятности. Европейский опцион пут. Биномиальная модель, европейский опцион колл. Европейский опцион пут и паритет пут — колл.

Оценка опционов американского типа с помощью биномиальных деревьев.

Риск-нейтральное оценивание. Существование риск нейтральных вероятностей.

Коэффициент дельта. Дельта-хеджирование.

Процессы поведения цен финансовых активов. Винеровский процесс. Геометрическое броуновское движение и логнормальное распределение. Лемма Ито.

Формула Блэка-Шоулза. Предположения. Вывод. Арбитражный портфель. Дельта-хеджирование в непрерывном времени. Вычисление коэффициента дельта. Другие коэффициенты чувствительности.

Подразумеваемая волатильность рыночными ценами опционов (implied volatility). Кривая волатильности, улыбка волатильности. Роль ненормального распределения активов.

Оценка опционов методом Монте-Карло. Дискретизация процесса геометрического броуновского движения.


Измерение риска: Value at Risk

Риск разорения и роль собственного капитала. Понятие экономического капитала. Value at Risk (VaR). Выбор параметров расчета VaR. Критика VaR. Когерентные меры риска. Expected shortfall. Методы расчета VaR: исторический, параметрический и Монте-Карло. Дельта-нормальный и дельта-гамма нормальный VaR. Коррекция по Корниш-Фишеру. Оценка эффективности с учетом риска: RAROC. Методы измерения дисперсии доходностей (изменений цен) при оценке VaR. Выборочная оценка. Оценка методом экспоненциального взвешивания (EWMA оценка) квадратов исторических доходностей. ARCH-GARCH оценки. Оценка на основе рыночных цен опционов на актив (implied volatility).

3. Тематика заданий текущего контроля

3.1 Примерные варианты контрольных работ


1. Объясните, как соотносится теория ожидаемой полезности с критерием принятия решений на основе мат. ожидания и дисперсии? В каких случаях эти подходы не будут противоречить друг другу? Какой из подходов к принятию решений более обоснован в ситуации, когда ничего не известно о форме вероятностного распределения негарантированных результатов?


2. Функция полезности инвестора имеет следующий вид:

.

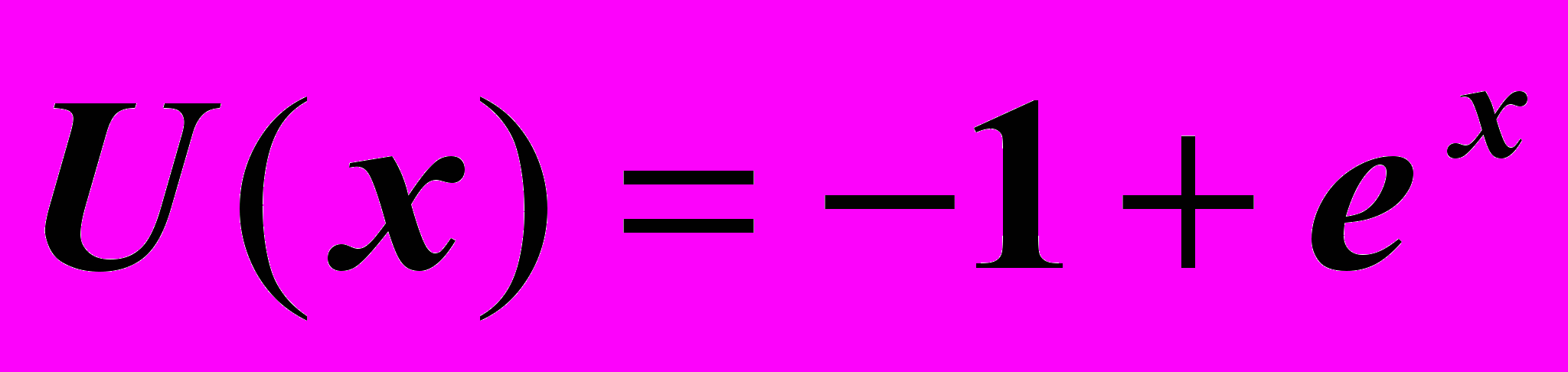а) Является ли инвестор нерасположенным (расположенным) к риску?

б) На основе коэффициентов абсолютной и относительной нерасположенности к риску проанализируйте как будет изменяться отношение к риску инвестора в зависимости от его уровня благосостояния.


3. Ваше сегодняшнее имущество составляет 50, а вашей функцией полезности является 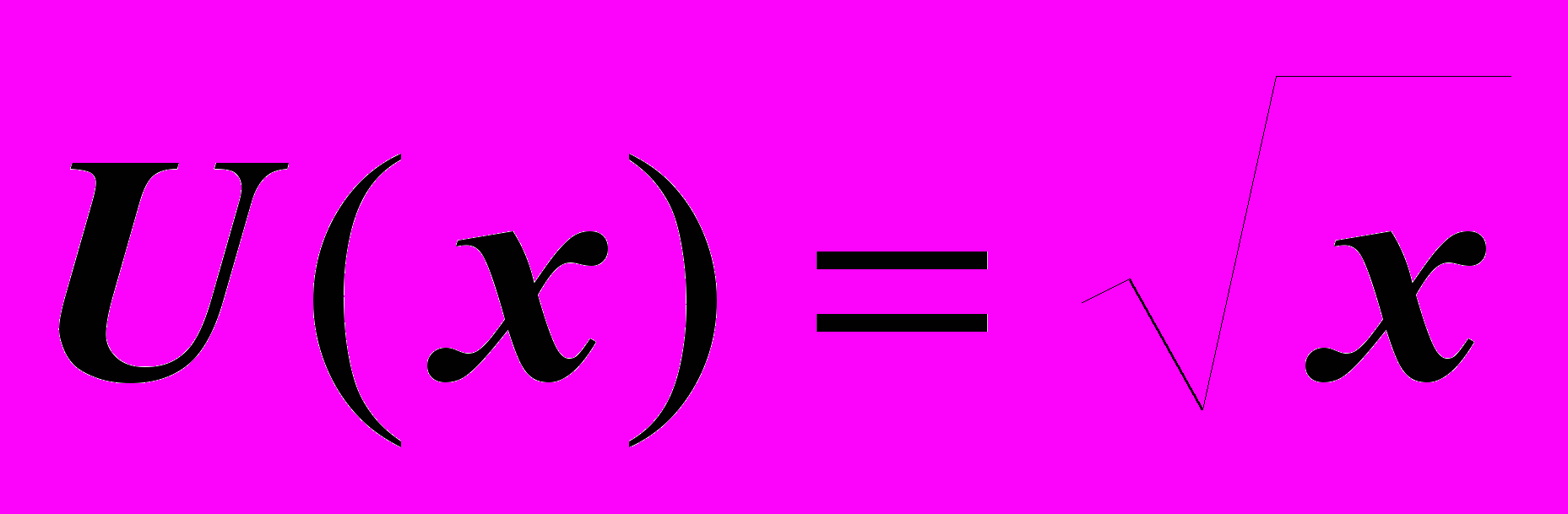. Какую сумму вы были бы готовы заплатить в качестве страховки от риска в следующей игре:

.


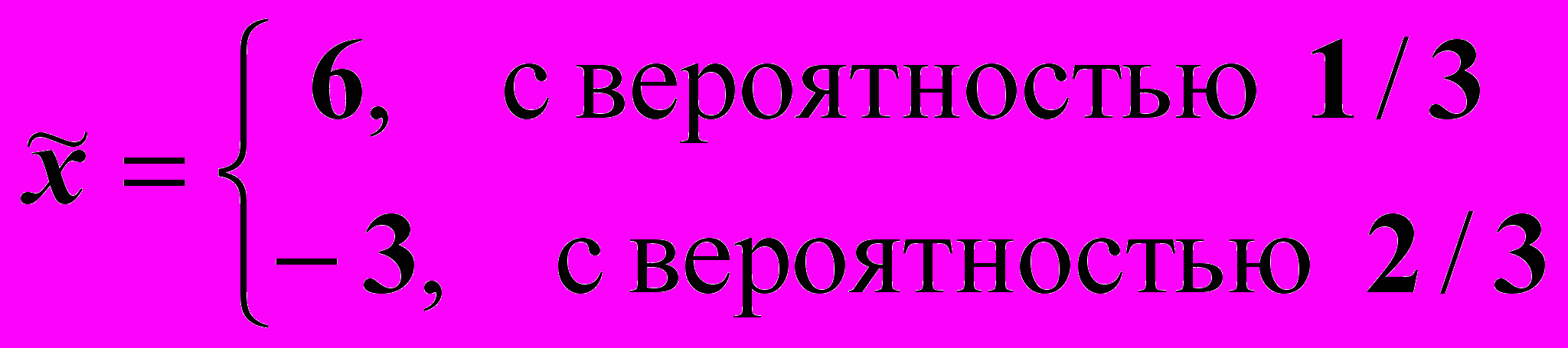4. На рынке капитала обращаются 3 финансовых актива, цены и денежные потоки которых приведены в таблице.

Финансовый актив	Денежные потоки в ситуации:			Цена
	1	2	3
1	10	5	3	10,7
2	5	8	5	9,5
3	0	0	7	2,8
Ц.б. компании XYZ	4	10	2	?

Вновь образуемая компания XYZ размещает на рынке свои акции. Через год они принесут владельцам, в зависимости от ситуации в экономике, доходы, указанные в таблице. Сколько будут стоить ц.б. компании XYZ, если рынок капитала не допускает возможностей арбитража?

Покажите, что арбитраж существует (составьте арбитражный портфель), если акции компании XYZ стоят 11 рублей.


3.2 Примеры письменного домашнего задания


Задание выполняется в Эксель, результаты оформляются в редакторе MS Word.

1. Выполнить в Эксель оценку в помощью метода Монте-Карло
   
   1. некоторого производного инструмента (европейский пут/колл опцион на акцию/валютный курс/фьючерс, спред опцион);
      
   2. VaR портфеля из нескольких акций/акции и облигации/облигации, номинированной в иностранной валюте;
      
2. Построить эффективную границу по Марковицу с помощью инструмента «Поиск решения»;
   
3. Оценить коэффициенты бета по историческим данным и построить эмпирическую линию рынка ценных бумаг для российского рынка;
   
4. Оценить VaR параметрическим/историческим методом для портфеля из заданного набора инструментов (исходными данными являются исторические цены).
   

3.3 Вопросы для подготовки к зачету

1. Межвременной выбор потребителя. Бюджетное ограничение и линия трансформации. Значение рынка капитала для выбора оптимального плана потребления. Математическое и графическое решение задачи оптимизации потребительского плана.
   
2. Выбор при наличии реальных инвестиций. Обоснование критерия сегодняшней приведенной стоимости.
   
3. Теорема Фишера о разделении инвестиционных решений и решений о потреблении
   
4. Принцип ожидаемой полезности
   
5. Отношение к риску
   
6. Выпуклость вверх функции полезности и нерасположенность к риску
   
7. Степень неприятия риска. Рисковая премия Марковица
   
8. Коэффициенты избегания риска Эрроу-Пратта
   
9. Эвристические меры риска. Дисперсия. Соотношение критерия ожидаемой полезности и выбора на основе мат. ожидания и дисперсии. Значение нормального распределения.
   
10. Стохастическое доминирование I-го и II-го порядков.
    
11. Модель рынка капитала с дискретным временем и конечным пространством состояний. Предположения.
    
12. Арбитражные возможности. Теорема доминирования и теорема аддитивности стоимости.
    
13. Условие отсутствия арбитражных возможностей. Примитивные ценные бумаги.
    
14. Безарбитражная оценка. Полнота рынка капитала.
    
15. Графическая иллюстрация наличия (или отсутствия) арбитражных возможностей для рынка с двумя ценными бумагами и двумя возможными состояниями.
    
16. Кривая доходности и временная структура процента.
    
17. Теории, объясняющие временную структуру процентных ставок.
    
18. Оценка облигаций.
    
19. Форвардная ставка процента.
    
20. Модель оценки капитальных активов. Предположения. Линия рынка ценных бумаг.
    
21. Доказательство CAPM Дженсена.
    
22. Теорема о двух взаимных фондах. Линия рынка капитала.
    
23. APT
    
24. Теорема Модильяни-Миллера с налогами и без.
    
25. Теорема Модильяни-Миллера. Доказательство на основе предположения об отсутствии арбитражных возможностей.
    
26. Оптимальная структура капитала. Издержки банкротства.
    
27. Оценка опционов для модели “два момента времени — две ситуации”.
    
28. Биномиальная модель.
    
29. Пут-колл паритет. Оценка опционов Пут.
    
30. Процесс геометрического броуновского движения.
    
31. Формула Блэка-Шоулза.
    

4. Учебно-методическое обеспечение курса

Литература по дисциплине


Базовый учебник

1. Крушвиц Л. Финансирование и инвестиции. — СПб.: «Питер», 2000.
   

Основная

2. Халл, Дж. К. Опционы, фьючерсы и другие производные финансовые инструменты. 6-е издание. Вильямс, 2008.
   
3. Уотшем Т., Паррамоу К. Количественные методы в финансах. М.: Финансы, ЮНИТИ, 1999.
   

Дополнительная

4. Бухвалов А.В., Дорофеев Е.А., Окулов В.Л. Лекции по избранным вопросам классических финансовых моделей.– СПб: Изд. ВШМ, 2010.
   
5. Крушвиц Л., Шефер Д., Шваке М. Финансирование и инвестиции: сборник задач и решений. СПб. : «Питер», 2001.
   
6. Финансовая математика. Математическое моделирование финансовых операций./ Под ред. В.А. Половникова, А.И. Пилипенко. М.: Вузовский учебник, 2005.
   
7. Шведов А.С. О математических методах, используемых при работе с опционами.// Экономический журнал ВШЭ, 3, 1998.— с. 385-409.
   
8. Cochrane J.N. Asset Pricing. Princeton University Press, 2001. Доступно по адресу: hicagobooth.edu/john.cochrane/research/papers/samplechapters.pdf
   
9. Copeland T.E., and J.F. Weston. Financial Theory and Corporate Policy. Addison-Wesley, Inc., 1993.
   
10. Campbell J.Y., Lo A.W., and A.C. MacKinlay. The Econometrics of Financial Markets. Princeton University Press, 1997.
    
11. Föllmer H., and A. Schied. Stochastic Finance An Introduction in Discrete Time.—2-nd ed. Walter de Gruyter, 2004.
    
12. Handbook of Quantitative Finance and Risk Management// Editors: Cheng-Few Lee, Alice C. Lee, John Lee. Springer, 2010.
    

5. Тематическое распределение часов

	Наименование разделов и тем	Аудиторные часы			Самост. работа	Всего часов
		лекции	семинары	всего
1.	Обзор моделей финансовых рынков	1	-	1	2	3
2.	Теорема Фишера	2	2	4	5	9
3.	Основы принятия решений в условиях неопределенности	2	2	4	5	9
4.	Оптимизация портфеля	2	2	4	5	9
5.	Теория арбитража	2	2	4	5	9
6.	Временная структура процентных ставок	2	2	4	6	10
7.	Модели оценки финансовых активов	3	2	5	6	11
	Контрольная работа 1		2	2		2
8.	Измерение риска: Value at Risk	3	3	6	8	14
9.	Теория структуры капитала	2	2	4	6	10
10.	Теория ценообразования опционов	5	3	8	12	20
	Контрольная работа 2		2	2		2
	Всего часов	24	24	48	60	108

Составил программу ст.преп. Косенко А.В.