Э. Кондильяк об искусстве рассуждения

Вид материала

Документы

Содержание Глава ix о блоке Посредством ряда О наклонной плоскости Когда направление Сила должна Скорость, с которой Его движение Как узнать Падает ли тело О маятнике Маятник производит Условия, необходимые Соотношение между Для определения длины маятника необходимо знать центр колебаний Предмет следующей книги Книга третья О метательном движении Этот снаряд Ь, дети находятся на линии ab Проходя ряд ... Полное содержание

Подобный материал:

• Тематика курсовых работ (доцент кафедры культурологи Н. Н. Гашева) Античные и библейские, 22.42kb.
• Урок на тему «Изображение пространства», 156.79kb.
• Конспект урока по развитию речи в 4 классе. Сочинение с элементами рассуждения «Что, 174.76kb.
• С, почему Лейбниц исключил из «Рассуждения о метафизике», построенного по плану типичного, 232.71kb.
• Н. К. Рерих об искусстве сборник статей, 2030.31kb.
• 5 класс Подготовка к сочинению-рассуждению «Для чего нужно заниматься спортом?», 124.23kb.
• Методические рекомендации к написанию сочинения-рассуждения егэ по русскому языку (часть, 201.83kb.
• Рекомендации по написанию сочинения-рассуждения, 39.14kb.
• Краткая история живописи, 99.09kb.
• Анализ текста как метод написания сочинения-рассуждения, 177.52kb.

ГЛАВА IX О БЛОКЕ

Блок — это маленькое колесо, укреп­ленное на оси в развилку и движу­щееся вокруг стержня, проходящего через его центр. Если к двум концам бечевки, перекинутой поверх блока (рис. 19), подвешены два равных груза, то будет иметь место равновесие. Ведь очевидно, что эти гру­зы действуют лишь на конец диаметра. Следовательно, Вы не должны считаться ни с верхней, ни с нижней частью бло­ка; представьте себе эти грузы как подвешенные на плечи весов на равном расстоянии от центра тяжести, или от точ­ки подвеса. Поэтому Вы должны применить к этому блоку все сказанное нами о весах.


Посредством ряда

блоков малая сила

поддерживает

большой груз
Один конец бечевки мы закрепим на крючке (рис. 20), а другой прове­дем по низу подвижного блока. Пере­кинем затем бечевку поверх не­подвижного блока. Груз весом в один ливр будет подвешен на этот конец бечевки, а груз в два ливра — на подвижный блок; Вы увидите, что установи­лось равновесие. Этот подвижный блок по существу явля­ется рычагом, где груз находится между двумя силами; ведь Вам надо считаться лишь с диаметром, а две бечевки представляют две силы а и Ь, каждая из которых удержи­вает половину Р, потому что груз находится на равном расстоянии от одной и от другой силы.

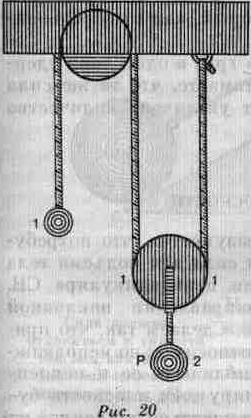
Поскольку а удерживает половину Р, оно удерживает один ливр. Таким образом, на один конец диаметра непод­вижного блока оказывает давление сила в один ливр и,



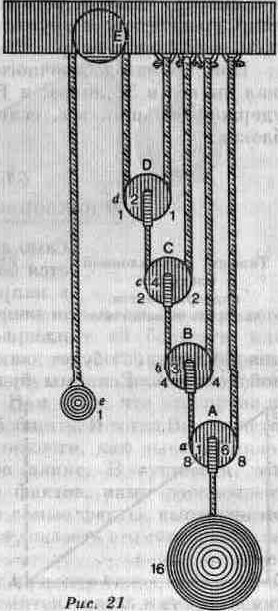
следовательно, уравновешивает груз в один ливр, поме­щенный на другом конце диаметра. С помощью пяти бло­ков, расположенных, как показано на рис. 21, вес одного ливра удержал бы груз в 16 ливров. Груз в 16 ливров, под­вешенный к нижнему блоку А, находится на равном рас­стоянии от точек приложения двух сил, действующих на два диаметра этого блока. Каждая из этих сил удерживает половину веса а и равна 8, значит, груз весит 8, а груз, под­вешенный к блоку В, становится весом в 8 ливров. Мы заметим также, что этот груз находится на равном расстоянии от двух сил, действующих на два конца диамет­ра блока В, и, следовательно, мы сочтем, что Ь, которое поддерживает половину груза, равно 4.

Аналогичным образом груз, подвешенный к блоку С, бу­дет весить 4 ливра и сила С будет действовать как 2 лив­ра. И наконец, груз, подвешенный к блоку D, будет весом в 2 ливра, а сила d, которая будет действовать как один ливр, уравновесится грузом е, который, как мы предпола­гаем, весит один ливр.

При помощи добавочного блока груз в один ливр удер­жал бы вес в 32 ливра; и Вы понимаете, что та же сила удержит больший вес, если будет увеличено количество блоков.

ГЛАВА X О НАКЛОННОЙ ПЛОСКОСТИ


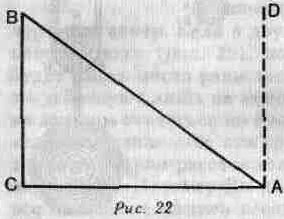
Само собой разумеется, что потребу­ется большая сила для подъема тела в направлении перпендикуляра СВ, нежели в направлении наклонной плоскости АВ. Сделаем так, что пря­мая ВА (рис. 22) будет двигаться относительно неподвиж­ной точки А. Если мы будем приближать ее к перпен­дикуляру AD, плоскость бу­дет становиться наклонной по мере того, как мы будем ее поднимать, и для того, чтобы удержать груз, понадобится большая сила. Если же, на­оборот, понижать ее, прибли­жая к горизонтальной линии СА, наклон плоскости будет уменьшаться по мере того,

как мы будем ее опускать, и такой же груз будет удержи­ваться меньшой силой. В первом случае наклонная пло­скость удерживает меньшую часть груза, а во втором — большую. Все это подтверждается опытом.

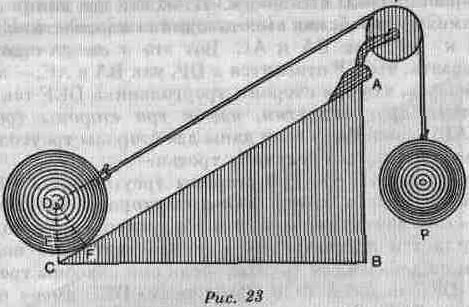
Если сила Р находится в равновесии с грузом D (рис. 23), когда направ­ление силы тяги TD параллельно плоскости, то, как только это направ­ление перестанет быть параллельным плоскости, равновесие нарушится, и груз потянет сила Р. Следователь­но, если угодно удержать тяжесть наименьшей силой, надо, чтобы направление тяги было параллельно плоско­сти. И это подтверждается опытом.



Но поскольку плоскость, по мере того как Вы придаете ей большую или меньшую высоту наклона, поддержи­вает большую или меньшую часть тяжести, Вам ясно, что это правило можно обобщить. И тогда Вы скажете:

сила всегда так относится к тяжести, как высота накло­на плоскости относится к ее длине. В сущности, это правило является следствием фактов, нами рассмотрен­ных. Оно не что иное, как эти самые факты, выраженные обобщенно. Теперь попытаемся доказать это согласно уста­новленным нами принципам.

Сила Р (рис. 23) действует на центр тяжести D, т. е. на конец линии FD; тяжесть стремится упасть в направлении

69

линии DEC перпендикулярно горизонту, и она упала бы в этом направлении, если бы ее частично не поддерживала плоскость. Вы можете рассматривать DFE как изогнутый рычаг, имеющий свою точку опоры в F; Вы видите, что прилагаемая сила воздействует в конце более длинного пле­ча рычага, а тяжесть давит на конец короткого плеча, на ко­нец линии FE, перпендикулярной DC; она давит на точку Е и упала бы перпендикулярно в С, если бы не была под­держана.

Следовательно, DF выражает расстояние, на которое точка приложения силы отдалена от точки опоры, a EF вы­ражает расстояние от этой самой точки, на которой нахо­дится тяжесть. Следовательно, две эти линии выражают условия, необходимые для равновесия, т. е. определенное соотношение силы и тяжести. Итак, эти две линии соотно­сятся между собой, как высота и длина плоскости: EF отно­сится к DF, как ВА к АС. Вот это и следует доказать.

Сказать, что EF относится к DF, как ВА к АС,— это зна­чит сказать, что три стороны треугольника DEF так же со­относятся друг с другом, как и три стороны треуголь­ника ABC, поскольку если даны две стороны треугольника, то тем самым определена и третья.

Ведь сказать, что три стороны треугольника EDF так относятся друг к другу, как три стороны треугольника ABC,— это значит сказать, что эти треугольники подобны; нам остается доказать, что они действительно подобны.

Они подобны один другому, если они подобны третьему. Итак, DEF подобен DCF. Во-первых, DEF имеет прямой угол F, a DCF также имеет прямой угол F — они подобны в том, что каждый имеет прямой угол. Во-вторых, они по­добны и в том, что угол CDF является общим для обоих. Стало быть, они одинаково подобны и третьему, так как, если даны два угла, третий определен.

Так же легко будет понять, что треугольник ABC подо­бен CDF, поскольку Вы видите, что каждый из них имеет прямой угол. Вы видите также, что наклонная линия АС падает на две параллельные линии АВ и CD и что, следова­тельно, угол DCA равен углу CAB. Вспомните сказанное нами, когда мы рассматривали углы, образующиеся при пересечении двух параллельных прямых третьей.

Когда какая-нибудь тяжесть находится в равновесии на наклонной плоскости, то доказано, что расстояние до точки опоры относится к расстоянию от точки приложе­ния силы до этой же точки, как высота относится к длине

плоскости, и что, следовательно, сила относится к тяжести, как высота плоскости — к ее длине.

Скорость, с которой

тело спускается

по наклонной

плоскости

Тело спускается с различной ско­ростью в зависимости от того, падает ли оно перпендикулярно к горизонту или же падает по наклонной плоско­сти. Оно не может спускаться иначе как с силой, равной той силе, которая удерживала бы его в равновесии. Стало быть, мы можем вывести общее правило: сила, с которой тело спускается по наклонной плоскости, относится к весу тела, как высота плоско­сти к ее длине. Теперь следует найти путь, который оно должно пройти по линии АВ за то же время, за какое оно проходит путь от А до С.

Начертим плоскость ABC (рис. 24), длина которой бу­дет вдвое больше высоты, и разделим АС и АВ на четыре части.



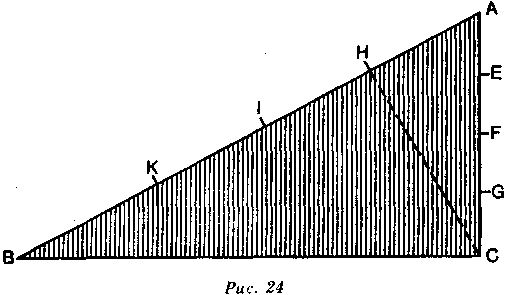
Я предполагаю, что АЕ, EF, FG и GC — четыре отрезка, которые тело должно пройти за две секунды.

Его движение

ускоряется

в пропорции

1, 3, 5, 7

На тело действует наполовину меньшая сила, когда оно падает из А в В, чем когда оно падает из А в С. Стало быть, оно должно иметь наполовину меньшую скорость, и потому оно достигает В лишь за четыре секунды. Итак, сила тяготения воздействует на тела одинаково, в каких бы на­правлениях они ни двигались, иначе говоря, в равные промежутки вре­мени ускорение движения составляет пропорцию 1, 3, 5, 7 и т. д. Стало быть, тела, падающие

из А в С, проходят в первую секунду отрезок пути АЕ, а в следующую — отрезки EF, FG, GC, и точно так же тело, падающее из А в В, в первые две секунды должно пройти отрезок АН, а в две следующие — отрезки HI, IK, КВ. Тело, двигающееся по этой наклонной плоскости, при­дет в Н за такое же время, как если бы оно падало перпен­дикулярно из А в С, т. е., падая но линии АВ в течение двух секунд, оно окажется не ниже, чем падая по линии АС в те­чение одной секунды. Ведь Е и Н находятся на равном расстоянии от горизонтальной линии СВ.

Если Вы опустите перпендикуляр на АВ, Вы увидите, что он падает точно в Н. Стало быть, чтобы узнать путь, который тело должно пройти по наклонной плоскости за такое же вре­мя, как если бы оно падало из А в С, нам нужно всего лишь опустить перпендикуляр из С на плоскость АВ.

Раз сила тяготения действует всегда одинаково, то из этого следует, что, каким бы ни был наклон плоскости, тело, когда оно опустится вниз, будет иметь ту же скорость, какую бы оно имело, если бы падало вдоль перпен­дикуляра.

Если плоскость имеет больший на­клон и потому короче, ускорение будет большим и эта скорость будет достигнута раньше; если плоскость менее наклонна, ускорение будет меньшим и та же скорость будет достигнута позднее. Стало быть, какой бы ни была линия, которую описывают несколько тел, достигнув низа, они имеют ту же силу всякий раз, когда падают с той же высоты.

ГЛАВА XI

О МАЯТНИКЕ

Начертим несколько наклонных пло­скостей между точкой А и горизон­тальной линией ВС и опустим пер­пендикуляры из С на эти плоскости. Наметим центр на равных расстоя­ниях от А и от С и начертим окруж­ность по угловым точкам D, Е, F. Линии AD, АЕ, AF (рис. 25) — хорды окружности; и мы

72

можем во второй полуокружности начертить прямые, ко­торые, будучи параллельны первым, будут им равны и одинаково наклонны.

Ведь очевидно, что все эти прямые играют ту же роль, что и плоскости, о которых мы только что говорили. Тело спустится вдоль каждой из них за такое же время, как если бы оно падало с верха диаметра вниз из А в С.

Сколько бы мы ни проводили хорд в вертикально поставленной окружности, тело всегда затратит одина­ковое время на прохождение каждой хорды, и время это будет равно тому, которое оно затратило бы на прохож­дение диаметра. Вы также заметите, что хорды пропор­ционально степени их наклона будут более длинными или более короткими.

Сила тяготения всегда действует пер­пендикулярно, и независимо от угла наклона плоскости тело, достигнув горизонтальной линии ВС, имеет ту же силу, как если бы оно падало перпендикулярно из А в С. Пусть тело подвешено (рис. 25) к центру М на нити, длина которой равна полудиаметру



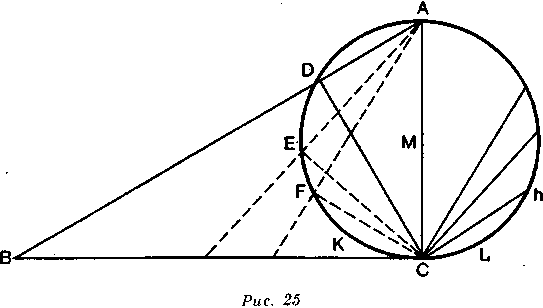
окружности. Это тело, опускаясь из h, не может упасть ниже С; но сила, приобретенная им при прохождении данного пути, может быть использована для прохожде­ния еще одного, равного ему пути, и оно вновь поднимется в F. Дойдя до этой точки, оно утратит всю свою силу и, таким образом, вновь упадет под действием своего тяго­тения, вновь обретет достаточную силу, для того чтобы

73

подняться в точку h, откуда оно снова упадет, и т. д.

Тело, подвешенное таким образом, называется маятни­ком. Оно может быть подвешено на веревке либо на прово­локе. Движение маятника из h в С и из С в h называется колебанием или качанием.

Оно падает ускоренным движением из h в С за то же время, за какое оно упало бы из А; и за такое же время оно поднимается в F затухающим движением.

Стало быть, если бы за эти два промежутка времени оно падало перпендикулярно из точки А, оно прошло бы четыре диаметра окружности.

Значит, тело, подвешенное в центре М, затратило бы на колебание такое же время, какое оно затратило бы, проходя перпендикулярно четыре диаметра, либо, что то же самое, проходя высоту маятника восемь раз.

Условия, необходимые

для изохронных

колебаний

Таково соотношение между движением колебательным и движением перпендикулярным, когда, по нашему пред­положению, маятник опускается и поднимается по хордам. Ведь поскольку дуги окружности тем менее отличаются от хорд, чем они меньше, предполагается, что соотношение остается тем же, когда маятник совершает колебание по ма­лой дуге LCK. По правде говоря, это допущение не совсем точно, поскольку геометры доказывают, что время, необхо­димое для того, чтобы опустить тяжелое тело по бесконечно малой дуге, относится к времени, необходимому для того, чтобы опустить его по хорде той же дуги, как длина окруж­ности — к четырем ее диаметрам, или приблизительно как 355 к 452. Между тем периоды колебания по сколь угодно малым дугам окружности равны, потому что они соотно­сятся как равные периоды падения по хордам этих дуг. Вам следует отметить, что во всем сказанном нами о движении мы упускаем из виду трение, а также сопротивление воздуха. Но трение тем менее ощутимо, чем длиннее маятник и чем меньшую дугу он описывает.

Если бы не существовало ни трения, ни сопротивления воздуха, маятник, раз качнувшись, вечно продолжал бы свои колебания в равные промежутки времени. Когда маят­ник короток, а дуги большие и трение и сопротивление воз­духа более ощутимы, то колебания происходят в неравные промежутки времени. А когда, наоборот, маятник длиннее, а дуги меньше, колебания могут без ощутимой ошибки рас­сматриваться как происходящие в одинаковые периоды

времени, до тех пор пока маятник не остановится. Подоб­ные колебания называются изохронными.

Соотношение между

длиной маятника

и продолжительностью

колебаний

Время колебаний тем меньше, чем короче сам маятник. Вот каково должно быть это соотношение (рис. 26). AGBE и D/Bi — две окружности, диаметры которых АВ и DB отно­сятся друг к другу как 4 к 1.

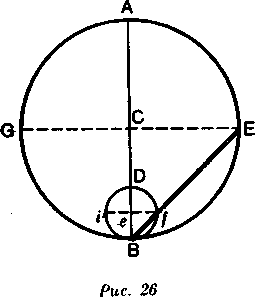
Мы доказали, что если тело падает из А в В за опреде­ленное время, то за промежуток времени, вдвое меньший,



оно может упасть лишь из D в В. Мы доказали также, что тело падает вдоль хорды окружности за то время, за какое оно падает вдоль диаметра. Стало быть, тело в Е упадет вдоль хорды BE за время, вдвое большее по сравнению с тем временем, в течение которого тело в f упадет вдоль хорды fВ. Итак, доказано, что если допустить, что дуги BE и fВ подобны или очень малы, то периоды падений по этим ду­гам, или периоды полуколебаний, соотносятся как периоды падений по хордам. Следовательно, время колебания маят­ника СВ будет вдвое больше, нежели время колебания маятника Be.

Если Вы хотите, чтобы колебания были в два раза мед­леннее, надо, чтобы маятник был в четыре раза длиннее, и, напротив, надо, чтобы он стал в четыре раза короче, если Вы желаете, чтобы колебания стали вдвое быстрее.

Для определения длины маятника необходимо знать центр колебаний

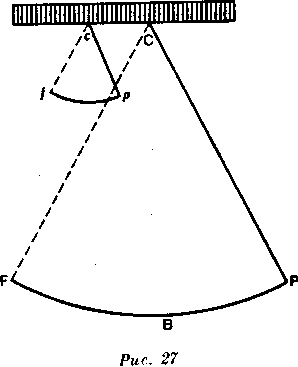
Но для того чтобы вымерить маятник, надо уметь определить центр колеба­ний, ведь длина маятника равна рас­стоянию от центра колебаний до центра подвешивания. Это один из труднейших вопросов. Всего того, что мы изучили до сих пор, недостаточно, чтобы научиться отыскивать точку, ко­торая и есть центр колебания. Ограничимся же тем, что составим понятие о данной проблеме.

Представим себе маятник СР (рис. 27) как рычаг, имеющий точку опоры в центре подвеса С, и, не учитывая силы тяготения рычагов, предположим, что вся тяжесть подвешенного тела сосредоточена в точке Р.

Предположим, что это тело упадет из Р в В со ско­ростью, пропорциональной массе, умноженной на расстоя­ние от центра тяжести до центра подвеса С, и центр колеба­ния будет тот же, что и центр тяжести. Если предположить то же относительно маятника ср, составляющего лишь одну четверть СР, центр колебания будет для него снова тот же, что и центр тяжести подвешенного тела. Итак, если эти два маятника совершают колебания по дугам, соотносящимся как окружности, частями которых они являются, то р дос­тигнет /, когда Р будет еще только в В; и р возвратится в точку, откуда оно вышло, когда Р достигнет F; р делает два колебания, в то время как Р делает одно, и если р затра­чивает полсекунды на каждое колебание, то Р затратит на каждое колебание целую секунду.

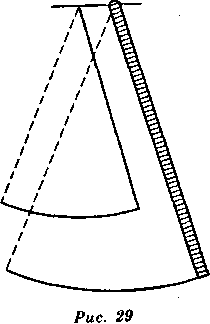
Вы также можете рассматривать (рис. 28) подвешен­ный рычаг АС, не учитывая силы тяготения, и, разделив его на четыре равные части, поместить на втором делении тело В весом в два ливра, а на конце — тело С весом тоже в два ливра.

Скорости В и С соотносятся как произведения их масс на их расстояние от А, и произведения будут 12. А ведь произведение массы на расстояние для тела весом в четыре ливра, помещенное в D, на третьем делении было бы тоже 12. Следовательно, колебания этого маятника будут происходить со скоростью, составляющей среднее арифме­тическое по отношению к скоростям В и С, как если бы вся тяжесть сосредоточивалась в D.

Из всех этих предположений Вам ясно, что, чем мень­шую тяжесть будет иметь нить по отношению к весу маят­ника, тем меньше поправок внесет сила тяготения рычага. Так именно и получается, когда тело значительного веса

подвешивают на очень тонкую стальную проволоку; наблю­дали, что маятник длиной 39,2 дюйма (в английской мере) от центра диска до точки подвеса совершает одно колебание в секунду и, следовательно, 3600 колебаний в час. Этот опыт был проведен с маятником весом 50 ливров, которому была придана чечсвицеобразная форма, чтобы уменьшить



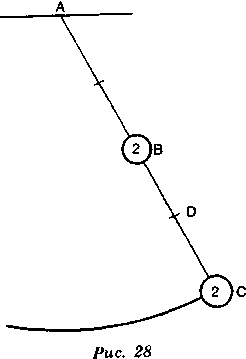
сопротивление воздуха; колебания продолжались целый день. Опыт (рис. 29) приблизительно показывает центр колебания бруска, однородного и имеющего одну и ту же плотность во всех своих частях, так как его колебания изохронны с колебаниями маятника, длина которого была бы равна третям длины бруска.

Предмет следующей книги

Я не склонен входить в дальнейшие подробности устройства механизмов. Принципов, изложенных мною, дос­таточно для объяснения того, как очевидность факта и оче­видность разума содействуют друг другу при достижении истины, и, поскольку эти принципы позволяют составить идею о системе планет, я дам Вам представление об этой системе в качестве нового примера рассуждений, ка­сающихся одновременно и очевидности факта, и очевидно­сти разума. Вы увидите, монсеньер, что вселенная — не что иное, как машина, подобная только что изученным нами; это — весы. Эта истина будет доказана Вам при помощи ряда теорем, тождественных теоремам второй книги.

КНИГА ТРЕТЬЯ

КАК ОЧЕВИДНОСТЬ ФАКТА

И ОЧЕВИДНОСТЬ РАЗУМА

ДОКАЗЫВАЮТ СИСТЕМУ НЬЮТОНА

тивоположном берегу и АВ — двое детей, играющих в во­лан в этой лодке. Итак, если за то время, пока волан пе­реходит из А в В, А вследствие движения лодки оказы­вается перемещенным в а и В в Ь, то В получит волан в Ь. Таким образом, под действием двух сил, направления которых образуют угол ВАа, волан прошел линию Аb —


ГЛАВА 1

О МЕТАТЕЛЬНОМ ДВИЖЕНИИ

(MOUVEMENT DE PROJECTION)


Действие

сопротивления

воздуха и силы

тяготения на снаряд,

выпущенный

горизонтально
Пушечное ядро, посланное горизон­тально, продолжало бы двигаться с одинаковой скоростью в одном и том же направлении, если бы ему не про­тиводействовала никакая причина. Но в то время как сопротивление воздуха уменьшает его скорость, сила, заставляющая его стремиться вниз, называемая силой тяготения, изменяет его направление. Если, предполагая, что ядро невесомо, мы будем учитывать лишь сопротивление воздуха, то мы пред­положим, что оно будет следовать своему первоначальному направлению, с каждым мгновением теряя скорость, так как оно не проложит себе путь, если не устранит частиц флюида, оказывающих ему сопротивление; оно не устранит их иначе, как придавая им движение, а сколько движе­ния оно им сообщит, столько его и потеряет. Следова­тельно, оно будет продвигаться все медленнее и наконец остановится в воздухе.

Но оно падает, потому что имеет вес; оно падает в каж­дое мгновение, так как не прекращает быть невесомым. Таким образом, с каждым мгновением оно отклоняется от горизонтального направления и описывает кривую. Это происходит оттого, что оно уступает в одно и то же время двум силам, направленным под углом друг к другу. Как же оно уступает этим двум силам? Какому закону оно подчиняется?

Этот снаряд

проходит диагональ

параллелограмма

в то же время,

в какое он прошел бы

одну из двух сторон

Для наглядности предположите (рис. 30), что TS — плоскость лодки, дви­жущейся в направлении TS по ка­налу HhgG.

Допустим, что dD — два неподвиж­ных предмета, например два дерева, которые находятся на берегу; Сс — два человека на про-



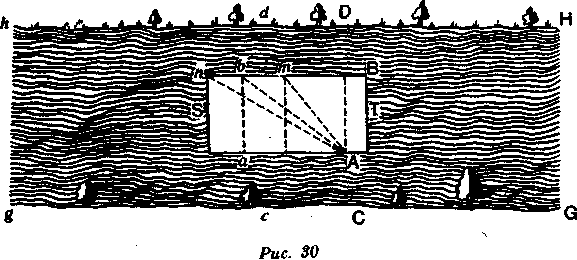
диагональ параллелограмма ABba; он прошел ее за та­кое же время, за какое он был бы перенесен из А в а, если бы не имел иного движения, кроме движения лодки, или за такое же время, за какое он был бы вытолкнут из А в В, если бы он имел лишь движение, сообщенное ему ракеткой в лодке, находящейся в покое.

Между тем волан кажется детям движущимся в направ­лении АВ, так как в то время, когда он попадает в Ь, дети находятся на линии ab, не замечая движения, в результате которого они переместились, и не сознавая того, что они принимают ab за АВ.

Но люди на берегу, находящиеся в Сс и устремляющие глаза на предметы dD, не могут спутать эти две линии и видят, что волан перешел из А в b.

Если, сохраняя прежнюю скорость волана, Вы увеличи­те или уменьшите скорость лодки, то диагональ будет прой­дена в такое же время, но она будет либо длиннее, либо короче. Если лодка движется быстрее, диагональ будет длиннее: она окончится, например, в точке п; если лодка движется медленнее, диагональ будет короче и окончится, например, в точке т.

Итак, мы можем обобщить этот закон: тело, приводимое в движение двумя силами, направленными под углом друг к другу, проходит диагональ параллелограмма за такое же

время, как если бы оно под воздействием одной из двух сил прошло одну из двух сторон.

Галилею возражали, что если бы Земля вращалась вокруг своей оси с запада на восток, то снаряд, выпущен­ный перпендикулярно горизонту, не упал бы в ту же точку, откуда поднялся, а упал бы, более или менее отклонившись к западу, в зависимости от того, насколько подвинулась бы эта точка к востоку за промежуток времени, который сна­ряд затратил бы, чтобы подняться и опуститься.

Это точно так, как если бы было сказано, что волан, бро­шенный из А к В, остался бы позади и упал бы за борт вне лодки; если бы, пока он двигался, лодка сама двигалась в направлении Аa.

Но волан подчиняется двум направлениям, поскольку он приводится в движение одновременно силой, приложенной к нему ракеткой, и силой, сообщаемой ему лодкой; так и предполагаемый снаряд имеет два направления: одно — перпендикулярное, которое мы ему придаем, другое — го­ризонтальное, сообщенное ему движением Земли. Стало быть, он должен подняться вдоль одной диагонали, по кото­рой он движется к востоку, и из наивысшей точки, достиг­нутой им, опуститься вдоль другой диагонали, которая также отклоняет его к востоку. Так и отвечал Галилей; в качестве доказательства он приводил тот факт, что на па­русном судне, как и на судне, стоящем на якоре, камень одинаково падает с верха мачты к ее подножию. Галилей справедливо полагал, что если камень падает перпендику­лярно, когда судно неподвижно, то, когда судно движется, он падает наклонно к горизонту и проходит диагональ па­раллелограмма, одна сторона которого равна расстоянию, пройденному судном, а другая — высоте мачты.

Итак, опыт доказывает, что тело, движимое двумя си­лами, направленными под углом друг к другу, проходит диагональ параллелограмма за такое же время, за которое оно прошло бы одну из его сторон. Теперь посмотрим, как, проходя ряд диагоналей, оно опишет кривую.

Проходя ряд

диагоналей, оно

описывает кривую

Пушечное ядро (рис. 31), приведен­ное в движение в горизонтальном направлении АВ, продолжало бы, как мы уже говорили, двигаться в данном направлении, если бы сила тяготения не отклоняла его в каждое мгновение; и если бы оно было вытолкнуто силой, способной придать ему скорость 4 фута в секунду, оно прошло бы в пять секунд 20 футов по линии АВ.

Точно так же, если, падая из А, это ядро приводилось бы в движение только той силой, которую оно получает от своего тяготения, оно продолжало бы двигаться в направле­нии АЕ, перпендикулярно горизонту, и, поскольку в пер­вую секунду оно прошло бы 1 фут, опускаясь из А в С, за пять секунд оно опустилось бы в Е, прошло бы 25 футов, поскольку это квадрат периодов времени.

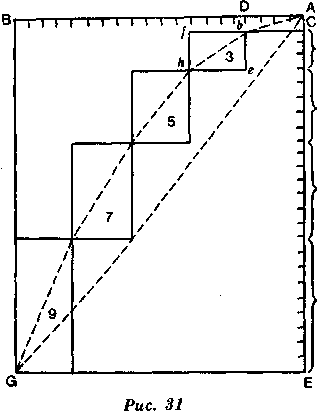
Но так как его при­водят в движение сразу две силы, из которых одна способна переме­стить его в В за то же время, за которое другая способна переместить его в Е, т. е. каждая за 5 се­кунд, оно подчинится обеим этим силам и, вместо того чтобы до­стичь В или Е, за 5 се­кунд упадет в G.

Если бы диагональ А параллелограмма ABGE представляла направле­ние падения, ядро слов­но проходило бы по пря­мой линии, но поскольку обе силы действуют каждое мгновение и в каждое мгно­вение каждая отклоняет ядро от того направления, ко­торое другая стремится ему придать, то очевидно, что мы приблизимся к описываемой ядром кривой лишь по мере того, как мы будем наблюдать его в самый короткий промежуток времени. Поэтому, если мы счи­таем, что ядро в А, толкаемое к С и к D, движется по диагонали Аb и что в 6, толкаемое к е и к /, оно движется по диагонали bh, и так далее вплоть до G, мы увидим, что оно движется по диагоналям 1, 3, 5, 7, 9, ряд которых обра­зует кривую, и нам становится ясно, что если бы мы на­блюдали движение ядра в более короткие промежутки времени, то каждая из этих диагоналей еще более искрив­лялась бы. Если бы это ядро (рис. 32) двигалось в направ­лении, наклонном к горизонту, как AI, то метательная сила заставила бы его пройти в равные промежутки рас­стояния АВ, ВС и т. д. Но так как сила притяжения заставляет его опускаться в каждое мгновение, оно будет

двигаться из А в Ь, вместо того чтобы двигаться из А в В. Следовательно, оно пройдет диагональ параллелограмма АВbа, сторона АВ которого представляет вытолкнувшую его силу, а сторона ВЬ, равная Аа, представляет силу тяготения.



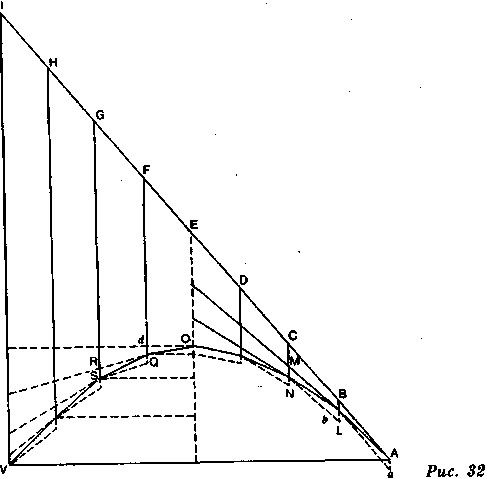
опустится так же, как и поднималось, т. е. от диагонали к диагонали, вплоть до низшей точки V. Значит, оно опишет кривую AOV за такое же время, за какое оно поднялось бы в I, если бы совершало только движение, вызванное вы­толкнувшей его силой.

Кривая, описываемая телом, брошенным горизонтально либо наклонно, называется параболой.

Таким образом, Вы можете представить себе параболу как ряд диагоналей, через которые проходит движущееся тело, когда оно одновременно подчиняется и выбросившей его метательной силе, и силе тяготения.

Вы можете заметить, что все сказанное нами в данной главе тождественно с какой-либо из двух теорем, доказы­ваемых наблюдением; первая: отрезки пути, пройденные падающим телом, равны квадратам времени; вторая: тело, приводимое в движение двумя силами, направленными под углом друг к другу, проходит диагональ параллелограмма в такое же время, в какое под действием одной из двух сил оно прошло бы одну из двух сторон. В сущности, мы лишь по-разному объясняем эти две теоремы, когда заключаем из этого, что тело, брошенное наклонно или горизонтально, описывает параболу. Вам надлежит освоиться с ними, что­бы с большей легкостью постичь их тождественность с дру­гими истинами, которые станут для Вас открытиями.

ГЛАВА II

ОБ ИЗМЕНЕНИИ, ПРОИСХОДЯЩЕМ С ДВИЖЕНИЕМ, КОГДА НОВАЯ СИЛА ПРИБАВЛЯЕТСЯ К ПЕРВОЙ

Точно так же, вместо того чтобы двигаться из Ь в М, подчиняясь лишь метательной силе, оно придет в N, так как подчиняется и силе тяготения, и пройдет диагональ парал­лелограмма bMNL. Таким образом, от диагонали до диаго­нали оно за четыре мгновения поднимется лишь на высоту точки О, вместо того чтобы подняться до Е, как это было бы, если бы оно двигалось под действием одной лишь метатель­ной силы. Итак, от О до Е шестнадцать отрезков пути, и это ровно столько, насколько оно должно опуститься за четыре промежутка времени, так как шестнадцать — квадрат четырех.

Но поскольку оно поднялось из А в О замедленным дви­жением, то из О в V оно опустится движением ускоренным. Вместо того чтобы двигаться из Q в R, оно будет двигаться из Q в S. Таким образом, под действием двух сил оно


Силы действуют

в одном и том же

направлении или

в различных

направлениях

Результат действия

сил, имеющих

одинаковое

направление
Две силы действуют либо в одном направлении, либо в противополож­ных направлениях, либо в направле­ниях, образующих угол. Надо рас­смотреть эти три случая. Пусть тело А направлено из А в L (рис. 33) с силой, способной заставить его пройти рас­стояние АВ в одну секунду; в сле­дующие секунды оно пройдет рас­стояние ВС, CD и т. д. потому, что все проходимые участки пространства равны первому. Если, когда оно находится в В, новая сила, равная пер­вой, действует на него в том же направлении, оно обретет двойную силу; значит, оно пройдет из В в D, из D в F за та-

кое же время, за какое оно прошло из А в В, т. е. оно прой­дет вдвое большую часть пространства в секунду, если добавленная вторая сила будет вдвое больше.

Результат действия сил, направления

которых противоположны

Если в то время, когда тело, движи­мое первой силой, проходит одинако­во АВ, ВС и т. д., на него будет дей­ствовать равная сила в обратном направлении LA, оно останется не­подвижным; так как эти две силы равны и противополож­ны, действие одной должно уничтожить действие другой. Если же последняя сила действует, лишь когда тело имеет тройную силу для прохождения трех отрезков пути за одну секунду, она уничтожит треть скорости. Следовательно, те­ло будет двигаться, как если бы оно подвергалось воздей­ствию лишь одной двойной силы в направлении AL, и оно пройдет лишь два отрезка пути в одну секунду. Наконец, если в то время, когда оно продвигается на три отрезка в секунду, на него будут действовать сразу две силы, равные первой, одна в направлении AL, а другая в направле­нии LA, оно будет продолжать двигаться с той же ско­ростью, так как результат двух новых сил будет равен ну­лю, поскольку они взаимоуничтожились. Таковы результа­ты действия сил, имеющих одинаковое направление, и сил, направленных в противоположные стороны.

А теперь посмотрим, что должно произойти в других случаях.

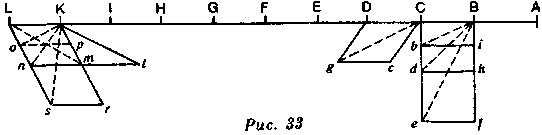
Скорость возрастает,

когда две силы

цействуют под прямым

углом друг к другу

Я предполагаю, что тело (рис. 33), двигаясь равномерно, проходит рас­стояние от А до В и от В до С за одну секунду и что новая сила, равная первой, действует на тело в В в на­правлении линии В/, перпендикулярной к AL; в данном случае эта сила действует под прямым углом к первой. Тело изменит направление и, как ясно из сказанного выше, опишет диагональ Bb. На том же основании, если бы новая сила была вдвое больше, тело описало бы диагональ Be,

а если бы она была вдвое меньше первой, тело описало бы лишь диагональ В/. Отсюда Вы видите, что, какова бы ни была новая сила, действующая под прямым углом, скорость тела непременно увеличится, так как оно проходит диаго­наль прямоугольного параллелограмма в такое же время, в какое под действием одной из двух сил оно бы прошло одну сторону этого параллелограмма. Одним словом, Вы увидите, что в предполагаемом нами случае предложения Скорость движущегося тела увеличится и Движущееся тело проходит диагональ прямоугольного параллелограм­ма идентичны. Вы увидите, что и следующие теоремы тождественны с указанными выше, и мне не нужно будет это подчеркивать.

Скорость возрастает

и тогда, когда силы

действуют под острым

углом

Если новая сила действует под ост­рым углом, то, как Вы понимаете, ее направление тем больше приближа­ется к направлению первой силы, чем острее угол. Отсюда мы делаем два вывода: что она уве­личит скорость и что она не увеличит ее так, как увели­чила бы, если бы действовала не под углом, т. е. в том же направлении.


Если вторая сила

образует с первой

тупой угол, скорость

либо останется

прежней, либо

уменьшится
Если, например, новая сила, равная первой, направлена по линии Сс, то DCc будет острым углом, образуемым дву­мя направлениями. Итак, чем острее данный угол, тем тупее gcC и тем больше диагональ Cg. Но ведь эта диаго­наль есть пройденный путь, и она выражает скорость тела. Следовательно, скорость увеличива­ется всякий раз, когда новая сила дей­ствует под прямым или острым углом, но, если новая сила действует под ту­пым углом, скорость либо останется прежней, либо слегка уменьшится. Предположим, что эта сила, равная первой, когда тело находится в К, действует в направлении Кm, тогда диаго­наль К« параллелограмма КLnm будет равна Km, так как параллелограмм разделен на два треугольника, стороны ко­торых равны. Тогда скорость тела останется прежней. Если бы новая сила была вдвое меньше первой, скорость тела уменьшилась бы, так как тогда [отрезок] Кр представ­лял бы новую силу и [отрезок] Ко, более короткий, нежели Кn, был бы пройденной диагональю.

Если новая сила вдвое больше и действует под тем же тупым углом (она изображается Кr), скорость, изображае­мая Ks, увеличится.

Если эта сила действует под более тупым углом и вслед­ствие этого в направлении более близком к противополож­ному, таком, как Кt, тело пройдет диагональ Km, равную KL, и, следовательно, его скорость не увеличится, несмотря на то что новая сила больше первой. Вы понимаете, что, если бы она была равна первой, скорость уменьшилась бы в той мере, в какой увеличился бы угол.

Положения данной

главы тождественны

с положениями

предыдущей

Все рассмотренные нами положения всего лишь различные приемы для выражения применительно к раз­личным случаям следующего положе­ния: движущееся тело пройдет диа­гональ, когда на него действуют две силы, направления которых образуют угол. Но рассмотренные выше положе­ния будут необходимы нам для уяснения других тожде­ственных им положений, т. е. других истин.

Закон, которому

подчиняется сила

тяготения, и закон,

которому подчиняется

тело, на которое

действуют две силы,

образующие угол,

окажутся

тождественными

со многими явлениями,

объясняемыми

в дальнейшем