Э. Кондильяк об искусстве рассуждения
| Вид материала | Документы |
- Тематика курсовых работ (доцент кафедры культурологи Н. Н. Гашева) Античные и библейские, 22.42kb.
- Урок на тему «Изображение пространства», 156.79kb.
- Конспект урока по развитию речи в 4 классе. Сочинение с элементами рассуждения «Что, 174.76kb.
- С, почему Лейбниц исключил из «Рассуждения о метафизике», построенного по плану типичного, 232.71kb.
- Н. К. Рерих об искусстве сборник статей, 2030.31kb.
- 5 класс Подготовка к сочинению-рассуждению «Для чего нужно заниматься спортом?», 124.23kb.
- Методические рекомендации к написанию сочинения-рассуждения егэ по русскому языку (часть, 201.83kb.
- Рекомендации по написанию сочинения-рассуждения, 39.14kb.
- Краткая история живописи, 99.09kb.
- Анализ текста как метод написания сочинения-рассуждения, 177.52kb.
Притяжение —
неизвестная причина
силы тяжести
Что мы разумеем под словом вес
Если тело, которое мы держим в руках, выпустить, оно упадет, и это явление Вы заметите во всех телах, находящихся вблизи Земли. Все они опускаются, если их не останавливает какое-либо препятствие. Вот это направление и есть так называемая сила тяжести. Это действие причины, нам неизвестной, которую мы назвали притяжением, так как мы предполагаем, что тело опускается не иначе как вследствие его притяжения к центру Земли. Под весом мы разумеем количество силы, с которой опускается тело. Полный вес тела — это совокупный вес всех частиц, его составляющих. Каждая из этих частиц — и когда они объединены, и когда они разъединены — имеет один и тот же вес; и данное тело может опускаться лишь так, как они опускались бы каждая в отдельности.
Вес подобен массе
Итак, два тела соотносятся по весу так же, как по массе, т. е. соответственно количеству содержащейся в них материи.
Тела должны падать
с одинаковой
скоростью
Из этого следует, что все тела падали бы с одинаковой скоростью, если бы не встречали сопротивления; это подтверждается опытом, В пустой камере и золотая монета и перо достигают дна в одно и то же время. Если в камеру впустить воздух, перо опустится медленнее, так как встретит большее сопротивление 19.
Но сопротивление
воздуха вносит
различия в скорость
их падения
Причиной этого явления оказывается тяжесть воздуха, поскольку воздух, как это будет доказано ниже, обладает весом. Вы понимаете, что перо может опускаться лишь потому, что оно разгоняет находящийся внизу воздух и понуждает его подняться и занять место вокруг него. Следовательно, падающее тело должно разогнать больше воздуха пропорционально своему большему объему, т. е. пропорционально большему пространству, им занимаемому.
Перо преодолевает большее сопротивление, чем золотая монета. Поэтому оно должно падать медленнее.
Как действует
притяжение,
наблюдаемое во всех
частях материи
Притяжение, которое Вы всегда рассматриваете как неизвестную причину тяжести, наблюдается во всех частях материи. Например, почему капля воды сферична? Потому что, раз все части притягиваются одинаково и взаимно, необходимо, чтобы они располагались в таком порядке, в каком они находятся на самом малом расстоянии друг от друга. А это возможно лишь при условии, что все точки поверхности помещены на том же расстоянии от центра, так как все они стремятся к общему центру.
Вы ясно увидите это притяжение, если сблизите две капли воды; как только они соприкоснутся, они сольются воедино. То же самое Вы сможете наблюдать в каплях расплавленного металла, и отсюда Вы сделаете вывод, что все их части взаимопритягиваются.
Если эти капли сплющиваются, соприкасаясь с плоской поверхностью,— это результат притяжения данной поверхности.
Представьте себе, что Земля и планеты подобны каплям воды, и Вам станет ясно, что все тола, из которых образованы Земля и планеты, и все тела, находящиеся на некотором расстоянии от их поверхности, тяготеют к общему центру. Вы предположите, что если двум каплям воды необходимо соприкоснуться для взаимопритяжения, то планеты, массы которых неизмеримо больше, взаимопритягиваются на больших расстояниях.
Итак, Вы узнаете, что всем телам свойственно взаимное притяжение, каковое Вам уже известно во всех частях одного тела. Отсюда явствует, что все тела и корпускулы, рассеянные во вселенной, тяготеют друг к другу; это называют всемирным тяготением.
Если Вы не всегда усматриваете это притяжение между всеми телами на поверхности Земли, то потому, что Земля, неизмеримо большая по массе, притягивает их с такой силой, что их взаимное притяжение становится незаметным. Есть философы, отвергающие тяготение,— это картезианцы. Их довод следующий: образовать для себя идею притяжения невозможно. Они стараются объяснить данное явление толчком, не замечая при этом, что толчок так же непонятен, как притяжение. Ньютонианцы, напротив, не отвергают толчка, но только отказываются понимать, каким образом толчок смог бы вызывать наблюдаемые нами явления. Однако нет необходимости вдаваться в этот спор. Для
53
52
Вас достаточно будет знать об этих возражениях и установить, способствуют ли они доказательству притяжения.
ГЛАВА V
ОБ УСКОРЕНИИ ДВИЖЕНИЯ
ПРИ ПАДЕНИИ ТЕЛ.
ПРОСТРАНСТВО, ПРОЙДЕННОЕ
В ПЕРВУЮ СЕКУНДУ
Замечено, что падающее тело (рис. 8) проходит одну английскую першу, или около 15 футов, в первую секунду; например, оно падает из А в В.
Предположение по данному вопросу
Если, рассматривая силу, заставляющую его опускаться из А в В, как толчок, данный в начале его падения, мы предполагаем, что тело впредь не получит иного толчка, то, значит, оно будет продолжать секунду за секундой опускаться на равные участки пространства — Bc, cd, dE, Е/ и т. д.— и число пройденных участков пространства будет равно числу секунд.
Но оно падает не так: видно, как его падение ускоряется от секунды к секунде. Мы, вероятно, ошиблись, полагая, что оно не получает новых толчков.
Другое предположение
В самом деле, если в точке А тяжесть, заставляющая тело падать в точку В, можно рассматривать как первый толчок, то в точке В она должна рассматриваться как второй толчок, поскольку в точке В тело получит второй толчок, равный первому. Но ведь два одинаковых толчка должны заставить его пройти двойное пространство. Значит, оно упадет из В в d за такое же время, за какое оно падало из А в В; и если бы оно не получило новых импульсов, оно продолжало бы проходить из секунды в секунду такие отрезки пространства, как df, fh, равные Bd. Но раз оно в В, в начале второго периода времени, получило второй толчок, то и в d, где начинается третий период времени, оно получит третий. Следовательно, оно пройдет пространство, равное тройному АВ. Оно опустится в третью секунду из d в g; а отрезки пути, проходимые из секунды в секунду, будут относиться друг к другу как числа 1, 2, 3, 4 и т. д.
Это было бы равномерно ускоренное движение, а так как мы склонны верить, что все происходит единообразно,
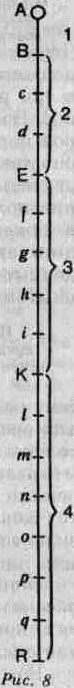
мы бы предположили, что именно так и ускоряется движение при падении тел. Но и это было бы ошибкой: наблюдение, являющееся для нас единственным правилом, ясно показывает, что ускорение увеличивается в другом соотношении; тело падает за три секунды из А в К (рис. 8), а, по нашим предположениям, оно должно было упасть лишь в g.
Как действует тяжесть
Мы предполагали, что, когда тело достигает точки В, тяжесть сообщает ему новый толчок, равный тому, какой она ему сообщила в точке А; и мы заключили, что оно падает из В в d за такое же время, за какое оно упало из А в В. Можно было бы предположить, что тяжесть действует лишь с интервалами,
притом только в начале каждой секунды; но такое предположение неверно. Раз тело не перестает быть тяжелым, тяжесть не прекращает своего действия.
Ее действие непрерывно или повторяется без интервалов в каждрй части секунды, и, следовательно, оно ускоряет движение в каждое мгновение. Тело же в начале своего падения не получает толчка для того, чтобы упасть в В за секунду: этот толчок оно получает последовательно, часть за частью; оно падает из А в В ускоренным движением.
Последнее предположение
Но поскольку мы не смогли бы представить себе закон этого ускорения в
столь краткое время, мы рассматриваем тяжесть, как если бы она воздействовала лишь в начале падения, и предполагаем, что толчок, побуждающий тело упасть из А в В, был дан сразу. Точно так же мы предполагаем, что, когда тело начинает падать из точки В, оно получает сразу второй толчок, равный первому, а поскольку оба толчка недостаточны для того, чтобы заставить его упасть так низко, как это показывает наблюдение, то не остается ничего иного, как предположить, что оно, падая, получает третий толчок, равный каждому из двух других.
54
55
В какой пропорции
возрастает сила,
которую сообщает
тяжесть
Итак, если первый толчок заставил пройти расстояние АВ (рис. 8) в первый период времени, то три толчка, каждый из которых равен первому, должны во второй период заставить пройти пространство в три раза большее, нежели АВ. И тогда тело опустится в Е. Но поскольку тело получило два новых толчка во второй период, я вправе предположить, что в третий период оно также получит два новых. Следовательно, его будут двигать пять толчков, и оно упадет в К. Наконец, я вправе предположить, что число импульсов увеличивается на 2 в каждый период времени и что между ними из секунды в секунду образуется пропорция 1, 3, 5, 7, 9 и т. д. Пройденные пути образуют ту же пропорцию. Это подтверждено опытом и согласуется с нашими предположениями.
Применение предположений в поисках истины
Мы различаем толчки, чтобы помочь нашему воображению, и мы их представляем возрастающими в числе в пропорции 1, 3, 5, 7, 9 и т. д. Между тем, поскольку первый толчок был сообщен постепенно, в то время, когда тело опускалось из А в В, то и два новых толчка также сообщаются постепенно и присоединяются к первому. И наконец, когда тело находится в Е, сила полученных им толчков равна силе трех предполагаемых нами толчков, и по существу уже не имеет значения, были ли эти силы сообщены ему одна за другой и каждая постепенно, или они были сообщены в три приема и каждая сразу. И опять-таки только в помощь нашему воображению я рассматриваю действие тяжести скорее как толчок, а не как притяжение; ведь для нее более привычно понятие силы толчка, нежели притягивающей силы.
Но, по правде сказать, метод, по которому мы только что рассуждали об ускорении движения при падении тел, не более чем нащупывание. Мы сделали предположение и ошиблись, затем мы сделали второе, чтобы исправить первое, и довели дело до того, что наши предположения оказались согласованными с опытом.
Вот пример поведения, на которое мы часто бываем обречены при изучении природы. Поскольку мы не всегда можем наблюдать точно с первого же раза и еще менее того способны отгадывать истину, мы блуждаем от предположений к ошибкам и от ошибок к предположениям, пока наконец не находим то, что ищем.
Именно так обыкновенно и делаются открытия. Прихо-
дилось строить предположения, подчас ошибочные, и эти ошибки бывали полезными, так как они вызывали необходимые дополнительные наблюдения и тем самым приводили к истине. Но когда истина найдена, ее доказывают" не предположения, а их согласованность с наблюдением и скорее даже само наблюдение 20.
Закон ускорения
движения при падении тел
Если бы явления не доказывали закона, которому подчинено ускорение при падении тел, не было бы уверенности в выводах, которые мы сделали о такой малоизученной причине, как тяжесть. Итак, доказано, больше наблюдениями, нежели нашими рассуждениями, что движение падающего тела ускоряется таким образом, что проходимые в равные промежутки времени части пространства соотносятся как числа 1, 3, 5, 7 и т. д. *
Сумма пройденных
частей пространства
равна квадрату
времени
Узнав этот закон, Вы увидите, что имеется соотношение между периодами времени и пройденными частями пространства, и легко заметите, что сумма частей пространства равна квадрату времени, т. е. числу единиц времени, помноженному само на себя. Например, тело, падающее за четыре секунды, проходит 16 першей, так как 16 есть квадрат четырех, или произведение числа 4, перемноженного само на себя.
Как можно узнать, на какую высоту поднялся снаряд
Вы заметите также, что, если тело метнуть в воздух, тяжесть должна замедлить движение в той же пропорции, в какой она ускоряет его при падении тела. Если в первую секунду поднимающееся тело проходит 7 футов, то во вторую оно пройдет 5 футов, в третью — 3 фута, а в четвертую — 1 фут.
В тот же промежуток времени оно, поднимаясь, теряет то же количество силы, какое оно приобрело бы, падая.
* Эту истину доказывают при помощи теории Галилея и другими методами, еще менее доступными читателям. Мне же нужен сам факт, и я довольствовался тем, чтобы сделать его наглядным путем предположения.
Отсюда можно узнать, на какую высоту поднялся снаряд наподобие бомбы. Надо лишь установить наблюдением число секунд, истекших с момента запала мортиры до момента падения бомбы; половина этого числа будет временем падения. Итак, квадрат времени равен числу футов. Если это время — 10, то бомба поднялась на 100 футов.
57
56
ГЛАВА VI О ВЕСАХ
Когда плечи коромысла
колеблются
относительно его
центра, то скорости
различных точек плеч
коромысла относятся
друг к другу так же,
как их расстояния
от центра
Предположим, что на прямую АВ (рис. 9) мы нанесли с обеих сторон несколько точек на равном расстоянии от центра. Если данная прямая движется относительно центра, то эти точки опишут дуги, которые будут иметь различную для разных точек длину. Эти дуги будут частями пространства, пройденными в одно и то же время всеми точками. А ведь мы уже видели, что пройденные части пространства равны произведению времени на скорость.
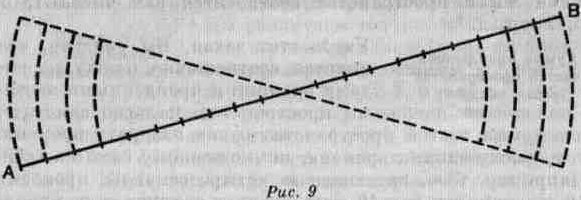
Время одинаково для всех точек, и поэтому скорости относятся друг к другу как части пространства и, следовательно, как расстояния от центра.
Сила, действующая
на тела, подвешенные
в этих точках, равна
произведению массы
на расстояние
Подвесим тела к этим точкам. Известно, что сила есть произведение массы на скорость. Вы только что видели, что скорости здесь относятся друг к другу, как расстояния. Сила, с которой каждое из этих тел будет стремиться вниз, будет пропорциональна произведению его массы на его расстояние от центра.
Случай, когда возникает равновесие
Предположим, что два тела равной массы (рис. 10) находятся на
равном расстоянии [от центра], например, в точке 10; они будут воздействовать одно на другое с одинаковой силой. А приложит к В точно такое же усилие, чтобы его поднять, какое В приложит к А. Поэтому ни одно из них не поднимется и не опустится. Это случай равновесия. Если, уменьшив массу А наполовину, мы поместим его на двойное расстояние, например в точку 6, в то время как В
находится в точке 3, оно выиграет в силе путем увеличения расстояния столько, сколько оно потеряло за счет уменьшения своей массы. И здесь также будет равновесие. Тела, подвешенные таким образом, называются грузами. Итак, грузы находятся в равновесии, когда их массы равны и они расположены на равном расстоянии от центра; если же их
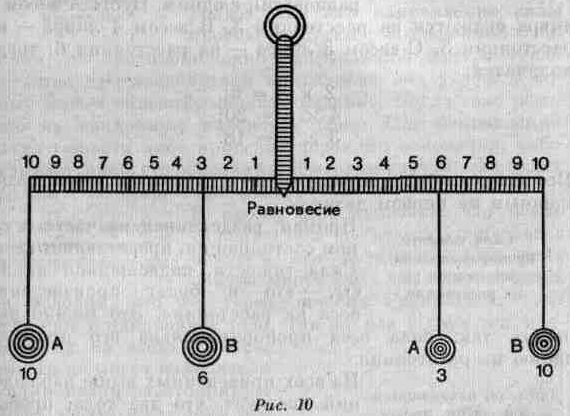
массы неравны — когда масса большего относится к массе меньшего, как расстояние меньшего к расстоянию большего. Равновесие между В, масса которого 6, и А, масса которого 3, возникнет лишь тогда, когда расстояние от В будет 3, а расстояние от А будет 6.
Случай, когда равновесие нарушается
Отсюда следует, что в случае равновесия произведение веса на расстояние остается и с той и с другой стороны одинаковым и что равновесие
нарушается, когда произведения разные. Произведение остается тем же, умножают ли 3 массы на расстояние 6 либо 6 масс на расстояние 3, и А уравновешивается с В. Но если изменить расстояние одного из них, произведение изменится и равновесие нарушится. Вы видите, что силы взаимно соотносятся так же, как произведения. Если А весом 4 ливра находится на четвертом делении, оно будет иметь силу, равную силе [тела] В весом 16 ливров, которое я подвешу на первое деление, потому что 1 умножить на 16,
59
58
как и 4 умножить на 4, равно 16. Если пододвинуть А ко второму делению, то его сила будет относиться к силе В как 1 к 16, так как 2 умножить на 4 равно 8, и равновесия не будет.
Несколько тел в равновесии с одним
Таким образом, Вам стало ясно, что несколько грузов могут оказаться в равновесии с одним. Пусть А весом 2 ливра окажется на расстоянии 3, В весом 4 ливра — на расстоянии 5, С весом 3 ливра — на расстоянии 6; тогда получится:
2 X 3 = 6; 4 X 5 = 20; 3 X 6 = 18.
Все эти тела будут в равновесии с грузом 44 ливра, помещенным на первом делении.
Сила тяжести пропорциональна произведению веса на расстояние
Прямая, разделенная на части в таком соотношении, представляет весы. Сила тяжести, подвешенной на весы, — это и будет произведение веса на расстояние. Это можно выразить так: сила веса пропорциональна его произведению на расстояние.
Два тела, находящиеся
в равновесии, имеют
один и тот же центр
тяжести
Все части шара
находятся
в равновесии
относительно одного
и того же центра
Из всех приведенных выше наблюдений явствует, что два тела, пребывающие в равновесии, имеют один и тот же центр тяжести и что вследствие этого они могут опуститься лишь при условии, что опустится их центр тяжести. Из этого Вам ясно, почему шар, помещенный на горизонтальной плоскости, остается неподвижным, хотя он касается лишь одной точки. Это происходит потому, что центр тяжести, вокруг которого все части находятся в равновесии, поддерживается этой плоскостью. Если бы не было равновесия, шар вращался бы, пока центр тяжести не расположился бы сколь возможно ниже.
Вес тела как бы
целиком собран
в его центре тяжести
Вы можете вывести заключение, что тело подпирается в точке, поддерживающей его центр тяжести, и Вы представите себе как бы собранной в этом центре всю силу, с которой оно стремится к Земле.
Направление центра тяжести
Направление центра тяжести вертикально, т. е. перпендикулярно к горизонту, и эта тяжесть исчезает в центре тяжести Земли.
Падение тела
по наклонной
плоскости
Вы понимаете, что, если поместить тело на наклонную плоскость, оно упадет, так как направление силы противодействия, создаваемой наклоном, не противоположно направлению центра тяжести. Сила противодействия направлена под углом и поэтому может только замедлить падение. Когда тело помещено на наклонную плоскость (рис. 11), направление центра тяжести либо проходит через его основание, либо оказывается вне его основания. В первом случае тело будет скользить, во втором оно покатится.
Различие между
центром тяжести
и центром величины
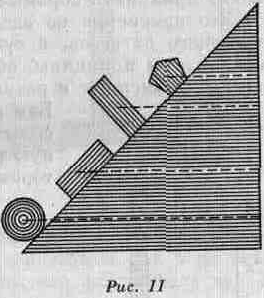
Я прошу Вас отметить, что центр тяжести тела не всегда совпадает с центром его величины. Оба этих центра могут быть совмещены лишь при условии, что это геометрически правильное, симметричное и однородное тело. Так же как у двух тел, подвешенных на весах, центры тяжести не могут находиться на одинаковом расстоянии от центра коромысла, если эти тела не равны между собой, так и части тела смогут быть в равновесии вокруг центра его величины только при условии тождественности массы и расстояний соответствующих частей этого тела. А ведь такое условие выполнимо, лишь если это геометрически правильное, симметричное и однородное тело. В данной главе очевидна тождественность всех положений, выводимых друг из друга. Следовательно, они доказаны в силу очевидности разума. Ведь все теоремы [данной главы] — это по сути одна и та же теорема, но выражена она различно. Рычаг, колесо, ворот и прочие механизмы, о которых мы еще будем говорить,— все это те же весы, по-разному устроенные. Вполне достаточно будет освоиться с проведенными нами наблюдениями над
60
61
весами, для того чтобы при беглом чтении понять последующие главы, где речь идет о рычаге, колесе и т. п., но если плохо усвоить, что представляют собой весы, трудно будет рассуждать о прочих машинах.
ГЛАВА VII О РЫЧАГЕ
Машины для рук суть то же, что методы для ума
Мы видели, как, придавая различные формы какому-нибудь положению, наш разум открывает истины, которых он [сам по себе] не усмотрел бы; точно так же при различном устройстве весов наша рука поднимает тела, которых она не смогла бы сдвинуть: машины для рук суть то же, что методы для ума.
Рычаг в сущности
тот же механизм,
что и весы
Рычаг, изображенный на рис. 12 линией АВ, поддерживается на подпорке С, вместо того чтобы быть подвешенным, как коромысло весов. Из точки подвеса мы делаем точку опоры, для того чтобы применить коромысло для других целей.
Это изменение не сделает из коромысла механизма, отличного от весов; в сущности, здесь остается тот же механизм, а принципы, объясняющие результаты работы одного, объясняют и результаты работы другого.
Принципы и для одного и для другого остаются те же
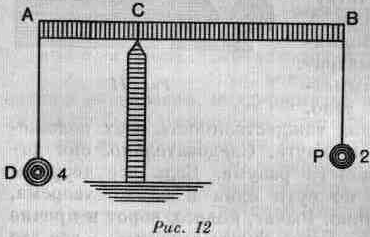
Вам понятно, что при малой затрате силы Вы сможете поднять значительную тяжесть, если расстояние, на котором Вы находитесь от точки опоры, относится к расстоянию до места нахождения тяжести так же, как сила этой тяжести относится к силе, Вами приложенной, или если произведение силы на расстояние одной части равно произведению силы на расстояние другой. Силой, способной удержать один ливр, Вы поднимете тяжесть в 100 ливров, находящуюся на расстоянии одного дюй-
ма, если будете действовать на расстоянии 100 дюймов.
Пусть прямая АВ (рис. 12) движется на своей опоре; тогда дуги, описываемые различными точками, пропорциональны их расстояниям от точки опоры. Скорости и, следовательно, приложенные к этим точкам силы будут пропорциональны расстояниям от опоры. Пусть тяжесть D, равная 4, будет помещена в точке, находящейся на расстоянии 2; сила, равная 2, будет в равновесии, так как она прилагается на расстоянии 4. Закон гласит, что равновесие устанавливается, когда произведение силы на расстояние одинаково и с той и с другой стороны, либо, что то же самое, когда D относится к Р, как расстояние от Р относится к расстоянию от D.
Следовательно, сила Р может быть тем меньшей, чем ближе к точке опоры будет находиться D.
Сочетая несколько рычагов, получают такой же результат, прилагая меньшую силу. На рис. 13 Вы видите три
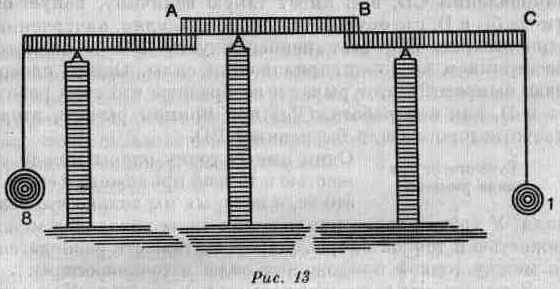
рычага; понятно, что если сила, для того чтобы быть в равновесии с тяжестью 8, должна действовать как 4 на точку А, то достаточно будет, чтобы она действовала как 2 на точку В и как 1 на точку С.
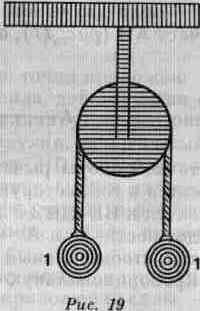
Если прибавить еще один блок, то вес одного ливра удержит вес в 32 ливра, и Вы понимаете, что одна и та же сила поддержит и больший груз, по мере того как будет увеличено число блоков.
Соображения об изогнутых рычагах
Правило для изогнутых рычагов то же, что и для других (рис. 14), т. е. равновесие устанавливается, когда расстояние до точки приложения силы так относится к рас-
63
62
стоянию до тяжести, как величина тяжести — к величине движущей силы. Но здесь следует привести некоторое дополнительное соображение. Возьмем, например, рычаг ABC, где В — точка опоры, a D — движущая сила.
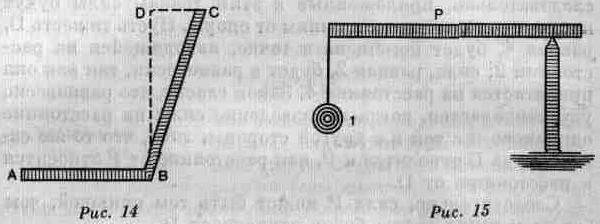
Вы бы ошиблись, приняв расстояние до точки приложения силы за длину линии ВС, потому что сила, действующая в направлении CD, в С имеет такую величину, какую она имела бы в D, где опускается перпендикуляр, начерченный относительно DC; этот перпендикуляр BD и является расстоянием до точки приложения силы. Одним словом, надо выпрямить этот рычаг и вообразить, что сила работает в D, как она работала бы при прямом рычаге, второе плечо которого было бы равным BD.
Существует три вида рычагов
Одни имеют точку опоры между тяжестью и точкой приложения силы — это те, о которых мы только что говорили. У других точка приложения силы находится между тяжестью и точкой опоры, у третьих тяжесть располагается между точкой приложения силы и точкой опоры.
В рычаге, где точка приложения силы (рис. 15) расположена между тяжестью и точкой опоры, если она нахо-
дится на расстоянии 1 от этой точки, когда тяжесть в один ливр находится на расстоянии 8, для установления равновесия необходимо, чтобы она была равна 8, а если переместить ее на 2, надо, чтобы она была равна 4.
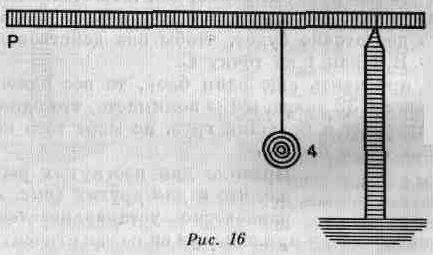
В рычаге, где тяжесть (рис. 16) находится между точкой приложения силы и точкой опоры, если тяжесть равна 4, находится на расстоянии 2, сила, равная 1, будет уравновешена на расстоянии 8. Но если ее переместить на 4, то надо будет, чтобы она была равна 2. Одним словом, закон таков, что сила относится к тяжести, как расстояние до этой тяжести относится к расстоянию до точки приложения силы.
Если два человека несут тяжесть, подвешенную к рычагу АВ (рис. 17), один по отношению к другому является
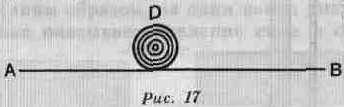
точкой опоры рычага, а та часть, которую несет В, относится к той, которую несет А, как AD к BD. Если AD относится к BD как 2 к 3 и если тяжесть равна 50 ливрам, В будет нести 20, а А — 30. Значит, можно поместить тяжесть так, чтобы сильный человек и ребенок несли каждый часть, пропорциональную своим силам.
ГЛАВА VIII О ВОРОТЕ
Ворот состоит
из множества
рычагов, вращающихся
вокруг точки опоры
Рычаг поднимает грузы лишь на небольшую высоту. Когда желают поднять их выше, пользуются воротом (рис. 18). Сила действует на периметр; поэтому спицы представляют для Вас плечи весов, а длина этих спиц является расстоянием, на которое сила отдалена от точки опоры.
относится
к расстоянию до точки
приложения силы,
как половина
диаметра вала
относится к спице
ворота
Расстояние до груза Вокруг вала, вращающегося вместе с воротом, наматывается веревка, на которую подвешивают груз. Полудиаметром вала становится расстояние, на которое груз отстоит от точки опоры. Равновесие получится, когда спица будет относиться к полудиаметру, как груз к силе. Например, один ливр, находя-
64
65
Но груз удаляется
от точки опоры,
по мере того как он
поднимается
щийся на краю спицы в 10 футов, уравновесит груз в 10 ливров, если полудиаметр вала равен одному футу. Вы заметите, что, по мере того как груз поднимается, требуется все большая сила, чтобы его удержать, потому что бечевка, наматываясь, увеличивает диаметр оси и, следовательно, груз оказывается на большем расстоянии от точки опоры.