Geum.ru

Учебно-методический комплекс для студентов, обучающихся по специальности 080102. 65 «Мировая экономика» Москва 2008

Вид материалаУчебно-методический комплекс
Тема 1.2. Конверсия валюты и нара­щение процентов.
Тема 1.3. Наращение процентов и налоги.
Тема 1.4. Наращение процентов и инфляция.
Тема 1.5. Математическая модель динамики внешнего долга с учетом инфляции и конверсии.
Раздел 2. Анализ потоков платежей
Тема 2.1. Наращенная сумма потока платежей.
Тема 2.2. Современная стоимость потока платежей.
Раздел 3. Математические модели оценки основных
Тема 3.1. Модели оценки облигаций.
Тема 3.2. Модели оценки акций.
Раздел 4. Математические модели формирования оптимальной структуры портфеля ценных бумаг
Тема 4.1. Вероятностные характеристики доходности ценных бумаг.
Тема 4.2. Вероятностные характеристики портфеля.
Тема 4.3. Модель Марковица.
Тема 4.4. Модель Тобина.
Раздел 5. Математические модели равновесия на конкурентном
Тема 5.1. Модель ценообразования на рынке капиталовложений (САРМ).
Тема 5.2. Цены равновесия на идеальном рынке.
Раздел 6. Моделирование динамики финансовых показателей
Тема 6.1. Модели стационарных временных рядов.
...
Полное содержание
Подобный материал:
1   2   3
Тема 1.1. Характеристики простейших финансовых операций. Операции на­ращения и дисконтирования. Процентные ставки и методы их начисления: простые и сложные процентные ставки, ставки наращения и учетные став­ки, дискретные и непре­рывные ставки и дисконты. Эффективная процентная ставка. Условия международного валютного паритета: паритет процентных ставок.

Тема 1.2. Конверсия валюты и нара­щение процентов. Конверсия валюты и нара­щение простых процентов. Определение критического значения темпа роста курса валюты для операции наращения по схеме простых процентов. Оптимизация операции наращения по схеме простых процентов. Конверсия валюты и нара­щение сложных процентов. Определение критического значения темпа роста курса валюты для операции наращения по схеме сложных процентов. Оптимизация операции наращения по схеме сложных процентов.

Тема 1.3. Наращение процентов и налоги. Международная практика налогообложения процентов от операции наращения. Начисление налогов на простые проценты от операции наращения. Реальные процентные ставки с учетом выплаты налога. Варианты начисления налогов на сложные проценты в долгосрочных финансовых операциях.

Тема 1.4. Наращение процентов и инфляция. Количественные характеристики инфляции: покупательная способность денег, индекс цен, темп инфляции. Влияние инфляции на наращенную сумму: наращение по схеме простых процентов, наращение по схеме сложных процентов. Эффект Фишера. Условия международного валютного паритета: паритет покупательной способности валют.

Тема 1.5. Математическая модель динамики внешнего долга с учетом инфляции и конверсии. Структура бюджетного дефицита. Механизмы урегулирования задолженности: конвертирование части внешнего долга в национальную валюту; списание части внутреннего долга. Спецификация модели с учетом конверсии. Спецификация модели с учетом инфляции. Анализ модели.

Раздел 2. Анализ потоков платежей

Современные финансовые операции обычно осуществляются не отдельными платежами, а некоторой их последовательностью во време­ни — потоком платежей. Например, периодическое поступление доходов от инвестиций, выплата пенсий, дивидендов, и т.д. Потоки платежей применяются при расчетах по внешнеэкономическим займам и кредитам. Обобщающие количественные характеристики потоков платежей (наращенная сумма, современная стоимость) позволяют лучше понять механизм долгосрочных финансовых операций.

Тема 2.1. Наращенная сумма потока платежей. Классификация потоков пла­тежей. Параметры финансовых рент. Определение наращенной суммы срочного аннуитета постнумерандо. Определение наращенной суммы срочного аннуитета пренумерандо. Определение наращенной суммы потока общего вида.

Тема 2.2. Современная стоимость потока платежей. Определение современной стоимости срочного аннуитета постнумерандо. Определение современной стоимости срочного аннуитета пренумерандо. Определение современной стоимости потока общего вида. Чистая приведенная величина. Вычисление эффектив­ной ставки методом последовательных приближений.


Раздел 3. Математические модели оценки основных

финансовых инструментов

В условиях рыночной экономики фондовый рынок приобретает ведущее значение в системе финансовых рынков. Процессы секьюритизации затронули большинство стран мира. Фондовые рынки превращаются в один из важнейших источников инвестиционных ресурсов, как для фирм развитых стран, так и для финансирования проектов в развивающихся государствах. Финансовые операции, связанные с ценными бумагами, относятся к рисковым операциям. Неопределенность эффективности операций на фондовых рынках требует привлечения аппарата прогнозирования (оценки) количественных характеристик финансовых инструментов. Основное внимание в данном разделе уделяется детерминированным моделям оценки основных финансовых инструментов и анализу эффективности операций с ними.

Тема 3.1. Модели оценки облигаций. Основные параметры и виды облигаций. Количественный анализ облигаций: расчет доходности и определение текущей цены для основных видов облигаций (бессрочных облигаций, облигаций с нулевым купоном, сберегательных облигаций, облигаций общего типа). Анализ влияния различных факторов на оценку облигаций. Характеристики поступления средств от облигации и измерение риска. Дю­рация.

Тема 3.2. Модели оценки акций. Классификация акций. Модели оценки привилегированных акций. Мо­дели оценки обыкновенных акций с равномерно возрастающими дивидендами (мо­дель Гордона). Модель оценки обыкновенных акций с изменяющимся темпом при­роста дивидендов. Моделирование влияния дивидендной политики фирмы на доходность акций.


Раздел 4. Математические модели формирования оптимальной структуры портфеля ценных бумаг

Современная теория инвестиций при исследовании влияния риска на принятие инвестиционных решений, опирается на теорию вероятностей и математическую статистику. Диверсификация портфеля, выполненная с учетом структуры ковариационной матрицы доходностей ценных бумаг, позволяет существенно снизить риск портфеля по сравнению с риском включенных в него ценных бумаг. В данном разделе рассматриваются две фундаментальные модели формирования оптимальной структуры портфеля ценных бумаг: модель Г. Марковица и модель Дж. Тобина.

Тема 4.1. Вероятностные характеристики доходности ценных бумаг. Факторы, определяющие доходность ценных бумаг. Математическое ожидание доходности. Дисперсия доходности. Коэффициент вариации доходности. Ковариация и корреляция между доходностями двух ценных бумаг. Правила доминирования рационального инвестора.

Тема 4.2. Вероятностные характеристики портфеля. Портфель ценных бумаг и его вероятностные характеристики. Доходность портфеля. Ожидаемая доходность портфеля. Дисперсия портфеля. Мера риска в портфельной теории. Влияние корреляции доходностей финансовых инструментов на риск портфеля ценных бумаг. Случай пря­мой корреляции. Случай полной обратной корреляции. Диверсификация портфеля.

Тема 4.3. Модель Марковица. Эффективная диверсификация портфеля по Марковицу. Спецификация модели. Определение оптимальной структуры рискового портфеля ценных бумаг. Дисперсия оптимального портфеля. Зависимость "риск-доходность" для рискового портфеля.

Тема 4.4. Модель Тобина. Распределение капитала между рис­ковыми и безрисковыми вложениями. Спецификация модели. Определение оптимальной структуры комбинированного портфеля ценных бумаг. Структура рисковой части комбинированного портфеля. Дисперсия оптимального портфеля. Зависимость "риск-доходность" для комбинированного портфеля.

Раздел 5. Математические модели равновесия на конкурентном

финансовом рынке

Взаимодействие спроса и предложения на конкурентном финансовом рынке приводит к состоянию равновесия. Состояние равновесия характеризуется равновесными ценами и объемами сделок. В классической теории равновесия, основоположником которой является Л. Вальрас, не учитывается риск, связанный с финансовыми операциями. В данном разделе рассматривается одна из простейших моделей равновесия конкурентного финансового рынка — модель САРМ (Capital Asset Prising Model), позволяющая оценить доходности ценных бумаг с учетом фактора риска.

Тема 5.1. Модель ценообразования на рынке капиталовложений (САРМ). Мера риска в модели САРМ. Коэффициент "бета" доходности ценной бумаги. Коэффициент "бета" портфеля ценных бумаг. Предпосылки модели. Вывод основного уравнения модели.

Тема 5.2. Цены равновесия на идеальном рынке. Моделирование оптимальной структуры портфеля ценных бумаг с учетом склонности инвестора к риску. Функция полезности модели. Модель равновесных цен в условиях неопределенности.

Раздел 6. Моделирование динамики финансовых показателей

При моделировании динамики финансовых показателей широкое применение нашли модели временных рядов. Примерами временных рядов могут быть финансовые индексы, ежедневные курсы валют, котировки акций, годовые объемы продаж, деловая активность и т.д., т.е. переменные, значения которых изменяются со временем. Наибольшую популярность среди моделей временных рядов нашли линейные модели (авторегрессионные, скользящего среднего, авторегрессии-скользящего среднего), что объясняется их простотой и высокой степенью аппроксимации широкого класса стационарных временных рядов при небольшом числе параметров.

Тема 6.1. Модели стационарных временных рядов. Определение стационарного временного ряда. Основные инструменты анализа временного ряда: автоковариационная и автокорреляционная функции, дисперсия, частная автокорреляционная функция. Авторегрессионные модели. Модели скользящего среднего. Смешанные модели авторегрессии-скользящего среднего.

Тема 6.2. Модели нестационарных временных рядов. Модель авторегрессии проинтегрированного скользящего среднего. Прогнозирование курсов акций и курсов валют по моделям нестационарных временных рядов.

Тематика и планы практических занятий

Занятие 1 (2 часа). Конверсия валюты и наращение процентов. Схемы операции совмещения наращения процентов и конверсии валюты. Определение критического значения темпа роста курса валюты для операции совмещения по схеме простых и сложных процентов. Оптимизация операции наращения.

Занятие 2 (2 часа). Наращение процентов с учетом налогов и инфляции. Начисление налогов на простые проценты от операции наращения. Варианты начисления налогов на сложные проценты в долгосрочных финансовых операциях. Влияние инфляции на наращенную сумму: наращение по схеме простых процентов, наращение по схеме сложных процентов.

Занятие 3 (2 часа). Наращенная сумма и современная стоимость потока платежей. Параметры p-срочных и m- срочных финансовых рент. Схемы потоков платежей. Определение наращенной суммы p-срочных и m- срочных рент. Определение современной стоимости p-срочных и m- срочных рент. Чистая приведенная величина.

Занятие 4 (2 часа). Модели оценки облигаций. Основные параметры и виды облигаций. Количественный анализ облигаций: расчет доходности и определение текущей цены для основных видов облигаций.

Модели оценки акций. Модели оценки привилегированных акций. Мо­дели оценки обыкновенных акций с равномерно возрастающими дивидендами (мо­дель Гордона). Модель оценки обыкновенных акций с изменяющимся темпом при­роста дивидендов.

Занятие 5 (2 часа). Контрольная работа.

Занятие 6 (2 часа). Вероятностные характеристики доходности ценных бумаг и портфеля ценных бумаг. Математическое ожидание, дисперсия, ковариационная матрица доходностей ценных бумаг.

Модель Марковица. Определение оптимальной структуры рискового портфеля ценных бумаг.

Занятие 7. (2 часа). Модель Тобина. Зависимость "риск-доходность" для комбинированного портфеля.

Модель ценообразования на рынке капиталовложений (САРМ). Зависимость доходности ценной бумаги, включенной в портфель, от степени ее риска. Определение коэффициента "бета" доходности ценной бумаги. Определение коэффициента "бета" портфеля ценных бумаг.

Занятие 8 (2 часа). Модели временных рядов. Авторегрессионные модели. Модели скользящего среднего. Прогнозирование курсов акций и курсов валют по моделям временных рядов.


Задания для самостоятельной работы

Задание 1. Конверсия валюты и наращение процентов

Операция совмещения объединяет операцию наращения (по схеме простых процентов) и конверсию валюты. Последовательность операции совмещения приведена на схеме:

руб. ® СКВ® СКВ® руб. ,

или, в принятых обозначениях (см. исходные данные)

.

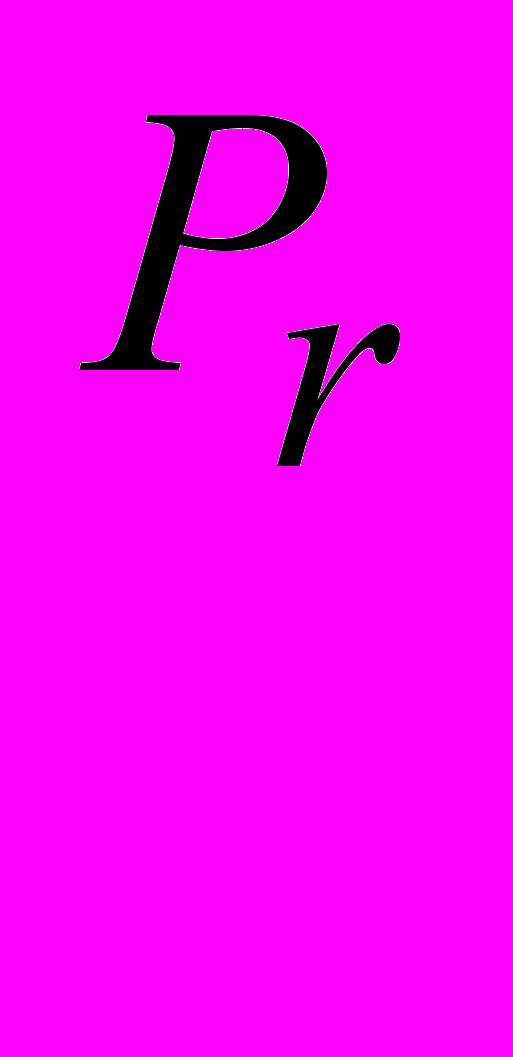
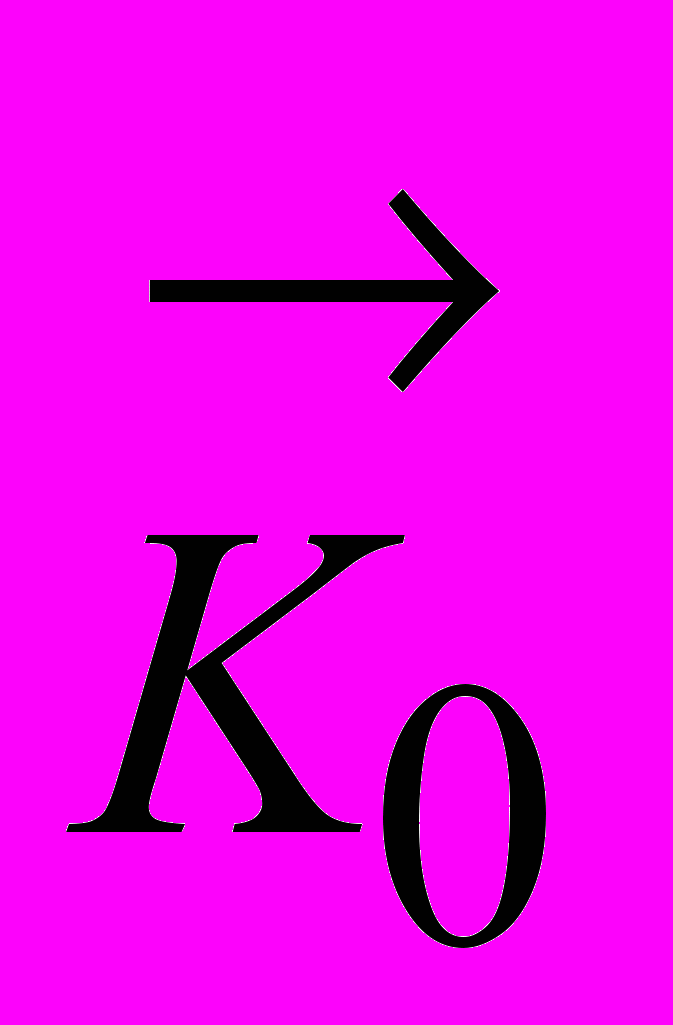
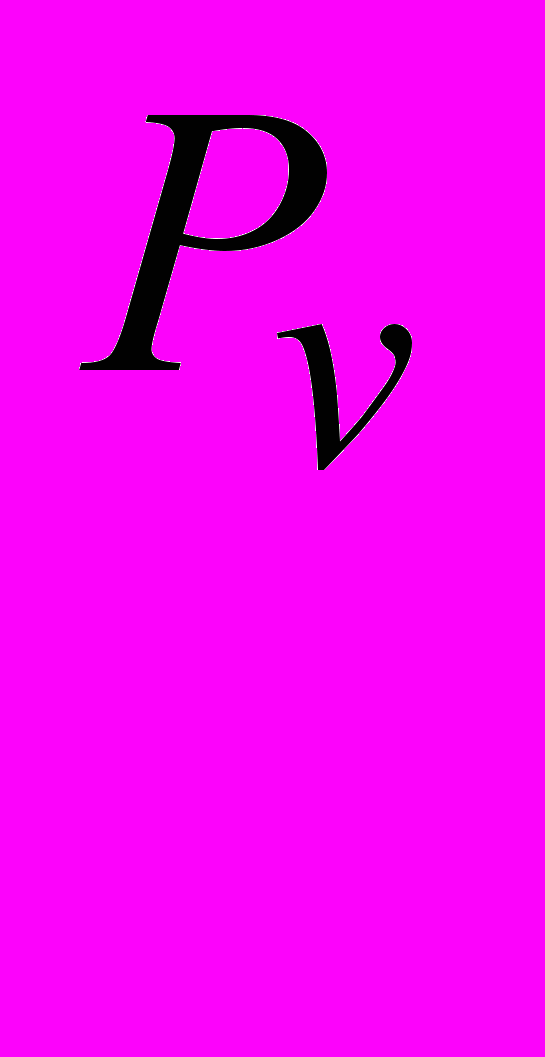
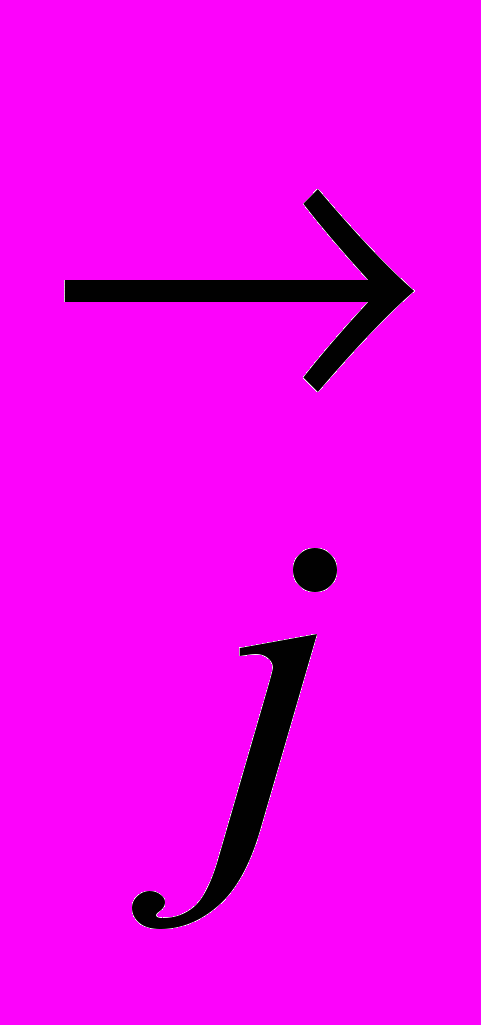
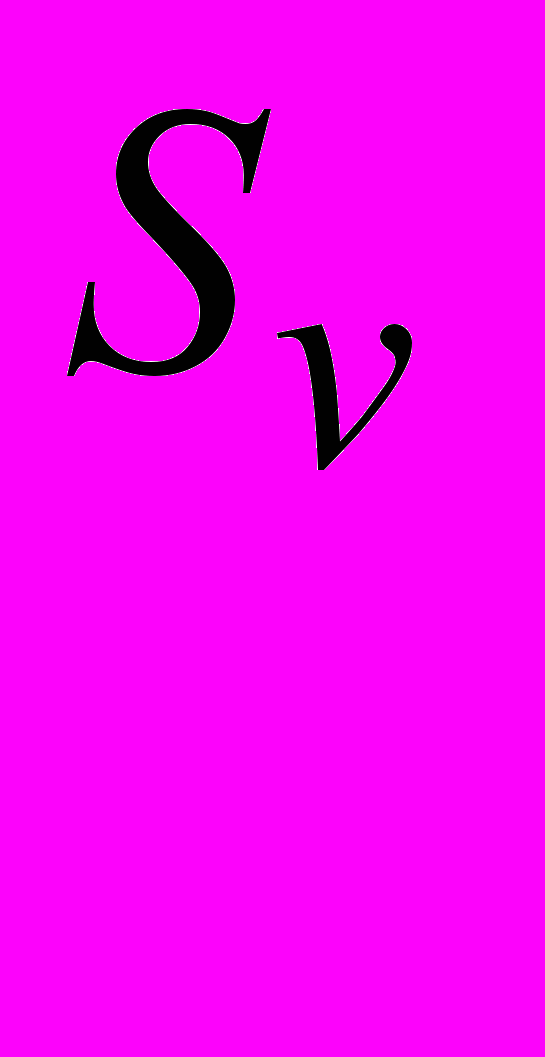
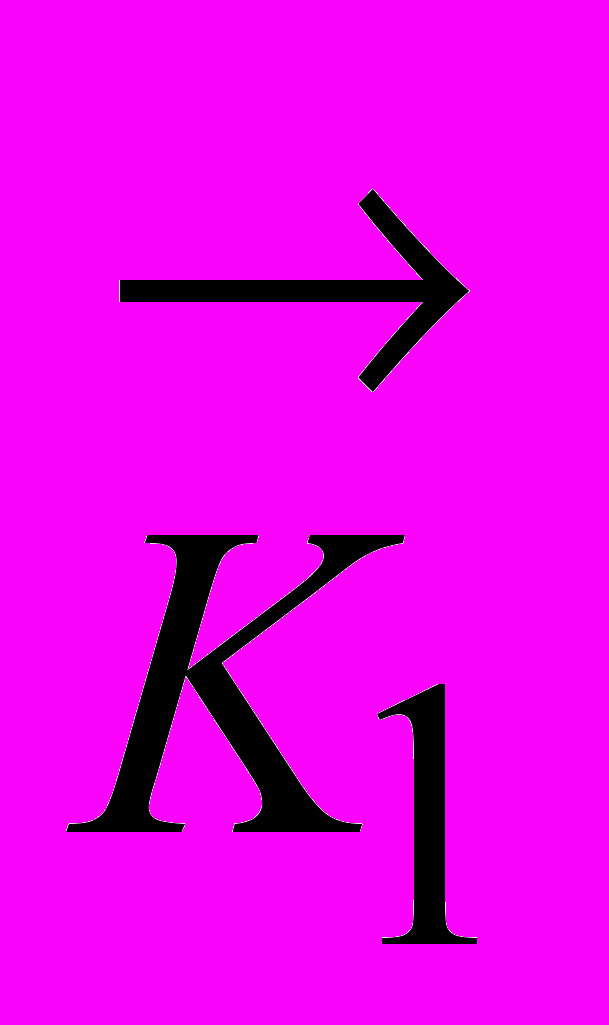
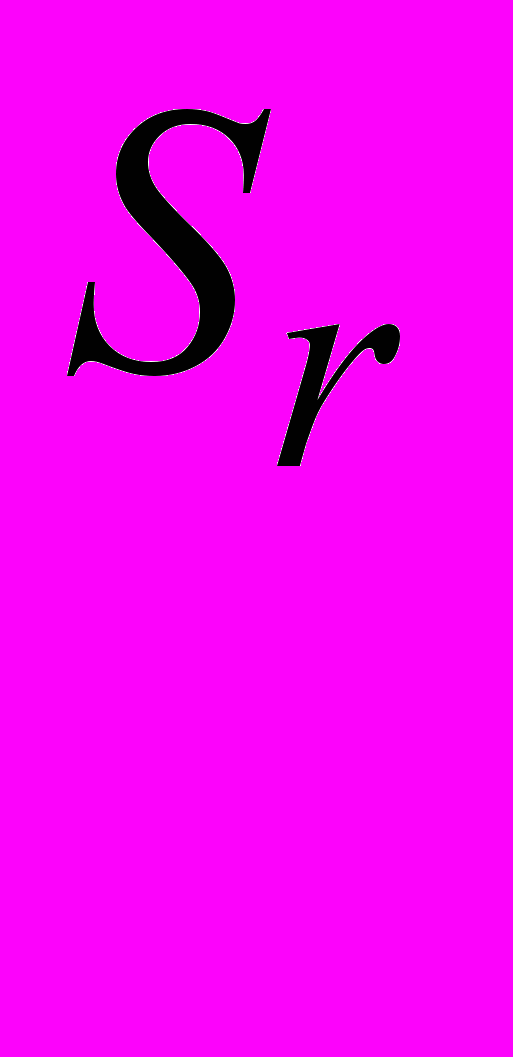Определить:

1) коэффициент наращения операции совмещения;

2) коэффициент наращения прямой операции;

3) критическое значение темпа роста курса, при котором эффективность операции совмещения равна нулю;

4) паритетное значение темпа роста курса, при котором эффективности операции совмещения и прямой операции совпадают;

5) наращенную сумму в прямой операции;

6) наращенную сумму в операции совмещения.

Исходные данные:

1) начальная сумма 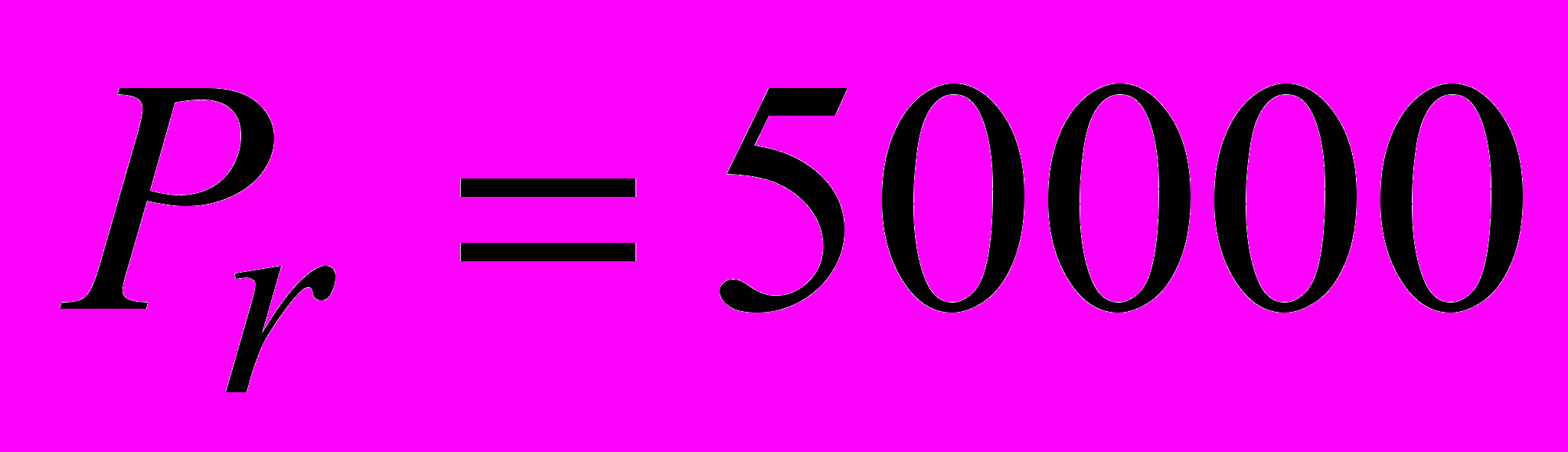руб.;

2) курс валюты в начале операции 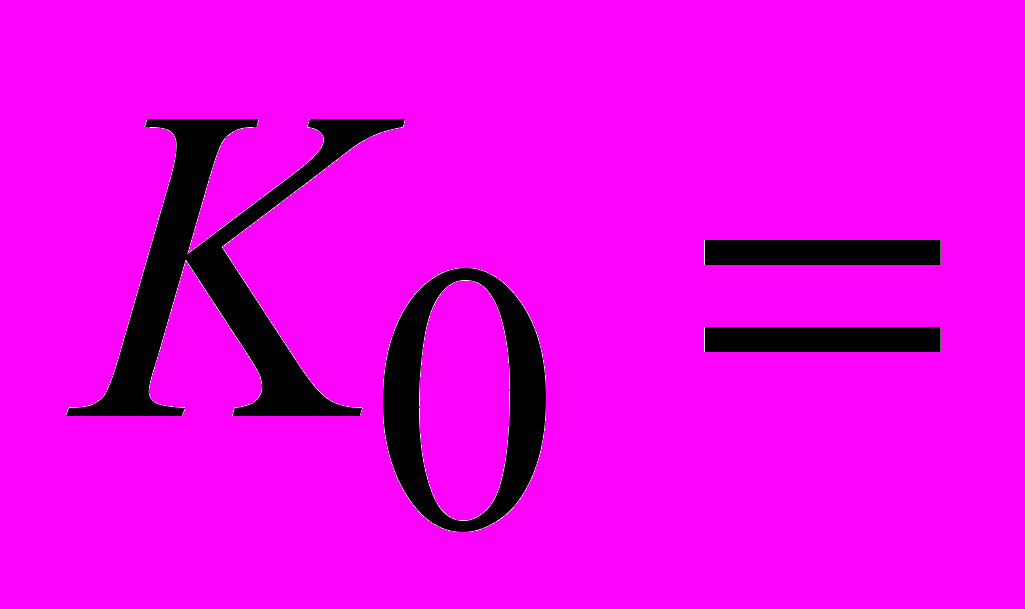25 руб. (курс СКВ в руб.);

3) курс валюты в конце операции 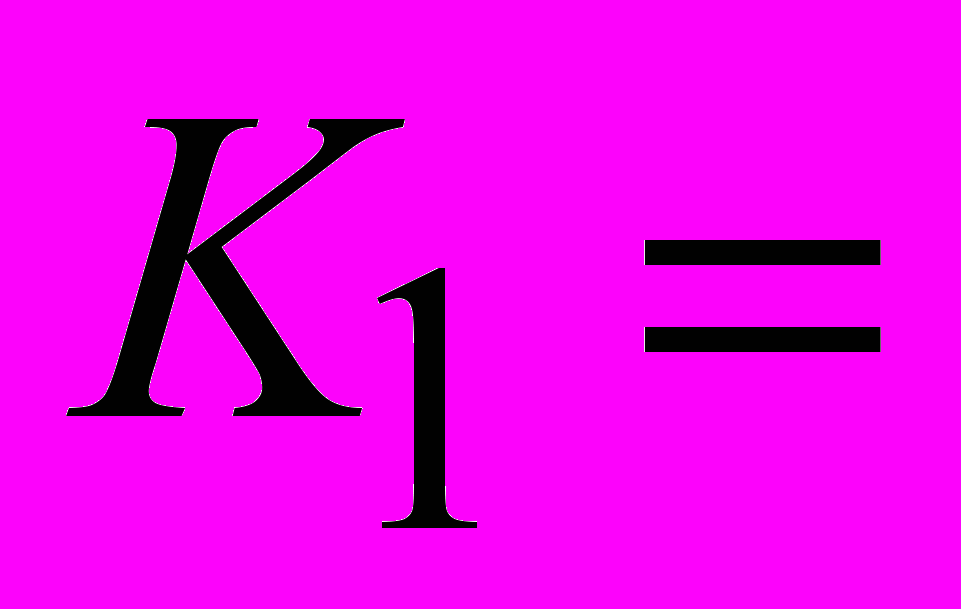30 руб. (курс СКВ в руб.);

4) срок проведения операции 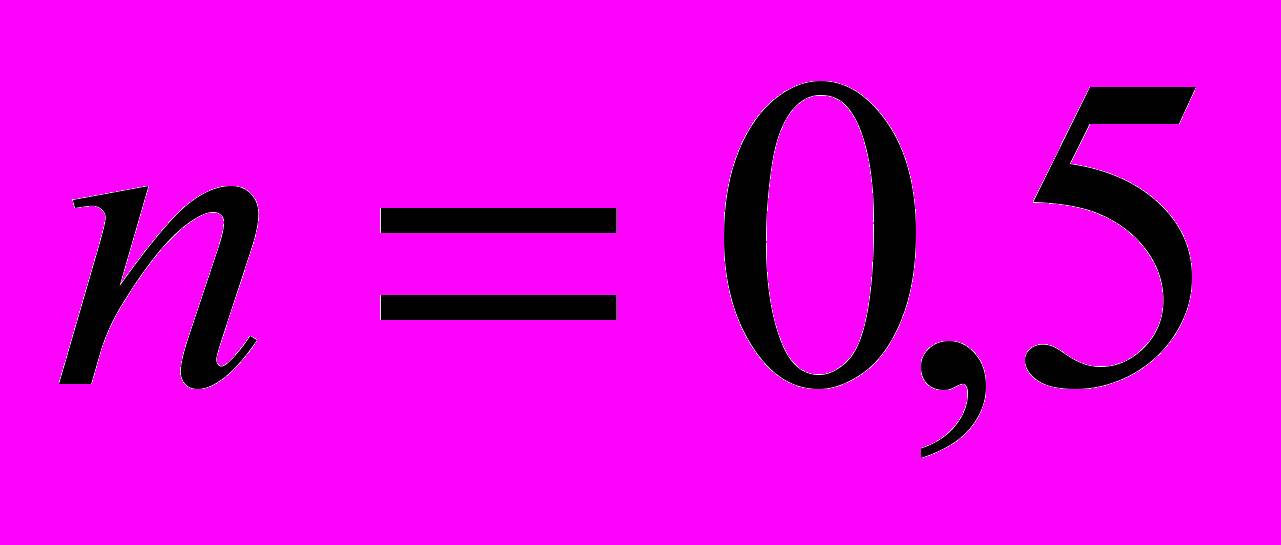года;

5) j = 0,15 — процентная ставка для СКВ;

6) 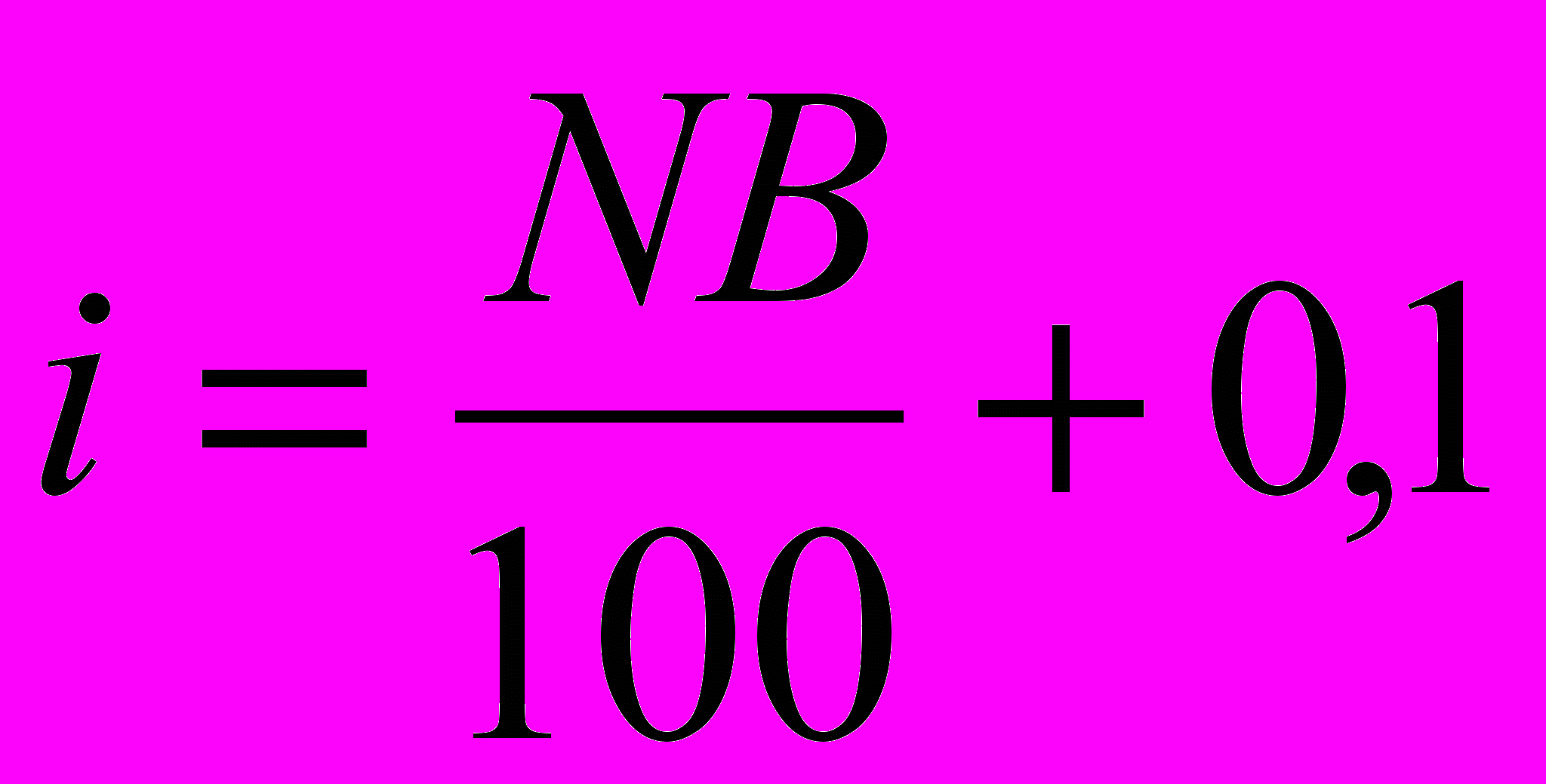— процентная ставка для рублевых сумм, где NB — номер варианта.

Задание 2. Наращение процентов и налоги

Исходные данные:

ставка налога на проценты ;

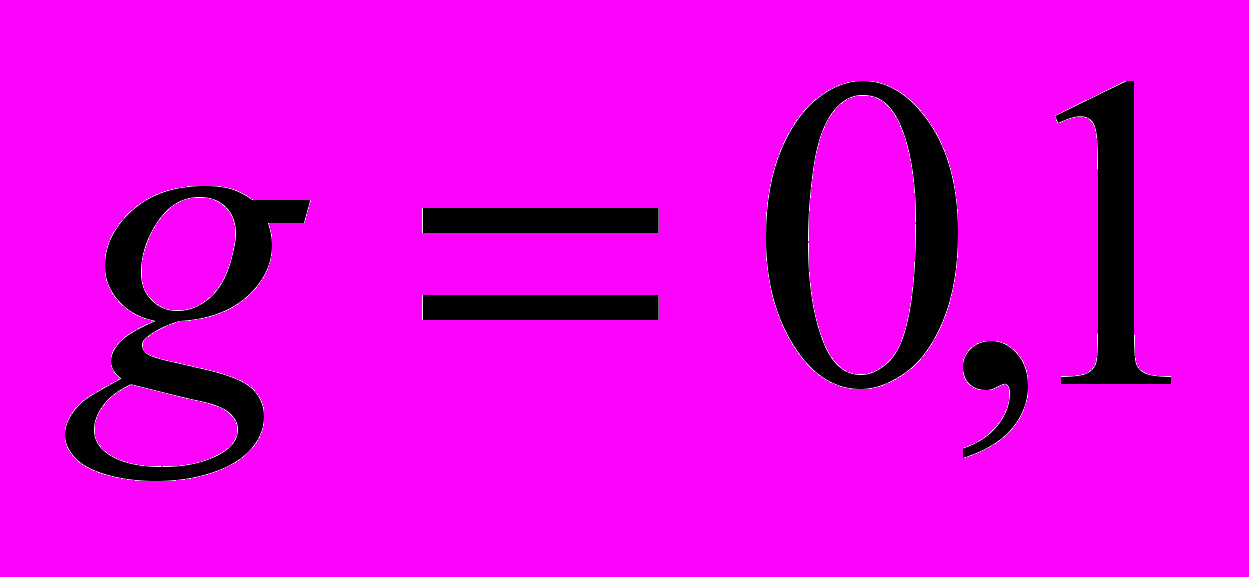годовая процентная ставка ;

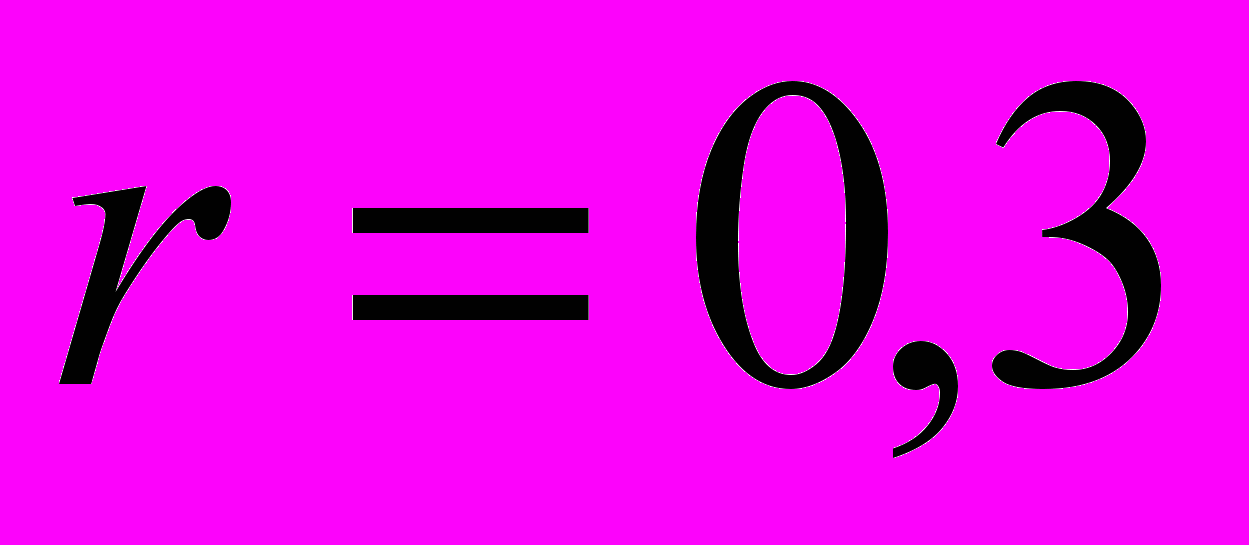срок начисления процентов 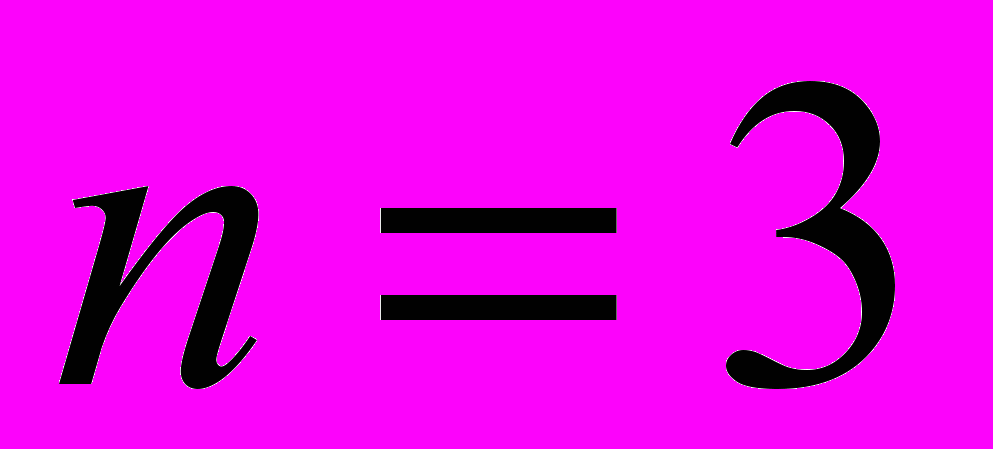года;

начальная сумма 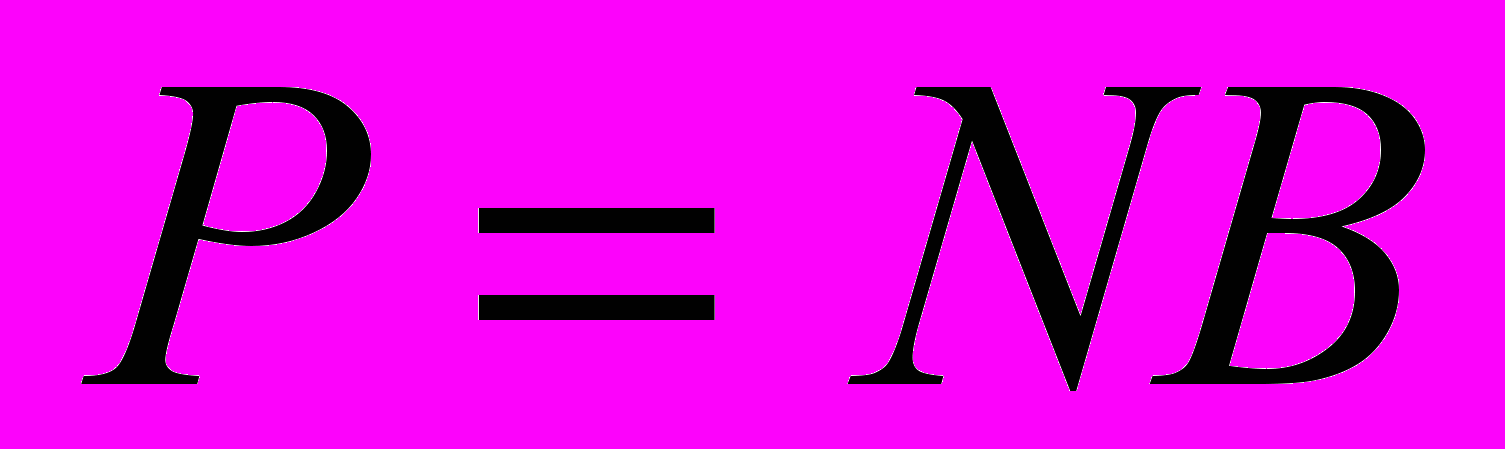(млн. руб.), где NB — номер варианта.

Определить:

1) для простых процентов:

· сумму налога G,

· наращенную сумму с учетом налога,

2) для сложных процентов:

· сумму налога G (налог начисляется на всю сумму сразу);

· сумму налога G по годам;

· наращенную сумму с учетом налогов.


Задание 3. Наращение процентов и инфляция

Исходные данные:

1) годовая процентная ставка ;

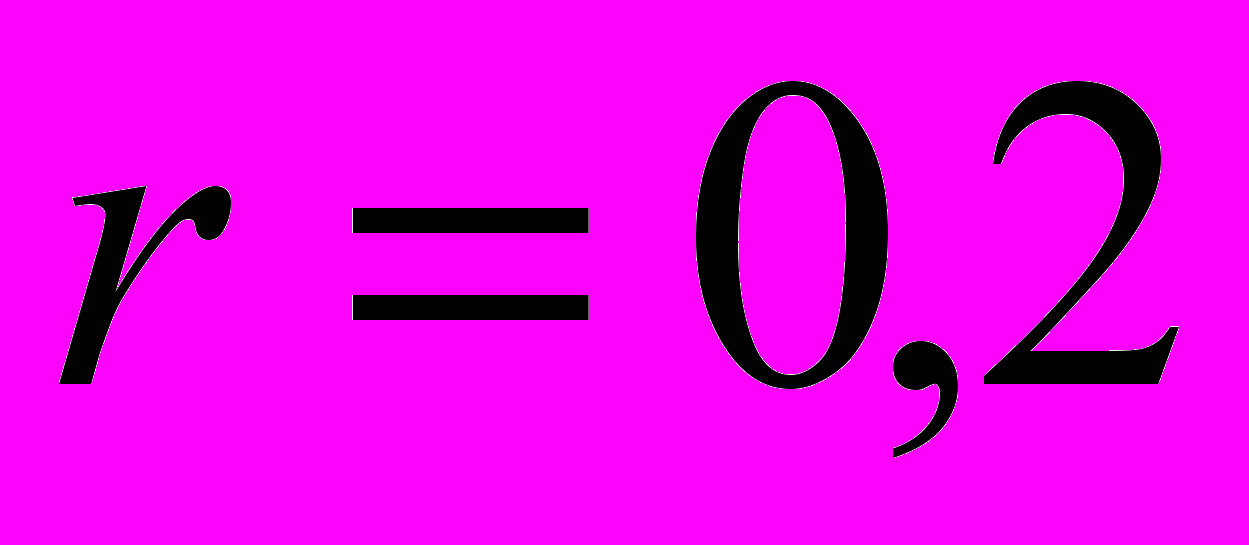2) срок начисления процентов: три месяца для простых процентов и три года для сложных процентов;

3) начальная сумма 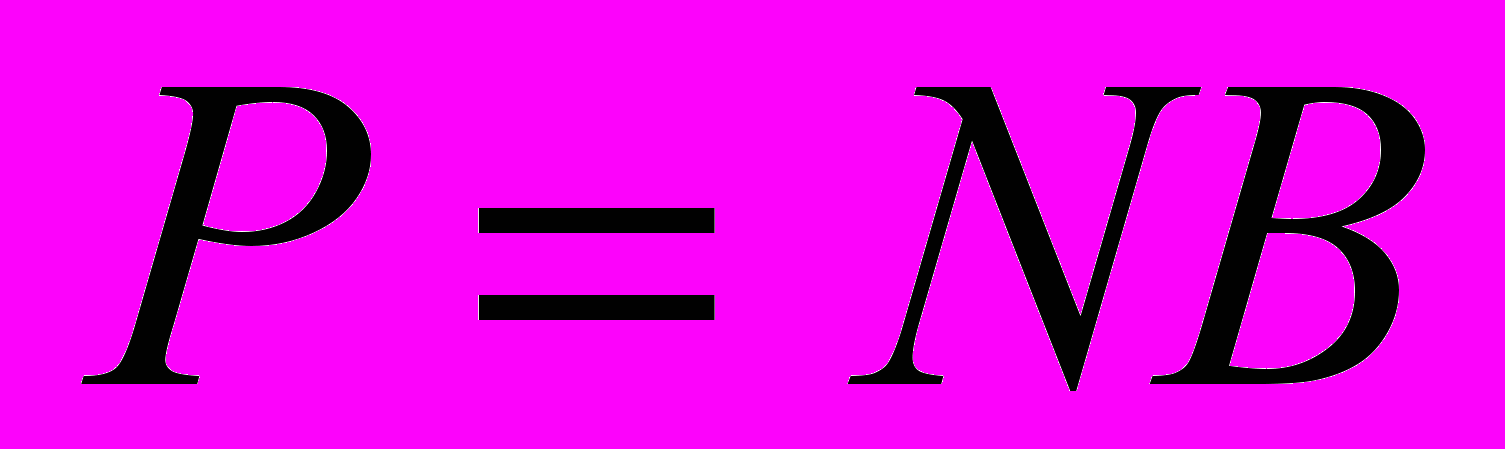(млн. Руб.);

4) темпы инфляции: 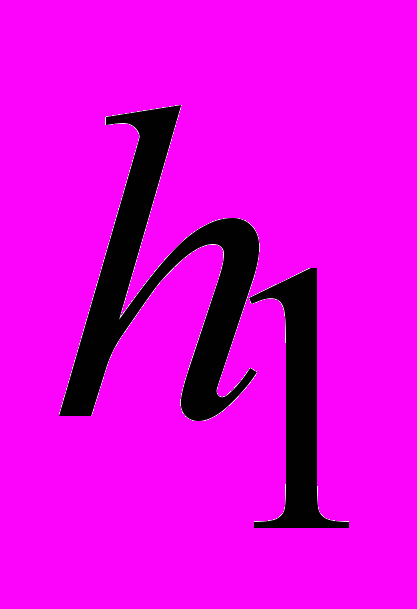=25+NB; 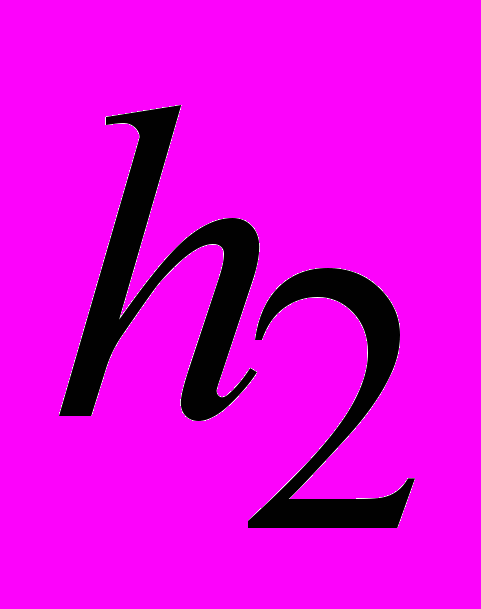=20+NB; 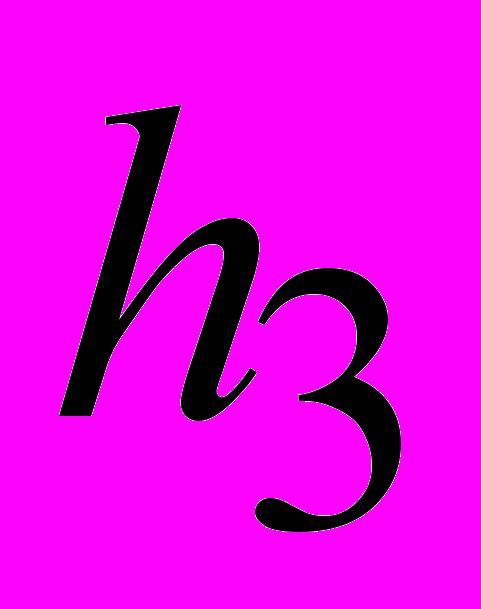=18+NB (по годам для сложных процентов, по месяцам для простых).

Определить: для начисления процентов по схеме простых и сложных процентов:

1) индекс цен за весь период;

2) темп инфляции за весь период;

3) процентную ставку 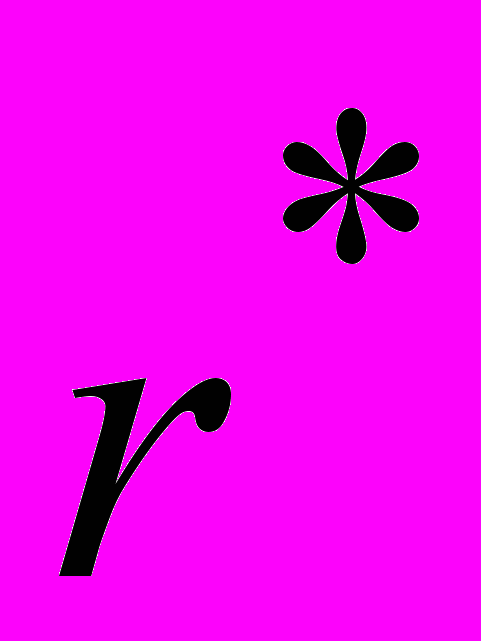, при которой наращение компенсируется инфляцией (эффективность операции наращения равна нулю).

4) брутто ставку, обеспечивающую доходность r .

5) наращенную сумму, которая обеспечивает доходность r в условиях инфляции с данными характеристиками.


Задание 4. Наращенная сумма и современная стоимость

p -срочных и m - срочных рент

Рассчитать наращенную сумму и современную стоимость для рент с параметрами (p — количество платежей в году, m — количество начислений процентов в году): 1) p =1; m =2; 2) p = 2; m =1; 3) p =2; m =2.

Исходные данные:

1) начальная сумма P = NB (в млн. Руб.), где NB — номер варианта;

2) процентная ставка 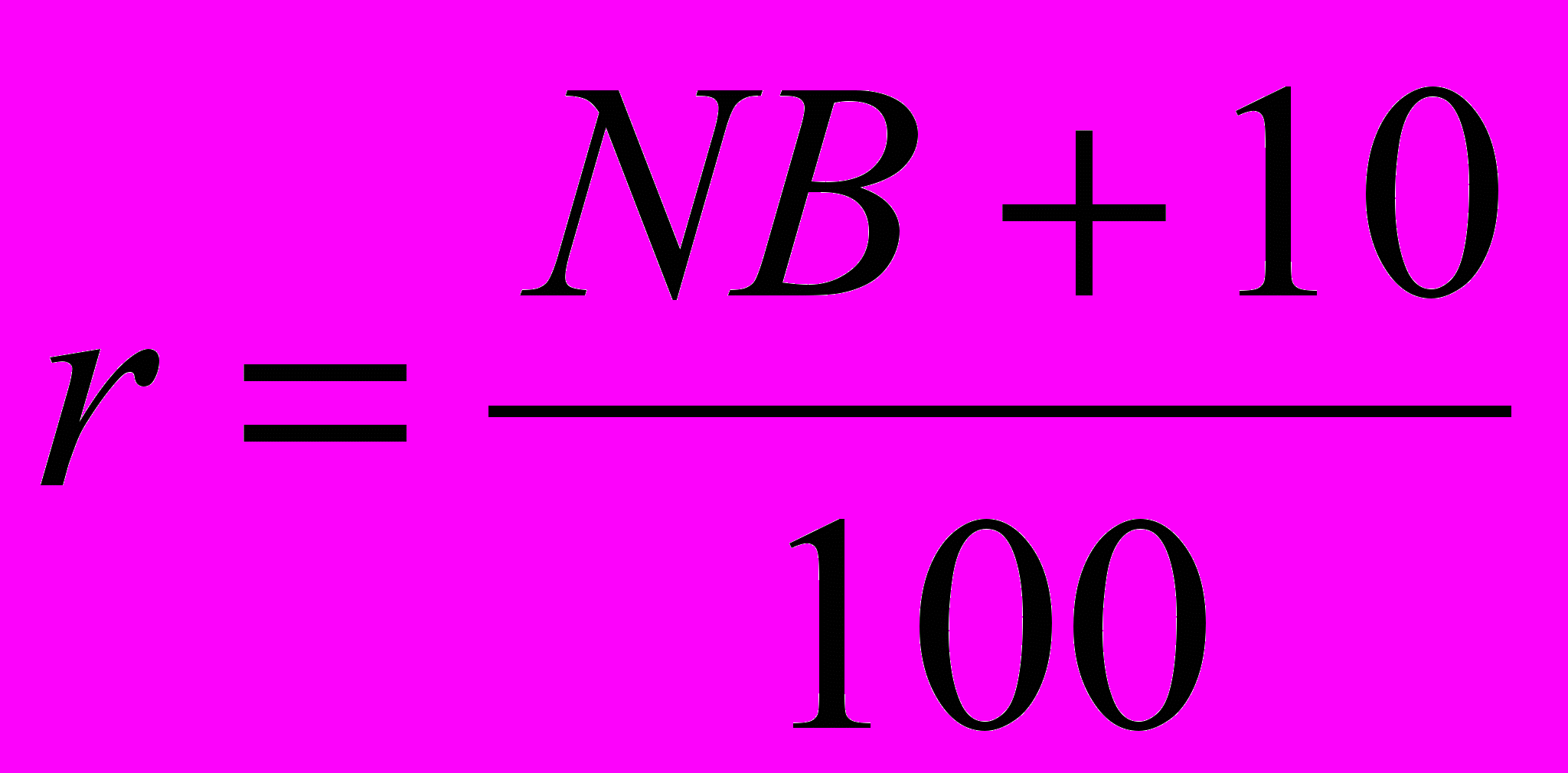(в долях единицы);

3) срок ренты 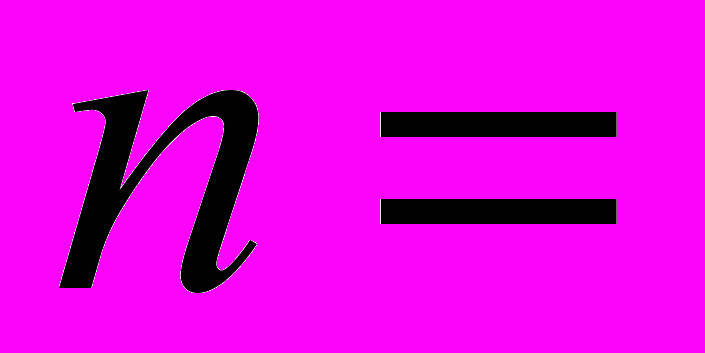2 года.


Задание 5. Оценка стоимости облигаций

1. Определить курс облигации общего вида (периодически выплачиваются проценты, в конце срока номинал). Срок облигации 5 лет. Купонная процентная ставка 8 % годовых. Годовая рыночная процентная ставка 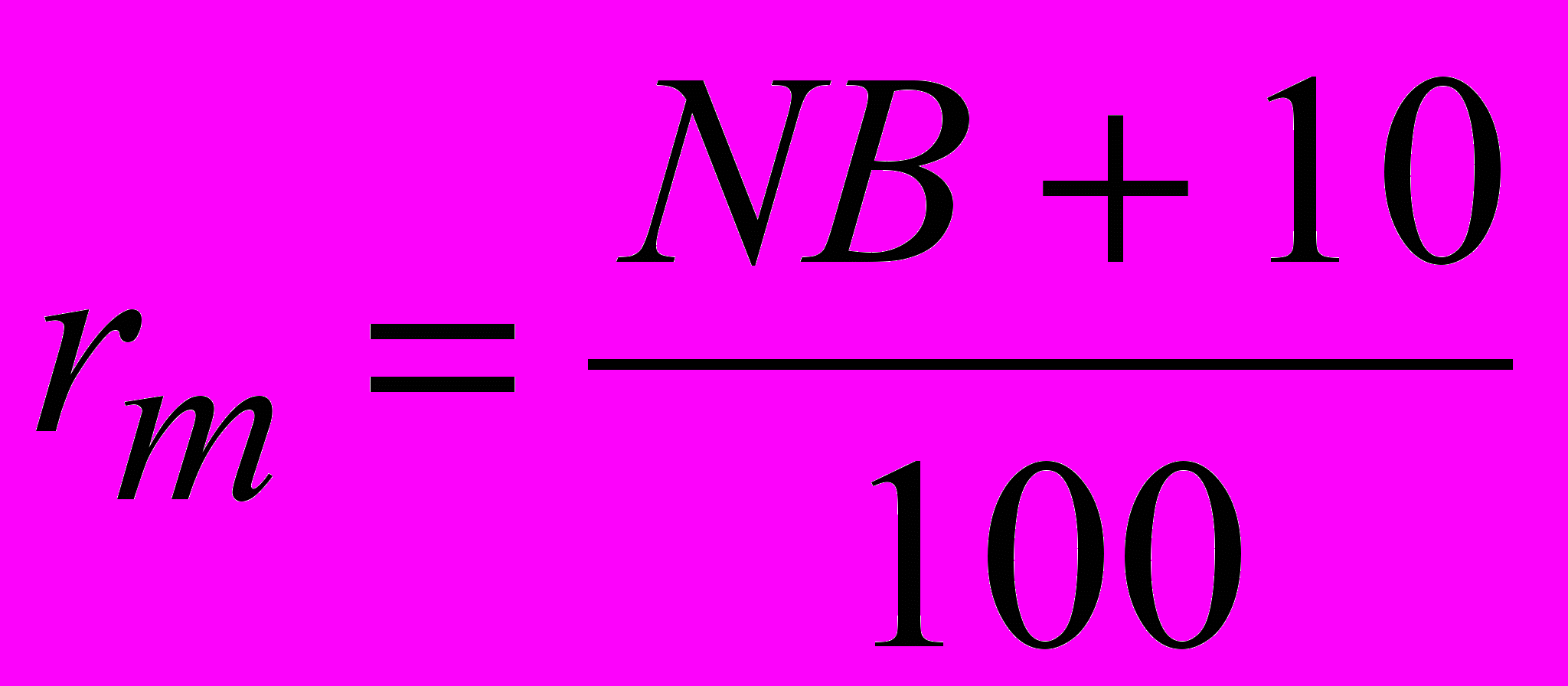, где NB — номер варианта. Проценты выплачиваются ежегодно.

2. Как изменится курс облигации, если проценты будут выплачиваться поквартально?

3. Как изменится курс облигации, если проценты будут начисляться поквартально?

Задание 6. Модели оценки акций

Ожидается, что дивиденды на обыкновенные акции (ОА) будут увеличиваться на 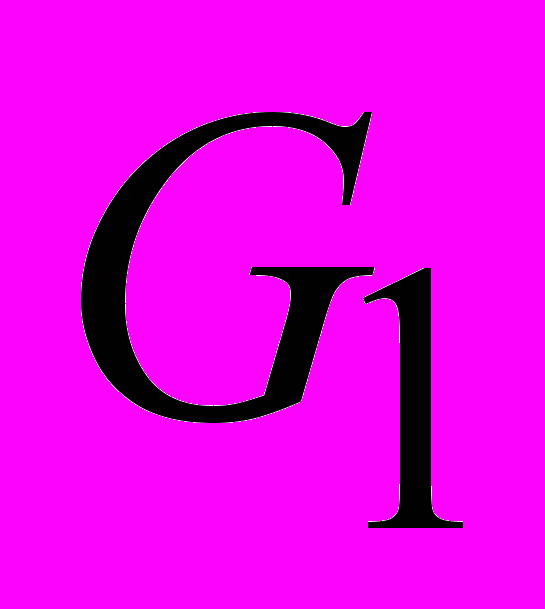процентов по сложной ставке на протяжении 5 лет, а затем на 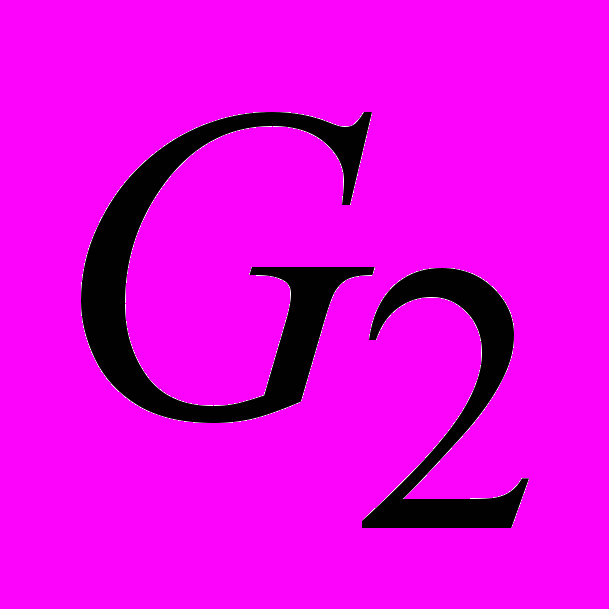процента. Рыночная процентная ставка r процентов годовых. Определить цену покупки, если базовая величина дивиденда 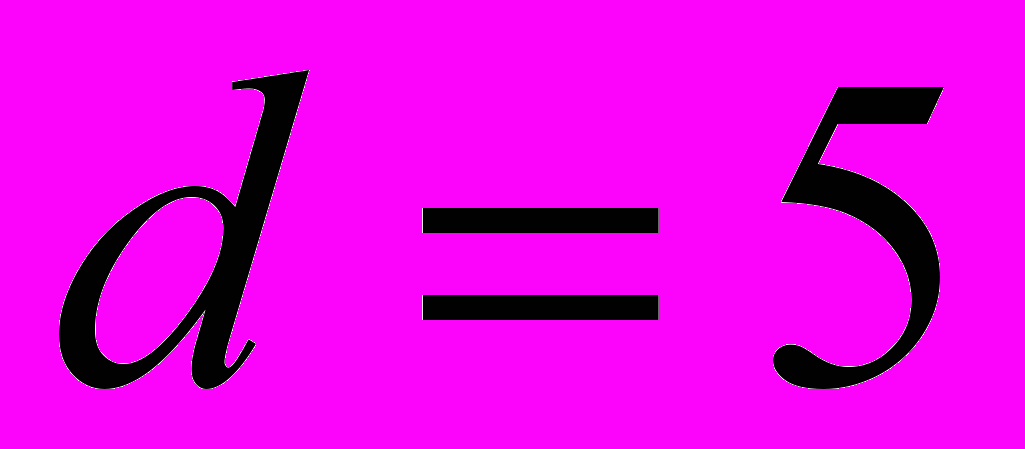долларов.

, , ,

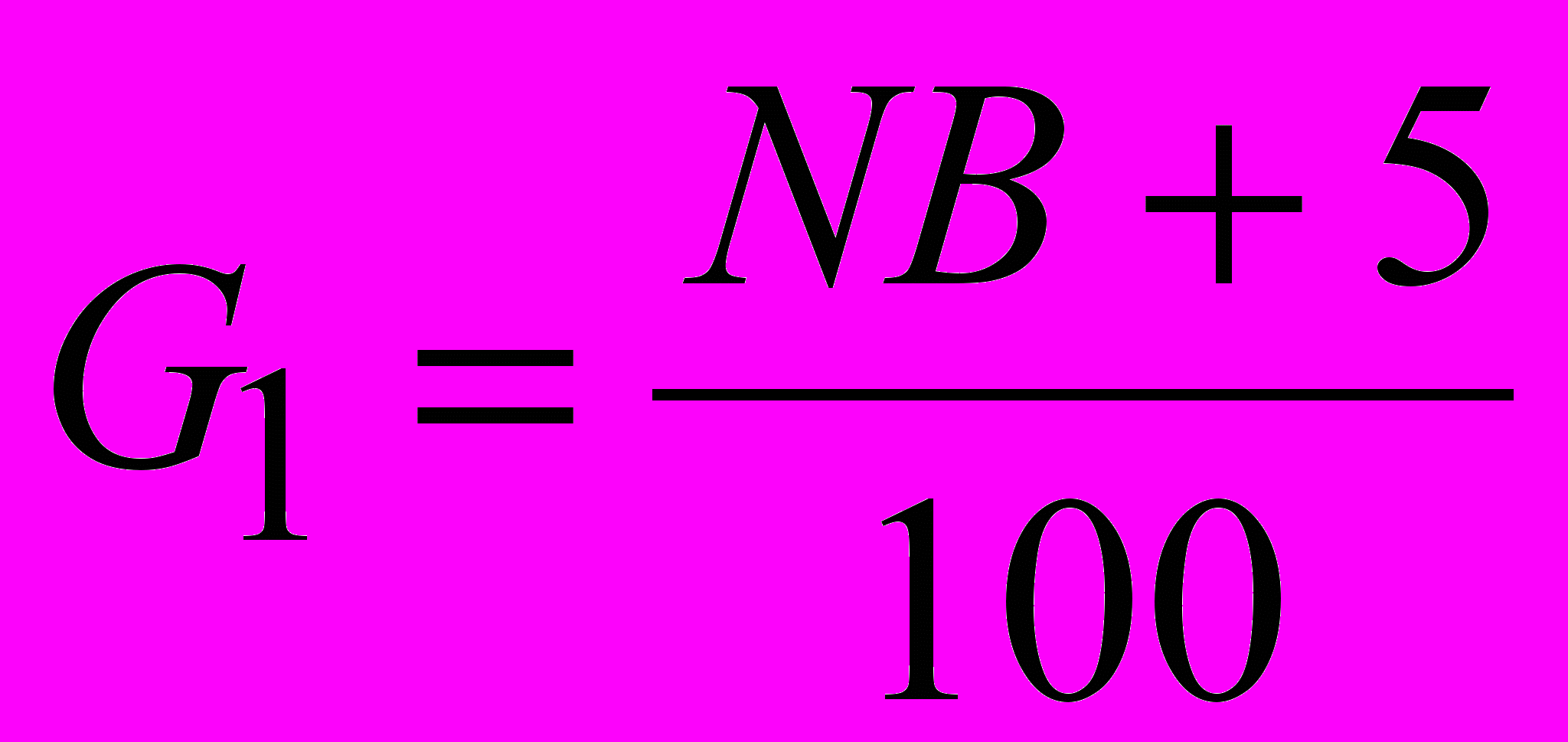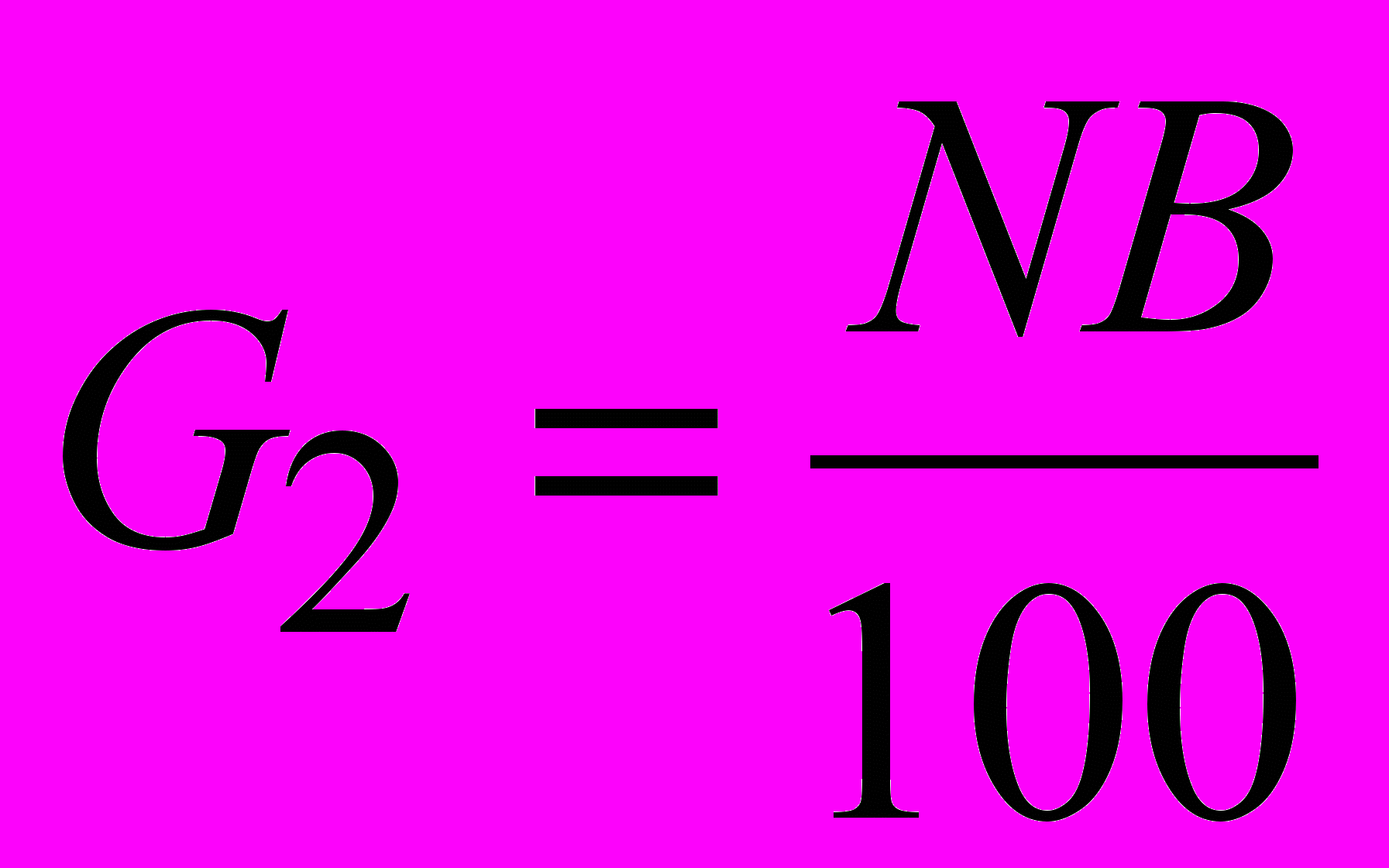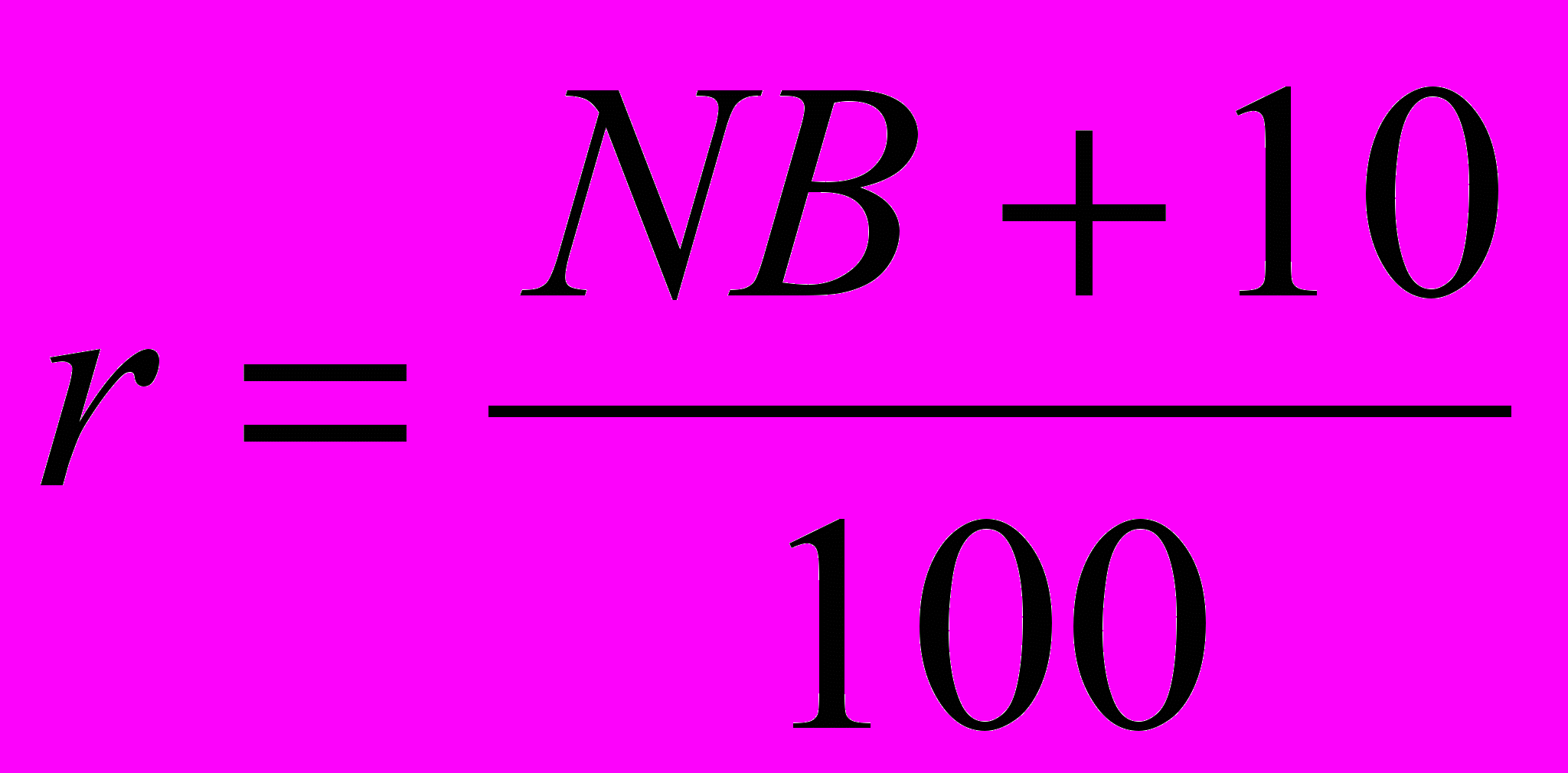NB — номер варианта.

Задание 7. Определение оптимальной структуры рискового

портфеля ценных бумаг

Используя данные, приведенные в таблице, определить оптимальную по Марковицу структуру портфеля ценных бумаг, включающего следующие инструменты: казначейские векселя, долгосрочные государственные облигации, долгосрочные облигации корпораций, обыкновенные акции.

Таблица

Годовые доходности по акциям, облигациям, казначейским векселям и изменения индекса потребительских цен в США за период 1926-1993 гг.1

№
Год
Казначейские векселя, %
Долгосрочные государственные облигации, %
Долгосрочные облигации корпораций, %
Обыкновенные акции %
Изменения индекса потребительских цен %

1
1926
3,26
7,77
7,37
11,62
-1,49

2
1927
3,12
8,93
7,44
37,49
-2,08

3
1928
3,56
0,10
2,84
43,61
-0,97

4
1929
4,75
3,42
3,27
-8,42
0,20

5
1930
2,41
4,66
7,98
-24,90
-6,03

6
1931
1,07
-5,31
-1,75
-43,34
-9,52

7
1932
0,96
16,48
10,82
-8,19
-10,30

8
1933
0,30
0,07
10,38
53,99
0,51

9
1934
0,16
10,03
13,84
-1,44
2,03

10
1935
0,17
4,98
9,61
47,67
2,99

11
1936
0,18
7,52
6,74
33,92
1,21

12
1937
0,31
0,23
2,75
-35,03
3,10

13
1938
-0,02
5,563
6,13
31,12
-2,78

14
1939
0,02
5,94
3,97
-0,31
-0,48

15
1940
0,00
6,09
3,39
-9,78
0,96

16
1941
0,06
0,93
2,73
-11,59
9,72

17
1942
0,27
3,22
2,60
20,34
9,29

18
1943
0,35
2,08
2,83
25,90
3,16

19
1944
0,33
2,81
4,73
19,75
2,11

20
1945
0,33
10,73
4,08
36,44
2,25

21
1946
0,35
-0,10
1,72
-8,07
18,16

22
1947
0,50
-2,62
-2,34
5,71
9,01

23
1948
0,81
3,40
4,14
5,50
2,71

24
1949
1,10
6,45
3,31
18,79
-1,80

25
1950
1,20
0,06
2,12
31,71
5,79

26
1951
1,49
-3,93
-2,69
24,02
5,87

27
1952
1,66
1,16
3,52
18,37
0,88

28
1953
1,82
3,64
3,41
-0,99
0,62

29
1954
0,86
7,19
5,39
52,62
0,50

30
1955
1,57
-1,29
0,48
31,56
0,37

31
1956
2,46
-5,59
-6,81
6,56
2,86

32
1957
3,14
7,46
8,71
-10,78
3,02

33
1958
1,54
-6,09
-2,22
43,36
1,76

34
1959
2,95
-2,26
-0,97
11,96
1,50

35
1960
2,66
13,78
9,07
0,47
1,48

36
1961
2,13
0,97
4,82
26,89
0,67

37
1962
2,73
6,89
7,95
-8,73
1,22

38
1963
3,12
1,21
2,19
22,80
1,65

39
1964
3,54
3,51
4,77
16,48
1,19

40
1965
3,93
0,71
-0,46
12,45
1,92

41
1966
4,76
3,65
0,20
-10,06
3,35

42
1967
4,21
-9,18
-4,85
23,98
3,04

43
1968
5,21
-0,26
2,57
11,06
4,72

44
1969
6,58
-5,07
-8,09
-7,50
6,11

45
1970
6,52
12,11
18,37
4,01
5,49

46
1971
4,39
13,23
11,01
14,31
3,36

47
1972
3,84
5,69
7,26
18,98
3,41

48
1973
6,93
-1,11
1,14
-14,66
8,80

49
1974
8,00
4,35
-3,06
-26,47
12,20

50
1975
5,80
9,20
14,64
37,20
7,01

51
1976
5,08
16,75
18,65
23,84
4,81

52
1977
5,12
-0,69
1,71
-7,18
6,77

53
1978
7,18
-1,18
-0,07
6,56
9,03

54
1979
10,38
-1,23
-4,18
18,44
13,31

55
1980
11,24
-3,85
-2,62
32,42
12,40

56
1981
14,71
1,86
-0,96
-4,91
8,94

57
1982
10,54
40,36
43,79
21,41
3,87

58
1983
8,80
0,65
4,70
22,51
3,80

59
1984
9,85
15,48
16,39
6,27
3,95

60
1985
7,72
30,97
30,90
32,16
3,77

61
1986
6,16
24,53
19,85
18,47
1,33

62
1987
5,47
-2,71
-0,27
5,23
4,41

63
1988
6,35
9,67
10,70
16,81
4,42

64
1989
8,37
18,11
16,23
31,49
4,65

65
1990
7,81
6,18
6,78
-3,17
6,11

66
1991
5,60
19,30
19,89
30,55
3,06

67
1992
3,51
8,05
9,39
7,67
2,90

68
1993
2,90
18,24
13,19
9,99
2,75


Расчет оптимальной структуры выполнить в Excel. Выборочные данные для каждого варианта сформировать по правилу ( NB — номер варианта):

1) номер первого наблюдения — NB;

2) номер последнего наблюдения — NB + 20;

3) объем выборки 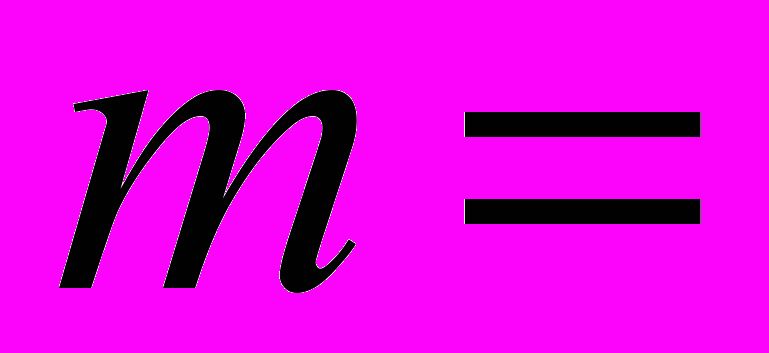21.

Например, для NB=2 используются данные с номера 2 по номер 22 включительно.

Построить зависимость риск-доходность для следующих значений ожидаемой доходности портфеля: 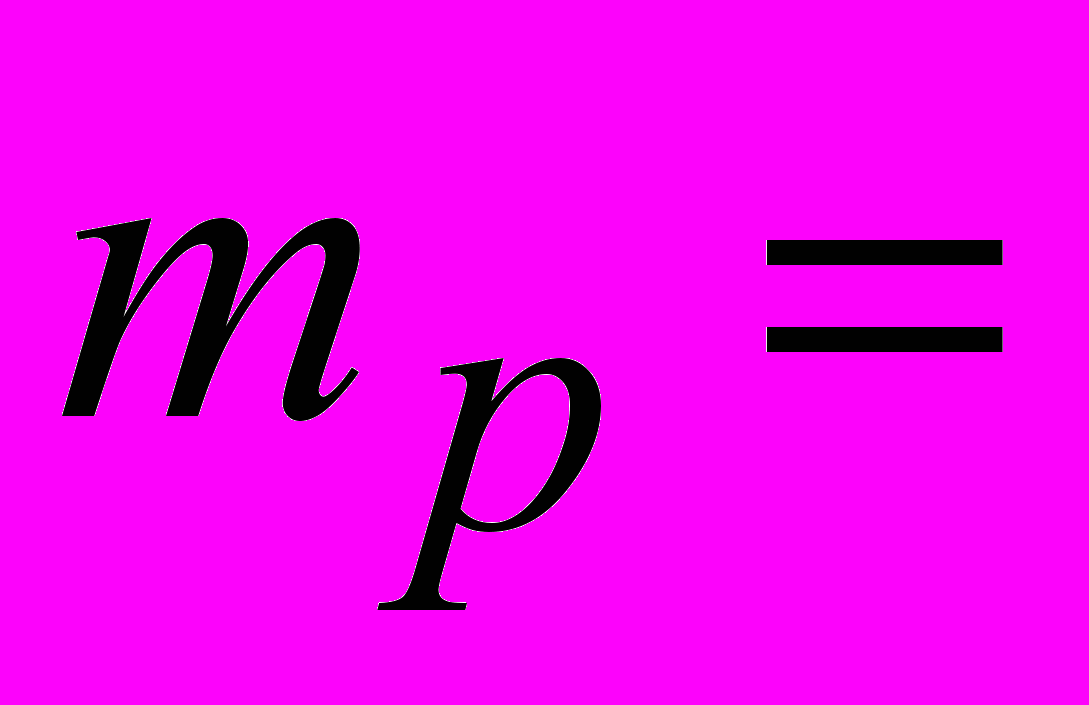4% ¸ 11%.