Системы управления товарно-материальными запасами при независимом спросе в этой главе

Вид материала

Пример 15.4. Величина заказа и точка очередного заказа
Q, а также точку повторного заказа R
Модели с фиксированным периодом
Модель с фиксированным периодом и уровень обслуживания
Т, а резервный запас, который необходимо иметь, равен zs
L — время выполнения заказа в днях (с момента размещения заказа до момента получения изделий по этому заказу); d
I — текущий уровень запаса (включает уже имеющиеся изделия). Примечание.
Специальные модели
Однопериодная модель (Single-Period Models).
Другие системы и проблемы

Подобный материал:

1 2 3 4 5

Пример 15.4. Величина заказа и точка очередного заказа

Ежедневная потребность в определенном изделии имеет нормальное распределение (среднее значение равно 60, а стандартное отклонение — 7). Источник поставок считается надежным и обеспечивает постоянное время выполнения заказа— 6 дней. Стоимость размещения заказа равняется $10, а годовые издержки хранения составляют $0,50 на одно изделие. Потерь, связанных с дефицитом изделий и невыполнением заказов, нет. Допустим, что продажи осуществляются на протяжении всего года. Определить величину заказа и точку повторного заказа, которые позволяли бы удовлетворить 95%-ную потребность из имеющегося запаса.

Решение

В нашем примере требуется вычислить величину заказа Q, а также точку повторного заказа R.

О

птимальная величина заказа будет

Чтобы вычислить точку очередного заказа, нам нужно вычислить количество изделий, используемое в течение времени выполнения заказа, и сложить его с резервным запасом.

Стандартное отклонение потребности в течение шести дней (период выполнения заказа) вычисляется на основе дисперсии по отдельным дням. Поскольку потребность для каждого дня является независимой величиной^²

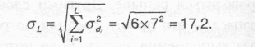
Дальше нам нужно знать, сколько требуется стандартных отклонений для обеспечения указанного уровня обслуживания. Как уже было показано,

К

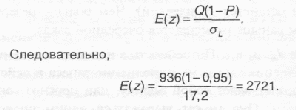
ак следует из табл. 15.2, для интерполяции E(z) = 2721 получаем z = -2,72. Точка очередного заказа:

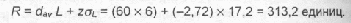
Полученный результат можно резюмировать следующим образом: заказ на 936 единиц размещается каждый раз, когда количество изделий, остающееся в запасе, сокращается до 313.

Обратите внимание, что в этом случае резервный запас zs_L. оказывается отрицательным. Это означает, что, если бы мы заказывали вычисленное нами количество изделий Q = 936, когда уровень запаса снижается до ожидаемой потребности в течение периода выполнения заказа (d_avL = 360), мы обеспечили бы более высокий уровень обслуживания, чем нам требовалось. Чтобы снизить его до 95%, нужно допустить больше нехваток, выдавая заказы в точке, расположенной несколько ниже вычисленной нами точки очередного заказа (313). Может, такой вывод покажется вам странным, но это действительно так. В этом случае мы фактически ожидаем дефицит изделий в каждом цикле заказа.

Мы можем проверить уровень обслуживания, обеспечиваемый в этом примере, указав, что нам пришлось бы размещать 23,4 заказов в год (60  365/936). В каждый из периодов нам пришлось бы сталкиваться с дефицитом 46,8 единиц (2,72  17,2). Таким образом, мы испытывали бы дефицит 1095 изделий в год (48,6  23,4). Следовательно, уровень обслуживания составит, как нам и требовалось, 0,95 = [(21 900-1095)/21 900].

Как следует из этих двух примеров, описанный метод определения уровней резервного запаса относительно прост и понятен. Он позволяет нам управлять запасом, обеспечивая требуемый уровень обслуживания.

Модели с фиксированным периодом

В системе управления запасами с фиксированным периодом запас подсчитывается только в определенные моменты времени, например раз в неделю или раз в месяц. Подсчет величины запаса и размещение заказов на периодической основе желательны в ситуациях, когда поставщики с определенной периодичностью навешают своих потребителей и принимают у них заказы на полную номенклатуру своей продукции либо когда покупатели пытаются комбинировать (объединять) заказы для экономии транспортных расходов. Многие фирмы предпочитают модель управления запасами с фиксированным периодом времени, поскольку она облегчает задачу планирования и учета запасов; например, дистрибьютор X наведывается к своим потребителям раз в две недели, и они знают, что с той же периодичностью необходимо проводить заказ продукции, поставляемой дистрибьютором X.

Модели с фиксированным периодом времени выдают размеры заказов, разные для различных циклов (в зависимости от нормы потребления). Это, вообще говоря, требует более высокого уровня резервного запаса, чем в системе с фиксированным объемом заказа. Система с фиксированным объемом заказа предполагает непрерывный подсчет наличного запаса, причем заказ размещается сразу же по достижении точки очередного заказа. В отличие от таких систем, в моделях с фиксированным периодом предполагают, что запас подсчитывается только в так называемые контрольные моменты времени. При этом возможно, что исключительно высокое потребление сведет весь запас к нулю сразу же после того, как заказ будет выполнен, и эта ситуация может оставаться незамеченной вплоть до наступления следующего контрольного момента. В таком случае можно оказаться без запаса изделий до поступления очередной партии заказанных изделий (т.е. в течение практически всего контрольного периода Т, плюс время выполнения заказа L). Таким образом, резервный запас должен защищать нас от дефицита изделий не только в течение контрольного периода, но и в течение времени выполнения заказа — с момента размещения заказа до момента получения изделий по этому заказу.

Модель с фиксированным периодом и уровень обслуживания

В системе с фиксированным периодом очередные заказы размещаются в контрольные моменты через время Т, а резервный запас, который необходимо иметь, равен zs_T₊_L.

На рис. 15.7 представлена модель с фиксированным периодом (контрольный период Т и период выполнения заказа L). В этом случае потребность характеризуется случайным распределением со средним значением d_av..

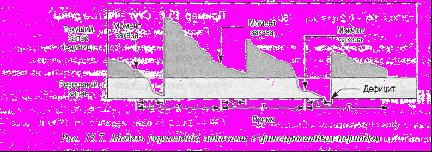
Рис. 15.7. Модель управления запасами с фиксированным периодом

Количество изделий, которые необходимо заказать q, равно:

Размер заказа =

= Средняя потребность в течение цикла +
+ Резервный запас — Текущий запас (плюс заказанное количество, если заказ уже размещен),

или

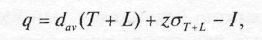
(15.10)

где q — размер очередного заказа;

Т — число дней между контрольными моментами;

L — время выполнения заказа в днях (с момента размещения заказа до момента получения изделий по этому заказу);

d_av. — прогнозируемая средняя дневная потребность;

z — число стандартных отклонений для заданного уровня обслуживания;

s_T₊_L — стандартное отклонение потребности в течение контрольного периода и периода выполнения заказа;

I — текущий уровень запаса (включает уже имеющиеся изделия).

Примечание. Потребность, период выполнения заказа, контрольный период и т.д. можно выражать любыми единицами времени (например, дни, недели или годы) — главное, чтобы в уравнении использовались одни и те же единицы измерения для всех величин.

В этой модели потребность d_av. можно, при желании, прогнозировать и пересматривать для каждого контрольного периода (можно использовать и ее среднегодовое значение). Мы предполагаем нормальный закон распределения потребности.

В

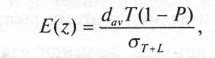еличину z можно получить из табл. 15.2 по E(z), которое определяется по формуле:

(15.11)

где E(z) — ожидаемая величина дефицита изделий, приведенная в табл. 15.2 при  = 1;

Р — требуемый уровень обслуживания, выраженный долей единицы (например, 0,95);

d_avT — потребность в течение контрольного периода, где d_av. — средняя дневная потребность, а Т — количество дней;

s_T₊_L — стандартное отклонение потребности в течение контрольного периода и периода выполнения заказа.

Пример 15.5. Величина заказа

Ежедневная потребность в определенном изделии составляет 10 единиц; стандартное отклонение— три единицы. Контрольный период — 30 дней, а период выполнения заказа — 14 дней. Руководство фирмы приняло решение создавать запас, обеспечивающий 98%-ное удовлетворение потребности. В начале данного контрольного периода в запасе есть 150 изделий.

Сколько изделий нужно заказать?

Решение

З

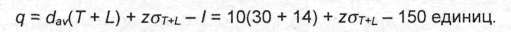
аказать нужно

Прежде чем решить это уравнение, нам нужно найти s_T₊_L и z. Чтобы найти s_T₊_L, мы, как и раньше, воспользуемся утверждением, что стандартное отклонение последовательности независимых случайных переменных равняется корню квадратному из суммы дисперсий. Следовательно, стандартное отклонение за период T+L равняется корню квадратному из суммы дисперсий за каждый день:

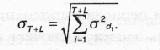
(15.12)

Поскольку каждый день независимый, a s_d— постоянная величина, то

Теперь, чтобы найти z, нам прежде всего нужно найти E(z) и отыскать соответствующее значение в табл. 15.2. В этом случае потребность в течение контрольного периода составит d_avТ, т.е.

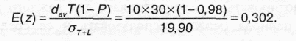
Из табл. 15.2 при E(z) = 0,302 путем интерполяции получаем z = 0,21.

Т

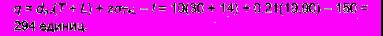
аким образом, количество изделий, которое нужно заказать, составит

Чтобы удовлетворить 98%-ную потребность в изделиях, нужно на этот контрольный период заказать 294 изделия.

Специальные модели

Рассмотренные модель с фиксированным объемом заказа и модель с фиксированным периодом времени, основанные на разных исходных посылках, все же имеют две общие характеристики — стоимость изделий остается постоянной при любом объеме заказа; процесс очередного размещение заказа предсказуем, т.е. изделия заказывались и помещались в запас в расчете на то, что потребность сохранится.

В этом разделе будут представлены две другие модели. Первая иллюстрирует изменение величины заказа в случае, когда цена единицы изделия меняется в зависимости от объема заказа. Вторая, называемая однопериодной моделью, или иногда статической моделью, представляет собой задачу, в которой определение размера заказа при каждой закупке требует поиска компромиссного варианта. Для этой модели решение отыскивается на основе анализа предельных показателей.

Модель со ступенчатой (переменной) ценой (Price-Break Models). Модель со ступенчатой (переменной) ценой учитывает то, что в действительности отпускная цена изделия зависит от объема заказа, причем зависимость цены от размера закупки обычно не прямо пропорциональная, а ступенчатая. Например, шурупы для дерева могут стоить $0,02 каждый при покупке от 1 до 99 таких шурупов, $1,60 — за сотню и $13,50 — за тысячу шурупов. Чтобы определить объем заказа изделий определенного типа, нужно рассчитать экономичный размер заказа для каждой цены, а также в "точках изменения цены". При этом не все значения экономичного размера заказа, определенные по формуле, будут подходящими. В примере с шурупами формула для Q_opt, может показать, что оптимальным объемом заказа при цене 1,6 центов за штуку является 75 шурупов. Однако это окажется невозможным, поскольку 75 шурупов стоили бы в этом случае по 2 цента каждый.

Оптимальный объем заказа определяют по наименьшим общим затратам на создание запасов для всех значений EOQ и Q, при которых происходит скачок цены. Для этого составляется таблица, в которой для всех возможных значений объема заказа (все EOQ и размеры закупок Q, при которых установлен скачок цены) рассчитывают все элементы затрат на создание запаса и находят общие затраты на создание запасов. По минимуму общих затрат определяется оптимальный объем закупки. При этом нужно учитывать, что не все значения EOQ имеют смысл, так как могут находиться в диапазонах цен, отличных от тех, по которым они рассчитаны. Рис. 15.8 иллюстрирует это по результатам примера 15.6.

Пример 15.6. Ступенчатые цены

Рассмотрим следующий случай:

D = 10000 изделий (годовая потребность);

S = $20 на размещение каждого заказа;

i = 20% стоимости (годовые затраты на перевозки, хранение, процент прибыли, старение и т.д.);

С = стоимость единицы (в соответствии с объемом заказа: заказ от 0 до 499 штук— $5,00 за одно изделие; от 500 до 999— $4,50 за одно изделие; от 1000 и выше— $3,90 за одно изделие).

Сколько изделий нужно заказать?

Решение

Подходящими формулами для этого случая будут формулы для модели с фиксированным объемом:

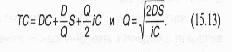
(15.13)

В табл. 15.3 приведены подробные расчеты суммарных затрат для экономичных размеров заказа при различных вариантах цены одного изделия, из которых следует, что оптимальный объем заказа составляет 1000 штук.

Отыскивая решение для экономичного размера заказа, получаем:

@ С = $3,90; Q = 716 неприемлемо.

@ С = $4,50; Q = 666 приемлемо, затраты = $45 599,70.

Скачок Q = 1000 → Затраты = = $39 590 → Оптимальное решение.

На рис. 15.8, который отображает результаты этого примера, необходимо обратить внимание на то, что каждая из трех кривых "объем заказа-затраты" имеет свой диапазон реальных значений и что в результате из трех кривых получается единственная (выделена жирной линией), которая отражает все допустимые значения. Это вполне объяснимо, поскольку, например, первый объем заказа определяет покупку 633 изделий по цене $5,00 за штуку. Однако, если закупать 633 изделия, цена составит $4,50, а не $5,00. То же самое справедливо для третьего объема заказа, равного 716 изделиям при цене $3,90 за штуку. Такая цена ($3,90) невозможна для заказов, объем которых составляет меньше 1000 штук.

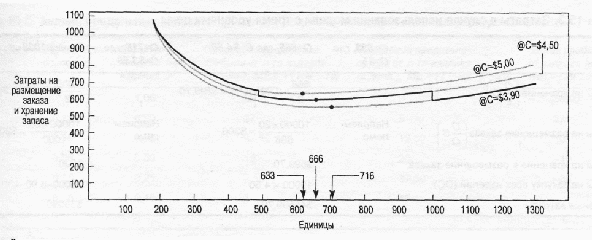
ис. 15.8. Зависимости суммарных затрат на создание запасов в ситуации
с тремя уровнями цены (жирная линия соответствует реально возможным объемам закупок)

Один из практических выводов для моделей со ступенчатыми иенами состоит в том, что ценовые скидки для крупных закупок часто делают экономически оправданным заказ изделий в количествах, превышающих Q_opt Таким образом, применяя данную модель, мы должны особенно тщательно следить за тем, чтобы получить правильный выбор с учетом увеличения потерь от устаревания продукции и затрат, связанных со складированием и хранением.

Однопериодная модель (Single-Period Models). В управлении запасами возникают ситуации, связанные с размещением заказов для покрытия потребности лишь на протяжении одного периода (цикла). Такие задачи, иногда называемые задачами одного периода, или "задачами уличного разносчика газет" (Сколько газет должен заказывать каждый день уличный разносчик газет?), можно решать на основе классического экономического подхода — анализа предельных показателей. В соответствии с анализом предельных показателей оптимальная величина запаса соответствует точке, в которой выгоды, извлекаемые от доставки на склад очередного изделия, оказываются больше возможных потерь из-за отсутствия этого изделия. Разумеется, набор конкретных выгод и затрат зависит от конкретной задачи. Например, мы можем сравнивать затраты на хранение с издержками, вызванными дефицитом изделий, или (как мы рассмотрим подробнее ниже) предельные доходы с предельными потерями.

Когда хранимые изделия продаются, оптимальным решением, — если пользоваться анализом предельных показателей, — будет решение хранить такой запас, при котором прибыль от продажи или использования последнего изделия будет не меньше, чем потери в том случае, если это последнее изделие не удастся продать. Математически это условие можно представить в следующем виде:

MPML,

где МР — прибыль от продажи n-го изделия;

ML — потери, если n-е изделие останется непроданным.

Применение анализа предельных показателей допустимо и в том случае, когда мы имеем дело с вероятностями тех или иных событий. В таких случаях мы сравниваем ожидаемую прибыль и ожидаемые потери. Если рассматривать вероятности, то взаимосвязь "предельная прибыль-предельные потери" принимает следующий вид:

Р(МР) (1- P)ML,

где Р — вероятность того, что изделие будет продано, а (1 — Р) — вероятность того, что изделие не будет продано (поскольку одно из этих событий обязательно произойдет, т.е. либо изделие будет продано, либо нет)^³.

Решая это неравенство относительно Р, получаем:

(

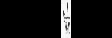15.14)

Это неравенство свидетельствует о том, что нам следует продолжать увеличивать объем запаса до тех пор, пока вероятность продажи последнего добавленного изделия не окажется равной или больше отношения ML/(MP+ML).

В сумму потерь можно легко включить ликвидационную стоимость или любые другие выгоды, извлекаемые из непроданной продукции. Это приводит к сокращению предельных потерь, что иллюстрирует следующий пример.

Пример 15.7. Ликвидационная стоимость в однопериодной модели

Отпускная цена на изделие установлена в размере $100, а его себестоимость постоянна и составляет $70. Каждое непроданное изделие имеет ликвидационную стоимость, равную $20. Ожидается, что в данный период потребность будет находиться в диапазоне от 35 до 40 изделий; 35 изделий наверняка будут проданы, а изделия свыше 40 штук наверняка не будут проданы. Вероятности спроса и связанное с ними распределение кумулятивной вероятности Р для этой ситуации показаны в табл. 15.4.

Предельная прибыль, если изделие продано, равна отпускной цене, минус затраты, или МР = $100 - $70 = $30.

Предельные потери в случае, если изделие не будет продано, равны себестоимости изделия, минус ликвидационная стоимость, или ML = $70 - $20 = $50.

Сколько изделий нужно заказать?

Решение

О

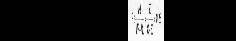
птимальная вероятность того, что последнее изделие будет продано, равна:

В соответствии с таблицей кумулятивной вероятности (последний столбец в табл. 15.4) вероятность продажи изделия должна равняться или быть больше 0,625, поэтому в запасе должно быть 37 изделий.

Вероятность продажи 37-го изделия составляет 0,75. Чистой выгодой от помещения в запас 37-го изделия является ожидаемая предельная прибыль, минус ожидаемая предельная потеря:

Net = Р(МР) - (1 - P)(ML) = 0,75($100 - $70) -- (1 - 0,75)($70 - $20) = $22,50 - $12,50 = $10.

Для иллюстрации в табл. 15.5 показаны все возможные решения. Последний столбец позволяет нам убедиться, что оптимальное решение равно 37 изделиям.

Другие системы и проблемы

Определение реальных величин расходов на размещение заказа, затрат на пуско-наладочные работы, транспортных расходов и издержек, связанных с дефицитом изделий на складе, — довольно трудная, а иногда и невозможная, задача. Иногда даже исходные предпосылки бывают нереальными. Например, на рис. 15.9 сравниваются затраты на размещение заказов, которые, по предположению, подчиняются линейному закону, с реальным случаем, когда добавление каждого нового заказа приводит к скачкообразному росту затрат, а не к линейному.

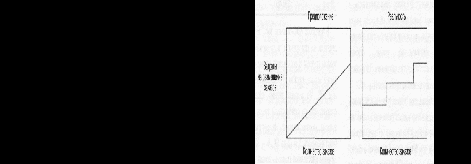
Рис. 15.9. Сравнение затрат на размещение заказов от количества размещаемых заказов:
предполагаемая линейная и реальная зависимость

Для всех систем управления товарно-материальными запасами характерно наличие двух серьезных проблем — осуществление надлежащего контроля над каждым элементом запаса и гарантирование точного сопровождения и отслеживания состояния наличных запасов. В этом разделе мы представим три простые системы, которые часто используются на практике (система с необязательным пополнением, однобункерная система и двухбункерная система), ABC-анализ (метод анализа запасов, основанный на значимости элементов) и циклический переучет.

Три простые системы управления товарно-материальными запасами

Blog

Системы управления товарно-материальными запасами при независимом спросе в этой главе