Тема Основные понятия статистики 5
| Вид материала | Контрольные вопросы |
| 3.6. Мода и медиана ряда распределения Вклады, грн Средняя зарплата, грн Процент высоколиквидных активов |
- Понятие, значение и задачи статистики. Основные понятия и категории статистики, 38.18kb.
- Тема: Основные понятия и определения, 121.92kb.
- Тема: Основные понятия и определения, 164.71kb.
- План урока: Орг момент. Повторение изученного. Объявление темы. Изучение нового материала., 66.27kb.
- Курс «Вероятность» является вторым в ряду вероятностно-эконометрических курсов Вероятность, 32.07kb.
- Задачи статистики рынка Система показателей статистики рынка Информационная база статистики, 1574.49kb.
- Структурно курс состоит из 15 тем: Тема Введение. Предмет, цели и задачи курса Тема, 140.87kb.
- Тема Психофармакотерапия и клиническая психология Тема Основные понятия в психфармакотерапии, 1195.06kb.
- Тема Территориальная организация населения: основные понятия и концепции, 2494.7kb.
- Тема Территориальная организация населения: основные понятия и концепции, 2373.94kb.
3.6. Мода и медиана ряда распределения
Кроме средних значений, характеристиками центра распределения принято считать также моду и медиану.
Мода – это значение признака х, при котором значение ряда распределения максимально.
Для полигонов, характеризующих распределения дискретных признаков, мода М0 определяется достаточно просто. Например, значение моды распределения размеров обуви группы из 20 студенток, заданного таблицей 3.1, равно М0=37.
Таблица 3.1
| xk | 35 | 36 | 37 | 38 | 39 | |
| nk | 2 | 5 | 9 | 3 | 1 | 20 |
В
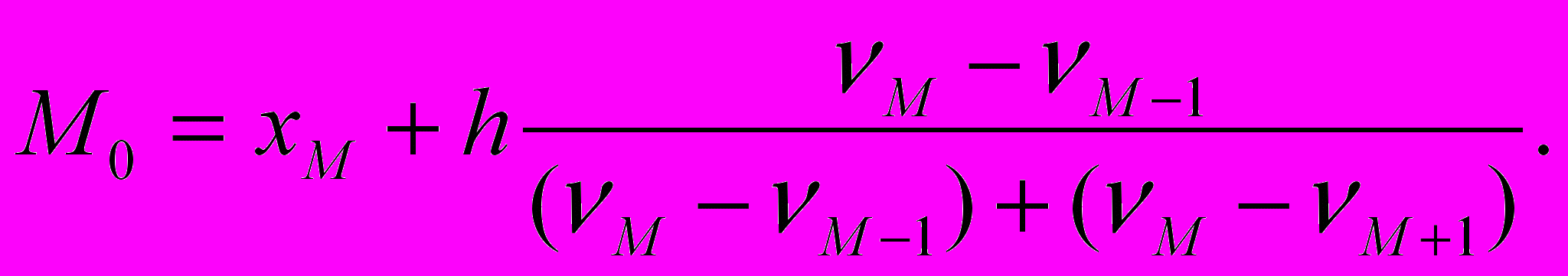
гистограмме значение моды определяется внутри модального интервала [xM ,xM+1] формулой Орженцкого (1863 – 1923)
Точка на оси х, определяющая это значение, может быть легко найдена графически как абсцисса точки пересечения двух прямых, проведенных в модальном интервале так, как показано на рис. 3.1.

Рис.3.1
М
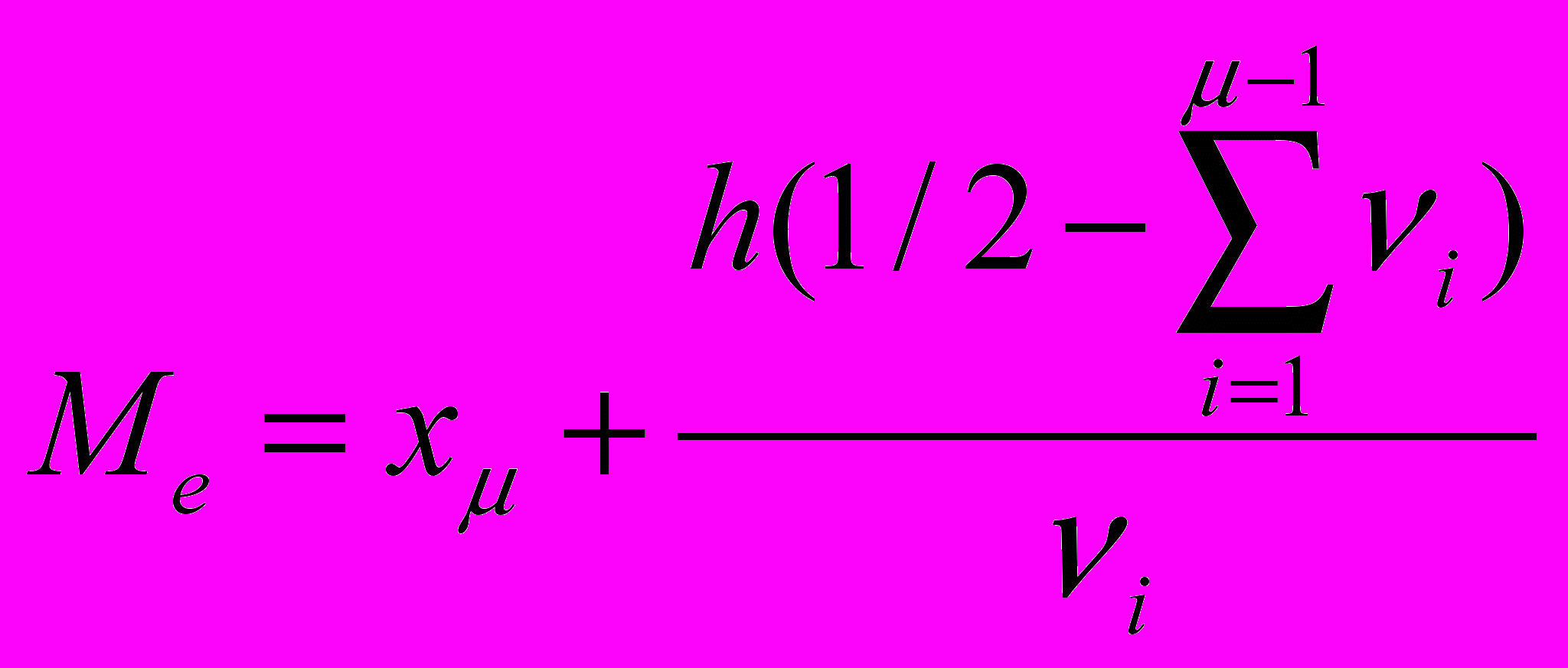
едиана – это значение признака х=Ме, которое делит площадь гистограммы пополам. Если обозначить х левую границу медианного интервала, то значение медианы гистограммы с равными интервалами ширины h определяется формулой
Пример 3.7. Распределение вкладов в банке представлено таблицей
| Вклады, грн | <1000 | 1000-1999 | 2000-2999 | 3000-3999 | >4000 |
| k, % | 19 | 34 | 25 | 13 | 9 |
Определить моду и медиану распределения.
О
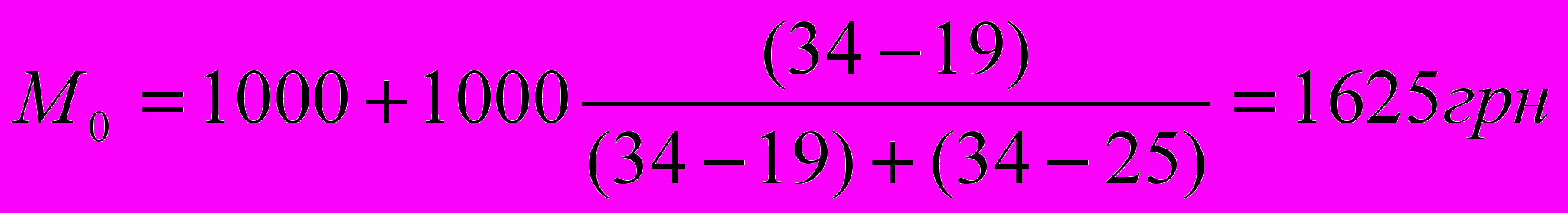
чевидно, модальный интервал лежит в области значений 1000-1999 грн. Согласно (3.7) получим значение моды
М
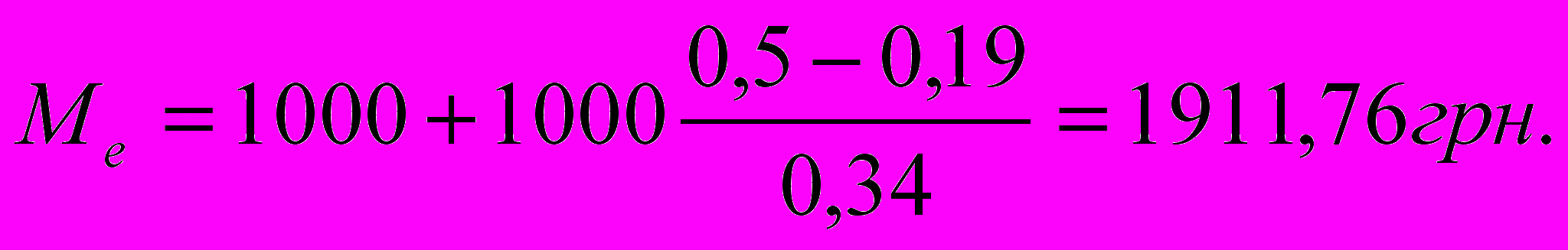
едиана этого распределения расположена в том же интервале и в соответствии с (3.8) равна
При симметричных рядах распределений все три параметра центра распределения – среднее арифметическое, мода и медиана – совпадают. В остальных случаях, которые, очевидно, преобладают, приходится производить отдельные расчеты для каждого параметра.
Задачи
- Имеются отчетные данные 20 заводов отрасли по объему валовой продукции (ОВП) за год (в млн. грн.)
{хi}(20)={4,5; 3,5;12,0; 3,4; 10,0; 8,8; 3,6; 9,5; 2,8; 6,5; 13,3; 9,9; 9,3; 8,7; 7,2; 6,2; 2,6; 3,7; 4,4; 4,1}.
Произвести группировку заводов по этому признаку с разбиением на 4 равных интервала. Построить гистограмму распределения ОВП для частот nk и относительных частот 100k%, определить средний ОВП, моду и медиану распределения. Данные о заработной плате работников двух цехов приведены в таблице
| № цеха | Январь | Февраль | ||
| Средняя зарплата, грн | Фонд зарплаты, грн | Средняя зарплата, грн | Число работников | |
| 1 | 380 | 41800 | 350 | 110 |
| 2 | 420 | 50400 | 400 | 130 |
Вычислить среднюю зарплату по заводу за январь, февраль и за два месяца.
- Распределение работников двух отраслей А и В по уровню квалификации характеризуется данными, %
| Отрасль | Тарифный разряд | ||||
| 2 | 3 | 4 | 5 | 6 | |
| А | 9 | 20 | 35 | 22 | 12 |
| В | 5 | 17 | 30 | 29 | 19 |
Для каждой отрасли определить средний уровень квалификации (по тарифному разряду) и моды распределений.
- По проценту высоколиквидных активов среди всех активов 20 банков распределяются следующим образом
| Процент высоколиквидных активов | 0 -10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 | 60-70 | >70 |
| Число банков | 1 | 4 | 7 | 3 | 3 | 1 | 1 | 0 |
Определить средний процент высоколиквидных активов, моду и медиану распределения.
5. Денежный оборот 3-х фирм оценивается данными: 200; 300; 700 грн/час. Определить среднее арифметическое и среднее гармоническое значение оборота. Каков финансовый смысл этих двух показателей?
