Тема Основные понятия статистики 5

Вид материала

Контрольные вопросы

Содержание 3.2. Cреднее гармоническое 3.3. Среднее геометрическое 3.5. Свойства среднего арифметического

Подобный материал:

• Понятие, значение и задачи статистики. Основные понятия и категории статистики, 38.18kb.
• Тема: Основные понятия и определения, 121.92kb.
• Тема: Основные понятия и определения, 164.71kb.
• План урока: Орг момент. Повторение изученного. Объявление темы. Изучение нового материала., 66.27kb.
• Курс «Вероятность» является вторым в ряду вероятностно-эконометрических курсов Вероятность, 32.07kb.
• Задачи статистики рынка Система показателей статистики рынка Информационная база статистики, 1574.49kb.
• Структурно курс состоит из 15 тем: Тема Введение. Предмет, цели и задачи курса Тема, 140.87kb.
• Тема Психофармакотерапия и клиническая психология Тема Основные понятия в психфармакотерапии, 1195.06kb.
• Тема Территориальная организация населения: основные понятия и концепции, 2494.7kb.
• Тема Территориальная организация населения: основные понятия и концепции, 2373.94kb.

3.2. Cреднее гармоническое

С


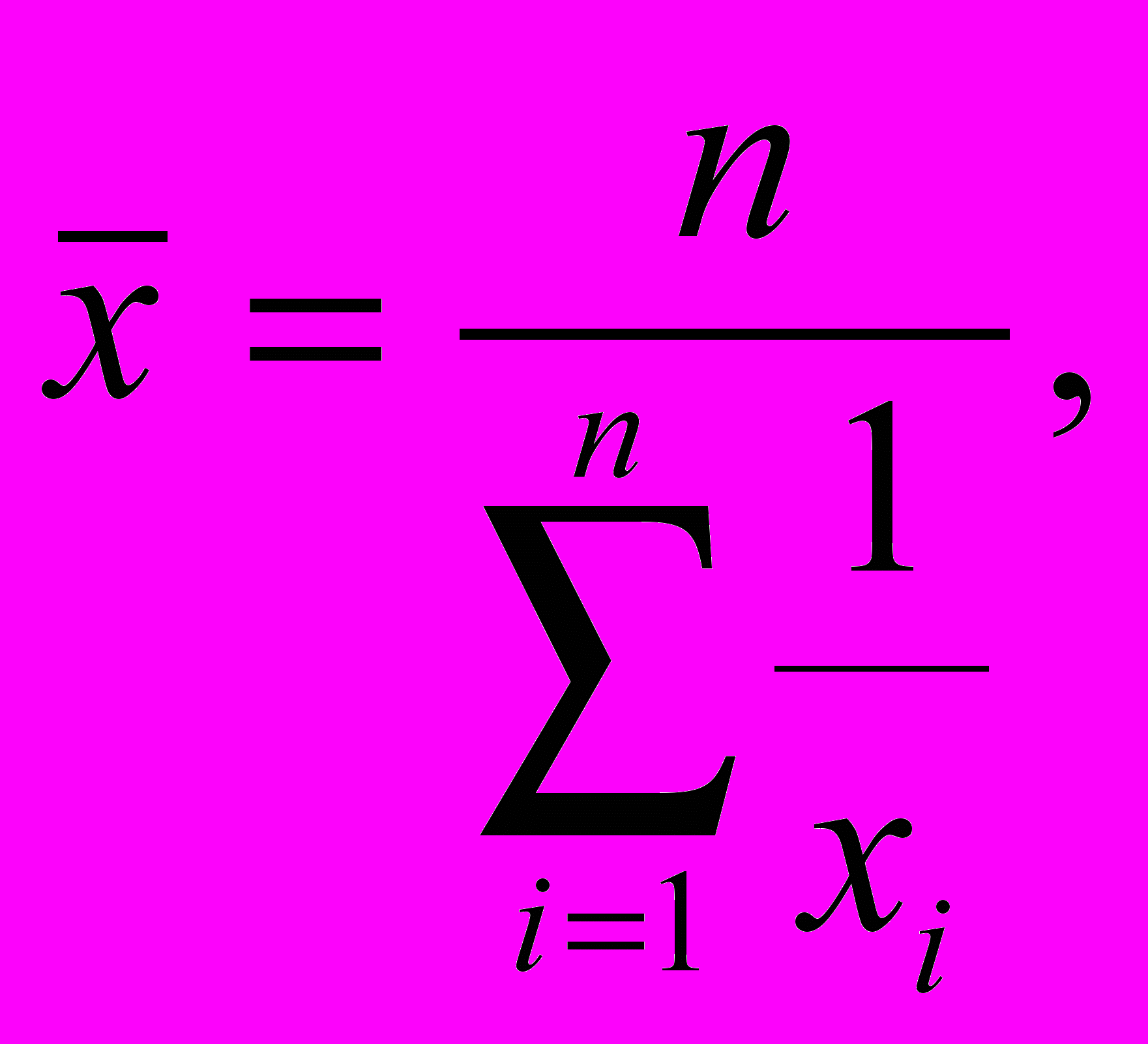
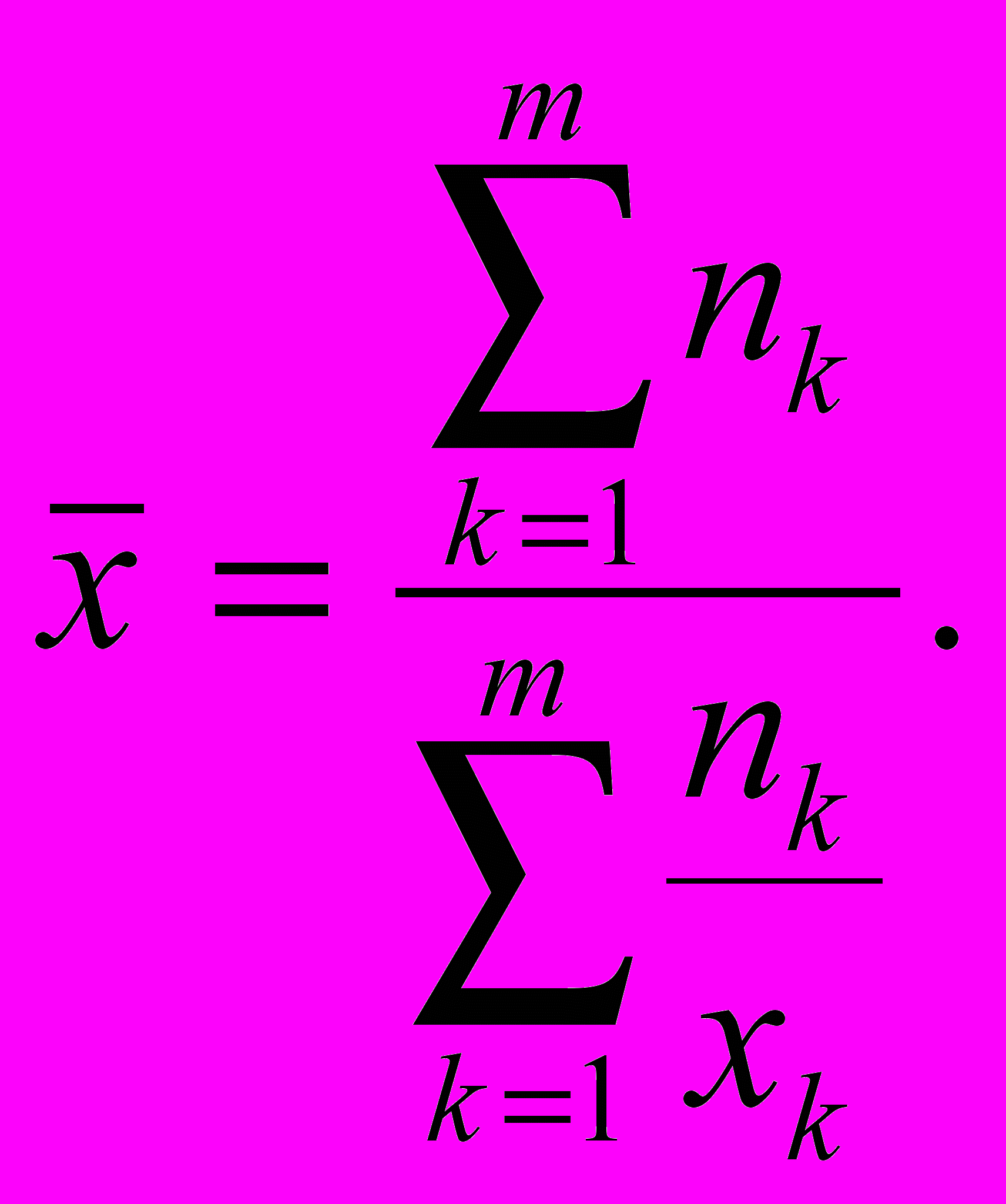
реднее гармоническое определяется формулами

З
десь (3.3) определяет невзвешенное, а (3.4) – взвешенное среднее.

Появление этого типа усреднения связано с двумя аспектами. С одной стороны, среднее гармоническое возникает при вычислении средней производительности при фиксации времени. Другое приложение- при вычислении обратных показателей. Рассмотрим примеры.

Пример 3.4. Из Киева до Белой Церкви грузовой автомобиль едет со скоростью V₁=80 км/час, а обратно со скоростью V₂= 60 км/час. Какова средняя скорость?

Среднее арифметическое, очевидно, равно 70 км/час. Если, однако, ввести условие одинакового времени при движении с заданными и со средней скоростью, то результат будет иным. Действительно, время в пути туда S/V₁ и обратно S/V₂ должно равняться времени движения 2S/V_ср со средней скоростью V_ср, то есть


S/V₁+S/V₂=2S/V_cp  V_cp=2/(1/V₁+1/V₂)=2/(1/80+1/60)=68,6 км/час.

Отсюда видно, что средняя скорость определяется как среднее гармоническое (3.3).

С
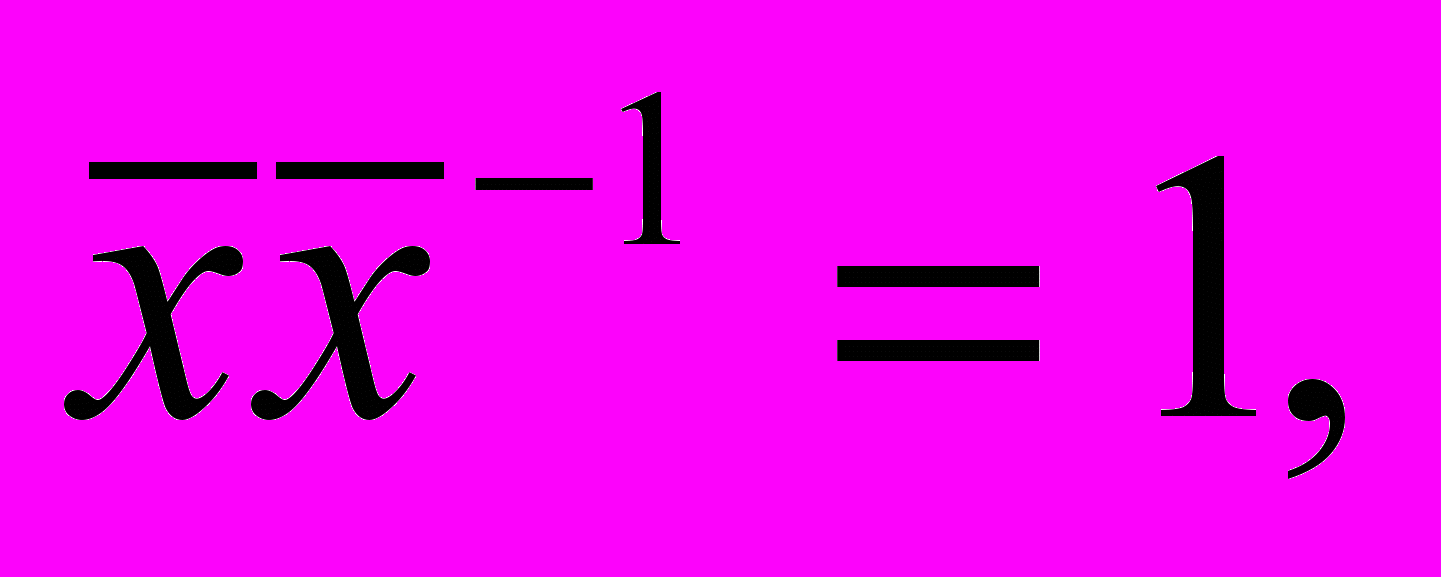
другой стороны, эта формула справедлива при вычислении так называемых обратных показателей. Обратными называют относительные показатели, имеющие обратные размерности. Например, измеряя производительность труда величиной х [деталей/час], можно пользоваться и обратным показателем х ^-1[час/деталь], определяющим трудозатраты времени на производство одной детали. Другие примеры: затраты капитала в единицу времени [грн/час] и время оборота денежной единицы [час/грн]; число заявок на обслуживание[заявок/час] и период времени поступления заявок [час/заявка]. Вычисляя прямой показатель как среднее арифметическое (3.1) и принимая


п
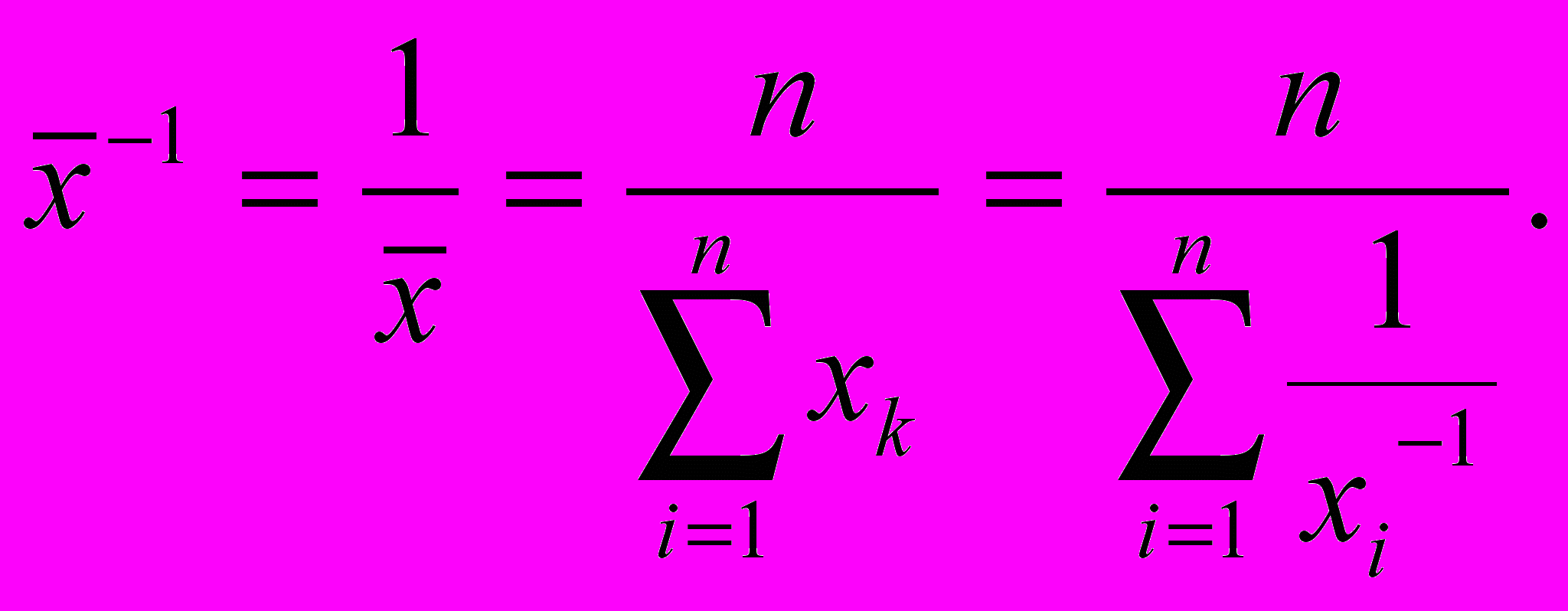
олучим для обратного показателя


Пример 3.5. Производительность труда Артема х₁=2 дет/час, Бориса х₂=3 дет/час и Влада – 7 дет/час. Каково среднее время выработки одной детали ?

Т
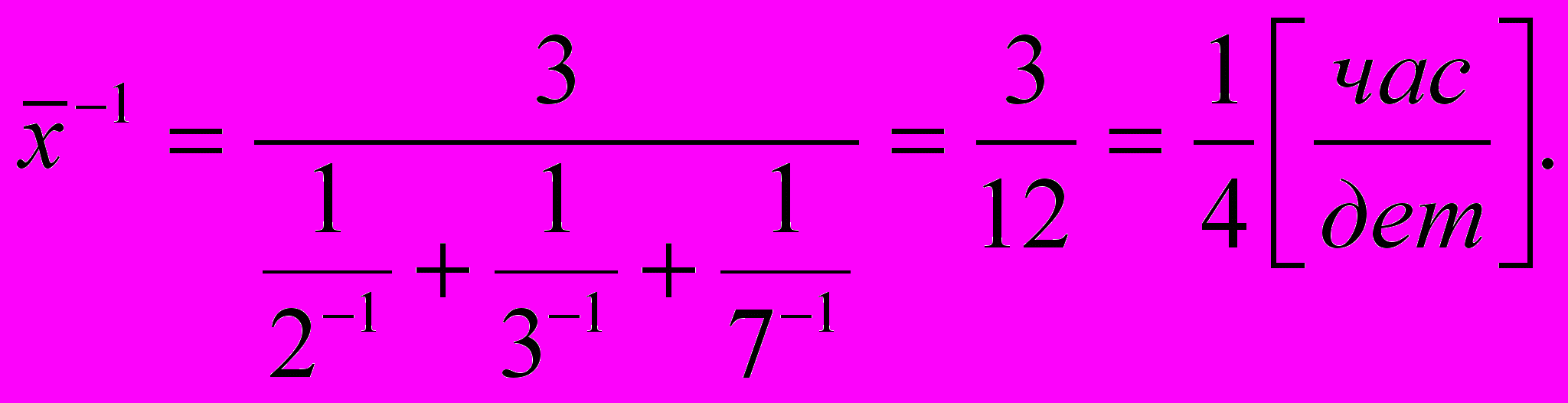
ак как средняя производительность этой бригады (2+3+7)/3=4 дет/час, то время на изготовление одной детали ¼ часа или 15 мин/дет. Тот же результат получим с помощью (3.3)

Иначе говоря, здесь среднее гармоническое есть не что иное, как обратное значение среднего арифметического.

3.3. Среднее геометрическое

В ряде случаев относительные показатели (например, темпы роста) не складываются, а перемножаются. В этом случае используется среднее геометрическое





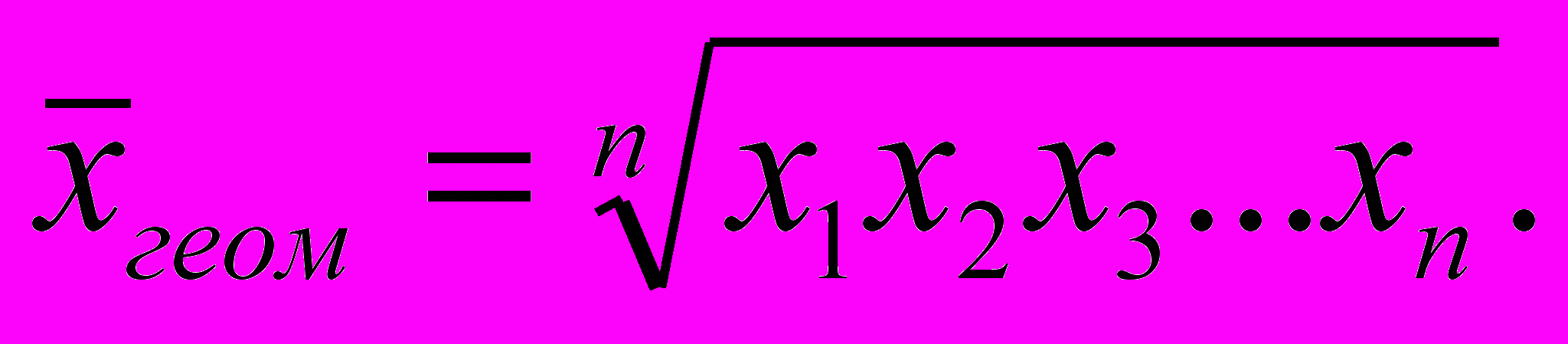
Этот вид усреднения встретится далее в теме “Индексы”.

3.4. Среднеквадратичное

О

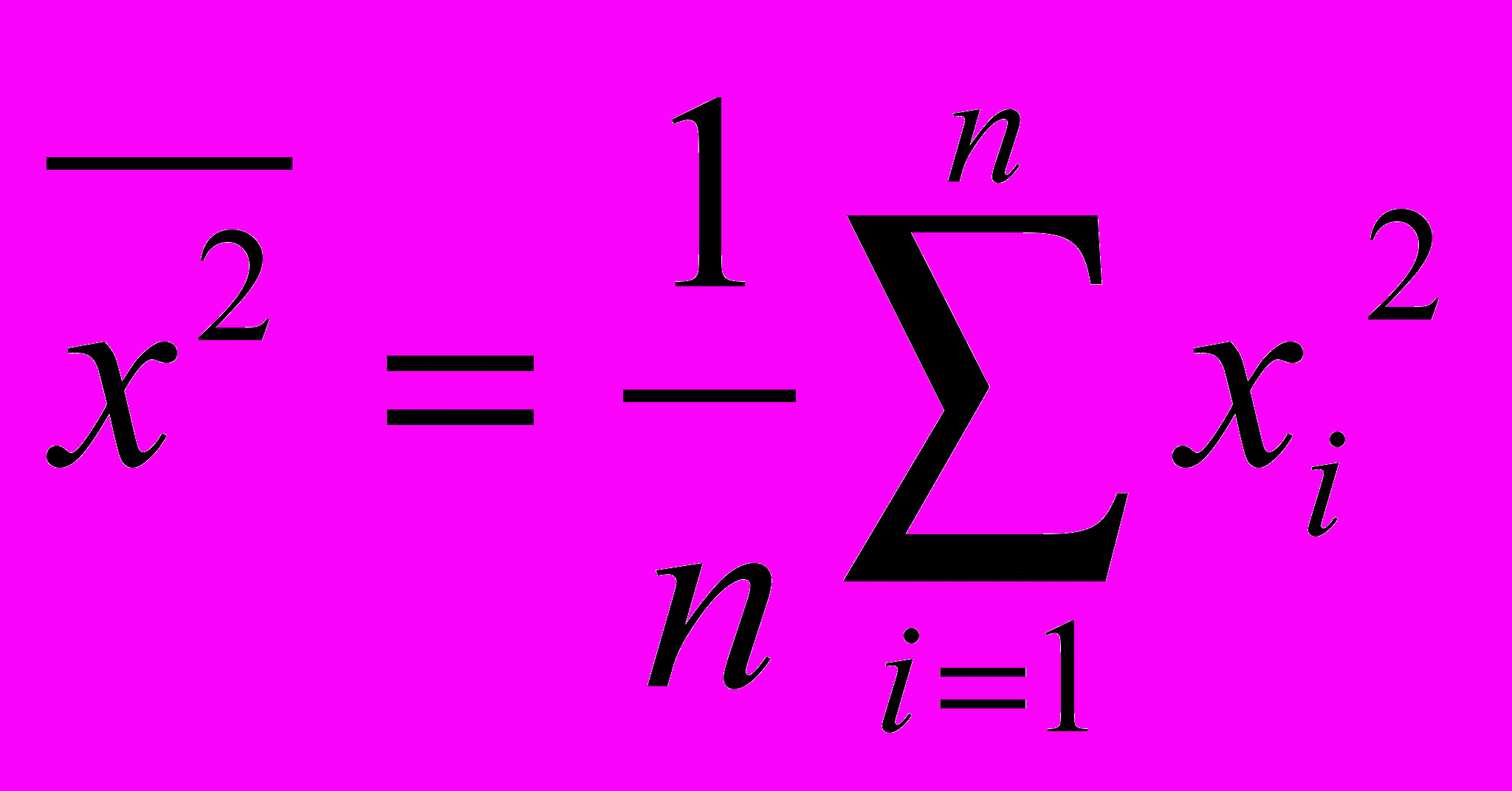
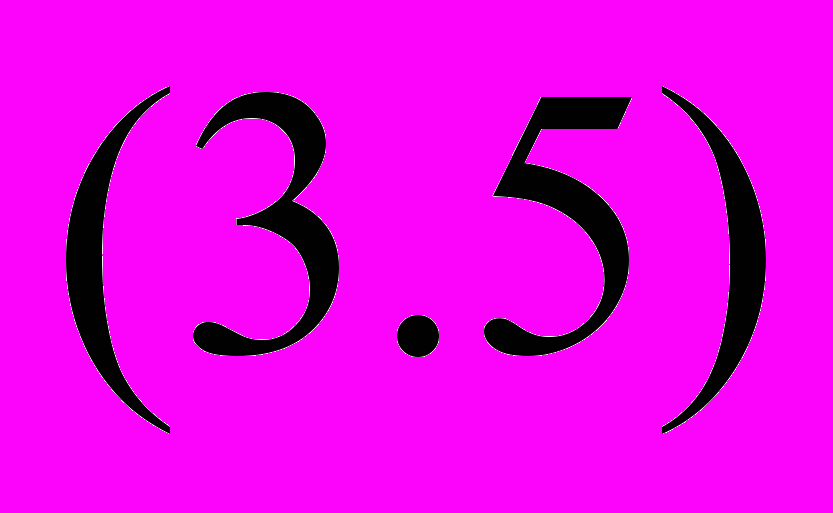
перацию арифметического усреднения применяют не только к исходным величинам x_i выборки, но и к квадратам x_i², в результате получим средний квадрат

п
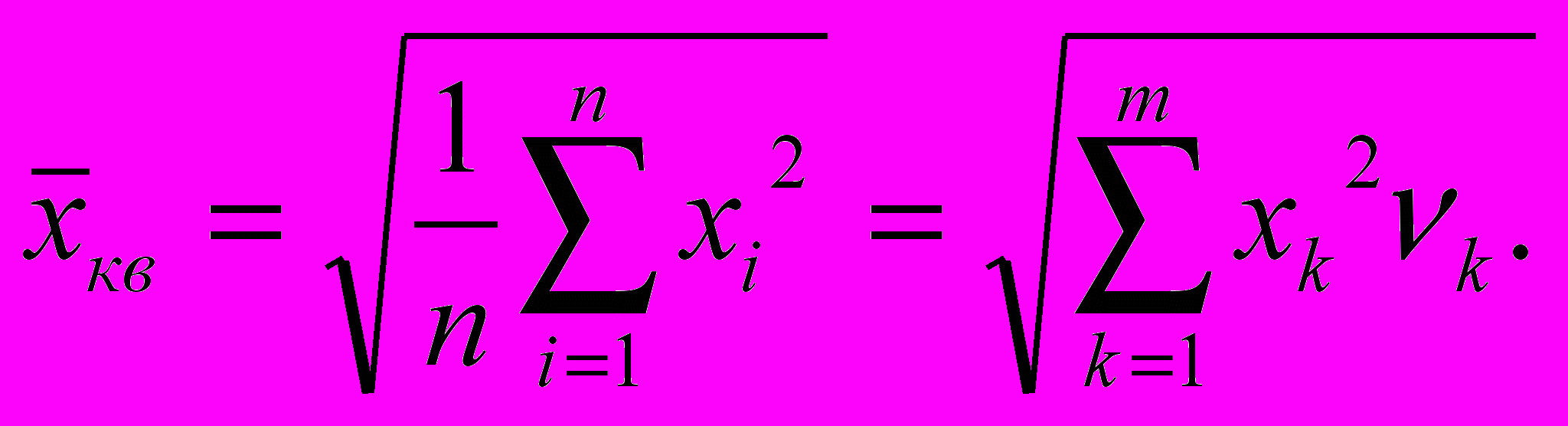
ри невзвешенном усреднении или

при взвешенном. Поскольку размерность среднего квадрата равна квадрату размерности х, возврат к исходной размерности х осуществляется извлечением квадратного корня из (3.5), (3.6)

Эта средняя величина называется среднеквадратичной. Она наиболее часто используется при оценке ошибок измерений.

И
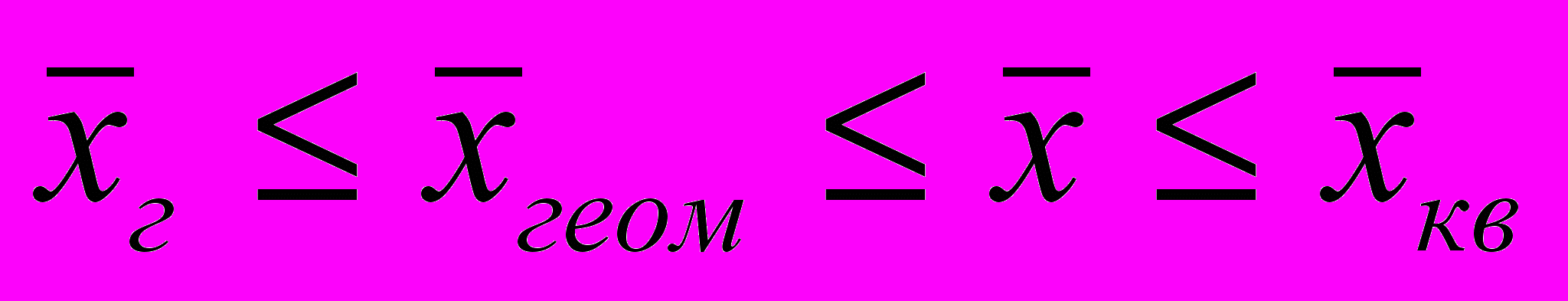
меет место следующее соотношение между средними величинами для одной и той же выборки

Следует отметить, что в подавляющем большинстве случаев в статистике используется среднее арифметическое. Эта величина наиболее проста и имеет ряд замечательных свойств.

3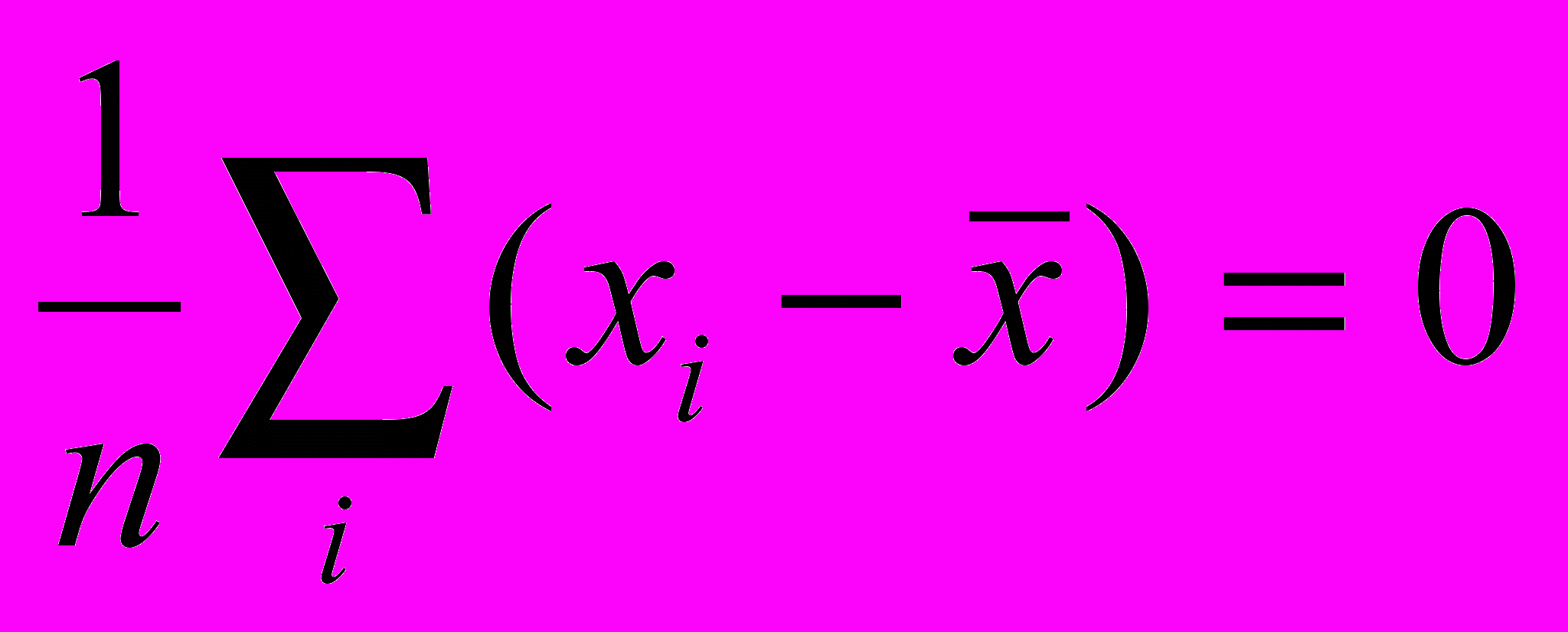
.5. Свойства среднего арифметического

1. Среднее арифметическое центрированных величин равно 0, т.е.
   
2. Д
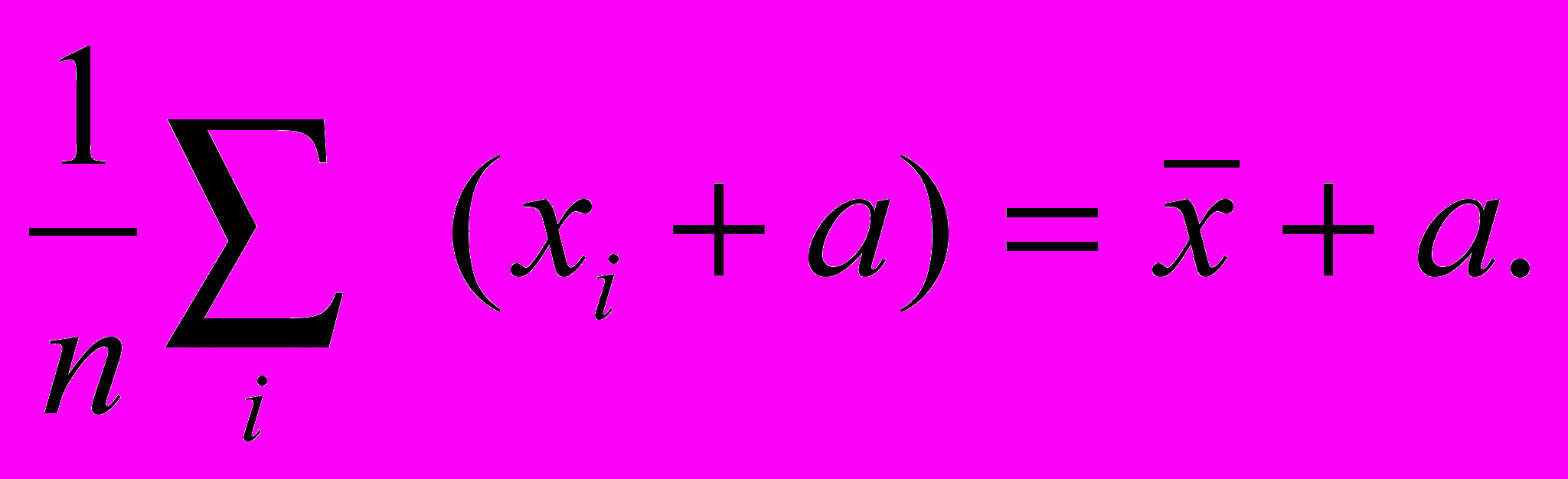
   обавление постоянной а к каждому элементу x_i изменяет среднее значение на ту же величину
   

3
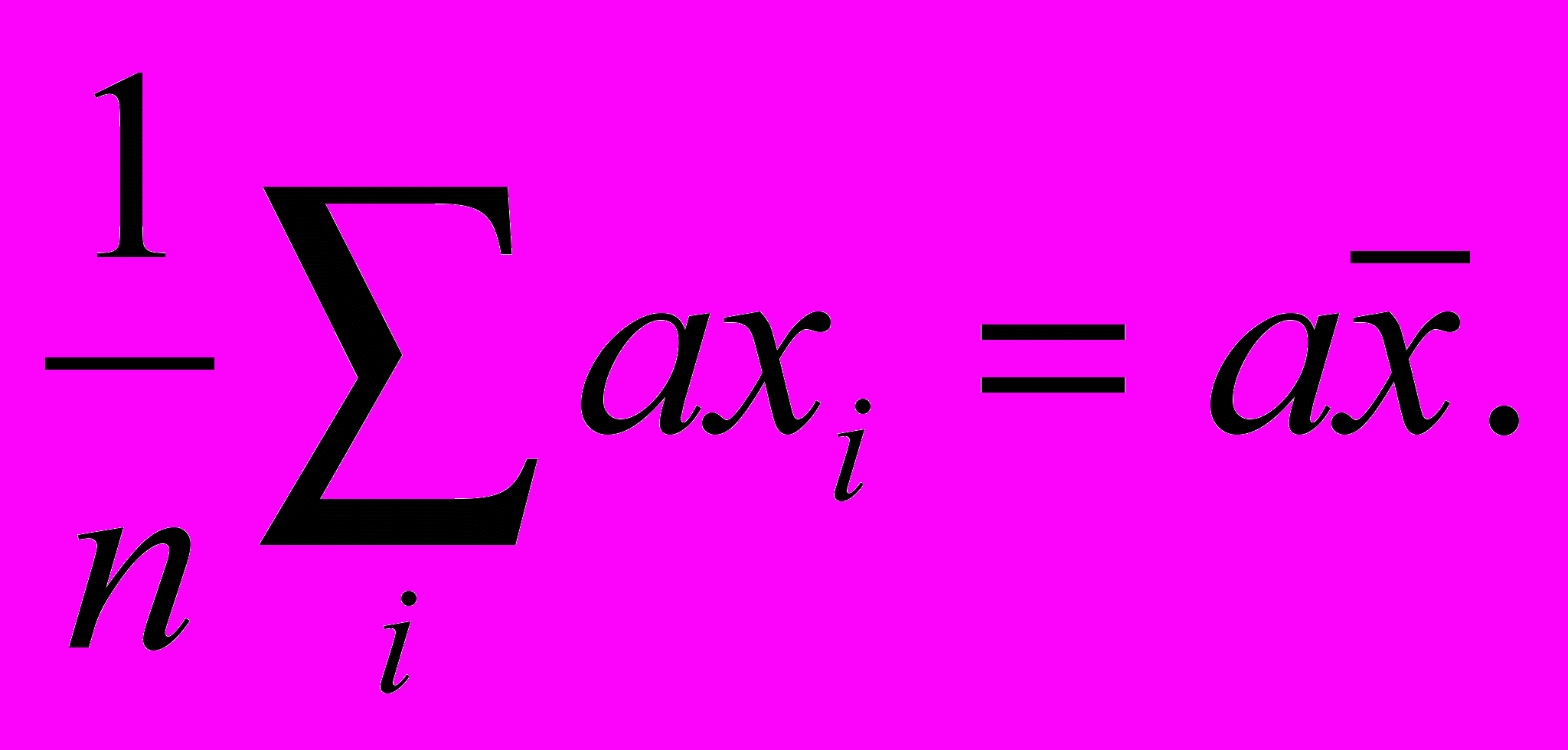
. Умножение каждого элемента х_i на постоянную величину а изменяет среднее арифметическое в а раз

4
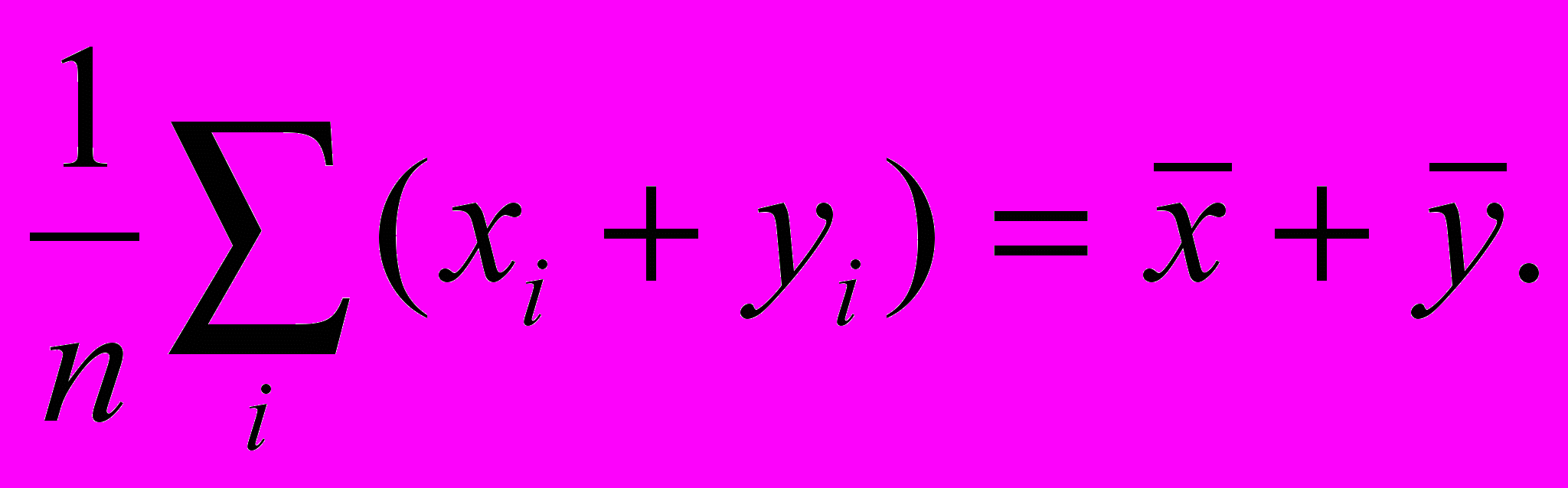
. Среднее арифметическое сумм двух выборок одинакового объема n равна сумме средних (свойство аддитивности)

Кроме этих достаточно очевидных свойств в математической статистике выборочное среднее (3.1), (3.2) рассматривается как оценка математического ожидания и обладает свойствами несмещенной, состоятельной и эффективной оценки. Это значит, что с ростом объема выборки среднее арифметическое приближается к математическому ожиданию и, кроме того, является наиболее точной оценкой. Все отмеченные свойства и предопределили широкое применение средней арифметической величины в статистике.