Geum.ru

Тема Основные понятия статистики 5

Вид материалаКонтрольные вопросы
2.2. Выбор интервалов группирования
2.3. Ряды распределения
Такие распределения, характерные для непрерывных величин, получили название гистограммы.
Таблица 2.4 (млн. грн.)
Подобный материал:
1   2   3   4   5   6   7   8

2.2. Выбор интервалов группирования


При использовании атрибутивных признаков группы образуются сравнительно просто (скажем, разделение людей по цвету глаз, волос). А как разбивать людей на группы по возрасту, росту, весу? Здесь границы интервалов условны и зависят от цели исследования. Если требуется одеть и обуть роту солдат, то надо знать размеры одежды и обуви каждого, а склад должен наполняться на основе статистических данных. Распределение мужчин по росту можно разбить на два интервала (выше среднего (>176см) и ниже среднего (<176cм)), а можно и с интервалом 1 см. Оба варианта мало пригодны: первый дает недостаточно информации, второй приводит к изломанным графикам распределений. Число m интервалов группирования, очевидно, зависит от объема выборки n. Чем больше выборка, тем больше статистической информации и тем больше интервалов группирования можно построить.

В области значений непрерывного признака X=[xmin,xmax] выборки объема n необходимо определить число интервалов группирования m. Чаще всего используется группировка с равными интервалами ширины h (равномерное квантование), при этом

h=( xmax - xmin)/m

В математической статистике рекомендуется оценивать m в зависимости от объема выборки формулой Стерджесса

m=[1+3,322lgn] (2.1)

где [.] означает округление до целого числа. Численные значения этой логарифмической зависимости приведены в таблице 2.1


Таблица 2.1

n N
10
50
100
1000

m M
4
7
8
11


Реже встречается неравномерное квантование области значений Х на интервалы с разной шириной hi, i=1,2,…,m. В этом случае может использоваться, например, метод равных частот.

Области значений Х внутри интервалов рассматриваются как сегменты [ximin ,ximax), замкнутые слева и открытые справа. Например, при разбиении целочисленной числовой оси на интервалы шириной 10 первый интервал включает значения 0 - 9, второй 10 – 19, третий 20 - 29 и т.д. На непрерывной числовой оси правые границы становятся равными 9,999, 10,999 и т.д., с числом знаков после запятой, задаваемым условиями задачи (к примеру, не существует 0,999 доллара).

2.3. Ряды распределения


Ряды распределения определяют наиболее общие закономерности группировок с количественными (вариационными) признаками. На их основе определяются частные характеристики (параметры распределения): средние величины, параметры вариации (отклонения от среднего), асимметрии, эксцесса и др.

В теории вероятностей изучаются родственные понятия ряда вероятностей и плотности вероятности. В статистике на основе ограниченного набора данных строятся ряды распределения частот или относительных частот по группам. Относительная частота события А, как следует из п.1.2, может рассматриваться как оценка вероятности.

Рассмотрим пример. Пусть k – число детей в семье (k=0,1,2,..,m-1), nk – число семей в городе, имеющих k детей, n – общее число семей, так что


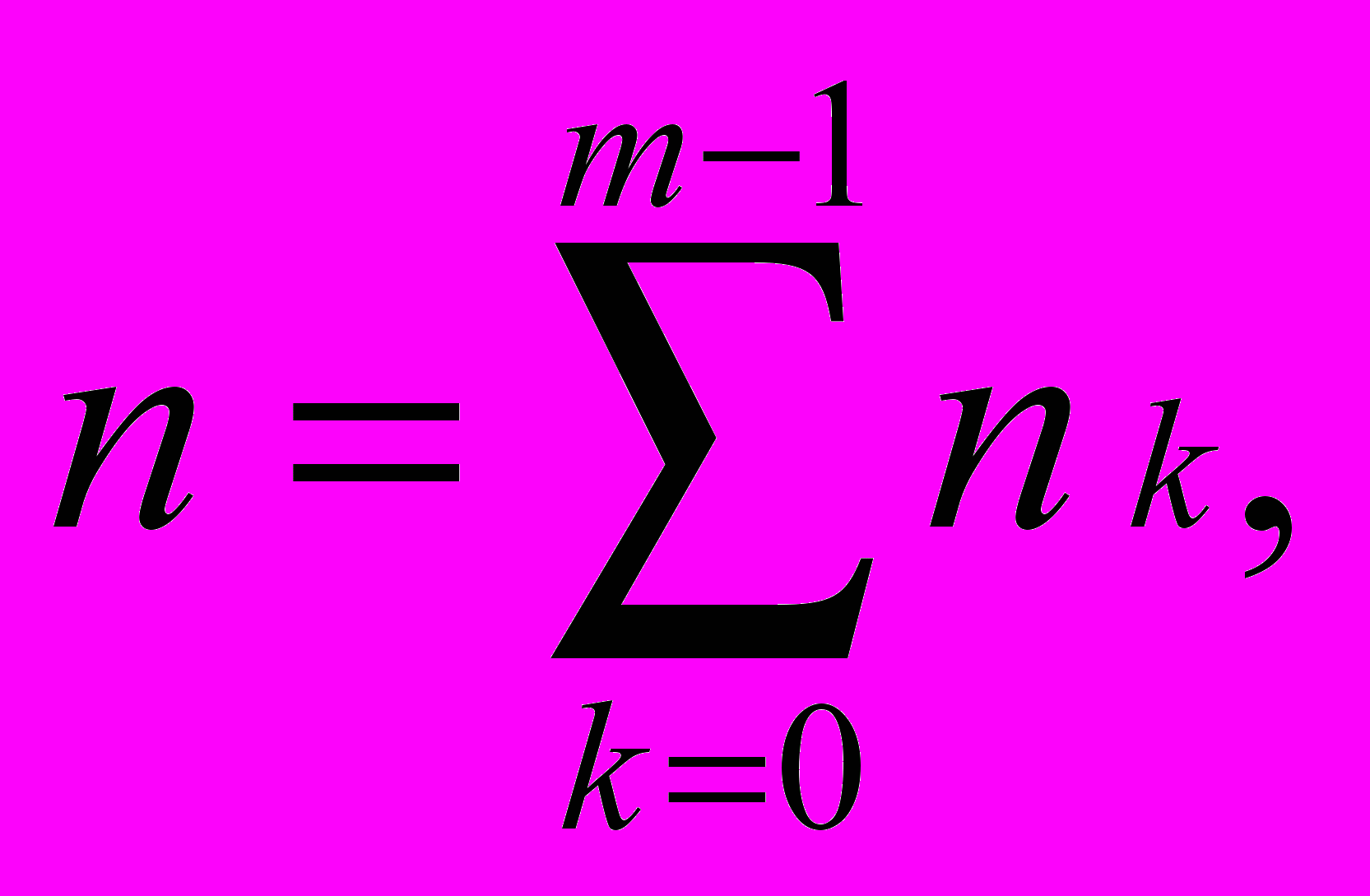
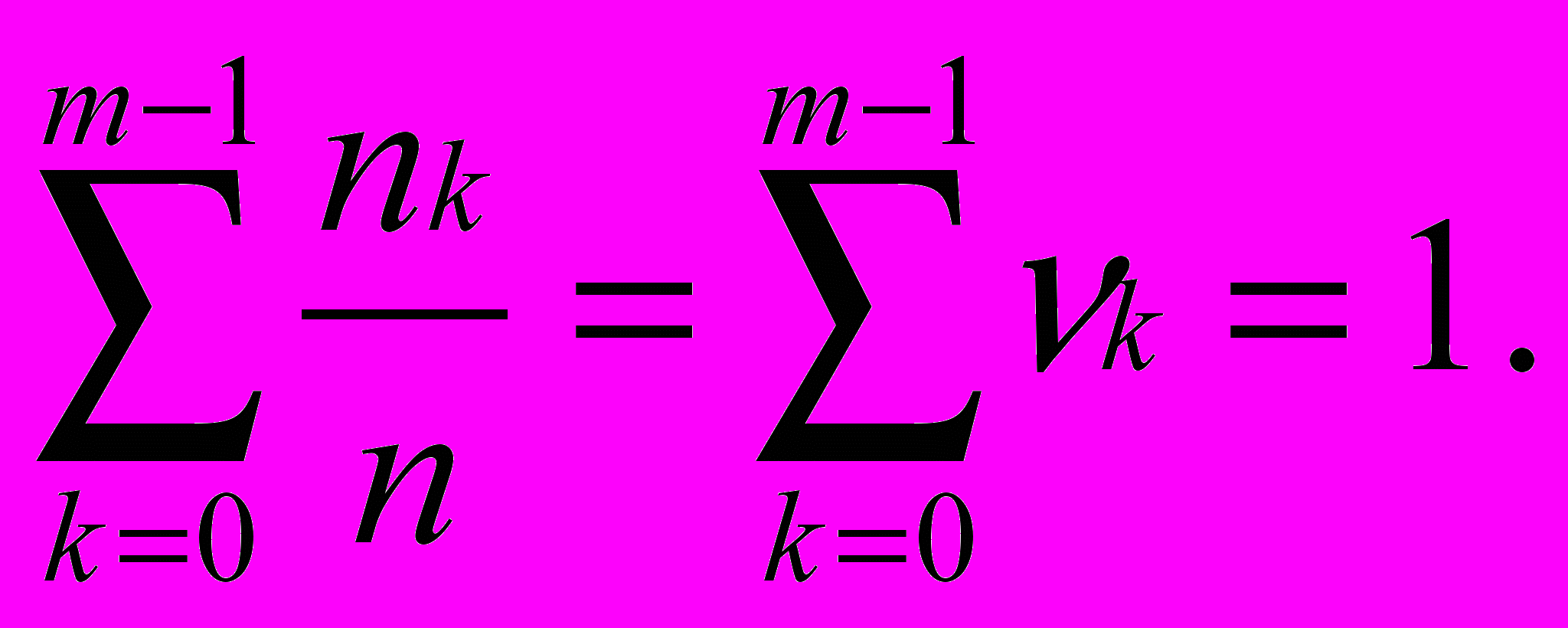(2.2)


Эти равенства называют условиями нормировки. Значения nk определяются как частоты k-й группы, а k – как относительные частоты (частости). В качестве примера в таблице 2.2 приведены данные о количестве семей г. Киева (в тыс.), имеющих до 5 детей (m=6). Отметим, что здесь группировка упорядочена, т.е. значения признака расположены в порядке нарастания. По приведенным данным нетрудно построить график


Таблица 2.2

К
0
1
2
3
4
5


nk, тыс.
79
258
205
86
23
3
645

k
0,12
0,39
0,31
0,13
0,035
0,005
1





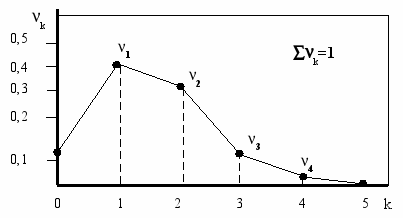
Рис. 2.1


ряда распределения частот (частостей) числа детей в семьях города, рис.2.1. Этот график называется полигоном распределения. Полигоны характерны для дискретных случайных величин.

Построение рядов распределения для непрерывных величин начинается с разбиения области значений Х на интервалы шириной h (при равномерном квантовании), при этом число интервалов рекомендуется выбирать в зависимости от объема выборки n согласно (2.1). В качестве примера приведем распределение числа банков nk в зависимости от уставного капитала до 30 млн. грн. с интервалами шириной h=5 млн. грн. Общее число банков равно n=120. Распределение дано в таблице 2.3 и изображено на графике рис.2.2а По вертикальной оси откладываются частоты nk или частости k, по горизонтальной – капиталы с интервалами по 5 млн. грн. Как и для полигонов, сумма частостей k равна 1.

Такие распределения, характерные для непрерывных величин, получили название гистограммы.


Таблица 2.3

Капитал, млн. грн.
0-

4,999
5-

9,999
10-

14,999
15-

19,999
20-

24,999
25-

29,999


nk
62
26
18
8
4
2
120

k
0,52
0,22
0,15
0,07
0,03
0,01
1

Fk
0,52
0,74
0,89
0,96
0,99
1,0









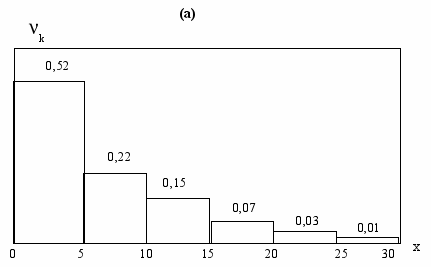
Рис. 2.2


Наряду с распределением относительных частот k иногда используют понятие накопленной частоты

F
k=k, k>=1,

для которой вместо полигона или гистограммы строят график кумулянтной кривой (рис.2.2б).


Пример 2.1. Число хi телевизоров, проданных магазином в i-й день, за 20 дней описывается выборкой

{xi}n={4, 3, 6, 6, 5, 3, 2, 3, 5, 4, 4, 2, 6, 7, 4, 7, 3, 5, 5, 5}.

Необходимо построить ряд распределения частот и относительных частот и кумулянтную кривую.

После упорядочения выборки в порядке возрастания хi нетрудно подсчитать распределение частот nk по группам, k=1 – 6, которое приведено в таблице 2.4. Здесь же даны частости k и накопленные частоты Fk. Соответствующие им графики приведены на рис.2.3a,б.


Таблица 2.4

xi
2
3
4
5
6

7


nk
2
4
4
5
3
2
20

k
0,1
0,2
0,2

0,25
0,15
0,1
1

Fk
0,1
0,3
0,5
0,75
0,9
1,0




В качестве следующего примера рассмотрим построение гистограммы с неравными интервалами группирования, формируемыми на основе метода равных частот. В этом случае в каждый интервал попадает равное число элементов выборки, а объем выборки n должен быть кратен числу m интервалов.







Рис.2.3


Пример 2.2. Веса 20 человек (в кг.) в порядке их нарастания описываются упорядоченной выборкой {xi}={(60, 62, 63, 65, 66 ); (68, 70, 70, 72, 73); (74, 76, 76, 77, 77); (78, 81, 81, 85, 86)}. Приняв m=4, построить гистограмму распределения весов.

В приведенной выборке группировка уже произведена и группы обозначены круглыми скобками. Ширина каждого интервала равна:

h1=68-60=8; h2=74-68=6; h3=77-73=4; h4=86-78=8.

Значения fk ряда определяются так, чтобы площадь под гистограммой на каждом интервале равнялась частости k (оценке вероятности), а суммарная площадь – 1 (как и под плотностью вероятности в теории вероятностей). Таким образом

f1=1/h1=1/32; f2=2/h2=1/24; f3=3/h3=1/16; f4=4/h4=1/32.

График этой гистограммы изображен на рис.2.4.




Рис.2.4


Результаты группирования величин или явлений часто представляются в виде прямоугольных или секторных диаграмм, которые привлекают своей наглядностью. Умноженные на 100 значения относительных частот дают их процентные соотношения.

В заключение заметим, что графики и диаграммы удобны при анализе распределения одномерной величины Х. Многомерные признаки чаще всего заставляют нас обращаться к табличному способу представления сгруппированных данных. В этих случаях используют так называемые статистические таблицы. В них показатели обычно располагаются по колонкам таблицы, а объекты – по строкам. Примером начала такой таблицы является таблица 2.4.


Таблица 2.4 (млн. грн.)

Банк

№
Капитал
Активы
Депозиты,

вклады
Кредиты,

инвестиции

1
2
3
4
5

1
27,0
137
37,2
73,8

2
24, 6
108,7
54,1
69,2

3













Ряды распределения содержат наиболее полную информацию о статистических закономерностях массовых явлений. На их основе определяются частные характеристики распределения: средние величины; параметры вариации, асимметрии, эксцесса; мода, медиана и др. Они изучаются в следующих темах.