Тема Основные понятия статистики 5

Вид материала

Контрольные вопросы

Содержание Контрольные вопросы Тема 3. Средние величины 3.1. Среднее арифметическое

Подобный материал:

• Понятие, значение и задачи статистики. Основные понятия и категории статистики, 38.18kb.
• Тема: Основные понятия и определения, 121.92kb.
• Тема: Основные понятия и определения, 164.71kb.
• План урока: Орг момент. Повторение изученного. Объявление темы. Изучение нового материала., 66.27kb.
• Курс «Вероятность» является вторым в ряду вероятностно-эконометрических курсов Вероятность, 32.07kb.
• Задачи статистики рынка Система показателей статистики рынка Информационная база статистики, 1574.49kb.
• Структурно курс состоит из 15 тем: Тема Введение. Предмет, цели и задачи курса Тема, 140.87kb.
• Тема Психофармакотерапия и клиническая психология Тема Основные понятия в психфармакотерапии, 1195.06kb.
• Тема Территориальная организация населения: основные понятия и концепции, 2494.7kb.
• Тема Территориальная организация населения: основные понятия и концепции, 2373.94kb.

Задачи

2.1. Число комнат в 24 квартирах дома описывается выборкой


x_i}={2, 3, 1, 3, 2, 2, 1, 3, 2, 3, 1, 3, 2, 2, 3, 2, 3, 3, 1, 2, 2, 3, 3, 2}.


Построить ряд распределения частот и частостей числа квартир в доме.

2.2. Возрастная структура населения характеризуется данными (млн. чел.)

Возраст, (лет)	0 – 20	20 – 40	40 – 60	60 – 80
Мужчины	12	15	16	9
Женщины	10	16	14	14

Построить гистограммы возрастных структур населения (в относительных частотах).

2.3. Задолженность предприятий (в млн. грн.) по краткосрочным кредитам в прошлом году составляла (по месяцам)


126 174 112 96 80 155 138 105 126 149 74 165


Построить гистограмму с разбиением на 3 интервала методом равных частот.

2.4. Процент работоспособного населения по районам страны определяется выборкой

{x_i}={82, 92, 66, 85, 63, 75, 71, 83, 79, 68, 58, 65, 62, 54}.

Построить гистограмму распределения работоспособного населения с группированием на 3 равных интервала.

2.5. Распределение семейных доходов Х (грн) населения характеризуется таблицей

Х	0-100	100-200	200-300	300-400	400-500	500-600	600-700	>700
k	1/3	2/9	1/6	1/9	1/18	1/18	1/36	1/36

Для 20 млн. семей построить ряды распределения частот, относительных и накопленных частот.

Контрольные вопросы

1. Что такое группировка статистических данных? С какой целью она проводится?

2. Какие величины называют дискретными, непрерывными? Как называют ряды распределения для дискретных и непрерывных величин (признаков)?

3. Дайте определение частоты, относительной частоты (частости), накопленной частоты.

4. Какие способы используются в статистике для представления рядов распределения? В каких случаях применяются графики, статистические таблицы?

5. Как выбираются интервалы группирования непрерывных величин? От чего зависит число возможных интервалов?

6. Что такое условие нормировки ряда распределения? Как его выразить в процентах?

7. Как строится гистограмма с неравными интервалами методом равных частот?

Тема 3. Средние величины

Наиболее распространенными и информативными статистическими показателями являются средние величины. Как правило, первым результатом обработки статистических данных является вычисление среднего значения изучаемой совокупности. Зная средний процент работоспособного населения, можно правильно планировать и распоряжаться трудовыми ресурсами. Средняя стоимость жилья позволяет оценивать возможные прибыли жилого строительства, а ввода и эксплуатации цифрового сотового телефона – прибыли телефонной компании. Чтобы рассчитать кубатуру большого лесного массива, не надо пересчитывать все деревья, достаточно знать среднюю плотность и площадь леса.

При вычислении средних величин не следует забывать, что изучаемая выборочная совокупность наблюдения должна быть репрезентативной и однородной. Хороший пример нарушения одного из условий: усредняя состояния одного миллиардера и тысячи нищих, заключаем, что в среднем все миллионеры.

В общей теории статистики принято рассматривать различные типы усреднения, приводящие к средним арифметическим, гармоническим, геометрическим, квадратичным величинам.

3.1. Среднее арифметическое

Д
ля выборочной совокупности {x_i}⁽ⁿ⁾={x₁,x₂,x₃,…,x_n} среднее арифметическое определяется как





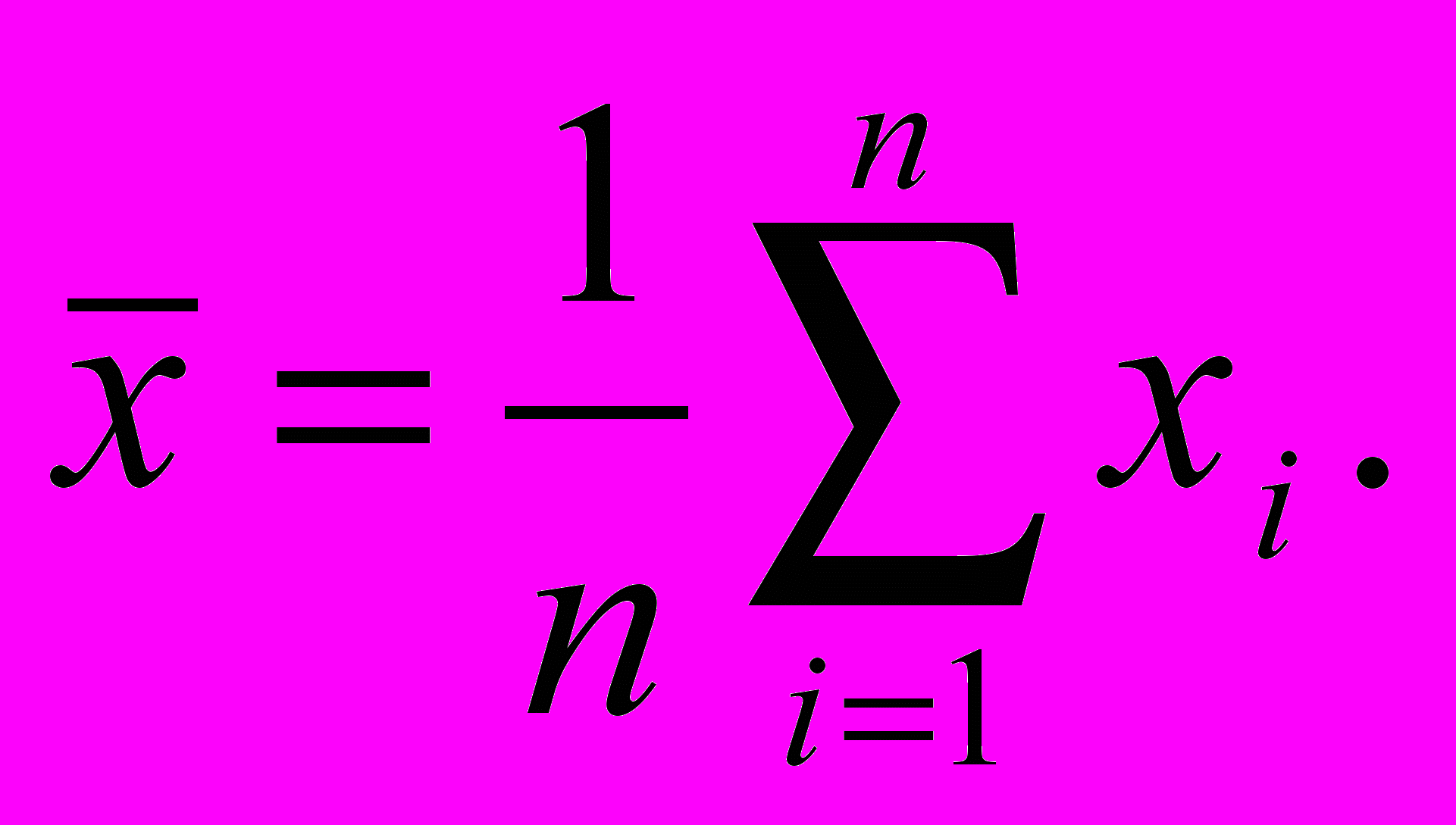
Э
та формула определяет так называемое невзвешенное среднее. При группировании выборки на m дискретных значений (для полигонов распределения) или m интервалов со средними точками х_k получим взвешенное среднее арифметическое





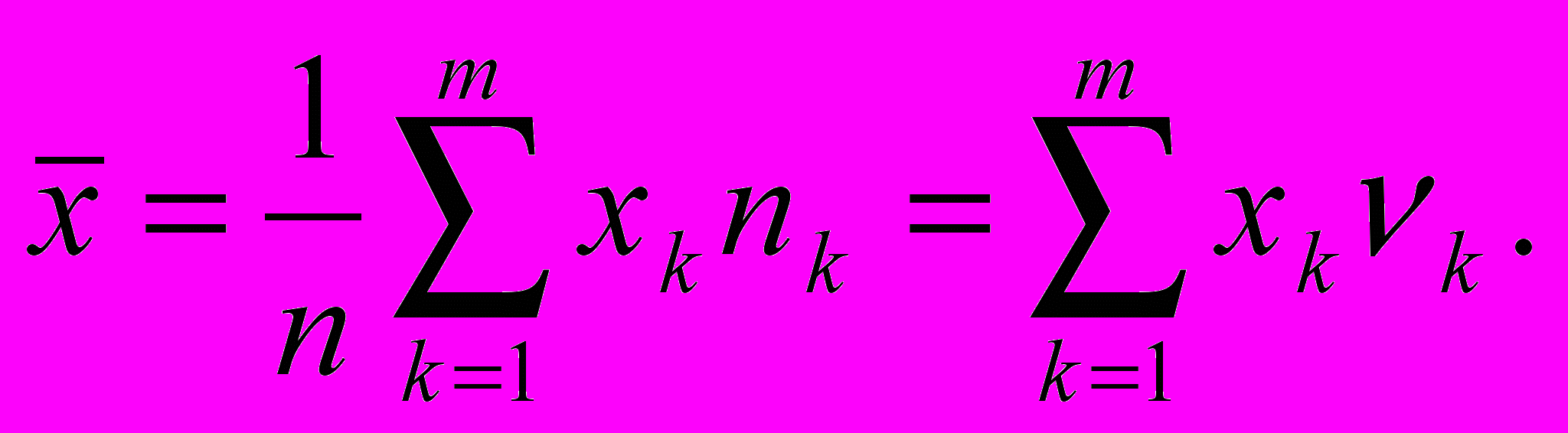
Здесь, как и ранее, n_k и _k – частоты и относительные частоты к-го значения дискретной величины (для полигонов распределения) или к-го интервала непрерывной величины (для гистограммы). Формулы (3.1), (3.2) еще называют выборочными средними.


Пример 3.1. Результаты сдачи экзамена по “Статистике” группой из 26 студентов: “отлично” – 4 студента, “хорошо” – 9 студентов, “удовлетворительно” – 10 студентов, “неудовлетворительно” – 2 студента. Определить средний балл.

С
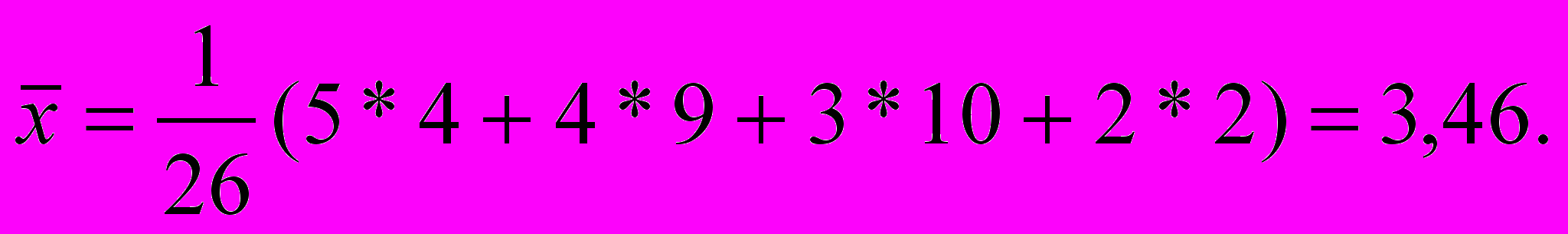
огласно (3.2) получим


Пример 3.2. Распределение доходов D (грн) 40 работников фирмы задано таблицей

D	100 - 200	200 - 300	300 - 400	400 - 500	500 – 600
nk	4	8	15	10	3

Определить средний доход работника.

П
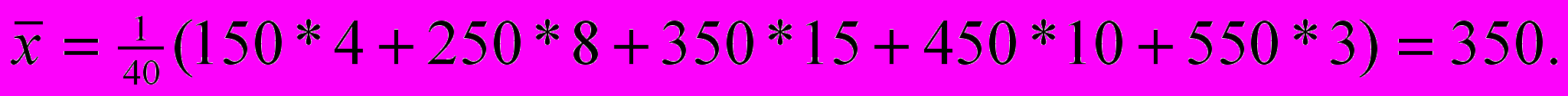
о формуле (3.2) имеем


Выборочное среднее в математической статистике рассматривается как оценка математического ожидания, тем более точная, чем больше объем выборки n.