Программа курса "Геометрия и алгебра"
| Вид материала | Программа курса |
- Рабочая программа учебной дисциплины «Алгебра и геометрия» Направление подготовки, 137.66kb.
- Рабочая учебная программа дисциплины (модуля) Алгебра и геометрия, 207.66kb.
- Примерная программа наименование дисциплины «Алгебра и геометрия» Рекомендуется для, 147.7kb.
- Рабочая программа по дисциплине б 2 математика. Алгебра и геометрия шифр и название, 370.36kb.
- Учебная программа по дисциплине алгебра и геометрия краснобаев Ю. Л. Требования к обязательному, 51.89kb.
- Правительство Российской Федерации Государственное образовательное бюджетное учреждение, 416.73kb.
- Календарный план учебных занятий по обязательной дисциплине «Алгебра и геометрия»,, 105.72kb.
- Программа курса :«Линейная алгебра и аналитическая геометрия», 38.96kb.
- Программа для поступающих на направление подготовки магистратратуры 010400 «прикладная, 30.56kb.
- Программа курса «Алгебра и геометрия», прикладная математика и информатика. 3 семестр,, 36.15kb.
Программа курса “Геометрия и алгебра”
1.Развитие понятия числа. Натуральные, целые, рациональные, вещественные, комплексные числа. Замкнутость числовых множеств относительно арифметических операций. Числовые кольца и поля. Теорема о минимальности поля рациональных чисел (среди числовых полей ). Иррациональные числа. Присоединение
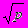к полю рациональных чисел, доказательство иррациональности 
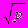, где p - простое число. Понятие об алгебраических и трансцендентных числах 2.Поле комплексных чисел. Сопряженные числа и действия c ними. Тригонометрическая форма комплексного числа. Формула Муавра, корни из единицы. Теорема о разложении многочлена в произведение линейных множителей над полем комплексных чисел ( без доказательства ) и ее вещественный аналог.
3. Отображения множества M в множество N, инъекции, сюръекции и биекции.
Размещения, сочетания, их число. Формула бинома Ньютона.
4. Мощность множества. Счетные и континуальные множества. Теоремы о счетности рациональных и алгебраических чисел. Теорема Кантора о мощности множества всех подмножеств множества M.
5. Линейное (векторное) пространство над числовым полем. Примеры: геометрические векторы, радиус-векторы, арифметическое n-мерное пространство, пространство многочленов. Следствия из аксиом. Теорема об обобщенной ассоциативности и коммутативности. Подпространства. Линейная зависимость. Отношение линейной выразимости между системами векторов и его транзитивность, умножение матриц. Эквивалентные системы векторов, теорема о замене. База и ранг системы векторов. Конечномерные и бесконечномерные линейные пространства. Базис и размерность. Координаты вектора в базисе. Изоморфизм линейных пространств. Изменение координат при изменении базиса. Пересечение и сумма подпространств. Прямая сумма. Построение базиса суммы.
6. Аффинная система координат (репер), изменение координат точки при изменении репера. Деление отрезка в заданном отношении, параметрическое задание прямой. Координаты центра тяжести.
7. Система линейных уравнений. Теорема Кронекера-Капелли. Метод Жордана- Гаусса и его матричная запись. Строчечный и столбцовый ранги матрицы и доказательство их равенства. Нахождение строчечной и столбцовой баз. Свойства матричных операций, обратная матрица, критерий ее существования, единственность. Решение матричных уравнений. Фундаментальная система решений однородной системы линейных уравнений. Связь множеств решений неоднородной и однородной систем; линейное многообразие, его размерность. Два способа задания подпространств и линейных многообразий. Задание прямых и плоскостей в аффинной системе координат, условия параллельности.
8. Евклидово и унитарное пространство. Длина вектора. Ортогональность. Запись скалярного произведения через координаты, матрица Грама. Неравенство Коши-Буняковского-Шварца, неравенство треугольника, теорема Пифагора. Линейная независимость ортонормированной системы векторов. Процесс ортогонализации, существование ортонормированного базиса. Изоморфизм унитарных пространств. Геометрический смысл линейного неравенства в декартовой системе координат. Условия перпендикулярности прямых и плоскостей.
9. Детерминант (определитель матрицы) и его свойства. Умножение подстановок. Разложение подстановок в произведение транспозиций. Сочетания, их число. Теорема Лапласа.
10. Правило Крамера. Интерполяционный многочлен. Ранг матрицы и его нахождение.
11. Линейные операторы, действия над ними, их матрицы. Изменение матрицы линейного оператора при изменении базисов. Ядро, образ, ранг, дефект линейного оператора. Линейные преобразования векторного пространства, подобие матриц. Инвариантные подпространства. Собственные векторы и числа. Характеристический многочлен. Теорема о существовании собственного вектора над полем комплексных чисел и ее вещественный аналог. Критерий подобия данной матрицы диагональной матрице.
12. Билинейные и квадратичные формы и их матрицы. Изменение матрицы квадратичной формы при изменении базиса. Теоремы Лагранжа и Якоби о приведении эрмитовой билинейной формы к каноническому виду. Закон инерции. Критерий Сильвестра положительной определенности билинейной формы, связь со скалярным произведением.
13. Аффинная классификация кривых и поверхностей 2-го порядка. Цилиндрические поверхности, конические поверхности.
14. Связь линейных преобразований и билинейных функций в унитарном пространстве. Сопряженное преобразование, свойства операции сопряжения. Нормальное преобразование унитарного пространства, существование у него базиса из собственных векторов. Комплексификация евклидова пространства. Теорема о нормальном преобразовании евклидова пространства. Унитарные (ортогональные) преобразования. Сопряженные (симметричные) преобразования. Неотрицательное самосопряженное преобразование, извлечение квадратного корня из него. Приведение квадратичной формы к главным осям. Одновременное приведение пары квадратичных форм к каноническому виду.
15. Ортогональная классификация кривых и поверхностей 2-го порядка. Инварианты и полуинварианты. Центр, асимптотические направления.
16. Алгебраические системы, их гомоморфизмы и изоморфизмы. Полугруппа, левый (правый) нейтральный и обратный элементы. Группа, подгруппа. Циклическая группа. Теорема о подгруппах циклической группы, ее применение для построения кругового многочлена. Разбиение группы на смежные классы по подгруппе, теорема Лагранжа. Фактор множество, факторгруппа. Нормальные делители и их связь с гомоморфизмами групп.
17. Кольцо, тело, поле, подкольцо, идеал. Кольца вычетов, матриц, формальных степенных рядов, многочленов; тело кватернионов. Теорема о правом (левом) делении многочленов (с коэффициентами из возможно некоммутативного кольца) с остатком, обобщенная теорема Безу , схема Горнера, матричные многочлены, теорема Гамильтона-Кели, минимальный многочлен.
18. Кольцо F[x] многочленов с коэффициентами из поля F. Алгоритм Евклида и представление d(x)=HOД(f(x), g(x)) в виде d(x)=u(x)f(x)+v(x)g(x). Три утверждения о взаимно простых многочленах. Теоремы о разложении многочлена в произведение неприводимых множителей. Теоремы о степени неприводимого многочлена над полями: комплексных, вещественных и рациональных чисел, над конечным полем.
Литература.
- Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. М., 1971.
- Беклемишева Л.А., Петрович А.Ю., Чубаров И.А. Сборник задач по аналитической геометрии и линейной алгебре. М., 1987.
Дополнительная литература.
- Воеводин В.В. Линейная алгебра. М., 1974.
- Курош А.Г. Курс высшей алгебры. М., 1971.
- Ильин В.А., Позняк Э.Г. Аналитическая геометрия. М., 1971.
- Погорелов А.В. Аналитическая геометрия. М., 1978.
- Шилов Г.Е. Математический анализ. Конечномерные линейные пространства. М., 1969.
- Гельфанд И.М. Лекции по линейной алгебре. М., 1966.
- Проскуряков И.В. Сборник задач по линейной алгебре. М., 1974.
- Моденов П.С., Пархоменко А.С. Сборник задач по аналитической геометрии., М., 1976.
- Фаддеев Д.К., Соминский И.С. Сборник задач по высшей алгебре. М., 1977.
- Икрамов Х.Д. Задачник по линейной алгебре. М., 1975.
- Бахвалов С.В., Моденов П.С., Пархоменко А.С. Сборник задач по аналитической геометрии. М., 1964.