Новый подход к оптимизации фондового портфеля в нечеткой постановке задачи

Недосекин А.О., ст. консультант Siemens Business Services, к.т.н.

Впервые мне довелось публично рассуждать об оптимизации фондового портфеля в нечеткой постановке задачи в 2000 году, в работе [1]. И прошло еще по меньшей три года, когда, с учетом накопленного опыта научных исследований (вызвавших, в том числе, создание системы оптимизации фондового портфеля [2, 3] и последующее ее внедрение в Пенсионном фонде РФ), мне захотелось вернуться к результату [1] и развить его. Слишком многое, на мой взгляд, свидетельствует в пользу этого подхода и нуждается в дополнительных исследованиях.

Существо подхода [1]

Рассматривается фондовый портфель из N модельных компонент и его ожидаемое поведение (прогнозный перфоманс) на интервале [0,Т]. Каждая из компонент портфеля i = 1..N характеризуется своей финальной доходностью r_i (оцененной в точке T как относительное приращение цены актива за период), причем r_i является нечеткой величиной. В отличие от классической возможностной оптимизации фондового портфеля, где доходности являются нечеткими случайными величинами [4, 5, 6], в [1] случайная составляющая финальной доходности не рассматривается, потому что предполагается, что отсутствуют достаточные основания вероятностного моделирования тенденций фондового рынка, и остаются только возможностные основы для моделирования.

Чтобы сделать ситуацию более понятной, рассмотрим модель из [6]. Там финальная доходность рассматривается как случайный процесс с линейным трендом, в сечении которого лежит нормально распределенная случайная величина, но параметры этого распределения – треугольные нечеткие числа (так называемое нечеткое гауссовское распределение). Таким образом, каждый актив в портфеле может быть описан двумя треугольными числами – среднеожидаемой доходности и риска. Помимо нечетких описаний самих активов, в модели присутствует описание связи между активами – корреляционной матрицы треугольных чисел.

Поскольку мы моделируем поведение актива гауссовским распределением, то актив характеризуется только двумя моментами (первым начальным и вторым центральным) этого распределения. Соответственно, возможно использование для оптимизации портфеля схемы Марковица в нечеткой постановке задачи. Тогда эффективная граница портфельного множества – это криволинейная полоса в координатах «риск-доходность», а оптимальный портфель в каждой точке полосы имеет расплывчатые границы. Этот принцип лежит в основе системы оптимизации модельного (индексного) портфеля [2, 3].

Есть несколько проблем, которые сдерживают применение подхода [6], как я имел возможность лично убедиться на практике, а именно:

Удалось преодолеть ограничение классического подхода Марковица, связанного с невиноровским характером ценовых процессов (мы перешли от модели текущей доходности актива к модели финальной доходности, с обоснованием квазистационарности процесса цены актива или индекса). Однако не удалось уйти от симметричной меры риска портфеля (роль которой выполняет среднеквадратическое отклонение от среднего). В то же время давно известно, что для собственника портфеля убытки воспринимаются по интенсивности гораздо более болезненно, нежели радость от прибыли. Такая асимметричность требует асимметричной меры риска (downside risk measure), что в рамках подхода Марковица недостижимо.
Еще в [1] указывалось, что корреляция – слово из эпохи классических вероятностных процессов – есть вещь, не существующая в природе фондового рынка. Достаточно изменять в широких пределах период для оценки корреляционной матрицы, и можно убедиться, что корреляционные коэффициенты в широких пределах меняют модуль своих значений, равно как и знак (потому что не обеспечивается условие однородности среды, в которой протекают фондовые процессы). В то же самое время в работах [7, 8] показано, что влияние колебаний значений корреляционной матрицы на решение - на порядок более низкое, чем влияние колебаний параметров доходности и риска активов портфеля. К тому же, общая тенденция рынка идет к тому, что, за счет введения в торговлю элементов телекоммуникации, все мировые фондовые рынки колеблются синхронно, т.е. «корреляция» ведущих индексов – почти полная положительная. В итоге, корреляция – это а) натяжка; б) низкоинформативный элемент модели. Значит, нужно стоить модель, где корреляция не играет роли.
Шесть скалярных параметров, характеризующих распределение доходности актива (два треугольных числа) – это слишком много. Можно, как это показано в [6, 9], находить параметры треугольных чисел доходности и риска актива, варьируя уровень доверия к ретроспективным данным (с точки зрения применимости ретроспективных оценок в прогнозах). Однако прошлое не определяет будущее, и поэтому ретроспективные оценки для прогнозов оказываются действительно малопригодными (чрезмерно размытыми). Поэтому, возможно, прогнозировать следует не параметры будущих вероятностных распределений, а непосредственно тенденции, причем не как случайные величины, но как возможности, что совсем не одно и то же. К тому же, видимо, достаточно по каждому активу знать две вещи в каждый момент: ожидаемые минимум и максимум цены, т.е. всего две прогнозные функции.

Сформулированные проблемы вызывают к жизни подход типа [1], где:

Риск портфеля – это не его волатильность, но возможность того, что ожидаемая доходность портфеля окажется ниже некоторой предустановленной плановой величины.
Корреляция активов в портфеле не рассматривается и не учитывается.
Доходность каждого актива – это детерминированное (неслучайное) нечеткое число (например, треугольного вида или интервального вида). Аналогично, ограничение на предельно низкий уровень доходности может быть как обычным скалярным, так и нечетким числом произвольного вида. Таким образом, мы сводим два источника информации (средняя доходность и волатильность актива) в один (расчетный коридор доходности или цены) и тем самым объединяем два источника неопределенности в один.

Поэтому оптимизировать портфель в такой постановке может означать, в частном случае, требование максимизировать минимум ожидаемой доходности портфеля в точке времени T при фиксированном уровне риска портфеля (по аналогии с тем, как это делается в [1] и [10]). Эффективная граница портфельного множества в этом случае – вогнутая линия в координатах «риск недопустимо низкой доходности портфеля – минимум ожидаемой доходности портфеля». Каждый точке эффективной границы отвечает оптимальный портфель с четкими границами. Таким образом, вся нечеткость, возможностность модели «прячется» в показателе риска недостаточной доходности.

Рассмотрим задачу на основе изложенной модели, в предположении самых широких допущений к виду нечетких параметров этой модели.

Возможностная оптимизация портфеля

Итак, мы договорились развивать подход, заявленный в [1], с целью исключить из модели все вероятностные описания. Таким образом, мы находимся в рамках детерминистской возможностной модели.

Пусть имеется фондовый портфель из N модельных компонент на интервале [0,Т]. Прогнозный перфоманс каждой из компонент портфеля i = 1..N на момент T характеризуется своей финальной расчетной доходностью r_i (оцененной в точке T как относительное приращение цены актива за период), причем r_i является нечетким числом. Эту нечеткое число мы можем задать, в зависимости от вида числа, либо как аналитическую функцию (например, для случая чисел LR-вида [11]), либо как совокупность сегментных интервалов [r_imin(), r_imax()] для каждого выбранного уровня принадлежности . Далее мы рассматриваем сегментный способ задания как наиболее общий. В вырожденном случае финальная доходность актива может быть просто четким числом (такое возможно, например, для облигаций и индексов на их основе).

Если известны расчетные доходности активов, то расчетная доходность по портфелю в целом составляет

[r_min(), r_max()] =

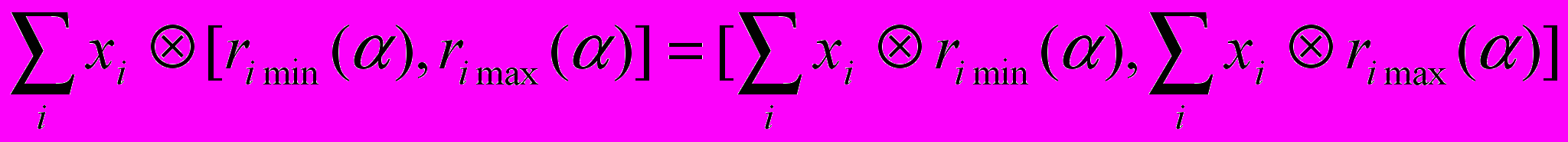
(1)

для всех [0,1], где x_i – вес i-го актива в портфеле, причем

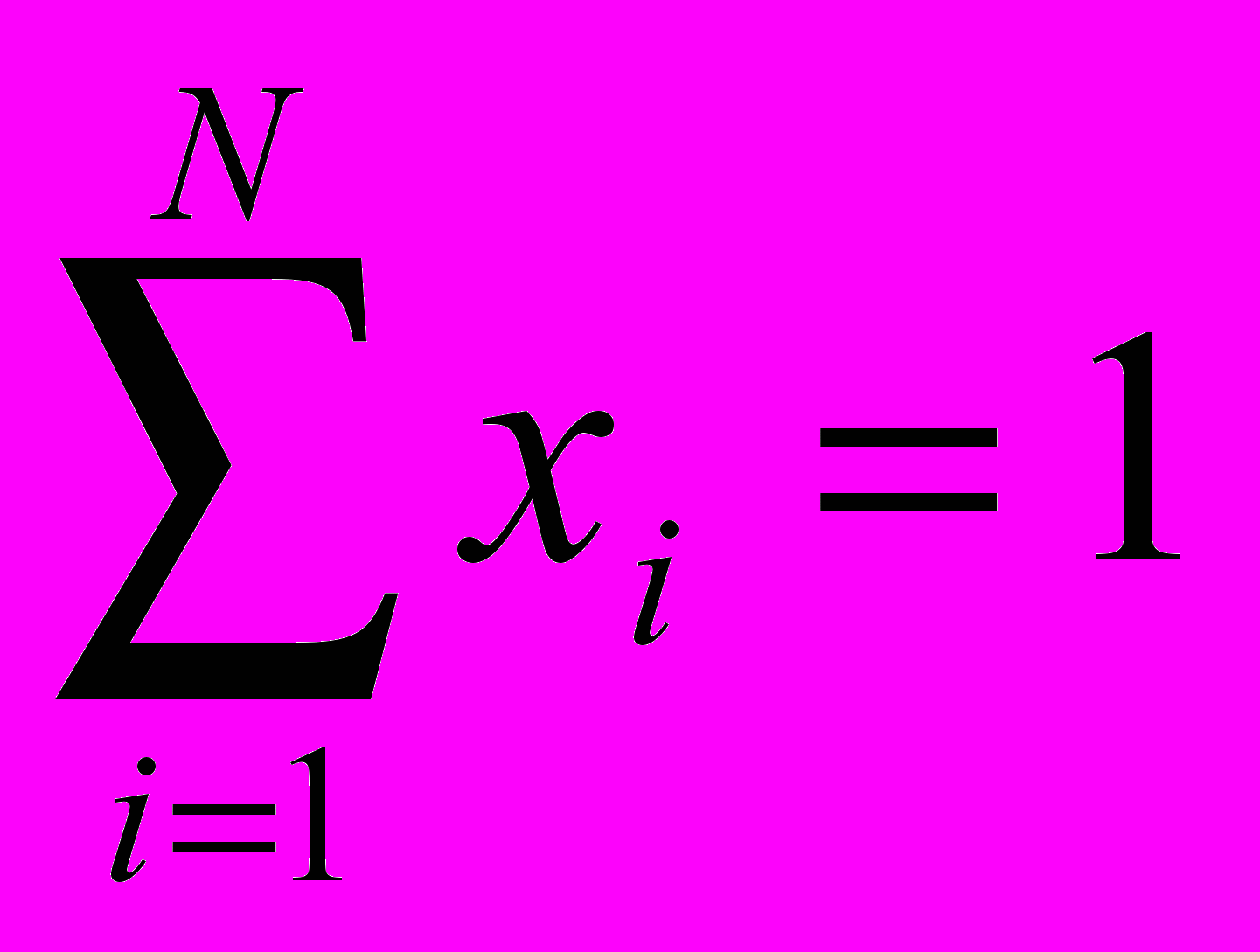, 0  x_i  1. (2)

Также определимся с нижней границей доходности портфеля на момент Т. Она также может быть нечетким числом произвольного вида [r_Pmin(), r_Pmax()]. В вырожденном случае это обычный числовой норматив r_P, например, 15% годовых.

Но в большинстве случаев владелец фондового портфеля не очень хорошо представляет себе, на что следует ориентироваться. Например, завтрашний уровень инфляции не известен вполне точно, он колеблется в некоторых пределах. Если нет выпуклого, наиболее ожидаемого значения инфляции, вокруг которого группируются прочие возможности, то имеет место обычный интервал. Соответственно, владелец портфеля желает, чтобы портфель по доходности опережал темп инфляции (вполне естественное ожидание), но он имеет расплывчатые ожидания, как о портфеле, так и об инфляции. Если ожидания портфеля и инфляции пересекаются на некоторых интервалах принадлежности, то налицо риск того, что портфель не «побьет» инфляцию, т.е. инвестиции окажутся неэффективными (подобная ситуация изображена на рис. 1).

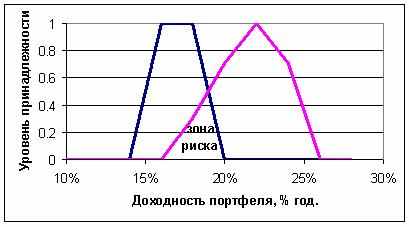
Рис. 1. Соотношение доходности портфеля и уровня инфляции

Соответствующий риск выражается формулой [12]:

Risk = Poss {r < r_P}

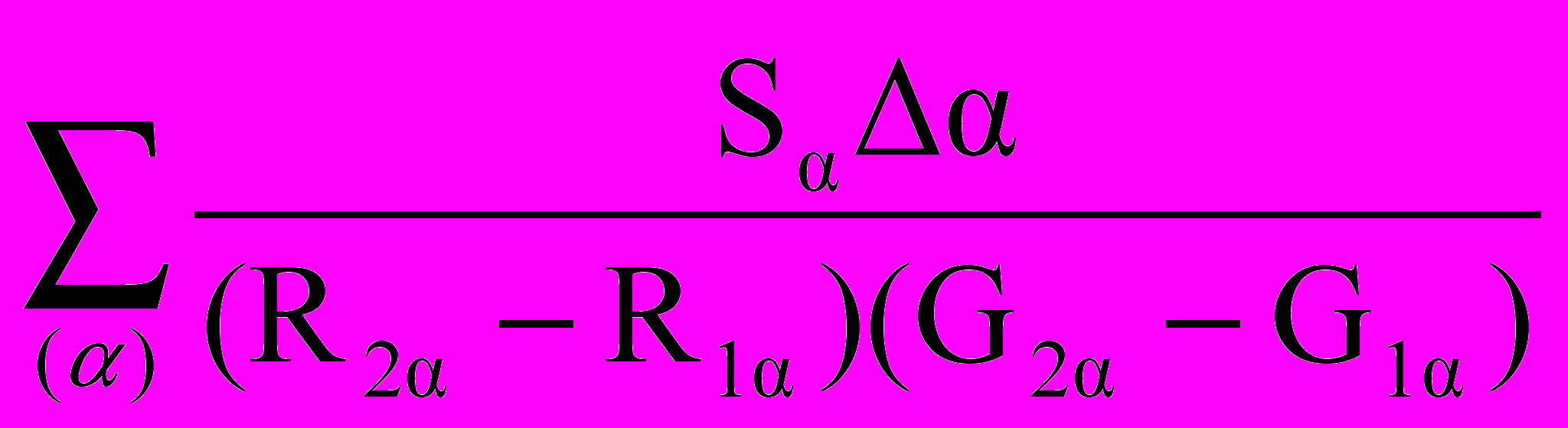, (3)

где  - уровень дискретизации по принадлежности  (например, 0.01), [R₁_, R₂_] = [r_min(), r_max()], [G₁_, G₂_] = [r_Pmin(), r_Pmax()] (сокращения, введенные для удобства записи), и

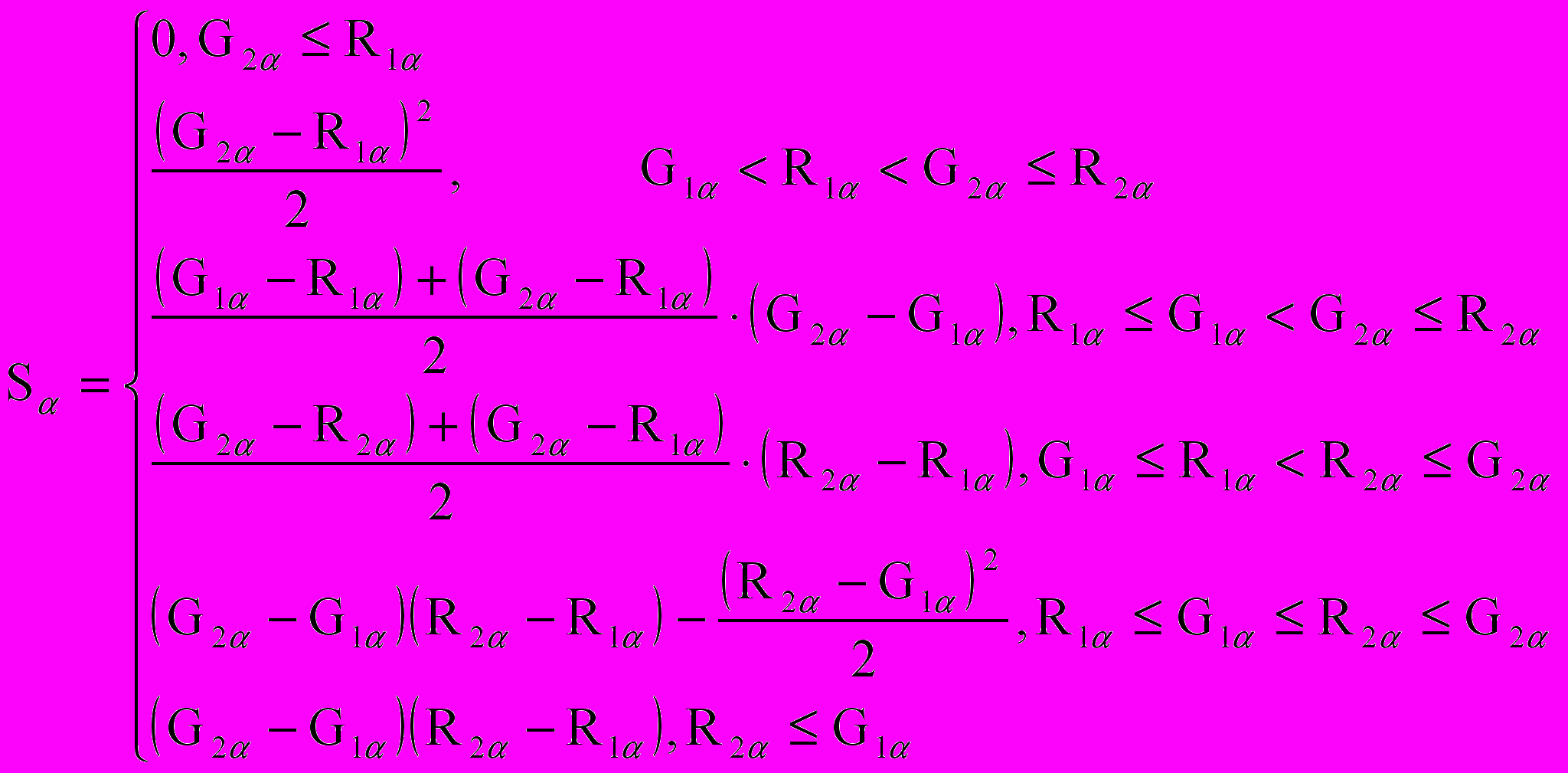. (4)

Таким образом, для каждого соотношения долей портфеля {x_i} мы умеем определять ожидаемую доходность портфеля как нечеткое число по (1) – риск портфеля как обычное скалярное число по (3) – (4). Теперь можно переходить к постановке и решению задачи оптимизации портфеля.

Будем считать, что оптимальным является портфель, у которого, при заданном уровне риска неэффективности (3), минимально возможное значение доходности является максимальным. В формульной записи это означает

r_min (=0)  max (5)

при ограничениях на размер долей портфеля вида (2) и вида равенства на размер Risk = Risk₀.

Поскольку не существует общего аналитического вида зависимости Risk (3), то не существует и общего решения задачи оптимизации (5). Эту задачу можно решить только приближенными методами, например, градиентным методом, который описывается следующим алгоритмом:

Мы строим эффективную границу портфельного множества в координатах «риск неэффективности портфеля – минимум доходности портфеля». Обозначим max {r_min (=0)} = Eff (от efficient frontier). Тогда уравнение для эффективной границы имеет вид

Eff = Eff (Risk₀) = Eff (Risk). (6)

Правая точка границы вида (6) определяется по активу с максимумом r_imin(=0). Обозначим номер этого актива как I. Тогда в соответствующем оптимальном портфеле

x_I = 1, x_i = 0, i  I (7)

Абсцисса правой точки границы (6) определяется по (3-4), обозначим ее Risk2. Ординату правой точки границы обозначим Eff2 = Eff(Risk2) = r_Imin (=0).

Контролируем вырождение границы. Если левый край границы совпадает с правым, то она вырождается в точку, и алгоритм останавливается. Контроль производится следующим образом. По каждому i-му активу, i  I, формируется относительно малое приращение доли x_i, сопровождаемое соответствующим снижением доли x_I, и замеряются соответствующие изменения уровней Eff и Risk. Назовем отношение Eff/Risk градиентом (по смыслу, это приближение первой производной эффективной границы). Тогда, если для каждого i-го актива градиент будет отрицательным (т.е. снижение доходности сопровождается ростом риска), то построение эффективной границы завершено, и алгоритм останавливается.

Вообще говоря, каждая точка эффективной границы обладает минимумом градиента, и это обуславливает вогнутость эффективной границы во всех точках. Если бы это было не так, то, как доказывается во всех учебниках по портфельной оптимизации, существовал бы портфель, лежащий выше эффективной границы, что противоречит определению эффективной границы.

Если вырождения эффективной границы нет (она не сжимается в точку), алгоритм градиентной оптимизации начинает работу. Выбирается пара активов (i, j), для которых, при снятии малой доли с i-го актива и при переносе ее на j-ый актив, положительный градиент обладает минимальным значением. На эффективной границе появляется новая точка с координатами (Risk_i, Eff_i), соответствующая портфелю с оптимально перераспределенными долями. И затем алгоритм возвращается на предыдущий шаг 3, с контролем завершения процесса восстановления эффективной границы (пока все возможные градиенты не сделаются отрицательными).

Градиентный метод, изложенный здесь, лежит в основе решения [2, 3]. Главным достоинством этого алгоритма является его адаптивность к любым координатным сеткам «риск – доходность», в том числе и к классической сетке Марковица. То есть вид риска и способ его вычисления для градиентного алгоритма не играет никакой роли.

Рассмотрим простейший расчетный пример.

Расчетный пример

Фондовый портфель содержит N = 4 актива, исходные данные по которым представлены в табл. 1. Все доходности сформулированы как интервальная оценка и, соответственно, являются прямоугольными нечеткими числами (интервальная оценка не зависит от уровня принадлежности). В интервальной форме задано также и ограничение на нижний размер доходности актива – r_P= 9.5%..11% годовых. В последней колонке табл. 1 произведен досчет уровня риска бизнеса относительно планового уровня доходности r_Pпо упрощенной формуле [12], вытекающей из (3-4) для интервального случая:

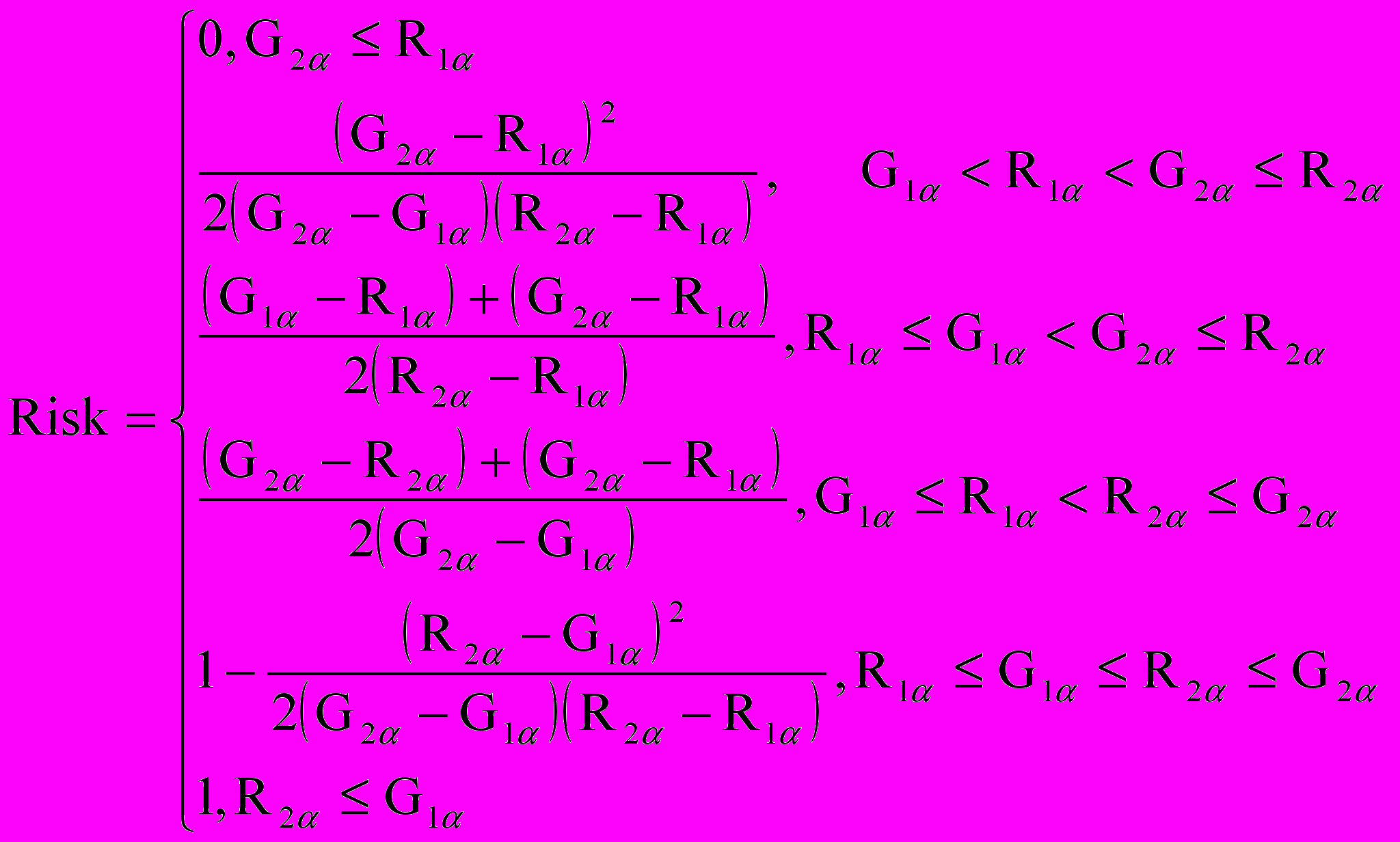. (8)

Табл. 1. Исходные данные по бизнесам (r_P = 9.5 -11% годовых)

Номер актива	r_min, % год	r_max, % год	Риск актива по уровню r_P
Номер актива	r_min, % год	r_max, % год	Риск актива по уровню r_P
1	9	14	0.250
2	8	18	0.225
3	6	25	0.224
4	5	30	0.210

По данным табл. 1 уже можно сказать, что все четыре актива (и, разумеется, произвольные их портфельные комбинации) обладают ненулевой мерой риска. Также видно, что с возрастанием номера актива растет неопределенность в части его ожидаемой эффективности. И тут как раз можно акцентировать несовпадение нашего подхода с подходом Марковица и производными от него. Монотонный рост волатильности и риска по Марковицу (с номером актива) не соответствует тенденции риска в нашем измерении. Потому что во всех случаях рост разбега доходности (риск по Марковицу) сопровождается удалением среднего значения доходности от пограничных величин, что вызывает снижение риска.

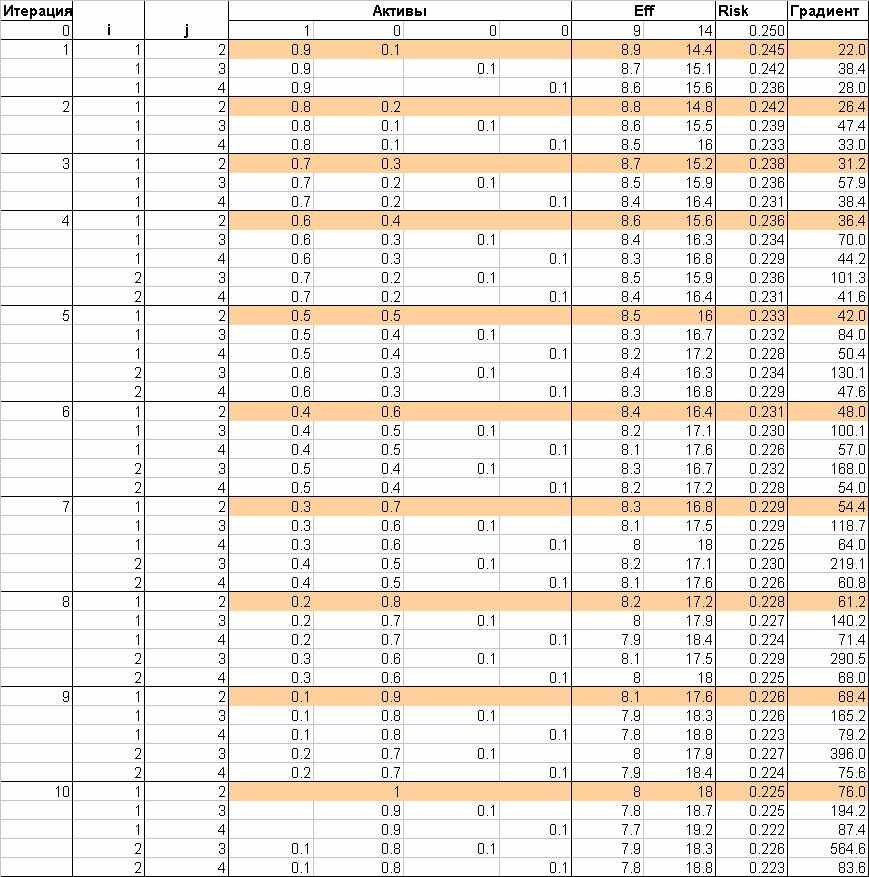
Итеративный алгоритм градиентной оптимизации дает нам результаты, представленные табл. 2. Соответствующая эффективная граница представлена на рис. 2.

Табл. 2. Решение задачи оптимизации

Окончание табл. 2.

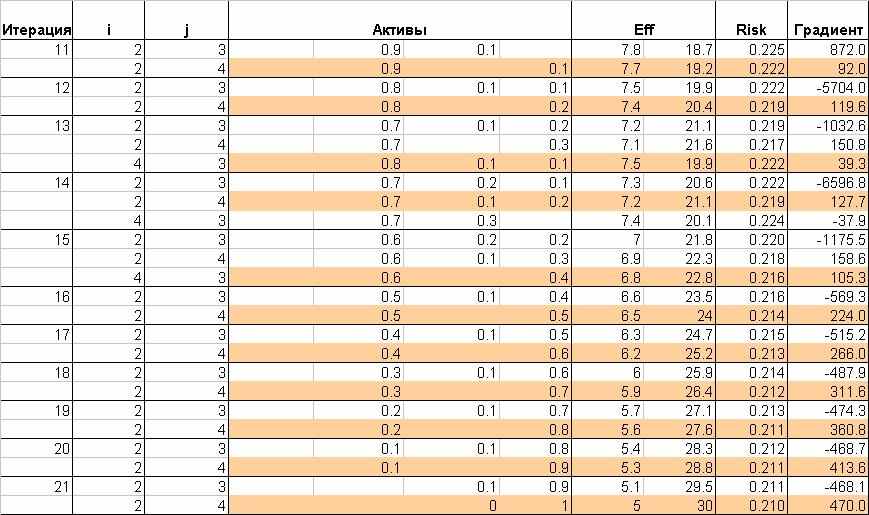
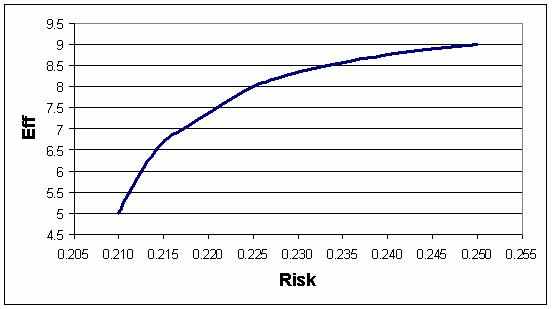
Рис. 2. Эффективная граница

Неровности и даже зигзаги на эффективной границе (следы которых присутствуют в табл. 2 на рис. 2 микшированы) обусловлены довольно большим шагом алгоритма (0.1 по уровню долей актива). Из рис. 2 видно, что минимальный градиент растет при обходе эффективной границы справа налево. Также видно, что все четыре актива участвуют в построении эффективной границы (актив 3, правда, практически незаметен на границе), причем минимальные доходности и риски убывают в одной последовательности, что характеризует этот портфель как монотонный [13] (в работе [13], кстати, показано, что все активы монотонного портфеля участвуют в построении эффективной границы портфельного множества).

Заключение

Совсем свежие результаты [10, 12], полученные в 2003 году, позволили нам производить сопоставление нечетких чисел произвольного вида, оценивая риск того, что одно из них будет больше другого в некоторый момент в будущем. Одновременно мы нашли, что оцениваемый нами риск может быть использован как критериальный параметр не только в инвестиционном проектировании, но и при оптимизации бизнес-портфелей произвольной природы. Все это, в совокупности с результатом [1], позволило нам вернуться к задаче оптимизации фондового портфеля в детерминистско-возможностной постановке и вообще посмотреть на имеющийся арсенал средств оптимизации другими глазами.

Нам начинает казаться, что компромисс, достигнутый при построении модифицированного метода Марковица (где доходность актива – нечеткая случайная величина или нечеткий случайный процесс), начинает вступать в противоречие с возможной точностью прогнозирования оценок. То, что реальный процесс курсового роста акций не является винеровским, известно давно. Также ясно, что рынок акций очень тесно связан с динамикой макроэкономических параметров и условиями рационального инвестирования [6]. Но прогнозы, которые можно сделать на этой основе, являются очень неточными, и это вступает в противоречие с точностью, требуемой для описания параметров нечеткой случайной величины. Ко всему прочему, остается проблема симметричного риска, которая не решается без полного разрыва с идеей Марковица.

Таким образом, мы вынуждены, скрепя сердце, отойти от метода Марковица в нечеткой постановке, сменив парадигму своих исследований. Мы исключаем вероятностные описания из модели роста активов безо всякого сожаления, потому что у нас нет абсолютно никаких предпосылок для того, чтобы подобные вероятностные формализмы строить. Зато у нас есть кое-какие наработки в прогнозировании фондовых индексов, в которых вероятностная проблематика тоже исчезает как бы сама собой, уступая место расчетным коридорам доходности. Сознательное загрубление модели, таким образом, приводит к повышению надежности результатов моделирования, а переход в сугубо возможностное пространство модели дает нам уже хорошо разработанный набор приемов для оценки риска портфеля и оптимизации в нечеткой постановке задачи. Кстати, в системе [2, 3] эта идея уже реализована для оценки бенчмарк-риска, когда сам бенчмарк – простое скалярное число, а расчетный коридор доходности портфеля – треугольная оценка. По сути дела, риск, который мы здесь оцениваем, - это бенчмарк-риск в чистом виде.

В работе [13] нами наглядно показано, что даже при наличии только отношений порядка доходностей и рисков активов можно производить оптимизацию портфелей и получать вполне достоверные результаты. Значит, в ближайшее время надо будет реконструировать аналогичный метод, но уже не в нечетко-вероятностном, а в возможностном пространстве. Отдельного места в этом новом исследовании заслуживает вопрос, что происходит при совместной оптимизации волатильных активов и активов с фиксированной доходностью, что появляется взамен бета-фактора Шарпа и т.д.

Подход, разработанный нами, может быть успешно применен как в фондовом менеджменте, так и при оптимизации бизнес-портфелей любой природы (например, бизнес-процессов в торговой сети или портфеля прямых инвестиций с масштабируемыми вложениями). Разумеется, эта же задача может быть решена с учетом дополнительных двусторонних ограничений на размер активов (эти ограничения будут учитываться в теле алгоритма градиентной оптимизации).

Список цитируемых источников

Недосекин А.О. Применение теории нечетких множеств к задачам управления финансами. Раздел 3 // Аудит и финансовый анализ, №2, 2000. – Также на сайте: ссылка скрыта .
Система оптимизации фондового портфеля (Сименс Бизнес Сервисез Россия). – На сайте ссылка скрыта .
Недосекин А.О. Система оптимизации фондового портфеля от Сименс Бизнес Сервисез // Банковские технологии, № 5, 2003. – Также на сайте: ссылка скрыта .
Puri M.D., Raleski D.A. Fuzzy Random Variables // J. Math. Anal. Appl., 1986, v. 114.
Язенин И.А. О методах оптимизации инвестиционного портфеля в нечеткой случайной среде // В кн.: Сложные системы: обработка информации, моделирование и оптимизация. Тверь, ТГУ, 2002.
Недосекин А.О. Фондовый менеджмент в расплывчатых условиях. – СПб, Сезам, 2003. – Также на сайте: ссылка скрыта .
Chopra V.K., Ziemba W.T. The Effects of Errors in Means, Variances, and Covariances on Optimal Portfolio Choice. – In: Worldwide Asset And Liability Modeling. – Cambridge University Press, 1998.
Бессонов Д.Н., Недосекин А.О. Корреляционная матрица и ее роль в оптимизации фондового портфеля. - На сайте: ссылка скрыта .
Недосекин А.О. Нечетко множественный анализ риска фондовых инвестиций. – СПб, Сезам, 2002. – Также на сайте: ссылка скрыта .
Недосекин А.О. Оптимизация бизнес-портфеля корпорации. – На сайте: ссылка скрыта .
Zimmerman H.-J. Fuzzy Sets Theory – and Its Applications. – Kluwer Academic Publishers, 2001. ISBN 0792374355.
Недосекин А.О., Кокош А.М. Оценка риска инвестиций для произвольно-размытых факторов инвестиционного проекта. – На сайте: ссылка скрыта .
Недосекин А.О. Монотонные портфели и их оптимизация // Аудит и финансовый анализ, №2, 2002. – Также на сайте: ссылка скрыта .

Blog

Новый подход к оптимизации фондового портфеля в нечеткой постановке задачи

Содержание