Проблемы и перспективы
| Вид материала | Документы |
- Состояние, проблемы и перспективы развития. Материалы VII международной научно-практической, 2398.87kb.
- Состояние, проблемы и перспективы развития. Материалы VIII международной научно-практической, 2761.66kb.
- Состояние, проблемы и перспективы развития. Материалы VI международной научно-практической, 1888.69kb.
- Состояние, проблемы и перспективы развития. Материалы V международной научно-практической, 1714.39kb.
- Состояние, проблемы и перспективы развития. Материалы IX международной научно-практической, 2233.33kb.
- Проект резолюции краевого налогового форума «Проблемы и перспективы налогового администрирования», 12.73kb.
- Программа II международной конференции «Возобновляемая энергетика: проблемы и перспективы», 673.06kb.
- Отчет о выступлении на Конференции «Альтернативы в энергетике и автомобилестроении:, 68.05kb.
- Консолидаци я потенциала «прикаспийской пятерки»: проблемы и перспективы, 898.41kb.
- Конференции, в которой планируется участие с докладом, 96.22kb.
В.К. Нусратуллин,
г.н.с. ЦСПИ АН РБ,
Р.Ф. Кинзягулов
ЭКОНОМИКО-МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ НАРОДОНАСЕЛЕНИЯ
Предварительные сведения. В экономической практике значения величин берутся в определенные дискретные или фиксированные моменты времени. Например, о выполнении плана судят по экономическим показателям на конец планируемого периода. Изменение показателя характеризуется разностью его значений на конец и начало периода, что можно записать в виде: у=у(t+1) — у(t), или у=у(t) у(t-1). Уравнение, связывающее разности экономических показателей в выбранный период времени, называется разностным. Иногда его называют конечно-разностным, поскольку количество рассматриваемых разностей конечно, то есть ограничено условиями конкретной задачи. Конечно-разностные методы достаточно универсальны и позволяют отобразить всякого рода циклические воспроизводственные процессы. Очень часто для облегчения конструирования конечно-разностной ЭМ-модели ее предварительно изображают графически.
Разностными или, вернее, конечно-разностными могут быть не только уравнения, но и неравенства. Определенным образом упорядоченная система и тех, и других называется конечно-разностной экономико-математической моделью (ЭМ-моделью). Конечно-разностные ЭМ-модели являются динамическими, то есть разворачивающими экономическое явление во времени. Причем горизонт охвата развития экономических явлений практически бесконечен. Свойства динамических моделей хорошо описаны в так называемой магистральной теории11.
Что значит упорядоченная система? Это, во-первых, ее соответствие выбранному способу решения задачи и требованиям алгоритма (и/или машинной программы) решения задачи по выбранному способу. Во-вторых, представление последовательности конструирования модели в виде определенного упорядоченного набора правил.
ЭМ-модели, построенные с помощью конечно-разностных методов могут явиться основой определенного сценария на будущее, программы развития, на достаточно продолжительный временный горизонт, способный включить не только единицы, но и десятки лет практически на любом уровне управления, в любой отрасли народного хозяйства и сферы деятельности, где присутствуют циклические воспроизводственные процессы. Они характеризуются тем, что: 1) представляют собой динамические процессы, протекающие во времени; 2) в них элементарные частицы воспроизводящихся систем проходят определенный отведенный им жизненный цикл, переходя из одной стадии развития к другой, взаимодействуя при этом между собой и проходя по альтернативным направлениям своего развития; 3) динамика развития воспроизводственных процессов сопровождается неравномерным во времени потреблением ресурсов и производством продукции. Иногда происходит накапливание и потребление ресурсов в предыдущих циклах развития элементов с тем, чтобы дать продукцию уже в зрелом возрасте; 4) хотя динамика развития воспроизводства всей системы в совокупности может не иметь циклического характера в своем развитии, но каждый из составляющих элементов системы проходит свой собственный цикл развития от рождения (зарождения, возникновения) до старости и смерти (устарения и списания), чаще всего, как было указано, по собственному пути развития, представляющего одну из альтернатив.
Примеры воспроизводственных процессов: 1) воспроизводство биологических популяций, в том числе домашних животных, сельскохозяйственных животных, человеческого сообщества и т.п.; 2) воспроизводство в экономике, которое совмещает в себе воспроизводство ОПФ, оборотных фондов, трудовых, природных ресурсов, жизненного пространства, экологии и т.п.
Соответственно могут быть построены различные динамические модели воспроизводства, в том числе, а может быть и главным образом, в целях прогнозирования и планирования. Например, модели: 1) структуры и оборота стада сельскохозяйственных животных12; 2) численности и структуры населения и трудовых ресурсов; 3) динамики капитальных вложений; 4) общественного воспроизводства и т.д.
ЭМ-моделирование народонаселения. ЭМ-модели народонаселения или воспроизводства человеческой популяции обычно разрабатываются и используются в целях прогноза численности и половозрастной структуры населения. Такое прогнозирование, например, в масштабах административного района, города, региона и т.д., является важнейшей составной частью анализа демографической ситуации, сложившейся или складывающейся в рамках каких-либо административно хозяйственных территорий.
В свою очередь, анализу демографической ситуации и прогнозу численности населения отводится видное место в прогнозировании и планировании социально-экономического развития административно-территориальных систем. При этом определяются половозрастная структура трудовых ресурсов, детей дошкольного и школьного возраста, возможный контингент лиц, обучающихся в профессионально-технических училищах, техникумах и вузах, а также лиц пенсионного возраста. Кроме того, по данным анализа и прогноза демографической ситуации в регионе рассчитываются возможные потребности населения и отдельных социальных групп в товарах и услугах.
Особо следует отметить потребности населения (как на момент составления прогноза, так и в будущем периоде) в объектах социального и культурно-бытового назначения (народного образования, здравоохранения, жилищно-коммунального хозяйства, бытового обслуживания, культуры, торговли, общественного питания и др.).
Прогноз половозрастной структуры населения осуществляют разными способами. Наиболее известным является метод, так называемой, передвижки возрастов. Общий смысл метода состоит в том, что все население территориальной системы (района, города, других территориальных единиц) разбивается на половозрастные группы. Численность каждой из них складывается из численности лиц в составе предшествующих групп, перешедших в соответствии со сроками прогноза в другие половозрастные группы, с учетом режима воспроизводства и миграции. В этом методе существуют свои сложности, вызванные, в первую очередь, привязкой теоретических схем передвижки возрастов к погодовой разбивке населения на возрастные группы. Эти схемы ориентированы на учет режима воспроизводства, заданного таблицами смертности населения. Последние рассчитываются преимущественно в погодовой разбивке.
Понятна в этом случае громоздкость работы как при подготовке информации, так и при реализации модели передвижки возрастов. Иногда это делает недоступным данный метод в широких исследованиях по воспроизводству населения и трудовых ресурсов. По сути дела, лишен указанных недостатков метод прогнозирования динамики населения, основанный на нашем подходе к моделированию воспроизводственных процессов, который вовсе не требует погодовой разбивки населения на возрастные группы, настраивания на режим воспроизводства, заданного таблицами смертности населения в разрезе годовых возрастных групп. Рассмотрим его методические особенности на примерах моделирования. Начнем с простейшей.
Исходная информация. В регионе проживает 5 млн. населения. Рождаемость в первый год на 1000 человек составит 23 ребенка и в каждый последующий год будет убывать на 1%, смертность — 20 человек на 1000 проживающих и будет увеличиваться в каждый последующий год на 0,5%. Трудоспособных на 100% населения приходится 50%. Производство национального дохода на одного трудоспособного в год равно 20 млн. руб. Из них на потребление расходуется 16 млн. руб.
Найти динамику воспроизводства национального дохода в зависимости от изменения численности населения и трудоспособных, в том числе с тем, чтобы узнать возможность его использования на накопление по годам прогнозного периода в течение последующих 5-ти лет.
Постановка задачи. Найти максимум использования национального дохода в данном регионе для использования на накопление в прогнозном периоде.
Построение графика (рисунок 1).
Рисунок 1. Динамика численности населения в регионе
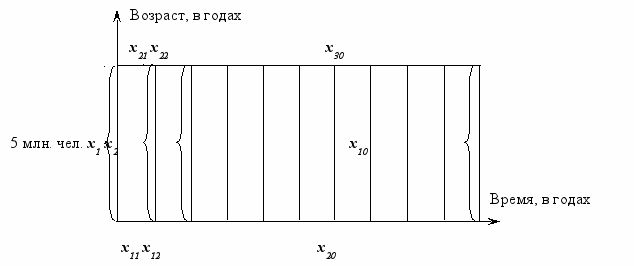
Переменные: 1) х1 — х10 численность населения на конец года, млн. чел.; 2) х11 — х20 численность родившихся в регионе за год, млн. чел.; 3) х21 — х30 численность умерших в регионе за год, млн. чел.
Ограничения: 1) по численности населения на конец 1-го года, млн. чел.: х1 = 5 + х11 — х21; 2) то же на конец 2-го года: х2 = х1 + х12 — х22; …; 10) то же на конец 10-го: х10 = х9 + х20 — х30; 11) по численности родившихся в 1-й год, не более, млн. чел.: х11 0,023× 5; 12) то же во 2-й год: х12 0,99 × 0,023х1; …; 20) то же в 10-й год: х20 0,91× 0,023х9; 21) по численности умерших в 1-й год, не более, млн. чел.: х21 0,02× 5; 22) то же во 2-й год: х22 1,005× 0,02х21; …; 30) то же в 10-й год: х30 1,045× 0,02х29.
Целевая функция — максимум национального дохода на накопление, млн. руб.: Z = (20–16)0,55+(20–16)0,5х1+…+(20–16)0,5х9 max.
Есть более сложные задачи воспроизводства населения. Рассмотрим одну из них.
Исходная информация. Население региона подразделено на следующие половозрастные группы: 1) учащаяся молодежь до 20 лет; 2) замужние женщины детородного (фертильного) возраста от 20 до 30 лет; 3) замужние женщины нефертильного возраста от 30 до 55 лет; 4) женщины, не вступавшие в брак от 20 до 55 лет; 5) женщины-пенсионеры от 55 до 70 лет; 6) мужчины от 20 до 60 лет; 7) мужчины от 60 до 65 лет.
Детей у женщин фертильного возраста, вышедших замуж, рождается двое, то есть в пять лет супружества 1 ребенок. Мальчиков и девочек рождается поровну. Стоимость жизни людей в год на 1 человека равна соответственно: учащаяся молодежь — 2 млн. руб.; замужние женщины от 20 до 30 лет — 5; тех же от 30 до 55 лет — 6; женщин, не вступивших в брак от 20 до 55 лет — 4; женщин-пенсионеров — 3; мужчин от 20 до 60 лет — 5,5 и мужчин-пенсионеров — 1,5 млн. руб. Производительность труда в млн. руб. зарплаты и других доходов в год: женщин, вступивших в брак от 20 до 55 лет — 10 млн. руб., женщин, не вступивших в брак от 20 до 55 лет — 15; мужчин трудоспособного возраста от 20 до 60 лет — 20 млн. руб.
Определить половозрастную структуру населения региона в процентах за период времени продолжительностью 5 лет, считая, что приведенные значения показателей в этот период неизменны для того, чтобы найти максимально возможный объем сбережений населения.
Постановка задачи. Отыскать оптимальную половозрастную структуру населения региона в целях регулирования демографической ситуации, максимизируя суммарные сбережения населения.
Построение графической модели (рисунок 2)
На рисунке изображен прямоугольник высотой в 70 лет и шириной в 5 лет, разделенный на ряд прямоугольных и квадратных секторов в соответствии с количеством лет, заключенных в возрастных интервалах половозрастных групп населения. Разрывы в некоторых секторах сжимают интервалы отдельных половозрастных групп, поскольку высота в 70 лет, отложенная хотя бы в 5 летнем масштабе, заняла бы значительное место, не вмещающееся в формат листа.
Переменные по численности: х1 учащейся молодежи до 20 лет, %; х2 замужних женщин фертильного возраста от 20 до 30 лет, %; х3 замужних женщин нефертильного возраста от 30 до 55 лет, %; х4 женщин, не вступивших в брак от 20 до 55 лет; х5 женщин-пенсионеров от 55 до 70 лет; х6 мужчин от 20 до 60 лет; х7 мужчин от 60 до 65 лет. При построении модели могут быть введены дополнительные переменные.
Рисунок 2. Динамика половозрастной структуры населения в регионе
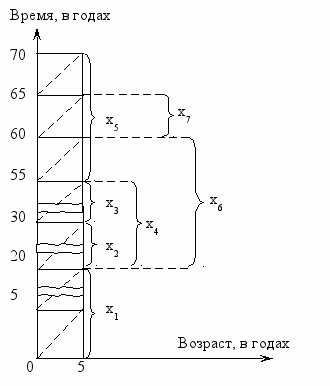
Ограничения: 1) по численности родившихся за 5 лет детей, %: 0,25 х1 = 1,00 х2, где 0,25 — так называемый коэффициент детерминации, выводимый из графической модели на рисунке 2 отношением периода прогнозирования (5 лет) на половозрастной интервал учащейся молодежи (20 лет); 1,00 — количество рождающихся детей за период в 5 лет на 1 женщину фертильного возраста; 2) по численности женщин и мужчин старше 20 лет, пополняемых за счет девушек и юношей до 20 лет, %: 0,5 х2 + 0,143 х4 + 0,125 х6 = 0,25 х1, где перед каждой переменной коэффициенты детерминации, каждый из которых исчисляется отношением периода прогнозирования (5лет) на половозрастной интервал группы населения, заданной соответствующей переменной; 3) половозрастная группа мужчин старше 20 лет может пополняться только за счет юношей до 20 лет, %: 0,125 х6 = 0,5 × 0,25 х1, где 0,5 — коэффициент, обозначающий долю юношей в общем количестве молодежи до 20 лет; 4) по взаимосвязи замужних женщин фертильного и нефертильного возрастов, %: 0,5 х2 = 0,2 х3; 5) по взаимосвязи женщин допенсионного и пенсионного возрастов, %: 0,2 х3 + 0,143 х4 = 0,333 х5; 6) по взаимосвязи мужчин допенсионного и пенсионного возрастов, %: 0,125 х6 = 1,0 х7; 7) по всей численности населения, %: х1 + х2 + х3 + х4 + х5 + х6 + х7 = 100.
Целевая функция — максимум сбережений населения, млн. руб.: Z = -2х1 + (10–5) х2 + (10–6) х3 + (15–4) х4 — 3х5 + (20–5,5) х6 — 1,5 х7 max.
Таким образом, разобранные примеры моделирования показали, что методика построения воспроизводственных моделей народонаселения достаточно проста и может быть использована в практике прогнозирования демографической ситуации в регионе или в целом по стране.
