Geum.ru

230100 – Информатика и вычислительная техника

Вид материалаДокументы

Содержание


ТЕМА 6. Мостиковые схемы
Подобный материал:
1   2   3   4   5   6   7   8   9   ...   20

 

 Примечание: для k > 10  можно воспользоваться свойством симметрии: Сл n = Cn - k n 

 

Поскольку для отказа системы "m из n" достаточно, чтобы количество исправных элементов было меньше m, вероятность отказа может быть найдена по теореме сложения вероятностей для k = 0, 1, ... , (m - 1):

 

Q = Σ Pk = Σ Cn k   pk  (1 - p)n-k

 

Аналогичным образом можно найти вероятность безотказной работы как сумму для k = m, m + 1, … , n:

 

P = Σ Pk = Σ Cn k  pk (1 - p)n-k


ТЕМА 6. Мостиковые схемы

Мостиковая структура:

 



 

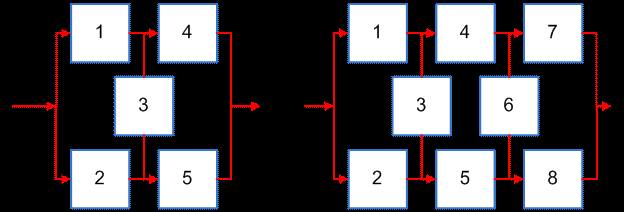
не сводится к параллельному или последовательному типу соединения элементов, а представляет собой параллельное соединение последовательных цепочек элементов с диагональными элементами, включенными между узлами различных параллельных ветвей (элемент 3 на левом рисунке, элементы 3 и 6 на правом рисунке).

 

Работоспособность такой системы определяется не только количеством отказавших элементов, но и их положение в структурной схеме. Например, работоспособность cистемы, схема которой приведена на левом рисунке будет утрачена при одновременном отказе элементов 1 и 2, или 4 и 5, или 2, 3 и 4 и т.д.

В то же время отказ элементов 1 и 5, или 2 и 4, или 1, 3 и 4, или 2, 3 и 5 к отказу системы не приводит.

 

Для расчета надежности мостиковых систем можно воспользоваться методом прямого перебора, как это было сделано для систем “m из n”, но при анализе работоспособности каждого состояния системы необходимо учитывать не только число отказавших элементов, но и их положение в схеме.

Все состояния системы занесены в таблицу (в таблице работоспособные состояния элементов и системы отмечены знаком “+” , а неработоспособные – знаком “-“):

 

 

№
состояния
Состояние элементов
Состояние системы
Вероятность состояния

 

1
2
3
4
5
в общем случае
при равнонадежных элементах

1
+
+
+
+
+
+
p1p2p3p4p5
p5

2
+
+
+
+
-
+
p1p2p3p4q5
p4 q1 = p4 (1 - p)

3
+
+
+
-
+
+
p1p2p3q4p5

4
+
+
-
+
+
+
p1 p 2 q3 p4 p5

5
+
-
+
+
+
+
p1q2p3p4p5

6
-
+
+
+
+
+
q1p2p3p4p5

7
+
+
+
-
-
-
p1p2p3q4q5
p3 q2 = p3 (1 - p)2

8
+
+
-
+
-
+
p1p2q3p4q5

9
+
-
+
+
-
+
p1q2p3p4q5

10
-
+
+
+
-
+
q1p2p3p4q5

11
+
+
-
-
+
+
p1p2p3p4p5

12
+
-
+
-
+
+
p1p2p3p4p5

13
-
+
+
-
+
+
p1p2p3p4p5

14
+
-
-
+
+
+
p1p2p3p4p5

15
-
+
-
+
+
+
p1p2p3p4p5

16
-
-
+
+
+
-
p1p2p3p4p5

17
+
+
-
-
-
-
p1p2p3p4p5
p2 q3 = p2 (1 - p)3

18
+
-
+
-
-
-
p1p2p3p4p5

19
-
+
+
-
-
-
p1p2p3p4p5

20
+
-
-
-
+
-
p1p2p3p4p5

21
-
+
-
-
+
+
p1p2p3p4p5

22
-
-
-
+
+
-
p1p2p3p4p5

23
+
-
-
+
-
+
p1p2p3p4p5

24
-
+
-
+
-
-
p1p2p3p4p5

25
-
-
+
-
+
-
p1p2p3p4p5

26
-
-
+
+
-
-
p1p2p3p4p5

27
+
-
-
-
-
-
p1p2p3p4p5
p1 q4 = p1 (1 -p)4

28
-
+
-
-
-
-
p1p2p3p4p5

29
-
-
+
-
-
-
p1p2p3p4 p5

30
-
-
-
+
-
-
p1p2p3p4p5

31
-
-
-
-
+
-
p1p2p3p4p5

32
-
-
-
-
-
-
p1p2p3p4p5
q5 = (1 - p)5