230100 – Информатика и вычислительная техника

Вид материала

Документы

Содержание Р системы и ее элементов р1 Вопросы для самоконтроля ТЕМА 4. Системы с паралельным соединением элементов Для отказа системы с параллельным соединением элементов в течение наработки необходимо и достаточно, чтобы все ее элементы отказ Вероятность безотказнойработы

Подобный материал:

• Рабочая учебная программа по дисциплине «Базы данных» Направление №230100 «Информатика, 115.03kb.
• Основная образовательная программа высшего профессионального образования Направление, 300.24kb.
• Образовательный стандарт по направлению 230100. 62 Информатика и вычислительная техника, 328.94kb.
• Рабочая учебная программа по дисциплине вычислительная математика специальность: 230100, 133.73kb.
• Рабочая программа учебной дисциплины днн. 02 Современные научные проблемы автоматизированных, 221.23kb.
• Образовательной программы по укрупненной группе 230000 Информатика и вычислительная, 933.17kb.
• Программа государственного экзамена по направлению 230100 «Информатика и вычислительная, 60.5kb.
• Рабочая учебная программа по дисциплине «Информатика» Направление №230100 «Информатика, 91.73kb.
• Рабочая учебная программа по дисциплине «Программирование на языке высокого уровня», 119.59kb.
• Образовательный стандарт по направлению 552800 «Информатика и вычислительная техника», 166.41kb.

 

По данным таблицы построены графики зависимости вероятности безотказной работы Р системы и ее элементов р₁ и p₂ от времени t её наработки:

 



 

Из анализа видно, что интенсивность отказов системы, состоящей из последовательно включенных элементов, больше, а средняя наработка меньше, чем у любого из её элементов: (принцип “хуже худшего”) и из малонадежных элементов нельзя создать высоконадежной cистемы при последовательным соединением её элементов.

Вопросы для самоконтроля

1. В чем состоит связь показателей надежности системы и её элементов ?

2. Когда можно применять метод прямого перебора всех возможных комбинаций системы для расчета безотказности системы ?

3. Чем достигается независимость отказов как случайных событий элементов системы ?

4. Сформулируйте теорему умножения вероятностей.

5. Может ли быть вероятность безотказной работы системы при последовательном соединении её элементо выше вероятности безотказной работы самого ненадежного из её элементов ?

6. Можно ли из малонадежных элементов создать высоконадежную систему при последовательном соединении элементов ?

7. Когда можно наблюдать простейший поток отказов ? Назовите основную причину простейших отказов.

ТЕМА 4. Системы с паралельным соединением элементов

Системой с параллельным соединением элементов называется система, отказ которой происходит только в случае отказа всех ее элементов:



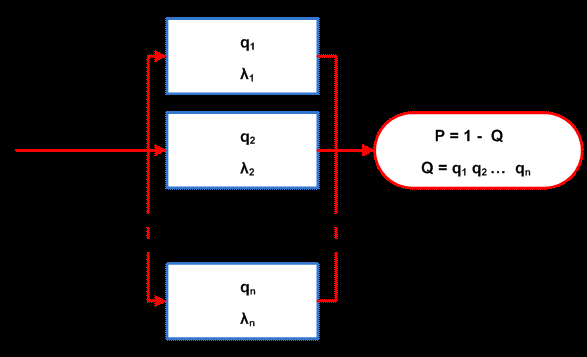
Такие схемы надежности характерны для систем, в которых элементы дублируются или резервируются, т.е. параллельное соединение используется как метод повышения надежности.
Однако такие системы встречаются и самостоятельно (например, системы двигателей четырехмоторного самолета или параллельное включение диодов в мощных выпрямителях).


Для отказа системы с параллельным соединением элементов в течение наработки необходимо и достаточно, чтобы все ее элементы отказали в течение этой наработки.

 

Поэтому отказ системы заключается в совместном отказе всех элементов, вероятность кторого (при допущении независимости отказов) может быть найдена по теореме умножения вероятностей как произведение вероятностей отказа элементов:

 

Q = q₁ q₂ ... q_n

 

Соответственно, вероятность безотказной работы cистемы с паралельным соединением элементов

 

P = 1 - Q

 

Для системы состоящей из параллельно включенных равнонадежных элементов (р_i = р)  вероятность отказа системы можно вычислить по формуле

 

Q = qⁿ

 

При этом вероятность  безотказной работы системы, состоящей из паралельно соединенных равнонадежных элементов, будет

 

P = 1 - qⁿ  = 1 - (1 - p)ⁿ ,  q = 1 - p

 

т. е. надежность системы с параллельным соединением повышается при увеличении числа элементов (например, при вероятности безотказной работы элемента системы р = 0.9 и количестве паралельно включенных элементов n = 2 вероятность безотказной работы системы будет Р = 0.99, а при n = 3 вероятность безотказной работы системы станет уже Р = 0.999 ).

 

Поскольку q_i  < 1, произведение Q = q₁ q₂ ... q_n  всегда меньше любого из со множителей, т.е. вероятность отказа системы не может быть выше вероятности самого надежного ее элемента (“лучше лучшего”) и даже из сравнительно ненадежных элементов возможно построение вполне надежной системы.

 

При экспоненциальном распределении наработки элементов системы p(t) = exp( - λ · t) вероятность безотказной работы системы можно найти по формуле:

 

Р = 1 - [ 1 - ехр( - λ · t) ]ⁿ

 

Средняя наработка на отказ (между отказами) есть математическое ожидание наработки до очередного отказа. Поэтому после интегрирования и преобразований получим формулу для вычисления средней наработки системы

 

T₀ = (1/λ ) Σ (1/i) = T_oi Σ (1/i)

 

где i = 1, 2, ... , n
Т_oi = 1/λ_i - средняя наработка элемента.

 

При больших значениях n для вычисления средней наработки на отказ можно применить приближенную формулу

 

Т₀ = T_oi (ln n + 1/2n +0,577).

 

Таким образом, средняя наработка системы с параллельным соединением больше средней наработки ее элементов (например, при n = 2 cредняя наработка системы на отказ будет  Т_o = 1.5 T_oi , при n = З   она уже увеличится и составит T₀ = 1.83 T_oi ).

Пример.  Два элемента системы с равными интенсивностями отказов λ = λ₁ =  λ₂ = 0,25 · 10 ^-6  ч^-1 соединены паралельно. Элементы системы работают в режиме нормальной эксплуатации (простейший поток отказов) и отказы их независимы друг от друга.

Построить график изменения вероятности безотказной работы системы от времени наработки. Сделать выоды о влиянии надежности элементов на надежность системы.

 

Решение.  Два равнонадёжных элемента p = p₁ = p₂ ( с равными интенсивностями отказов  λ ) соединены паралельнольно. Для отказа системы с параллельным соединением элементов в течение наработки необходимо и достаточно, что бы все элементы отказали в течение этой наработки. Вероятность такого события ( при допущении независимости отказов элементов ) может быть найдена по теореме умножения вероятностей как произведение вероятностей отказов элементов:

 

Q = q₁ · q₂ = q² ,  q = q₁ = q₂ . 

 

Соответственно, вероятность безотказной работы системы

 

P = 1 - Q = 1 - q² = 1 - ( 1 - р )² , q = 1 - p ,  p = p₁ = p₂

 

P = p ( 2 - p ) .

 

Так как все элементы системы работают в периоде её нормальной эксплуатации ( простйший поток отказов ), то вероятность безотказной работы элемента

 

р = exp ( - λ · t ) = exp ( - 0,25 · 10^-6 · t ) .

 

Результаты расчетов сведены в таблицу

 

Вероятность безотказной работы:	Время наработки системы t · 106  ч
	0,5	1,0	1,5	2,0	2,5	3,0
элемента р	0,8825	0,7788	0,6873	0,6065	0,5353	0,4724
системы Р	0,	0,	0,	0,	0,	0,