Geum.ru

Рабочая программа по дисциплине б высшая математика (шифр и название дисциплины)

Вид материалаРабочая программа

Содержание


Типовые задачи к зачету по разделу «Теория вероятностей»
Подобный материал:
1   2   3
Тематика контрольных домашних заданий

1 семестр

1. Линейная алгебра и аналитическая геометрия

2. Графики функций +

3. Производная и исследование функций

2 семестр

1. Неопределенный и определенный интегралы

2. Дифференциальные уравнения

3. Кратные и криволинейные интегралы

3 семестр

1. Числовые и степенные ряды

2. Теория функций комплексного переменного

3. Задачи математической физики

4 семестр

1. Основные теоремы теории вероятностей

2. Случайные величины и законы распределения

3. Обработка выборки методами математической статистики

Образцы оценочных средств текущего контроля успеваемости

Контрольное домашнее задание № 2 (первый семестр) «Функции и пределы»

Задание 1. Построить графики функций:

1) , 2) Y = 2 + x + x2, 3) 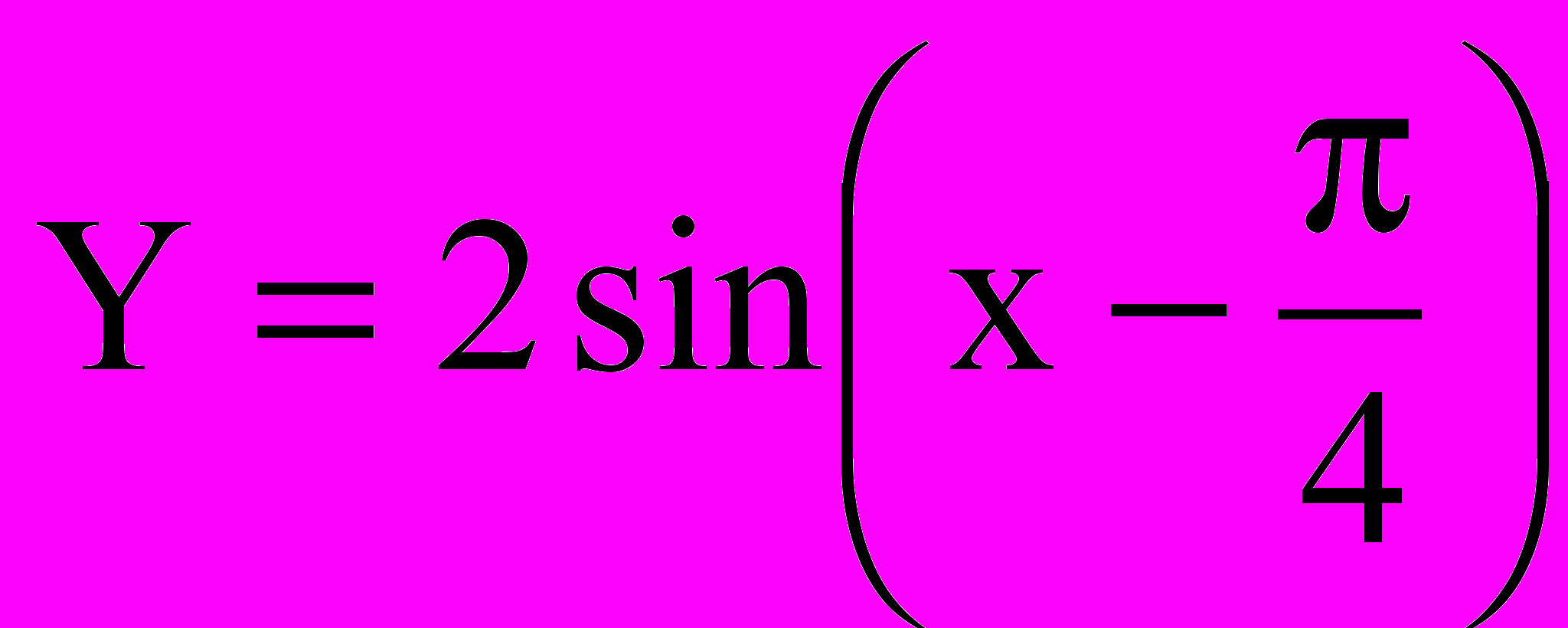, 4) Y = sin2x – cos2x, 5) Y = ctg0,5x, 6) z = 2sin

Задание 2. Найти обратные функции и построить график прямой и обратной функции:

1) , 2) Y = –logx + 3, 3) Y = 1 + e–x

Задание 3. Графически решить уравнение 1 + log2 (x + 1) = 2x

Задание 4. Найти точки разрыва функции. Определить характер разрывов:

А) 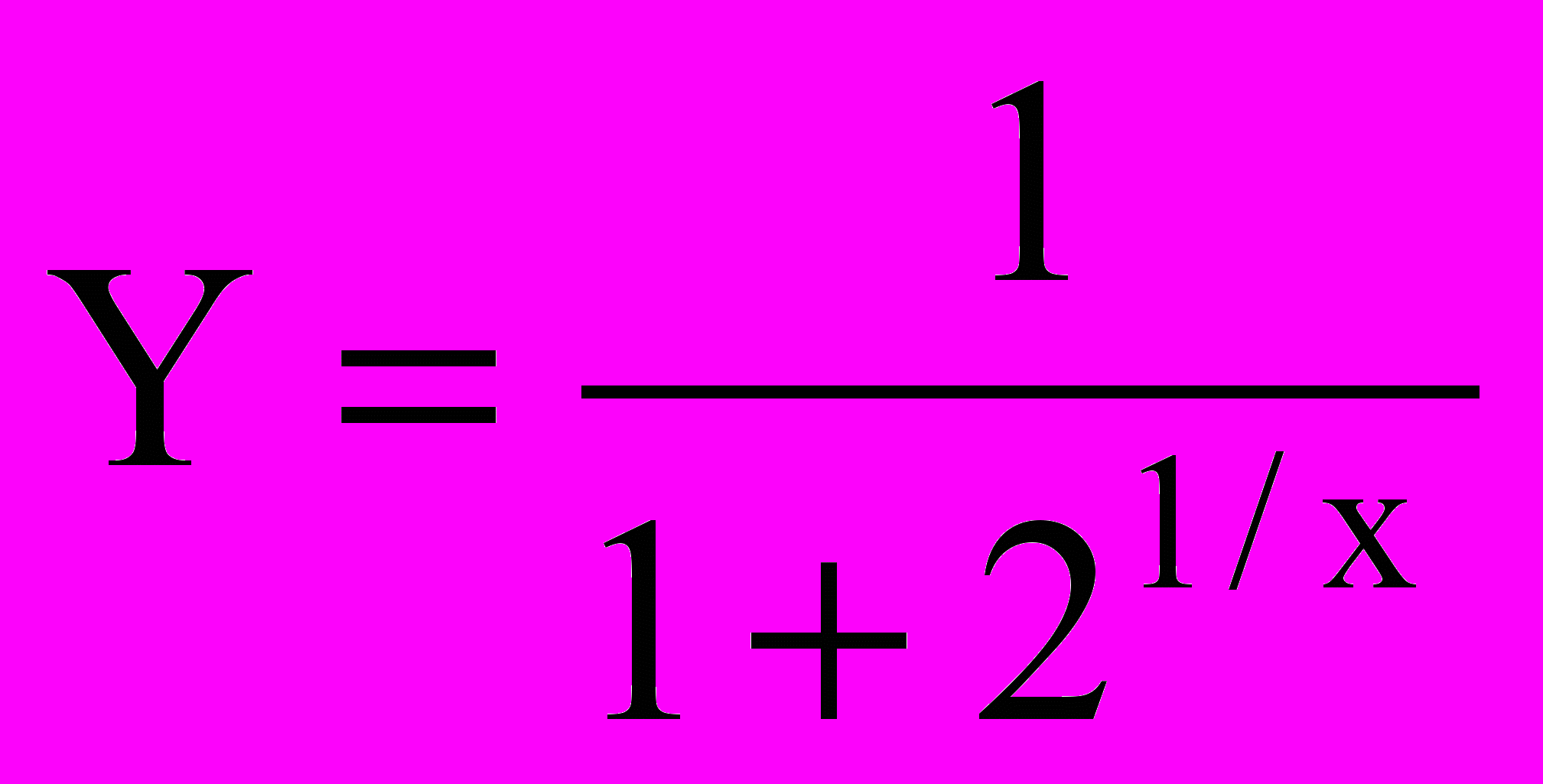, Б)

Теоретические вопросы к рубежному контролю № 2 (второй семестр) по разделу «Дифференциальные уравнения»
  1. Что называется дифференциальным уравнением первого порядка?
  2. Дать определение частного решения. В чем состоит начальное условие для уравнения первого порядка?
  3. Сформулировать теорему существования и единственности решения уравнения первого порядка.
  4. Что называется общим решением дифференциального уравнения первого порядка?
  5. Дать геометрическую иллюстрацию частного и общего решений дифференциального уравнения первого порядка.
  6. Дать определение дифференциального уравнения с разделяющимися переменными и указать метод его интегрирования.
  7. Какое уравнение первого порядка называется однородным? Как оно решается?
  8. Какое уравнение первого порядка называется линейным? Изложить способ его решения.
  9. Что называется дифференциальным уравнением второго порядка?
  10. Каков геометрический смысл начальных условий дифференциального уравнения второго порядка?
  11. Сформулировать теорему существования и единственности решения для уравнений второго порядка.
  12. Изложить способы приведения уравнений второго порядка.
  13. Дать определение дифференциального уравнения n-го порядка и его общего решения. Указать, как задаются начальные условия для уравнения n-го порядка.
  14. Что называется линейным дифференциальным уравнением второго порядка?
  15. Сформулировать и доказать теорему об общем решении линейного уравнения без правой части.
  16. Сформулировать и доказать теорему о структуре общего решения линейного уравнения с правой частью.
  17. Описать способ решения линейного уравнения второго порядка без правой части с постоянными коэффициентами. Какое уравнение называется характеристическим? Как оно составляется?
  18. Какой вид имеет общее решение линейного уравнения второго порядка без правой части с постоянными коэффициентами при действительных и различных корнях характеристического уравнения? При равных корнях?
  19. Доказать, что если комплексная функция является решением линейного уравнения с действительными коэффициентами, то ее действительная и мнимая части также являются решениями.
  20. Указать вид решения в случае комплексных корней характеристического уравнения.
  21. Как можно находить решение уравнения с правой частью, если правая часть его представлена в виде суммы нескольких функций
  22. Что называется системой дифференциальных уравнений? Что называется решением такой системы?
  23. Какая система дифференциальных уравнений называется нормальной?
  24. Описать приемы сведения одного уравнения высшего порядка к нормальной системе. Как осуществляется обратный переход и всегда ли он возможен?

Типовые задачи к зачету по разделу «Теория вероятностей»
  1. Событие А означает, что хотя бы один из трех проверенных приборов бракованный, событие В – все три прибора стандартные. Что означает события а)А+В, б)АВ?
  2. Монета брошена два раза. Найти вероятность того, что хотя бы один раз выпадет герб.
  3. Наудачу взятый телефонный номер состоит из пяти цифр. Какова вероятность, что в нем все цифры различные?
  4. На 12 карточках напечатаны числа от 11 до 22. Наудачу выбираются 4 карточки. Какова вероятность того, что сумма чисел на них будет равна 82?
  5. В урне 5 белых и 10 черных шаров. Из урны вынимают один шар, затем второй. Найти вероятность, что оба шара будут белыми.
  6. Схема состоит из трех последовательно соединенных элемента. Вероятность безопасной работы (надежность) каждого элемента равна 0,9. Найти надежность схемы в целом.
  7. Вероятность хотя бы одного попадания в мишень при трех выстрелах равна 0,875. Найти вероятность попадания при одном выстреле.
  8. Приборы изготавливаются двумя заводами. Первый завод поставляет вдвое больше изделий, чем второй. Надежность (вероятность безотказной работы) прибора первого завода равна 0,8, второго – 0,9. Определить вероятность безотказной работы случайно выбранного прибора.
  9. Вероятность нормального расхода горючего в автопарке равна 0,7. Определить вероятность того, что в течение недели (7 дней) нормальный расход горючего будет в течение не менее 5 дней.
  10. Стрелок производит три выстрела по мишени. Вероятность попадания в цель при одном выстреле равна 0,6. Случайная величина Х – число попаданий в мишень. Составить закон распределения этой случайной величины.
  11. Определить М(х), D(х), и σ(х) для случайной величины, заданной законом

    X
    -1
    0
    1
    2

    Р
    0,3
    0,2
    0,3
    0,2
  12. Случайная величина Х распределена по закону f(x)=A/(1+x2). Найти а) константу А, б) Вероятность попадания в интервал(0;π/4)
  13. Найти М(х), D(х), и σ(х) случайной величины, распределенной равномерно на отрезке (0,2]. Найти так же вероятность попадания в интервал (1;15)
  14. Плотность вероятности показательного распределения f(x)=3e-3x, х≥0. Найти М(х), D(х), σ(х), вероятность попадания этой величины в интервал (0,1;0,7)
  15. Вычислить вероятность попадания в интервал (1;4) для случайной величины, распределенной нормально с плотностью
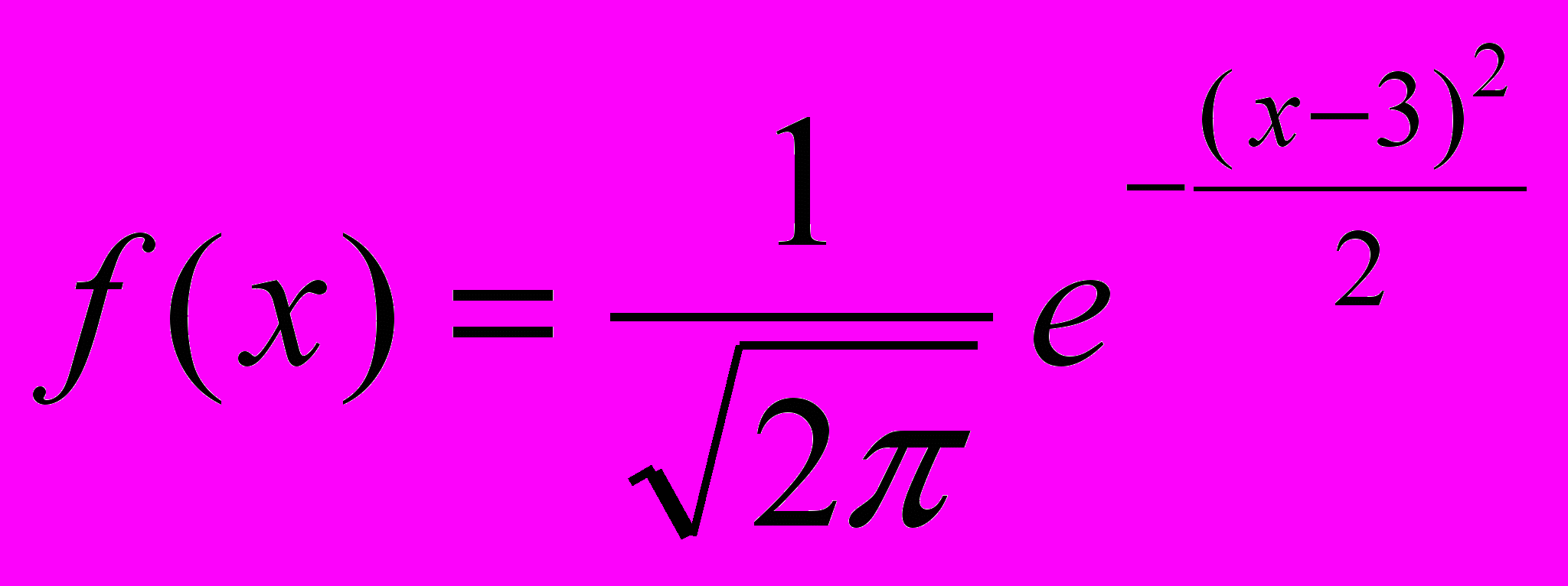
  16. Найти вероятность Р (|xn-10|<3), если случайная величина распределения нормально и σ=1
  17. При измерении длины детали (распределение длины – нормальное со средним знанием а=15мм и средним квадратическим отклонением σ=2мм). Требуется найти интервал, в котором с вероятностью 0,9544 попадают значения измеряемой длины


7. Учебно-методическое и информационное обеспечение дисциплины (модуля)

а) основная литература:
  1. Письменный Д.Т. Конспект лекций по высшей математике. – М.: Айрис Пресс, 2007.
  2. Бермант А.Ф. и Араманович И.Г. Краткий курс математического анализа (для втузов). – М.: Наука, 1973.
  3. Бугров Я.С. Никольский С.М. Дифференциальное и интегральное исчисление. – М.: Наука, 1980, 1988.
  4. Бугров Я.С. Никольский С.М. Дифференциальные уравнения. Кратные интегралы. Ряды. – М.: Наука 1981, 1985.
  5. Араманович И.Г. и др. Функции комплексного переменного. Операционное исчисление. – М.: Наука, 1968.
  6. Под ред. Л.В. Ефимова и Б.П. Демидовича. Сборник задач по математике для втузов. – М.: Наука, 1986.
  7. Задачи и уравнения по математическому анализу (для втузов). Под редакцией Б.П. Демидовича. – М.: Наука, 1978 и последующие издания.
  8. Письменный Д.Т. Курс лекций по теории вероятностей, математической статистике и случайным процессам. – М.: Айрис Пресс, 2007.
  9. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высшая школа, 1979 и последующие издания

б) дополнительная литература:
  1. Минорский В.П. Сборник задач по высшей математике. – М.: Наука, 1978.
  2. Шипачев В.С. Высшая математика. – М.: Высшая школа, 1990.
  3. Шипачев В.С. Задачник по высшей математике. – М.: Высшая школа, 1998.
  4. Данко П.Е. и др. Высшая математика в упражнениях и задачах. Ч. 1, 2. – М.: Высшая школа, 1986.

в) программное обеспечение и Интернет-ресурсы:

программа тестового контроля знаний;

информационно-справочная база учебно-методического материала;

сайт кафедры Высшей математики vm.mstuca.ru.


8. Материально-техническое обеспечение дисциплины (модуля)

– лаборатория персональных ЭВМ,

– проекционная компьютерная система.