Лекция Силы, действующие в атмосфере. Уравнение статики атмосферы и его следствия Закон сохранения массы, из которого следует уравнение неразрывности, является первым из основных законов механики.
| Вид материала | Лекция |
- Программа по курсу механики сплошных сред Основные понятия механики сплошных сред, 9.75kb.
- 4 Универсальное уравнение состояния идеального газа, 171.14kb.
- § Тема. Некоторые определения и обозначения, 1005.59kb.
- Решение кубического уравнение в общем виде. От общего кубического уравнения к упрощённому, 14.77kb.
- Самостоятельная работа Повторение основных понятий, определений, законов из курса механики, 251.69kb.
- Содержание уравнения математической физики (нм-3) Уравнения математической физики (нп-3), 92.05kb.
- Урок учителя математики Гукасовой А. П. Тема урока: «Уравнение касательной», 52.29kb.
- План-конспект Тема урока : Движение жидкостей и газов. Уравнение Бернулли, 43.29kb.
- Л. Н. Гумилева Физико-технический факультет Экзаменационные билеты, 42.99kb.
- Ассистент Андрей Алексеевич Шошин Плотность и поток энергии в мгд. Простые следствия, 53.62kb.
- -
Лекция 6. Силы, действующие в атмосфере. Уравнение статики атмосферы и его следствия
Закон сохранения массы, из которого следует уравнение неразрывности, является первым из основных законов механики. Вторым основным законом является закон изменения импульса или второй закон Ньютона, согласно которому изменение количества движения (импульса) за единицу времени равно сумме сил, приложенных к рассматриваемому телу. В гидромеханике второй закон Ньютона используется в форме принципа Даламбера, согласно которому при движении контрольного объема все силы, приложенные к нему уравновешивают друг друга. Для того, чтобы выяснить, как описываются математически силы, действующие на частицу атмосферного воздуха, следует рассмотреть важный частный случай – состояние покоя.
Силы, действующие на воздушные частицы
Объемные и поверхностные силы
Объемные (массовые) силы: величина этих сил пропорциональна объему (массе) жидкости, на который они действуют. Объемная сила, действующая в контрольном объеме, выражается формулой
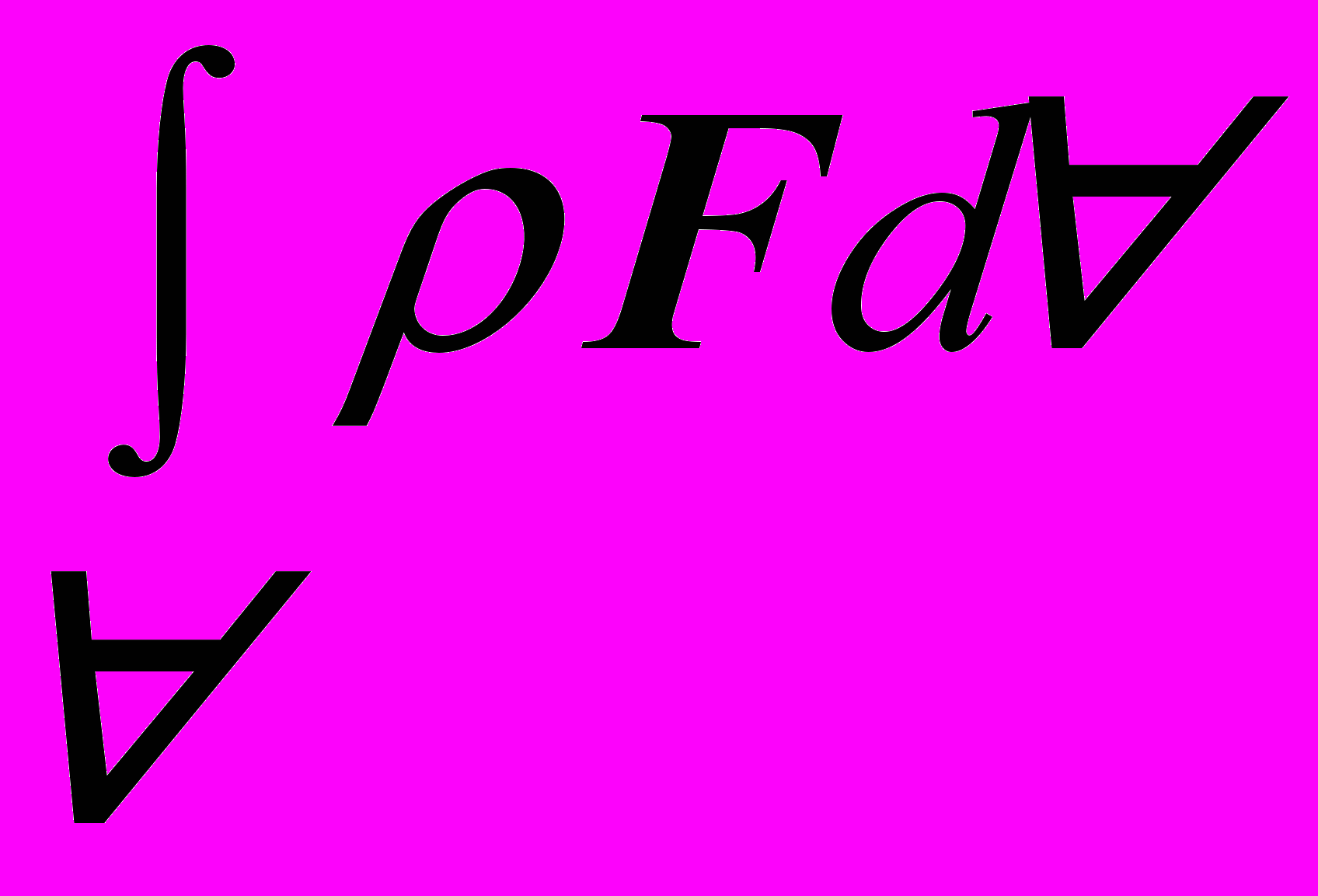 , в которой характеристикой объемной (массовой) силы в каждой точке является плотность распределения этой силы в пространстве, векторная величина, равная силе, действующей на единицу объема (массы)
, в которой характеристикой объемной (массовой) силы в каждой точке является плотность распределения этой силы в пространстве, векторная величина, равная силе, действующей на единицу объема (массы) 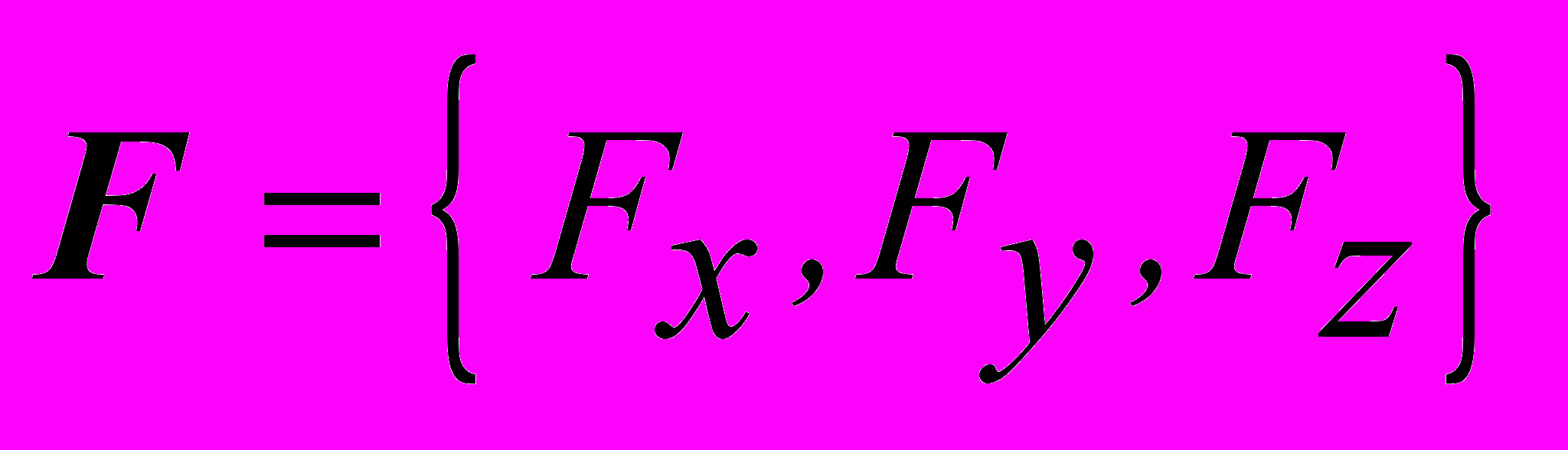 . Примером объемной силы является сила тяжести. В этом случае плотность распределения представляет собой силу, приходящуюся на единицу массы сплошной среды.
. Примером объемной силы является сила тяжести. В этом случае плотность распределения представляет собой силу, приходящуюся на единицу массы сплошной среды.Поверхностные силы, действуют между частями данного объема жидкости. Они не могут изменить количество движения этого объема, так как внутри него каждая внутренняя сила уравновешивается равной ей по модулю внутренней силой, имеющей противоположное направление. Вместе с тем работа внутренних сил может изменить кинетическую и (или) потенциальную энергию рассматриваемого объема жидкости. Величина этих сил пропорциональна площади поверхности, на которую они действуют. Характеристикой поверхностной силы на заданной поверхности является плотность ее распределения, которую называют напряжением. Это векторная величина. Её направление, в общем случае, не совпадает с направлением нормали к заданной поверхности. Проекцию напряжения на эту нормаль называют нормальным напряжением, а проекцию напряжения на касательную плоскость к заданной поверхности называют касательным напряжением.
Ниже приведены основные сведения об объемных и поверхностных силах, действующий в атмосфере.
Сила тяжести – объемная сила
Вектор силы тяготения согласно закону Ньютона может быть записан в виде
F = f m1m2 /r2 iF
,где f = 6.673 10-11 [н м2/кг2 или м3/с2] – гравитационная постоянная, iF – орт направления силы от меньшей массы (m2) к большей (m1). В дальнейшем принимается, что m1 = m (для Земли M), m2 = 1 кг (единичная масса). Выбирая единичную массу притягиваемого тела, силовое поле массы M начинают описывать с помощью ускорения силы тяжести. (В дальнейшем будет использована и геоцентрическая гравитационная постоянная fM=3,086 1014 [м3/с2]).
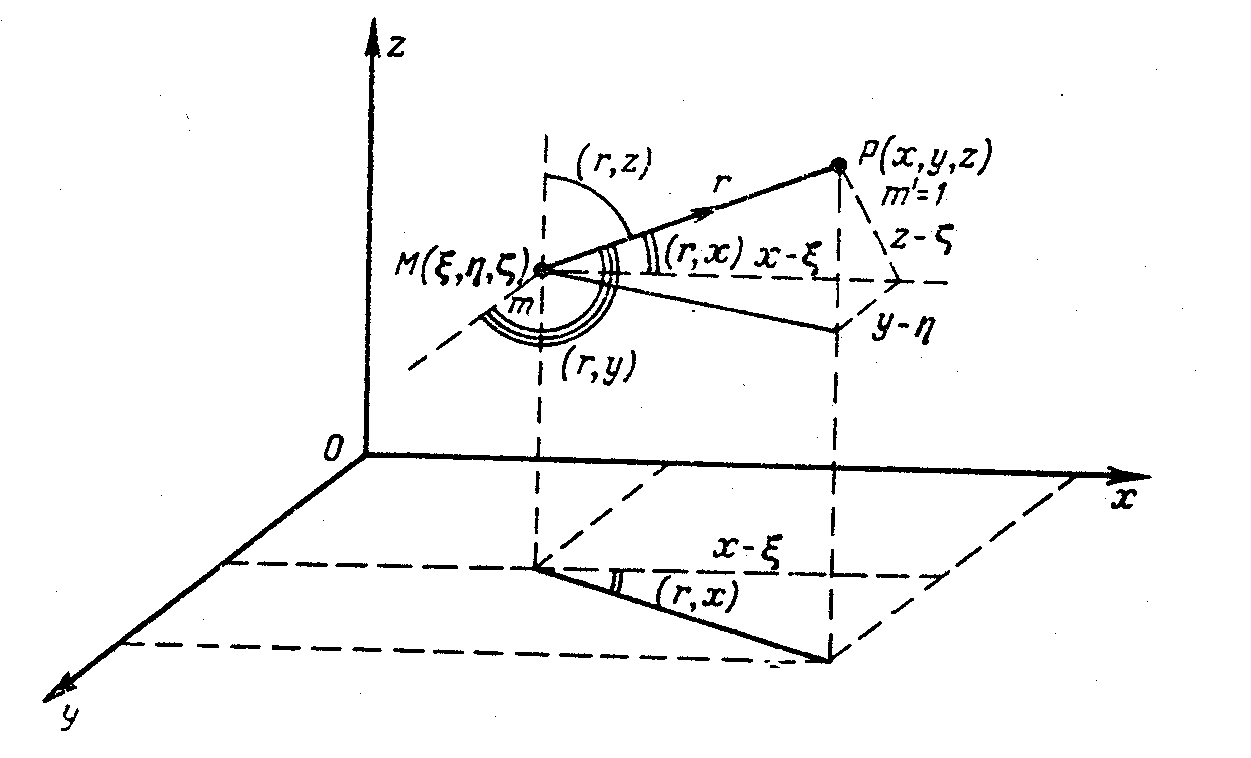
Если, как показано на рисунке, если масса M расположена в точке {ξ, η, ζ}, а единичная масса расположена в точке{x,y,z}, то вектор направления силы противоположен вектору расстояния r2 = (x2-x1)2 + (y2-y1)2 +(z2- z1)2 до притягиваемой точки.
Если dF =dFx i + dFy j + dFz k – вектор силы притяжения элементом dm массы M, единичной массы в проекциях на оси декартовой системы координат с центром в центре тяжести тела M , то вычисление силы притяжения телом конечного объема может быть выполнено с использованием объемного интеграла.
dFx = dF cos(F x)= - dF cos(r x) = - (f dm/r2) (x2-x1)/r Fx = - f cos(r x) /r2 dm
dFy = dF cos(F y)= - dF cos(r y) = - (f dm/r2) (y2-y1)/r Fy = - f cos(r y) /r2 dm
dFz = dF cos(F z)= - dF cos(r z) = - (f dm/r2) (z2-z1)/r Fz = - f cos(r z) /r2 dm
Если ось Z совместить с направлением действующей силы, то Fx=Fy=0. Тогда
Сила притяжения единичной массы со со стороны массы M, выражается формулой
 (6.1)
(6.1)Притяжение однородного шара
Пусть центр притягиваемой массы находится на расстоянии ρ от центра сферы. Произвольная точка A на притягивающей сфере находится на расстоянии r от притягиваемой точки, причем r2 = R2 + ρ 2 –2R ρ cosоткуда следует, что R/ ρ dr=R2sind/r
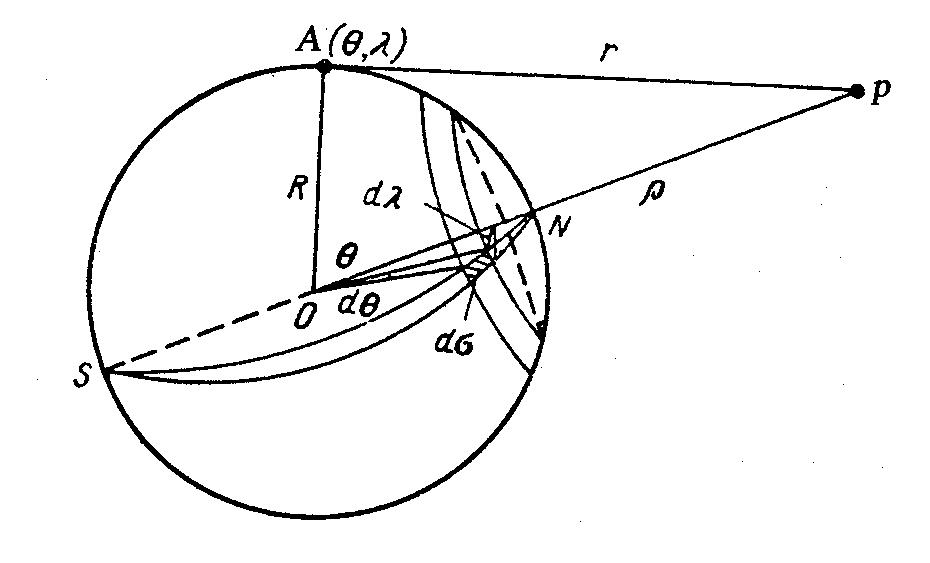
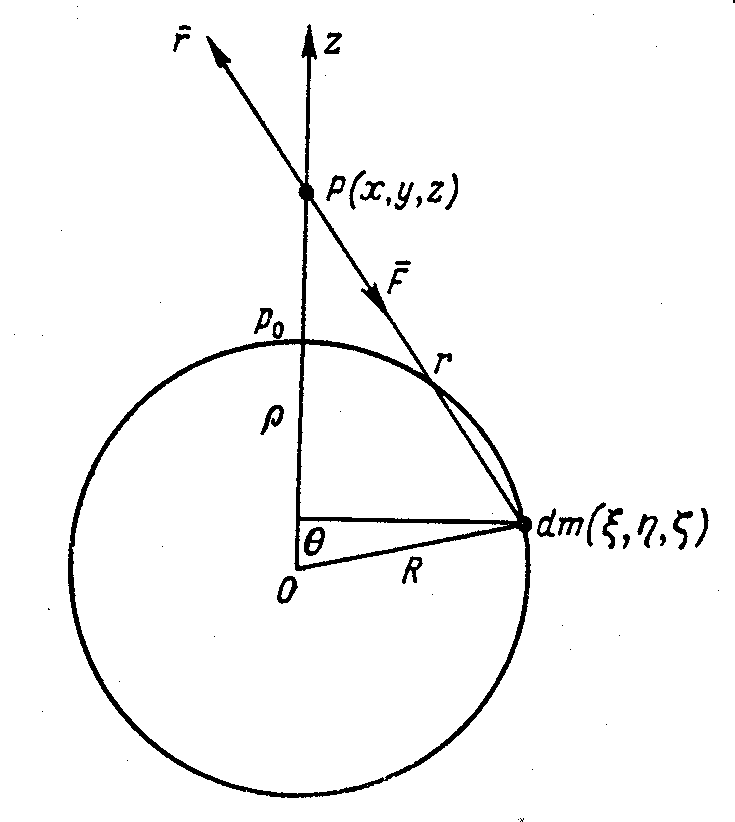
Элемент притягивающей массы, расположенной на участке поверхности dσR2sin()dd можно найти по формуле
dm = dσR2sin()dd (6.2)
где З(R)dR поверхностная плотность (объемная плотность обозначена З(R)). Сила притяжения элемента массы участка поверхности dm, вычисляется по формуле
dF= -f μ cos(r,z)dσ =- f μ(ρ-Rcosθ)/r dσ = f μ(ρ2-R2+r2)/2ρr dσ , (6.3)
в которой Rcosθ выражен через расстояния.
Сила притяжения всей сферической поверхности может быть вычислена путем интегрирования dF по все поверхности сферы
F = f
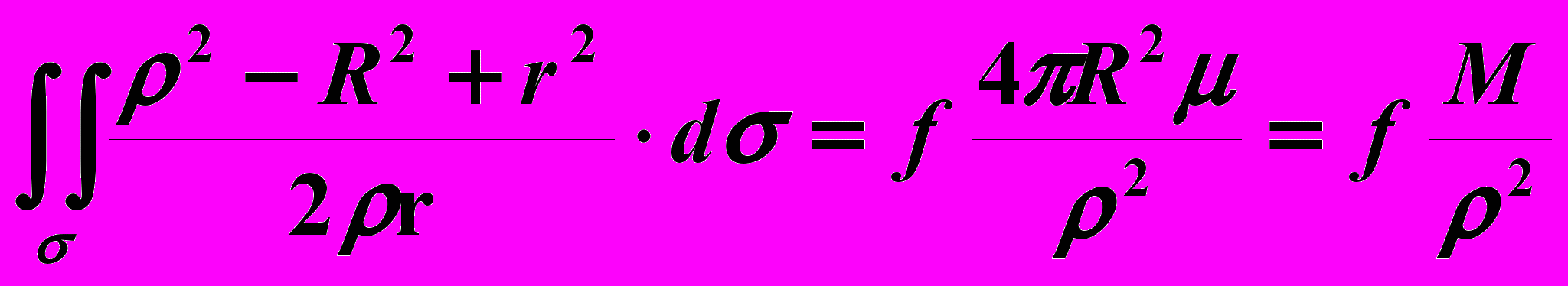 (6.4)
(6.4)Cилу притяжения шара можно вычислить, выразив поверхностную плотность через постоянную объемную плотность З =dR , суммируя воздействие всех внутренних бесконечно тонких слоев dR и учитывая, что в пределах атмосферы высоты z ( 0- 50 км) почти в тысячу раз меньше радиуса Земного шара Rш (6400 км), по формуле
F =
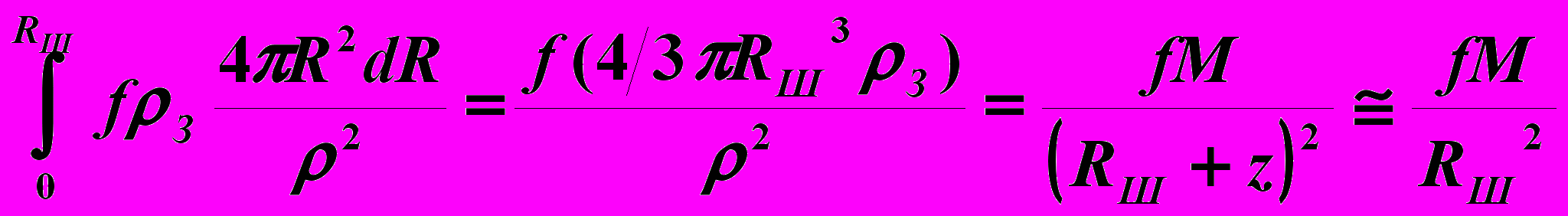 =9,8 м/с2 =g (6.5)
=9,8 м/с2 =g (6.5)Таким образом, показано, что при оценке силы тяжести можно считать, что сила притяжения Земного шара сосредоточена в его центре и вычисляется по закону Всемирного тяготения для материальных точек. Это значит, что на каждую частицу воздуха действует сила P, направленная к центру Земли, называемая весом этой частицы и вычисляемая по формуле
 (6.6)
(6.6)Потенциал силы тяготения и геопотенциал
Если V/ x = Fx, V/ y = Fy , V/ z = Fz , то скалярное поле V(x,y,z) – потенциал векторного поля F(x,y,z). Для поля силы тяжести Земного шара в метеорологии можно ограничиться только приближенной оценкой его вертикальной составляющей по формуле
dV= V/ x dx+ V/ y dy + V/ z dz = Fx dx + Fy dy + Fz dz =g dz
Учитывая, что потенциал является полным дифференциалом, он определяется путем интегрирования по произвольному контуру между двумя точками поля
V(B) – V(A) = A B dV = A B Fx dx + Fy dy + Fz dz =
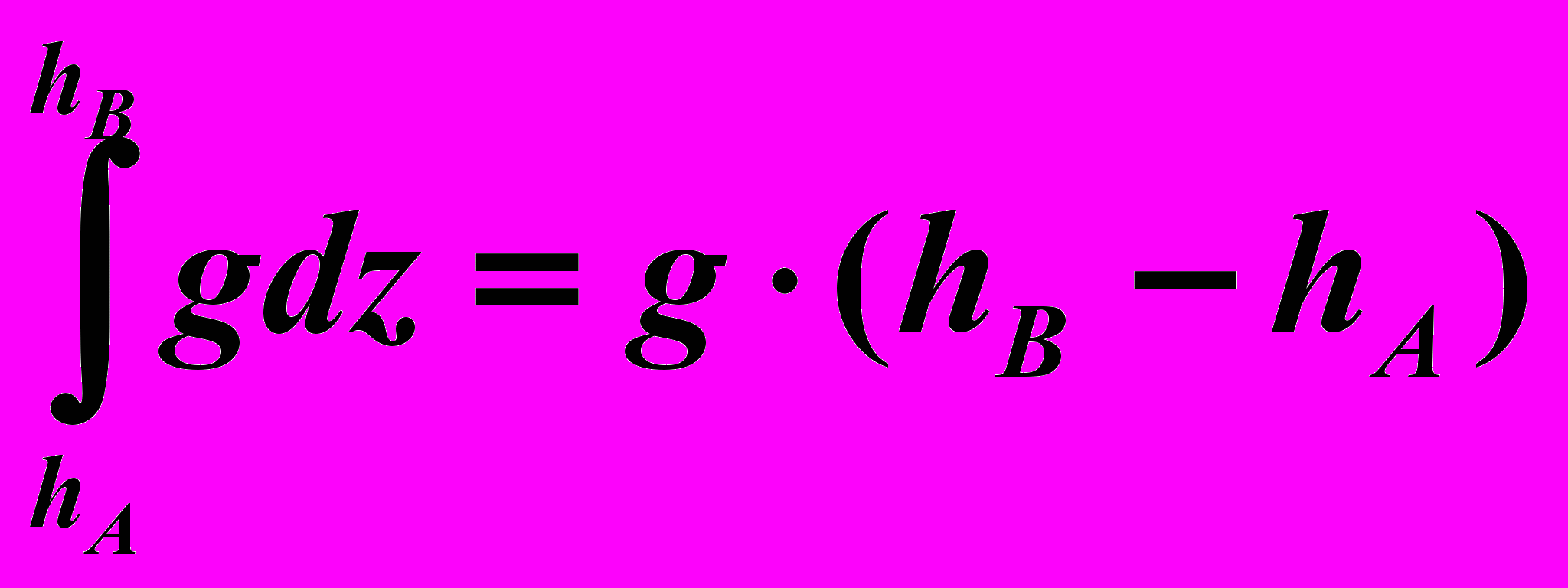
По физическому смыслу потенциал -это работа силы земного тяготения по перемещению единичной массы между точками A B. С большой точностью можно считать, что она зависит только от перепада высот между точками. В метеорологии принято его называть геопотенциалом. Полезно помнить, что для центральных векторных полей, к которым относится поле силы тяжести, для вектора силы F(x,y,z) потенциал обратно пропорционален расстоянию до точки (V = f M/r). Между этими определениями нет несоответствия, так как последнее переходит в первое при использовании предположения 1/r =1/( Rш+z)≈ -z/ Rш2 .
Тензор напряжений – форма записи поверхностных сил
Д
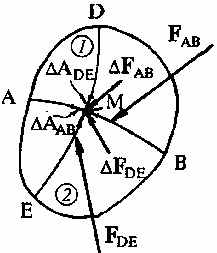 ля того, чтобы показать, почему существуют поверхностные силы, разделим, как принято в механике сплошных сред, произвольную часть контрольного объема сплошной среды поверхностью АВ на две части (см. рисунок). При этом часть 1 будет действовать на часть 2 с силой ΔFAB . Обозначив часть площади поверхности АВ, расположенную в точке M через ΔАAB , можно записать формулу для вектора напряжения PAB , действующего на эту площадку, в виде
ля того, чтобы показать, почему существуют поверхностные силы, разделим, как принято в механике сплошных сред, произвольную часть контрольного объема сплошной среды поверхностью АВ на две части (см. рисунок). При этом часть 1 будет действовать на часть 2 с силой ΔFAB . Обозначив часть площади поверхности АВ, расположенную в точке M через ΔАAB , можно записать формулу для вектора напряжения PAB , действующего на эту площадку, в виде 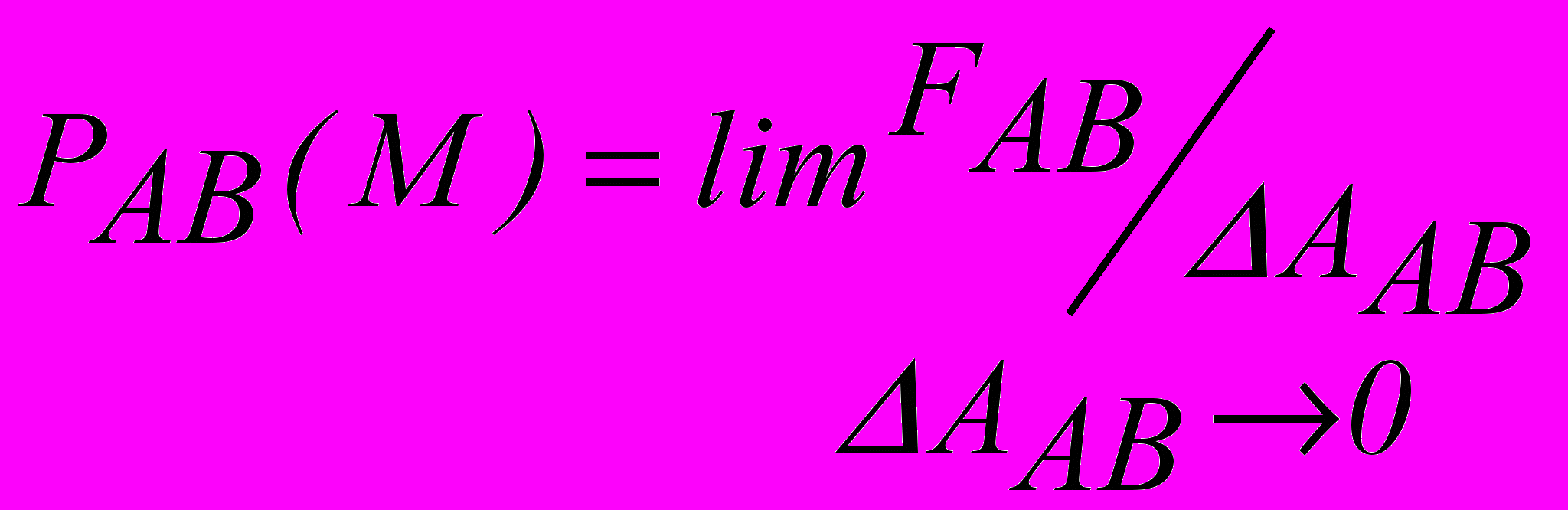
Следует обратить внимание, что на часть площади ΔАDE поверхности DE, расположенную в той же точке M, действует другой вектор напряжения
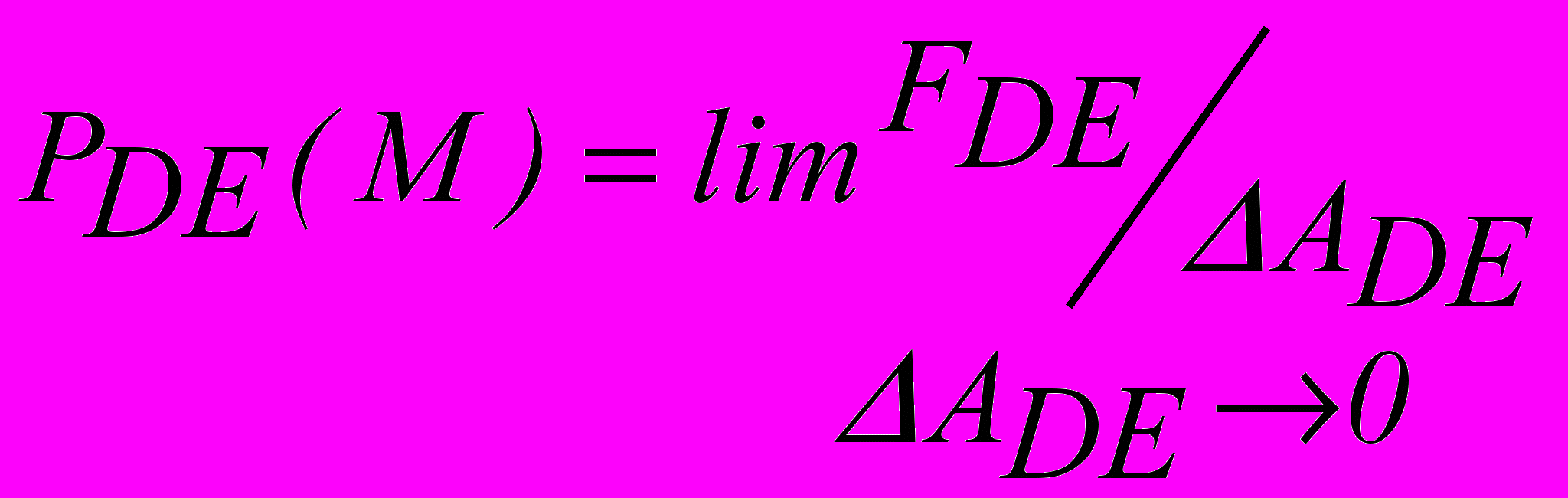
Это значит, что векторное представление поверхностных сил в одной и той же точке атмосферы неоднозначно, оно зависит от ориентации элементарной площадки. Для того, чтобы отделить однозначное описание напряженного состояния в точке от влияния ориентации площадки, нужно учесть, что для любой площадки, ориентация которой задается вектором нормали
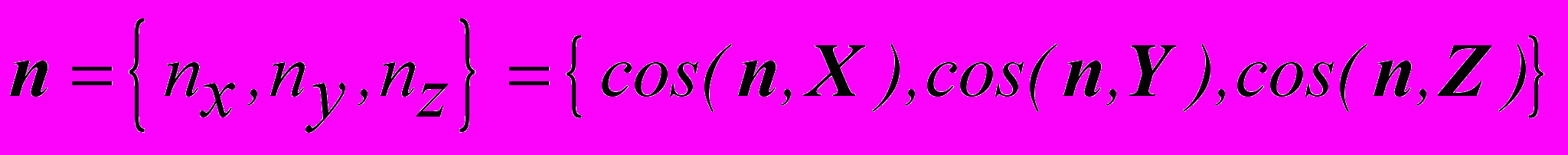 вектор напряжения P разлагается по трем не компланарным векторам, в соответствие с выбранной координатной системой. (см. рисунке). Каждый из векторов PX, PY , PZ представляет напряжение, действующее в точке на координатные плоскости. В общем случае эти вектора могут не быть перпендикулярными координатным плоскостям. Поэтому каждый из них имеет трехкомпонентное представление.
вектор напряжения P разлагается по трем не компланарным векторам, в соответствие с выбранной координатной системой. (см. рисунке). Каждый из векторов PX, PY , PZ представляет напряжение, действующее в точке на координатные плоскости. В общем случае эти вектора могут не быть перпендикулярными координатным плоскостям. Поэтому каждый из них имеет трехкомпонентное представление.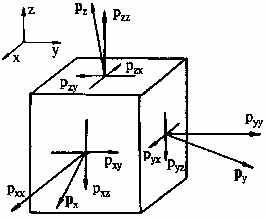
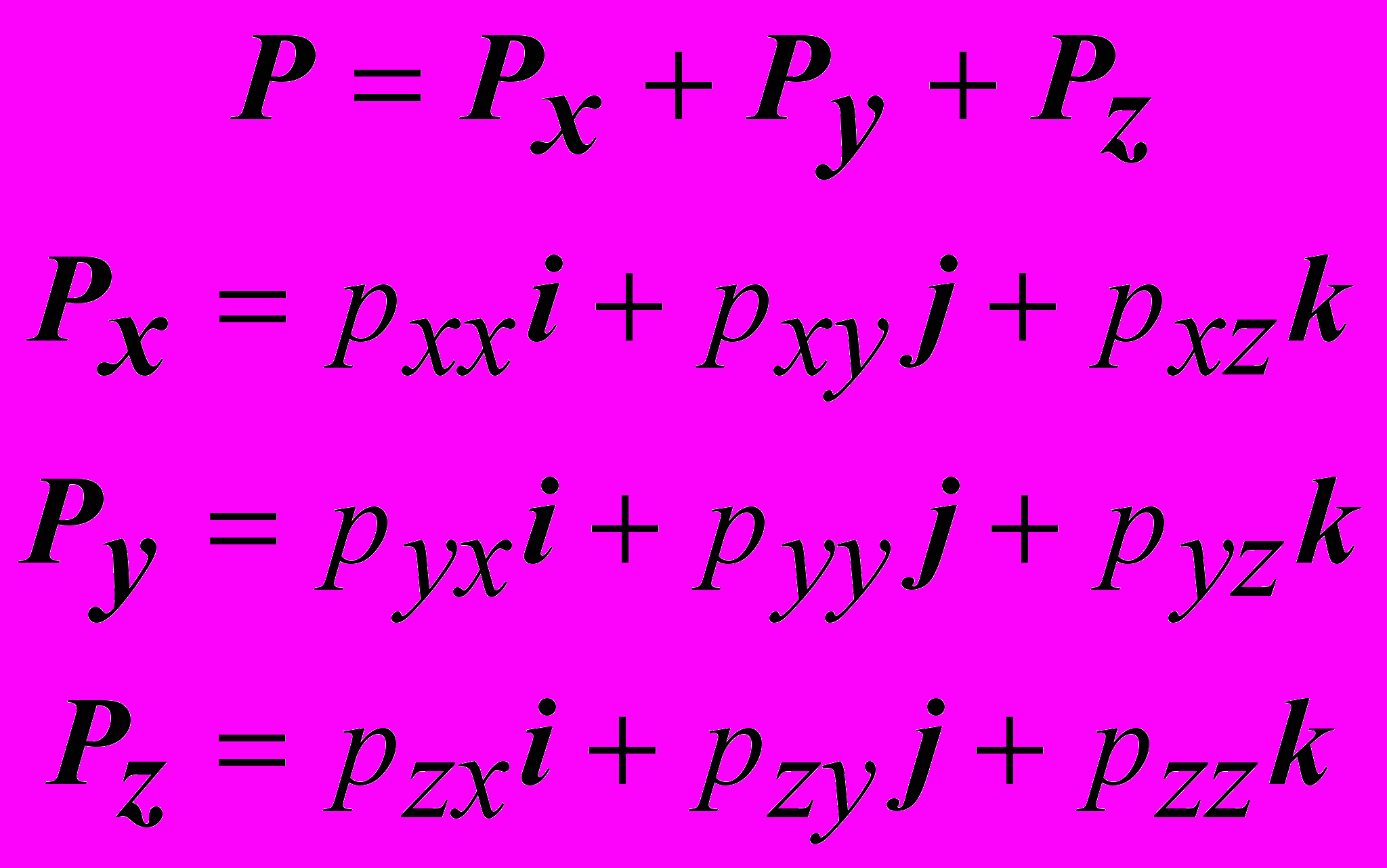
Компоненты PXX, PYY, PZZ являются нормальными напряжениями, а остальные компоненты – касательными напряжениями.
Если рассмотреть равновесие контрольного объема в форме пирамиды с вершиной в точке M (см. рисунок), т
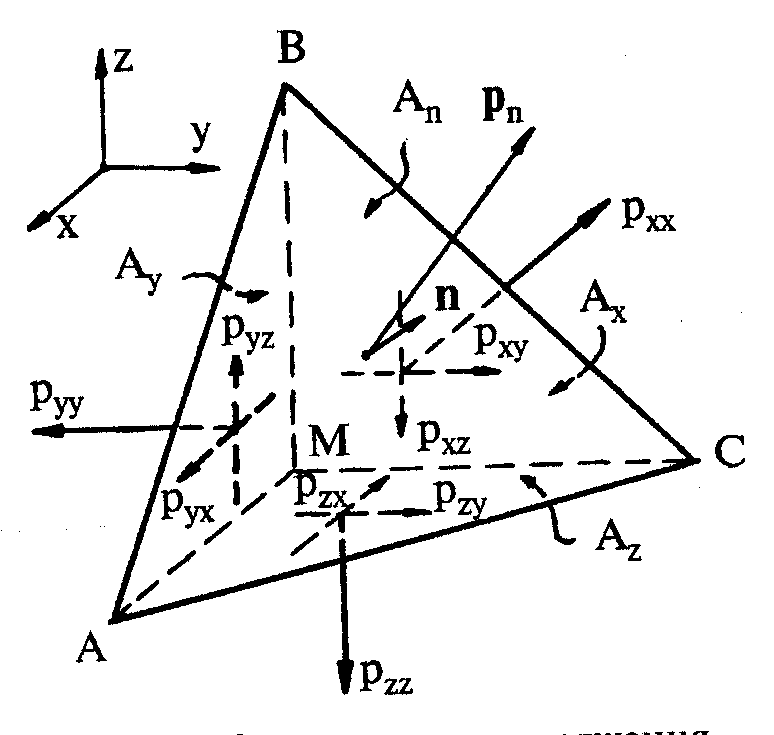 о проекции грани ABC, имеющей площадь An , на координатные плоскости выражаются формулами
о проекции грани ABC, имеющей площадь An , на координатные плоскости выражаются формулами 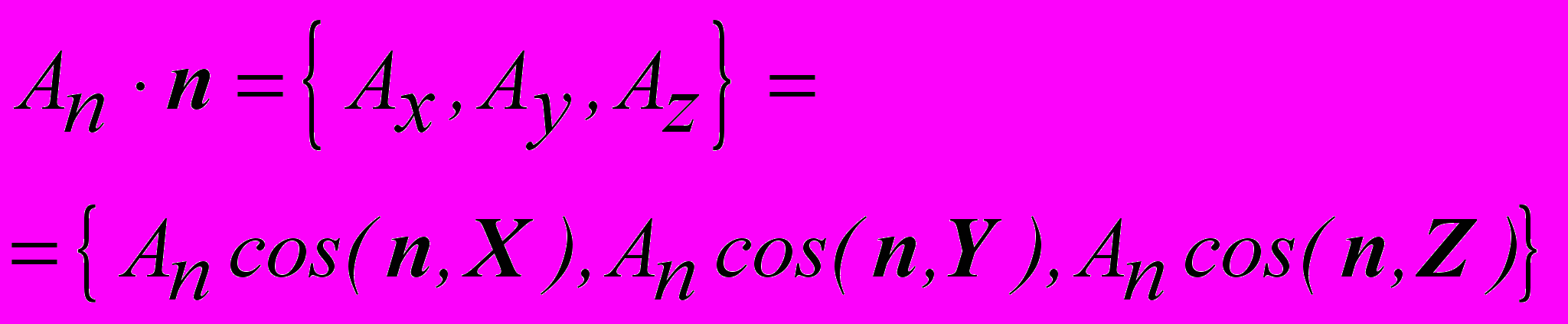 . Вектор напряжений, действующий на эту грань, представляется в виде
. Вектор напряжений, действующий на эту грань, представляется в виде  , причем вектора напряжений, действующих параллельно координатным осям, имеют компоненты
, причем вектора напряжений, действующих параллельно координатным осям, имеют компоненты 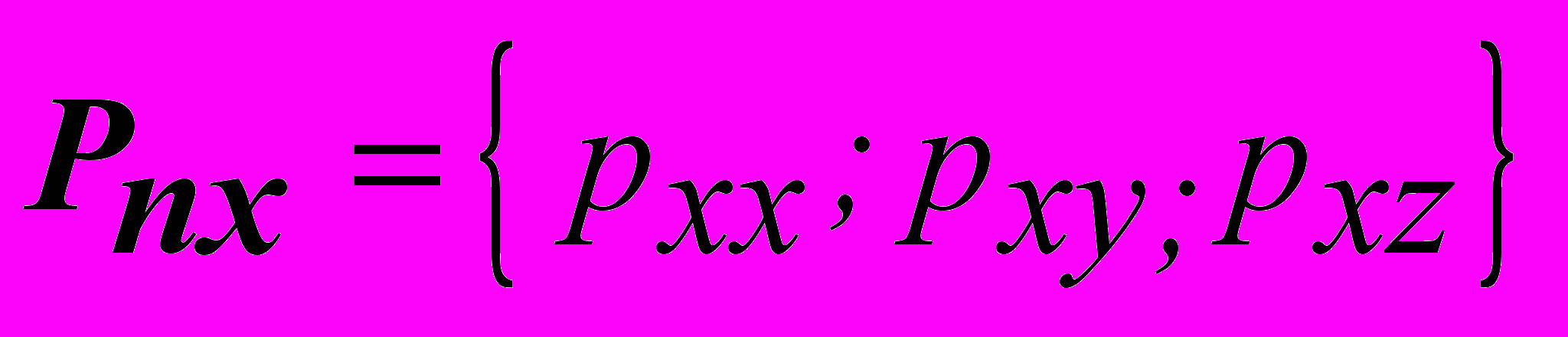 ,
, 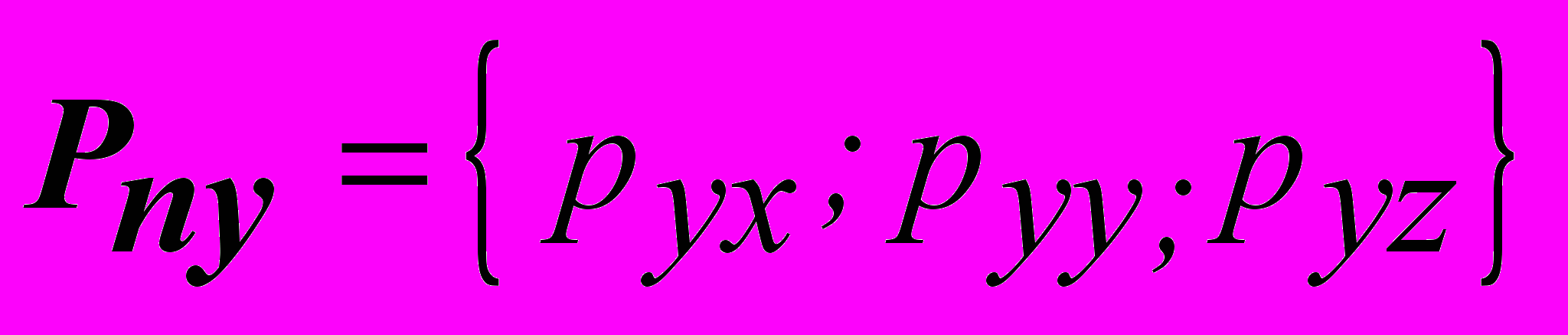 ,
, 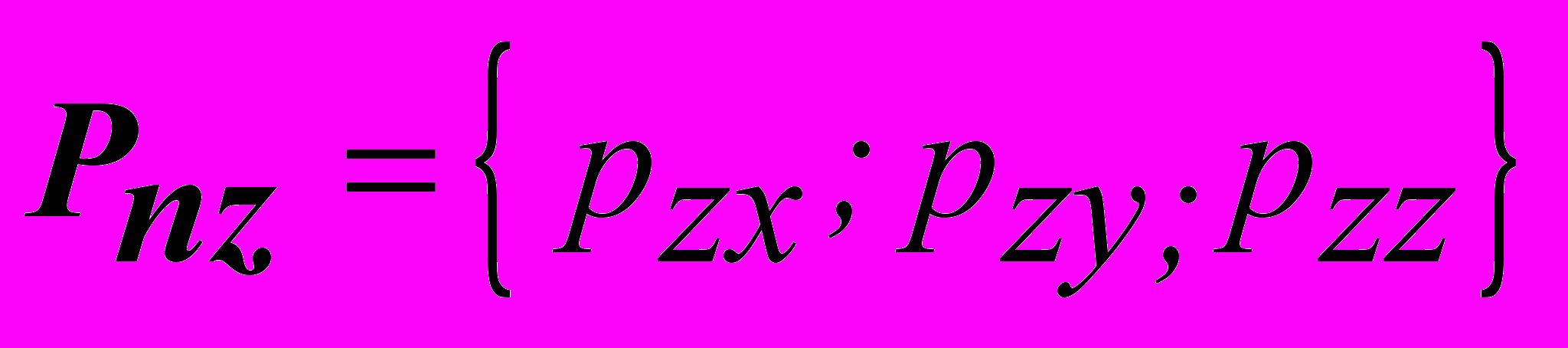
Для того, чтобы пирамида находилась в равновесии проекции всех сил на координатные оси должны быть уравновешены. Отсюда следуют равенства
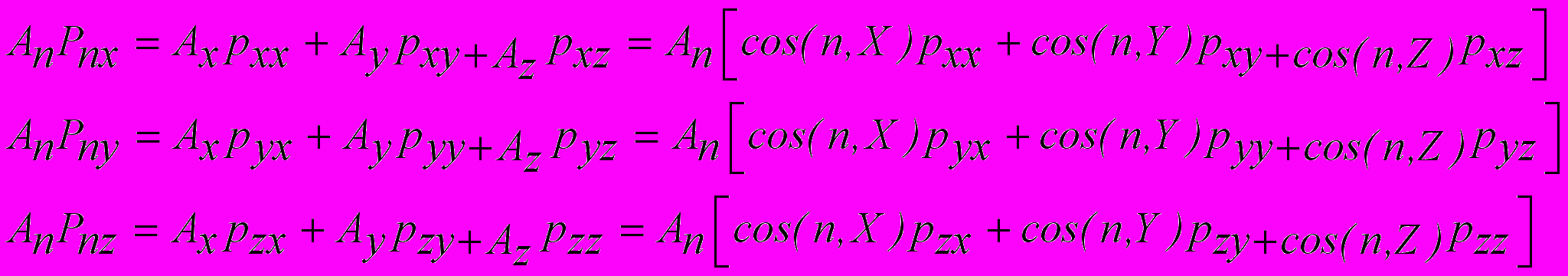 Если сократить An и представить эти равенства в матричной форме, то эти равенства можно переписать в виде
Если сократить An и представить эти равенства в матричной форме, то эти равенства можно переписать в виде (6.7)
(6.7)Становиться видно, что эффект ориентации грани ABC, выражаемый вектором нормали к этой грани n и эффект действующих в точке M напряжений, выражаемый таблицей П (3х3), разделяются.
Таблица
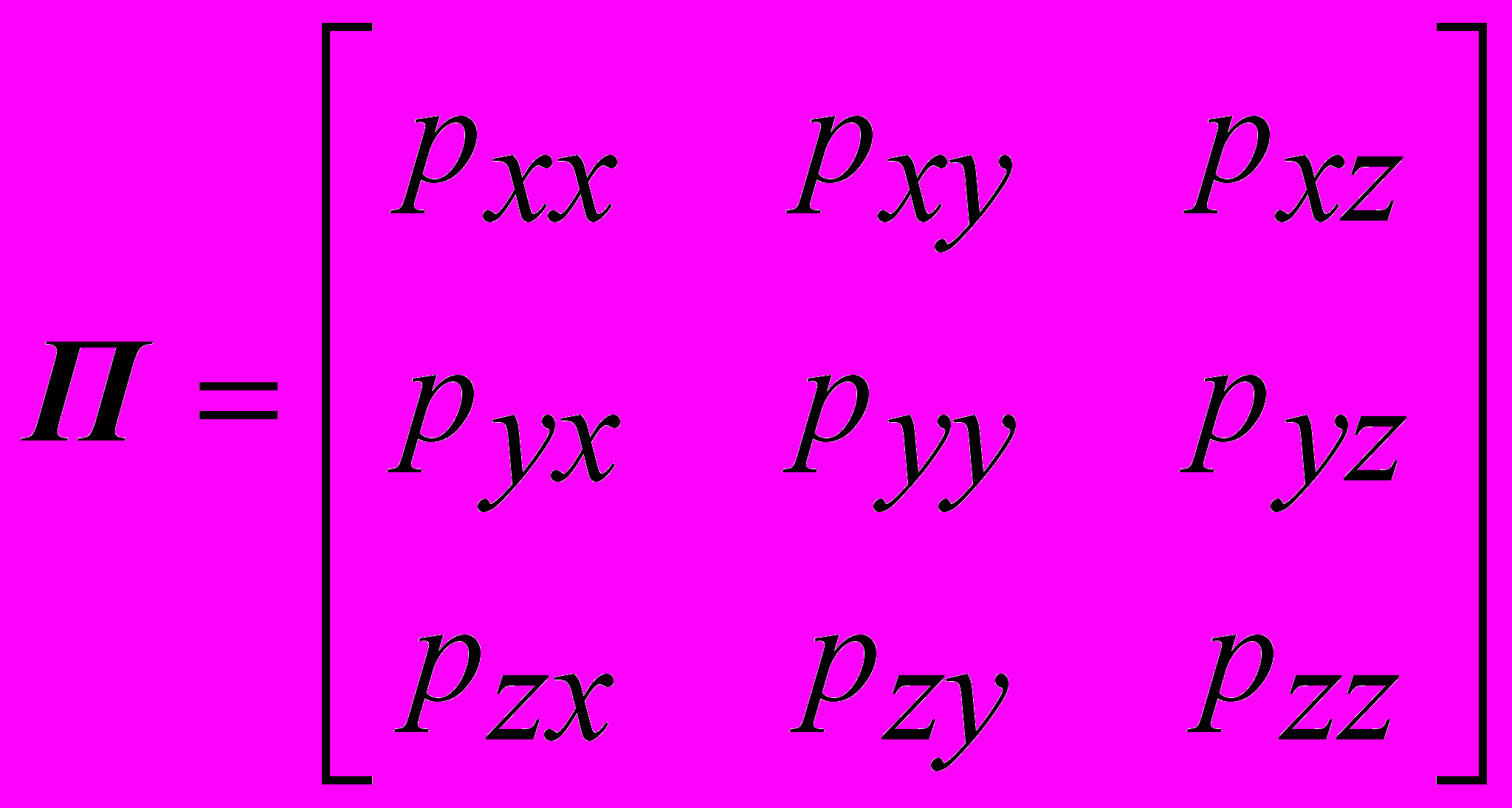 называется тензором напряжений.
называется тензором напряжений. Свойства тензоров напряжений в любой сплошной среде
1. П - это матрица. Справедливы все свойства матриц.
2. Если от системы (x,y,z) перейти к (x',y',z'), то П' = А П , П' - тензор в новой системе, А - матрица перехода (известна). Это значит, что П' предсказуем и не зависит от ориентации площадки, тензор напряжений однозначно определяет поверхностные силы, действующие в точке сплошной среды.
3. При смене координат сохраняются ИНВАРИАНТЫ тензора П:
а) След (pxx+ pyy+ pzz), б) Миноры; в) Определитель.
4. Так как вектор n безразмерен, то размерность [pij] = Н/ м2
Свойства тензоров напряжений жидкости.
Текучестью называется способность частиц жидкости приходить в движение при любом, даже бесконечно малом касательном напряжении. Отсюда следует, что в состоянии покоя, когда нет движения, нет и касательных напряжений, то есть тензор напряжений в жидкости (и газе) является диагональной матрицей, то есть
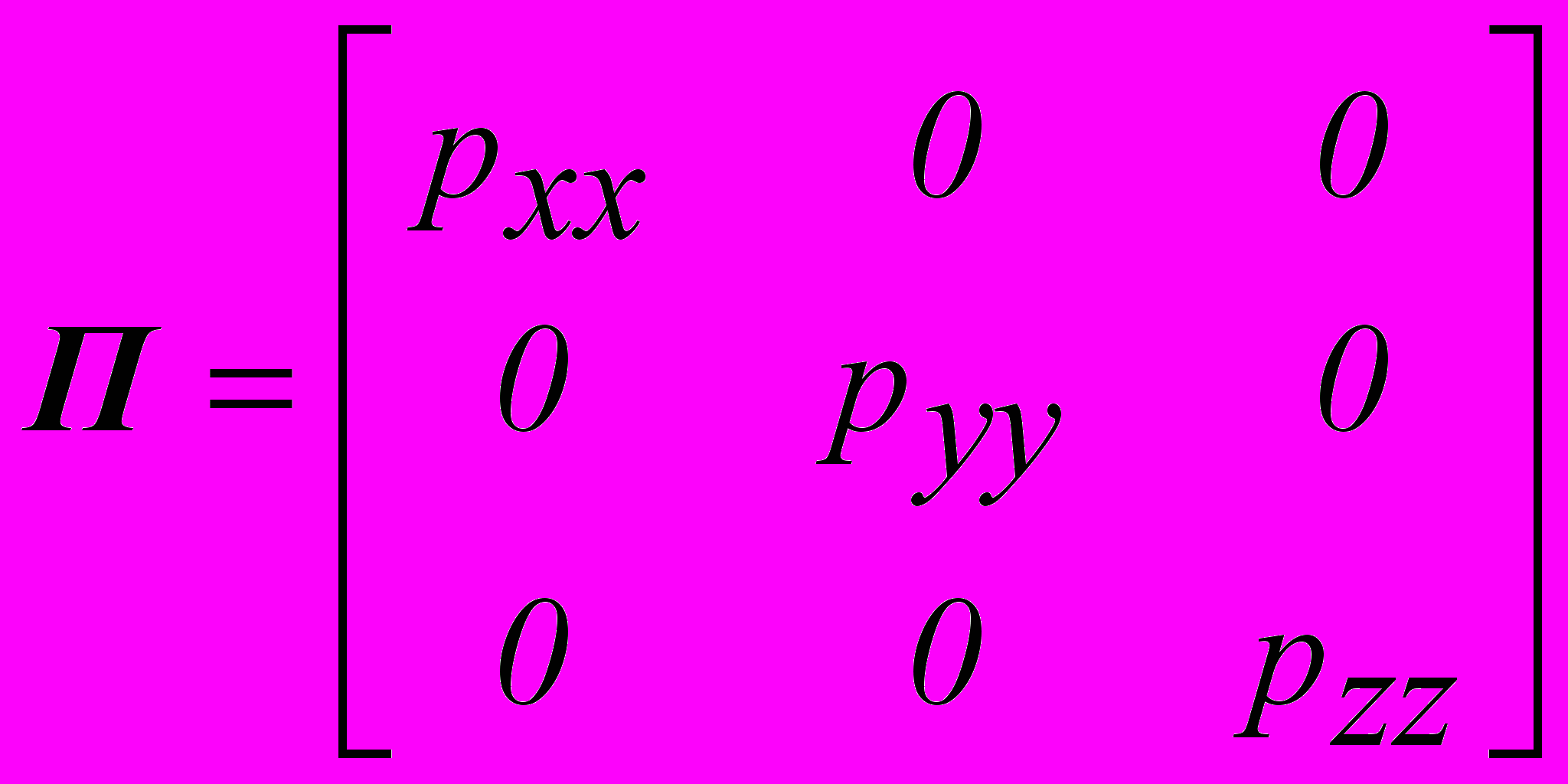
Так как для произвольно ориентированной площадки вектор напряжения в жидкости перпендикулярен к ней, то PN = n |PN|. В тензорном представлении PN = n П. Сравнивая эти два определения, получим, что
n |PN| = {nx |PN|; ny |PN|; nz |PN|} = n П = {nxpxx+0+0; 0+nypyy+0; 0+0+nzpzz}.
Откуда следует, что
|PN|= pxx = pyy = pzz = - p и
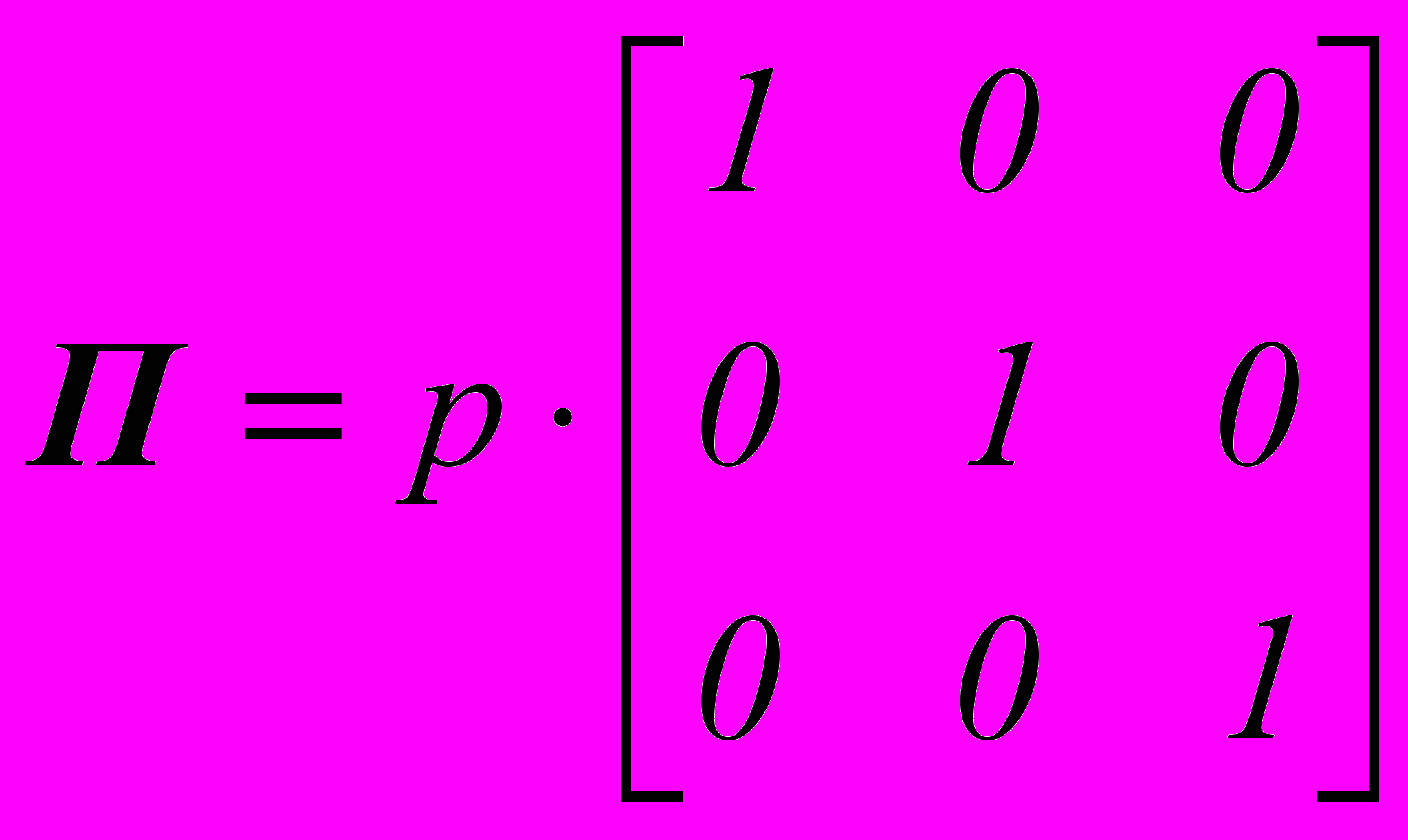
В покоящейся жидкости (и газе) тензор напряжений полностью определяется одной скалярной величиной p,которая называется гидростатическим давлением
Закон Паскаля: В покоящейся жидкости напряжения по любому направлению одинаковы и направлены по нормали к площадке
Определение силы давления площадку ∆A совпадает с термодинамическим ∆F = - p n ∆A Определение силы барического градиента, порождаемой разностью давлений и действующей н
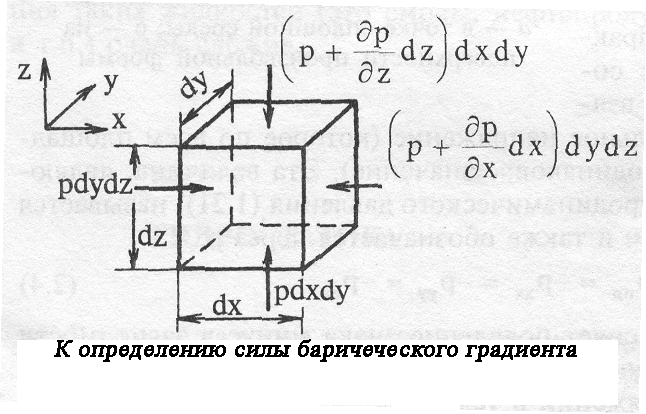 а элемент объема ∆V = dx dy dz иллюстрирует рисунок. На нем p - сила давления на площадку dydz, расположенную в точке (x,y,z.), -(p +∂p/∂xdx)- сила давления на площадку dydz, расположенную в точке (x+dx,y,z.).На элемент объема в направлении x действует составляющая силы давления p dydz -(p +∂p/∂xdx) dydz = - ∂p/∂x dx dydz
а элемент объема ∆V = dx dy dz иллюстрирует рисунок. На нем p - сила давления на площадку dydz, расположенную в точке (x,y,z.), -(p +∂p/∂xdx)- сила давления на площадку dydz, расположенную в точке (x+dx,y,z.).На элемент объема в направлении x действует составляющая силы давления p dydz -(p +∂p/∂xdx) dydz = - ∂p/∂x dx dydzНа элемент ∆V действует вектор силы давления, который в метеорологии принято называть силой барического градиента. Он равен - grad p dx dydz,где grad p = { - ∂p/∂x, - ∂p/∂y, - ∂p/∂z}.
Закон гидростатики. Статика атмосферы
В покоящейся жидкости вектор силы тяжести, действующей на элемент, уравновешен градиентом давления:
( ρ f - grad p ) dx dy dz = 0
В проекциях на оси:
{ ρ fx - ∂p/∂x=0, ρ fy - ∂p/∂y=0, ρ fz - ∂p/∂z=0}
Принято направлять ось z в зенит, тогда f = { 0, 0, -g} и баланс сил тяжести и барического градиента сводится к равенствам
∂p/∂x=0, ∂p/∂y=0, ∂p/∂z= - ρ g
В покоящейся атмосфере изобары параллельны геосфере. Последнее из равенств называется законом гидростатики.
Статика атмосферы.
В атмосфере закон гидростатики действует совместно с уравнением состояния
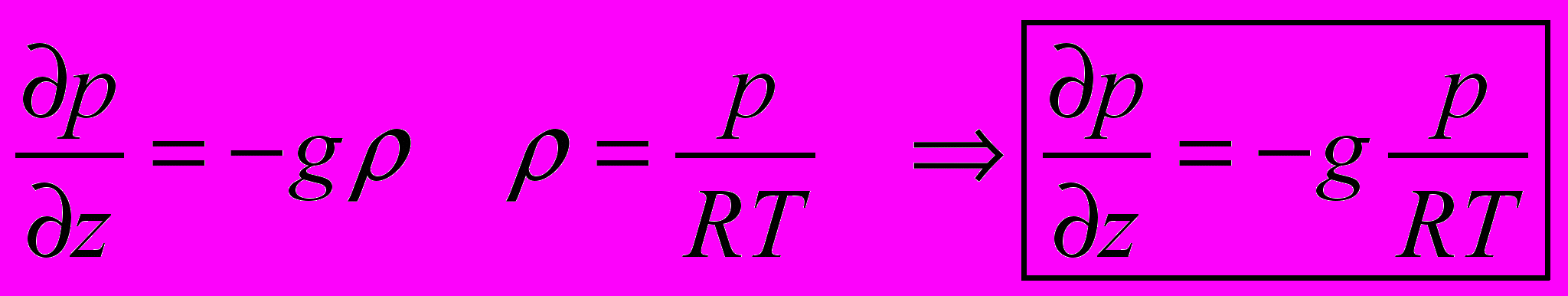
О
 тсюда следует, что распределение давления по вертикали в атмосфере определено полностью, если известен вертикальный профиль температуры и давление на каком-либо одном уровне. Физически правильно было бы использовать значениние давления на самых верхних уровнях, но в силу малой точности наблюдений, применяют давление на уровне подстилающей поверхности.
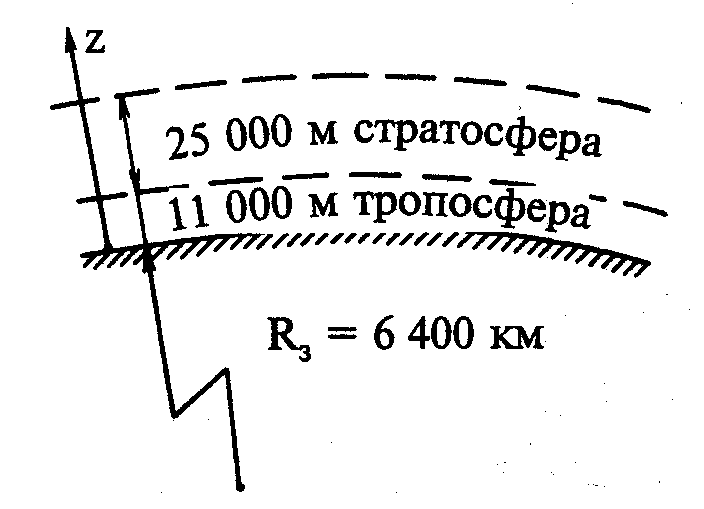
тсюда следует, что распределение давления по вертикали в атмосфере определено полностью, если известен вертикальный профиль температуры и давление на каком-либо одном уровне. Физически правильно было бы использовать значениние давления на самых верхних уровнях, но в силу малой точности наблюдений, применяют давление на уровне подстилающей поверхности.Для различных оценок полезно знать, как приблизительно изменяется давление с высотой в стандартной атмосфере, то есть при линейном падении температуры (политропная атмосфера) до 11 км, свойственном тропосфере, и при постоянной температуре (изотермическая атмосфера), что является упрощенным описанием стратосферы (см. рисунок).
В политропной атмосфере (тропосфере)

На верхней границе тропосферы z=z11=11000 м, T=T11=217 oK, p=p11=225 гПа
В изотермической атмосфере (стратосфере)
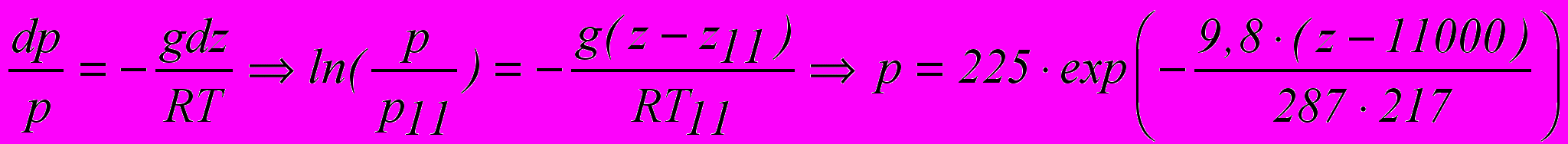
В
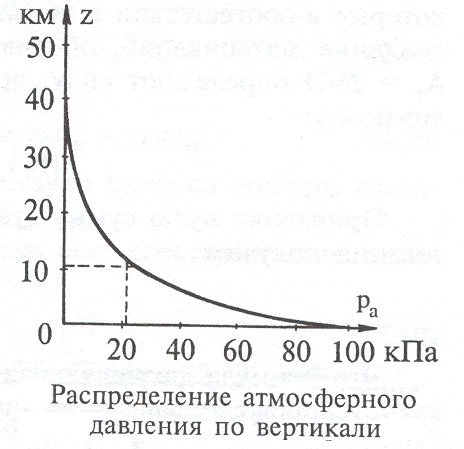 ертикальное распределение давления, полученное по этим зависимостям, приведено на рисунке
ертикальное распределение давления, полученное по этим зависимостям, приведено на рисункеСледствия уравнений статики и состояния
Масса единичного столба атмосферы

Внутренняя энергия единичного столба атмосферы
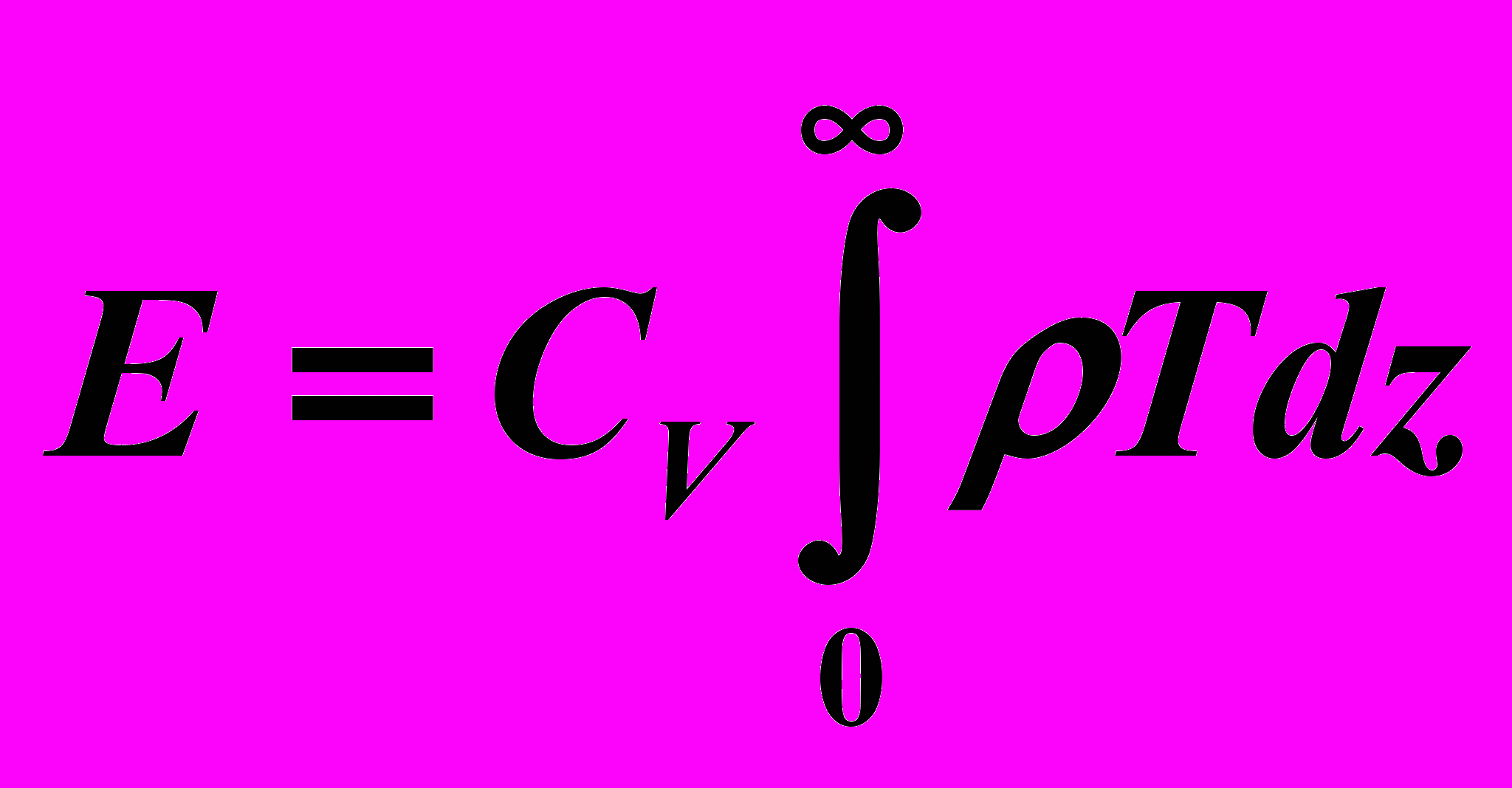
Потенциальная энергия и ТЕОРЕМА ДАЙНСА
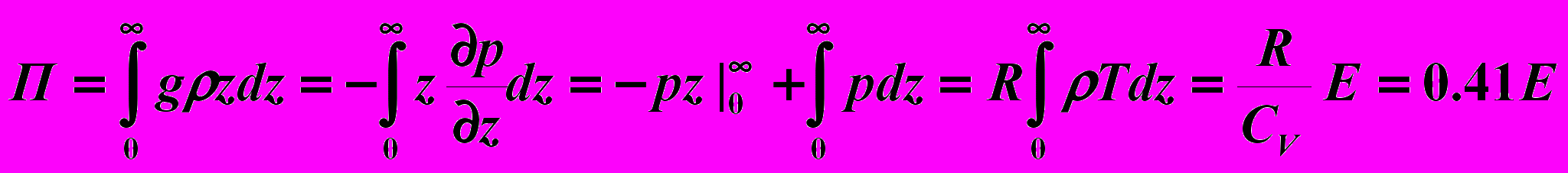
Запись теоремы Дайнса через высоту центра тяжести и среднюю температуру

Выполнимость теоремы Дайнса на уровне максимума ψ
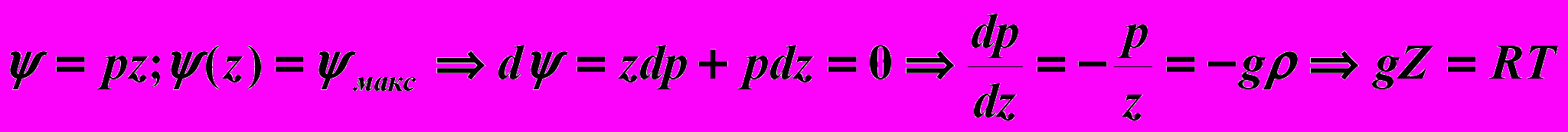 Доказательство изопикничности среднего энергетического уровня
Доказательство изопикничности среднего энергетического уровня
Приближенные значения переменных для среднего энергетического уровня

