Урок учителя математики Гукасовой А. П. Тема урока: «Уравнение касательной»
| Вид материала | Урок |
СодержаниеУравнение касательной Усложним условие задачи №89 I вариант |
- План-конспект Тема урока : Движение жидкостей и газов. Уравнение Бернулли, 43.29kb.
- Урок №13 Тема урока: Музыкальная гармония пропорций, 53.89kb.
- Урок математики в 5 классе. Тема урока: Сложение и вычитание натуральных чисел, 76.55kb.
- Десять способов построения касательной к окружности, 19.97kb.
- Урока математики в начальной школе, 26.21kb.
- Тема урока: Нестандартные методы решения уравнений. Цель урока, 24.43kb.
- § Тема. Некоторые определения и обозначения, 1005.59kb.
- Тематическое и поурочное планирование. Урок это зеркало общей и педагогической культуры, 409.5kb.
- Урок по литературе. 9 класс. Тема урока: А. С. Грибоедов. Личность и судьба. «Горе, 29.98kb.
- Тема: «Эффективный урок стимул к успеху ученика и учителя», 140.15kb.
Открытый урок учителя математики Гукасовой А.П.
Тема урока:
«Уравнение касательной»
Цель урока: вывести уравнение касательной к графику функции и находить его для конкретных функций
- Ребята, мы научились с вами находить производные простых и сложных функций, решать неравенства методом интервалов и, наконец, изучили геометрический смысл производной функции в точке. Итак, цель нашего сегодняшнего урока:
- Проверить все полученные вами знания по этим темам
- вывести уравнение касательной к графику функции в заданной точке
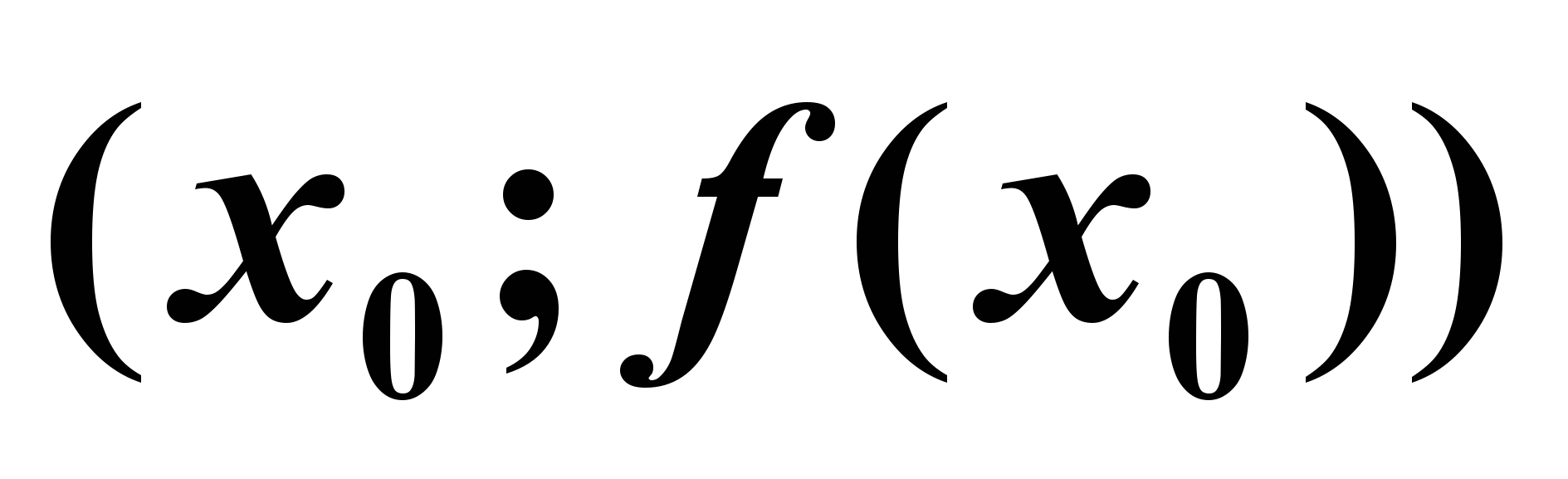
- Проверить все полученные вами знания по этим темам
- В начале урока проведём тест (на 10-12 мин) - тест в Приложении №1
- пишут на двойных листах, выписывая ответы в свои тетради
- после того как работы собраны учителем, ученики проверяют верность своих решений по ответам, выписанным на обратной стороне доски.
- пишут на двойных листах, выписывая ответы в свои тетради
- Решим у доски задание, аналогичное тому, что было задано на дом. Это задание поможет в объяснении новой темы.
Итак, открываем учебник Калягин, стр. 34, №80 (б)
Дано:
α = П/6 1) Уравнение прямой имеет вид y=kx+b
X0 = 6 2) Что показывает коэффициент k?
Y0 = -5 k =tg α = tg П/6 =
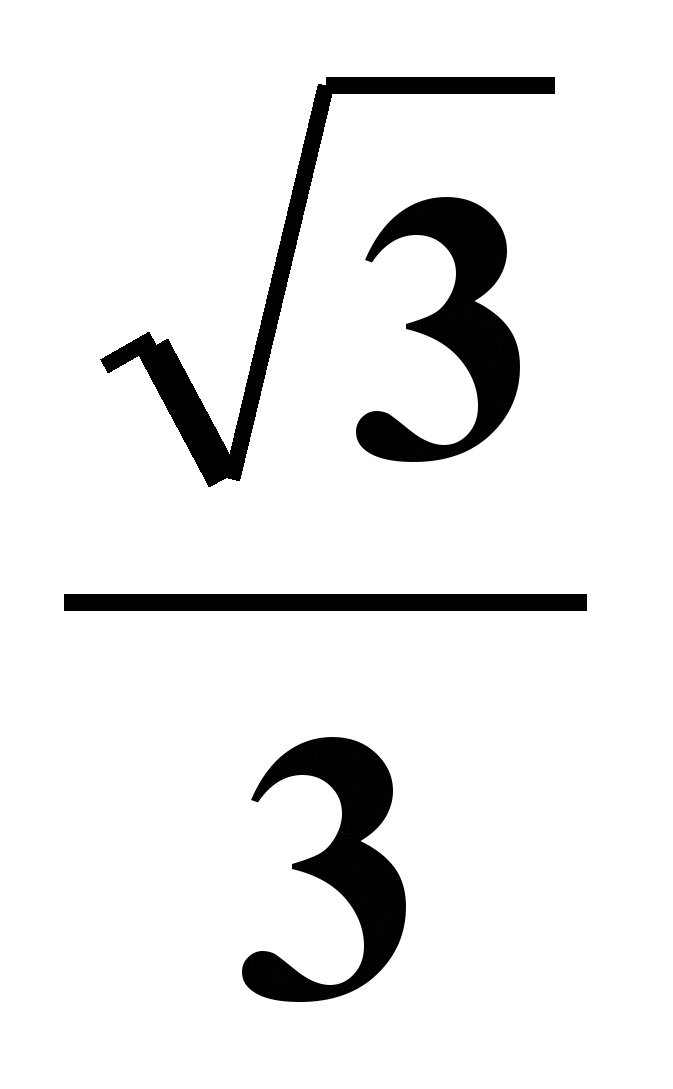
Составим уравнение прямой y =
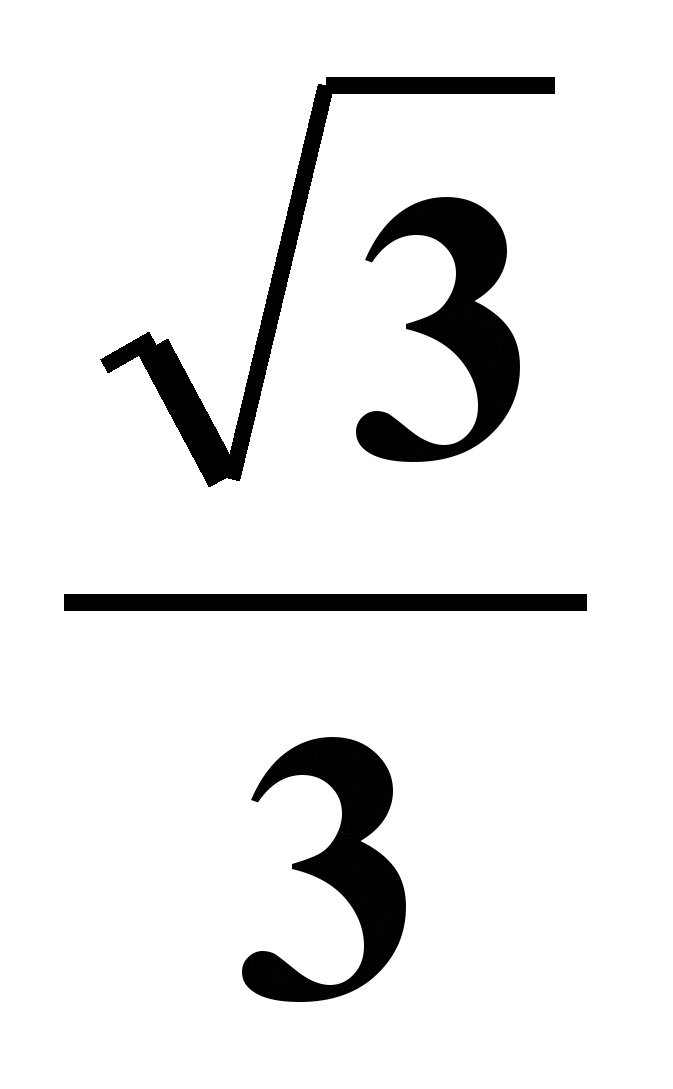 x + b
x + b3) т.к. точка (X0, Y0)
 этой прямой, то
этой прямой, то -5 =
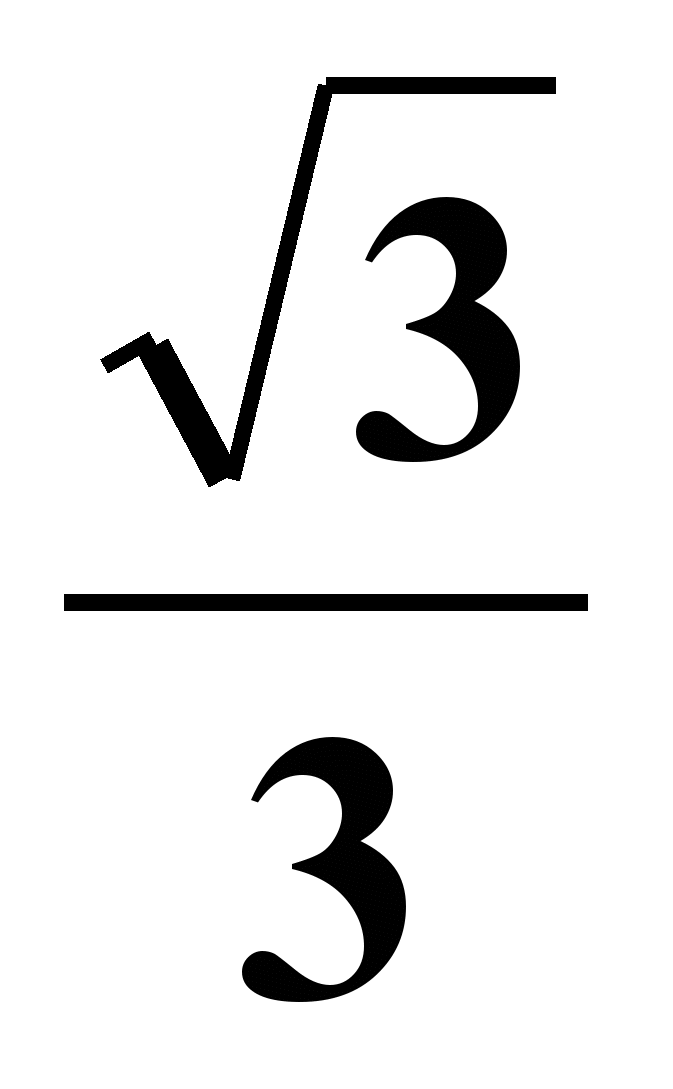 *6+b
*6+b-5 = 2
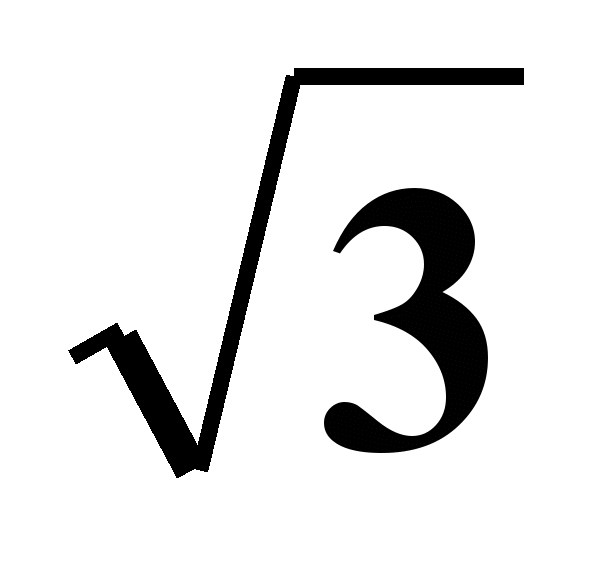 +b
+bb = -5- 2
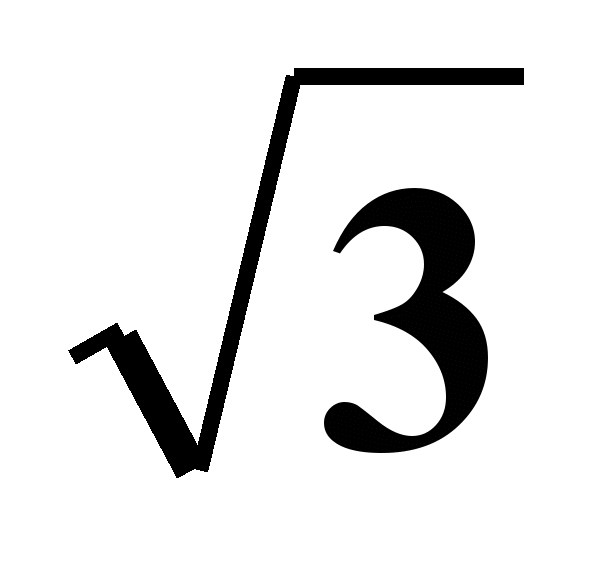
4) уравнение имеет вид y =
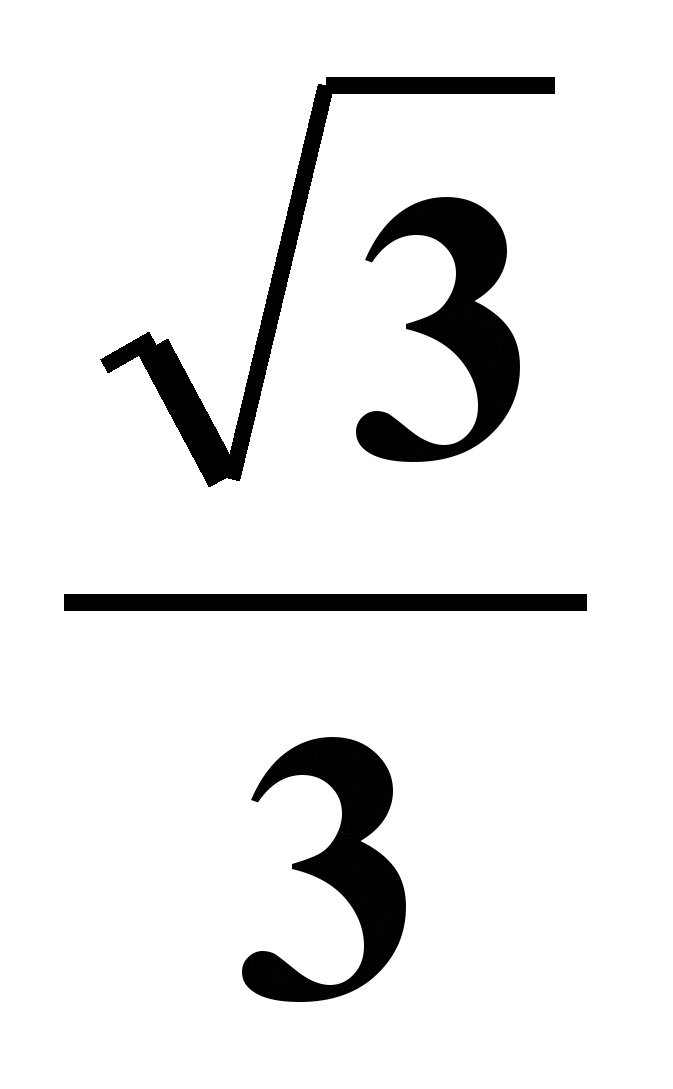 x -5-2
x -5-2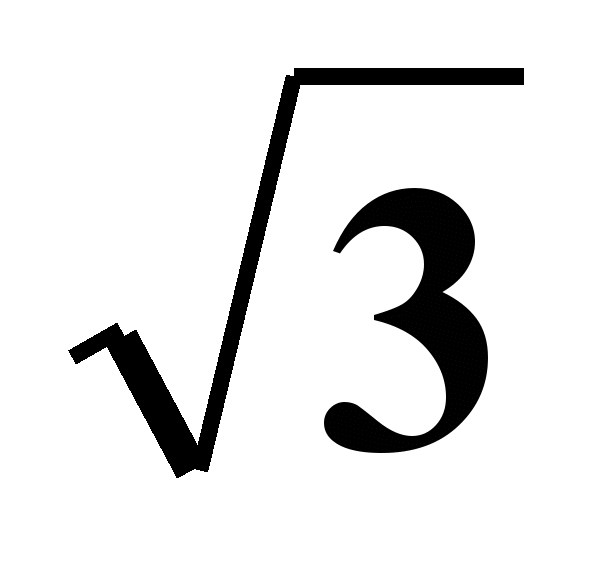
Дополнительные вопросы:
- Какая прямая называется касательной к графику функции
- В чем состоит геометрический смысл производной
- Если
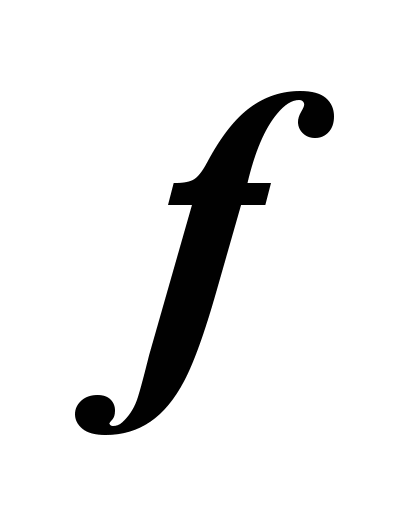 `(x)<0, то какой угол образует касательную с положительным направлением оси OX. А если
`(x)<0, то какой угол образует касательную с положительным направлением оси OX. А если 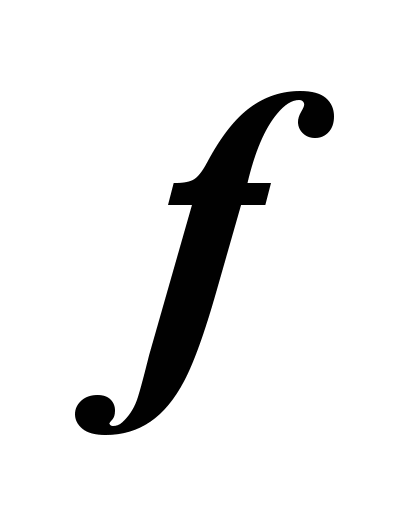 `(x)>0 ? А если
`(x)>0 ? А если 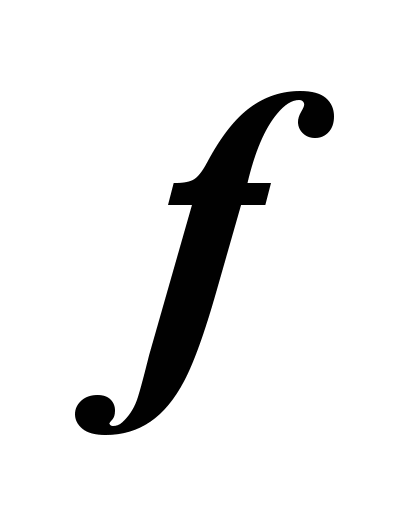 `(x) = 0?
`(x) = 0?
Ребята, а если бы задача звучала бы так:
Составить уравнение прямой, имеющей с графиком функции y=
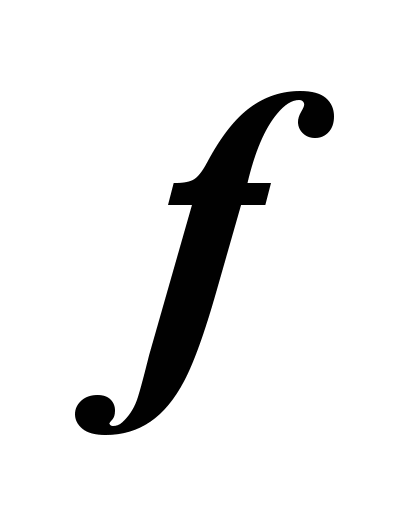 (x) единственную точку (6; -5) и образующую с положительным направлением оси OX угол α=П/6
(x) единственную точку (6; -5) и образующую с положительным направлением оси OX угол α=П/6Тогда, как бы мы назвали эту прямую? Необходимо знать y =
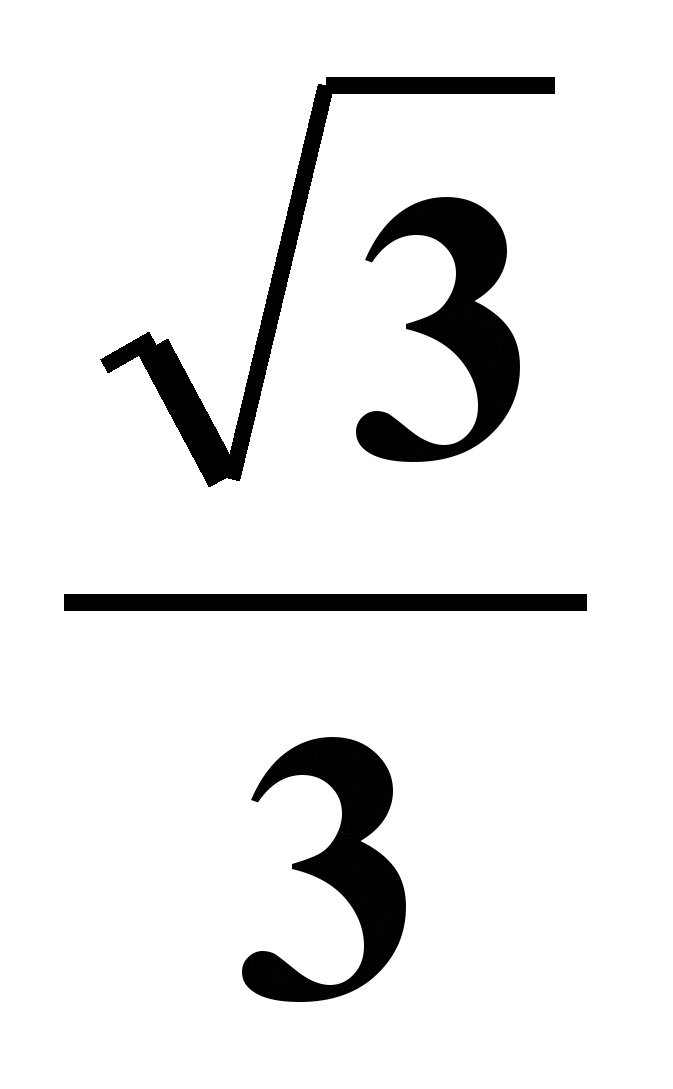 x -5-2
x -5-2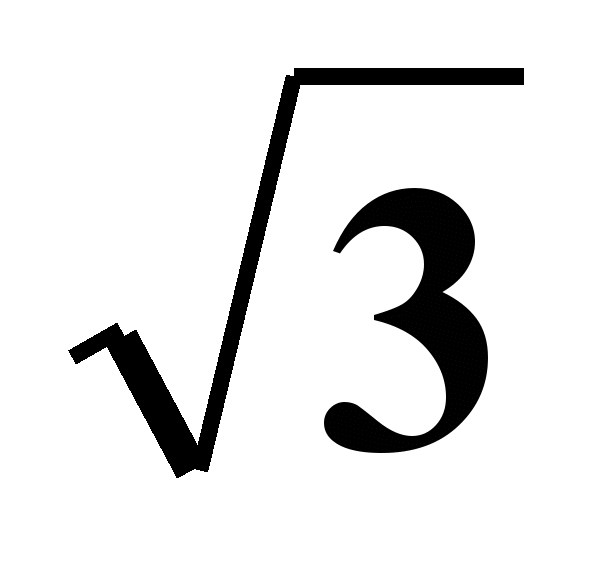 - уравнение касательной к графику функции y=f(x).
- уравнение касательной к графику функции y=f(x). Решение задачи поможет в составлении уравнения касательной к графику функции в точке
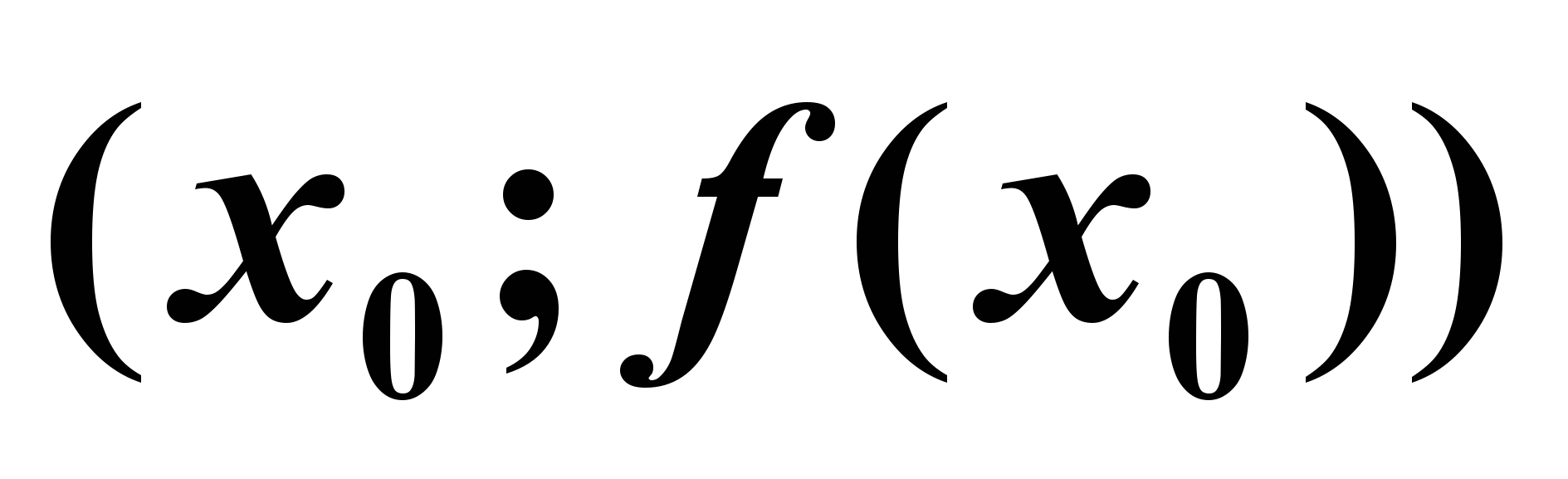
Запишем тему урока « Уравнение касательной»
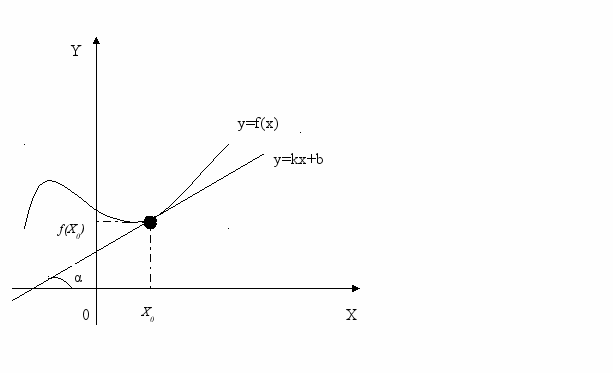
Пусть нам дана дифференциальная функция y = f(x)
Точка
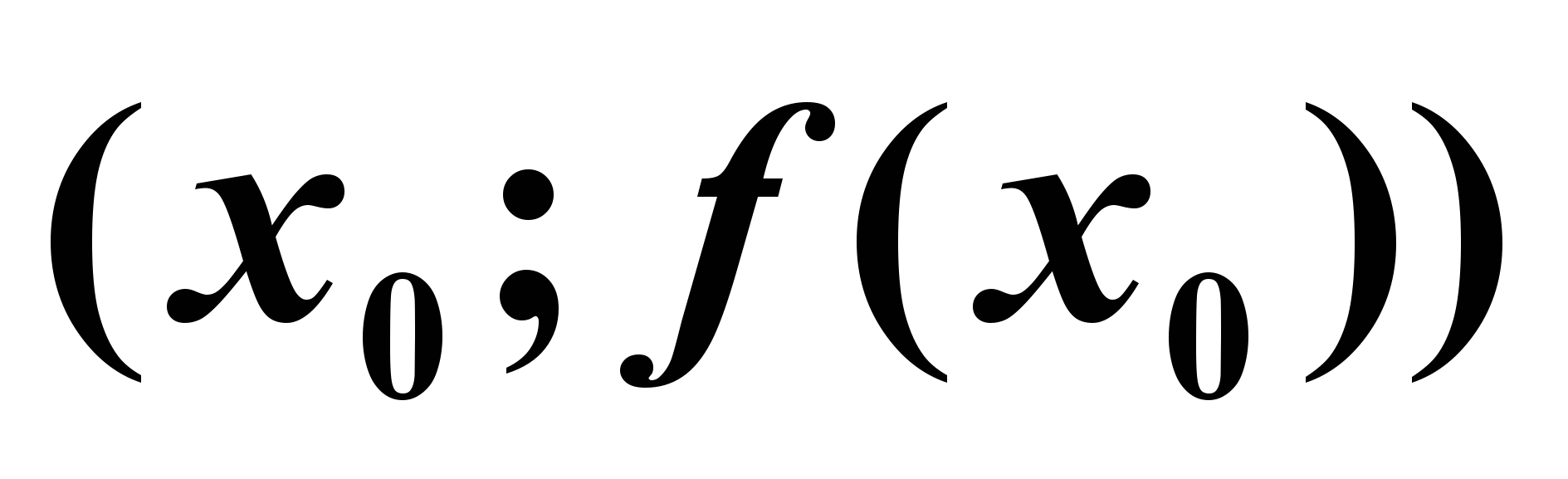 - точка касания графика функции y=f(x) с прямой y=kx+b
- точка касания графика функции y=f(x) с прямой y=kx+by=kx+b, т.к. k=
 `(X0), то уравнение примет вид y =
`(X0), то уравнение примет вид y =  `(X0)*x+b (*)
`(X0)*x+b (*)т.к. касательная проходит через точку
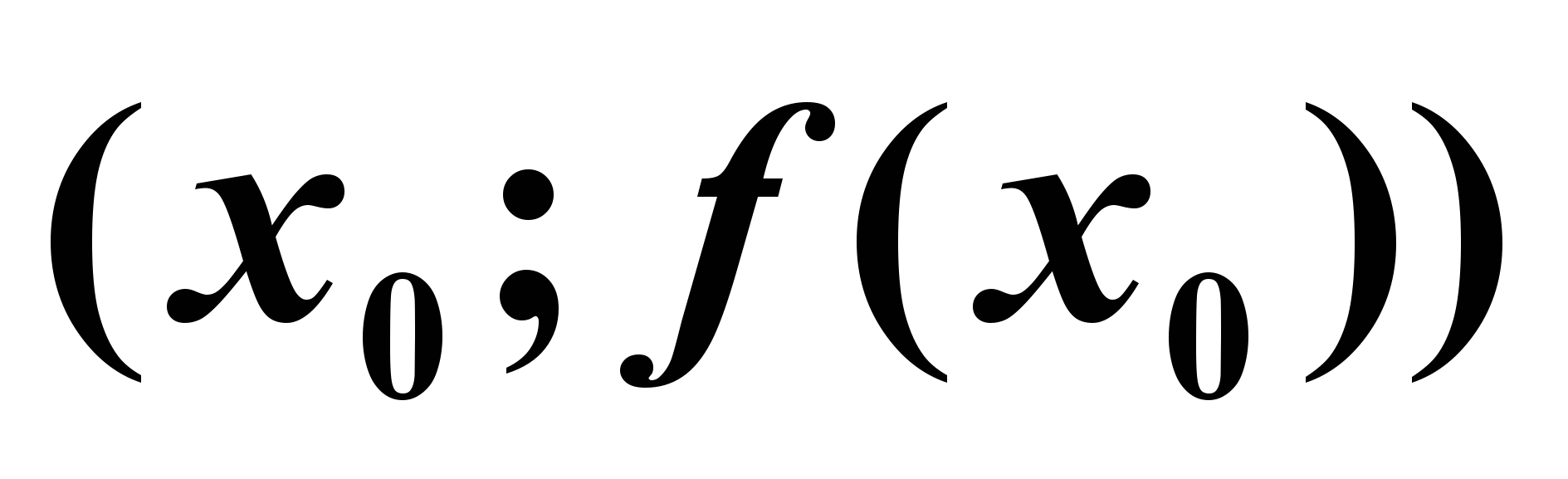 , то координаты этой точки удовлетворяют уравнению
, то координаты этой точки удовлетворяют уравнениюY0=
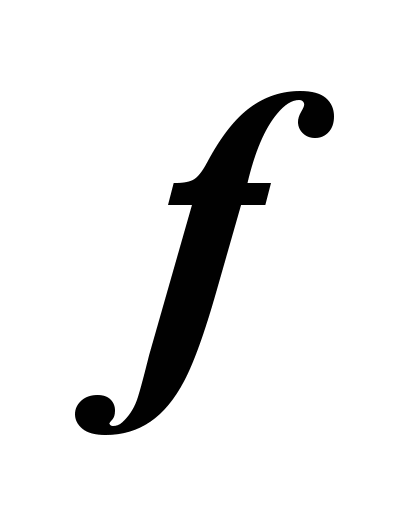 `(X0)*x+b, т.е. Y0=
`(X0)*x+b, т.е. Y0=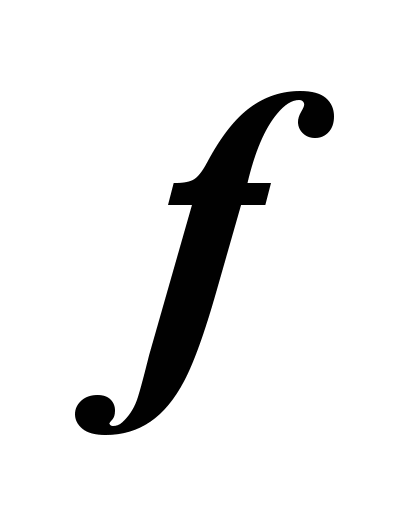 `(X0)*X0+b
`(X0)*X0+bОтсюда b=
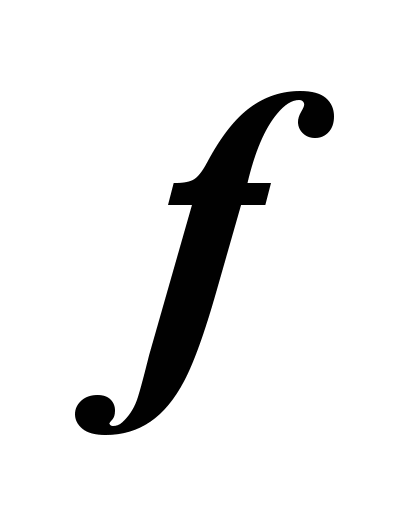 (X0) -
(X0) -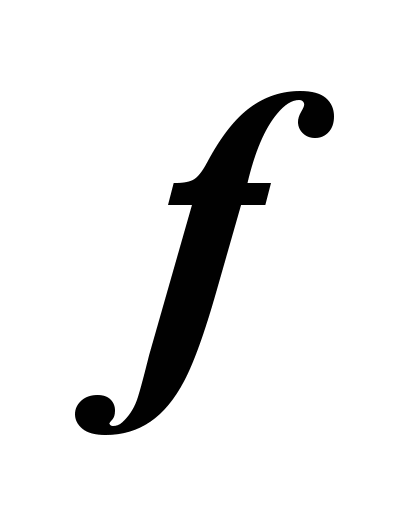 `(X0)*X0
`(X0)*X0Y=
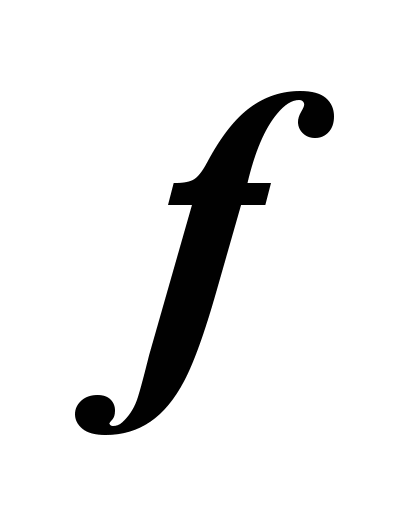 (X0) +
(X0) +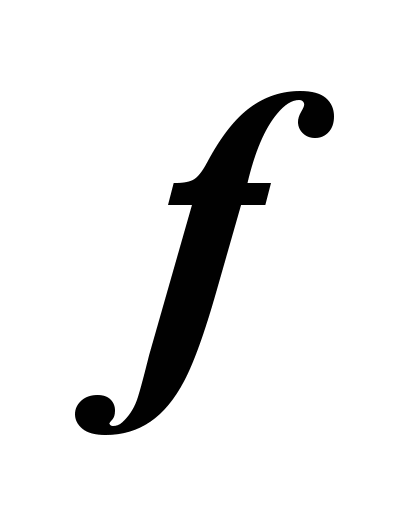 `(X0)*(X-X0)
`(X0)*(X-X0)Мы вывели уравнение касательной, где
 - координаты точки касания.
- координаты точки касания. (x, y) – координаты любой точки этой касательной.
Пример №1 (№84(2), стр.35)
Дано: y=f(x0) + f `( x0)(x-x0)
f(x)=x-3x2 1) f(x0)=2-3*4=-10
x0=2 2) f `( x)=1-6x
___________________ 3) f `( x0)=1-6*2=-11
Написать уравнение 4) y=-10-11*(x-2)
касательной y=-10-11*x+22
y=-11*x+12
Запишем алгоритм решения:
- вычислить f(x0)
- найти f `(x)
- вычислить f `( x0)
- подставим в уравнение касательной Y=
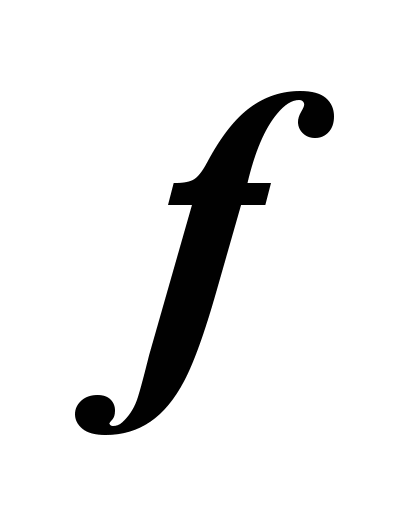 (X0) +
(X0) +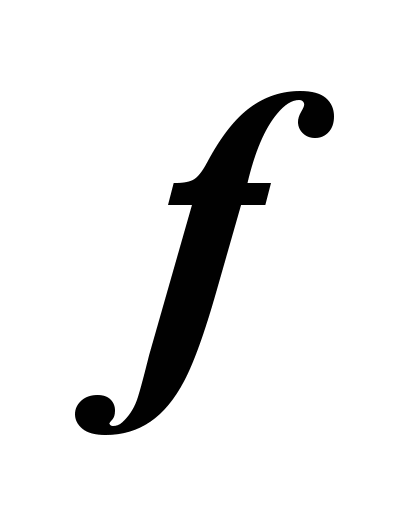 `(X0)*(X-X0)
`(X0)*(X-X0)
Пример №2 (№85(3))
Дано: y=f(x0) + f `( x0)(x-x0)
f(x)=
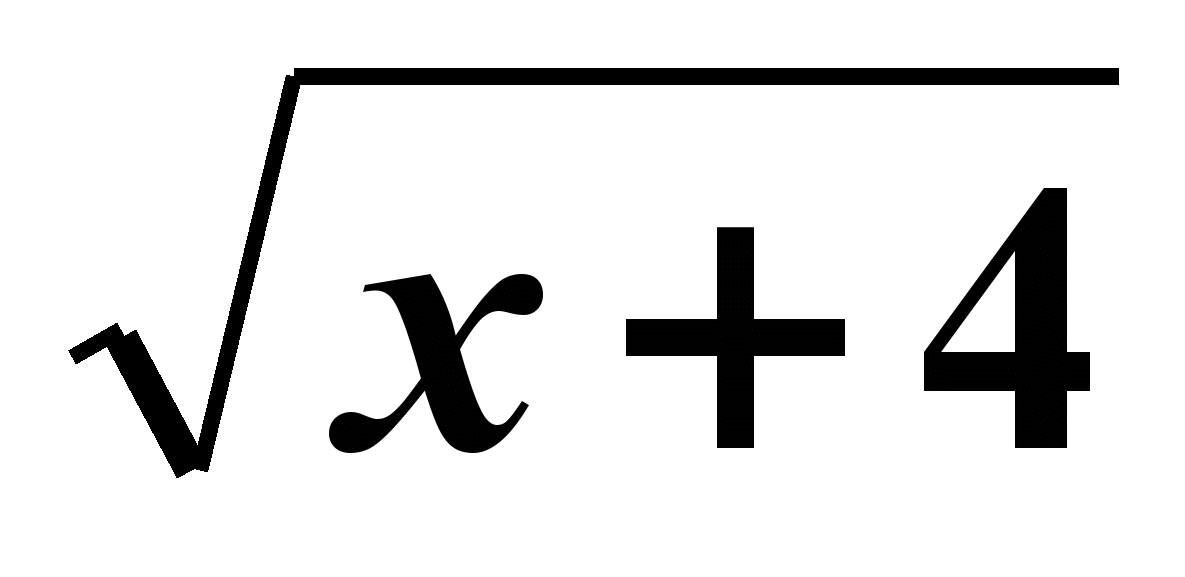 1) f(x0)=
1) f(x0)= 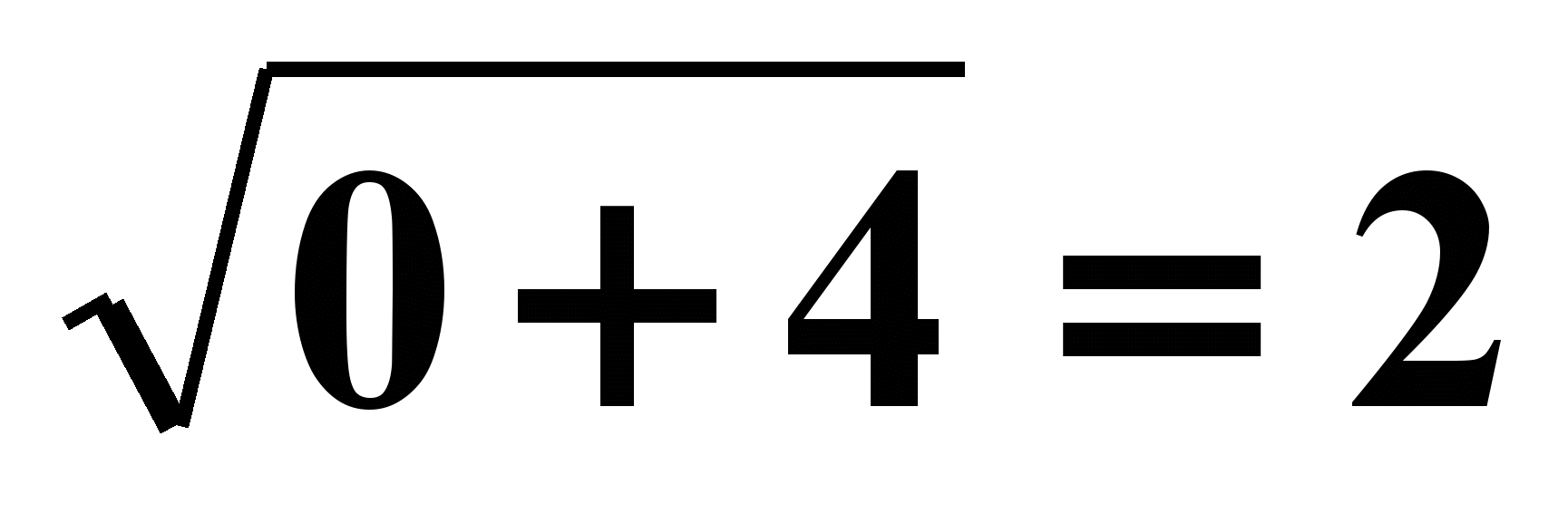
x0=0 2) f `( x)=
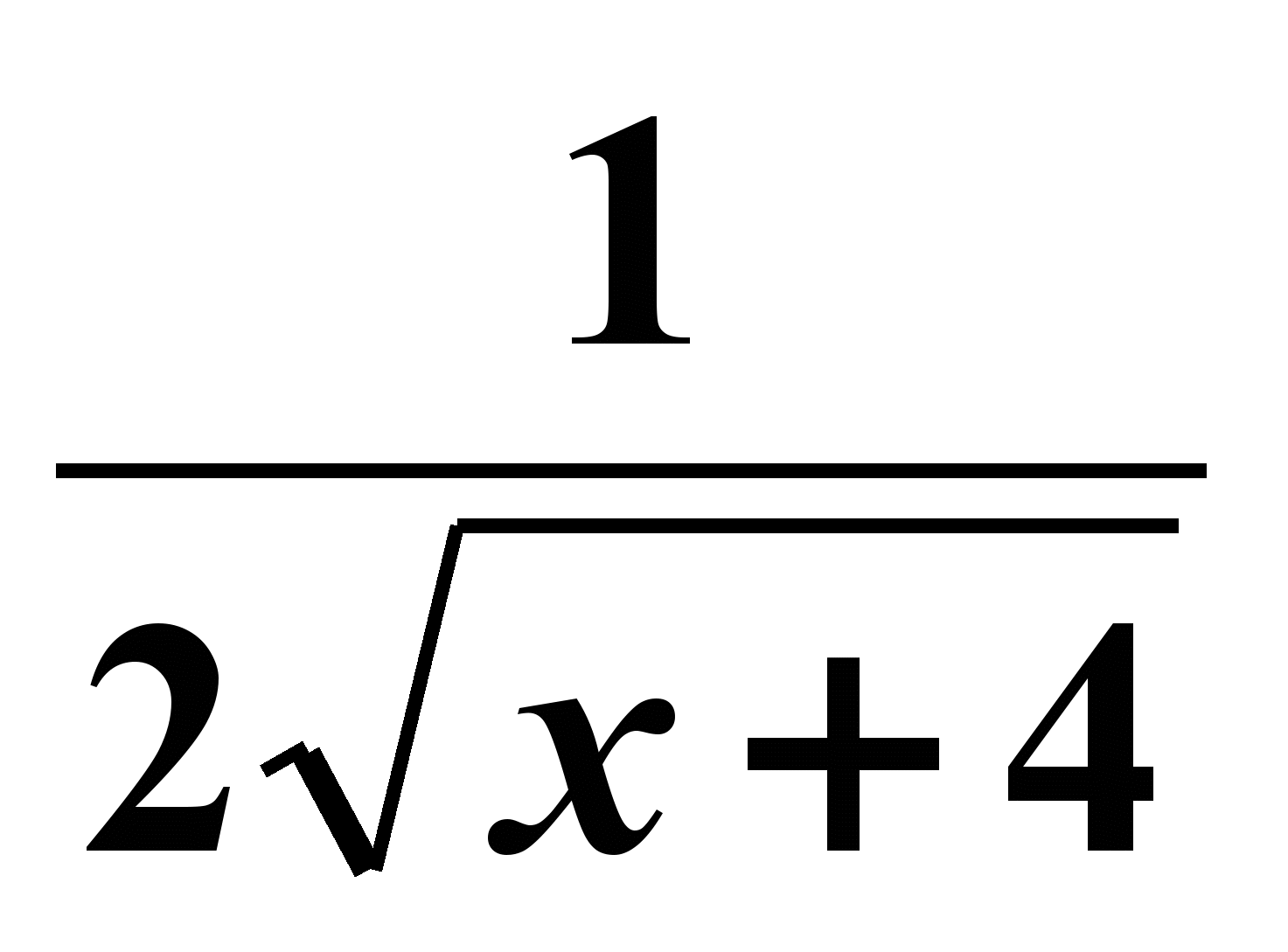
___________________ 3) f `(0)=
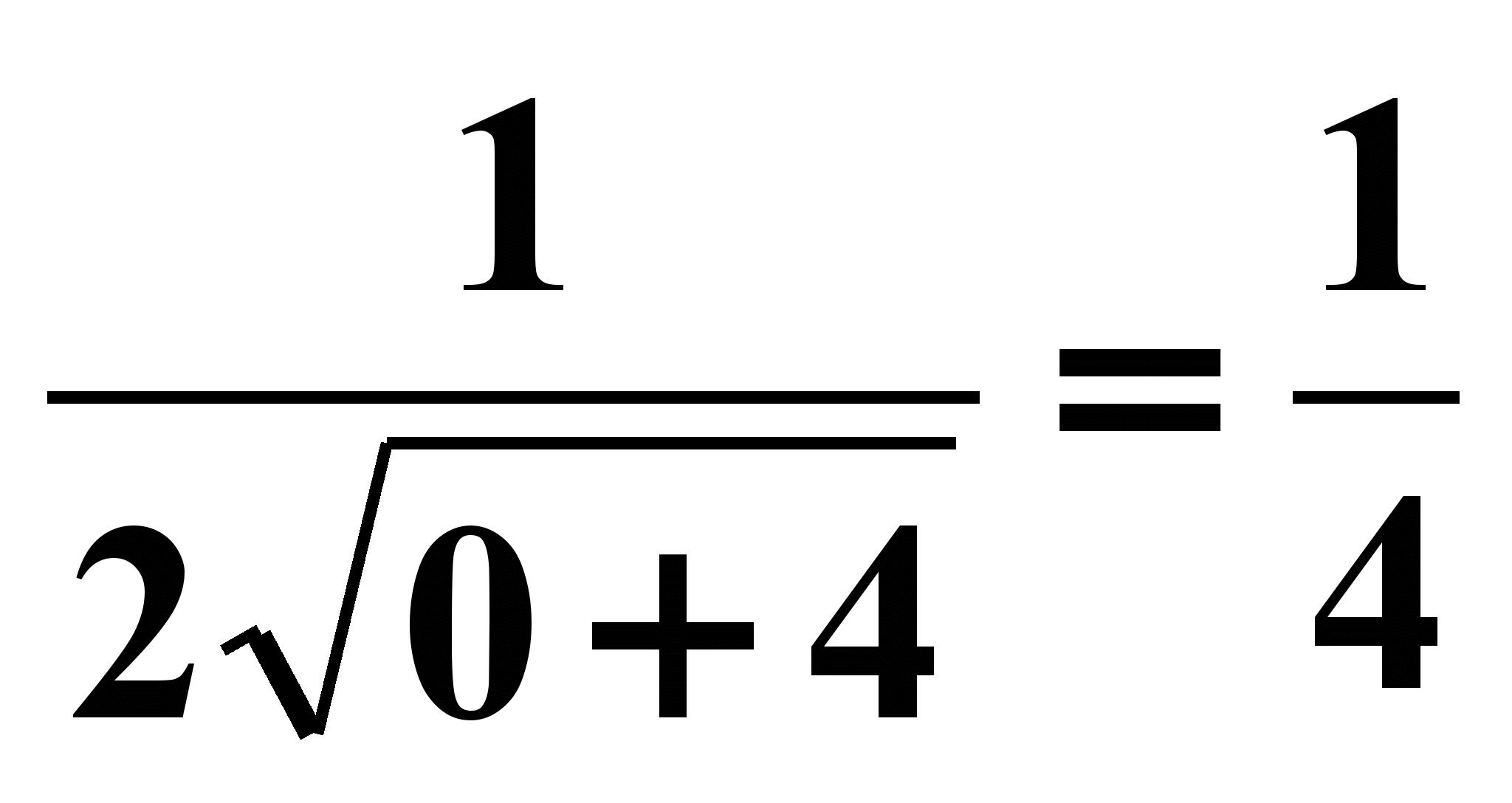
Написать уравнение 4) y=
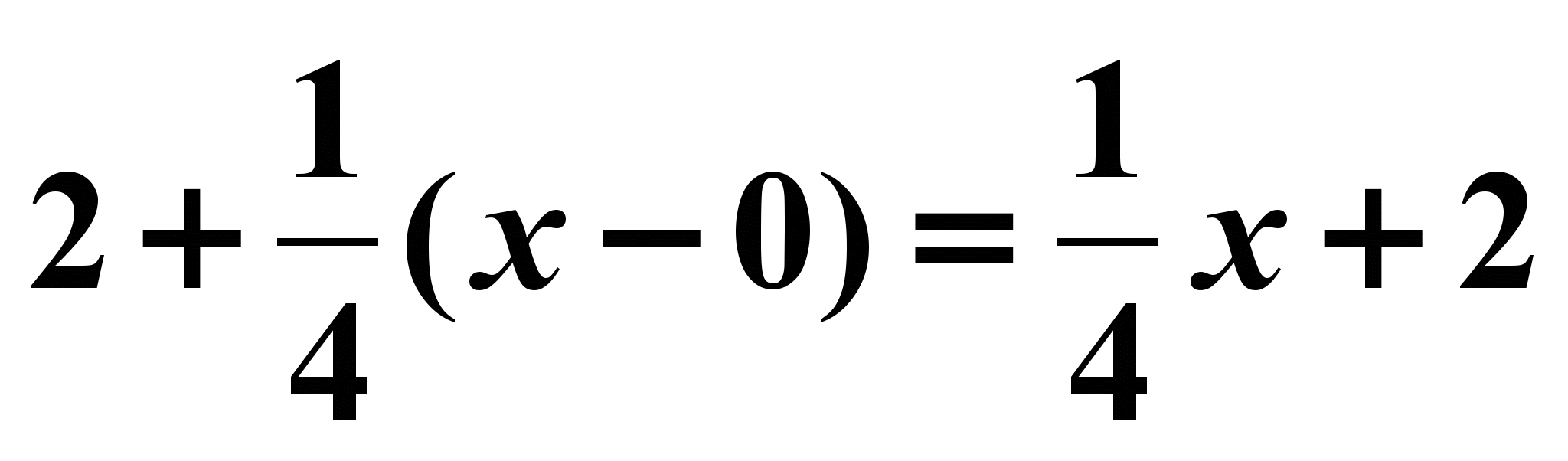
касательной
Вопрос Какой угол образуется касательной с положительным направлением оси OX?
- Самостоятельная работа (№84(1) и 84(4))
- На оборотах доски учениками решаются эти задания
№84(1) Решение:
f(x)=x2+x+1 1) f(x0)=3
x0=1 2) f `( x)=2x+1
- f `(1)=3
- y=3+3(x-1)
y=3x
№84(4) Решение:
f (x) =
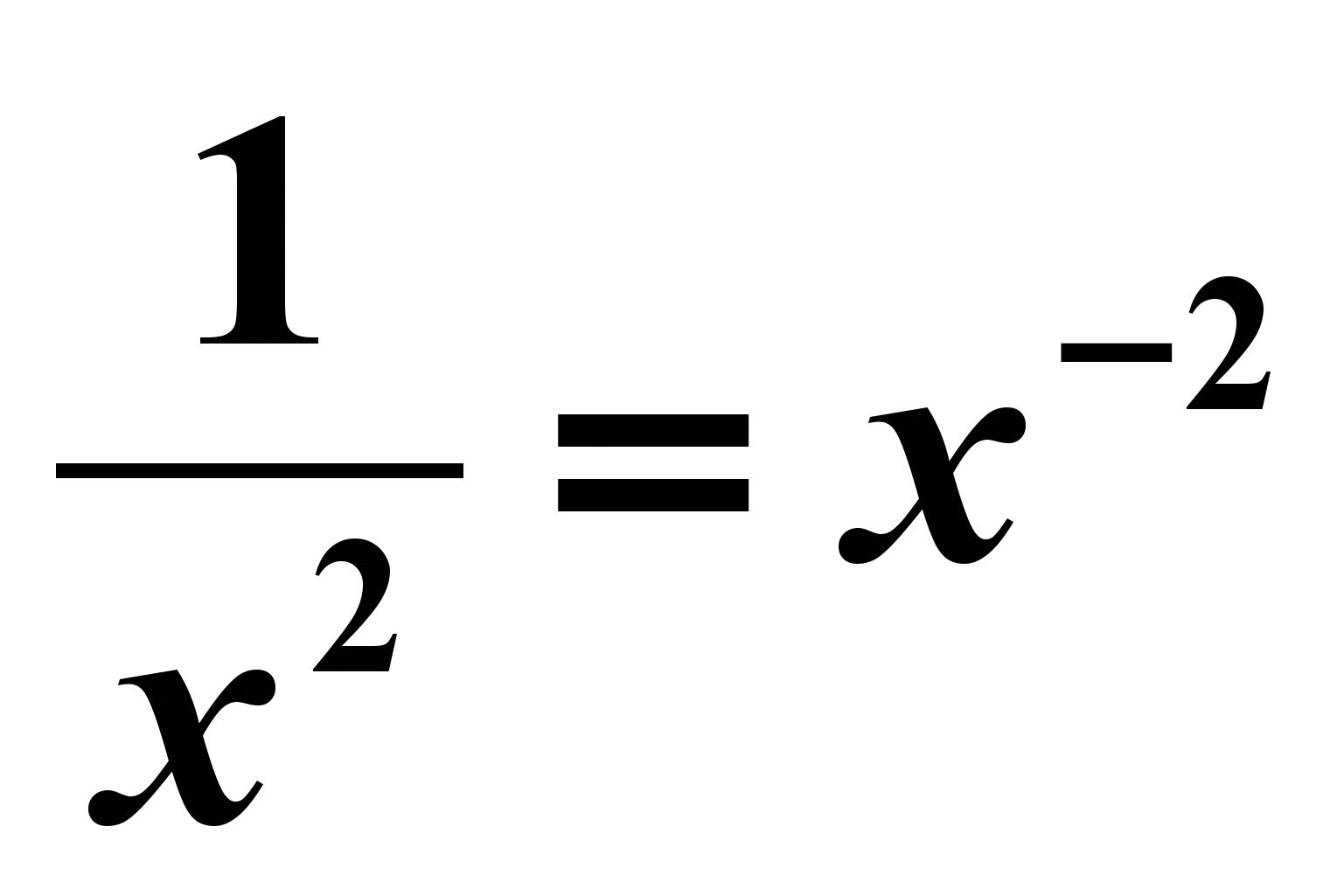 1) f(x0)=
1) f(x0)=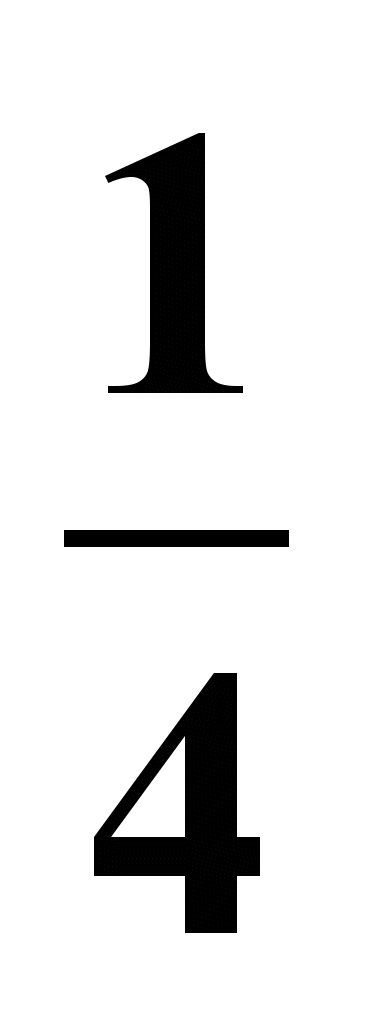
x0=-2 2) f `( x) = -2x-3=
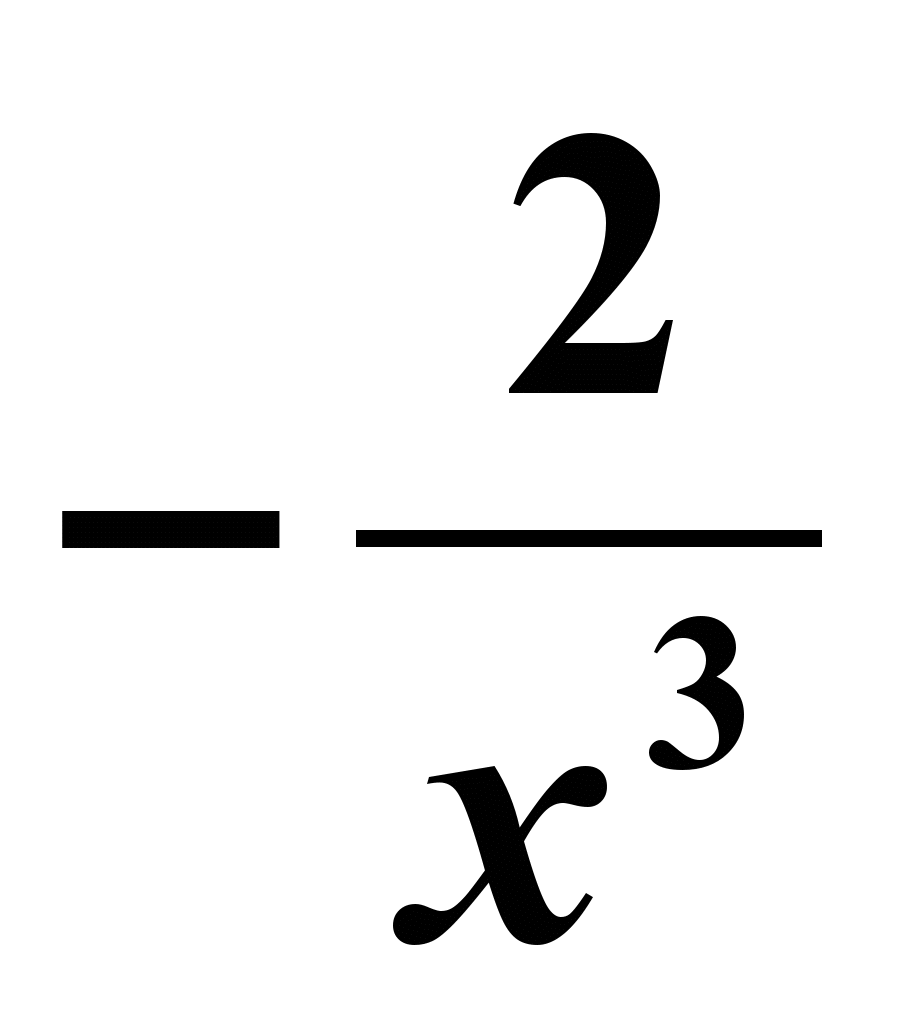
3) f `( x0) =(-2)/(-8)=
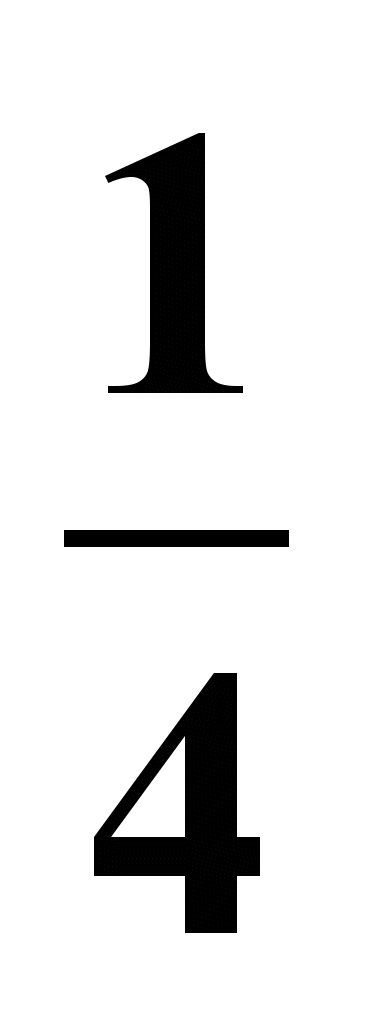
4) y=
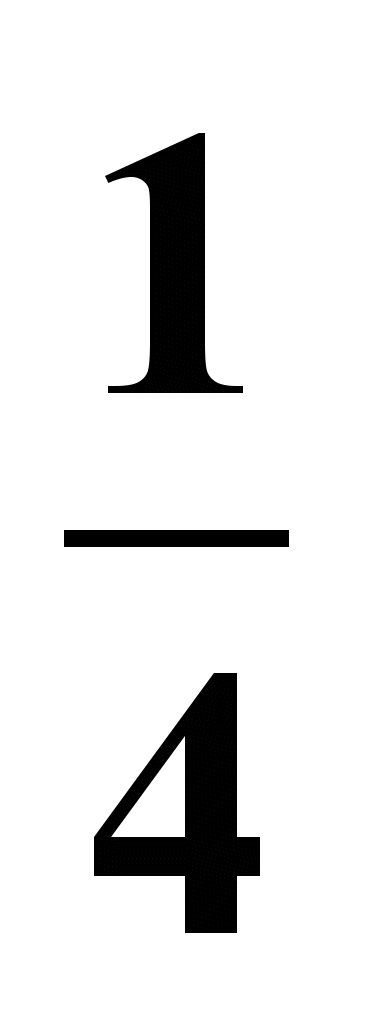 +
+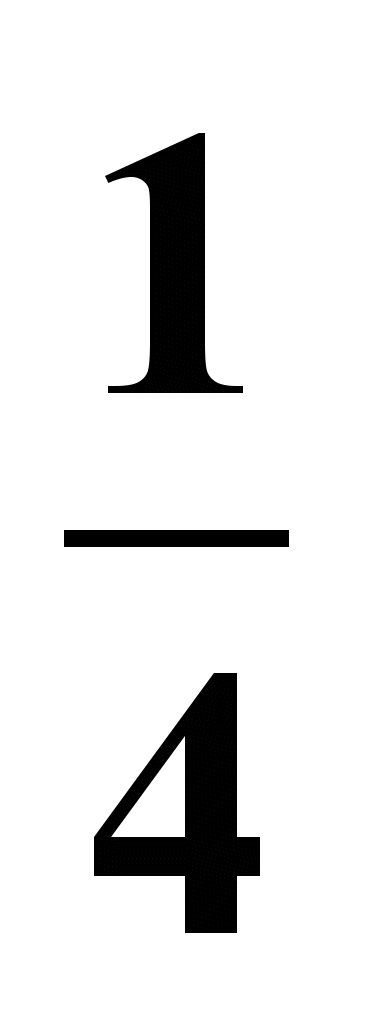 (x+2)=
(x+2)= 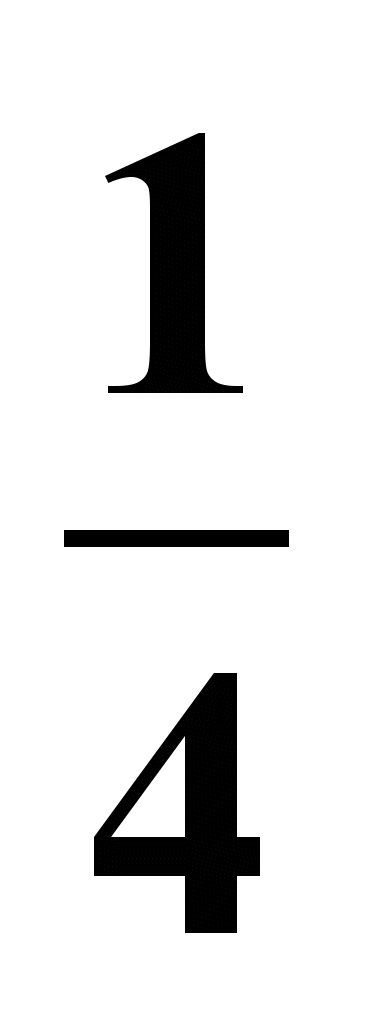 x+
x+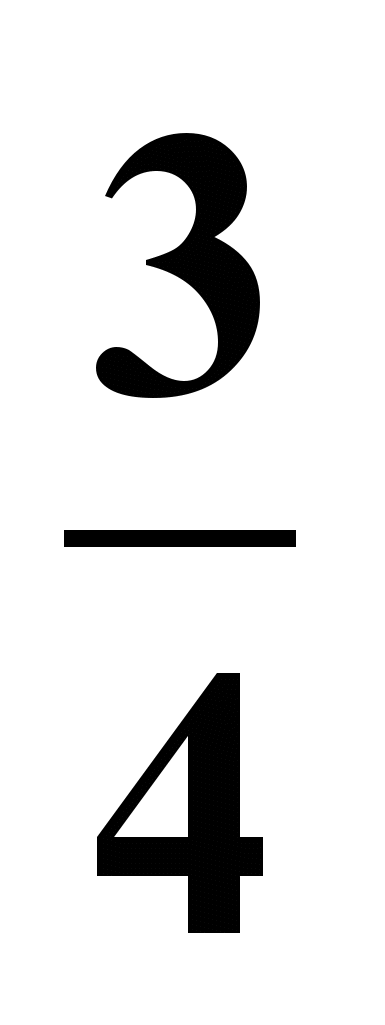
y =
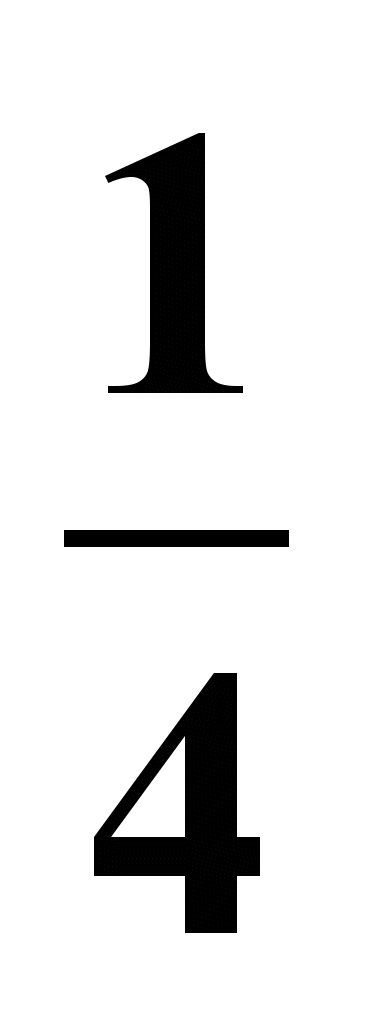 x+
x+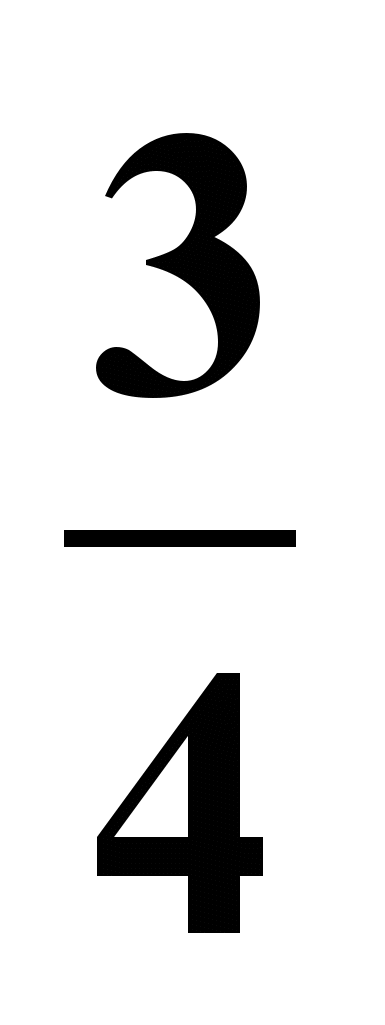
Вернёмся к домашнему заданию №89(6). В ней надо было найти точки графика функции y=f(x), в которой касательная к этому графику параллельна прямой y=kx
Вспомним условие II двух прямых: если две прямые параллельны, то их угловые коэффициенты равны.
Усложним условие задачи №89
Дана функция f(x)=x2-3x+4.Составим уравнение касательной,параллельной прямой y=3x-1
f(x)= x2-3x+4 Т.к. касательная параллельна прямой y=3x-1, то k=3
y=3x-1 Зная, что k= f `( x0), имеем
2x0-3=3
2x0=6
x0=3
Y=
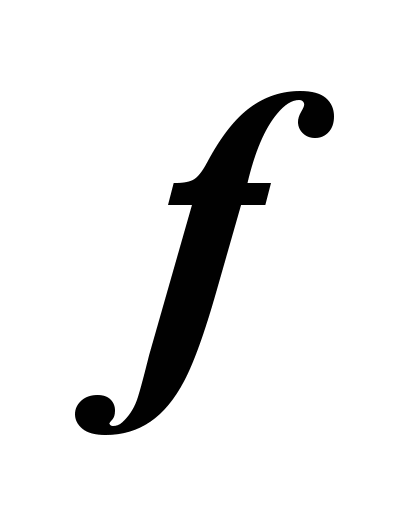 (X0) +
(X0) +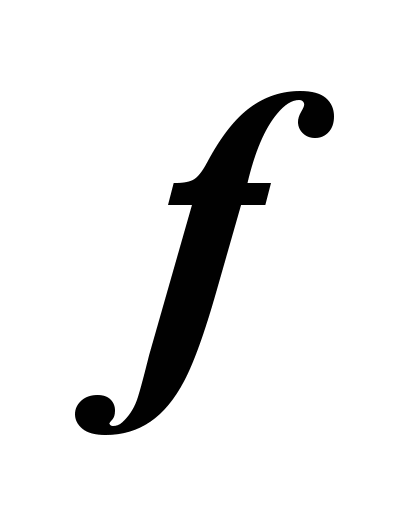 `(X0)*(X-X0)
`(X0)*(X-X0)Пусть
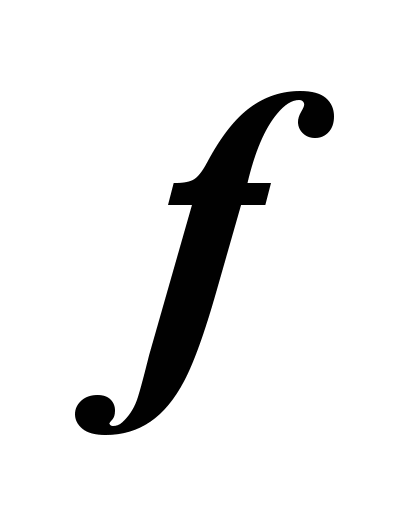 `(X0)=K
`(X0)=K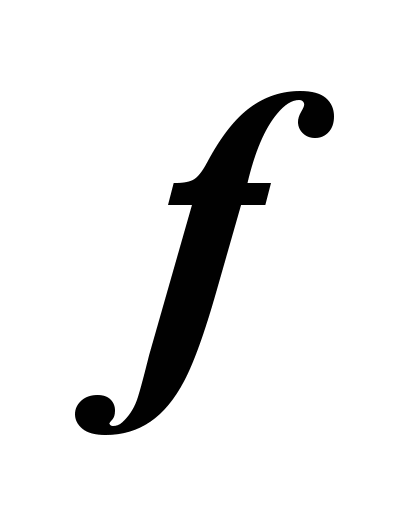 (X0)=32-3*3+4=4
(X0)=32-3*3+4=4Y=4+3(x-3)=4+3x-9=3x-5
Y=3x-5
Подведём итоги урока:
- Перечислить пункты алгоритма. Составить уравнение касательной.
- Если надо составить уравнение касательной, параллельной данной прямой, с чего надо начинать решение таких заданий?
Домашнее задание учебник Калягина, стр.32 №84 (3, 5, 8),
№85(1, 2, 4)
Приложение
| I вариант | II вариант |
f(x)=(x+1)(x+2)-(x-1)(x-3)=(x+1)(x+2)-(x-1)(x-3) 1) -7 ; 2) -1; 3) -7; 4) 1 |
f(x) = 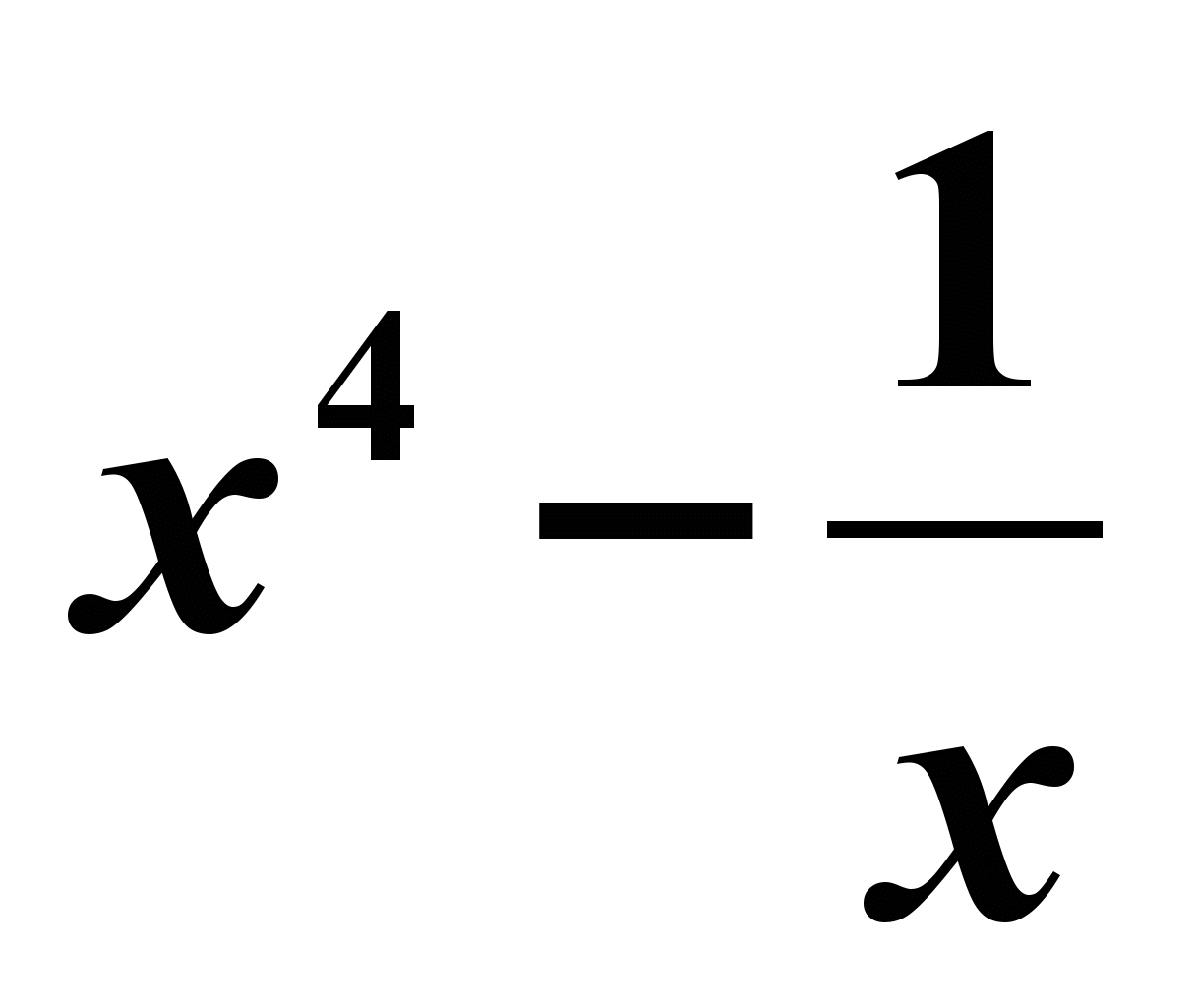 1) 4x - 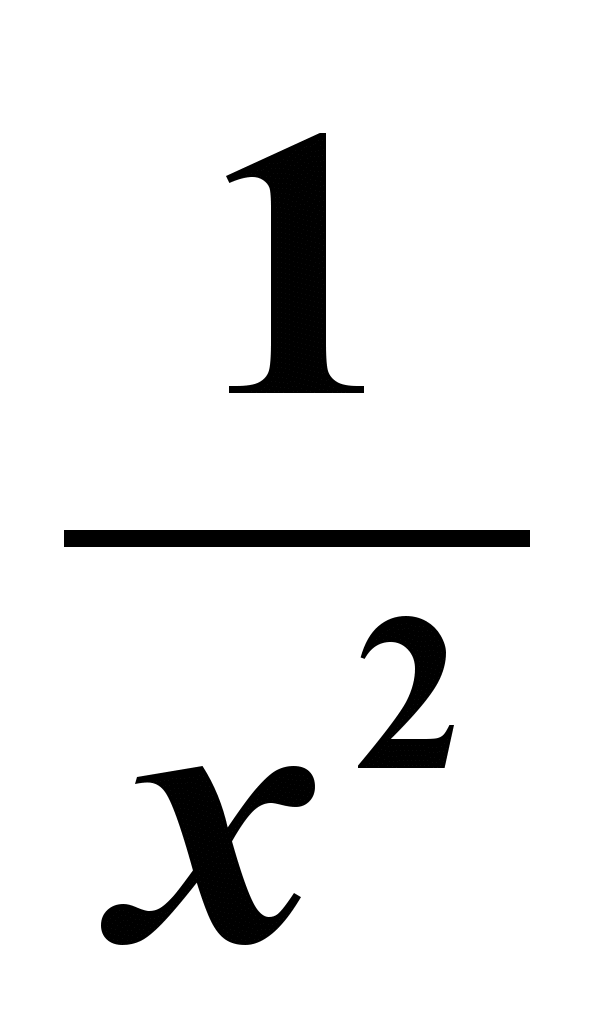 ; 2) 4x3 - ; 2) 4x3 - 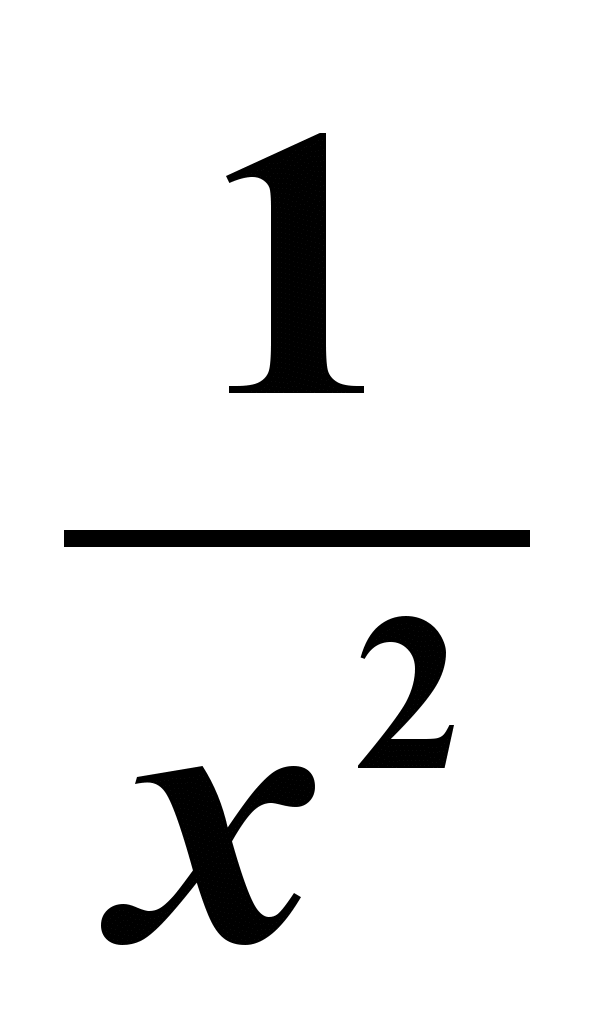 ; 3) 4x + ; 3) 4x +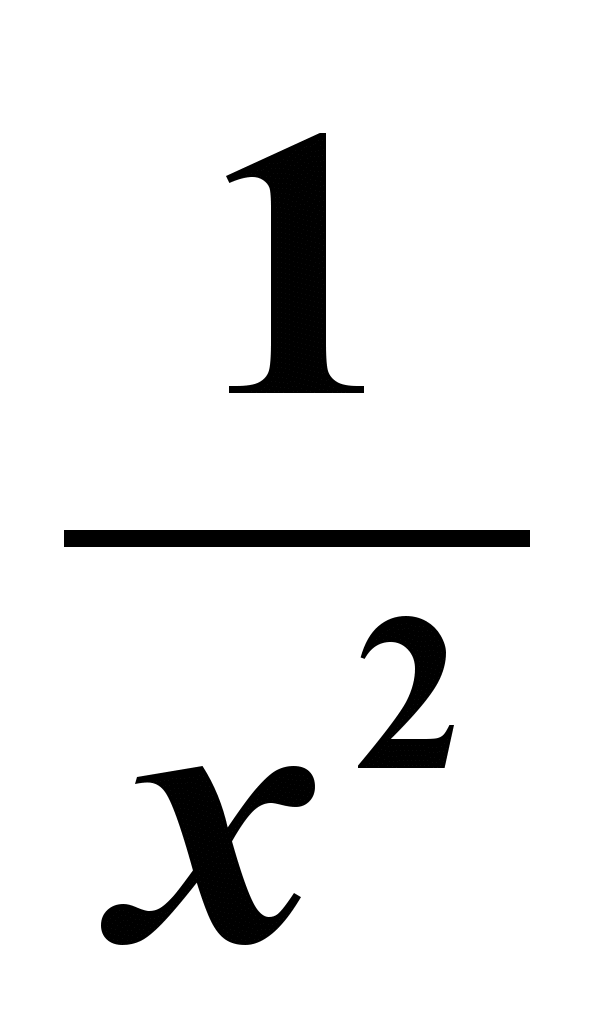 ; 4) 4x3 + ; 4) 4x3 +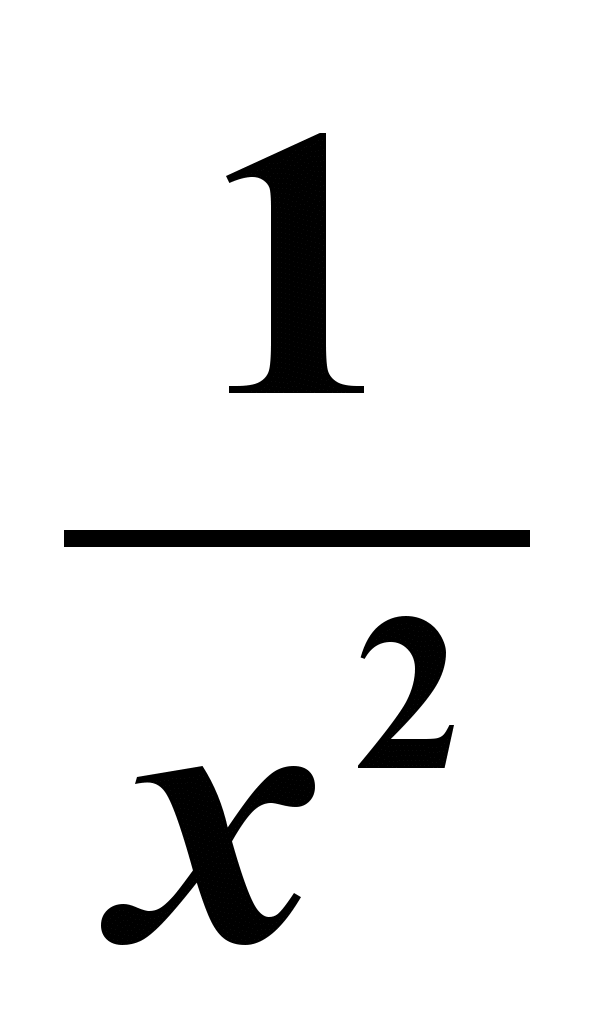 |
| 2.Найдите тангенс угла наклона касательной, проведённой к графику y = 6x - 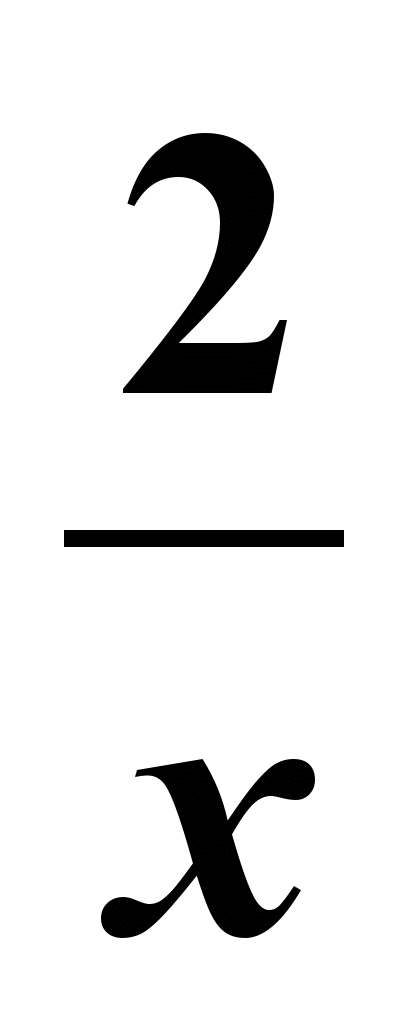 в его точке с абсциссой (-1) в его точке с абсциссой (-1)1) -4; 2) -6; 3) 6; 4) 8 | 2. Найдите угловой коэффициент касательной, проведённой к графику функции y=sin 2x в его точке с абсциссой 0 1) 0; 2) 1; 3) 2; 4) -1 |
| 3. Решить неравенство f `( x)>0, если f ( x)=-x2-4x-2007 1) (2; +∞) ; 2) (-2; +∞) ; 3) (- ∞; 2) ; 4) (- ∞; - 2) | 3. Решить неравенство 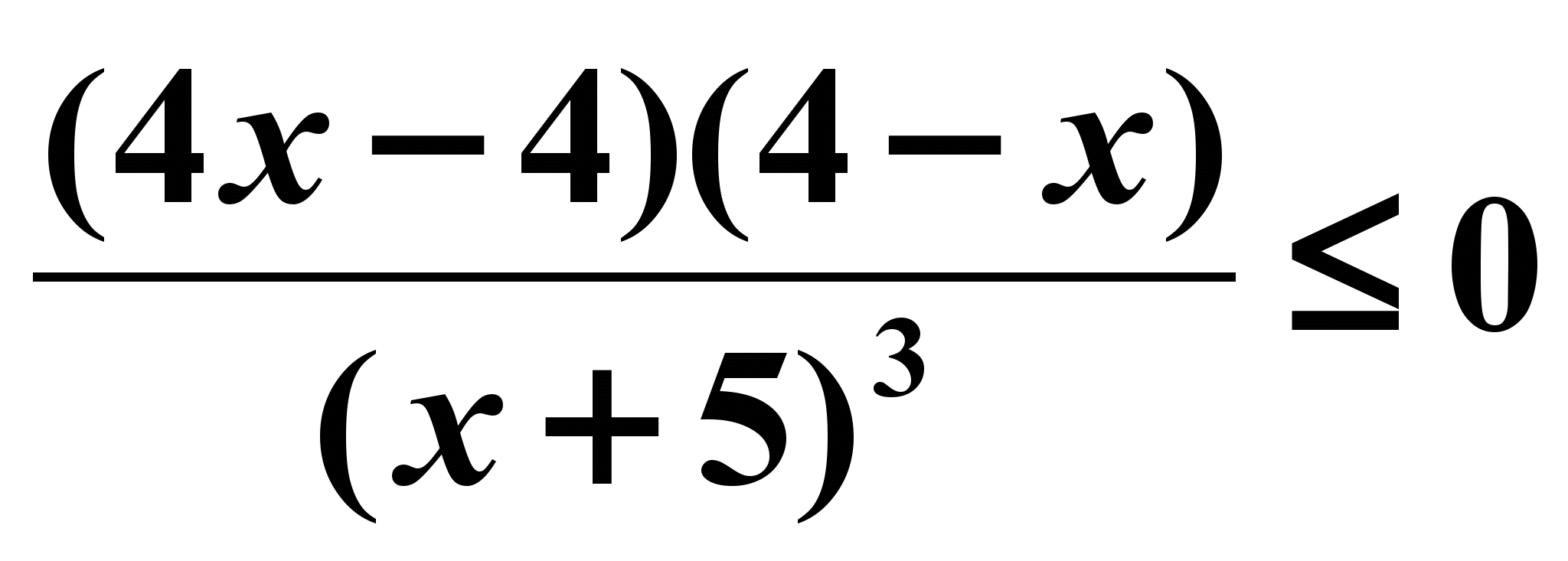 1) (- ∞; -5) 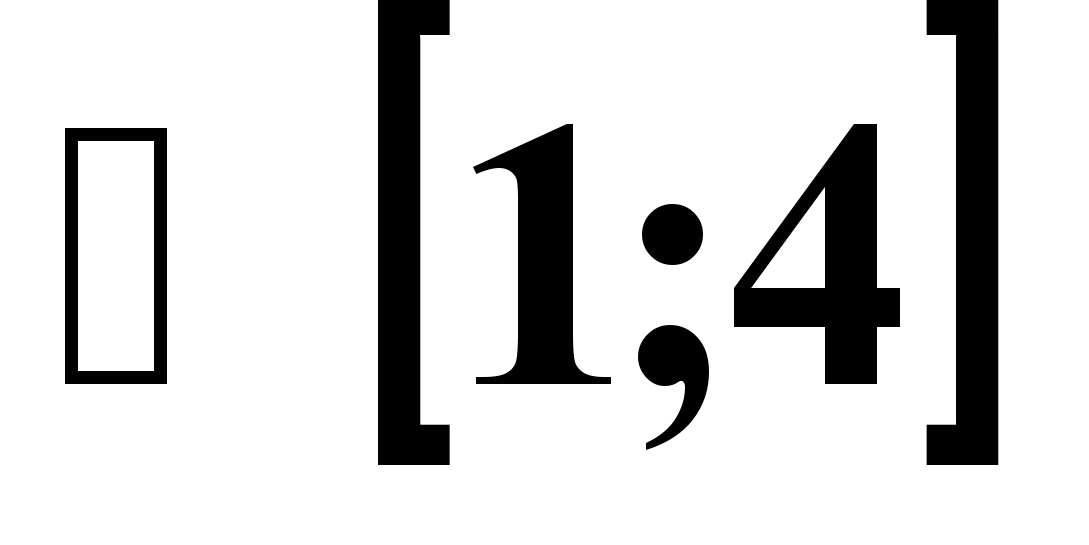 ; 2) (-5; 1) ; 2) (-5; 1) 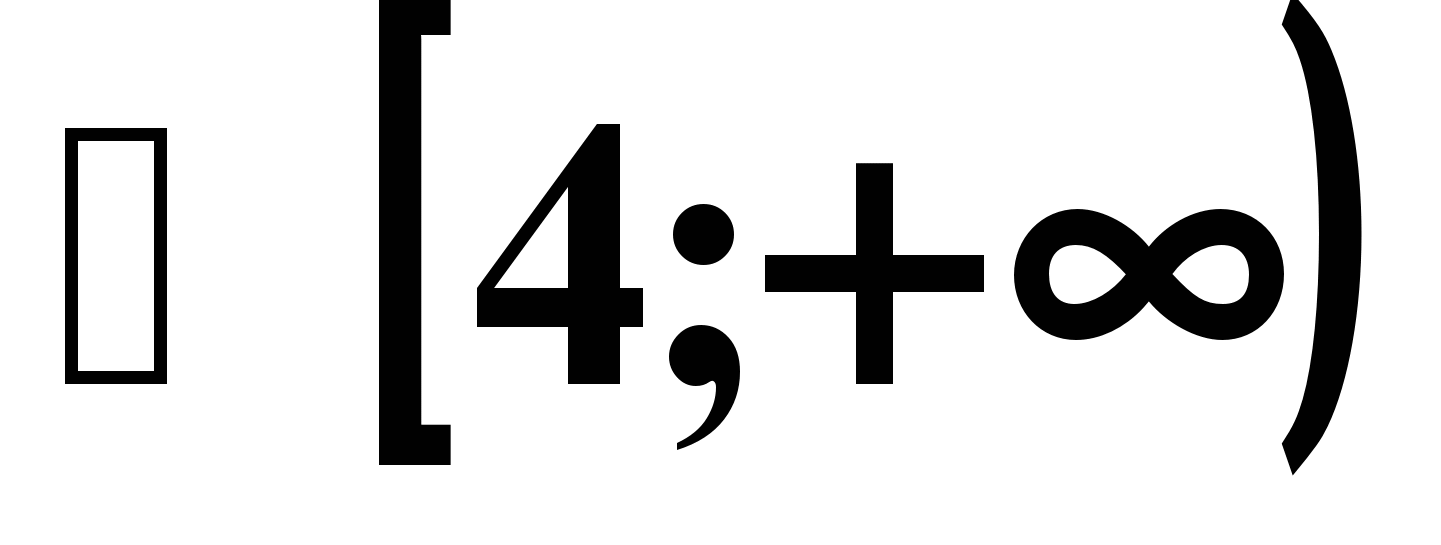 ; ;3) (- ∞; -5) 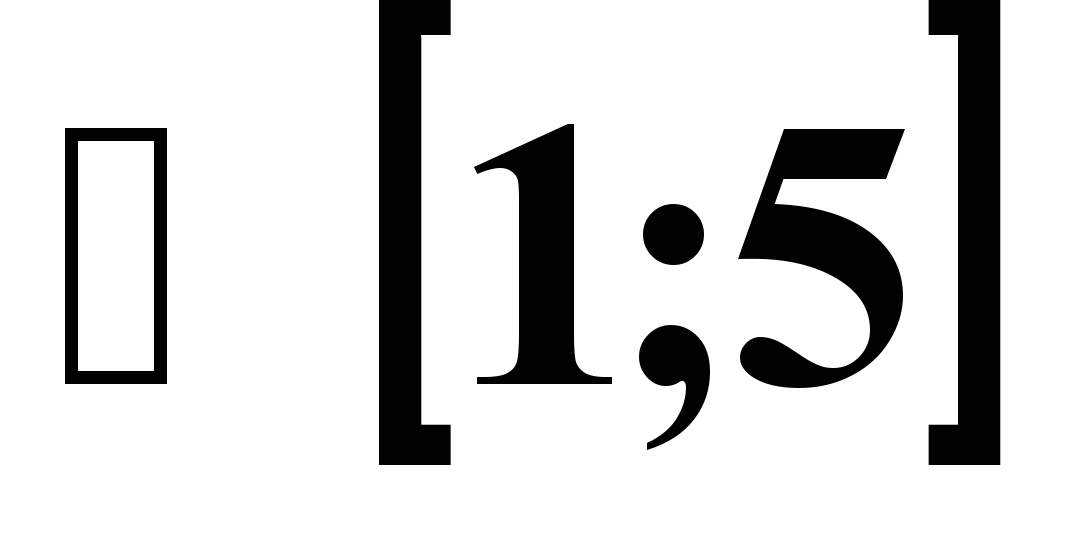 ; 4) (-5; 1) ; 4) (-5; 1) 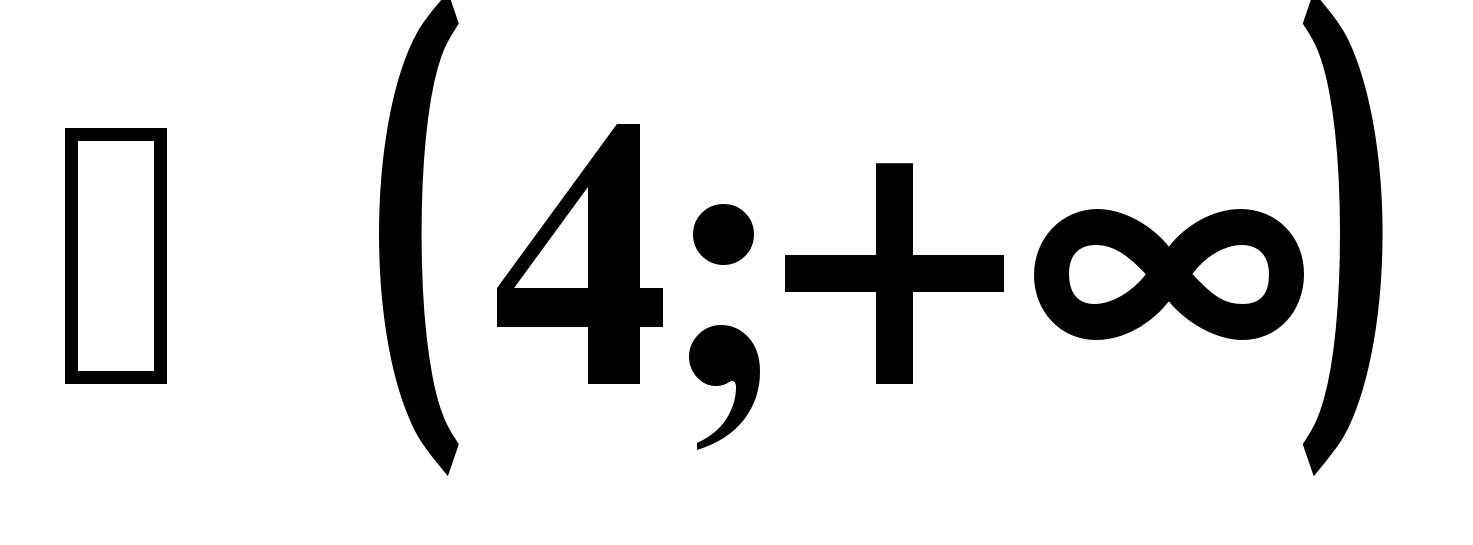 ; ; |
| 4. Найти производную y = 2 sin x +cos x - 3 1) y`( x) = tg x +7; 2) y`( x) = 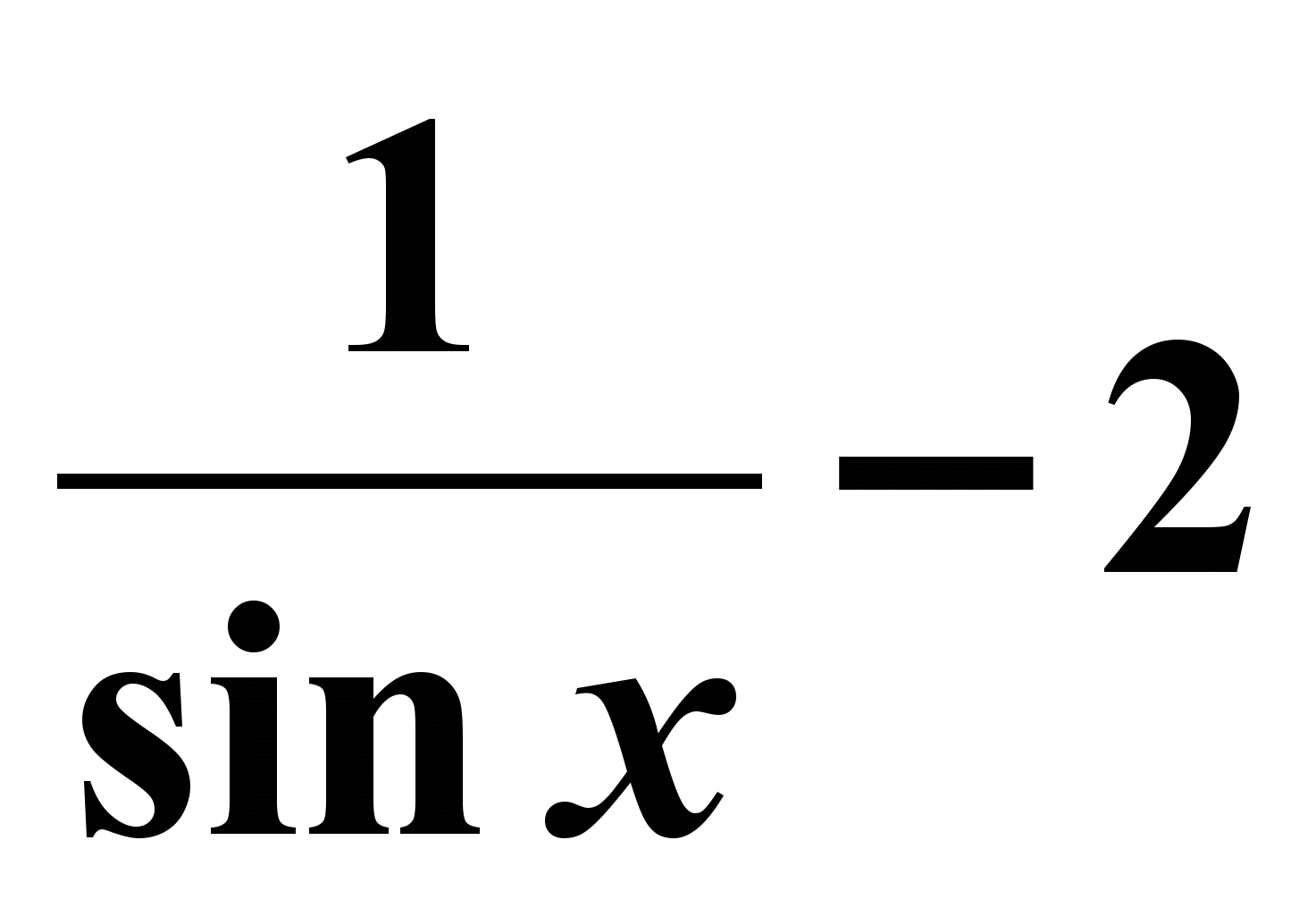 ; ;3) y`( x) = 3 sin x - 2; 4) y`( x) = 2 cos x – sin x | 4. Найти производную 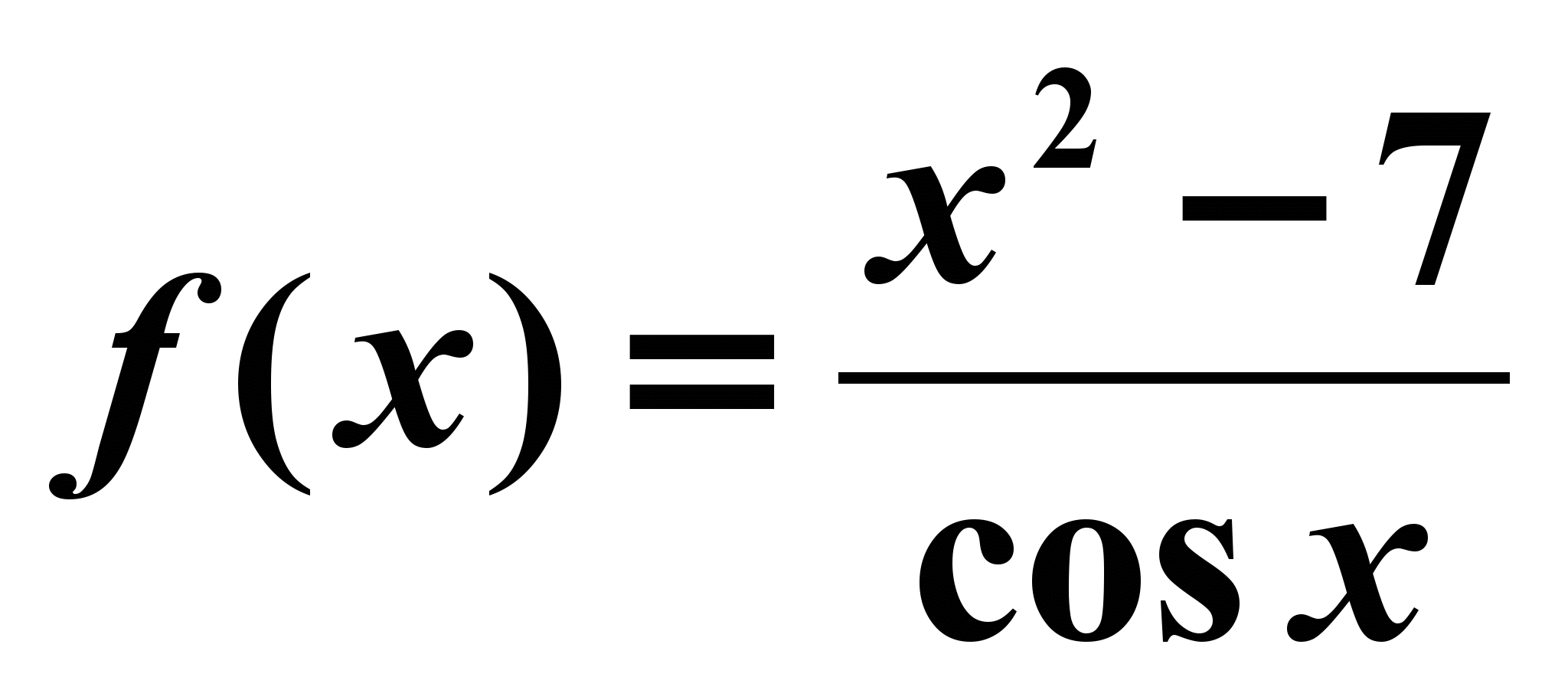 1) f `( x) = 2x + 7 sin x ; 2) f `( x) = 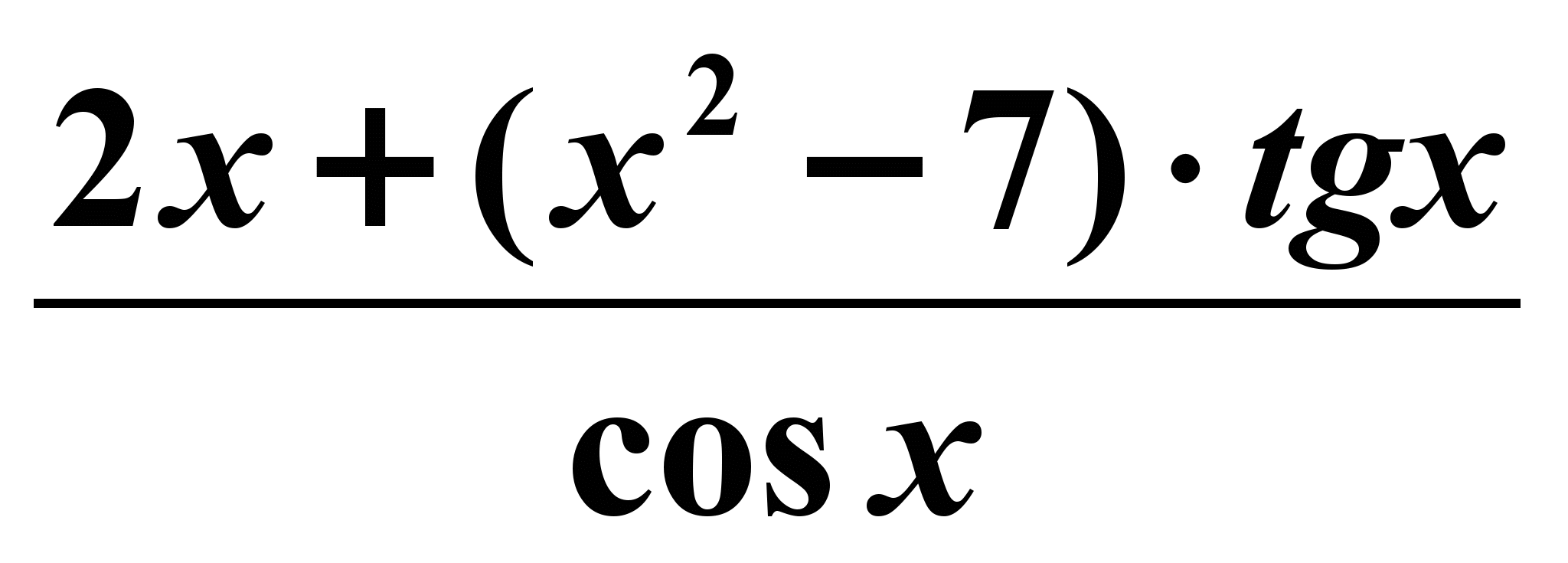 ; ;3) f `( x) = 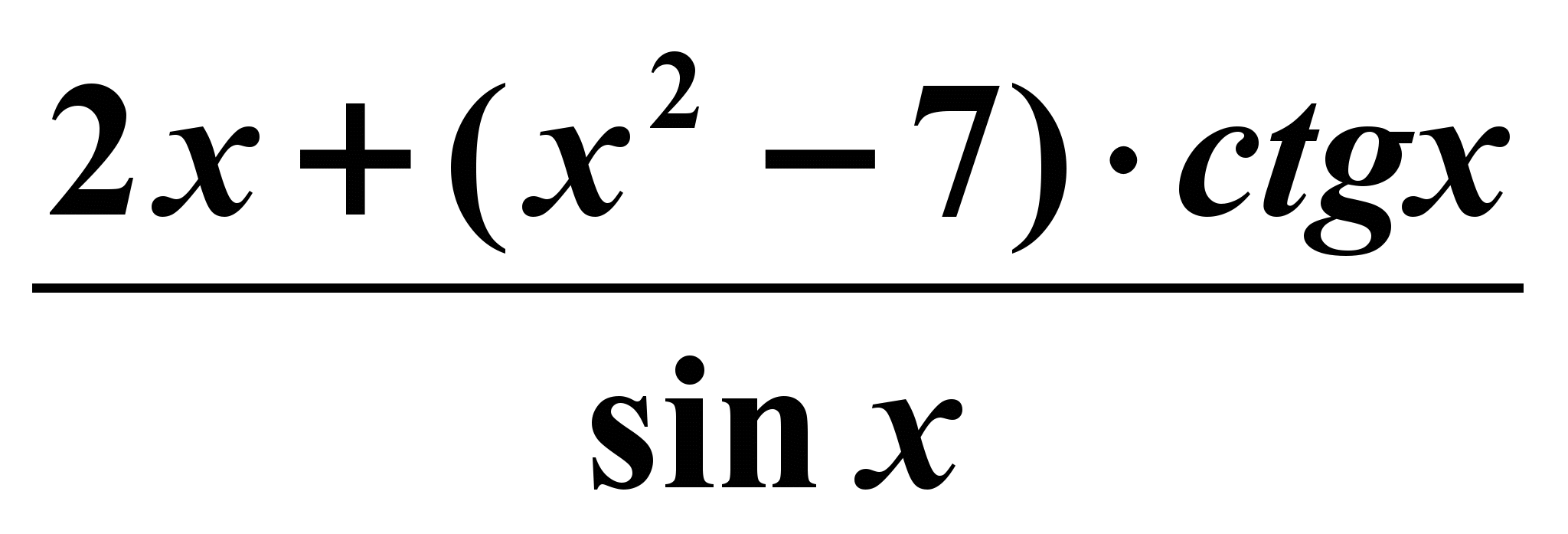 ; ;4) f `( x) = 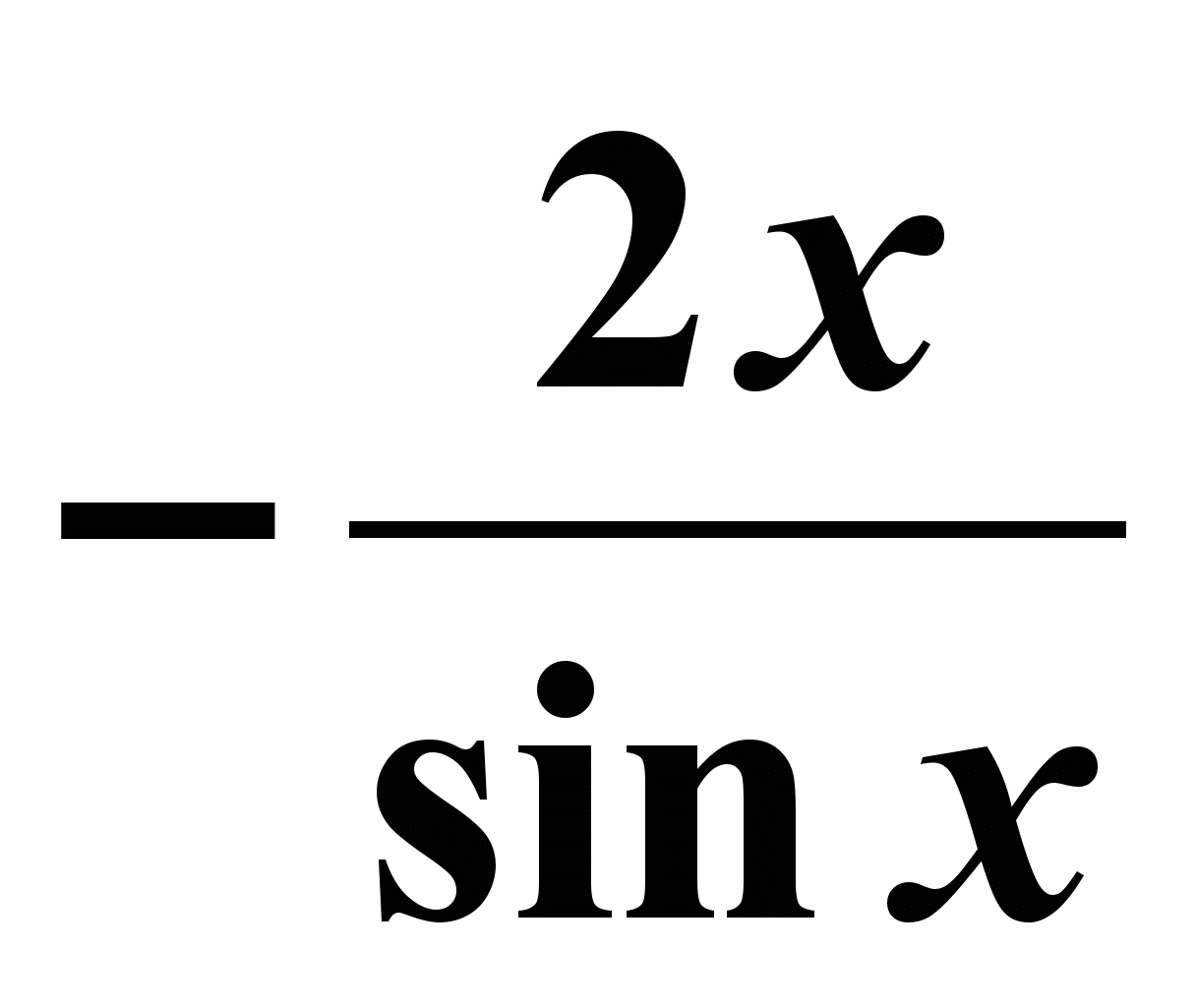 ; ; |
Ответы: вариант I – 3444,
вариант II - 1312
