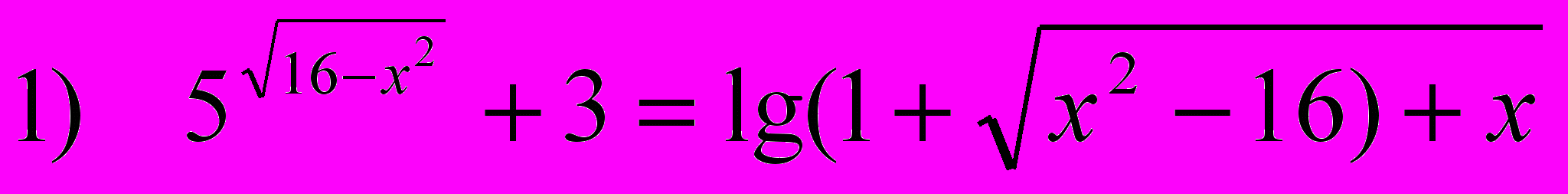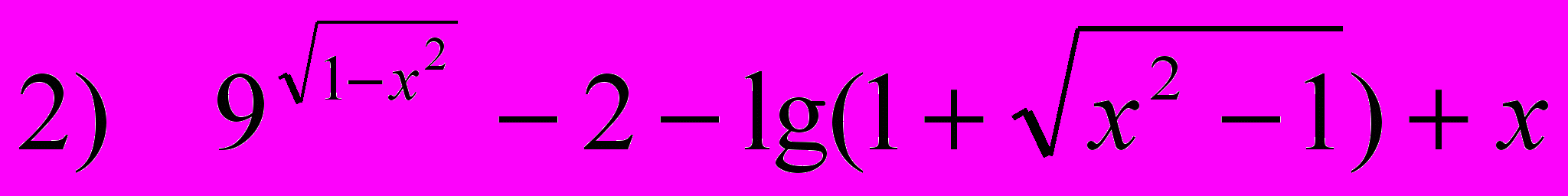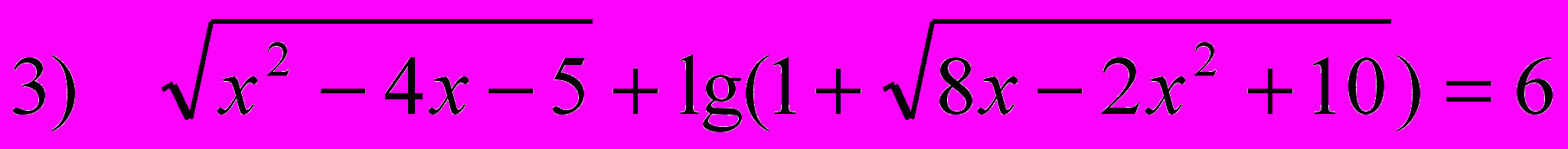Тема урока: Нестандартные методы решения уравнений. Цель урока

Вид материала

Урок

Содержание II. Изложение новой темы. Ответ: нет решений.III. Итог урока.

Подобный материал:

• Тема урока: Теорема Безу. Корни многочленов, 114.7kb.
• Решение линейных уравнений Цель урока, 126.51kb.
• Конспект урока. Тема урока. Функционально-графические методы при решении тригонометрических, 66.13kb.
• Старые методы для решения новых систем уравнений Тип урока, 38.55kb.
• Старые методы для решения новых систем уравнений Тип урока, 37.32kb.
• Конспект урока «Методы решения иррациональных уравнений», 56.45kb.
• План-конспект интегрированного урока в 1 классе Тема урока, 91.29kb.
• Тема: Решение иррациональных уравнений, 89.67kb.
• Конспект урока по теме «Методы решения систем рациональных уравнений», 20.25kb.
• Методические рекомендации к проведению урока: «Методы решения уравнений и неравенств., 15.21kb.

Тема урока: Нестандартные методы решения уравнений.

Цель урока: научить решать уравнения с использованием свойств функций, входящих в это уравнение.

Развивающие задачи:

- развивать творческую сторону мышления;

- учить осуществлять исследовательскую деятельность.

Воспитательная задача: формировать навыки умственного труда – поиск рациональных путей решения.

Тип урока: урок-лекция

Ход урока.

I. Информационный ввод.

Имеется довольно много уравнений, которые можно (и нужно) решать с использованием свойств функций, входящих в это уравнение. Часто оказывается, что такой метод дает возможность решить уравнение, чем с помощью стандартных методов, а иногда решить их в тех случаях, когда стандартные методы не дают такой возможности.

II. Изложение новой темы.

1. Использование областей существования функций.

Если при рассмотрении уравнения выясняется, что обе части определены на множестве М, состоящем из одного или нескольких числе, то нет необходимости приводить какие-либо преобразования уравнения, достаточно проверить, является или нет каждое из этих чисел решением данного уравнения.

Пример 1. Решим уравнение: 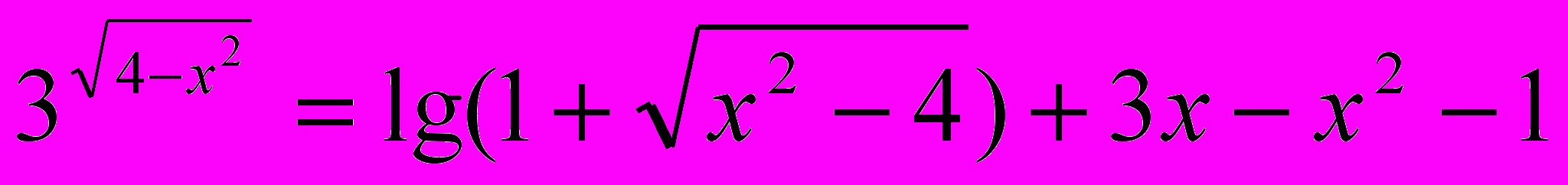(1)

Обе части уравнения (1) определены только для тех х, которые удовлетворяют системе неравенств:



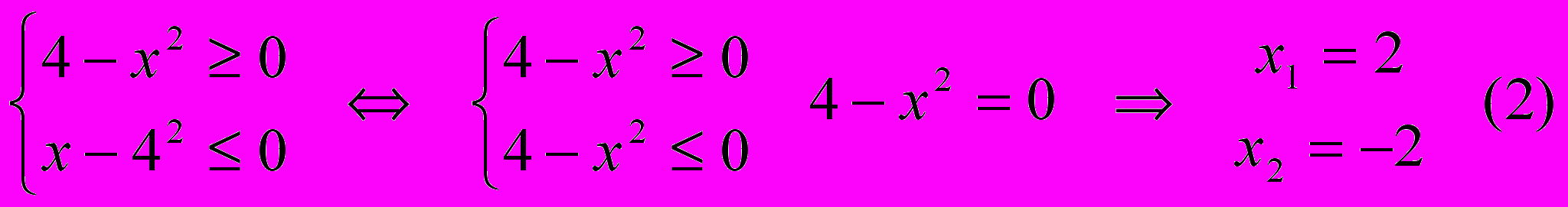
Все решения системы (2) состоят из двух чисел: х₁=2 и х₂=-2. Поэтому если уравнение (1) имеет решения, то они могут быть только среди этих двух чисел.

Проверка:

х=-2

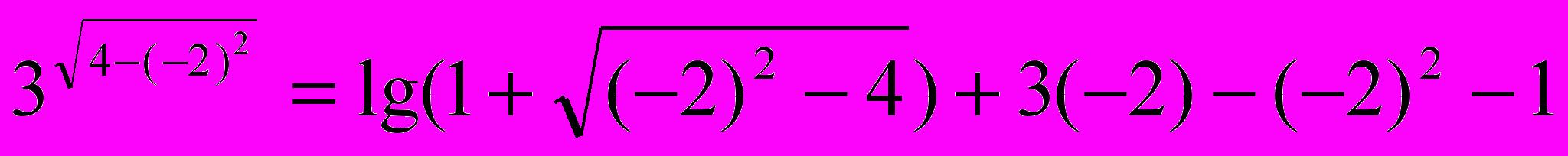
3⁰=lg(1)+(-6)-4-1

1=-11 (не верно)

х=2

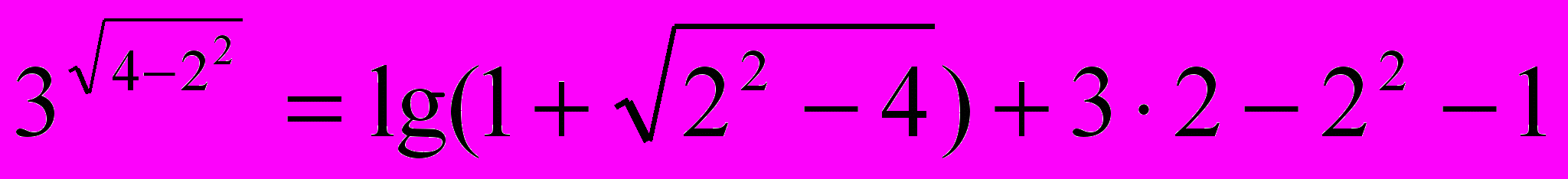
3⁰=lg(1)+(6)-4-1

1=1 (верно)

Ответ: х=2

2. Решить уравнение



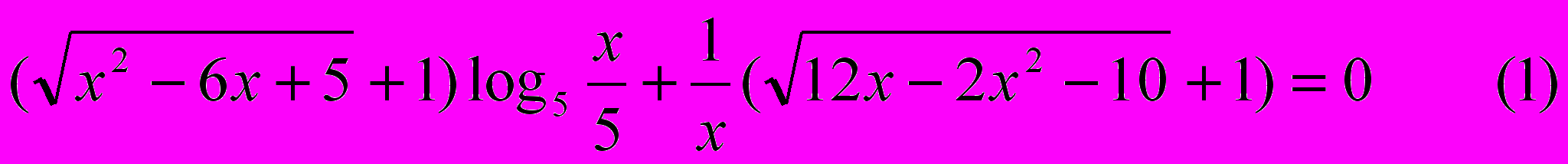
Уравнение определено только для тех х, которые удовлетворяют системе неравенств:

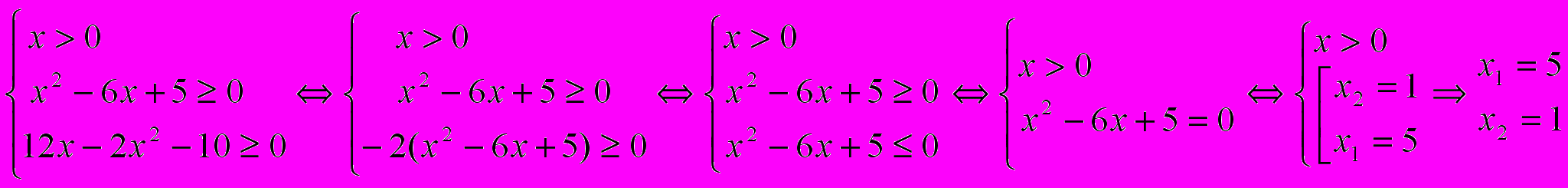Системе неравенств удовлетворяют лишь два числа х₁=5 и х₂=1. Поэтому если уравнение (1) имеет решения, то они могут быть только среди этих двух корней.

Проверка.

х=5





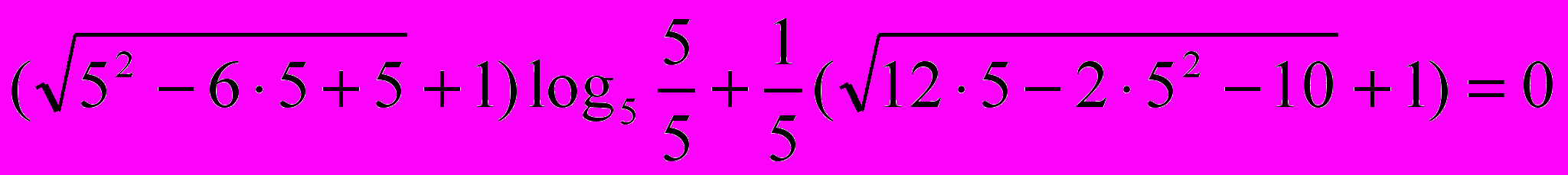
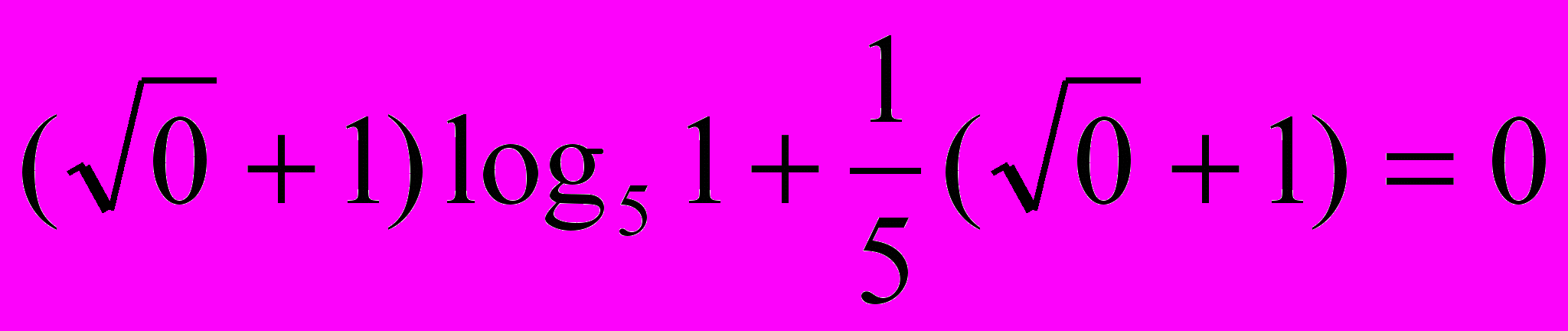
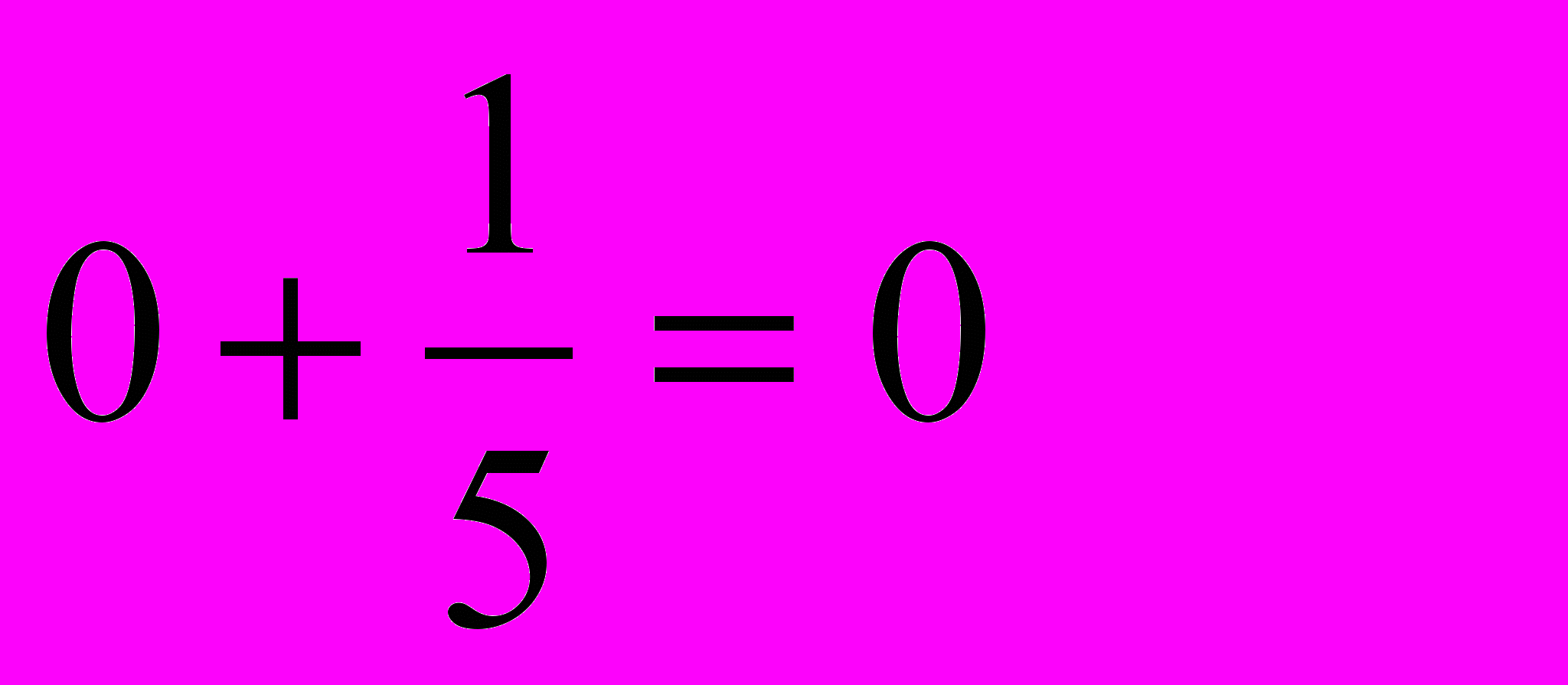неверно

х=5 не является корнем

х=1





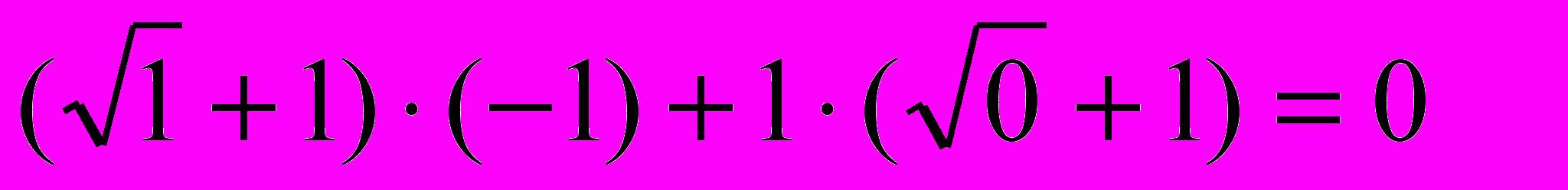
2(-1)+1=0

-1=0 неверно

х=1 не является корнем

Ответ: уравнение не имеет решений.


3. Решить уравнение



Уравнение определено только для тех х, которые удовлетворяют системе неравенств:



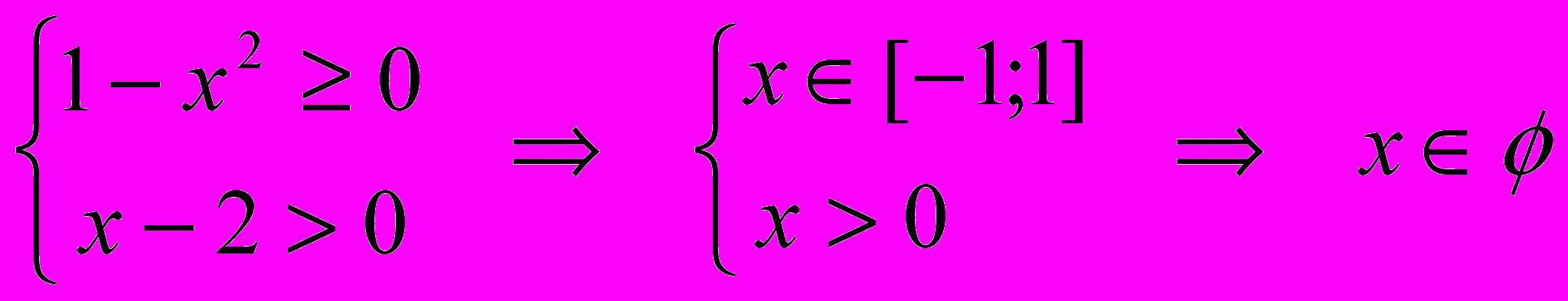
1-х² ≥ 0

(1-х)(1+х) ≥ 0



Эта система неравенств не имеет решений. Следовательно, уравнение не имеет решений.

Ответ: нет решений.


III. Итог урока.

Решение данных уравнений показало, что использование свойств функций, входящих в эти уравнения, дает возможность решить уравнение проще, чем с помощью стандартных методов, а иногда решить их в тех случаях, когда стандартные методы не дают такой возможности. Этот метод можно применить при решении заданий С₁, С₂. На следующем занятии разберем применение этого метода при решении неравенств.


IV. Домашнее задание.

Решить уравнения