Тема урока: Теорема Безу. Корни многочленов
| Вид материала | Урок |
Содержание2. Изучение нового материала Пример 2. Решите уравнение 4. Итоги урока. Домашнее задание. Ход урока 2. Изучение нового материала. |
- Элективный курс «Отработка основных методов и приёмов решения уравнений» 10класс. 2010/2011, 51.02kb.
- Программа Учебный курс предпрофильной подготовки «Деление многочленов. Теорема Безу»., 55.16kb.
- План-конспект открытого урока по теме: «Разложение многочленов на множители», 74.23kb.
- Разложение многочленов на множители” (7 класс), 38kb.
- Программа междисциплинарного экзамена по специальности 010101 "Математика", 115.77kb.
- Андрияновой Наталии Анатольевны 5 класс Русский язык Тема: Корни с чередованием букв, 96.91kb.
- Програма н/к "Основи мсс" курс- 3, семестр-1, 54год лекц, 28.91kb.
- Тема. Теорема Пифагора, 72.28kb.
- Конспект урока тема Сложение многочленов Учитель математики Iкатегории Пак Валентина, 165.69kb.
- История теорема Пифагора, 154kb.
-+
Тема урока: Теорема Безу. Корни многочленов.
Цель урока: Познакомить учащихся с методом решения уравнений, основанном на применении теоремы Безу. Научить использовать его при решении уравнений.
Задачи: вырабатывается умение: логически мыслить, анализировать, решать уравнения высших степеней.
Ход урока
1. Проверить усвоение изученного.
Повторить алгоритм деления многочлена на многочлен.
а) Выполнить деление:
(х3-4х2-11х+30): (х-2)
б) Найти значение многочлена
х3-4х2-11х+30 при х=2
в) Выполнить деление
(х3-4х2-11х+30): (х-3)
г) Найти значение многочлена
х3-4х2-11х+30 при х=3
2. Изучение нового материала
Любой многочлен R(x) можно представить в виде:
P(x)= (х-а) Q(х) + r, где r=P(a)
Пример 1. Найти остаток от деления х4-6х3+8 на х+2
Теорема Безу. Если уравнение а0хn + a1xn-1+ … + an-1x+an = 0,
где все коэффициенты целые, имеет целые корни, то это делители свободного члена.
Пример 2. Решите уравнение
х3-8х2+19х-12=0
Свободный член – 12 имеет делители 1, 2, 3, 4, 6, 12.
При x=1 значение многочлена равно 0. Это означает, что 1 является корнем уравнения, а х3-8х2+19х-12 делится на x-1.
Выполнив деление, получим уравнение х2-7х+12=0 , решая которое, получим что x=3 или x=4.
Ответ: 1; 3; 4.
Сформулировать обобщенную теорему Безу
3. Решение задач.
1) Решить уравнения:
а) х3-3х2-4х+12=0,
б) х3+4х2+5х+2=0,
в) х4+4х3+х2-12х-12=0,
г) х4+4х3-х2-16х-12=0.
2) Доказать, что уравнение не имеет целых корней:
а) х2-х-1=0,
б) х4-5х2+6=0,
в) х4+х3+х2+х+1=0.
3) Уравнение х3+17х2+bх-17=0 имеет три различных целях корня. Найти b
4. Итоги урока.
Какие уравнения можно решить с помощью теоремы Безу? Можно ли решить уравнение этим методом, если коэффициенты дробные? Какие еще методы применяются при решении таких уравнений?
Домашнее задание. Выучить теорему Безу.
1) Решить уравнение:
а) х3+3х2-5х-10=0,
б) х4-5х3+11х2-25х+30=0,
в) х4+3х2-3х3+12х-28=0.
2) Решить уравнение двумя способами:
а) х3-5х2-4х+20=0,
б) х3-3х2-3х+1=0,
в) 6х4-35х3+62х2-35х+6=0.
Индивидуальное задание: изучить схему Горнера и на следующем уроке сделать сообщение.
Тема урока: Дробно-рациональные уравнения.
Цель урока: Познакомить учащихся с различными методами решения дробно-рациональных уравнений. Научить правильно выбирать метод решения уравнений.
Задачи: выработать умение: логически мыслить, анализировать, пользоваться методом интервалов.
Ход урока
1. Проверка домашнего задания.
Проверить решение двух уравнений:
а)
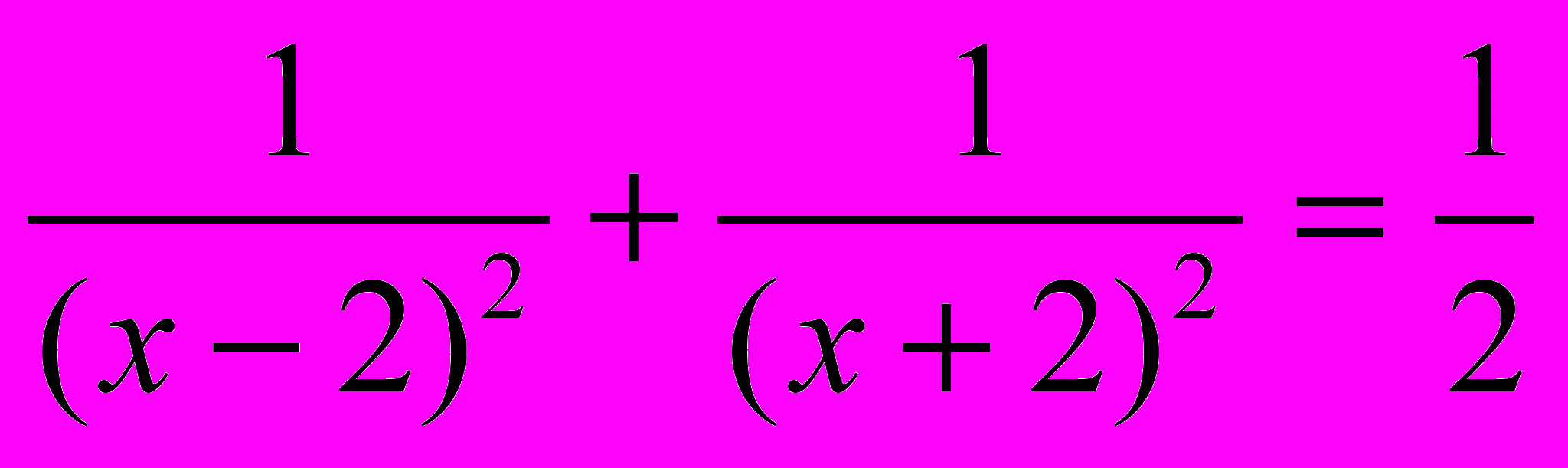 ,
,уравнение решается по общей схеме.
Вопрос: как лучше выполнить умножение
 (х-2)2(х+2)2.
(х-2)2(х+2)2.Выбрать более простой способ.
б)
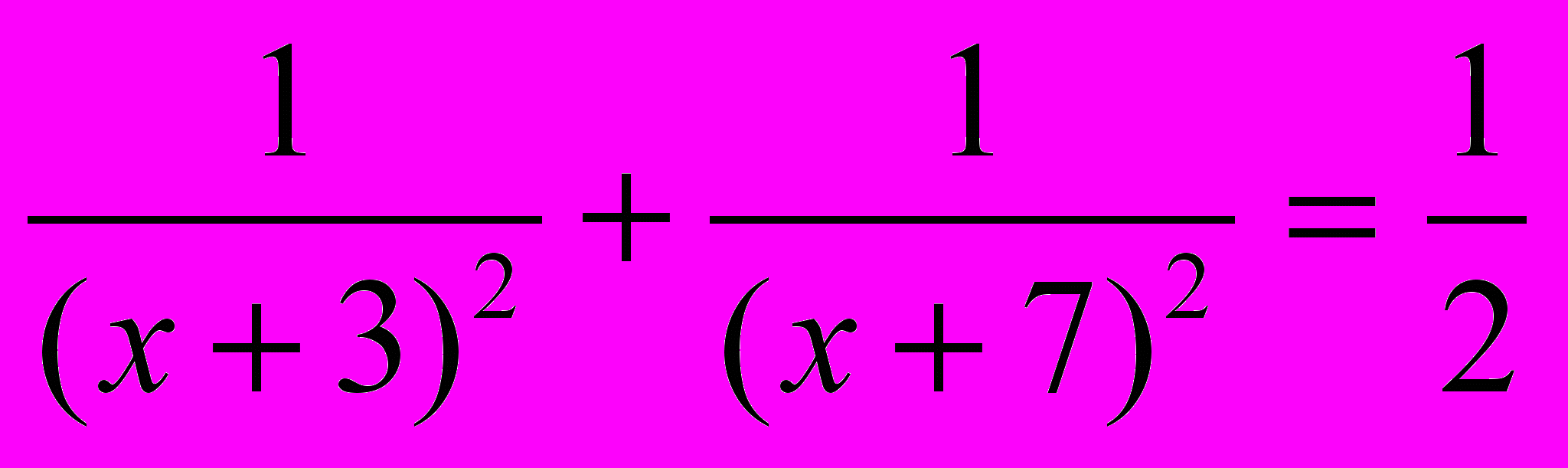 .
.Вопрос: можно ли это уравнение с помощью замены привести к уравнению вида а)?
2. Изучение нового материала.
Рассмотреть на примерах различные методы решения дробно-рациональных уравнений.
1) Общая схема решения уравнения:
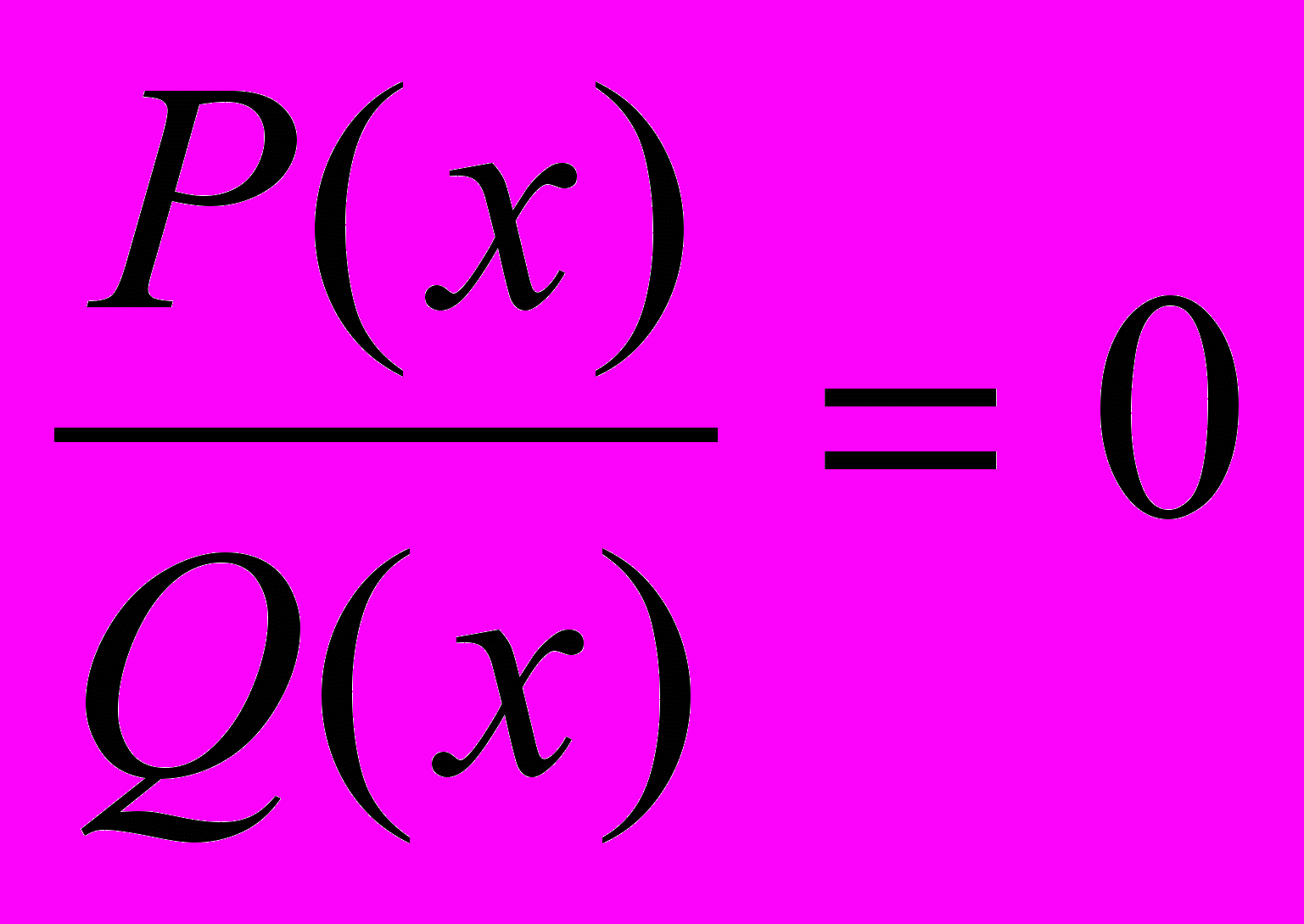 . Уравнение равносильно системе:
. Уравнение равносильно системе: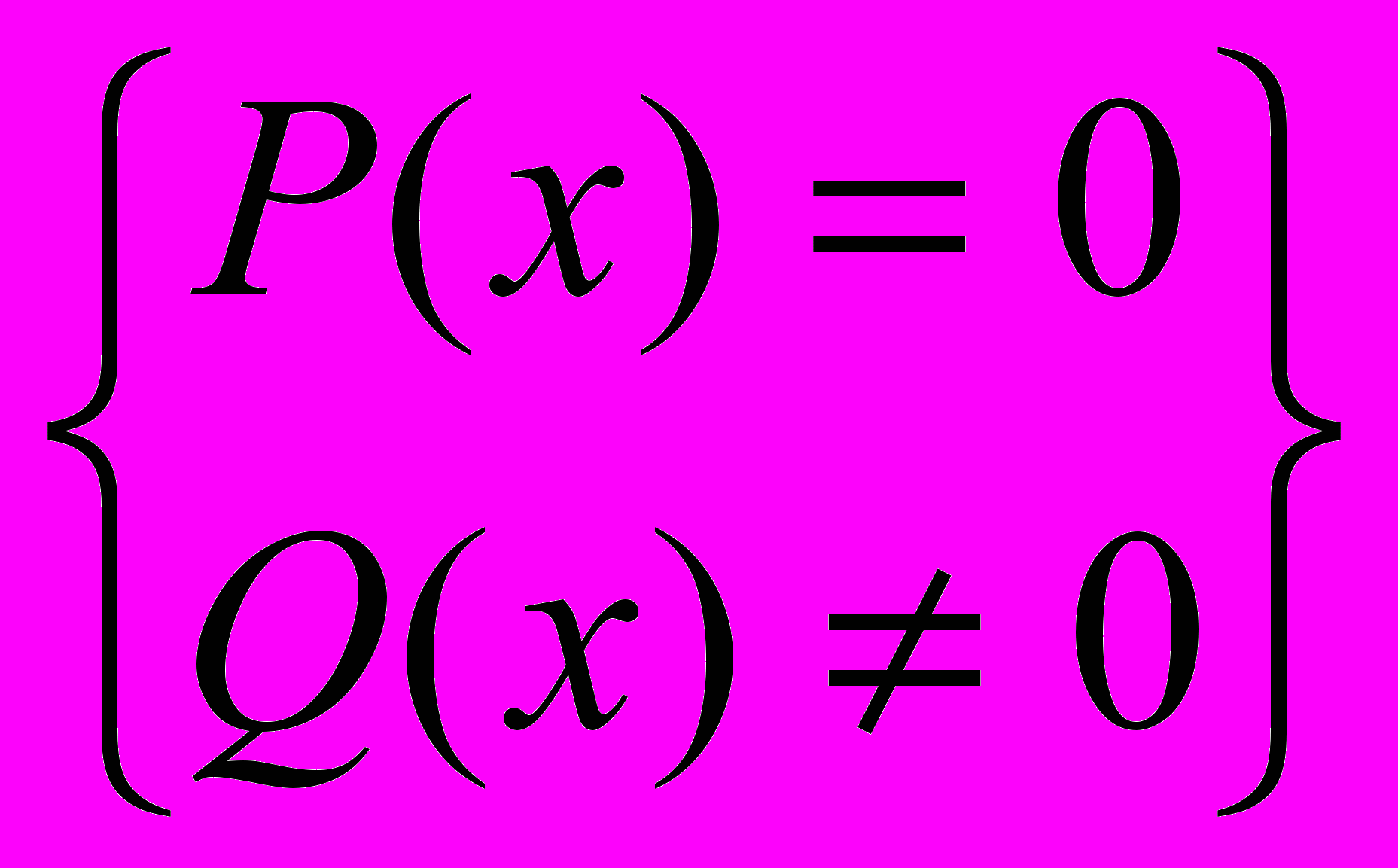
Пример 1. Решить уравнение:
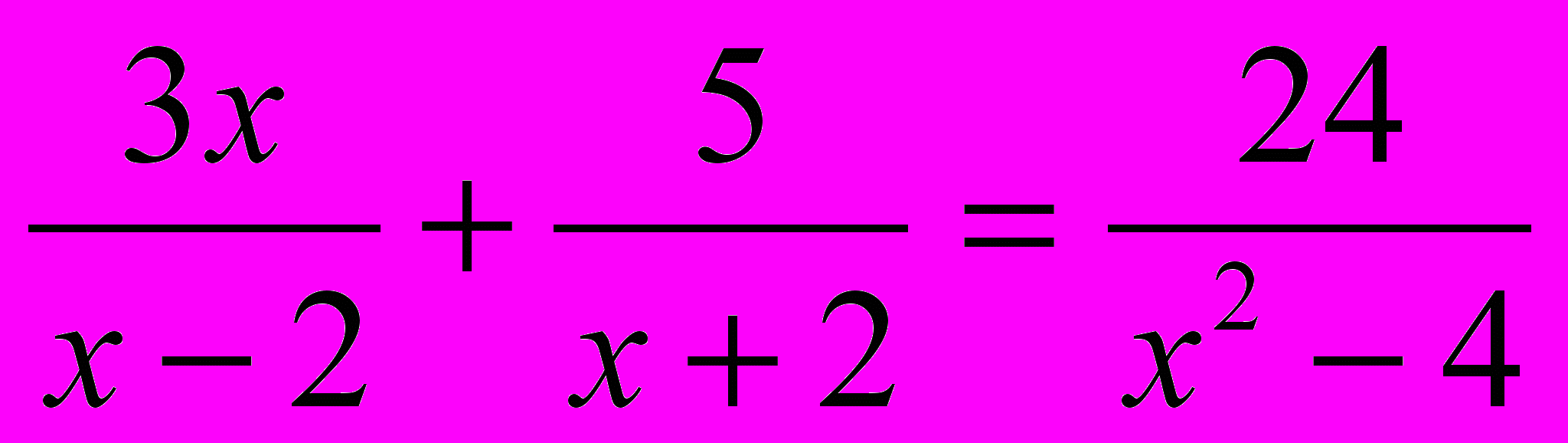
2) Метод замены переменных.
имерППППппрррПример 2. Решить уравнение:
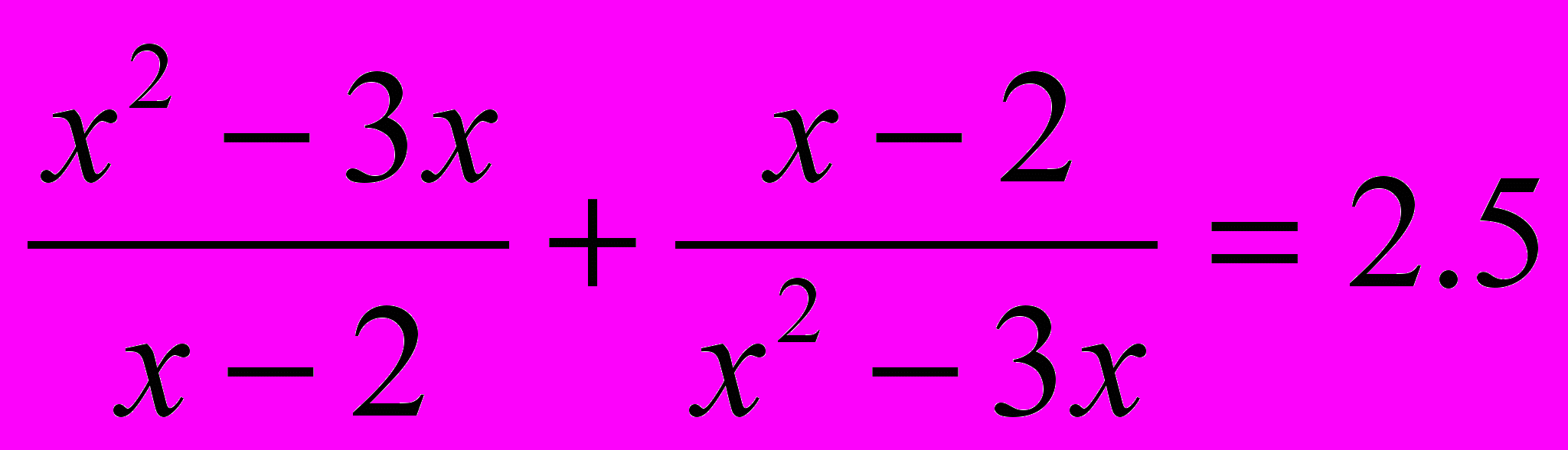
Замена
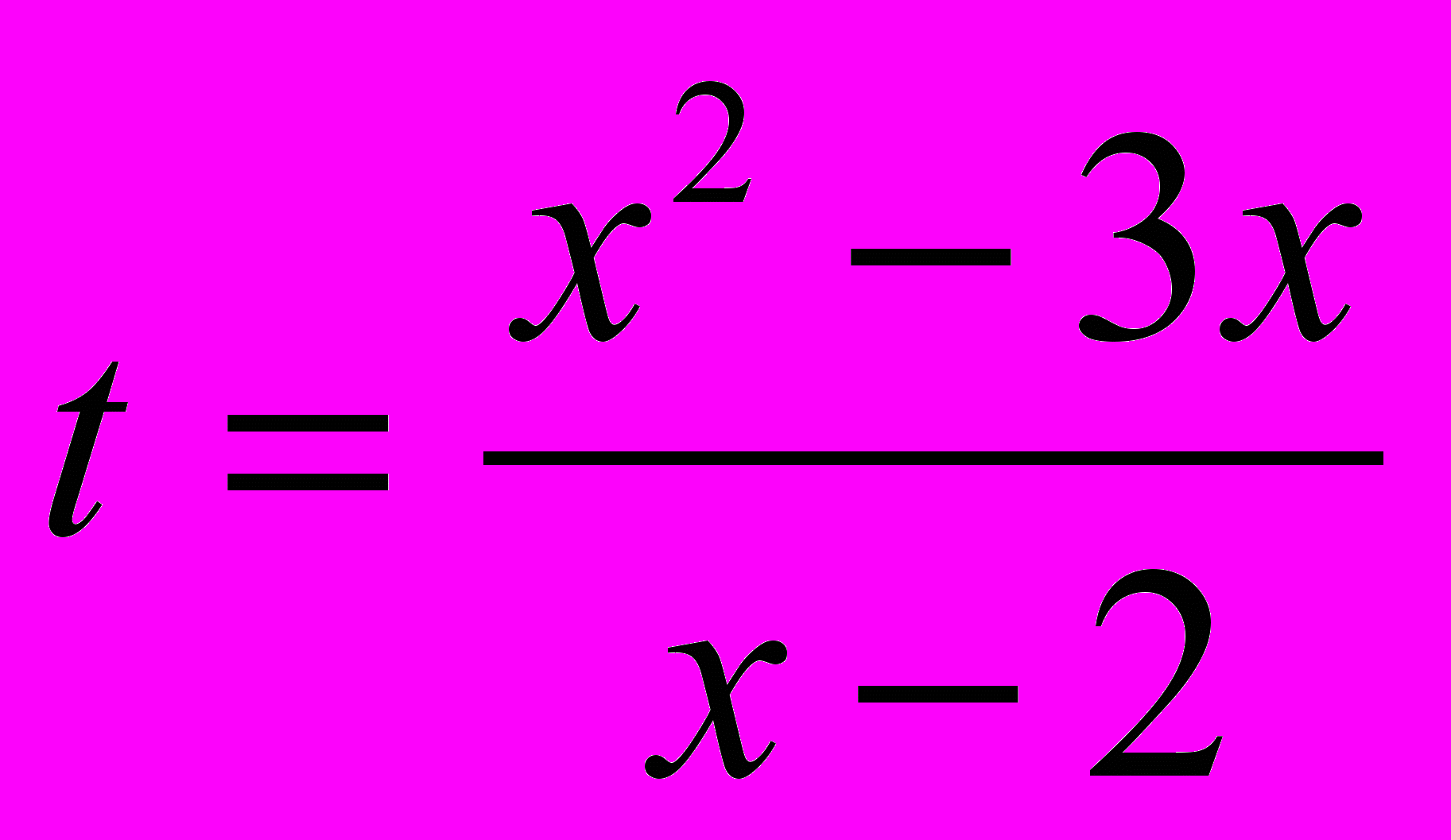 приводит к квадратному уравнению
приводит к квадратному уравнению 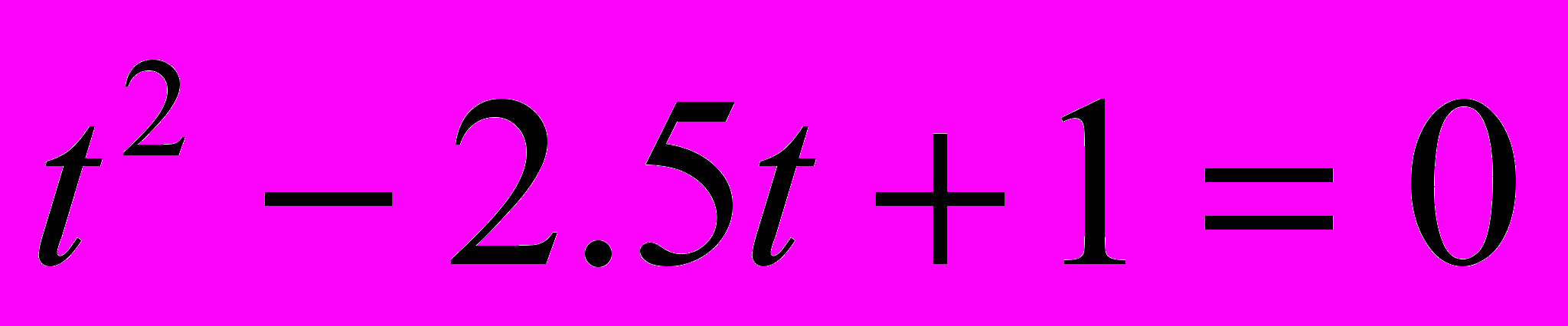 , которое имеет корни: t1=0,5; t2=2. Решая далее уравнения:
, которое имеет корни: t1=0,5; t2=2. Решая далее уравнения: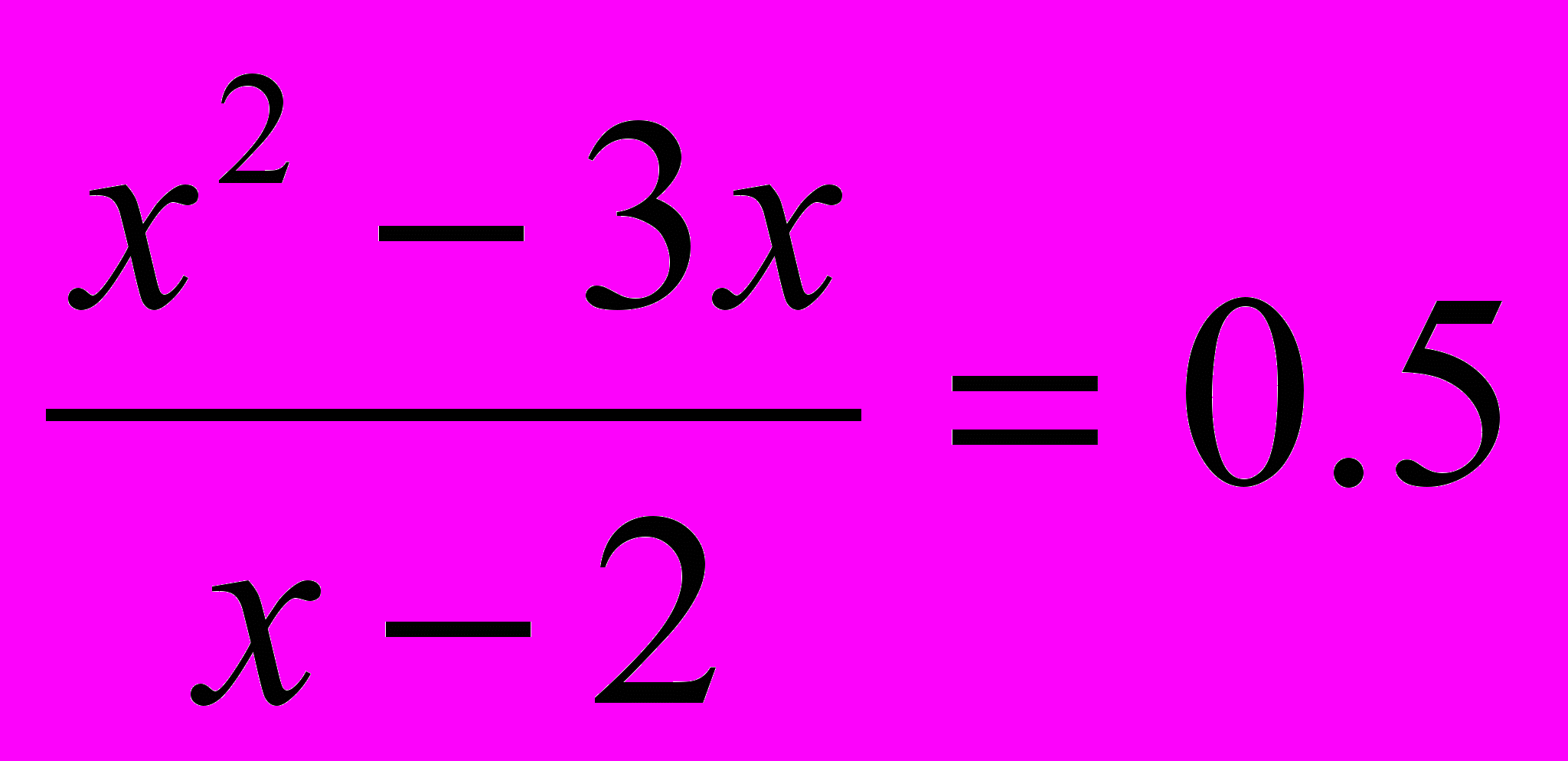 и
и 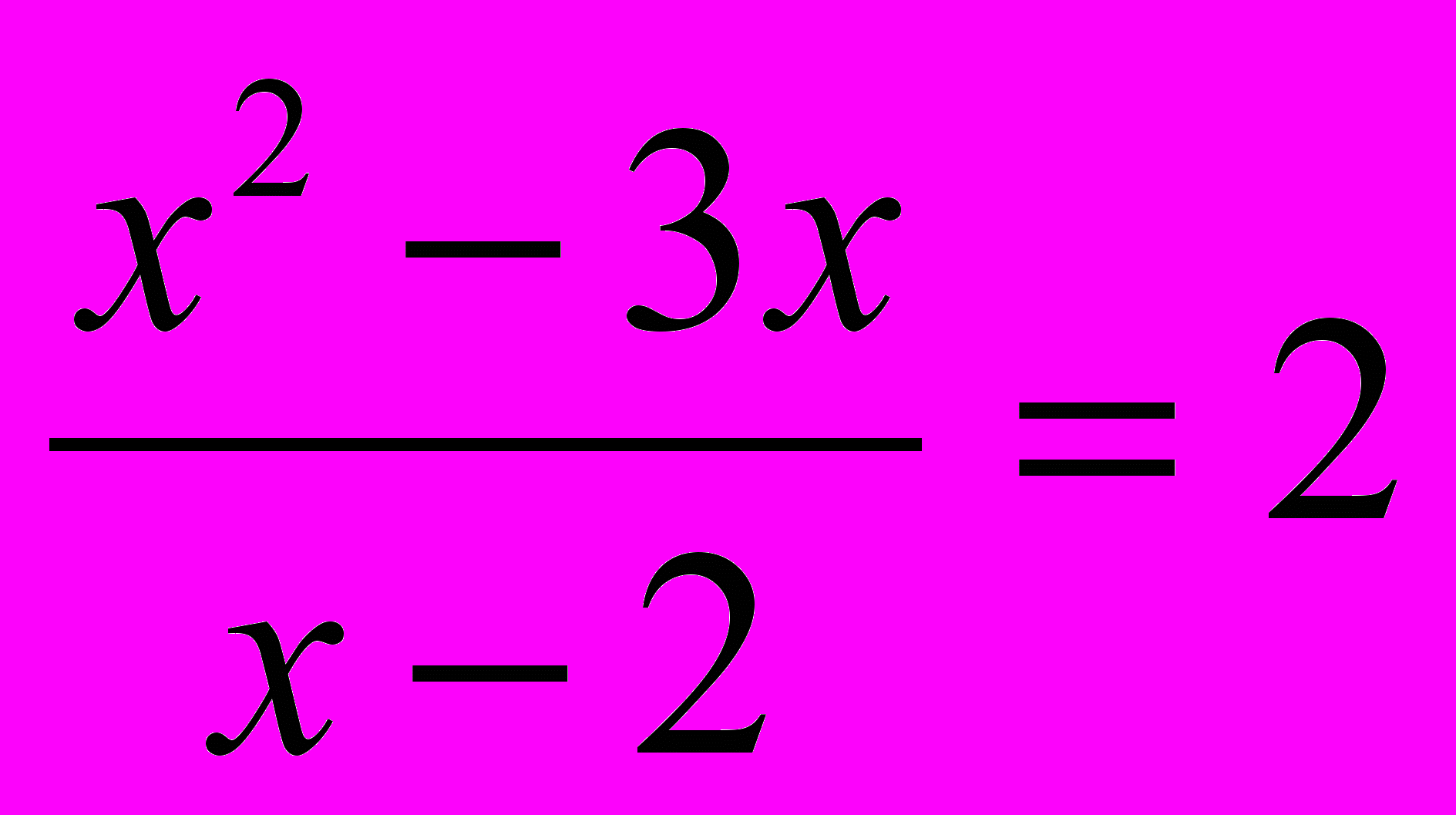 ,
, получим корни заданного уравнения:
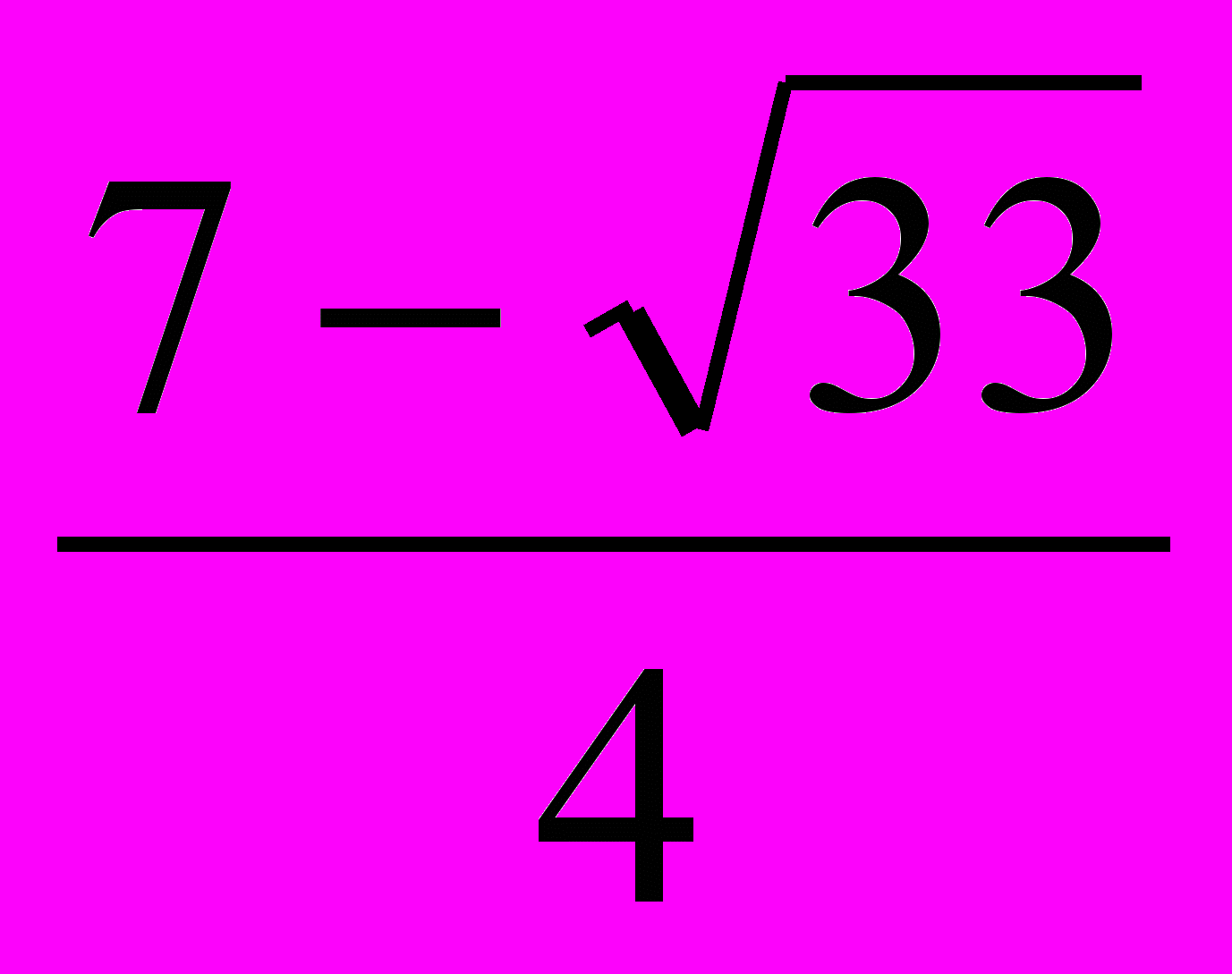 ;
; 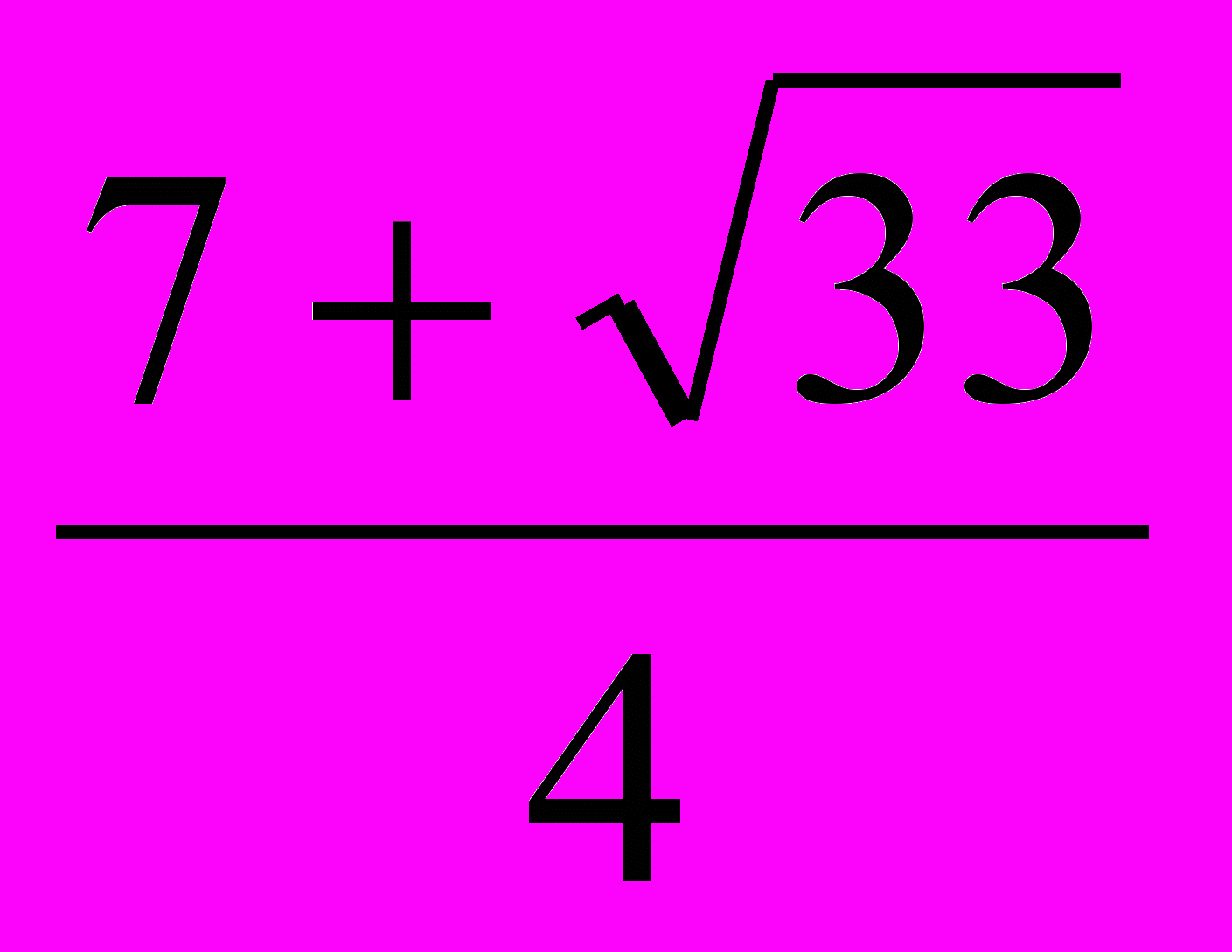 ; 1; 4.
; 1; 4.3) Применение основного свойства дроби
Пример 3. Решить уравнение
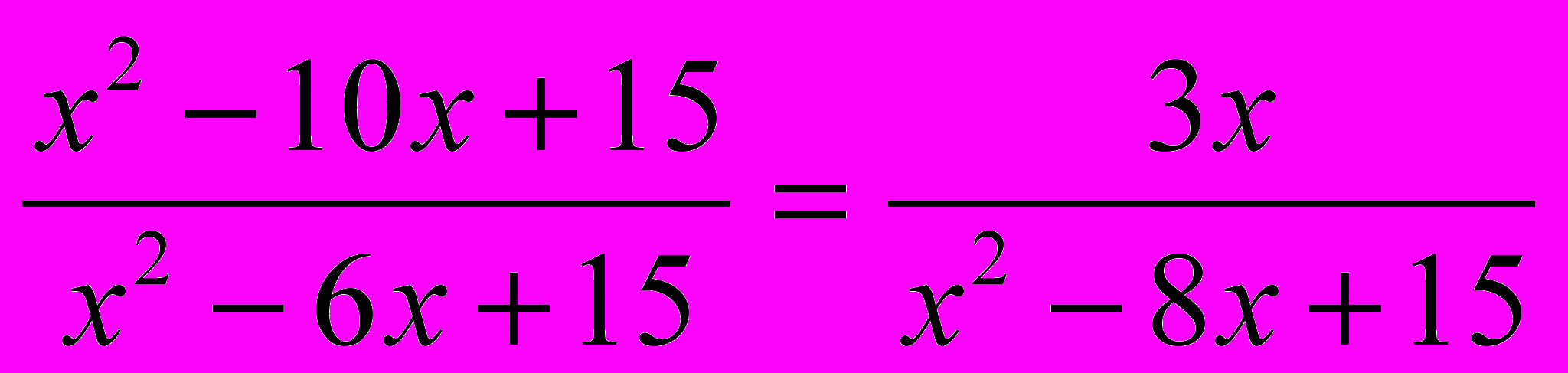
Замечаем, что повторяется выражение x2+15, но замена: t= x2+15 не приводит к более простому уравнению.
Проверим, что 0 не является решением уравнения и разделим числитель и знаменатель каждой дроби на x. Получим уравнение:
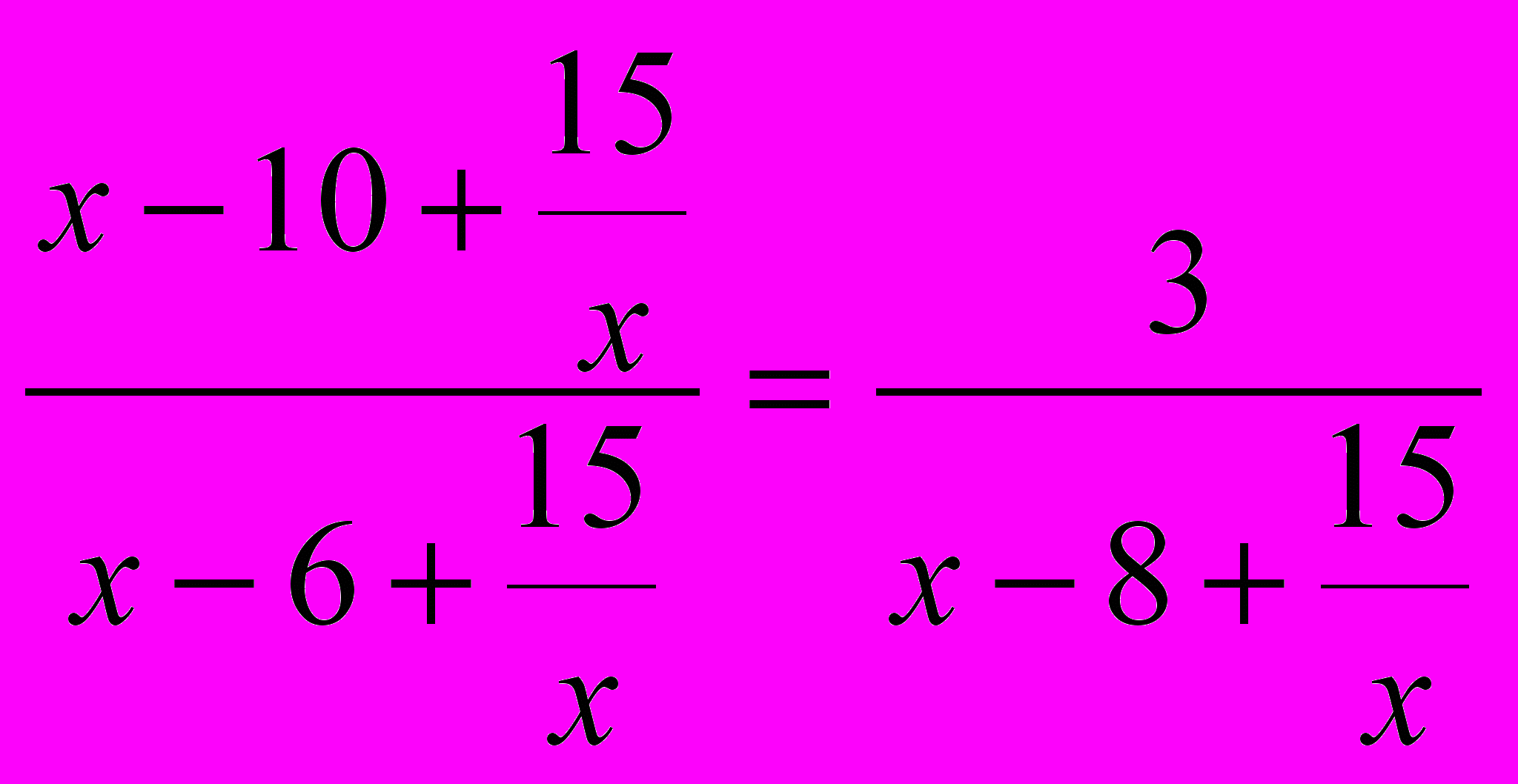
Далее делаем замену:
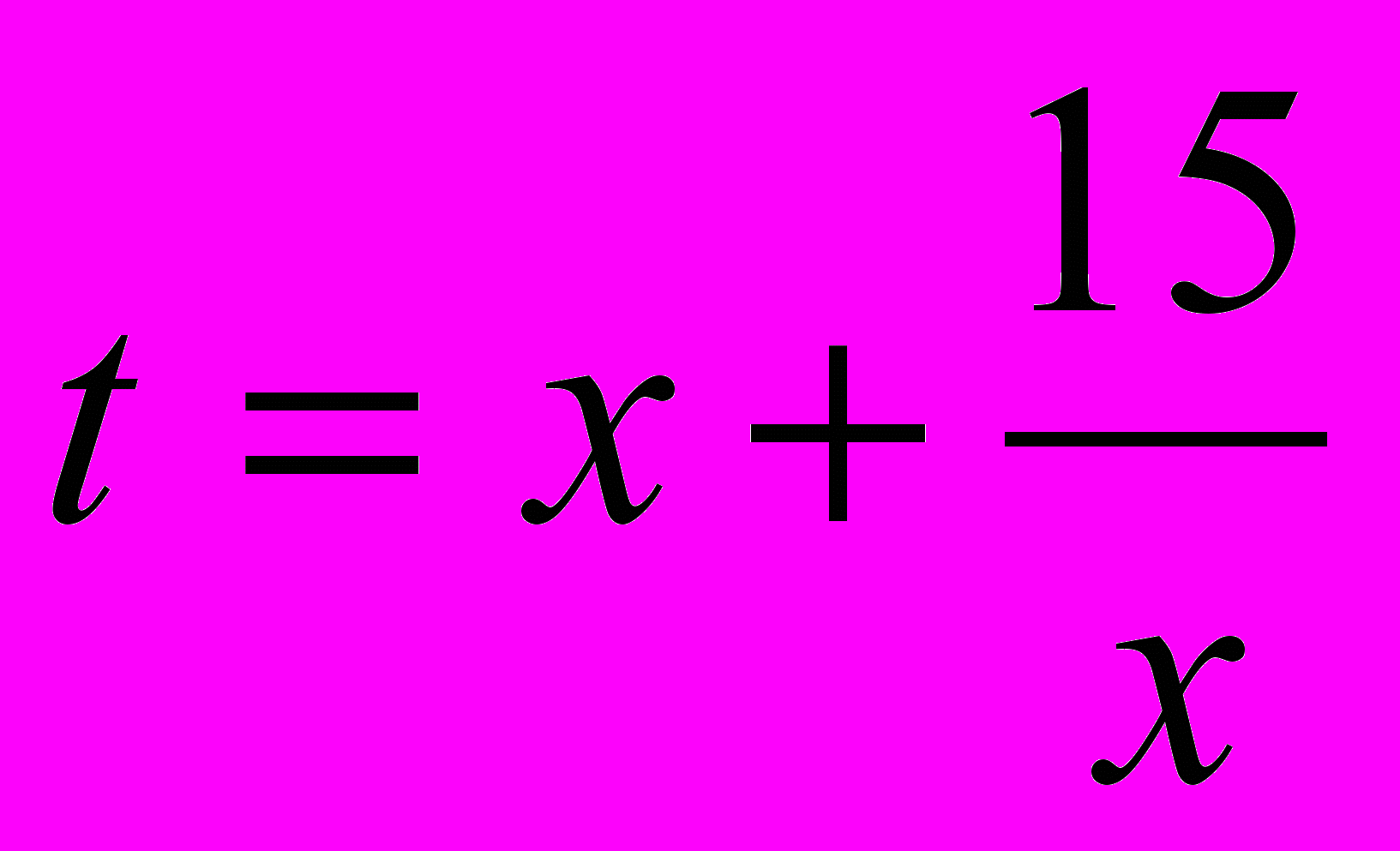 и получаем уравнение:
и получаем уравнение: 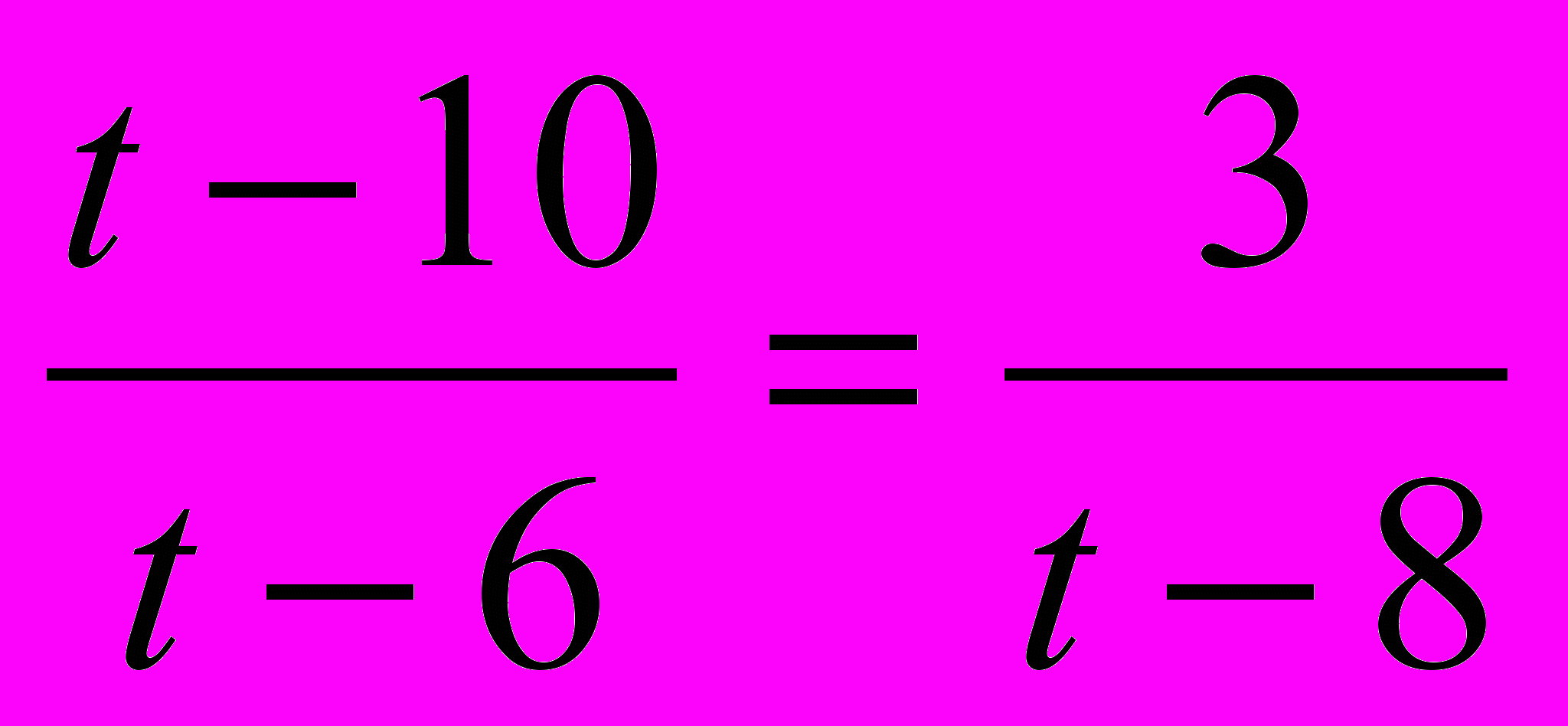
Откуда t=7 или t=14. Решая уравнения:
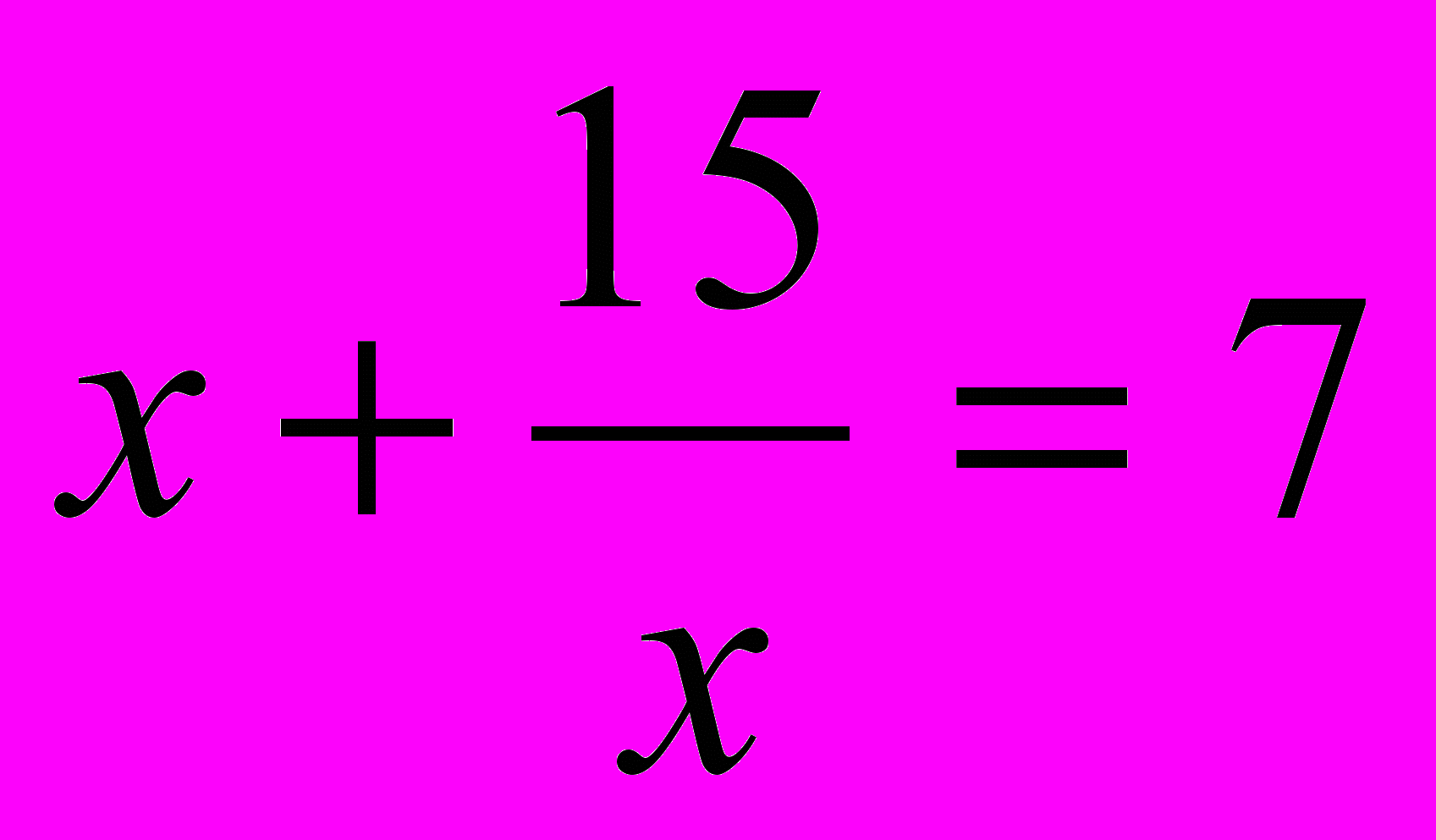 и
и 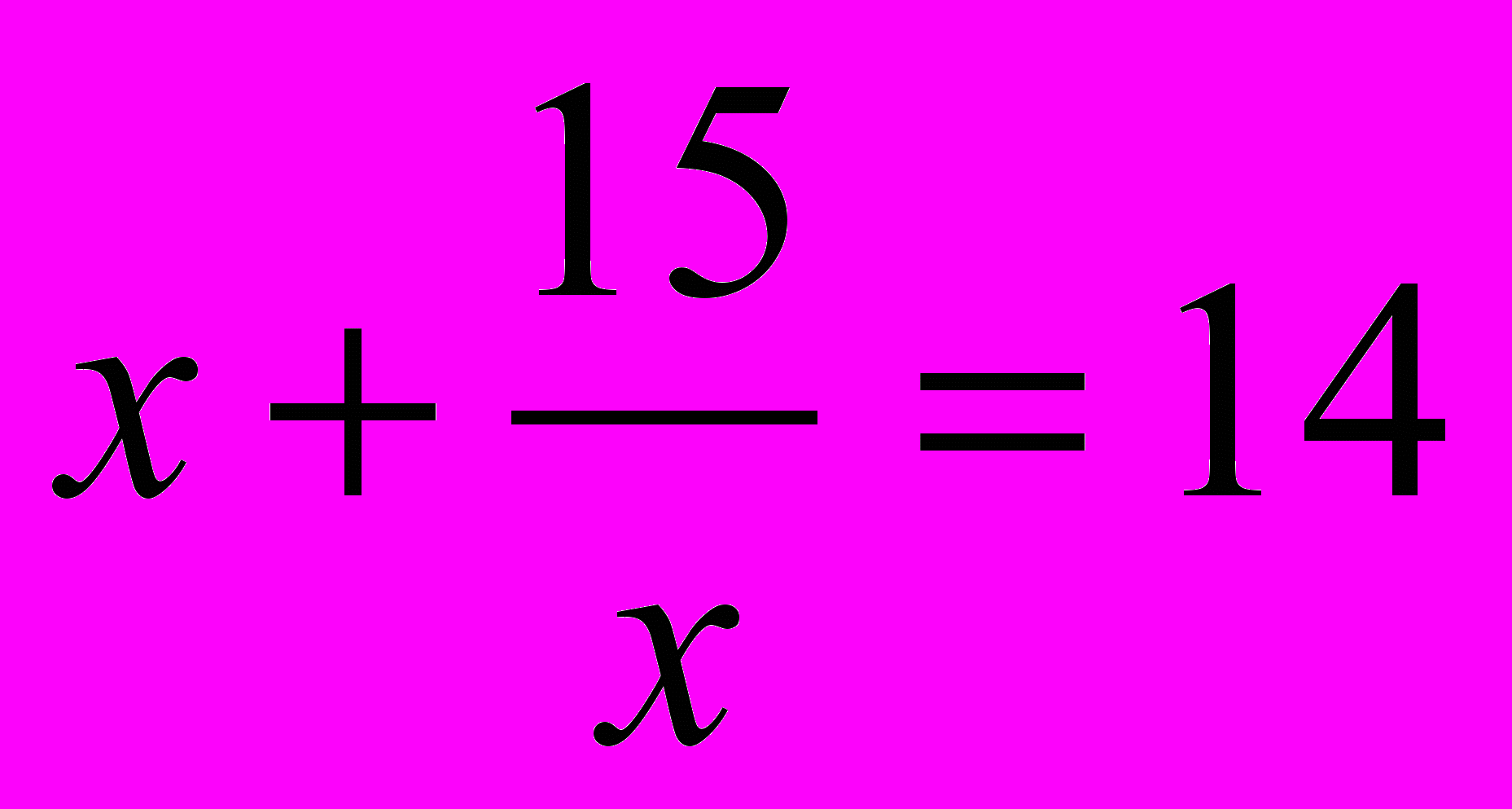 , получим корни уравнения:
, получим корни уравнения: 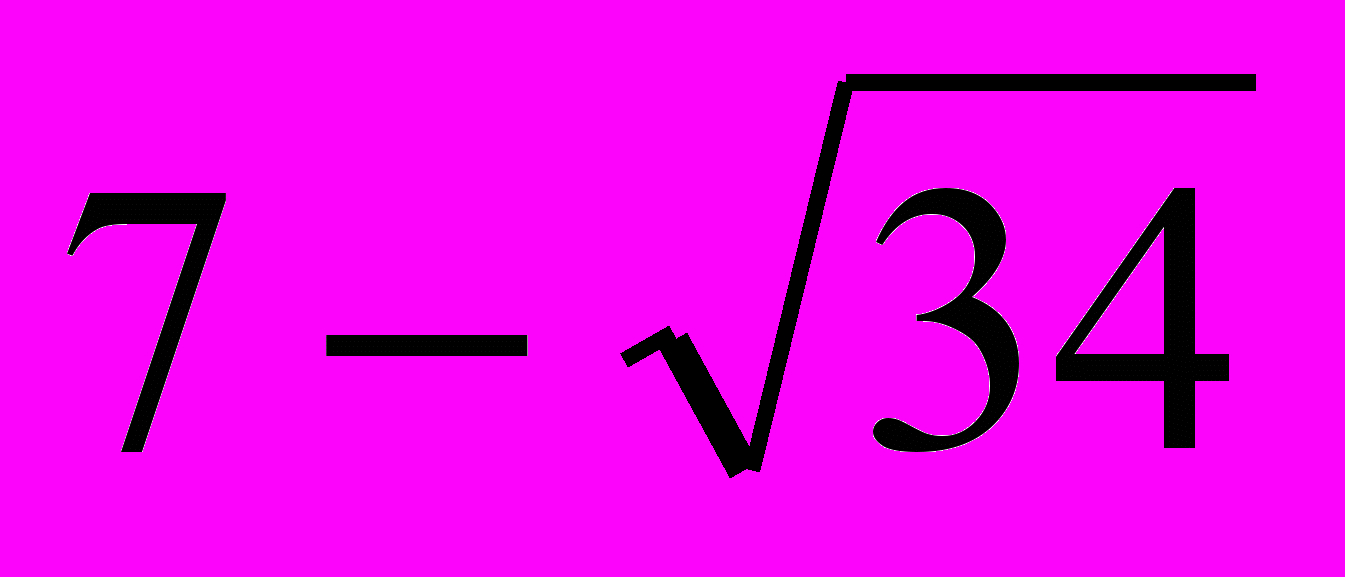 и
и 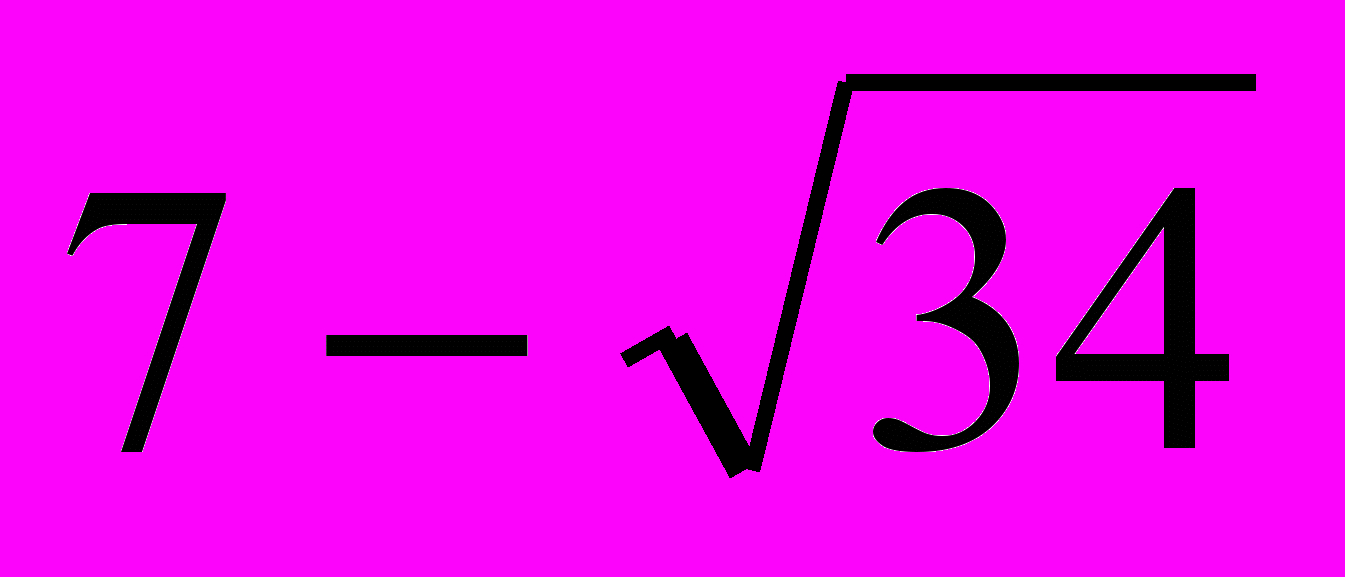 .
.Заметим, что если 0 является решением, то его следует записать в ответ.
3. Решение задач.
Решить уравнения:
а)
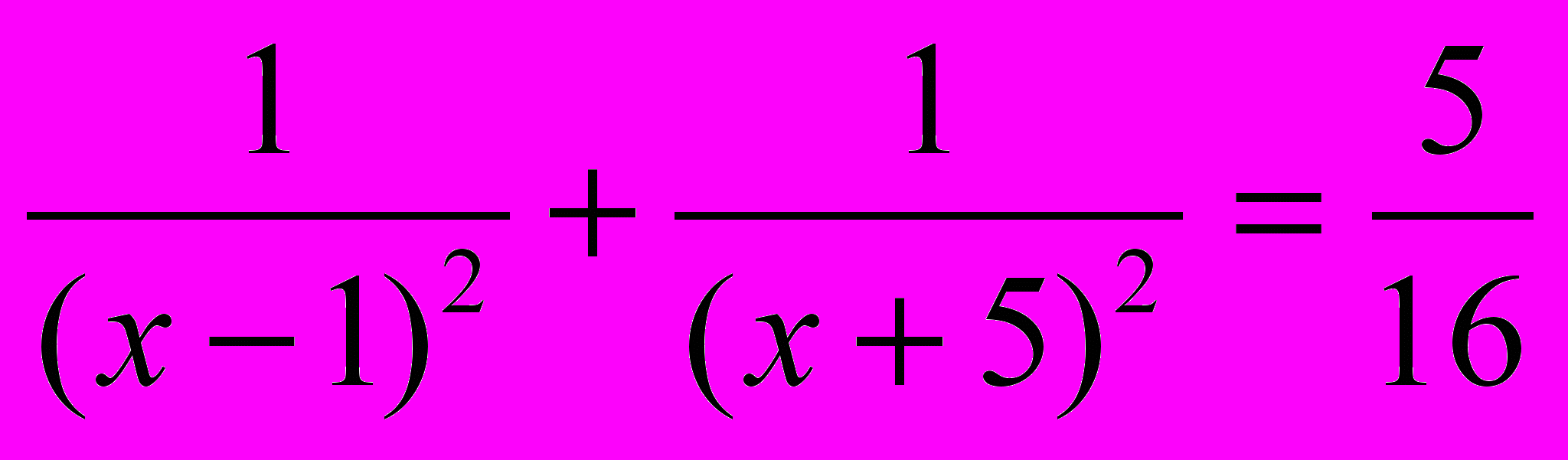 ;
;б)
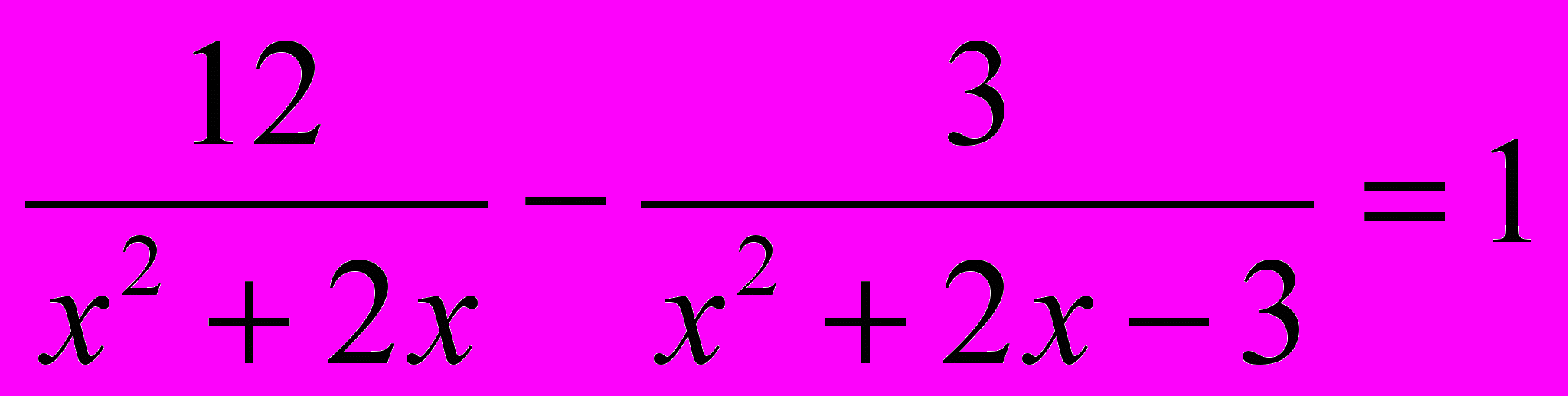 ;
;в)
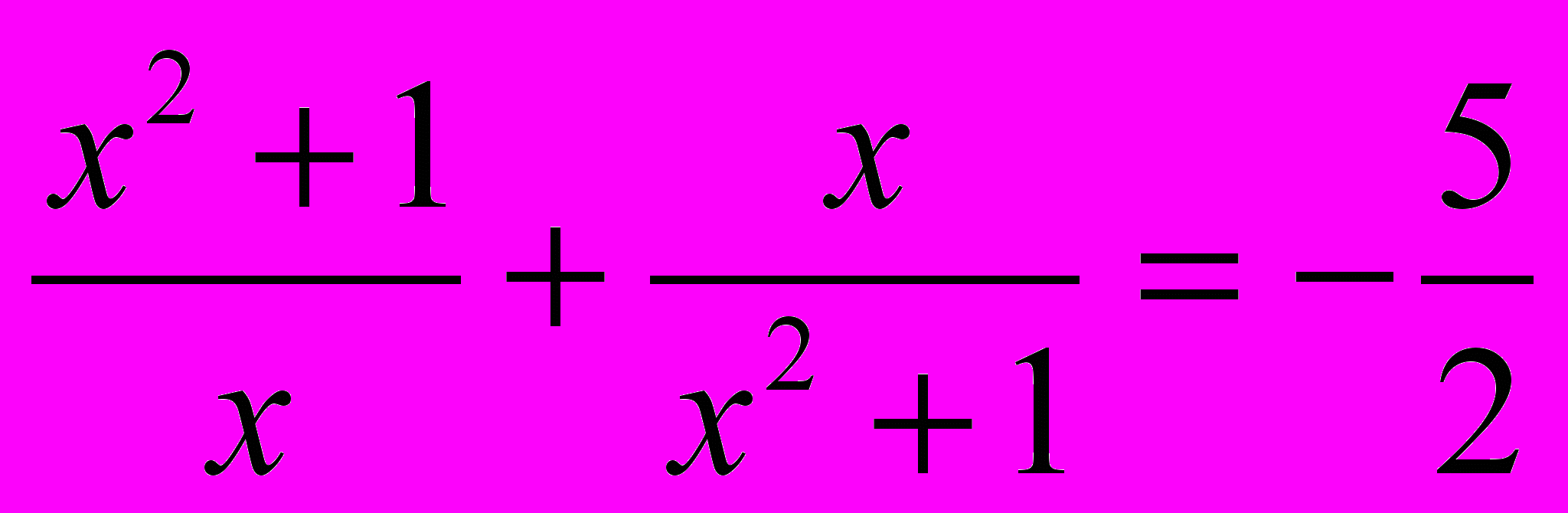 ;
;г)
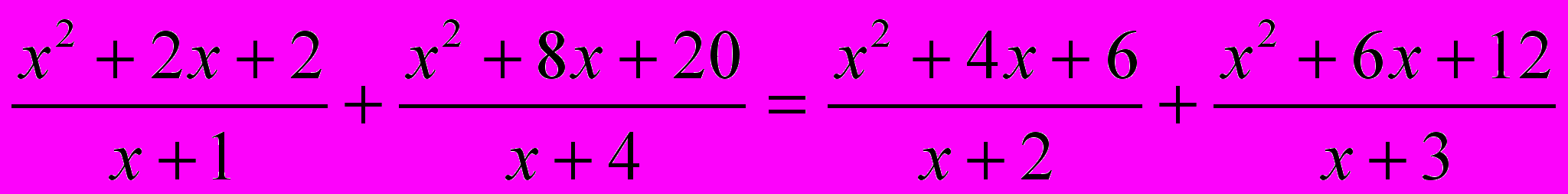 .
.4. Итоги урока. Какие методы можно применять при решении дробно-рациональных уравнений?
5. Домашнее задание
Решить уравнения:
а)
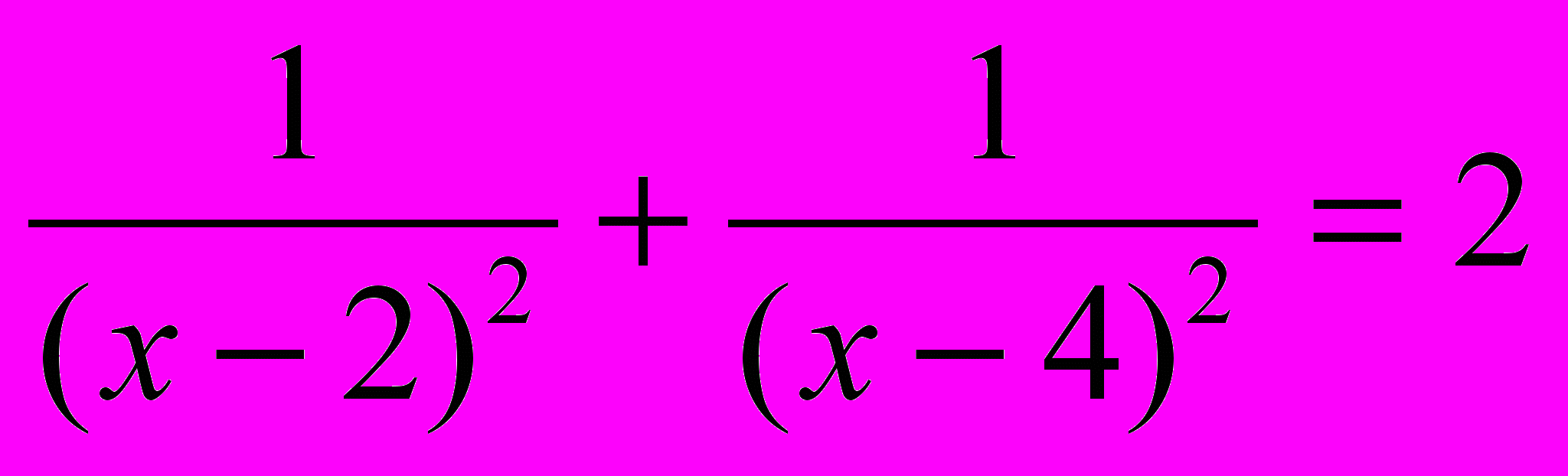
б)
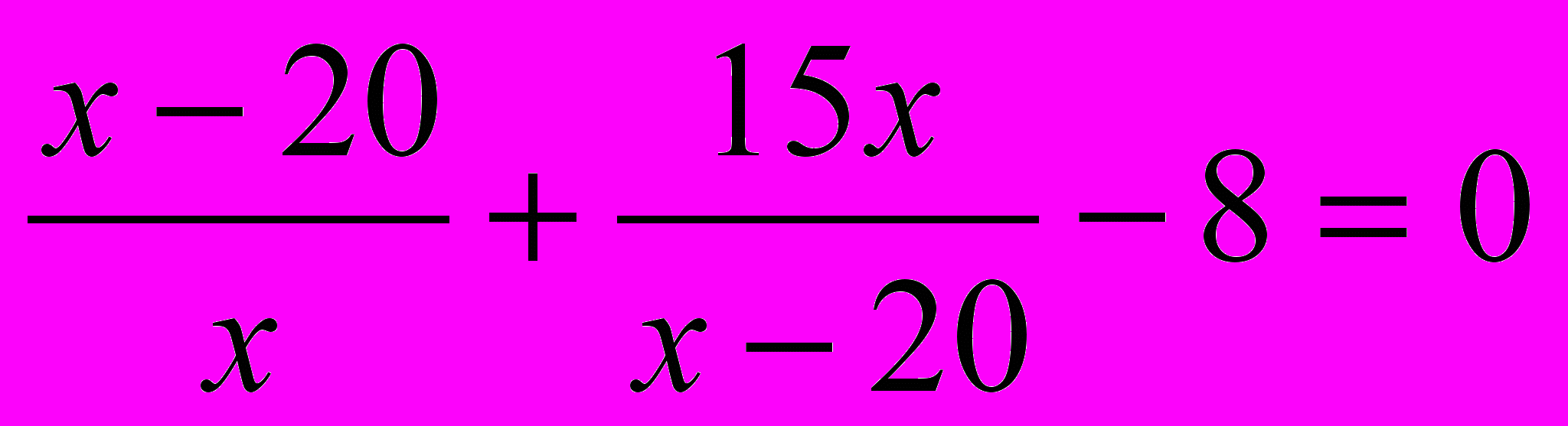
в)
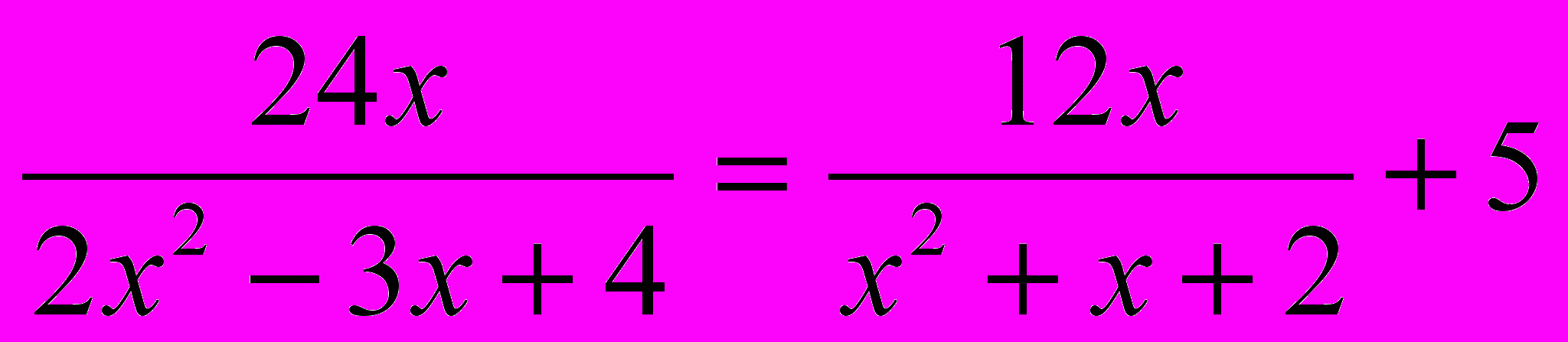
г)
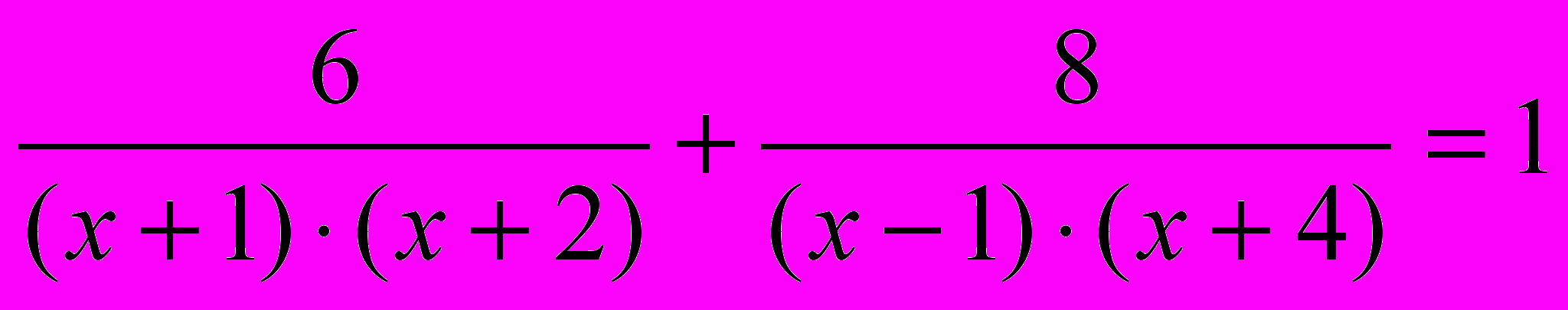
Творческое задание: решить уравнение:
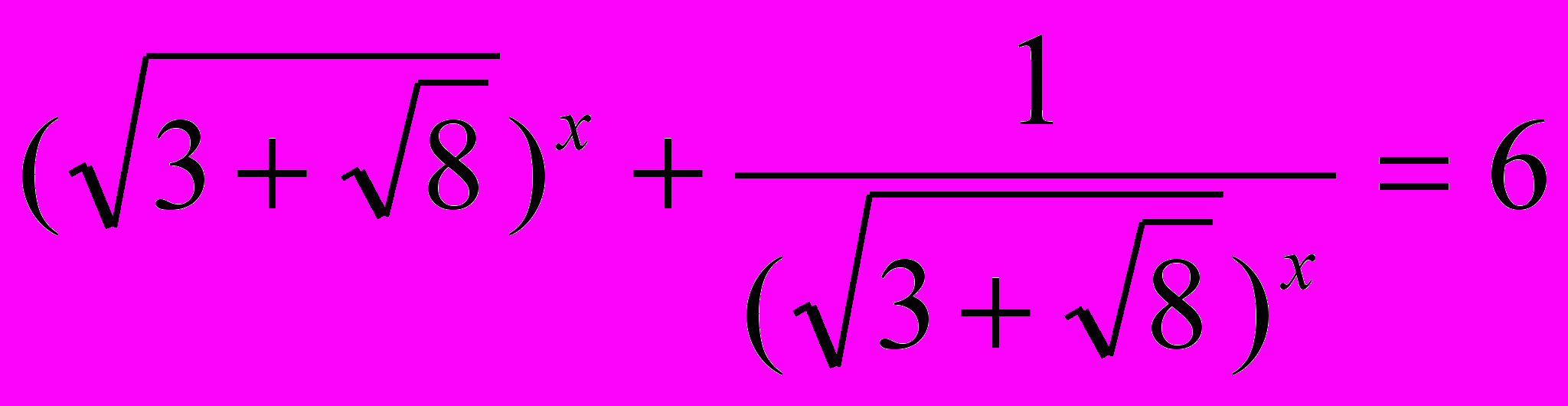
Самостоятельные работы
Самостоятельная работа 1
Вариант 1
1. Преобразовать в многочлен:
а) (2а2 – 3в)3,
б) (а + 2)6.
2. Разложить на множители:
а) 27х3 + 108х2 +144х + 64,
б) 64х6 – у6.
3. Разделить многочлен на многочлен:
а) (х3 + 8х2 + 11х – 20) : (х + 5),
в) (х3 + 2х2 – 7х – 14) : (х + 2),
с) (2х4 + 4х3 – 11х2 – 10х +15) : (2х2 – 5).
Вариант 2
1. Преобразовать в многочлен:
а) (3а4 + 2в)3,
б) (х – 4)5.
2. Разложить на множители:
а) 8х3 – 60х2 +150х – 125,
б) 243х5 – у5.
3. Разделить многочлен на многочлен:
а) (х3 - 7х2 + 14х – 8) : (х – 2),
в) (х3 + 4х2 – 5х – 20) : (х + 4),
с) (2х4 + 6х3 – 9х2 – 21х +7) : (2х2 – 7).
Самостоятельная работа 2
Вариант 1
1. Сократить дробь:
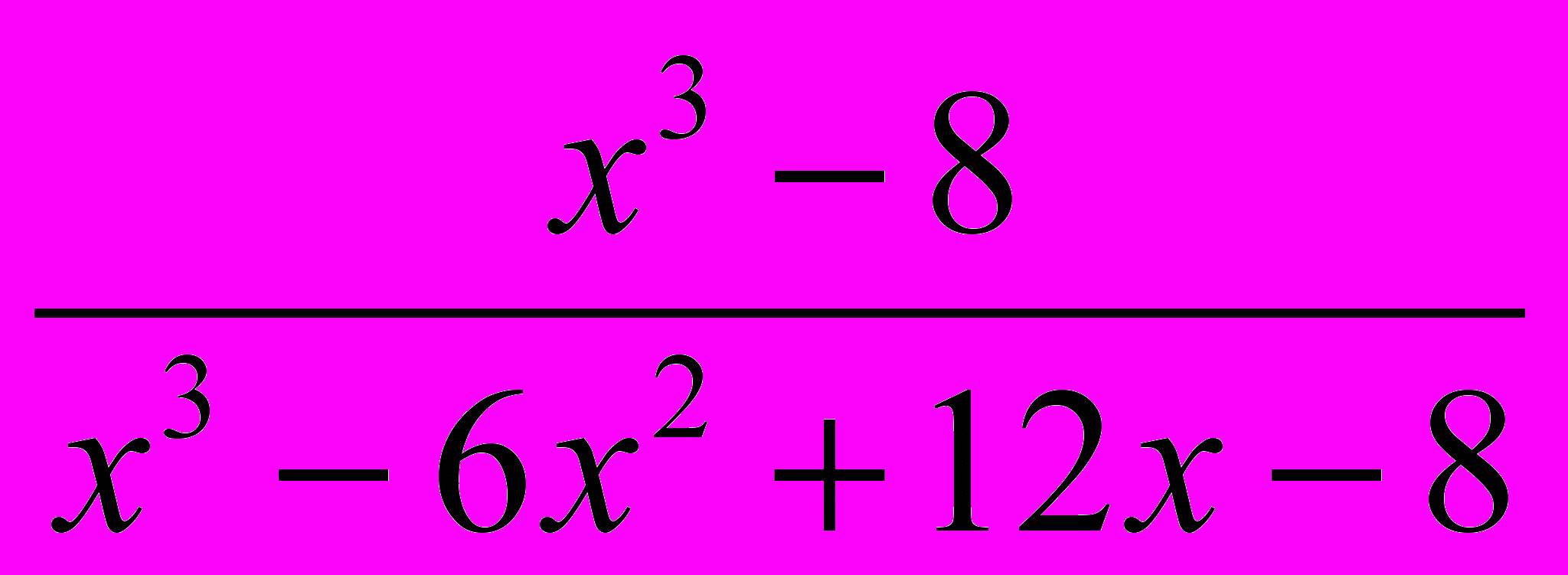 .
.2. Выделить целую часть: а)
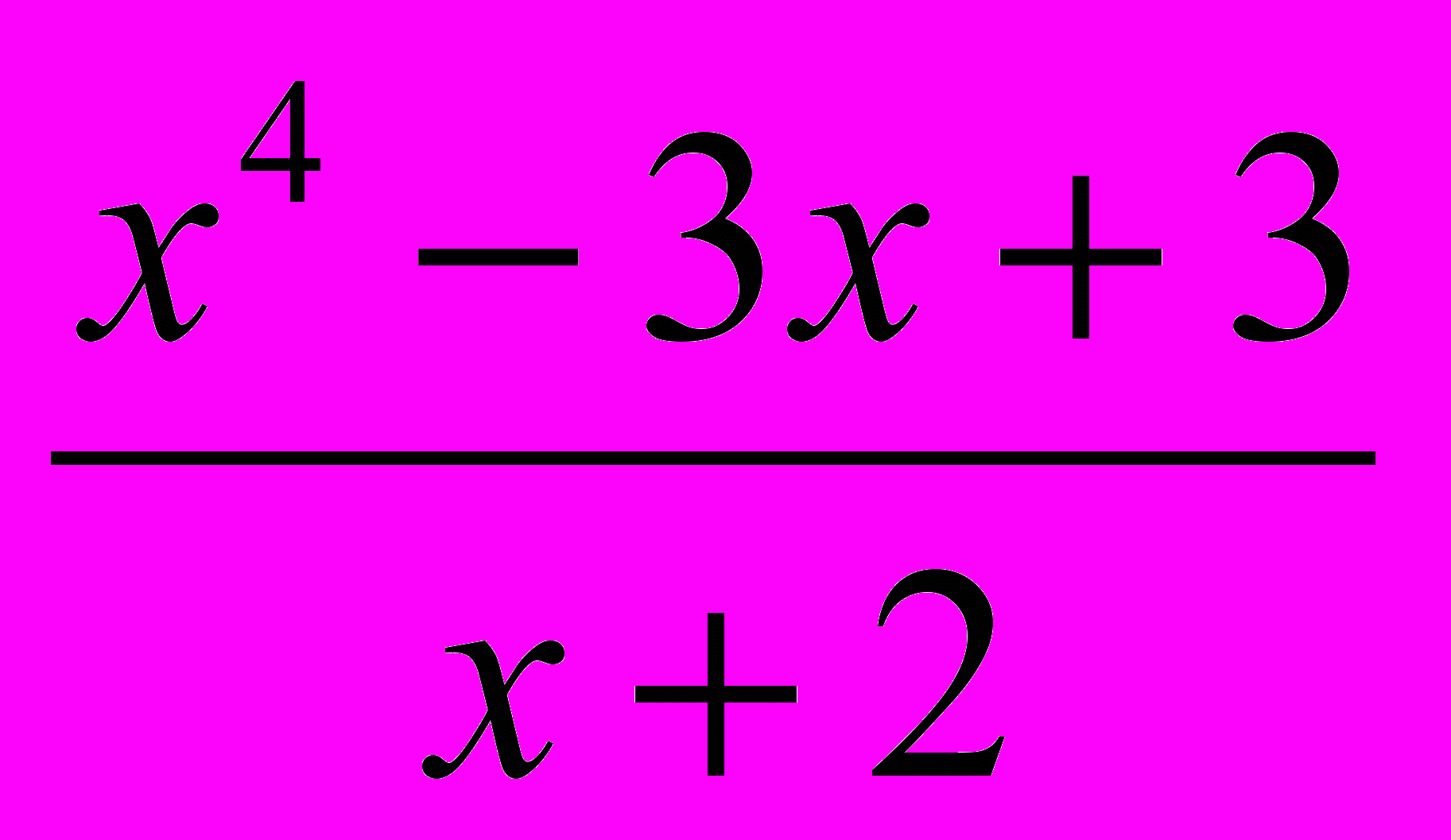 ; в)
; в) 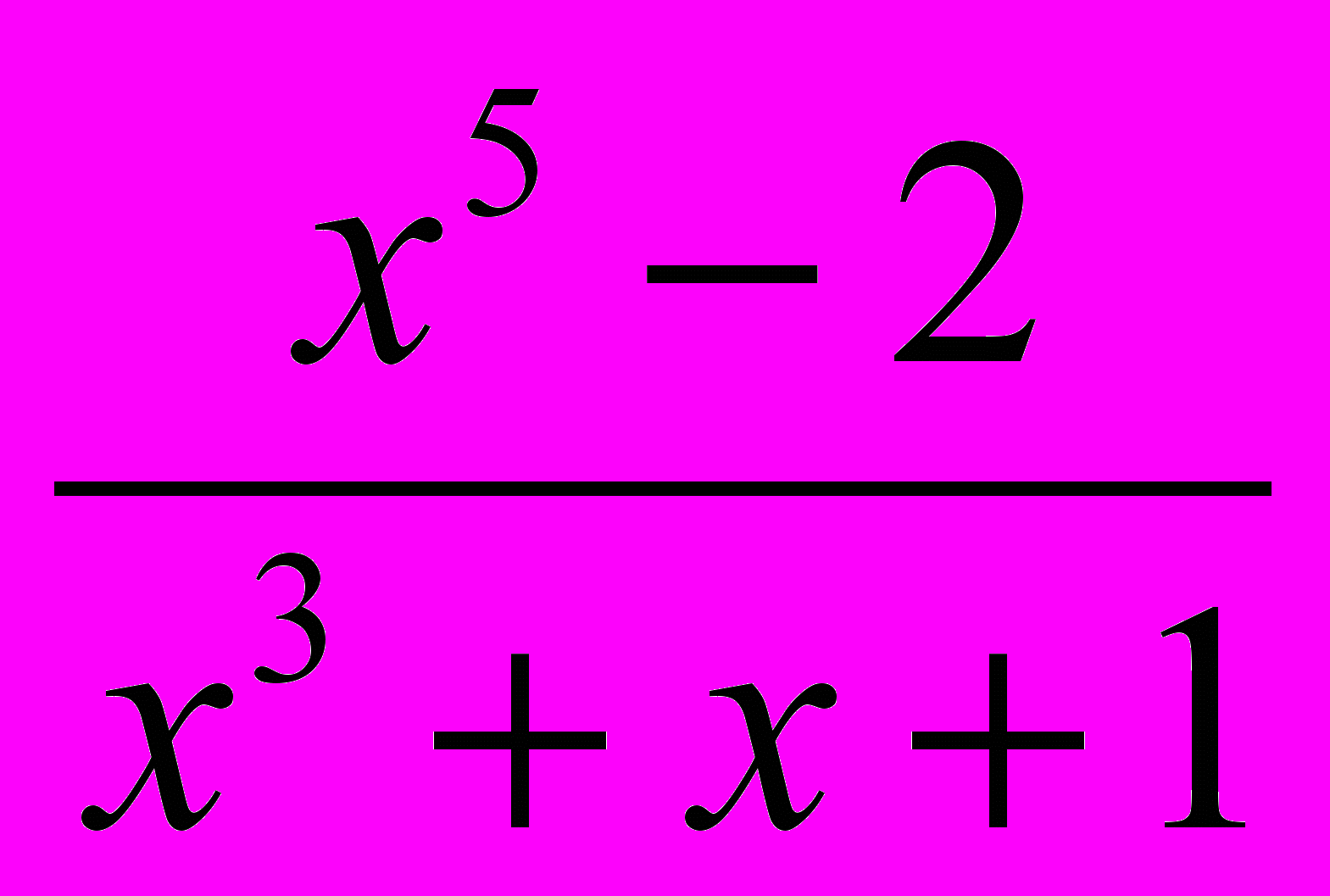 .
.3. Решить уравнения с помощью теоремы Безу:
а) х3 – 6х2 + 11х – 6 = 0,
в) х3 – 5х2 – 2х + 24 = 0,
с) х4 + 3х3 – 13х2 – 17х + 26 = 0.
Вариант 2
х3 + 9х2 + 27х + 27
1. Сократить дробь: х3 + 27 .
х4 + 5х – 2 х5 + 4
2. Выделить целую часть: а) х – 3 ; в) х3 – 2х + 1 .
3. Решить уравнения с помощью теоремы Безу:
а) х3 – 7х2 + 14х – 8 = 0,
в) х3 – х2 – 14 х + 24 = 0,
с) х4 + 4х3 – 9х2 – 16х + 20 = 0.
Самостоятельная работа 3
Вариант 1
1. Решить уравнения:
а)
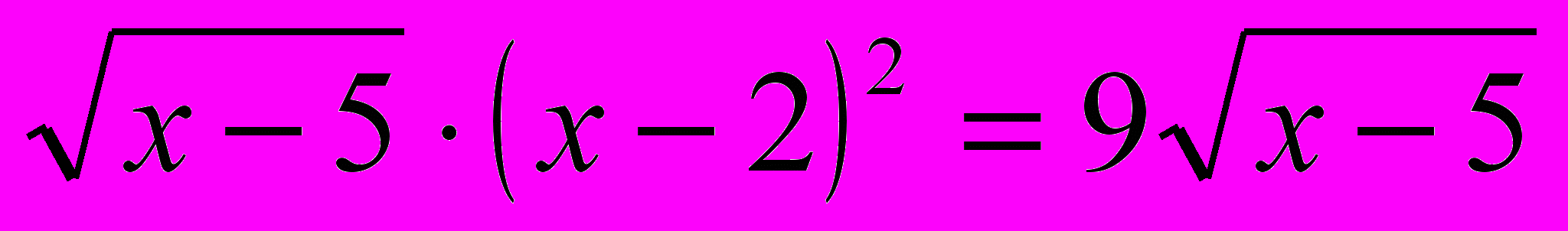 ,
,б)
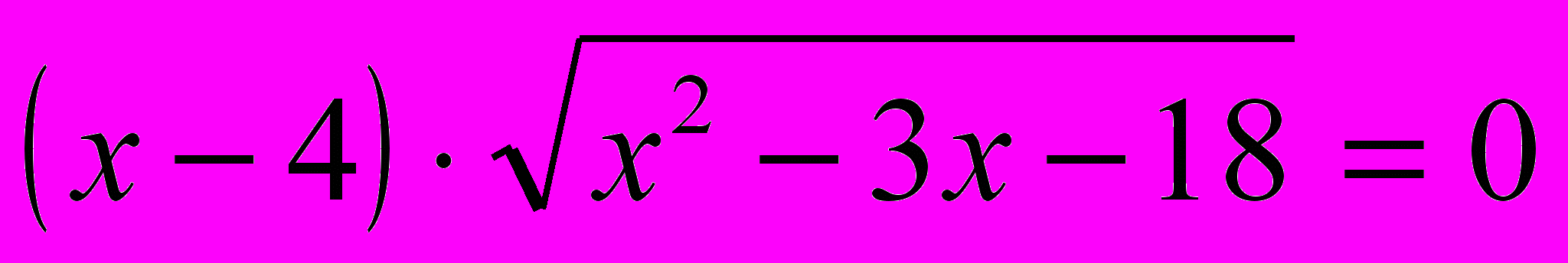 ,
,в)
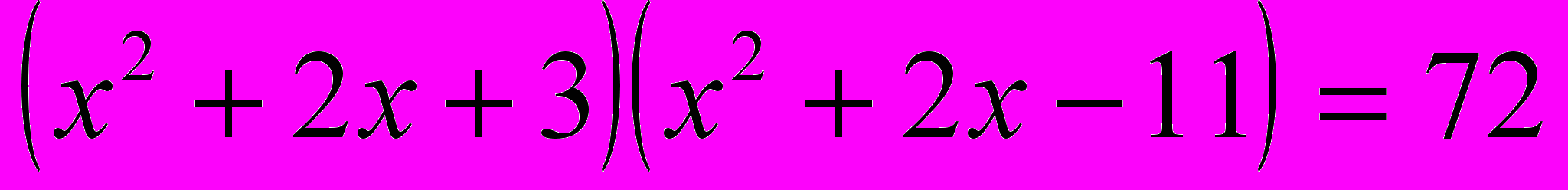 .
.г) (х +2) (х + 4) (х + 6) (х + 8) = –15,
д)
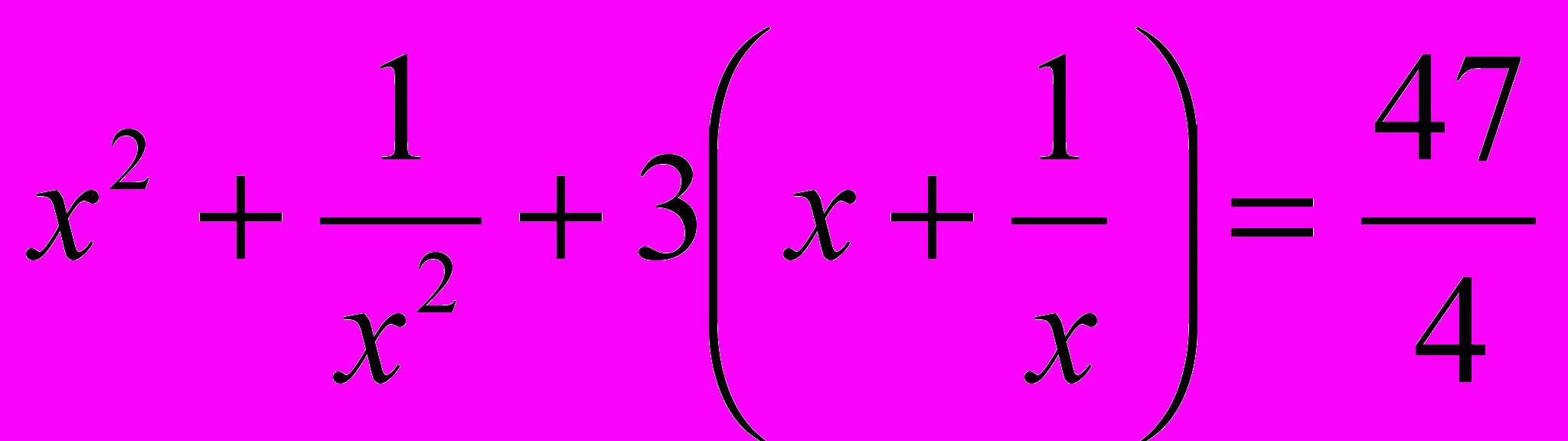 .
.Вариант 2
1. Решить уравнения:
а)
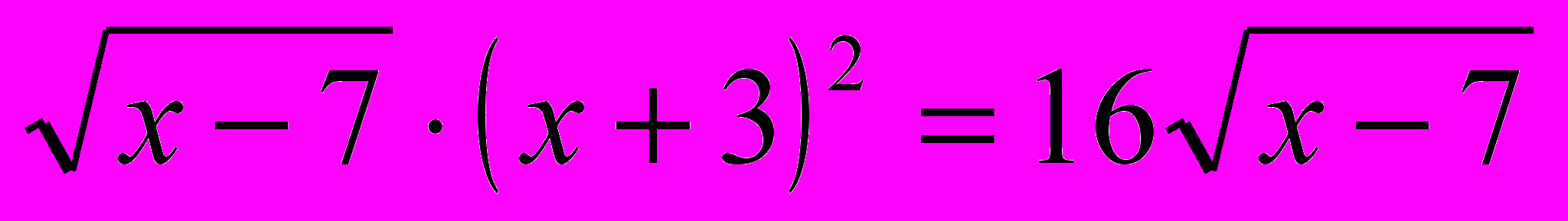 ,
,б)
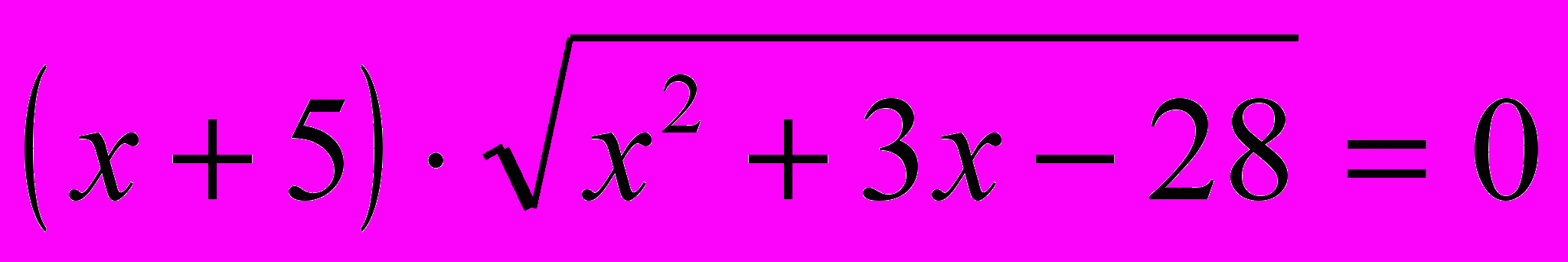 .
.в) (х2 +3х – 4) (х2 +3х –7 ) = 18,
г) (х – 2) (х – 4) (х – 6) (х – 8) = –15,
д)
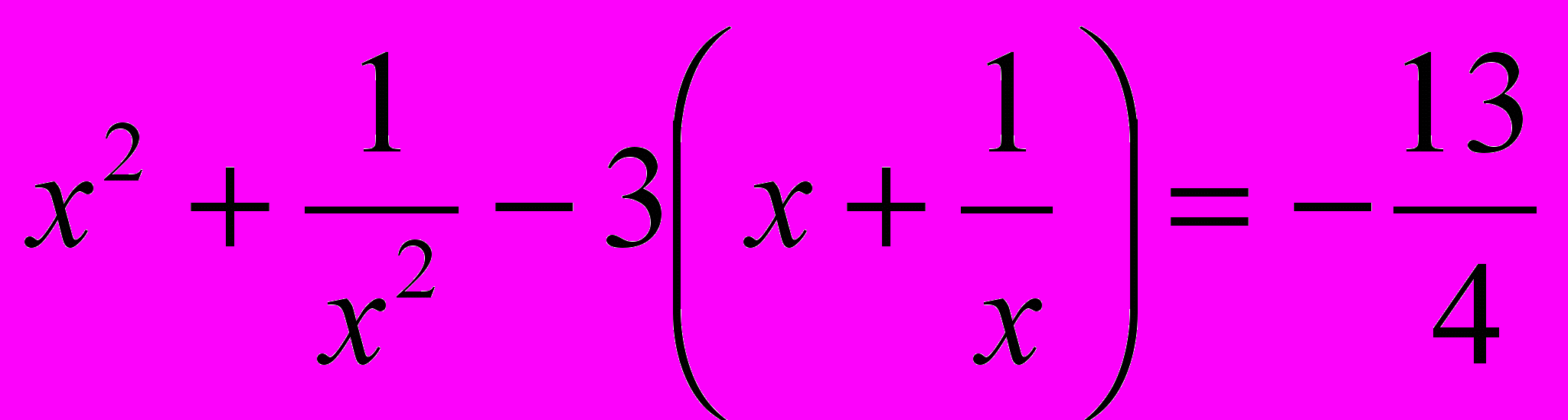 .
.Самостоятельная работа № 4
Вариант 1
- Решить возвратные уравнения:
- 4х3 – 5х2 – 5х + 4 = 0,
- 3х4 + 5х3 –
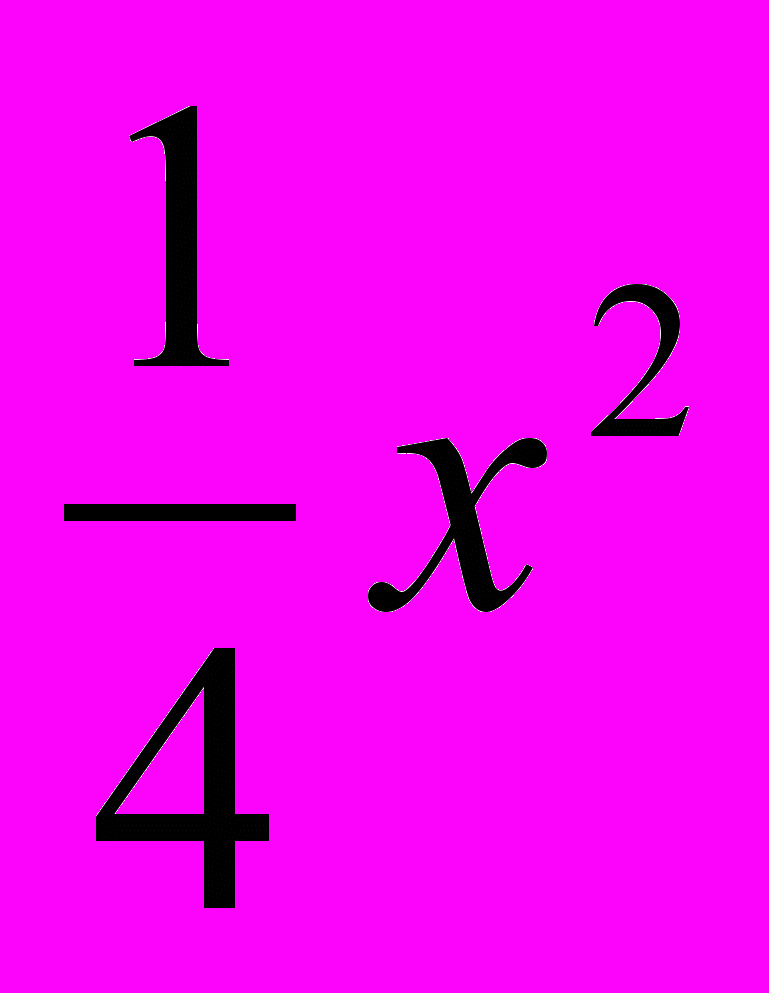 + 5х + 3 = 0.
+ 5х + 3 = 0.
- 4х3 – 5х2 – 5х + 4 = 0,
- Решить однородные уравнения:
- 3(х2 – 5)2 + 4(х2 – 5) (х + 7) – 7 (х + 7)2 = 0,
- (х – 2)4 + 5(х + 2)4 = 6(х2 – 4)2.
- 3(х2 – 5)2 + 4(х2 – 5) (х + 7) – 7 (х + 7)2 = 0,
Вариант 2
- Решить возвратные уравнения:
- 5х3 – 4х2 – 4х + 5 = 0,
- 2х4 – 5х3 + 4х2 – 5х + 2 = 0.
- 5х3 – 4х2 – 4х + 5 = 0,
- Решить однородные уравнения:
- 3(х2 + 5)2 + 4(х2 + 5) (х – 7) – 7 (х – 7)2 = 0,
- (х-3)4 + 4(х + 3)4 = 5(х2 – 9)2.
Самостоятельная работа № 5
Вариант 1
- Решить дробно-рациональные уравнения:
а)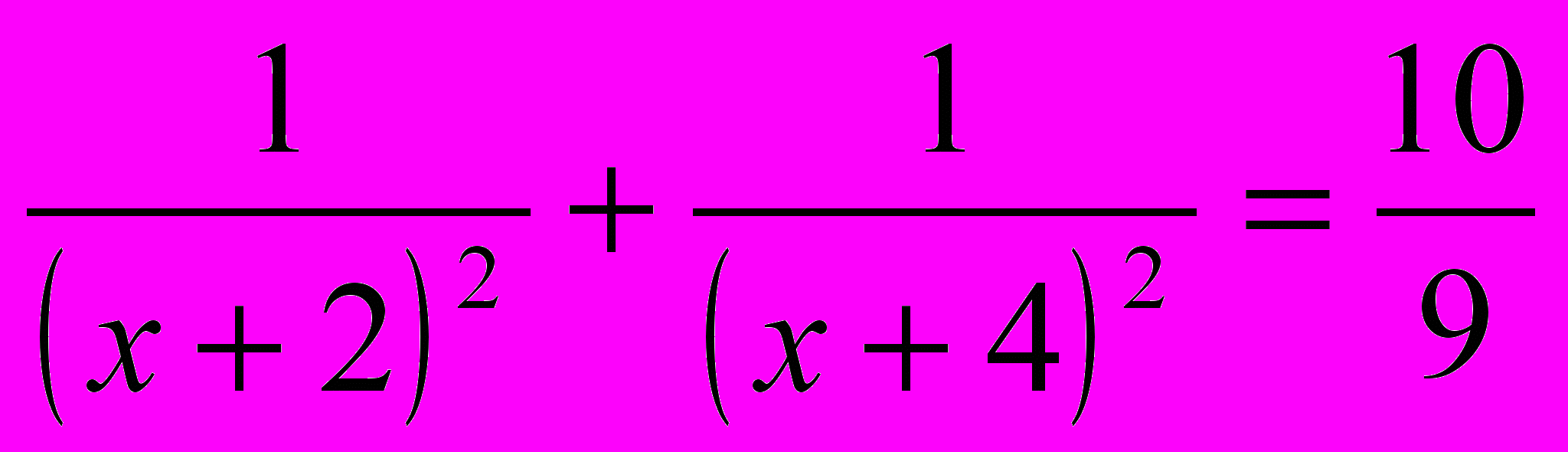 ,
,
б)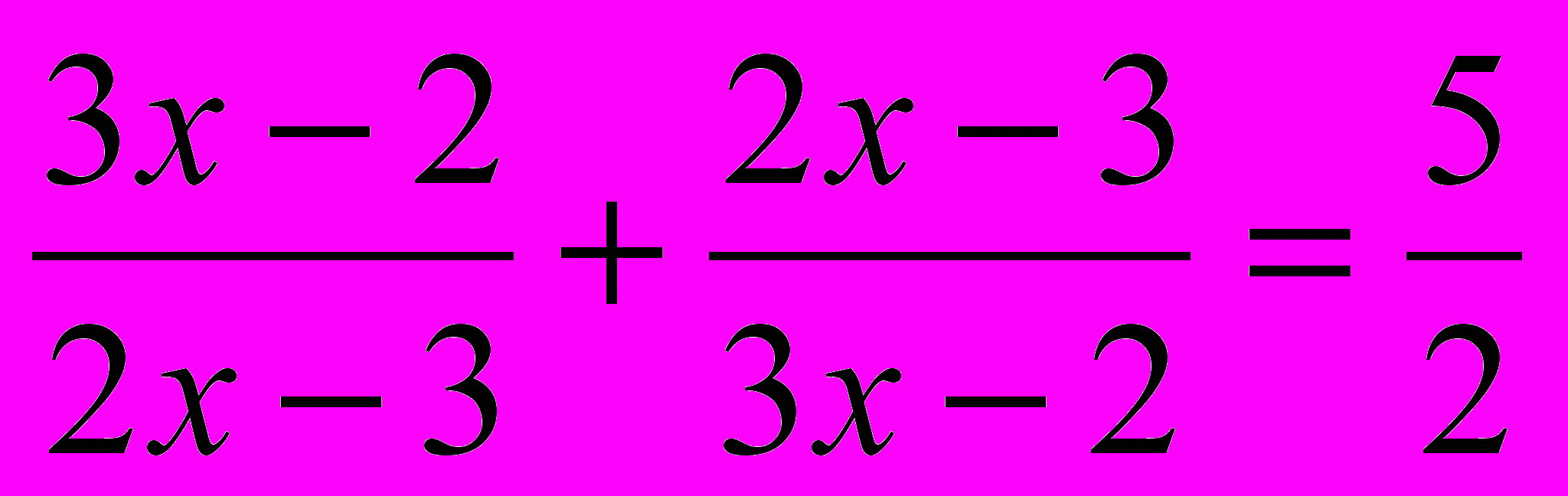 .
.
- Решить уравнения:
- |х - 5| + |х + 2| = 7,
- |2х – 3| + |2х – 5| = 2,
- 5|х|2 – 3|х| = 2.
- |х - 5| + |х + 2| = 7,
Вариант 2
- Решить дробно-рациональные уравнения:
а)
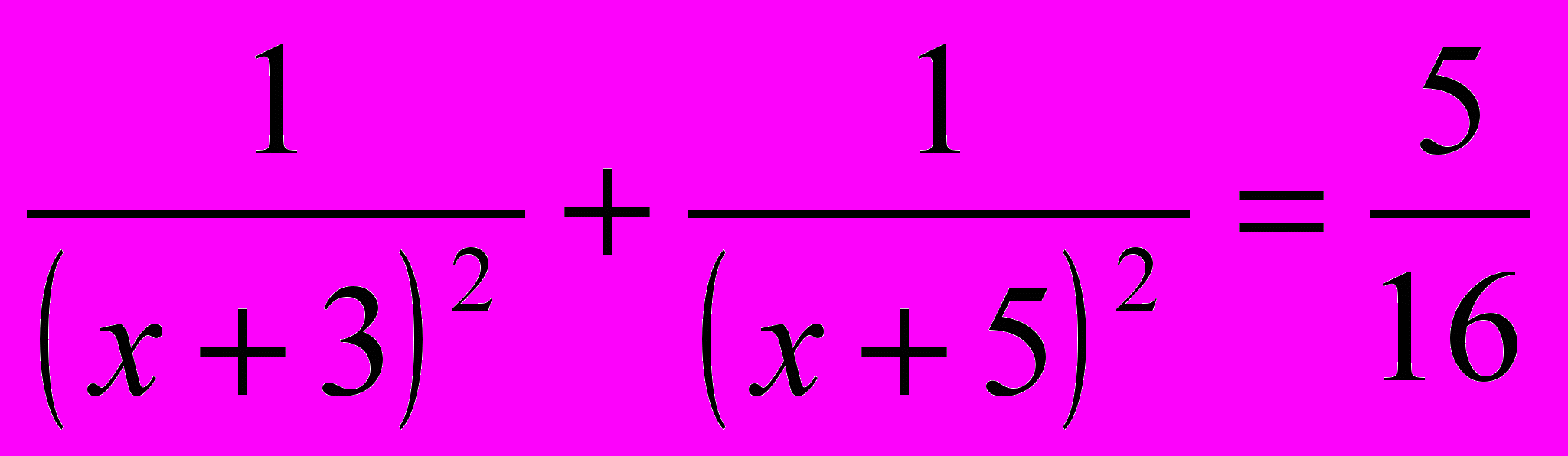 ,
,б)
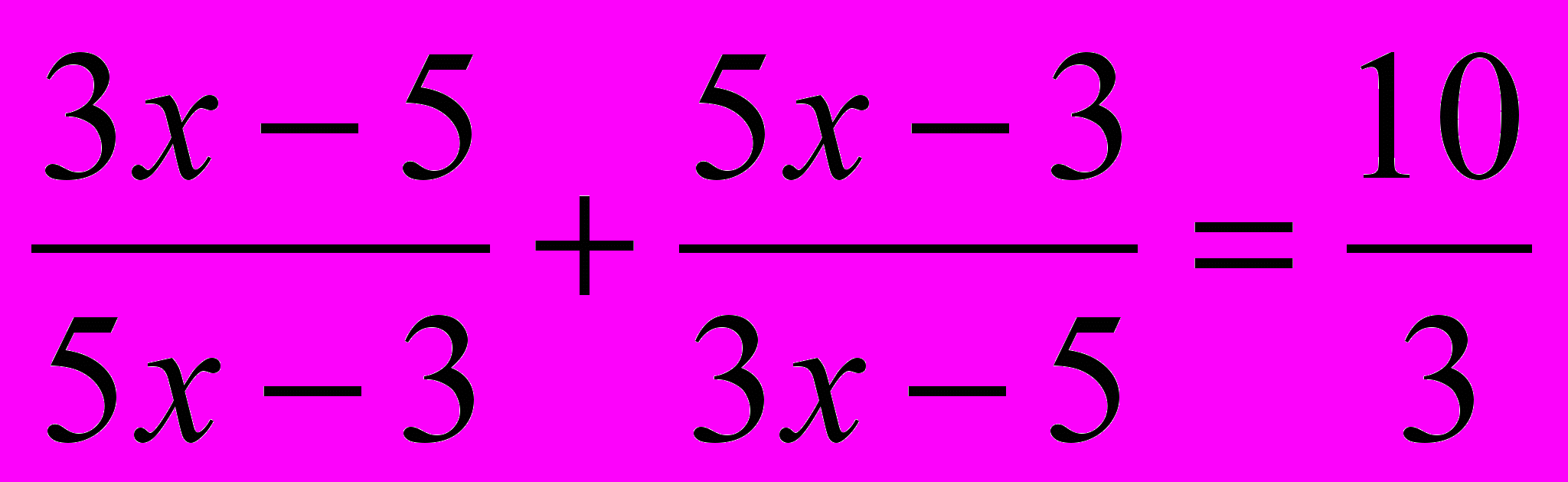 .
.- Решить уравнения:
- |х + 4| + |х - 7| = 11,
- |2х + 3| + |2х – 5| = 8,
- 7|х|2 – 4|х| = 3.
- |х + 4| + |х - 7| = 11,
Самостоятельная работа № 6
Вариант 1
- Решить уравнения:
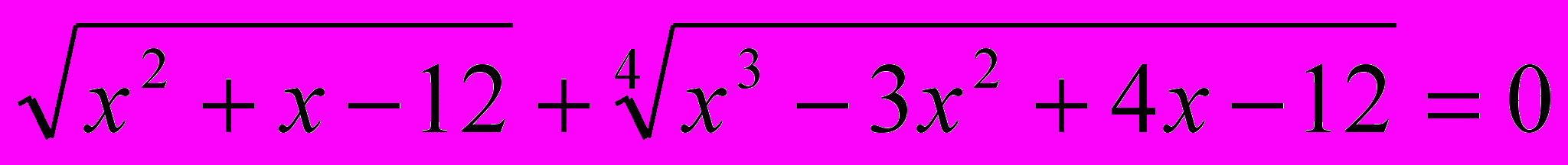 ,
,
- sin 2x – 3cos 4x = 4,
- sin x = х2 + 4х + 5.
- Найти значения а, при которых уравнение
3sin x – 7 cos x = a
имеет корни.
Вариант 2
- Решить уравнения:
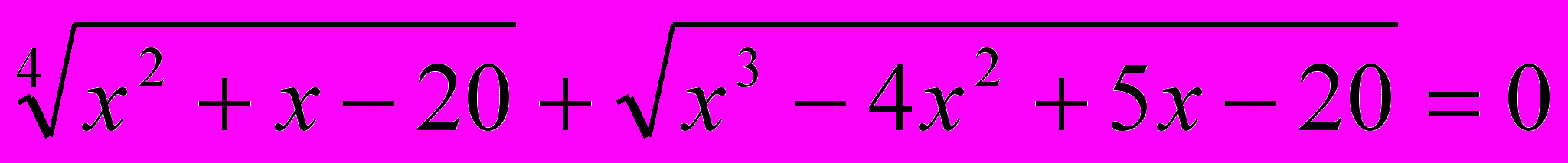 .
.
- sin 2x – 4 cos 4x = 5,
- cos x = х2 + 6х + 10.
- Найти значения а, при которых уравнение
4 sin x – 5 cos x = a
имеет корни.
Самостоятельная работа № 7
Вариант 1
- Решить систему уравнений:
а
 ) х2 + ху + у2 = 37,
) х2 + ху + у2 = 37,х + у = 7;
б
 ) 5х2 – 7ху + 2 у2 = 0,
) 5х2 – 7ху + 2 у2 = 0,3х2 + у2 = 4;
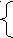
в) х2 + у2 + 3ху = 31,
ху = 6.
Вариант 2
- Решить систему уравнений:
а
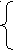 ) х2 - ху + у2 = 21,
) х2 - ху + у2 = 21,х + у = 9;
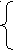
б) 4х2 – 9ху + 5у2 = 0,
5х2 + 2у2 = 7;
в
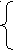 ) х2 + у2 + 5ху = 60,
) х2 + у2 + 5ху = 60,ху = 8. .
Самостоятельная работа 8
Вариант 1
Решить систему уравнений:
а
 )
) 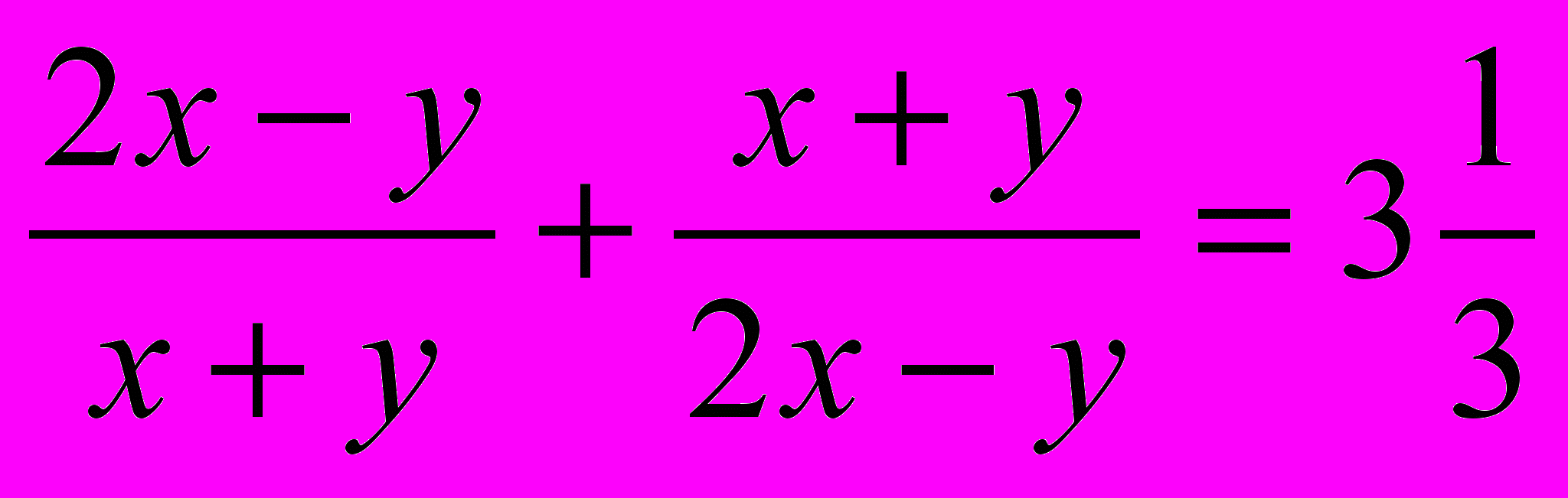 ,
,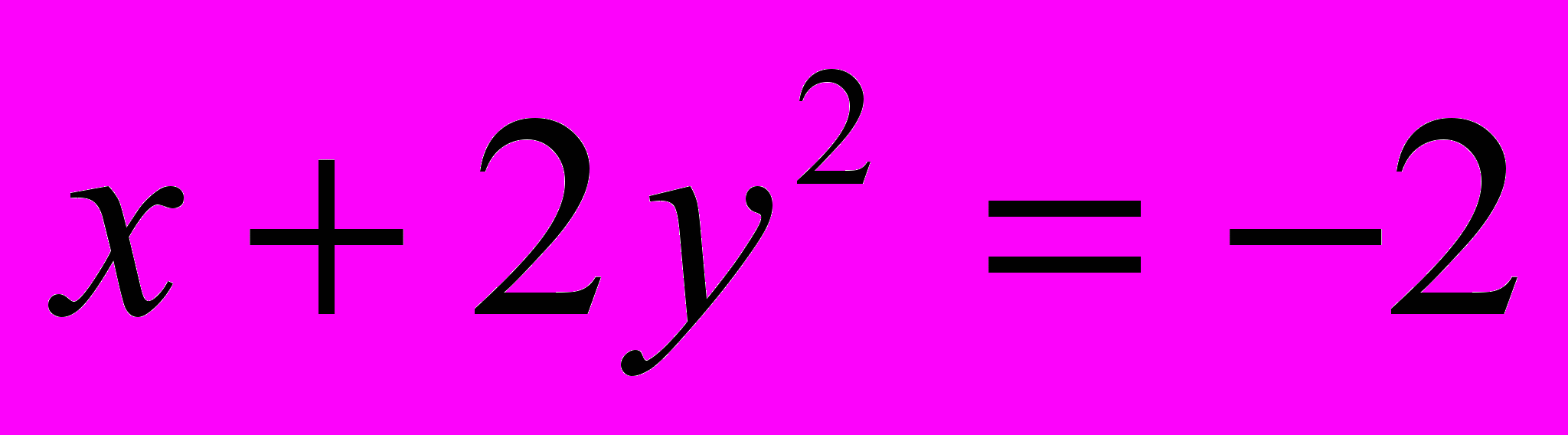 ;
; x + y + 3z = 1,
x + y + 3z = 1,б) 2x – y + 2z = 5,
–x + 2y – 5z = –4;
в) ах +2у = 6,
3ах - у = 2.
Вариант 2
Решить систему уравнений:
а
 )
) 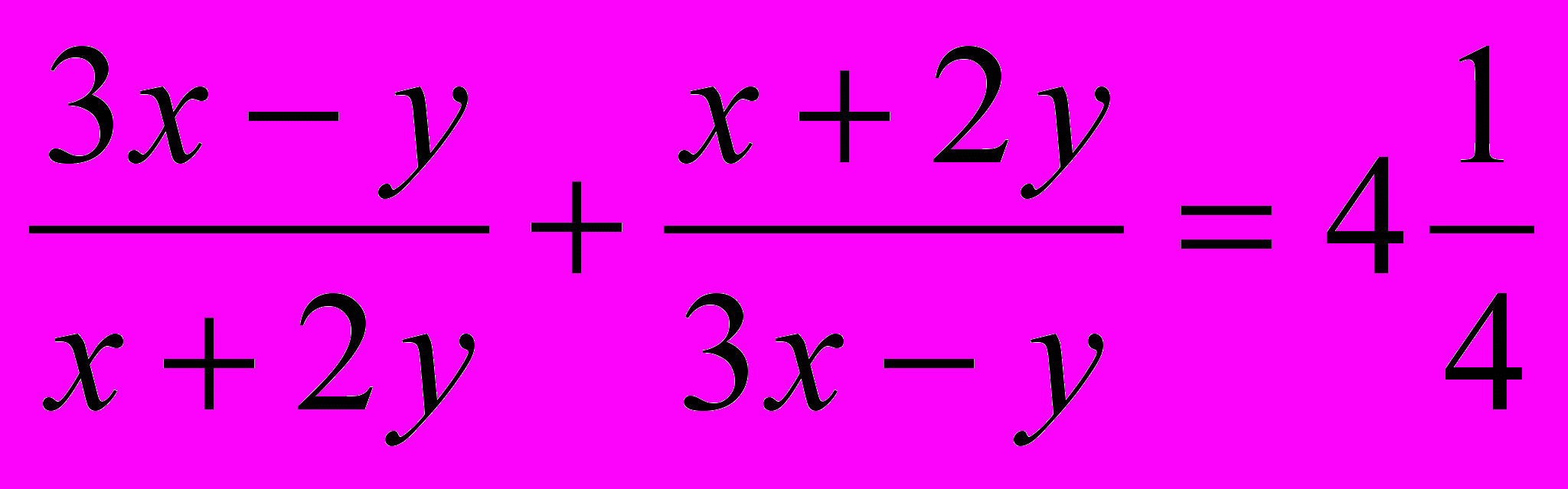 ,
,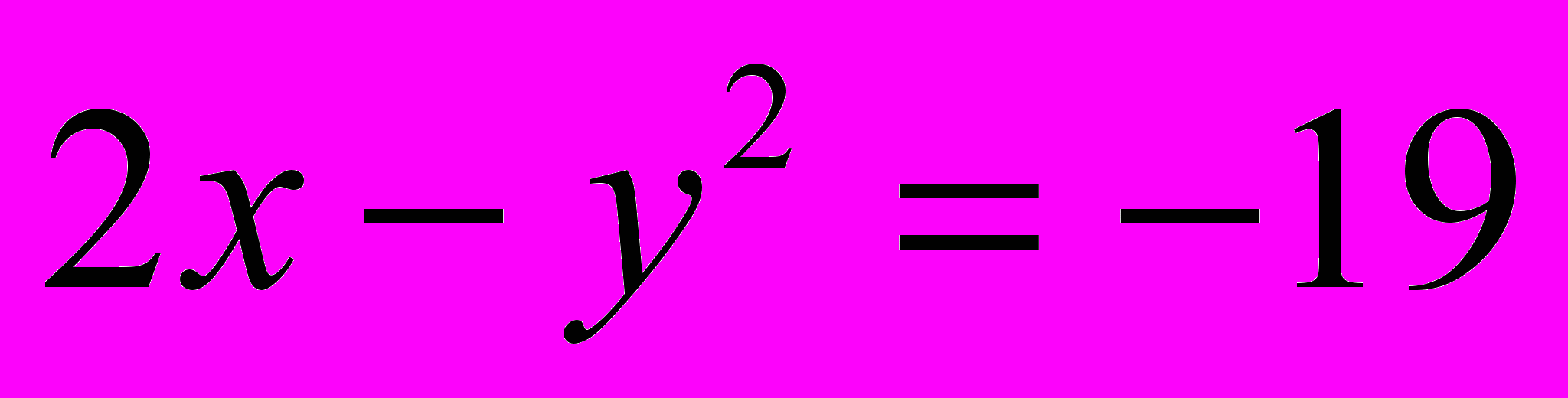 ;
; x + 2y – 4z = –1,
x + 2y – 4z = –1,б) 2x – y + 3z = 9,
–x + 4y – 2z = –5;
в
 ) х – 3ау = 4,
) х – 3ау = 4,3х + ау = 7.
Самостоятельная работа 9
Вариант 1
1. Решить неравенства:
а)
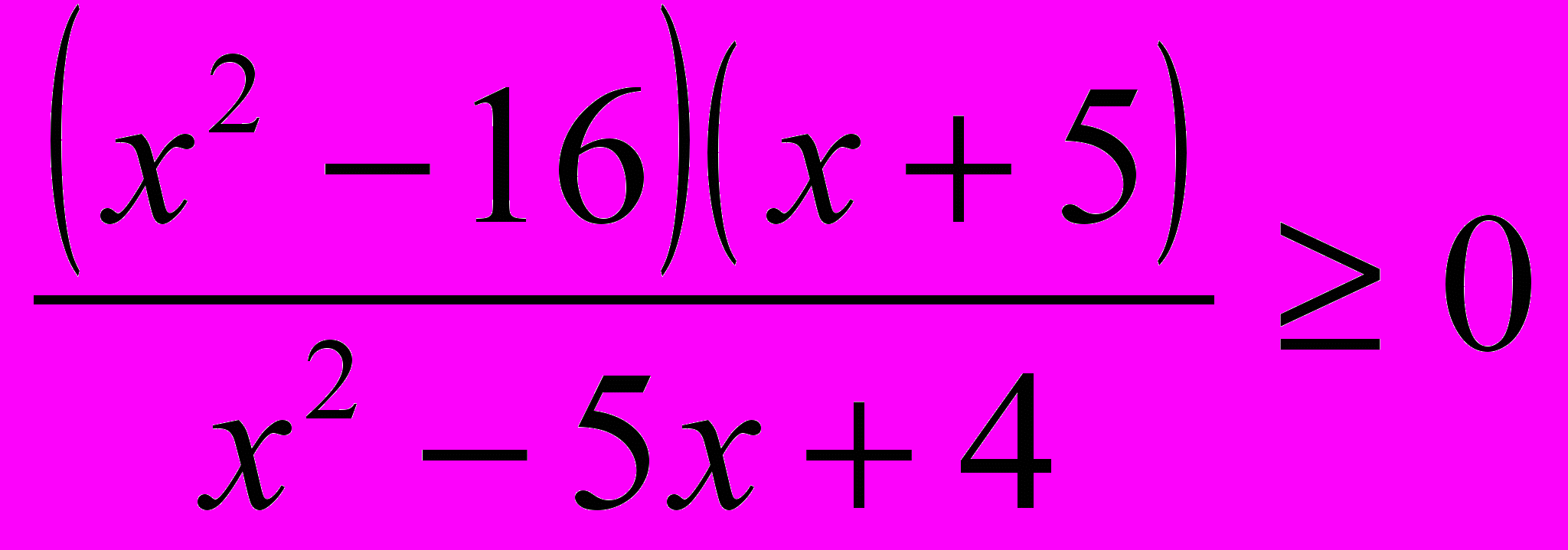 ,
,б)
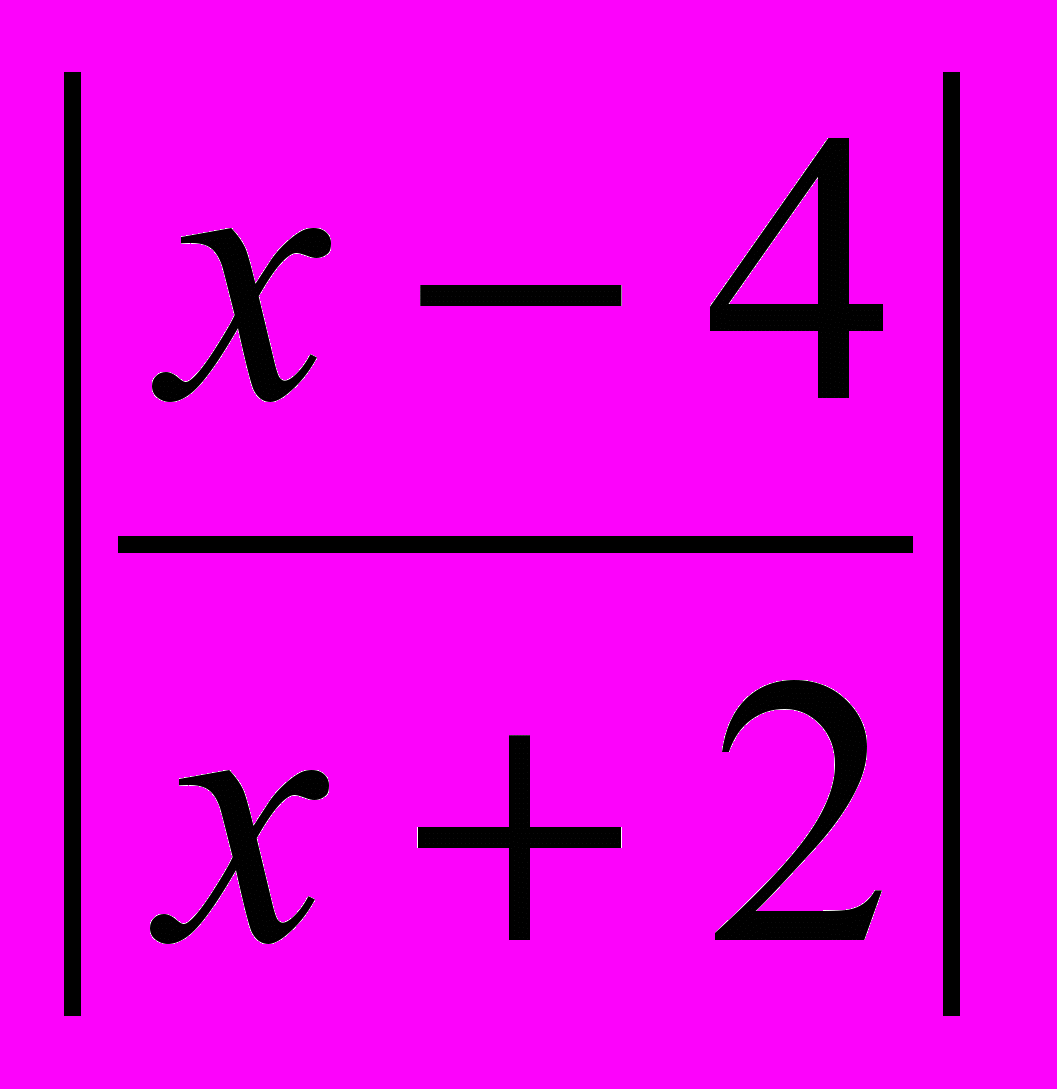 5.
5.2. Изобразить на плоскости множество решений неравенства:
а) 2х – 5у + 10 0,
б) ху –6.
Вариант 2
1. Решить неравенства:
а)
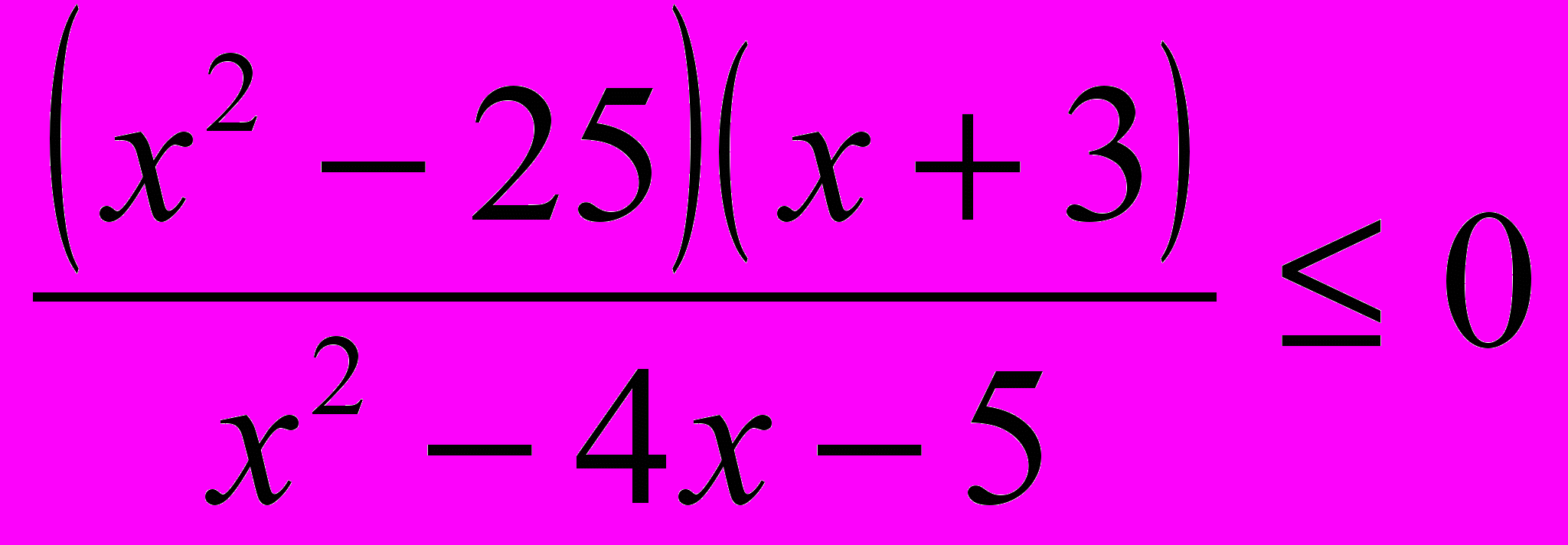 ,
,б)
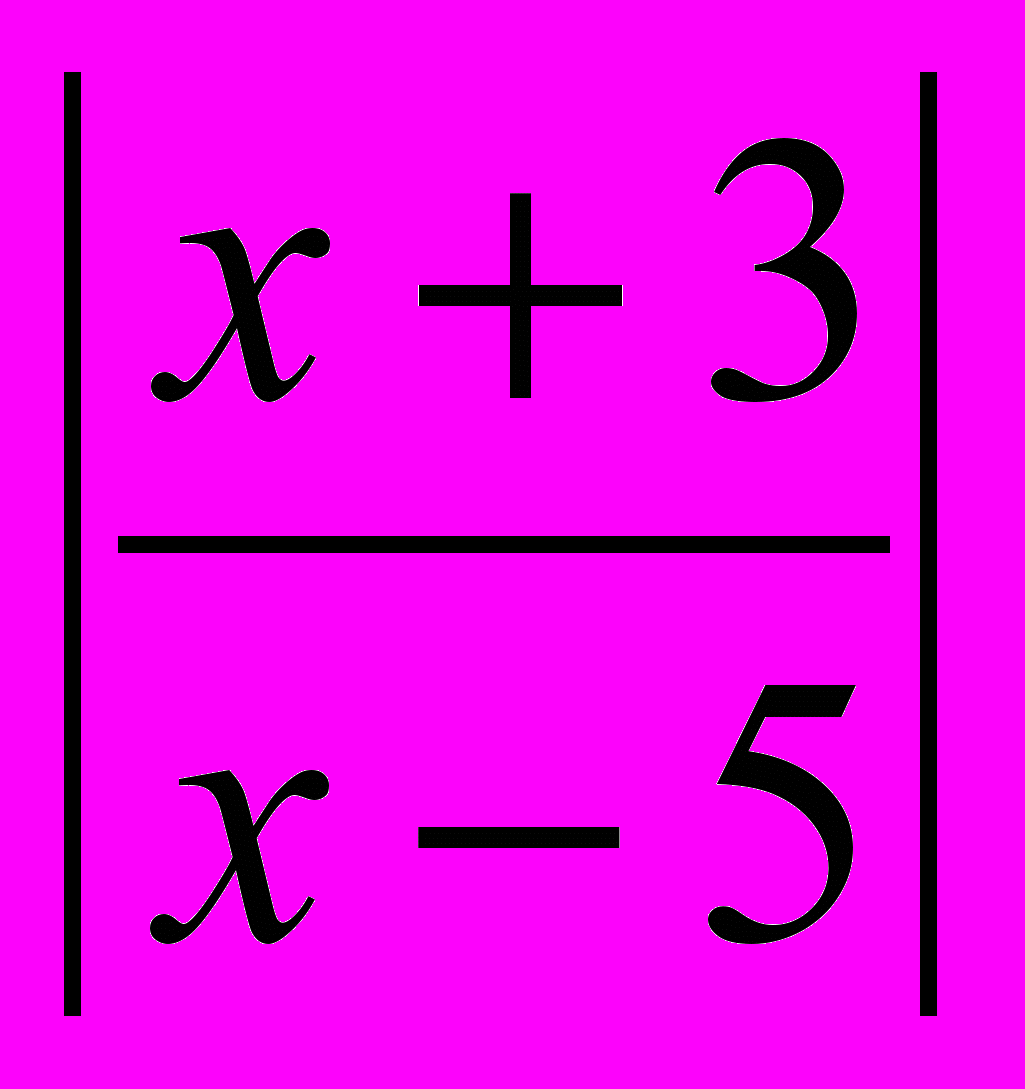 4.
4.2. Изобразить на плоскости множество решений неравенства:
а) 3х + 2у – 8 0,
б) ху –8.
Зачет № 1
по теме «Алгебраические уравнения»
Вариант 1.
- Теорема Безу.
Решить уравнение: х3 – 8х2 + 19х – 12 = 0.
- Какое уравнение называется следствием из другого уравнения?
Какое из данных уравнений является следствием другого уравнения:
2(х + 3) + х (х – 4) = (х – 4) (х + 3 )
или
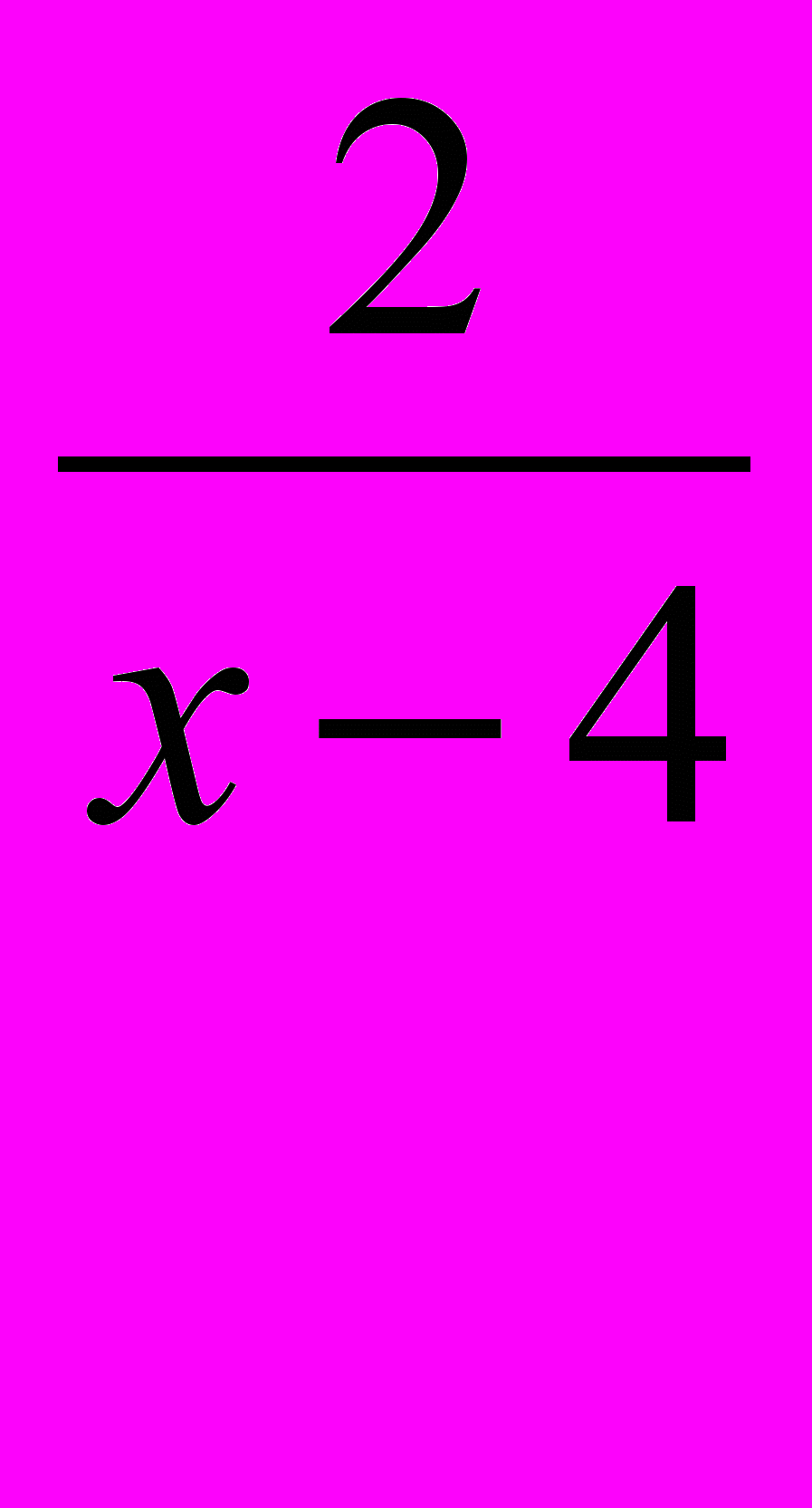 +
+ 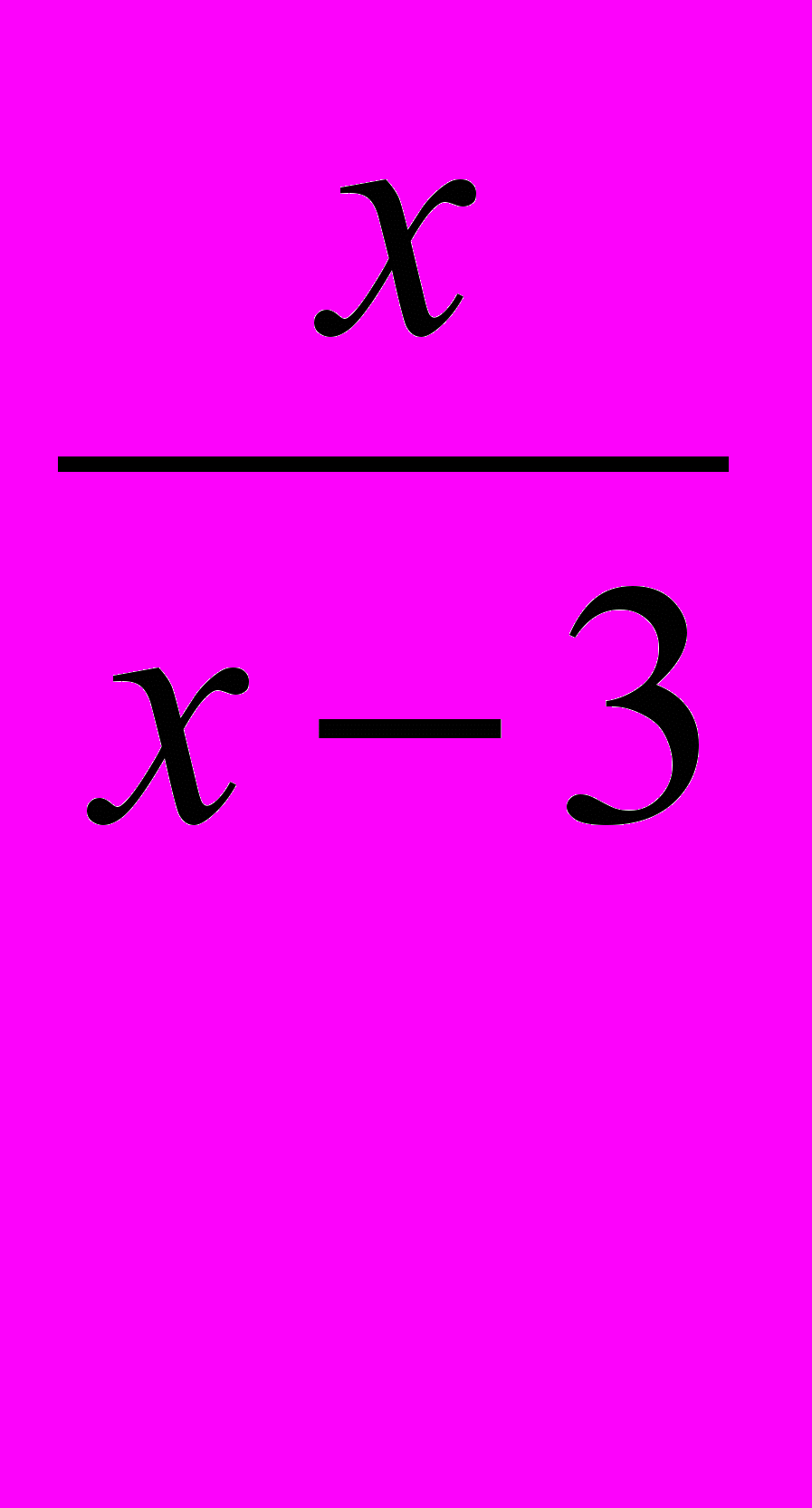 = 1 ?
= 1 ? - Какое уравнение называется однородным? Привести пример уравнения с двумя переменными. Решить уравнение:
2(х2 – 1)2 – 5(х2 – 1) (х2 + 4х) + 2 (х2 + 4х)2 = 0.
- Решить уравнения:
- 5х3 – 6х2 – 6х + 5 = 0,
- 2х4 + 3х3 – 16х2 + 3х + 2 = 0.
Вариант 1.
- Обобщенная теорема Безу.
Решить уравнение: 2х3 + 5х2 – х – 1 = 0.
- Какие уравнения называются равносильными? Привести пример.
Равносильны ли уравнения:
(х – 3) (х + 5) = 0 и
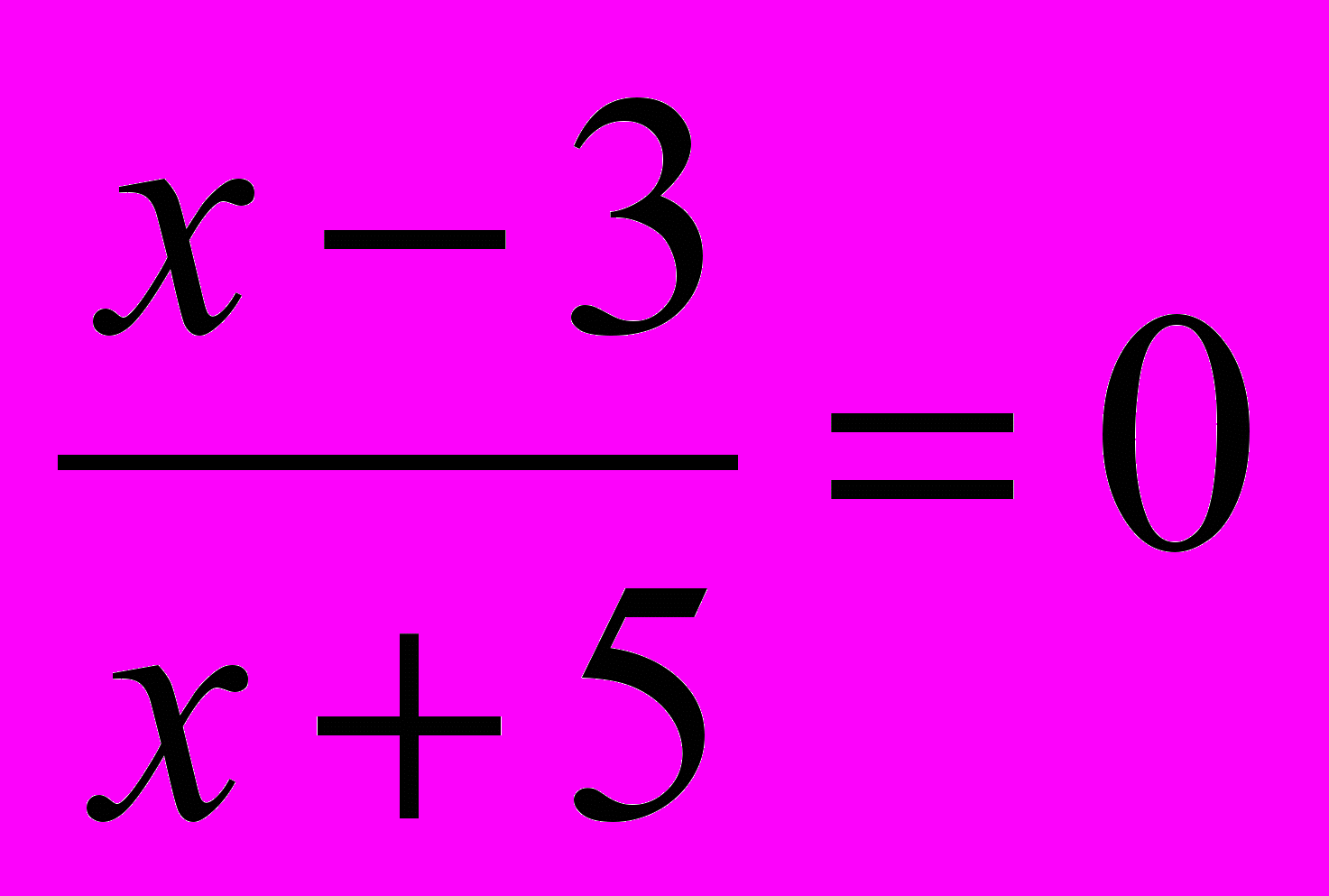 ?
?- Какие уравнения называются возвратными? Решить уравнения:
- 12х4 – 20х3 – х2 – 20х + 12 = 0,
- х3 – 5х2 – 5х + 1 = 0.
- 12х4 – 20х3 – х2 – 20х + 12 = 0,
- Решить уравнение: 2(х2 – 4)2 + 5(х2 – 4) (х2 – 2х) – 3(х2 – 2х)2.
Зачет № 2
по теме «Алгебраические уравнения»
Вариант 1.
- Дробно-рациональные уравнения. Методы решения. Решить уравнения:
а)
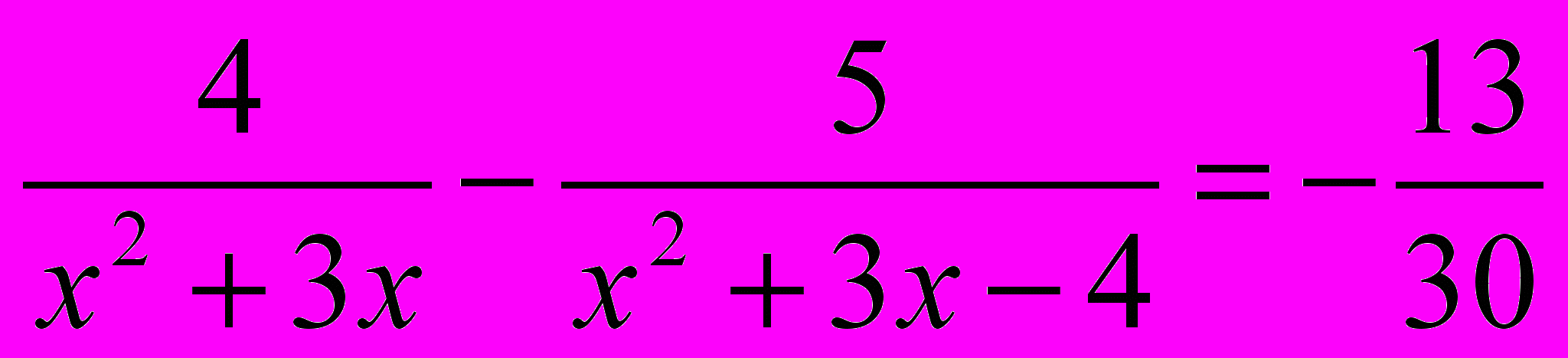 ;
;б)
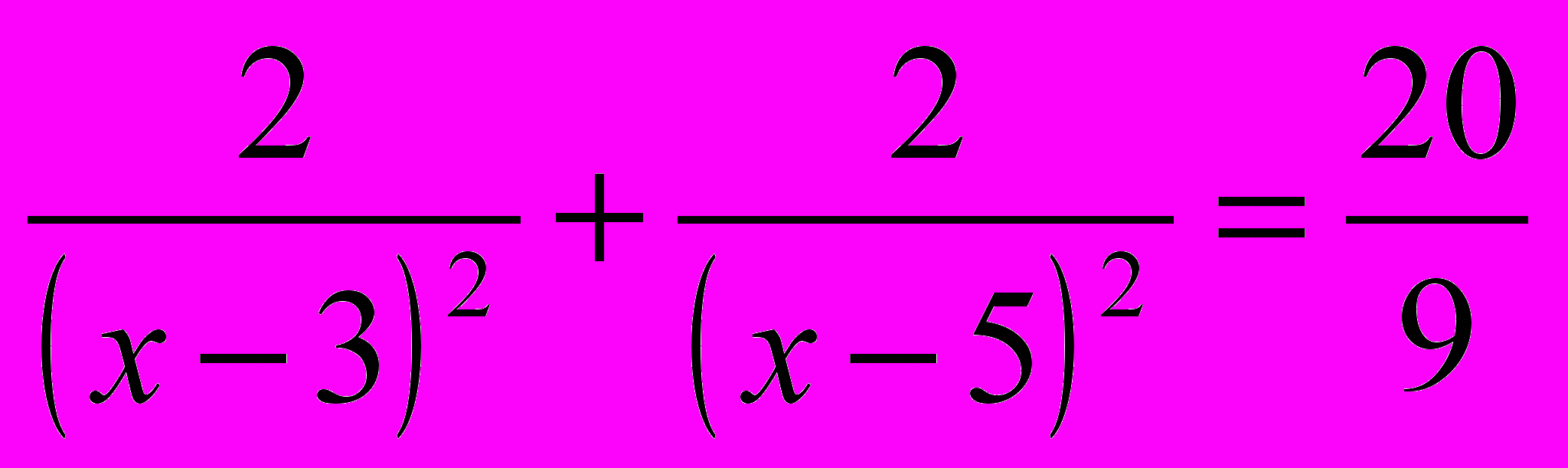 .
.- Что значит решить уравнения с параметрами? Решить уравнения:
- х2 – 2ах + а2 – 1 = 0;
- (а2 – 9) · х + а + 3 = 0.
- х2 – 2ах + а2 – 1 = 0;
- Решить уравнения, содержащие знаки модуля:
- |х – 7| – |4 – 2х| = 2;
- х2 – 5|х| – 6 = 0.
- |х – 7| – |4 – 2х| = 2;
Вариант 2.
- Методы решения уравнений, содержащих знаки модуля. Решить уравнения:
- |х2 – 5х| = 5х - х2,
- |х + 5| - |6 – 3х| = 3.
- Метод оценки. Решить уравнения:
а) |х2 – 5х - 6| +
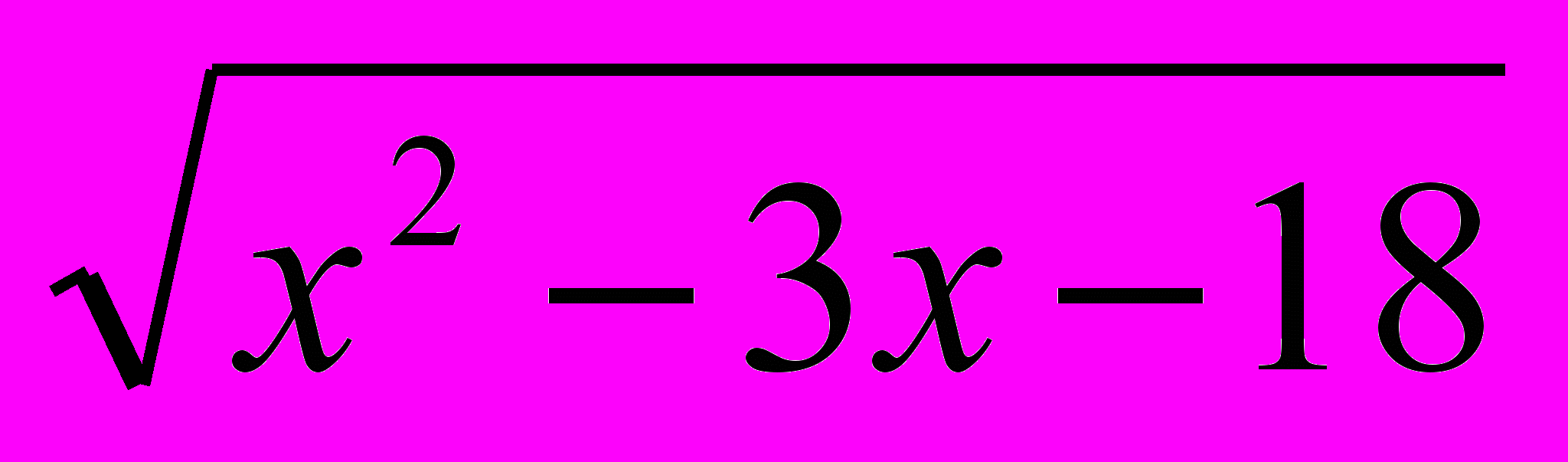 = 0,
= 0, б) 3 sin 4х – 4 cоs 2х = 7.
- Решить уравнения:
- х2 – 6ах + 9а2 – 2а + 2 = 0.
- х2 – 6ах + 9а2 – 2а + 2 = 0.
б)
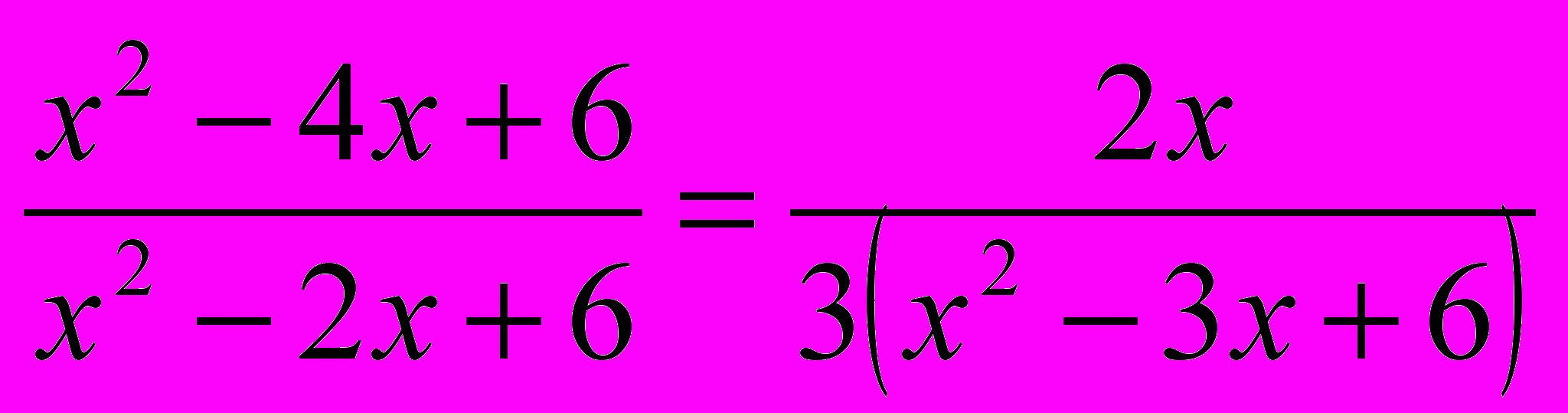 .
.Зачет № 3
по теме «Системы алгебраических уравнений и неравенств»
Вариант 1.
- Методы решения систем уравнений с двумя переменными.
Решить системы уравнений:
а
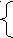 ) х2 + у2 – ху = 13,
) х2 + у2 – ху = 13,ху = 12 ;
б
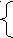 ) (3х – 4)2 + (5у – 2)2 = 328,
) (3х – 4)2 + (5у – 2)2 = 328,(3х – 4) (5у – 2) = 36;
в
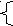 ) х2 – 4ху + 3у2 = 0,
) х2 – 4ху + 3у2 = 0,х2 – 5у2 = – 8.
- Метод интервалов. Решить неравенство:
(х – 3)2 (х + 7)
≥ 0.
2 – х
- Изобразить множество решений неравенства:
а) у ≥ 2х2,
б) (х – 3)2 + (у + 2)2 ≤ 9.
Вариант 2.
Методы решения систем уравнений с двумя переменными.
Решить системы уравнений:
а
 ) х2 + у2 + 3ху = 31.
) х2 + у2 + 3ху = 31.ху = 6 ;
б
 ) (5х – 4)2 + (3у + 2)2 = 65,
) (5х – 4)2 + (3у + 2)2 = 65,(5х – 4) (3у + 2) = 36;
в
 ) х2 + 5ху – 6у2 = 0,
) х2 + 5ху – 6у2 = 0,2х2 + 5у2 = 63.
Метод интервалов. Решить неравенство:
| (х – 5) (х + 2) 2 | ≥ 0. |
| 4 – х |
Изобразить множество решений неравенства:
а) у ≤ – х2,
б) (х + 2)2 + (у – 3)2 ≥ 16.
