Конспект урока тема Сложение многочленов Учитель математики Iкатегории Пак Валентина Николаевна Кострома

Вид материала

Содержание

Ход урока
2. Актуализация знаний.
Сложение многочленов
4. Первичное закрепление с проговариванием во внешней речи.
5. Самостоятельная работа с самопроверкой по эталону.
6. Включение в систему знаний и повторение.
7. Рефлексия деятельности.
Тема: «Сложение и вычитание многочленов».
1. Записываем заданные многочлены через сумму скобок
2. Раскрываем скобки, оставляя знаки слагаемых без изменения
3. Приводим подобные слагаемые
1. Записываем заданные многочлены через разность скобок
2. Раскрываем скобки, изменяя знаки слагаемых на противоположные
3. Приводим подобные слагаемые
Самоанализ урока

Подобный материал:

Муниципальное общеобразовательное учреждение

средняя общеобразовательная школа № 8 города Костромы

Конспект урока

тема

Сложение многочленов

Учитель математики I категории

Пак Валентина Николаевна

Кострома

2009

Цели урока:

Образовательные:

повторить и закрепить понятие многочлена, его членов, понятие стандартного вида многочлена, приведение подобных членов.
закрепить навыки раскрытия скобок:
отрабатывать умения применять полученные алгоритмы при решении заданий.

Развивающие:

учащиеся «открывают» способ сложения и вычитания многочленов;

развивать познавательный интерес;
развивать математическую речь, логическое мышление, память, внимание, творчество;
формировать математическую культуру.

Воспитательные:

воспитать устойчивый интерес к изучаемому предмету;
воспитать ответственность за коллективное решение;
проявить положительное отношение к знаниям.

Задачи урока:

вывести алгоритм сложения и вычитания многочленов, построить правило составления алгебраической суммы многочленов;
четкая организация работы в парах.

Знать:

Понятие многочлена, двучлена, трехчлена, стандартный вид многочлена.
Правила раскрытия скобок.
Алгоритмы сложения и вычитания многочленов
Правило составления алгебраической суммы многочленов.

Уметь:

Применять правила при раскрытии скобок, перед которыми стоит знак « + », « - ».
Использовать приведение подобных слагаемых и взаимное уничтожение членов

многочлена для записи многочлена в стандартном виде.

3. Использовать алгоритмы сложения и вычитания многочленов, правило составления

4. Анализировать полученные результаты.

Достигать цели с применением имеющегося практического опыта.
Выполнять задания в паре.

Методы:

Наглядный
Иллюстративный.
Творческий

Форма организации учебной деятельности:

парная

Оборудование:

подготовленная классная доска;
учебник;
дидактический материал: карточка учебной деятельности (приложение 1), схема (приложение 2); карточки алгоритмов (приложение 3, 4), рефлексия (приложение 5).

Этапы урока:

Самоопределение к деятельности.
Актуализация знаний.
«Открытие» учащимися нового знания.
Первичное закрепление с проговариванием во внешней речи.
Самостоятельная работа с самопроверкой по эталону.
Включение в систему знаний и повторение.
Рефлексия деятельности.

Тип урока: «Открытие» нового знания.

Эпиграф: «Сначала я открывал истины, известные многим, затем стал открывать истины известные не многим, и, наконец, стал открывать истины, ещё никому не известные».

К.Э. Циолковский

Ход урока

1. Самоопределение к деятельности.

Цель этапа:

включить учащихся в учебную деятельность;
определить содержательные рамки урока: продолжаем работу с многочленами.

Организация учебного процесса на этапе 1:

- Добрый день. Начинаем наш урок. Я надеюсь, что Вы с хорошим настроением приступаете к работе.

(Учащиеся занимают свои места и настраиваются на урок.)

- В какой деятельности вы сейчас находитесь? (В учебной.)

- Из каких частей состоит учебная деятельность? (Надо выяснить чего мы не знаем и самостоятельно найти выход из затруднения.)

(На доске открываются карточки №1.)

- Но прежде чем выяснить, чего мы не знаем, что необходимо сделать? (Выяснить, что нам известно.)

2. Актуализация знаний.

Цель этапа:

актуализировать учебное содержание, необходимое и достаточное для восприятия нового материала: определение многочлена, членов многочлена, операция приведения подобных членов многочлена, приведение многочлена к стандартному виду.
актуализировать мыслительные операции, необходимые и достаточные для восприятия нового материала: сравнение, анализ, обобщение;
зафиксировать все повторяемые понятия и алгоритмы в виде схем и символов: в виде правил;
зафиксировать индивидуальное затруднение в деятельности, демонстрирующее на личностно значимом уровне недостаточность имеющихся знаний.

Организация учебного процесса на этапе 2:

- В какой большой теме мы с вами сейчас работаем? (Многочлены.)

- Вспомните план, по которому мы изучали тему «Одночлены»? (1. Понятие, 2. Арифметические действия).

- Что из перечисленного мы уже изучили? (Определение многочлена.)

- Давайте вспомним основные моменты:

Что называют многочленом?
Приведите примеры многочленов.
Как называются слагаемые многочлена?
Как называется многочлен, состоящий из 2-х, 3-х членов?
Рассмотрите пример 3аb²∙ 2 а²b – 4а – 8а - 3b² - 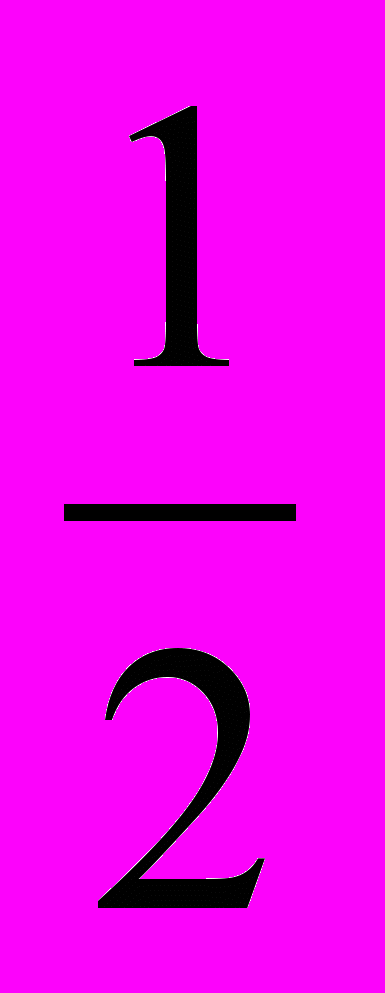а³ b² ·4b + 2b² (пример записан заранее на откидной доске) и ответьте на вопросы: является ли данное выражение многочленом, всё ли вам нравится в его записи и что надо сделать, чтобы его запись была наиболее удобна?

(Учащиеся должны привести многочлен к виду 6а³b³– 4а – 8а - 3b² - 2а³b³ + 2 b², а затем к виду 4а³b³– 12а - b²).(Работают в тетрадях парами, затем кто-то из учеников записывает полученный ответ на доске, а все остальные проверяют ответ и корректируют, если это необходимо).

Выполнение каких операций позволило Вам получить такой ответ и как теперь называется данный многочлен?

(На доске открывается схема №1.)

- К какому шагу приступим на этом уроке? (Будем изучать арифметические действия с многочленами.)

- С какого действия начнем? (Конечно со сложения.)

- Сформулируйте тему урока. ( Сложение многочленов.)

(Тема записывается в тетради и на доске).

- Сформулируйте цель урока. (Научиться складывать многочлены)

- Чтобы достичь этой цели, какую задачу поставим перед собой? (Вывести алгоритм или правило сложения многочленов)

3. «Открытие» учащимися нового знания.

Цель этапа:

организовать коммуникативное взаимодействие для построения нового способа действия;
зафиксировать новый способ действия в знаковой, вербальной форме и с помощью эталона.
организовать решение исходной задачи, данной для пробного действия.
уточнить общий характер пробного знания.

Организация учебного процесса на этапе 3:

Организуется работа в парах по выполнению задания. Пары работают в тетрадях. Одновременно задание выполняется на доске. Результаты, полученные на доске, проверяются и обсуждаются предпринятые шаги для полного завершения задания. Анализируются результаты. Ответы могут быть разные, как и ошибки. После подробного анализа на доске остаётся только верный ответ.)

- Какую из известных Вам операций можно выполнить в данном выражении: (2х²+ 3х – 8) + (5х + 2) (Раскрыть скобки)

(Раскрывают скобки, работая в тетрадях. Один ученик выполняют данную работу на откидной доске. Проверяем ход работы и анализируем все ли операции выполнены?)

- Как раскрываются скобки, перед которыми стоит знак «+»? (Формулируют правило)

- Как называются выражения, стоящие в скобках? (Многочлены или трехчлен и двучлен.)

- А какой знак действия? (Сложения.)

- Значит, какую операцию мы сейчас с вами выполнили? (Сложение многочленов.)

- Какое выражение должно получится в ответе, чтобы можно было считать, что задание выполнено верно? (Многочлен стандартного вида.)

- Сформулируйте алгоритм сложения многочленов.

(Несколько учащихся проговаривают шаги алгоритма сложения многочленов А1, который фиксируется на доске)

- А какое ещё правило раскрытия скобок Вы знаете? (Перед которыми стоит знак « - «)

- А как по - другому можно назвать теперь это действие? (Вычитание многочленов)

- Вспомните правило раскрытия скобок, перед которыми стоит знак « - « ?

(Формулируют правило)

- Найдите разность многочленов: (х³+ у³+ 2х + 3у + 5) – (х³- у³- 5х + 3у - 7)

(Раскрывают скобки, работая в тетрадях, в парах. Один ученик выполняют данную работу на откидной доске. Проверяем ход работы и анализируем все ли операции выполнены верно?)

- Сформулируйте алгоритм вычитания многочленов.

(Несколько учащихся проговаривают шаги алгоритма вычитания многочленов А2, который фиксируется на доске)

- Вспомните, какое общее название у следующих выражений:

р₁(х) + р₂(х) + р₃(х);

р₁(х) - р₂(х) + р₃(х);

р₁(х) - р₂(х) - р₃(х);

р₂(х) - р₃(х) + р₁(х)? (Алгебраическая сумма многочленов)

- А теперь, используя данный термин, сформулируйте правило составления алгебраической суммы многочленов.

(Формулируют правило. Заслушиваем несколько учащихся, внося изменения, оттачивая формулировку)

- А теперь откройте учебник на странице 107 и прочитайте Правило 1.

(Сначала читают про себя, а затем один ученик читает вслух)

- Как вы думаете, помогут вам новые алгоритмы достичь цели сегодняшнего урока? (Да).

- Каков следующий шаг? (Отработать умения, закрепить алгоритмы, потренироваться).

4. Первичное закрепление с проговариванием во внешней речи.

Цель этапа: организовать усвоение детьми нового способа действий при решении типовых задач с их проговариванием во внешней речи.

Организация учебного процесса на этапе 6:

Решаем № 25.1 (б), 25.2 (б), 25.4 (б), 25.5 (в) в тетрадях и на доске с проговариванием шагов алгоритма.

(Ученики по очереди у доски).

5. Самостоятельная работа с самопроверкой по эталону.

Цель этапа: проверить своё умение применять алгоритм сложения в типовых условиях на основе сопоставления своего решения с эталоном для самопроверки.

Организация учебного процесса на этапе 7:

- Можете ли вы теперь уверенно сказать, что научились складывать и вычитать многочлены? (Нет, нам надо выполнить самостоятельную работу и проверить себя).

Самостоятельная работа. Учащиеся выполняют в тетрадях № 25.1, 25.2, 25.4 (пример а) 25.5 (пример б)- I вариант, № 25.1, 25.2, 25.4 (пример в), 25.5 (пример г) – II вариант. Выполнив задания, учащиеся выполняют проверку по эталону.

(Выполняется самопроверка по эталону, который выдан каждому ученику. Если допущена ошибка, то отмечается шаг алгоритма, в котором она допущена).

6. Включение в систему знаний и повторение.

Цель этапа: использование нового содержания для определения дальнейших действий многочленами.

Организация учебного процесса на этапе 8:

- Ребята, а можем мы, используя полученные знания, решать уравнения? (Да)

- Проверьте это на примере задания № 25.6(а)

(Два ученика выполняют данную работу на откидных досках.)

7. Рефлексия деятельности.

Цель этапа: зафиксировать новое содержание, оценить собственную деятельность.

Организация учебного процесса на этапе 9:

Домашнее задание: § 25 правило выучить, № 25.1, 25.2, 25.4, (пример г), 25.5 (а) доп-но № 25.13 (а)

(Ученики отвечают на вопросы фронтально).

- Выполнили вы сегодня условия учебной деятельности?

- Какую цель ставили перед собой на уроке?

- Смогли ли ее достичь?

- Выполнили ли основную задачу урока?

- Какой алгоритм еще удалось получить?

- Что более всего понравилось на уроке?

- Оцените свою деятельность на уроке с помощью карточки самооценки 5.

(Если ученик поставил все плюсы или есть один плюс-минус, то это оценка 5. 4 ставиться если нет минусов и плюс-минус встречается больше одного раза. Оценка 3 на уроке не ставиться.)

- Напиши, над чем тебе надо еще поработать дома и на следующем уроке.

- Оцените свое настроение на сегодняшнем уроке. (Оценка происходит с помощью цветных карточек Учащиеся вывешивают их на доску).

- Молодцы. Вы хорошо поработали на уроке. Урок окончен.

Приложения к конспекту урока в «Технологии деятельностного метода»

по учебнику А.Г. Мордковича «Алгебра, 7 класс».

Тип урока: «Открытие» нового знания

Тема: «Сложение и вычитание многочленов».

Автор: Пак В.Н., руководитель МО, учитель математики первой квалификационной категории МОУ СОШ № 8, г. Кострома.

К1:Структура учебной деятельности (2 шага)

Схема 1

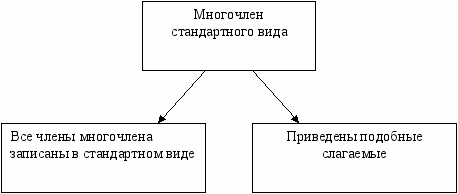
К
ЗАДАЧА: вывести алгоритм сложения многочленов

ЦЕЛЬ: научиться складывать многочлены.

2 К3

А 1: Алгоритм сложения многочленов

1. Раскрыть скобки, перед которыми стоит знак «+»

2. Привести подобные слагаемые

А 2: Алгоритм вычитания многочленов

1. Раскрыть скобки, перед которыми стоит знак «-»

2. Привести подобные слагаемые

К 4: Эталон для самопроверки Самостоятельной работы

В - 1		В - 2
№25.1 (а)	№25.2 (а)	№25.1 (в)	№25.2 (в)
1. Записываем заданные многочлены через сумму скобок
(2а + 5) + (3а – 7)	(2х³+5) + (3х³+ 7)	(3а - 4) + (11 - 3а)	(6х²- 4) + (5х²- 10)
2. Раскрываем скобки, оставляя знаки слагаемых без изменения
2а + 5 + 3а – 7	2х³+5 + 3х³+ 7	3а - 4 + 11 - 3а		6х²- 4 + 5х²- 10
3. Приводим подобные слагаемые
5а – 2	5х³+ 12	7		11х²- 14
№25.4 (а)	№25.5 (б)	№25.4 (в)		№25.5 (г)
1. Записываем заданные многочлены через разность скобок
(2у³+ 8у – 11) – (3у³- 6у + 3)	(5с⁴+ 3c² d) – (2с²+ 3с²d+ d²)	(у³- у + 7) – (у³+ 5у + 11)		(с²+ 2cd+ d²) - (5с²– 6cd - 7d²)
2. Раскрываем скобки, изменяя знаки слагаемых на противоположные
2у³+ 8у – 11 – 3у³+ 6у - 3	5с⁴+ 3c² d – 2с²- 3с²d- d²	у³- у + 7 – у³- 5у – 11		с²+ 2cd+ d² - 5с²+ 6cd + 7d²
3. Приводим подобные слагаемые
- у³+ 14у - 14	5с⁴– 2с²- d²	- 6у – 4		- 4с²+ 8сd+ 8d²

К5: Карточка самооценки

Этап урока	Оценка (+ ± -)
1.Задание на раскрытие скобок, перед которыми стоит знак «+»
2. Конструирование алгоритма сложения десятичных дробей
3.Задание на раскрытие скобок, перед которыми стоит знак «-»
4. Конструирование алгоритма вычитания десятичных дробей
5. Конструирование правила составления алгебраической суммы многочленов
6. Выполнение упражнений по образцу
7. Самостоятельная работа

«+» - все верно

«±» - допущена ошибка

«-» - больше половины заданий выполнено неверно.

Фамилия и имя __________________________________________________

Оценка ___________________

Над чем еще надо поработать?_________________________________

Самоанализ урока

№ п/п	Наименование	Результат
	Основные дидактические требования	Целенаправленная и систематическая работа над развитием всех учащихся
	Особенности методической системы	Процессуальность (постоянный возврат к ранее пройденному на основе связи старого с новым), Вариантность (использование различных способов общения между учителем и классом, варьирование меры помощи ученикам, системы заданий как по уровню трудности, так и по времени их предъявления).
	Тип урока	Урок «открытия» нового знания.
	Структура учебной деятельности а. Мотивация б. Целеполагание и постановка учебных задач в. Учебные действия (через мыслетехники)	Успеха и познавательной новизны Учитель организует так деятельность учащихся, что они сами ставят цели и задачи Обобщение, рефлексия, осмысление Со стороны учителя – создание положительного эмоционального настроя, Со стороны учеников – самоконтроль и самооценка.
	Подбор содержания на урок	Логическая целостность урока в системе уроков по теме, соответствие цели. Использование разнообразных дидактических средств обучения с целью контроля и рефлексии.
	Реальные учебные возможности	1.Задание на раскрытие скобок, перед которыми стоит знак «+» - 98 % 2. Конструирование алгоритма сложения десятичных дробей – 100 % 3.Задание на раскрытие скобок, перед которыми стоит знак «-» 80 % 4. Конструирование алгоритма вычитания десятичных дробей – 100 % 5. Конструирование правила составления алгебраической суммы многочленов - 80% 6. Выполнение упражнений по образцу - 82% 7. Самостоятельная работа – 69 % Хороший уровень интеллекта учащихся.
	Место урока	В разделе – тема изучение нового материала, в курсе – ключевая.
	Связь с предыдущими темами	Раскрытие скобок, перед которыми стоит знак «+», «-«, приведение подобных слагаемых
	Работа на последующие темы	Преобразование различных алгебраических выражений
	Специфика урока	Урок в технологии деятельностного метода обучения
	Задачи, решаемые на уроке: Обучающая: Развивающая: Воспитывающая	а) повторить и закрепить понятие многочлена, его членов, понятие стандартного вида многочлена, приведение подобных членов, закрепить навыки раскрытия скобок, отрабатывать умения применять полученные алгоритмы при решении заданий. b) учащиеся «открывают» способ сложения и вычитания многочленов; развивать познавательный интерес; развивать математическую речь, логическое мышление, память, внимание, творчество; формировать математическую культуру. с) воспитать устойчивый интерес к изучаемому предмету, ответственность за коллективное решение, проявить положительное отношение к знаниям.
	Комплексность задач	Обеспечена комплектность и взаимосвязь решаемых задач.
	Главная задача	Самостоятельность, мыслительный процесс.
	Особенности класса	Задания подобраны среднего уровня, т.к. в классе большая часть учащихся имеет хороший потенциал.
	Время	Распределено равномерно, на каждый этап выделено фиксированное количество времени. Одно вытекает из другого, идет нарастание уровня сложности. Между этапами присутствуют логические связки.
	Акцент урока	Технология деятельностного метода обучения, общие приемы работы с текстом учебника, решение заданий по теме урока.
	Методы	Наглядный, иллюстративный, творческий.
	Формы обучения для раскрытия материала	Деятельностный метод обучения, выполнение заданий + самостоятельная работа.
	Контроль усвоения ЗУН	Выполнение заданий + самостоятельная работа
	Учебный кабинет	Используется доска + учебник + методический материал + иллюстративный материал + дидактический материал
	Работоспособность учащихся	Активная работоспособность обеспечивается за счет деятельностного метода обучения, обусловлена высоким темпом. Критерии самооценки почти по всем показателям соответствуют оценке «4» и «5»
	Психологическая атмосфера	Поддерживается непринужденной беседой, обсуждением, ответами, защитой своего мнения. Рефлексия показала, что форма проведения урока понравилась всем учащимся, новую тему поняли..
	Перегрузки	Перегрузок нет, т.к. постоянно идет смена учебной деятельности. Нормы СанПиН выдержаны.
	Методическое мастерство учителя на уроке	Создание педагогических ситуаций, позволяющих ученику проявить самостоятельность, инициативу, самореализацию.
	Запасные методические ходы учителя	Необходимы для более слабых учащихся индивидуальная помощь со стороны учителя + дополнительные задания для более «продвинутых» учащихся..

Вывод

Смена форм и видов деятельности, разнообразие дидактического материала, оптимальный контроль каждого задания позволяет сформировать, закрепить и систематизировать знания учащихся. Необходимо откорректировать выявленные пробелы в знаниях и способах действий учащихся, в рамках изученной темы.

Blog

Конспект урока тема Сложение многочленов Учитель математики Iкатегории Пак Валентина Николаевна Кострома

Содержание

Ход урока