Старые методы для решения новых систем уравнений Тип урока
| Вид материала | Урок |
- Старые методы для решения новых систем уравнений Тип урока, 38.55kb.
- Реферат по математике. На тему: «основные методы решения систем уравнений с двумя переменными», 140.92kb.
- Конспект урока по теме «Методы решения систем рациональных уравнений», 20.25kb.
- Конспект урока «Методы решения иррациональных уравнений», 56.45kb.
- Методические материалы для студентов, 104.19kb.
- Методические рекомендации к проведению урока: «Методы решения уравнений и неравенств., 15.21kb.
- Ядрышникова Вера Викторовна, учитель муниципальной общеобразовательной школы №168, 40.13kb.
- Тема урока: Нестандартные методы решения уравнений. Цель урока, 24.43kb.
- «Численные методы», 64.5kb.
- Практических: 0 Лабораторных:, 21.53kb.
Тема: Старые методы для решения новых систем уравнений
Тип урока: урок- исследование.
Класс: 9
Количество часов: 1час.
Цели:
- Изучить методы решения систем уравнений, одно из которых является уравнение I-ой степени, а другое II-ой степени.
- Выяснить, сколько решений может иметь такая система.
- Отработка навыков решения систем уравнений.
Ход урока:
I. Постановка цели урока.
Учитель: Мы сегодня проведём «урок-исследование», цель которого выяснить: - подходят ли «старые» методы для решения новых систем уравнений.
Выясним, сколько решений может иметь такая система.
Разберёмся, от чего зависит решение системы.
А начнем мы наш урок с теоретической разминки. Дома вы повторяли тему «Системы линейных уравнений». Проверим ваши знания.
II. Теоретическая разминка.
Вопросы к учащимся:
- Что значит: решить систему уравнений?
- Что является решением системы уравнений?
- Какие системы называются равносильными?
- Перечислить методы решения систем линейных уравнений
- В чём заключается сущность каждого метода?
У
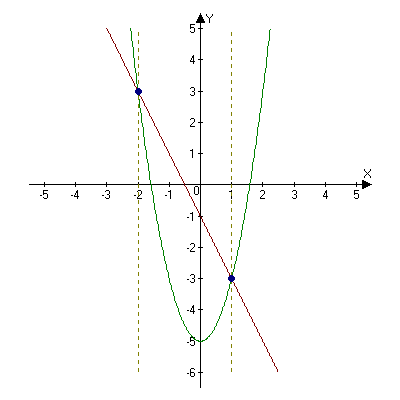читель: Посмотрите на рисунок.Какие задачи составили бы вы, глядя на этот рисунок?
Учащиеся:
1) Найти абсциссы точек пересечения графиков.
2) Найти координаты точек пересечения параболы с прямой.
3) Решить систему уравнений.
4)Указать, сколько решений имеет система.
5) Вычислить площадь фигуры, ограниченной параболой и прямой.
6) Определить длину отрезка, отсекаемого параболой от прямой.
Учитель: Итак, среди сформулированных задач вы, наверное, обнаружили те, которые решали, причем не единственным образом. Нашли задачи, методы, решения которых на данный момент совершенно не ясны. Увидели и задачи, которые есть смысл решать, привлекая аналогию. (Это решить систему; найти координаты точек пересечения.) А подойдут ли «старые» методы для решения систем уравнений?
III. Исследовательская работа учащихся (каждый учащийся выполняет самостоятельно)
Учитель:
1. Что из себя представляет система
Учащиеся: 1 - уравнение 2-ой степени, 2 – уравнение 1-ой степени.
Учитель: Попробуйте решить ее разными способами: (Идет самостоятельная работа в группах – группы составлены по уровню знаний).
| 1 группа | 2 группа | 3 группа |
| Методом сравнения | Методом сложения | Подстановкой |
| | | |
Решение систем проверим.
Решение:
     |   |  |
Учитель: Сверьте решение системы с решением системы, полученным графическим способом (см. рисунок) и сделайте вывод.
Физкультминутка.
2. Учитель: А сколько же решений может иметь такая система? Решите данную систему своей группы любым способом.
| 1 группа | 2группа | 3группа |
 |  |  |
(1-ая система имеет бесконечно много решений; 2-ая система имеет 1 решение; 3-ья система вообще не имеет решений).
Делаем общий вывод: Система может иметь: 0 решений, 1 решение, 2 решения, много решений.
3.Учитель: А сейчас нужно выяснить: сколько решений может иметь система и от чего это зависит? Рассмотрим систему:
Каким способом можно ее решить?
Учащиеся: Подстановкой.
Получим:
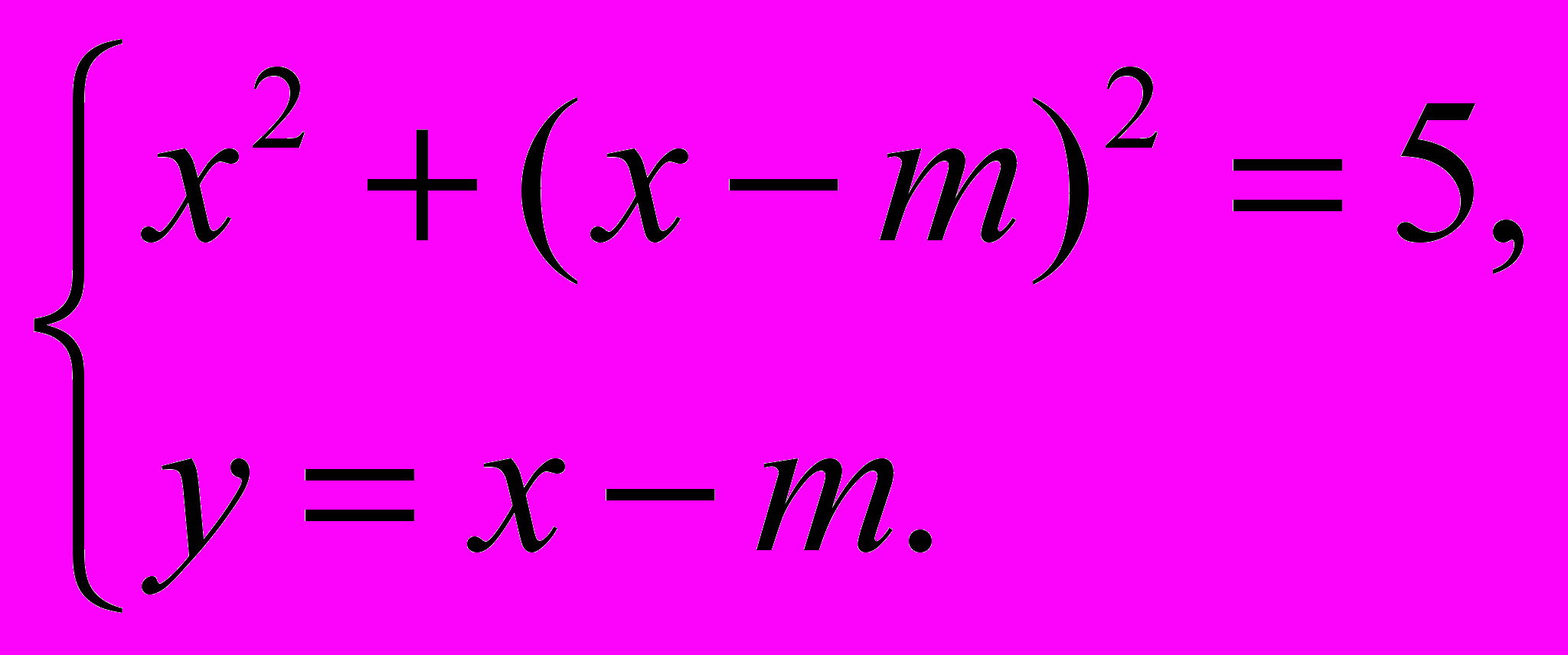
Задания по группам:
| 1 группа | 2 группа | 3 группа |
| Чему равен дискриминант Если  D>0, D<0? | Чему равен дискриминант? | Какое получили квадратное уравнение? |
| Ответ 1):  2)  | Ответ: Д=0 при  | Ответ:  |
4. Решить красиво систему уравнений:
Учитель: Проверим решение систем..
IV. Домашнее задание задается по группам.
V. Подведение итогов урока.