Конспект урока. Тема урока. Функционально-графические методы при решении тригонометрических уравнений

Вид материала

Урок

Подобный материал:

• План конспект па алгебре и началам анализа в 10 классе Тема урока: Тригонометрические, 109.55kb.
• Тема урока: Теорема Безу. Корни многочленов, 114.7kb.
• Тема урока: Нестандартные методы решения уравнений. Цель урока, 24.43kb.
• Решение линейных уравнений Цель урока, 126.51kb.
• Задачи урока: повторить свойство монотонности и ограниченности показательной функции;, 91.6kb.
• Цель: Рассмотреть способы решения тригонометрических уравнений, 43.07kb.
• Конспект урока по теме «Методы решения систем рациональных уравнений», 20.25kb.
• Основные методы решения тригонометрических уравнений, 22.36kb.
• Конспект урока «Методы решения иррациональных уравнений», 56.45kb.
• План-конспект урока информатики в 7 классе Тема: «Растровая и векторная графика. Растровые, 51.02kb.

Конспект урока.

Тема урока. Функционально-графические методы при решении тригонометрических уравнений.

Цели урока.1. Повторить и обобщить знания по темам «Решение тригонометрических уравнений», «Графики и свойства тригонометрических функций».

2. Научиться применять функционально - графический метод для решения тригонометрических уравнений и неравенств.

3. Развивать логическое мышление, наблюдательность.

4. Воспитывать активность, творческую инициативу, внимательность к окружающим.

План урока.

1. Организационный момент.
   
2. Мотивация учебной деятельности.
   
3. Актуализация опорных знаний.
   
4. Изучение новых знаний: функционально- графический метод решения нестандартных тригонометрических уравнений.
   
5. Закрепление знаний: первичное, комплексное, творческое.
   
6. Проверка усвоения материала: «Шапка вопросов.»(резерв времени)
   
7. Подведение итогов: оценки, подарки, домашнее задание.
   

План урока в цитатах (кроме оргмомента)

1. «Мир математики – ни что иное, как отражение в нашем сознании реального мира.» Гиппократ.
   
2. Кто не знает, в какую гавань он плывет, для того нет попутного ветра. Сенека.
   
3. Геометрия приближает разум к истине. Платон.
   
4. Не будем спорить – будем вычислять. Г.Лейбниц.
   
5. О мир! Пойми! Певцом – во сне – открыты Закон звезды и формула цветка. Марина Цветаева.
   

Необходимы материалы для каждого ученика.

1. Сигналы с рожицами .
   
2. Бумага в клеточку для рисунков, чертежные инструменты.
   
3. Задания для этапов актуализации, закрепления, домашнего задания.
   

Содержание.

Эпиграф: А синуса график волна за волной

по оси абсцисс пробегает…

(Из студенческой песни)

1. Оргмомент. Сообщение темы, целей урока. Правила работы с семафором. Слайды 1-3
   
2. Мотивация осознанного обучения. Распространение тригонометрических функций в природе. Сообщение учителя (слайды 4-5-6)
   

Тригонометрические функции в природе.

Они служат прежде всего для описания разнообразных периодических процессов, с которыми человек сталкивается повсюду. Восход и заход солнца, изменение фаз луны, чередование времен года. Биение сердца, циклы в жизнедеятельности организма, вращение колеса, морские приливы и отливы, заполненность городского транспорта, , эпидемии гриппа ,- в этих многообразных процессах можно найти общее: они периодичны, а , значит, их математические модели описываются тригонометрическими функциями. Если бы зрение людей обладало способностью видеть звуковые, электромагнитные и радиоволны, то мы видели бы вокруг себя и предметов которые нас окружают многочисленные синусоиды всевозможных видов. Ведь все эти явления: звук, электрический ток, радио и связанные представляют собой колебания различной частоты и амплитуды .

3. Актуализация опорных знаний. Повторение знаний по темам «Тригонометрические функции», «Тригонометрические уравнения». Задания на слайдах:
   

Запишите название функций, графики которых изображены на рисунках:



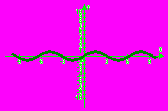
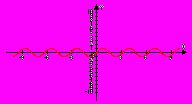
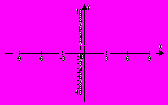
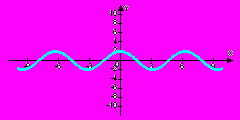
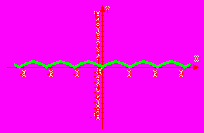
Запишите решение по рисунку единичной окружности


Найдите ошибку в решении уравнения: (правильные ответы выделены цветом)

1. cos 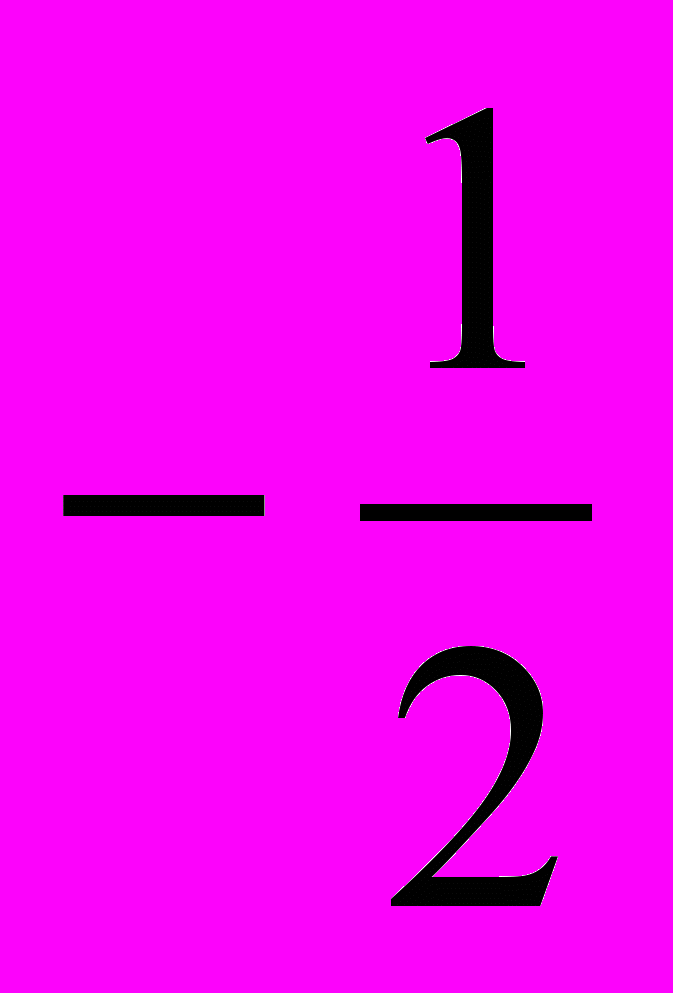x =, x=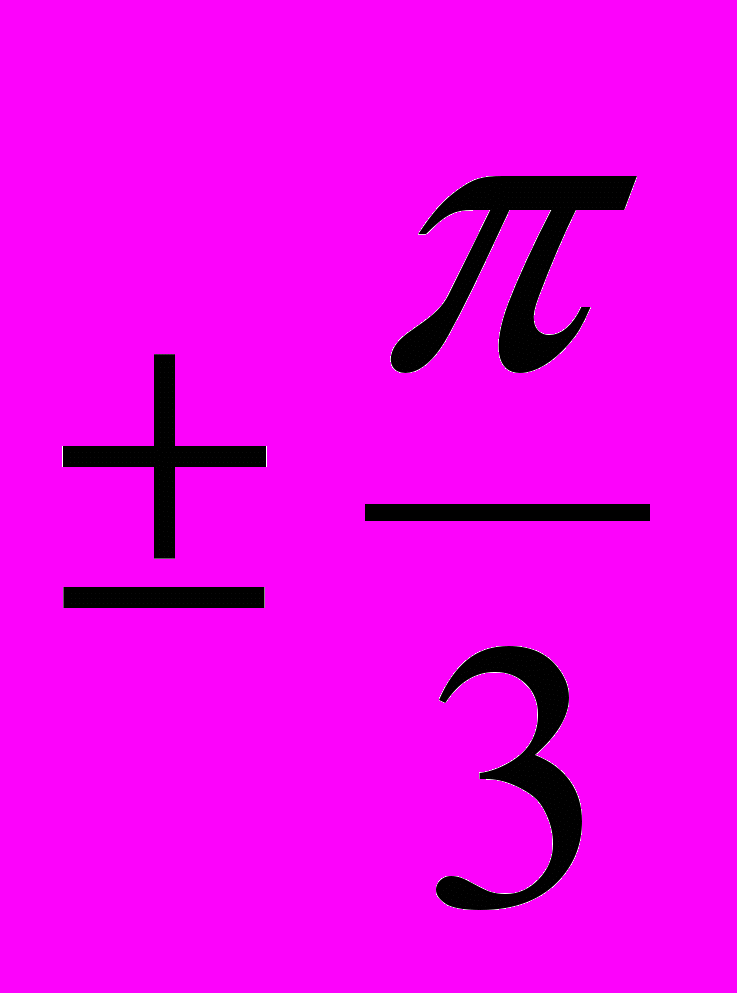+2πn, n.

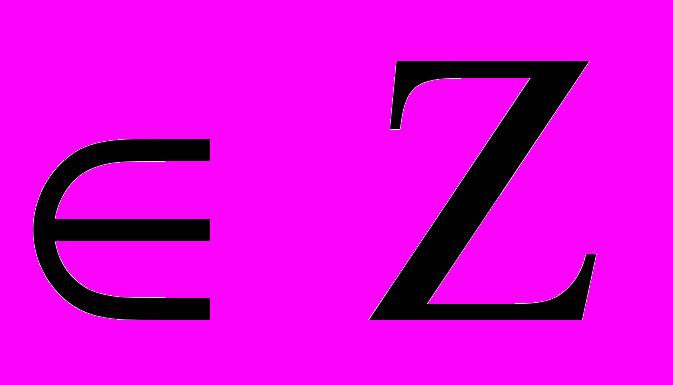2. tg x =1, x= 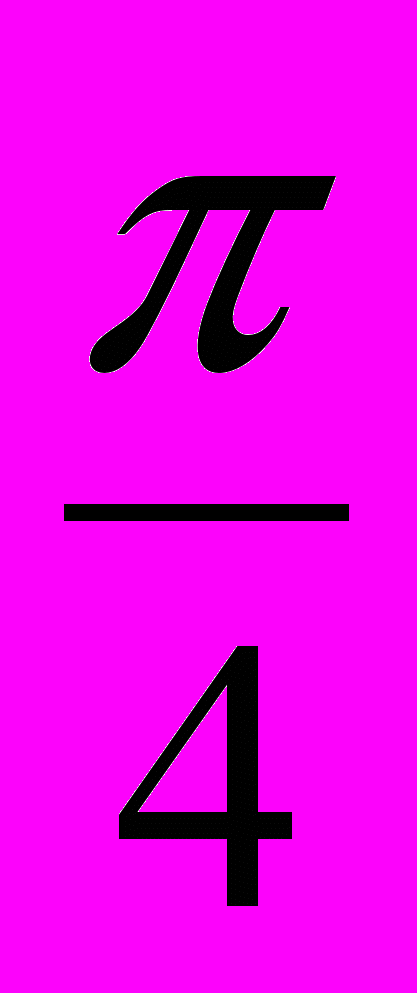+2πn, n.

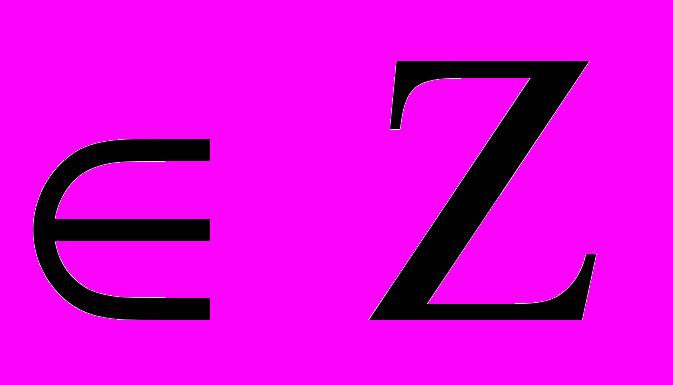3. sin²x+sinx-2=0.

Пусть t=sin x, t²+t-2=0,

D=9, x=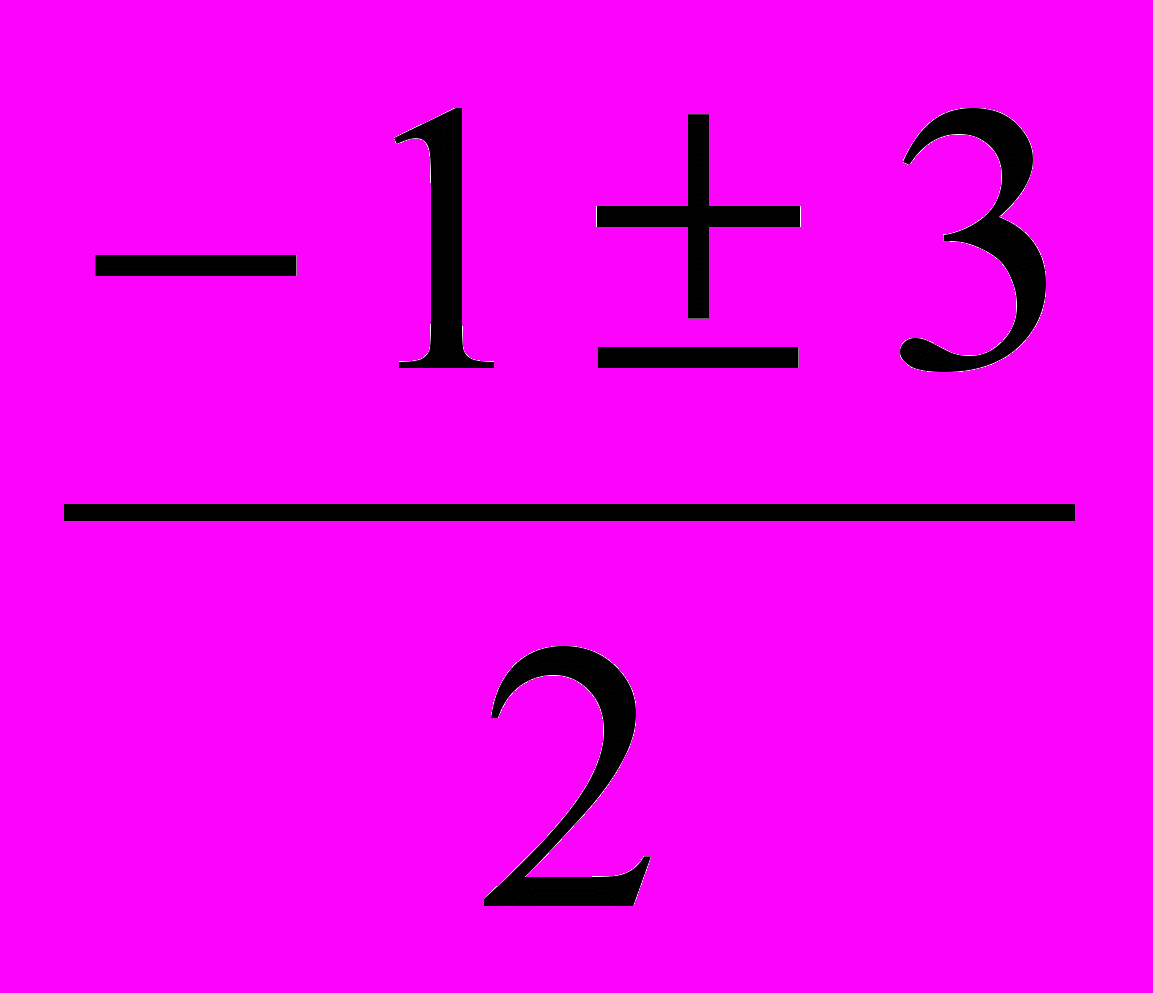, x₁=-2, x₂=1.

Ответ: -2,1.

4. sinx cosx + sinx=0.

Разделим обе части уравнения на sinx0: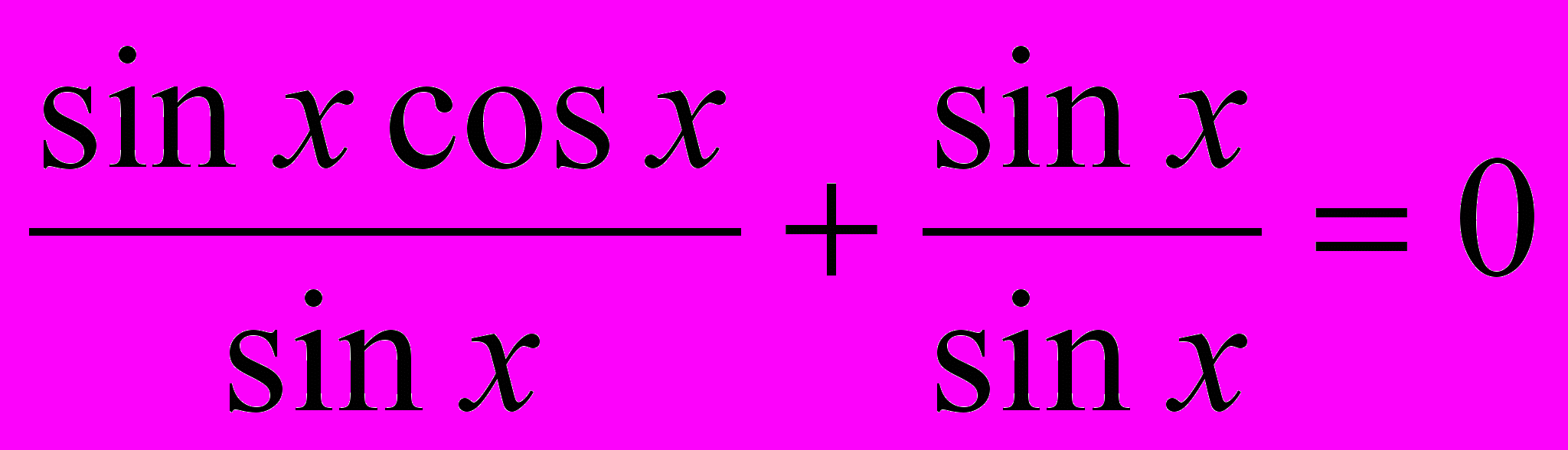

, cosx + 1=0,

cosx = -1, x= π+2πn, n.

5. sinx + cosx = 1.

Разделим обе части уравнения на cosx0.

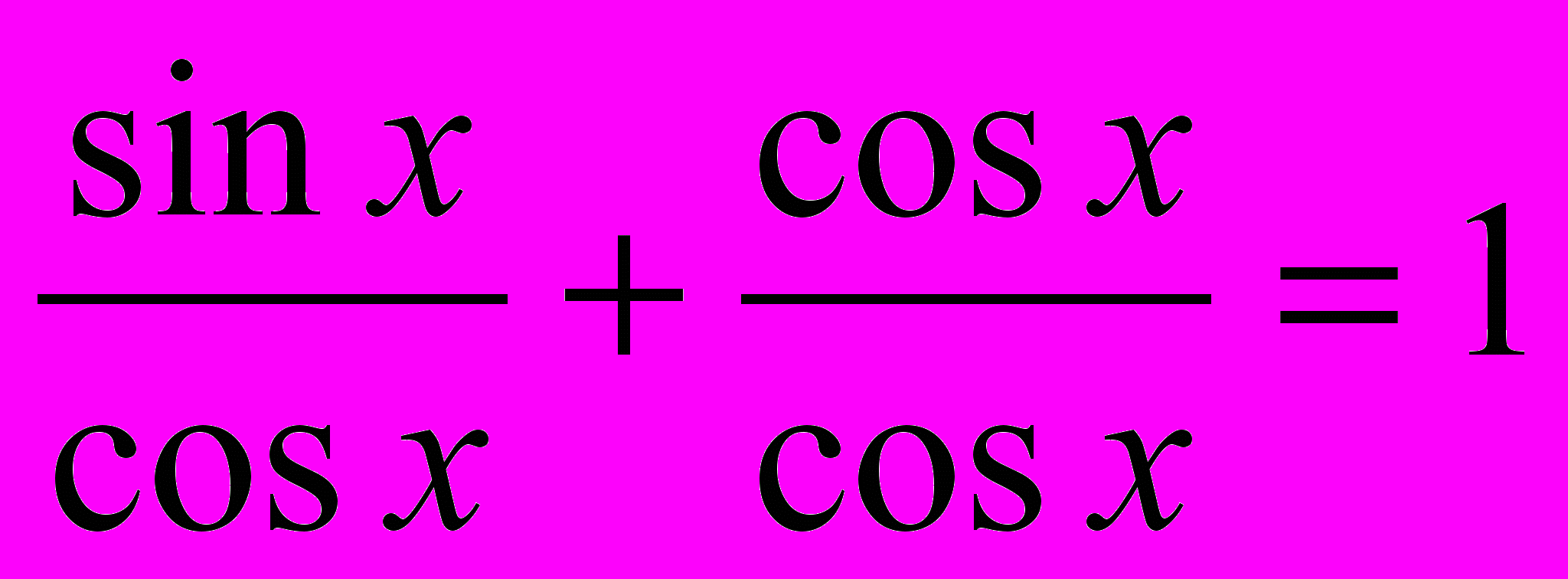, tgx+1=1, tgx=0, x=πn, n.

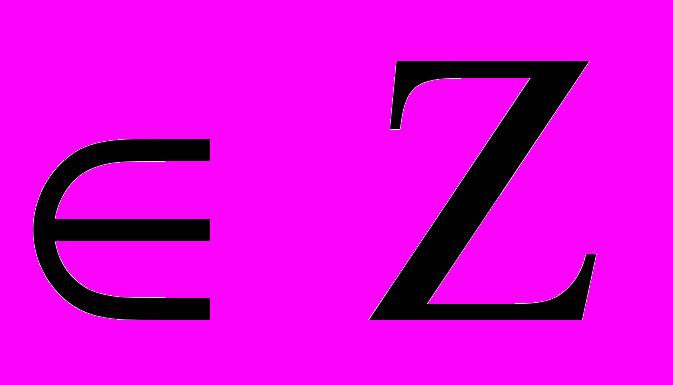Найдите ошибку в решении:

1. sin=.

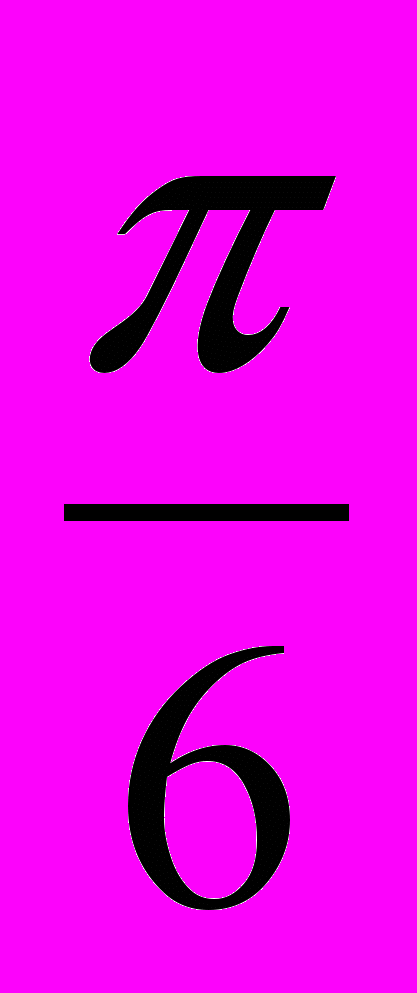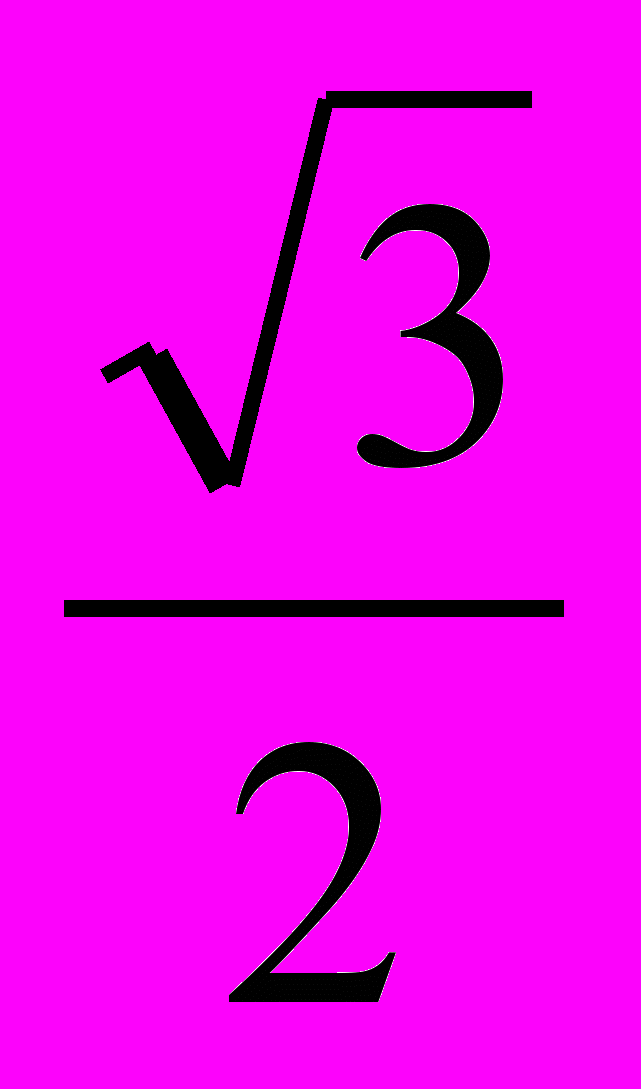2. cos(-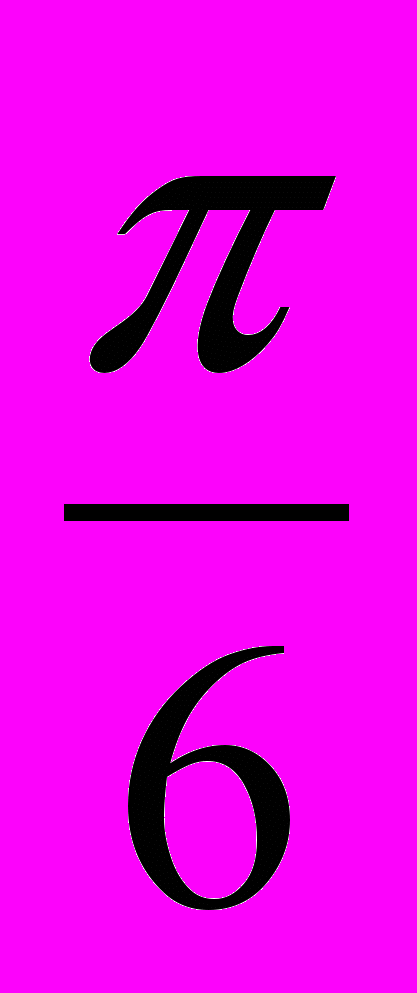)= -cos=-.

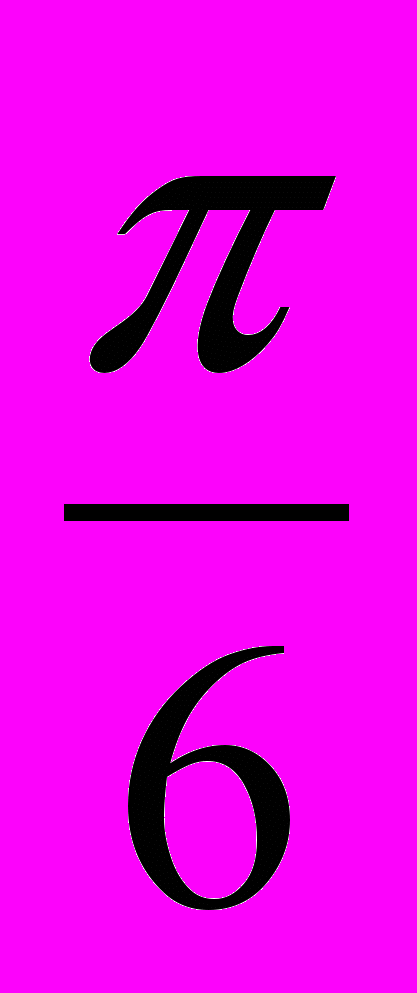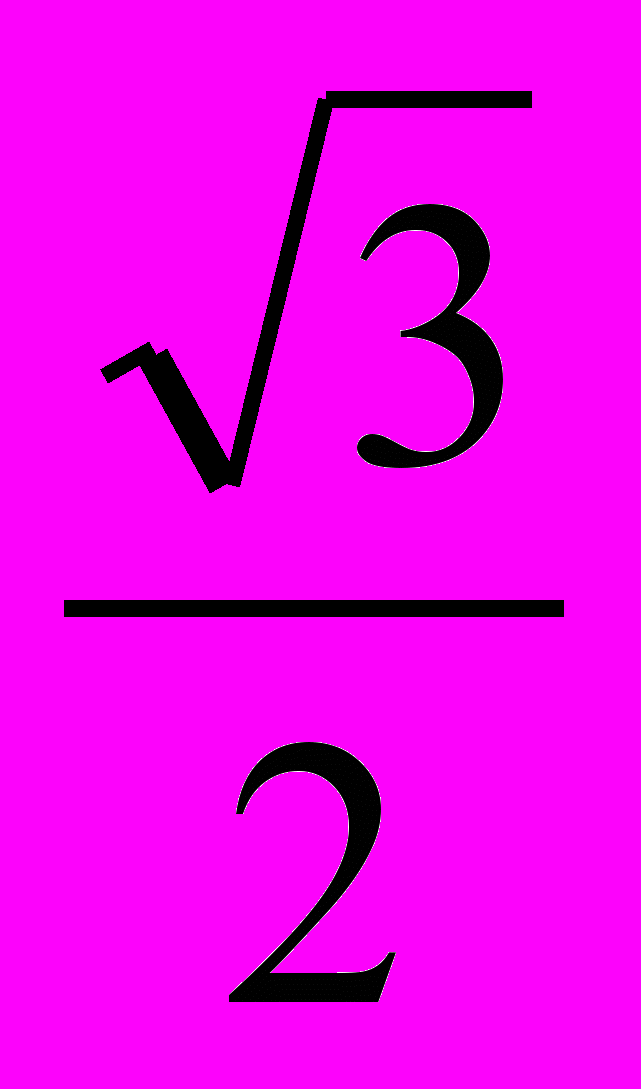3. ctg(-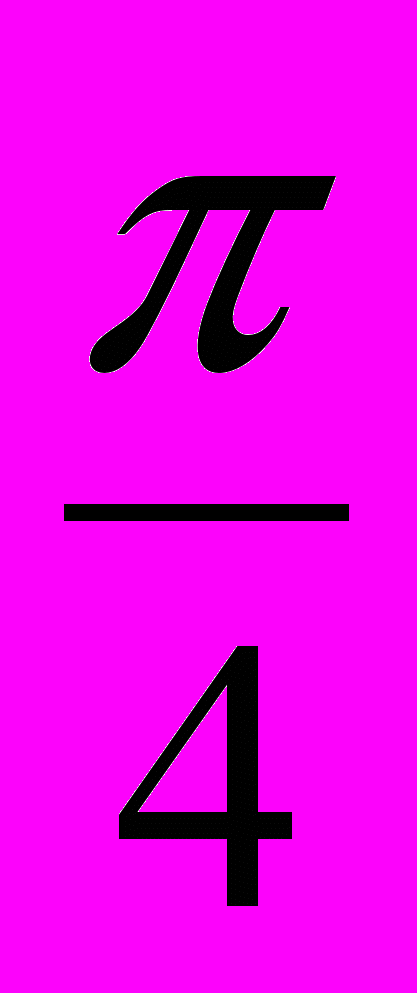)=-1.

4. cos0=0.

5. .

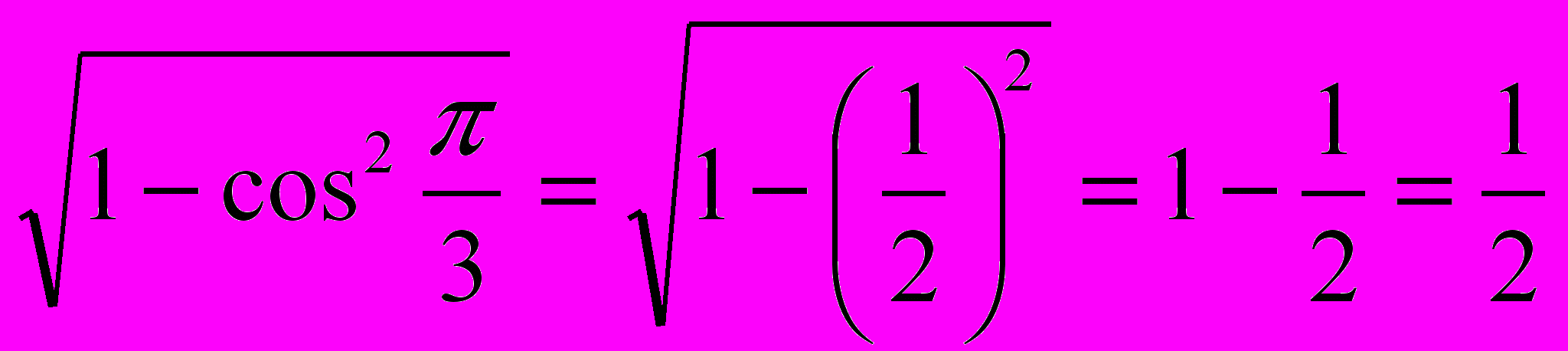4. Изучение новых знаний.(слайды) На примере уравнения sin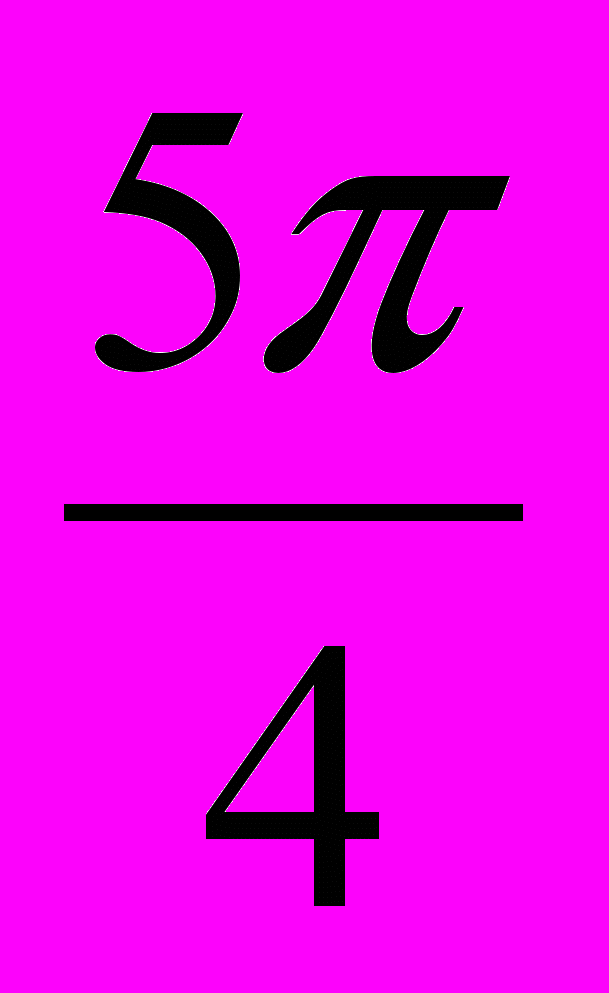x=x²-4x+5 графиков его правой и левой частей объясняется функционально – графический метод решения уравнений которые удовлетворяют условию теоремы:
   

Если на некотором промежутке

наибольшее значение функции f равно А,

а наименьшее значение функции g тоже равно А,

т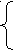о уравнение f=g равносильно системе:

f=A;

g=A.

Записывается алгоритм решения уравнений функционально – графическим методом

• Сделать эскизы графиков
  
• Если функции удовлетворяют условию теоремы, составить систему.
  
• Решить систему и сделать проверку.
  

5. Закрепление знаний, выработка умений и навыков.
   

Решаются задания (на слайдах): постройте эскизы графиков функций

1. y=x² +3;
   
2. y=-x²-5;
   
3. y=|x| +2;
   
4. y=x²-6x+10;
   
5. y=|cos x|.
   

Решите уравнения:

1. x² +3=cosx+2;
   
2. cosx=|x|+1;
   
3. x²-6x+10=|cos x|.
   

4)-cos 7πx =x²-6x+10.

Решите уравнение с параметром: 14=13+cos10πx-(6a+5)².

Составьте условие уравнения

6. Поведение Итогов. Если осталось время – «Шапка вопросов». Оценки, подарки.