Основные методы решения тригонометрических уравнений

Вид материала

Документы

Содержание II Замена переменной V Метод преобразования уравнения с помощью тригонометрических формул.

Подобный материал:

• Методы решения тригонометрических уравнений, 53.9kb.
• Конспект урока. Тема урока. Функционально-графические методы при решении тригонометрических, 66.13kb.
• Реферат по математике. На тему: «основные методы решения систем уравнений с двумя переменными», 140.92kb.
• Цель: Рассмотреть способы решения тригонометрических уравнений, 43.07kb.
• План занятия элективного курса в 10 классе по теме: «Решение тригонометрических уравнений,, 39.39kb.
• Учебного заведения, 120.64kb.
• План конспект па алгебре и началам анализа в 10 классе Тема урока: Тригонометрические, 109.55kb.
• Приближенные методы решения уравнений, 78.01kb.
• Старые методы для решения новых систем уравнений Тип урока, 38.55kb.
• Старые методы для решения новых систем уравнений Тип урока, 37.32kb.

Основные методы решения тригонометрических уравнений.


I Приведение к простейшим тригонометрическим уравнениям.


Схема решения.

1). Выразить тригонометрическую функцию через известные компоненты.

2). Найти аргумент функции по формулам:

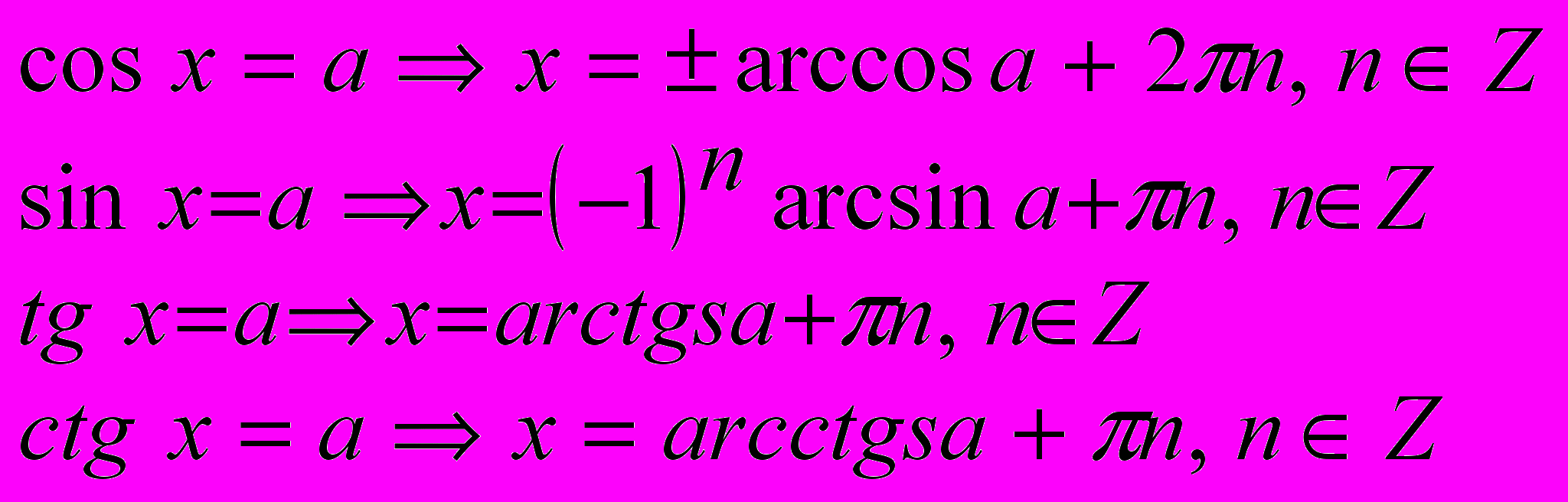3). Найти неизвестную переменную.


Пример.

Решение.

1). ;

2).

;

3).

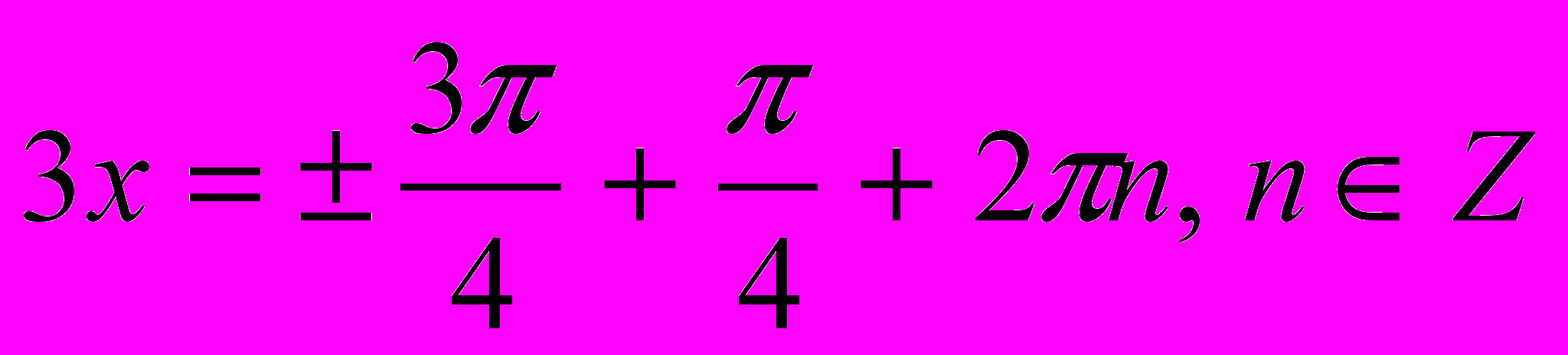
Ответ: .


II Замена переменной


Схема решения.

1). Привести уравнение к алгебраическому относительно одной из тригонометрических функций.

2). Обозначить полученную функцию переменной t

(ели необходимо, ввести ограничения на t)

3). Записать и решить полученное алгебраическое уравнение.

4). Сделать обратную замену.

5). Решить простейшее тригонометрическое уравнение.

Пример.

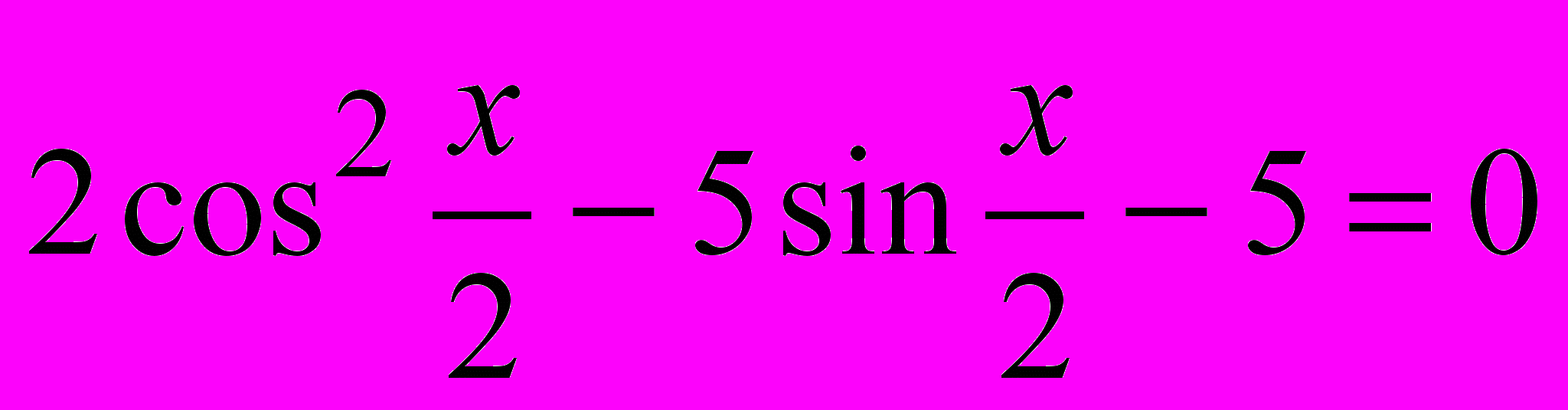
Решение.

1).

;

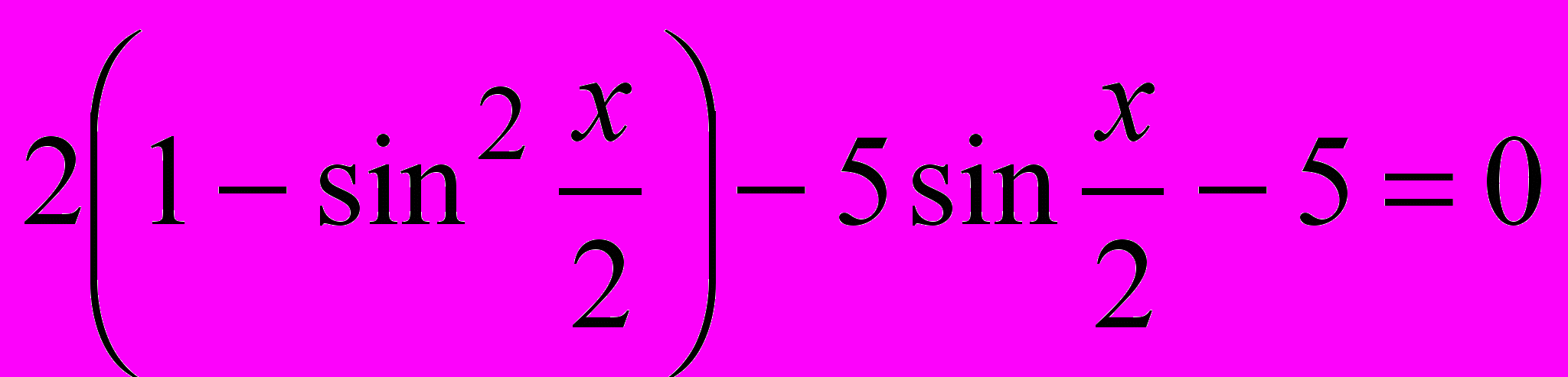
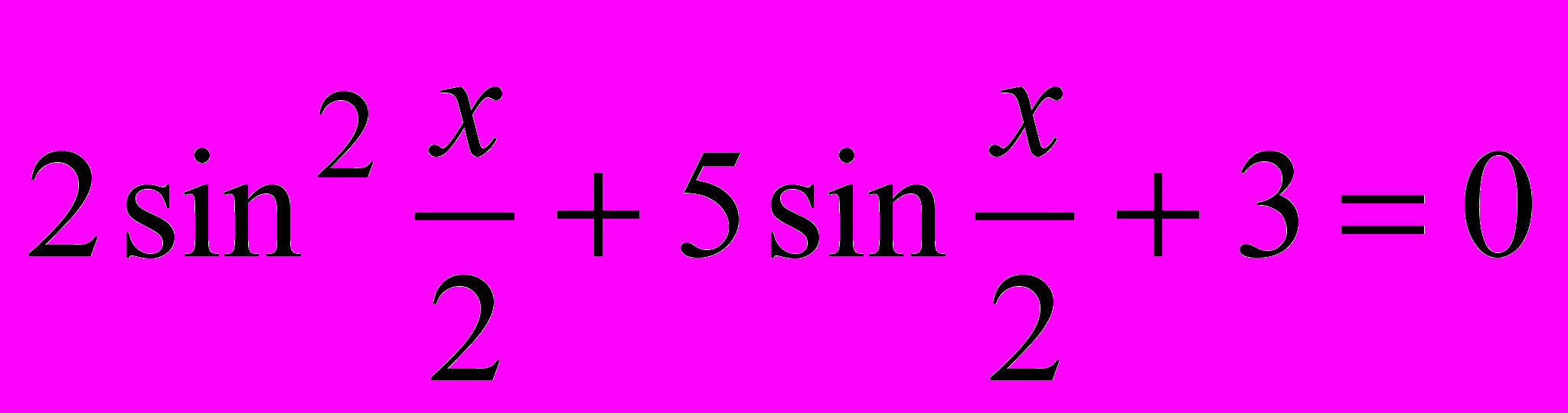2). Пусть .

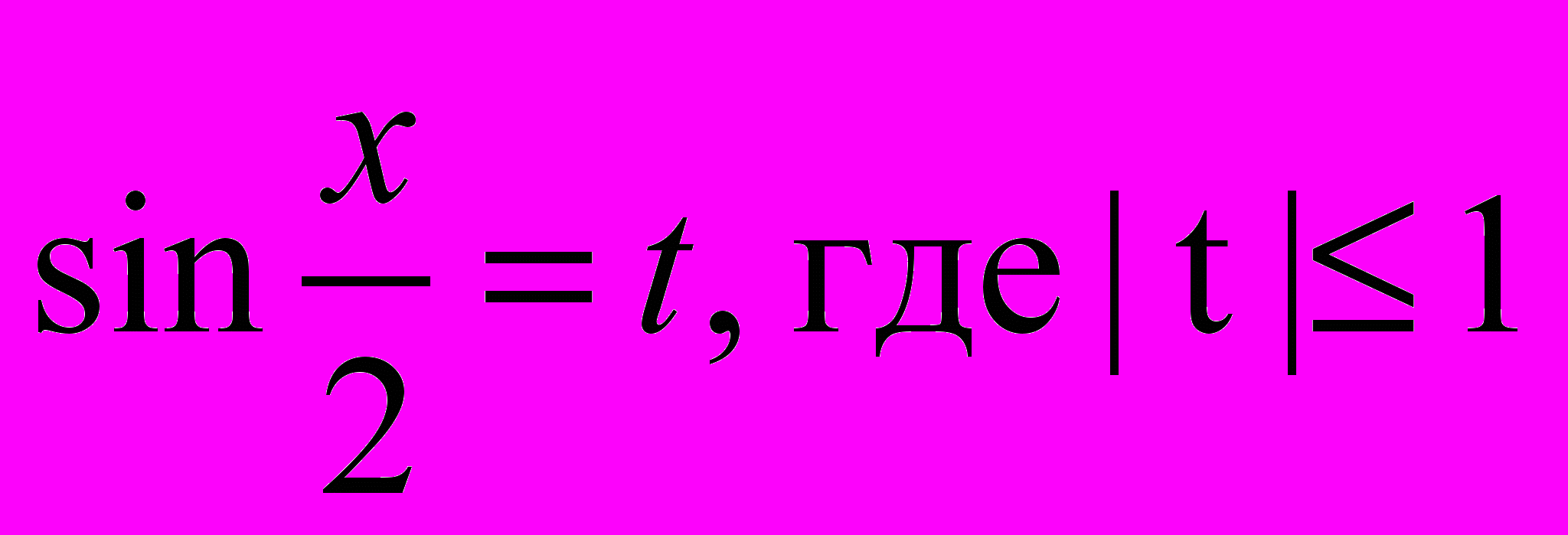3). ;



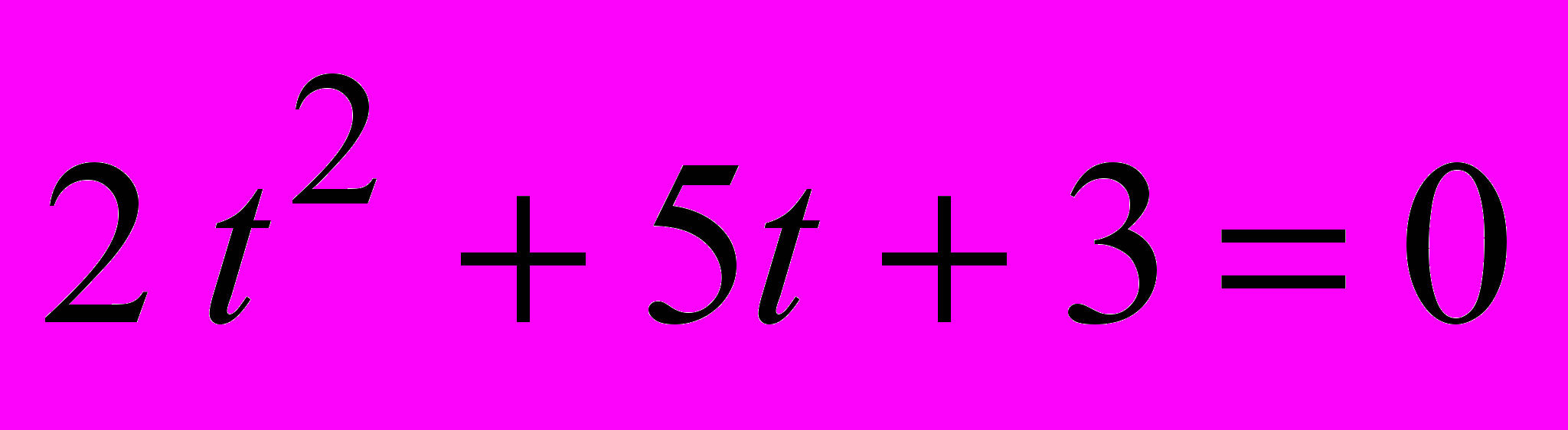4).

5).



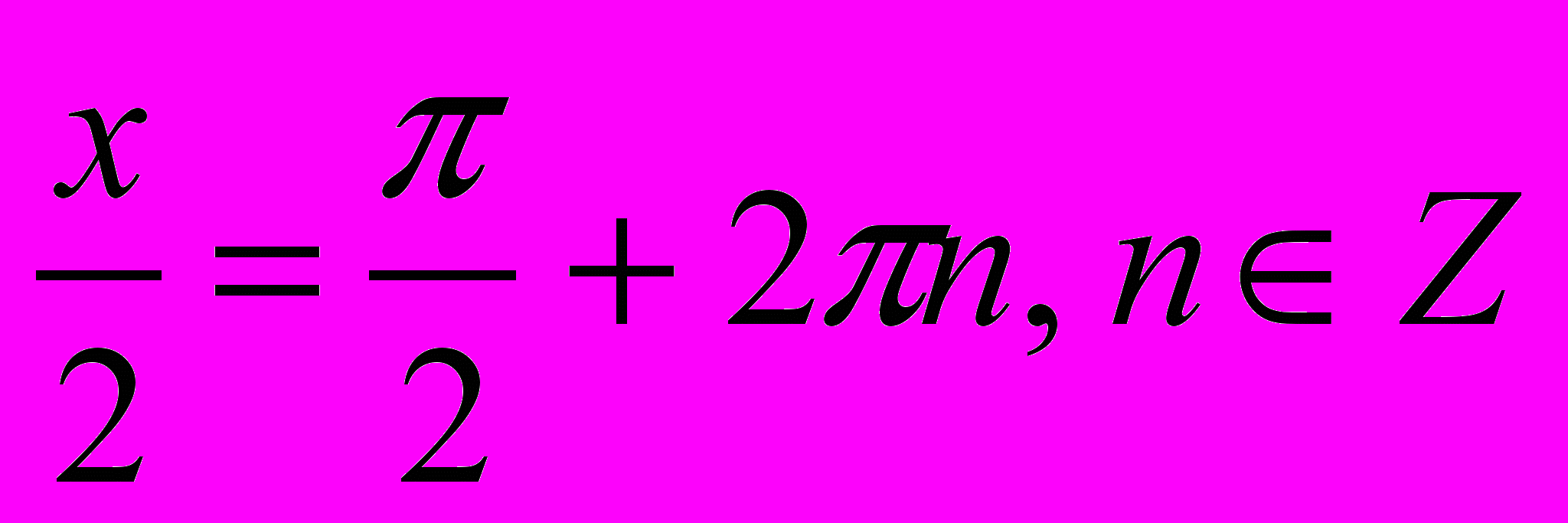
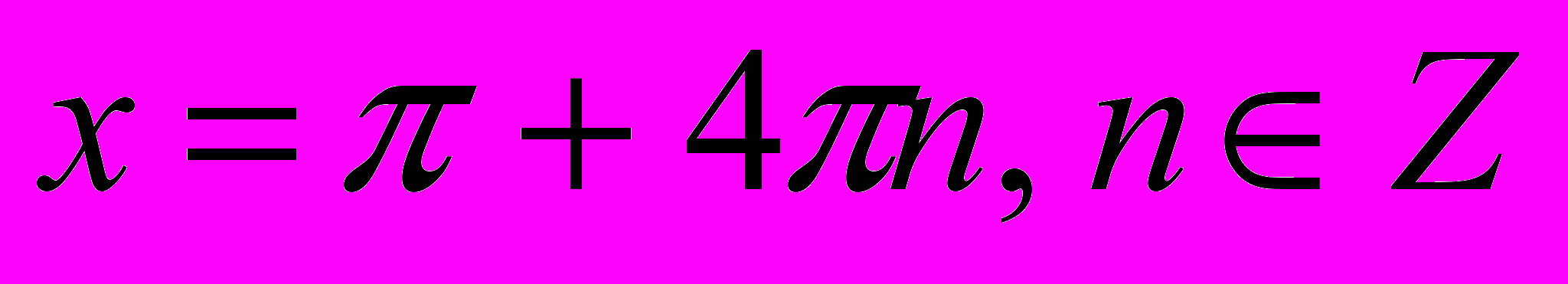
Ответ:


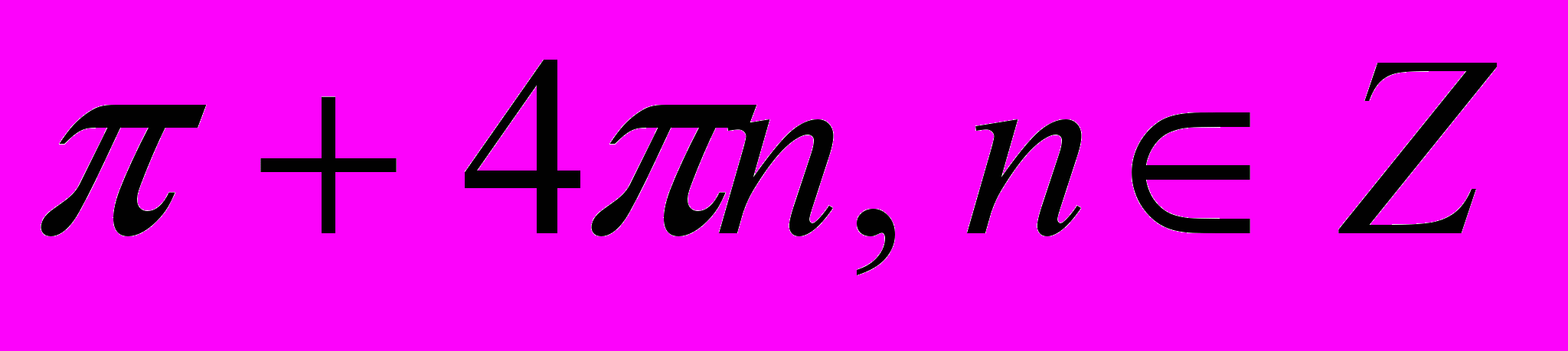
III Метод понижения порядка уравнения.


Схема решения.

1). Заменить данное уравнение линейным, используя формулы понижения степени:



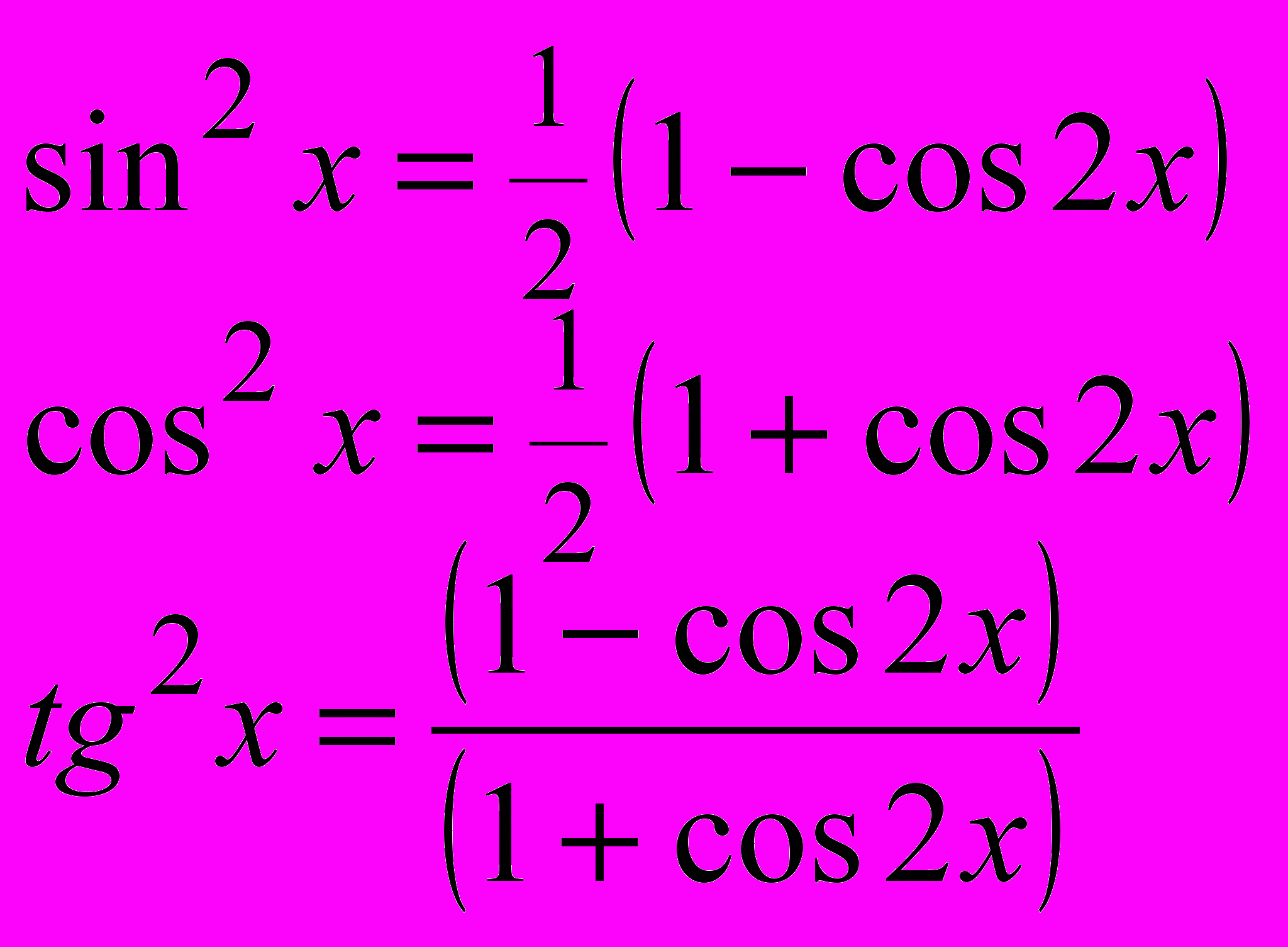
2). Решить полученное уравнение с помощью методов I и II.


Пример.

Решение.

1).

2).









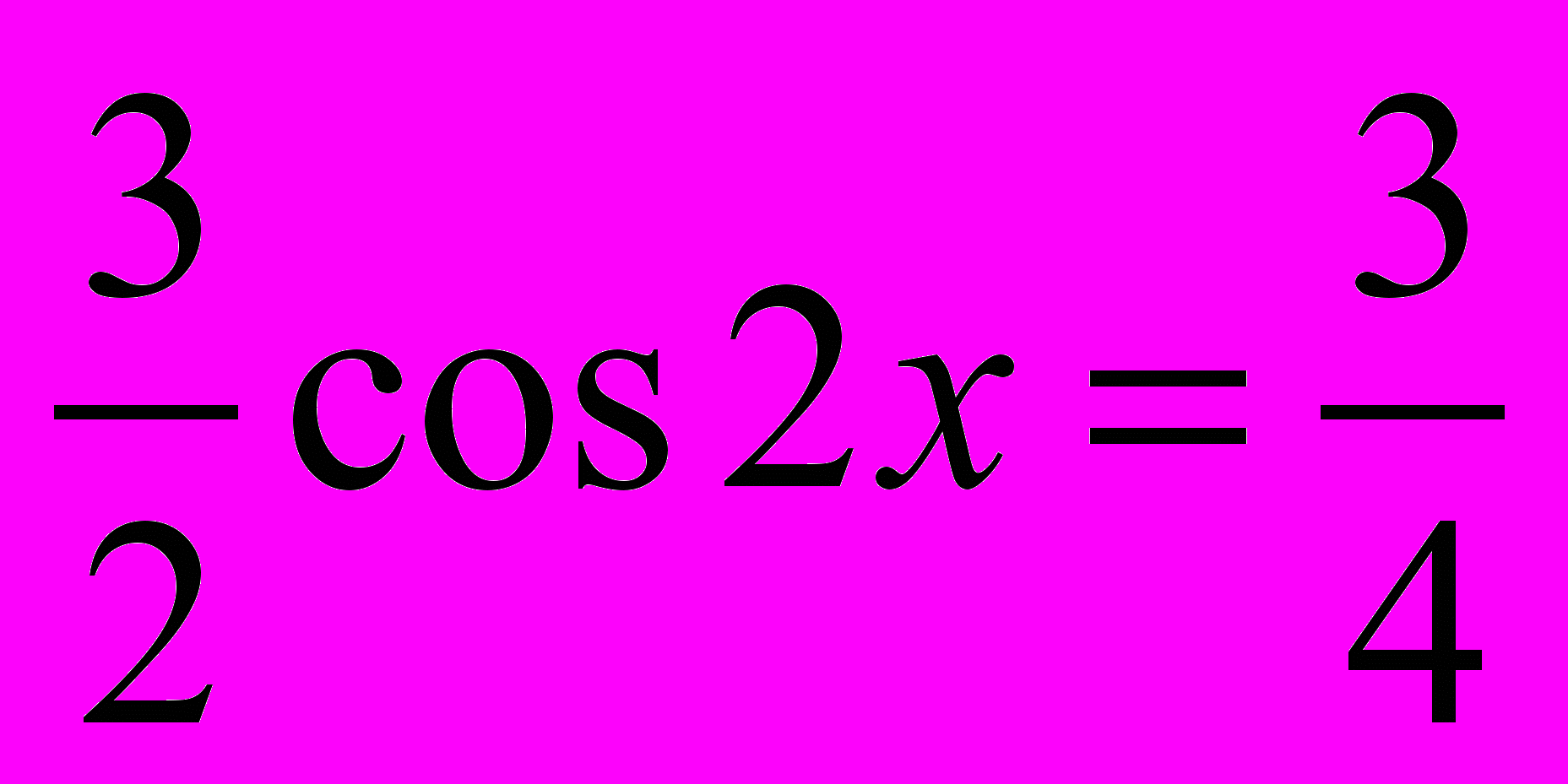
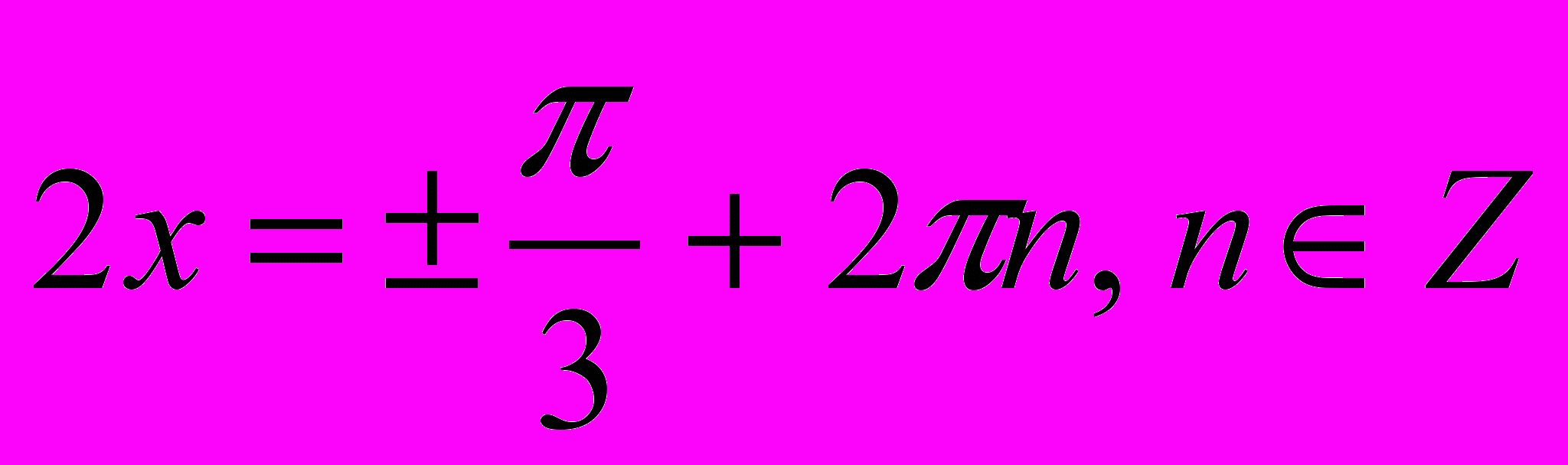
Ответ:


IV Однородные уравнения.


Схема решения.

1) Привести уравнение к виду

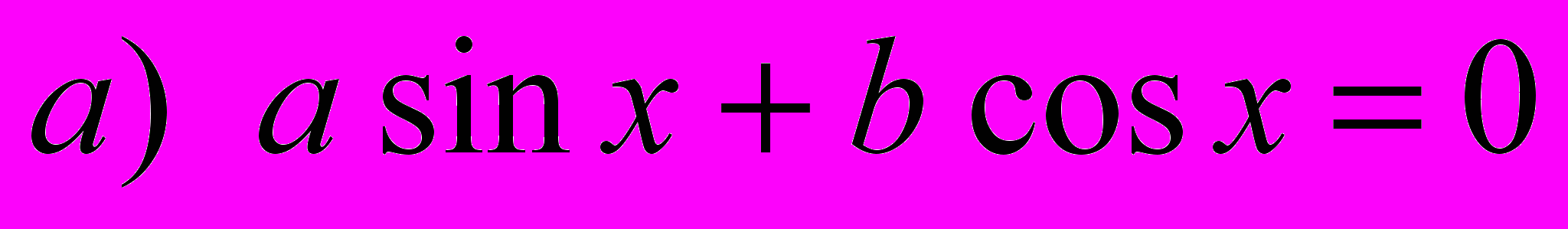или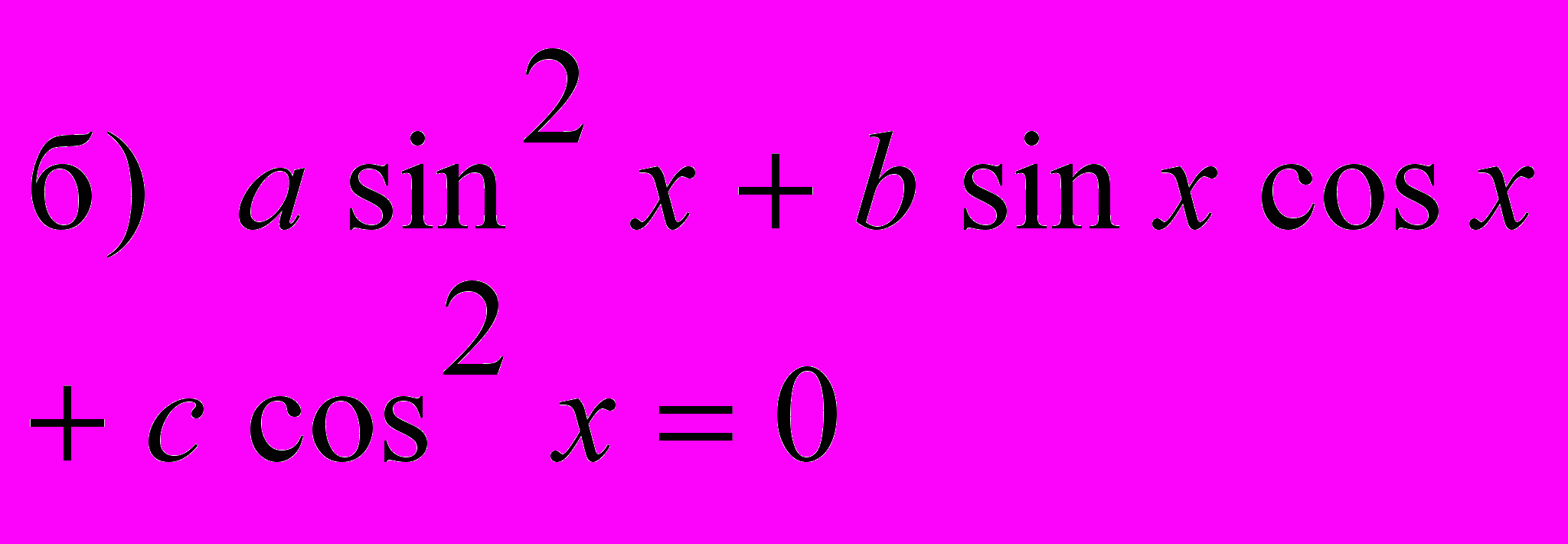

2). Разделить обе части

уравнения на

а) и получить уравнение относительно :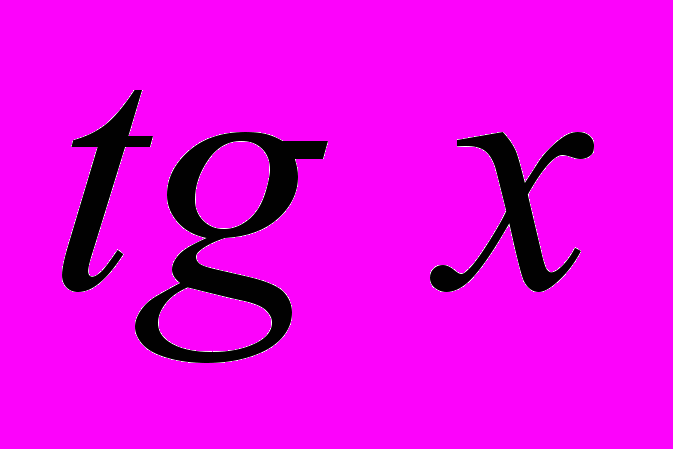





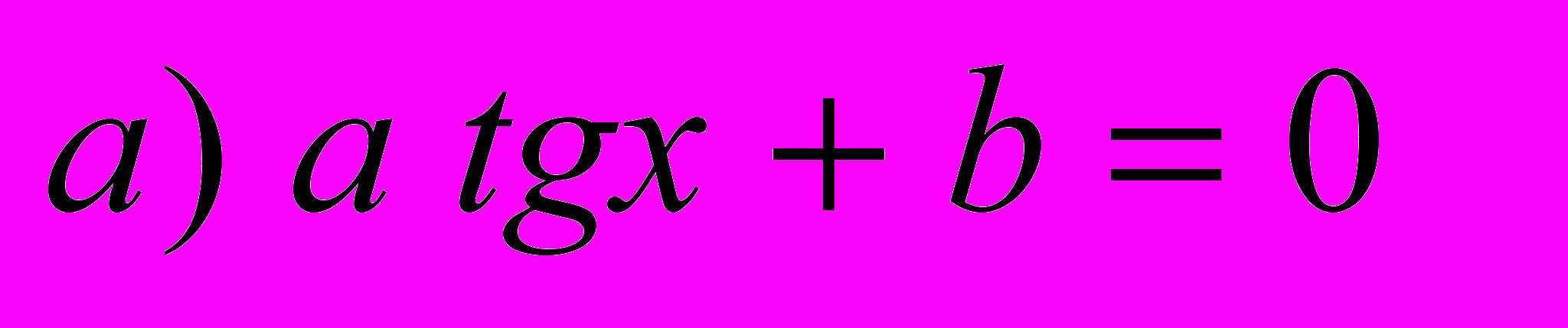
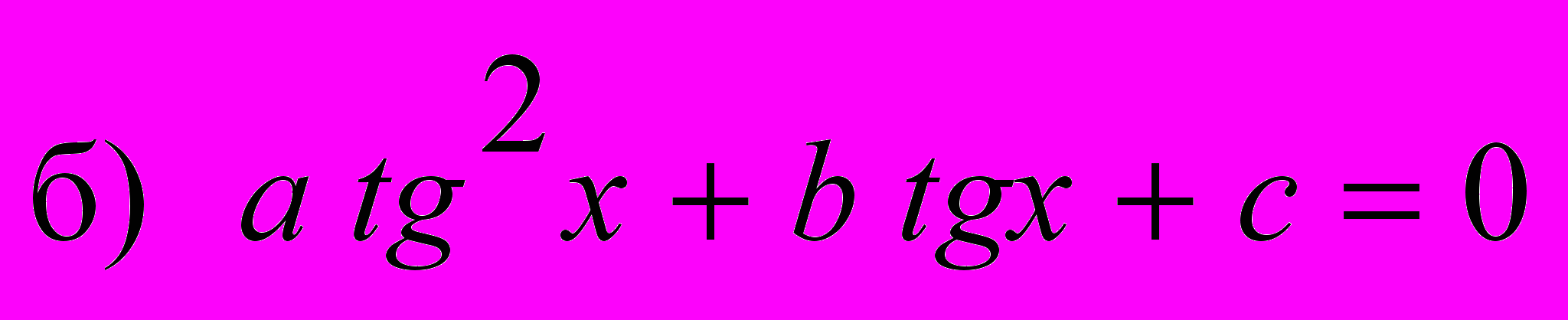
3). Решить уравнение известными способами.


Пример.

Решение.

1).

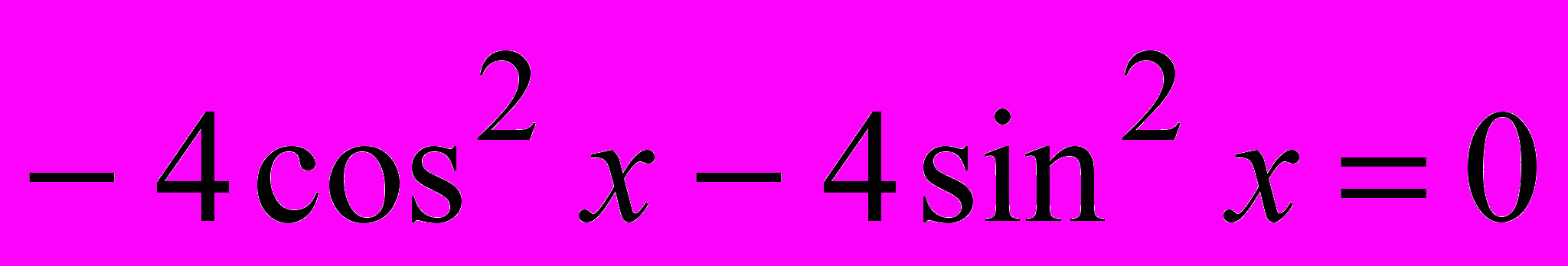
2).

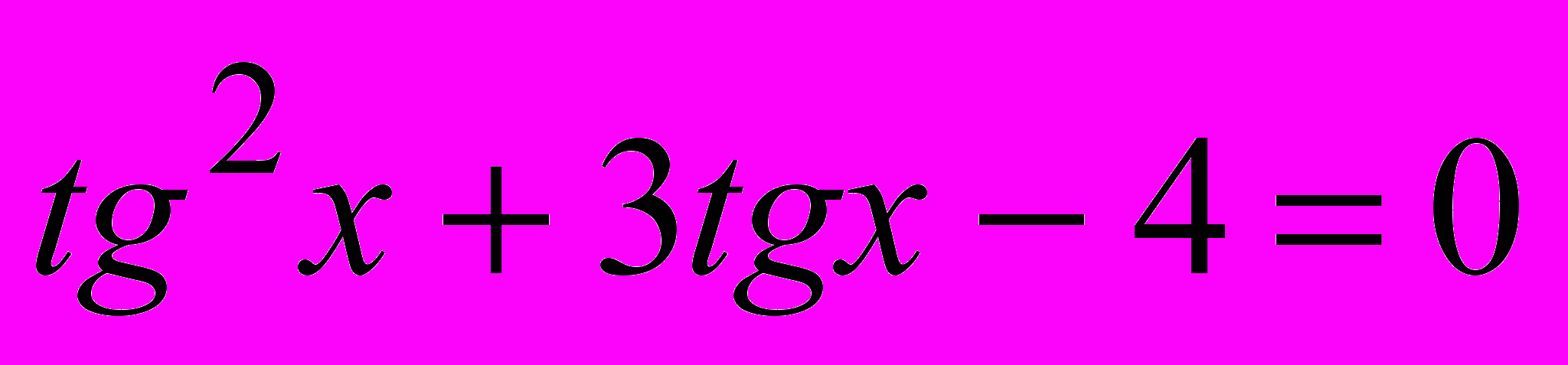
3). Пусть 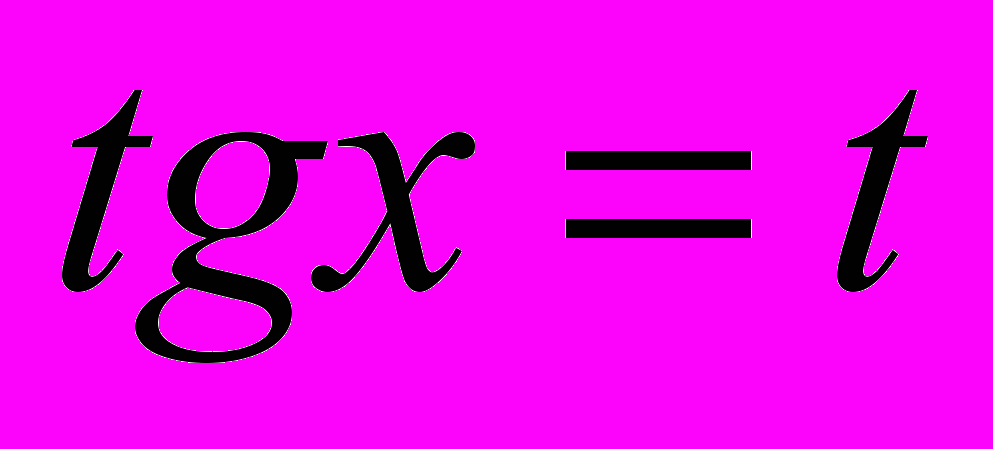, тогда







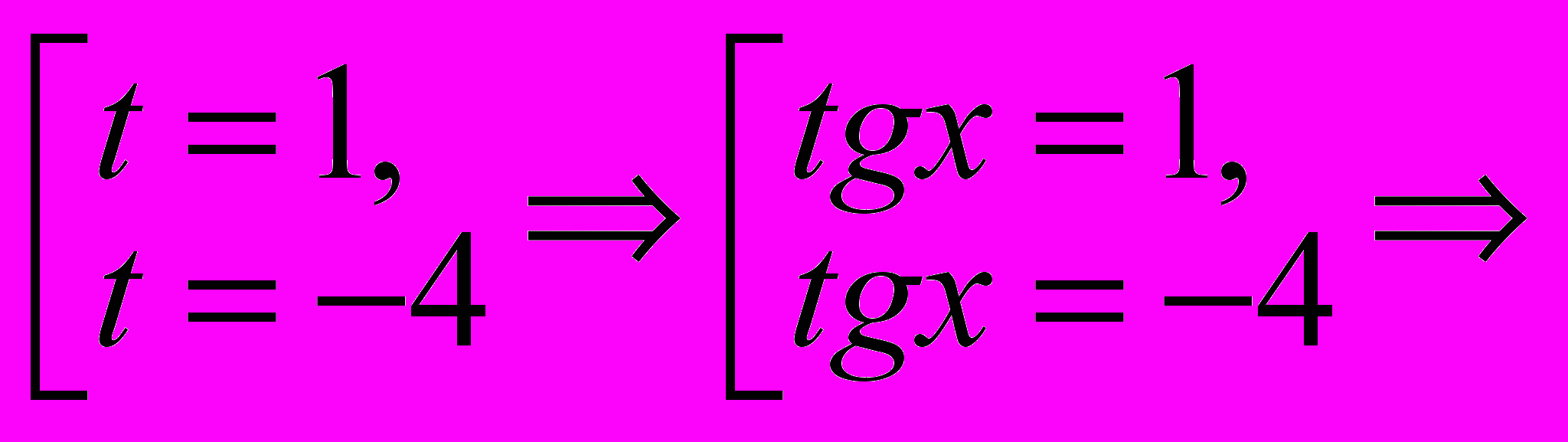
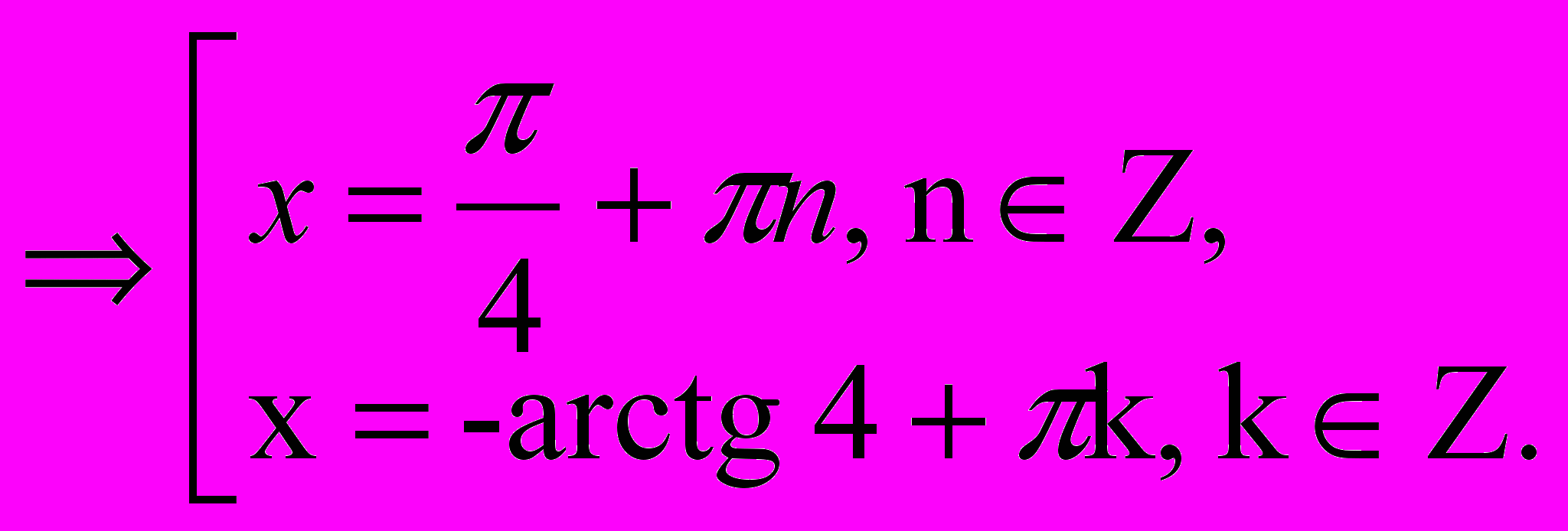
Ответ:

V Метод преобразования уравнения с помощью тригонометрических формул.


Схема решения.

1). Используя тригонометрические формулы, привести уравнение к уравнению, решаемому методами I,II,III,IV.


2). Решить полученное уравнение известными методами.


Пример.


Решение.

1). ;



2). ;



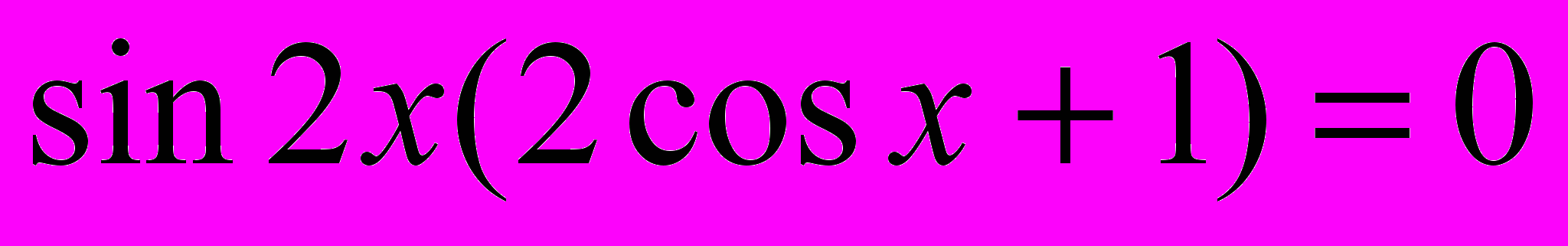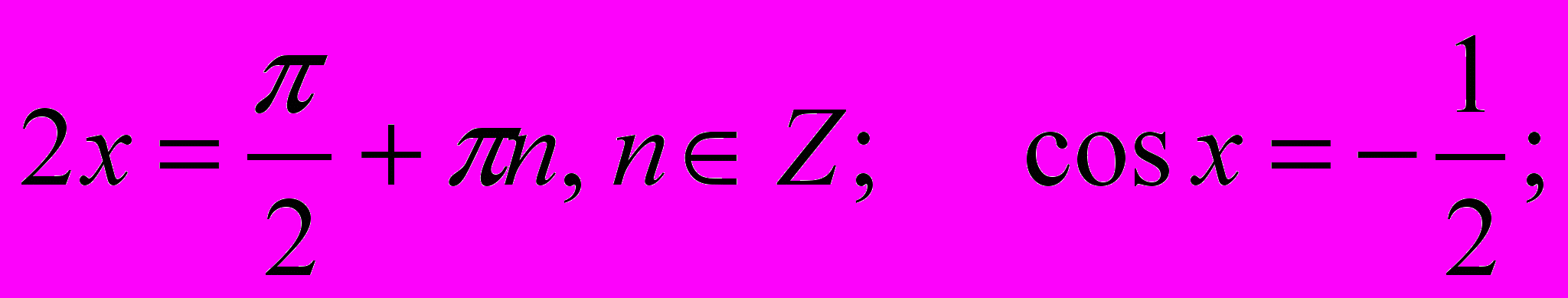
Ответ: