План занятия элективного курса в 10 классе по теме: «Решение тригонометрических уравнений, содержащих знак абсолютной величины»
| Вид материала | Решение |
- План конспект па алгебре и началам анализа в 10 классе Тема урока: Тригонометрические, 109.55kb.
- Конспект урока. Тема урока. Функционально-графические методы при решении тригонометрических, 66.13kb.
- Методы решения тригонометрических уравнений, 53.9kb.
- Методика изучения уравнений в курсе алгебры 7-9 классов Примерное содержание, 12.53kb.
- Программа элективного курса «решение алгебраических уравнений высоких степеней», 84.18kb.
- Методический комплекс по теме: «Решение тригонометрических уравнений и неравенств», 157.93kb.
- Урок итогового повторения по теме «Решение тригонометрических уравнений и неравенств», 22.26kb.
- Тема: «Решение квадратных уравнений с помощью номограммы», 98.28kb.
- Программа элективного курса по математике для учащихся 9-11, 194.16kb.
- "Решение тригонометрических уравнений", 94.47kb.
План занятия элективного курса в 10 классе по теме:
«Решение тригонометрических уравнений, содержащих знак абсолютной величины».
Цель: научить учащихся применять алгоритм решения уравнений с модулем к тригонометрическим уравнениям.
I. Вступление.
На предыдущих занятиях мы работали с типовыми заданиями по тригонометрии. Это задания группы А и В. Сегодня проверим как вы усвоили этот уровень.
- 1) Контроль знаний в форме теста. Учащиеся в тетрадях оформляют решение, а в бланки ответов заносят решения (см. приложение).
2) Один учащийся работает с интерактивной доской – решает тригонометрические уравнения.
Собираются работы учащихся и сверяются с правильными ответами на доске.
Проверяются задания учащегося у интерактивной доски.
- Результаты показали, что основная часть усвоила типовые задания по тригонометрии. Кому-то есть еще над чем поработать. Сегодня мы рассмотрим тригонометрические уравнения, содержащие знак абсолютной величины. В прош8лом году мы изучали на элективных занятиях тему «Модуль» - преобразовывали алгебраические выражения, решали алгебраические неравенства и уравнения с модулем. Давайте вспомним, как решались уравнения с модулем. Презентацию подготовили Числов Максим и Боброва Юлия.
Презентация
«Решение уравнений,
содержащих знак абсолютной величины».
Модулем числа а называют расстояние (в единичных отрезках) от начала координат до точки А (а).
 .О .А (а)
.О .А (а) а
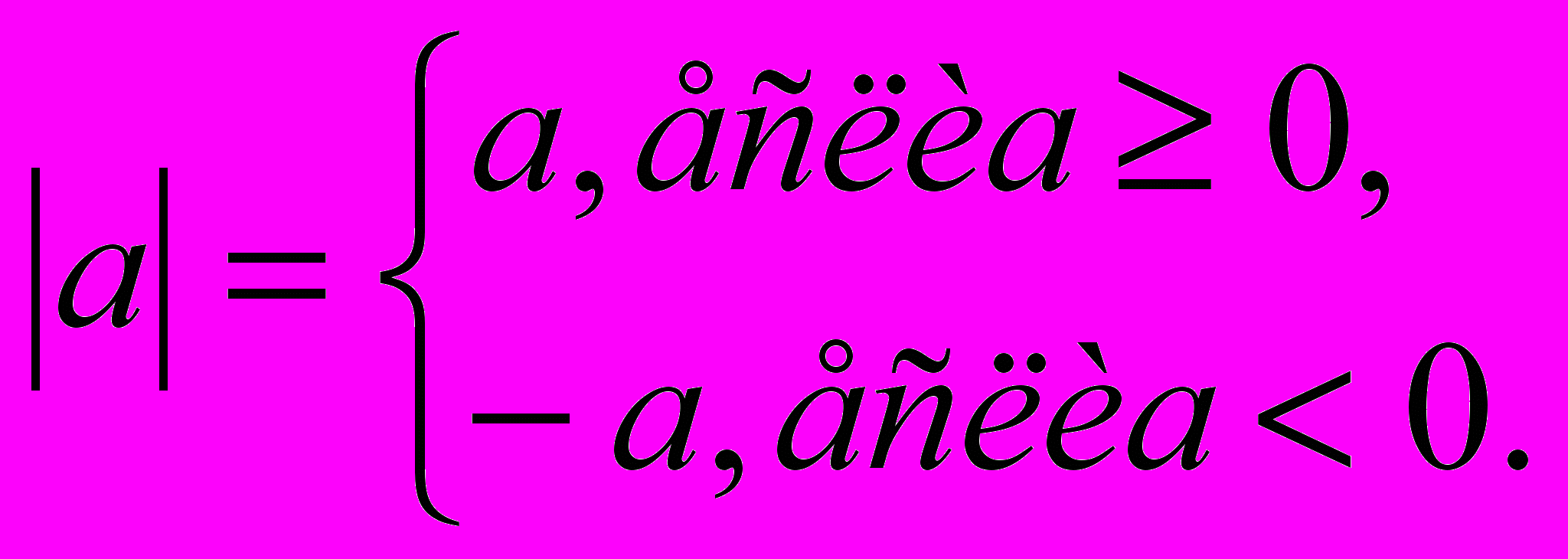
Уравнения с модулем.
1.
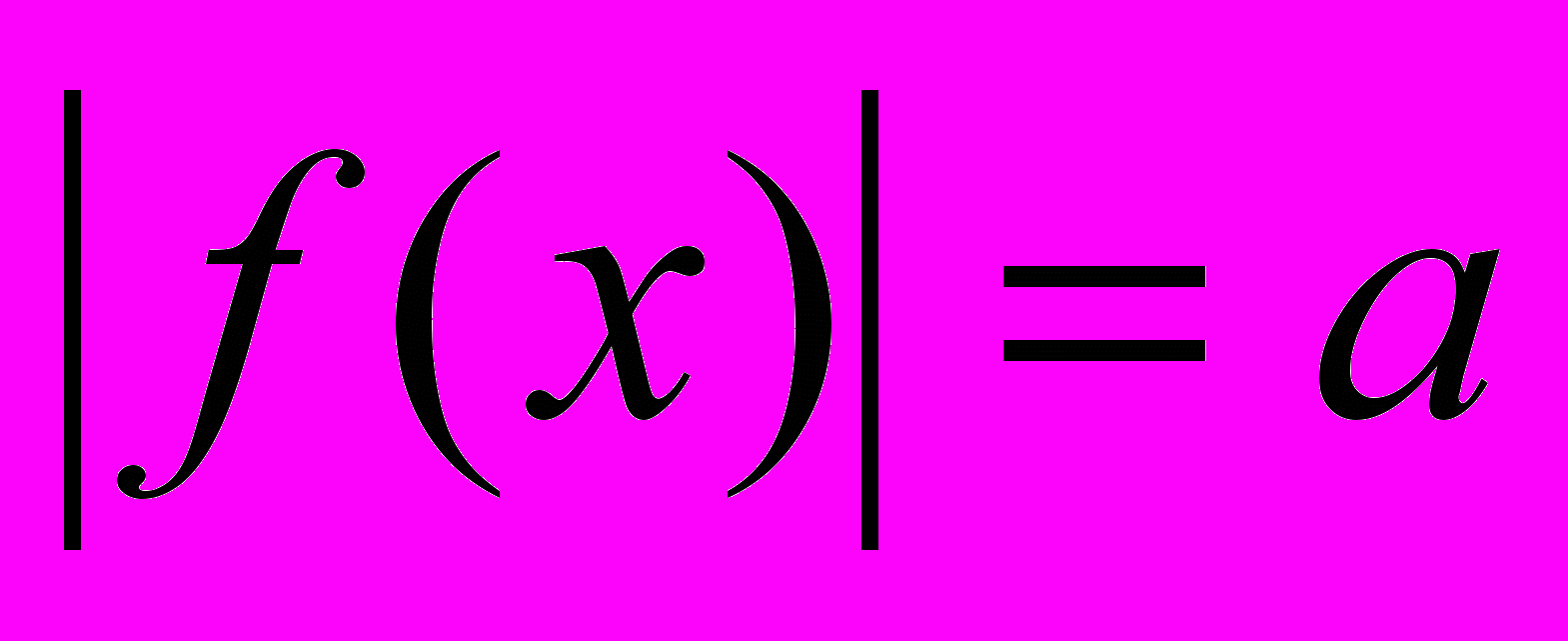
а)
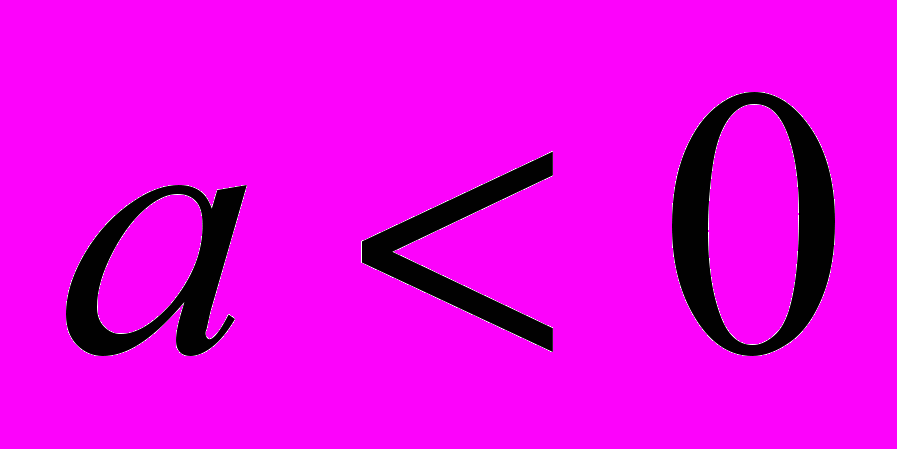 , решений нет.
, решений нет.б)
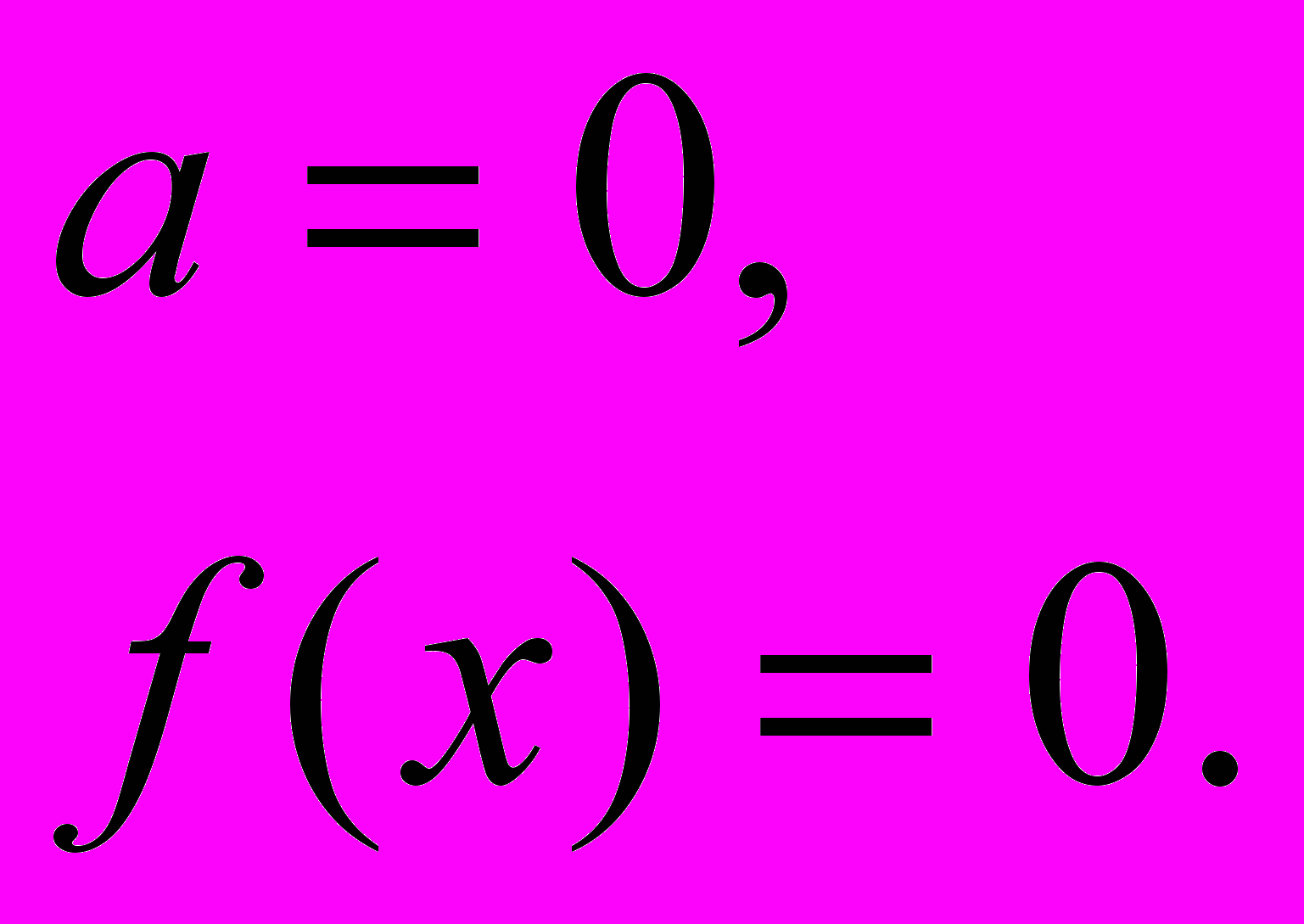
в)
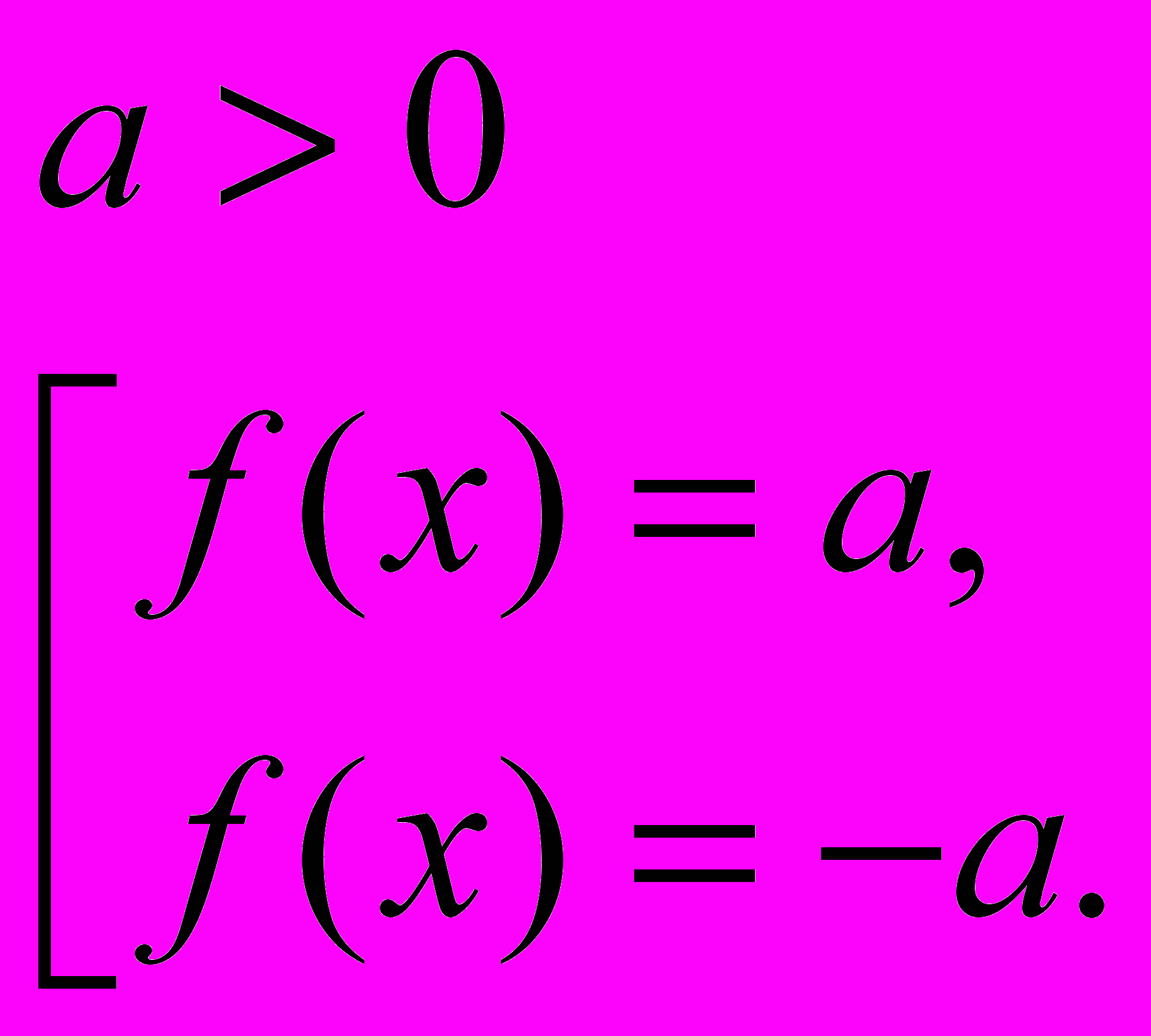
2.
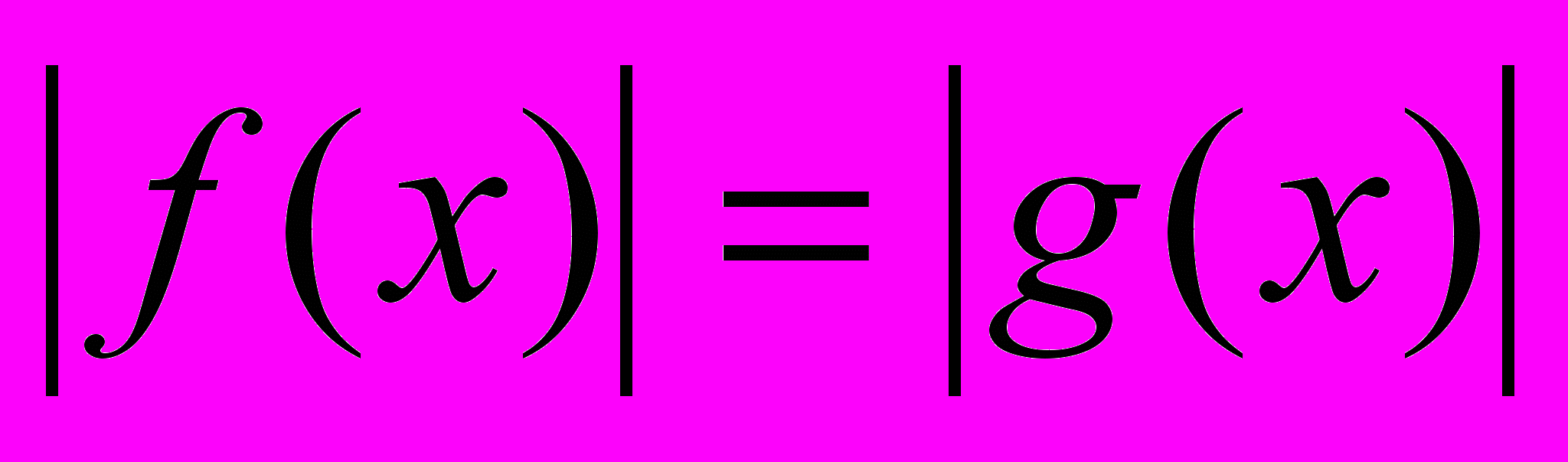
равносильно объединению уравнений:
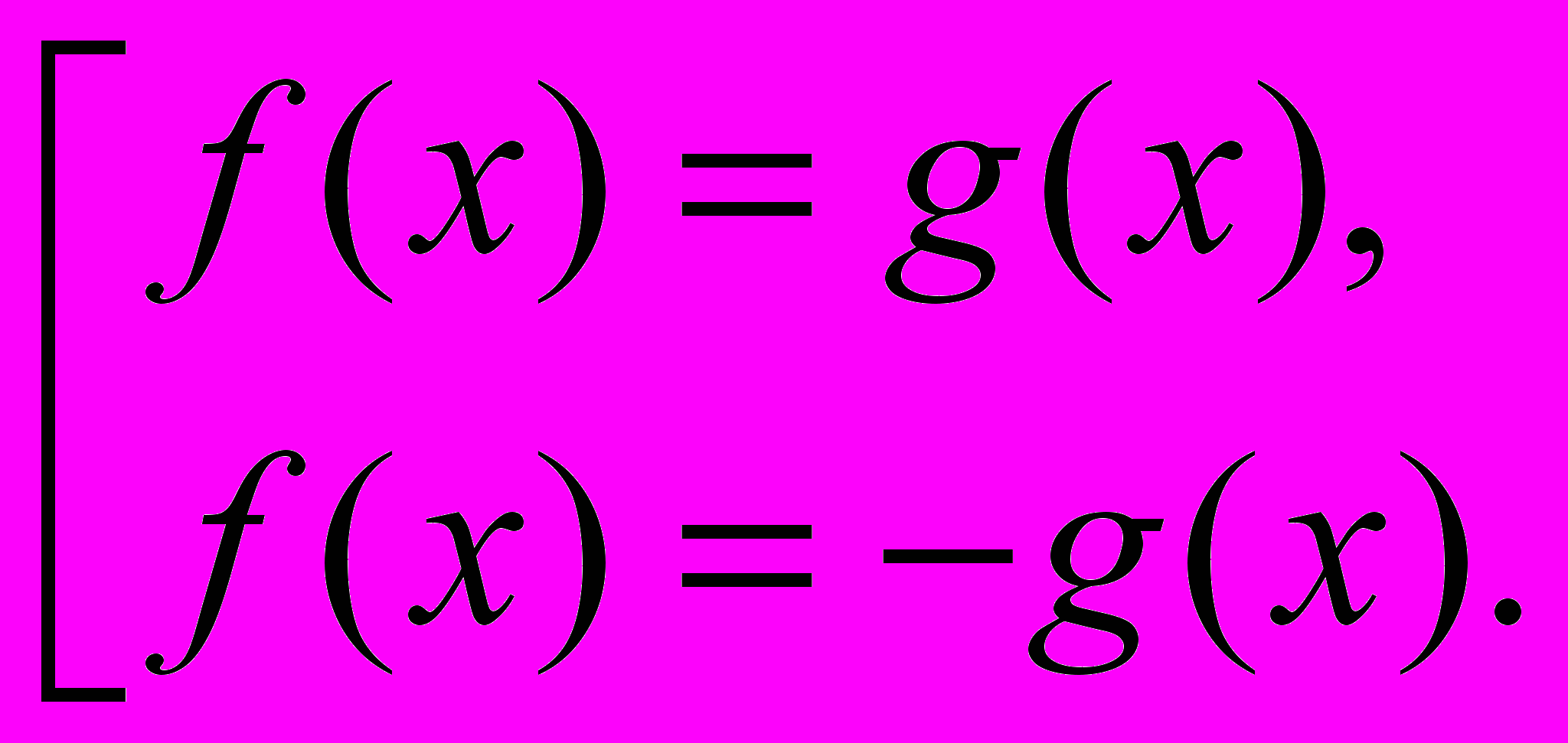
3.
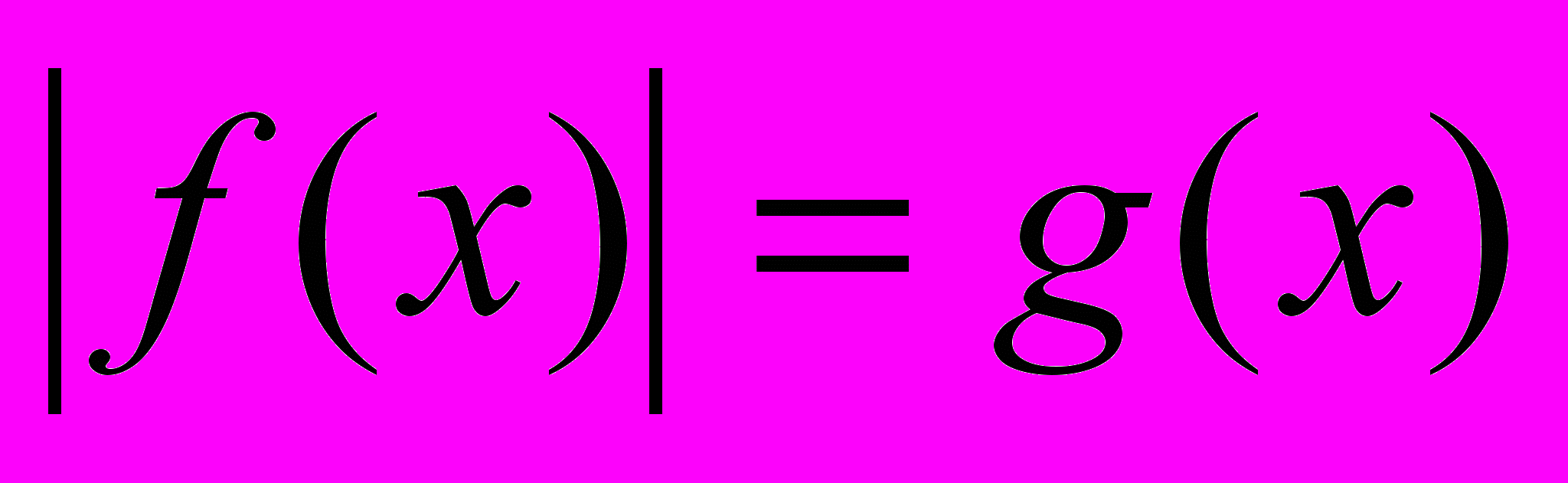
равносильно системе уравнений:
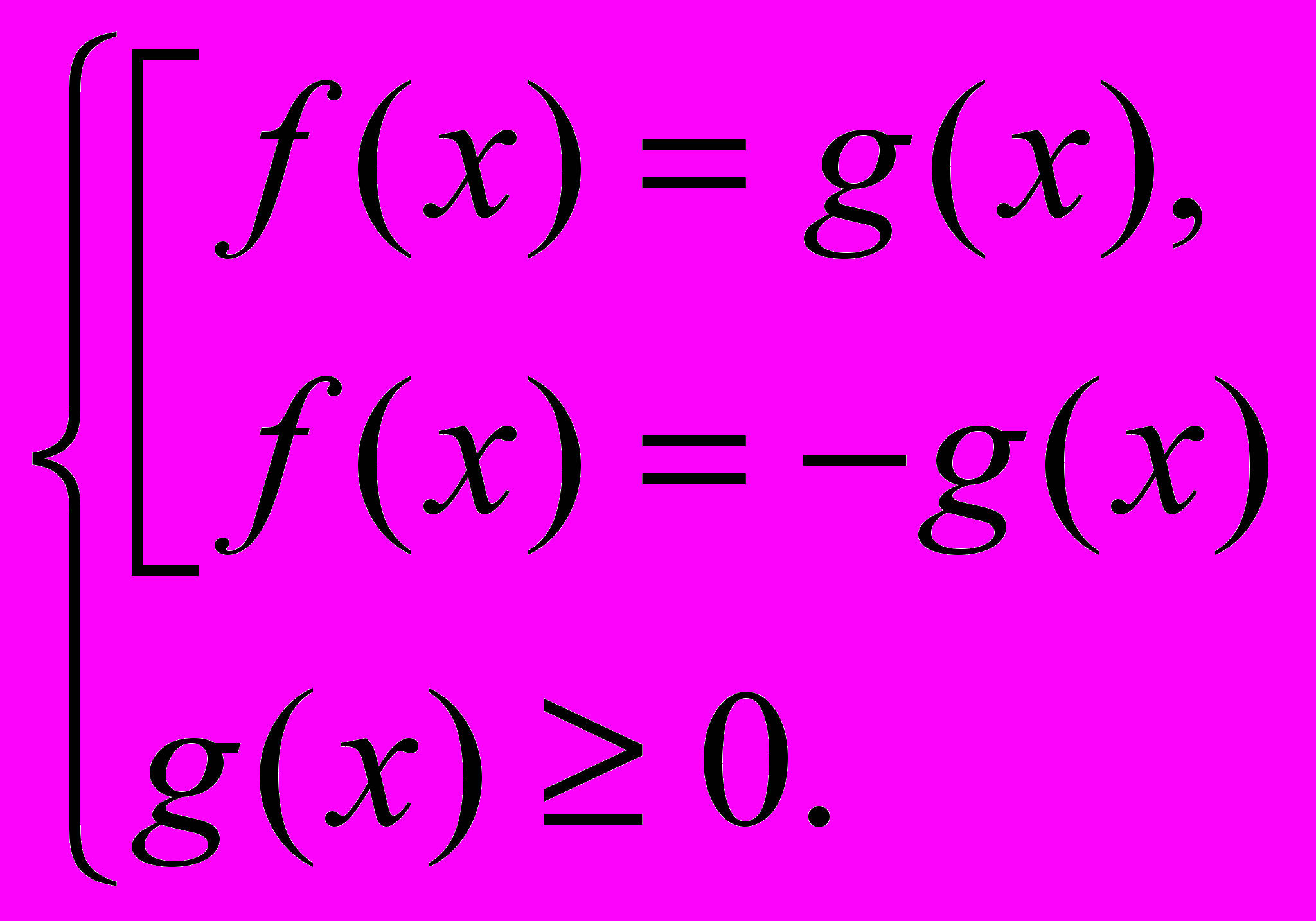
4. Алгоритм решения уравнений с переменной под знаком модуля на числовых промежутках.
а) Найти точки, в которых выражение под знаком модуля обращаются в нуль.
б) Разбить числовую ось на промежутки найденными точками.
в) Раскрыть модуль отдельно на каждом промежутке в соответствии с определением модуля и решить получившиеся уравнения. Проверить принадлежность значения переменной данному промежутку.
г) Объединить решения, полученные на каждом промежутке.
- Закрепление.
Теперь попробуем применить известные нам знания на примере темы «Тригонометрические уравнения, содержащие знак абсолютной величины».
1)
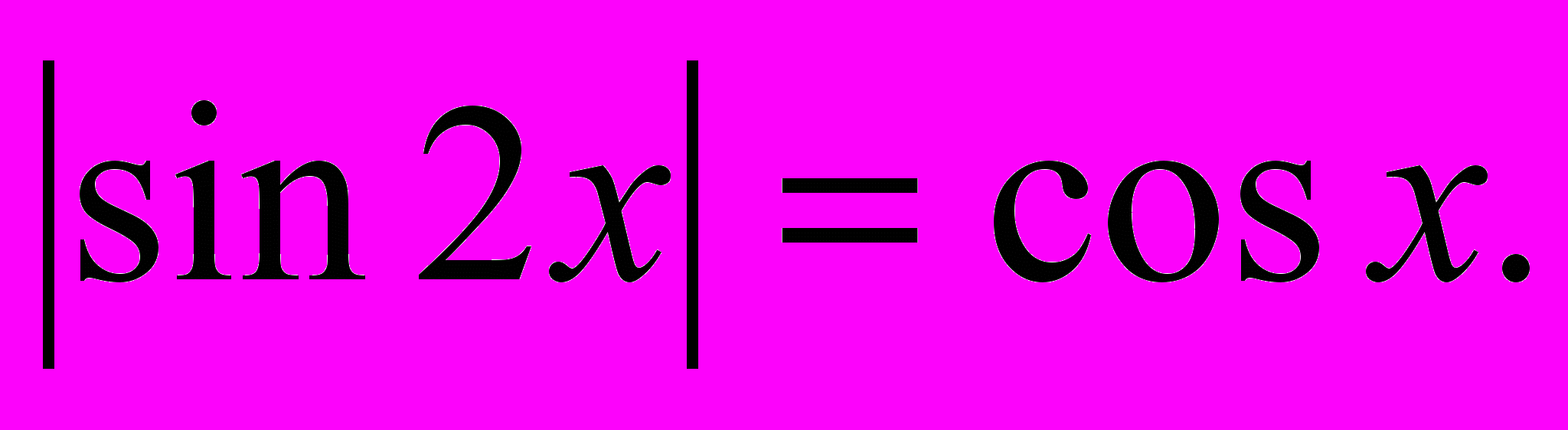
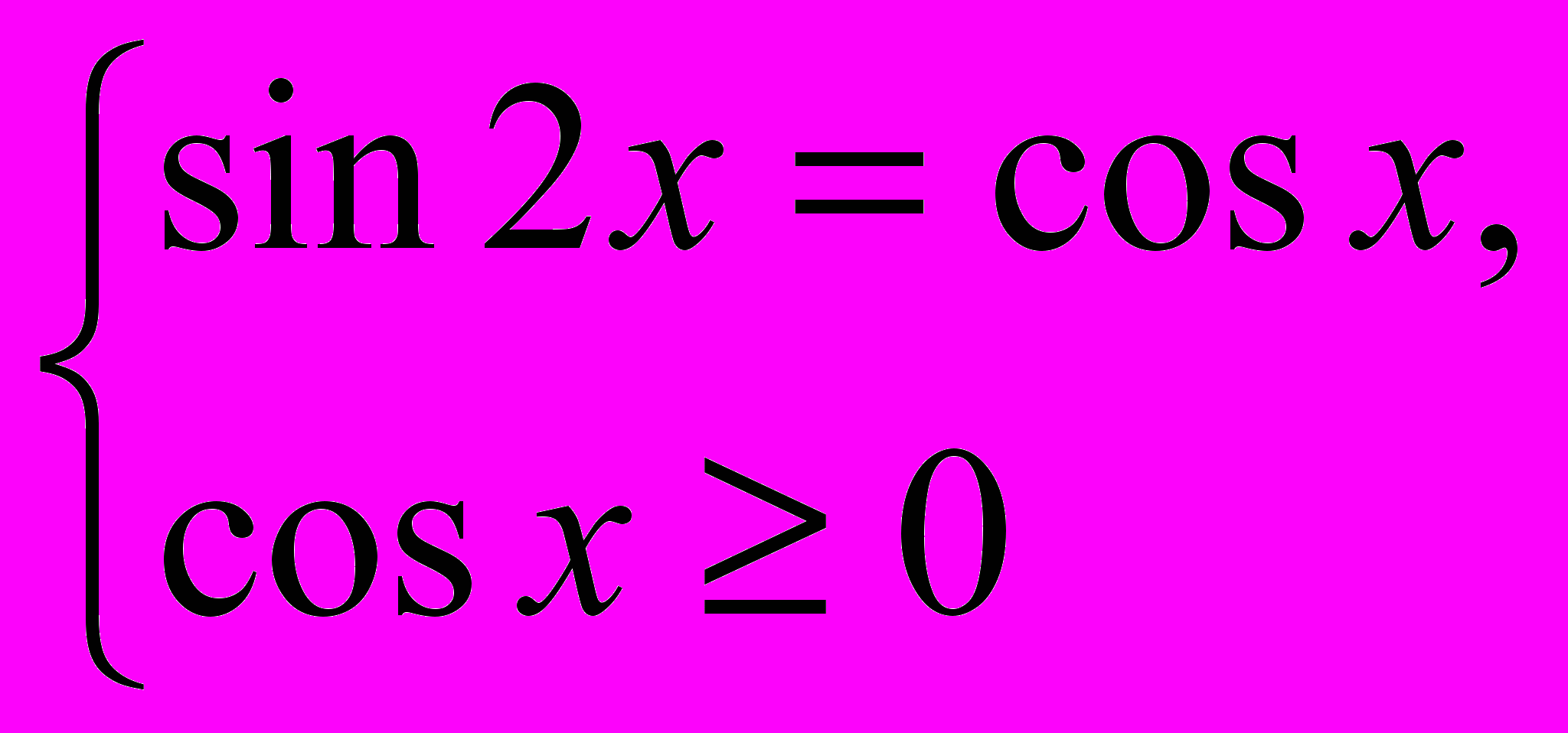 или
или 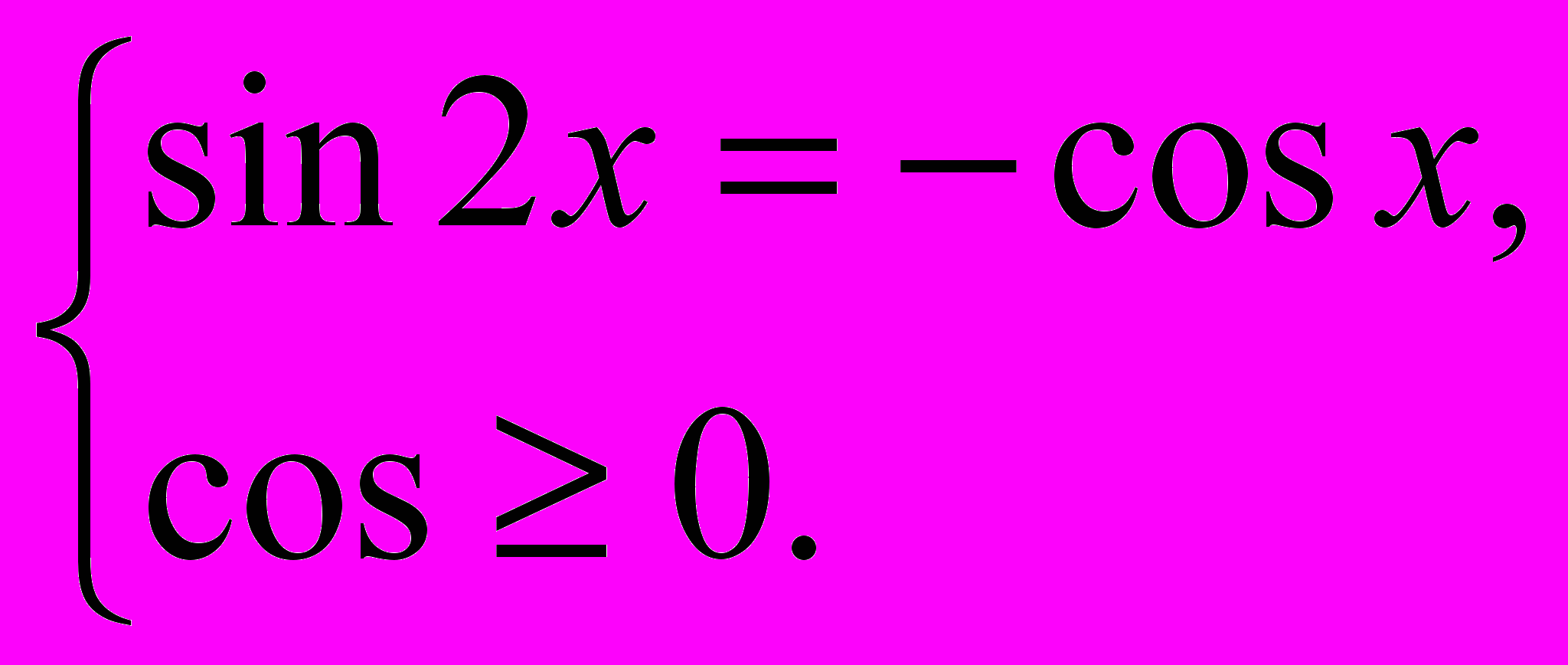
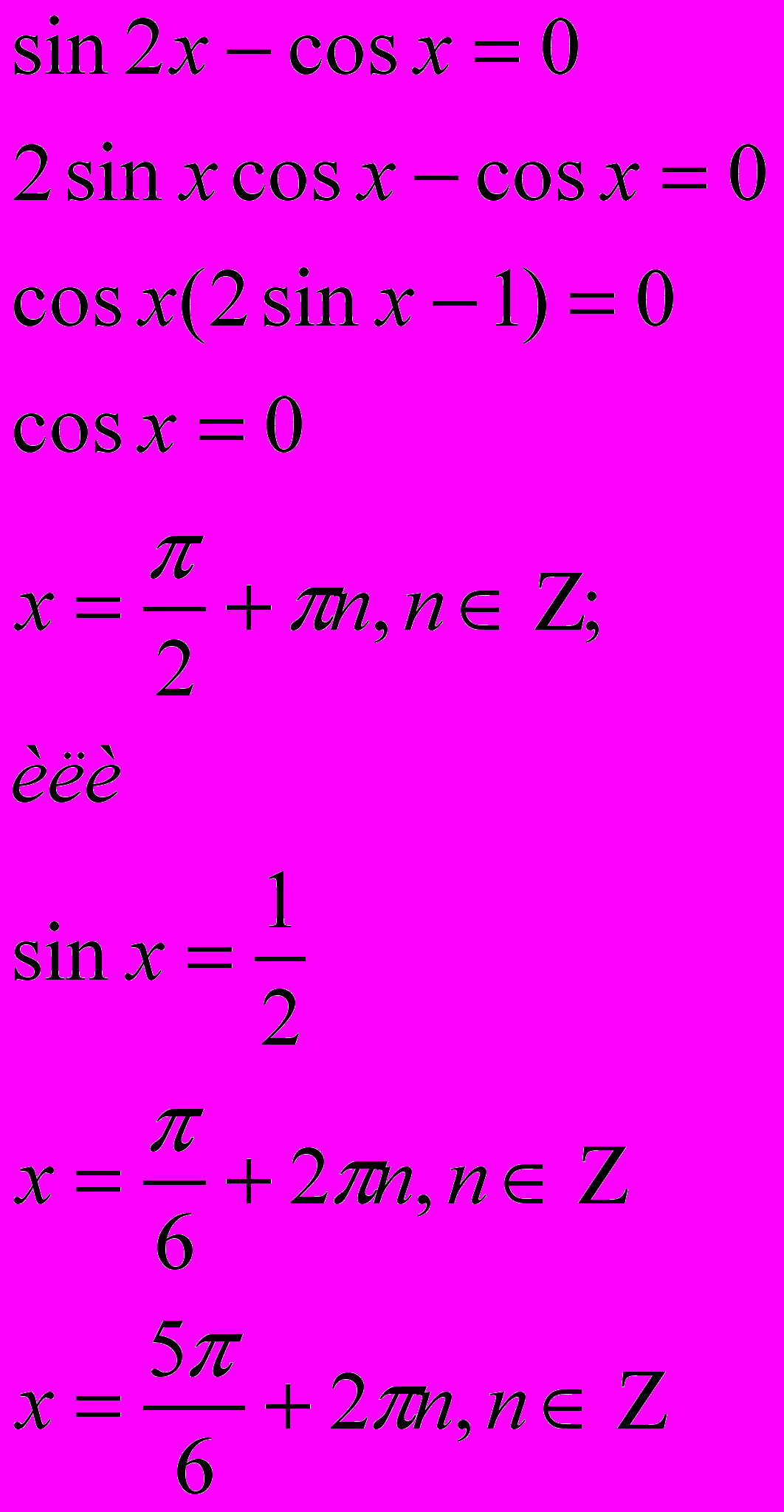
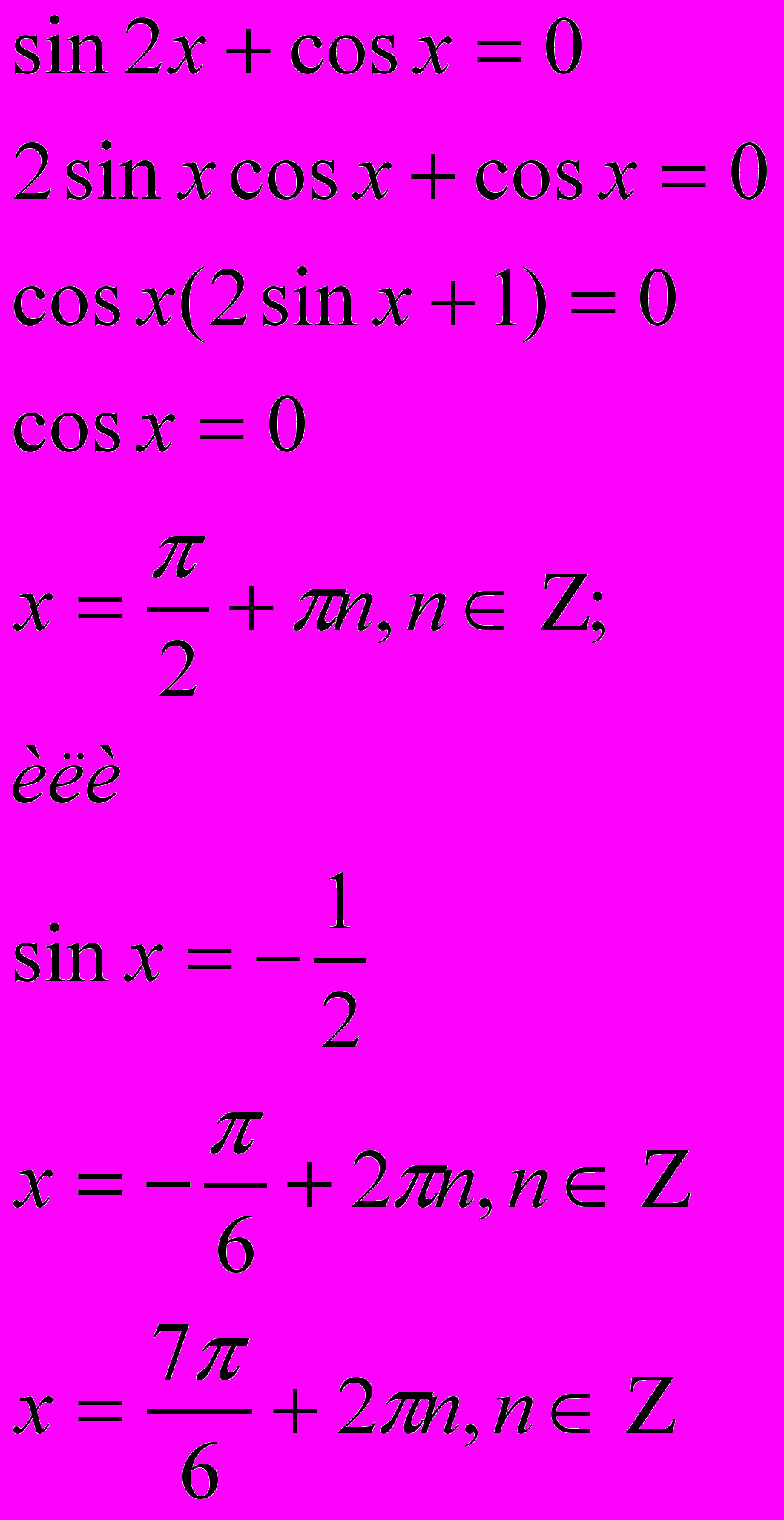
- не удовлетворяет условию - не удовлетворяет условию
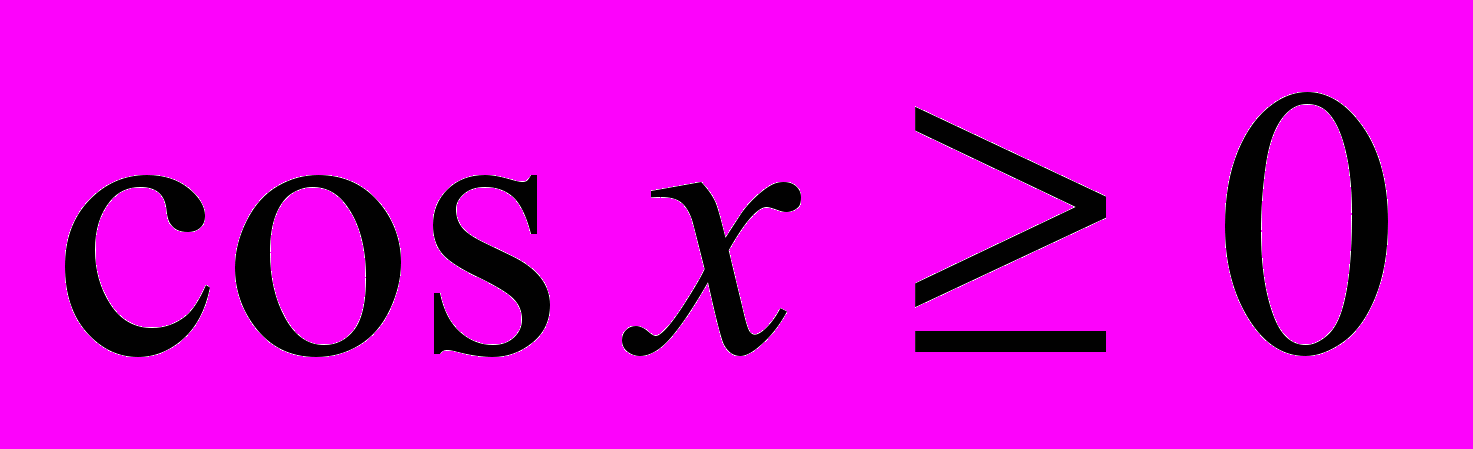 .
. 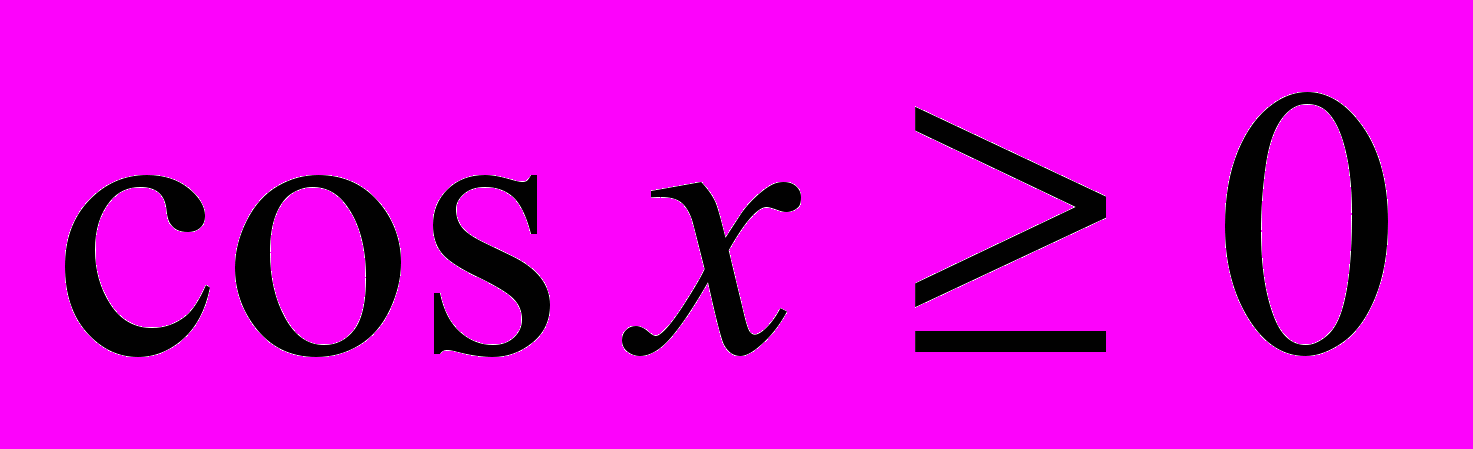 .
.Ответ:
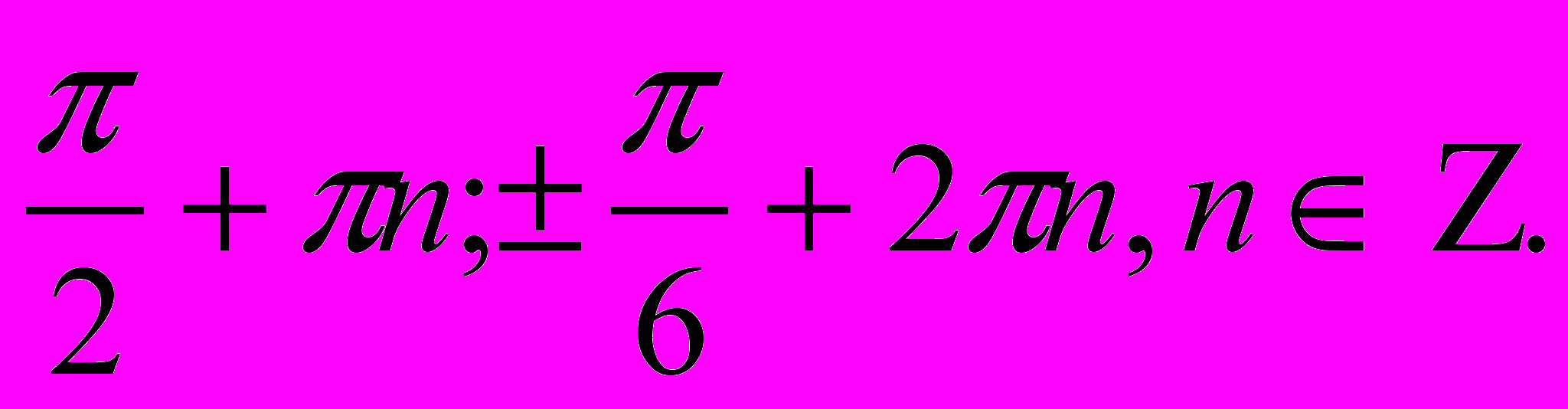
2).
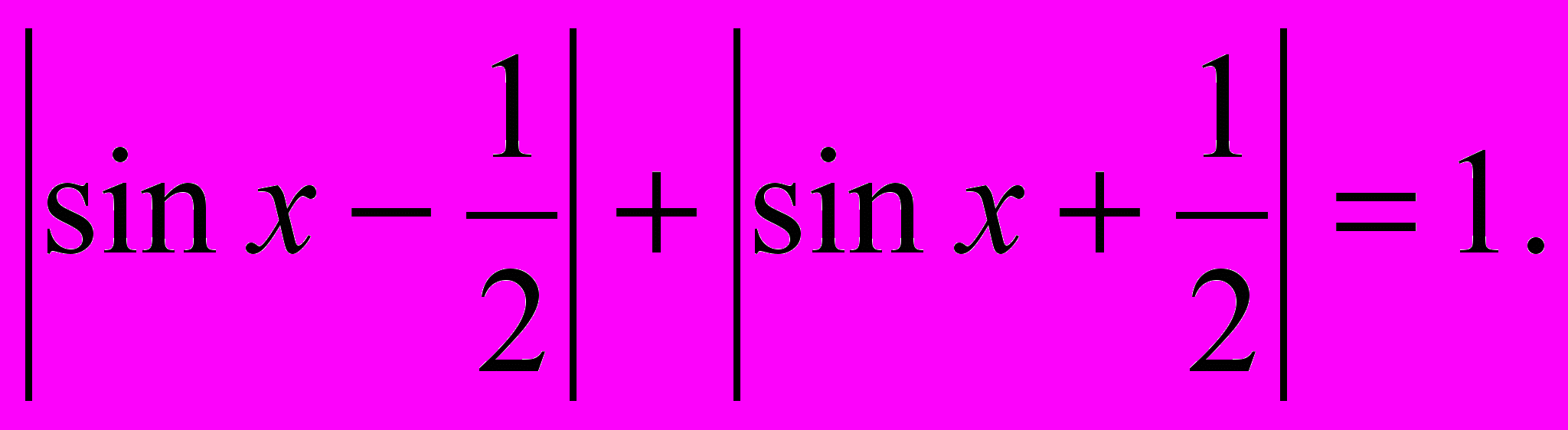
Пусть
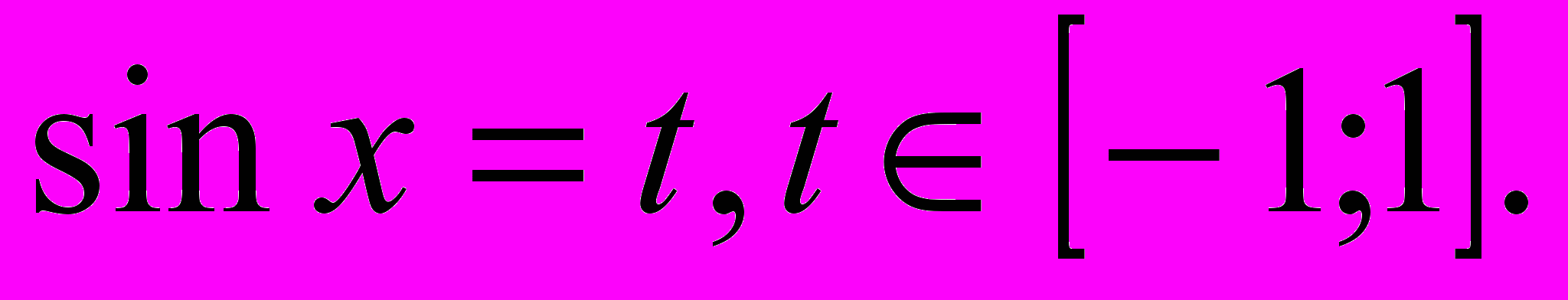
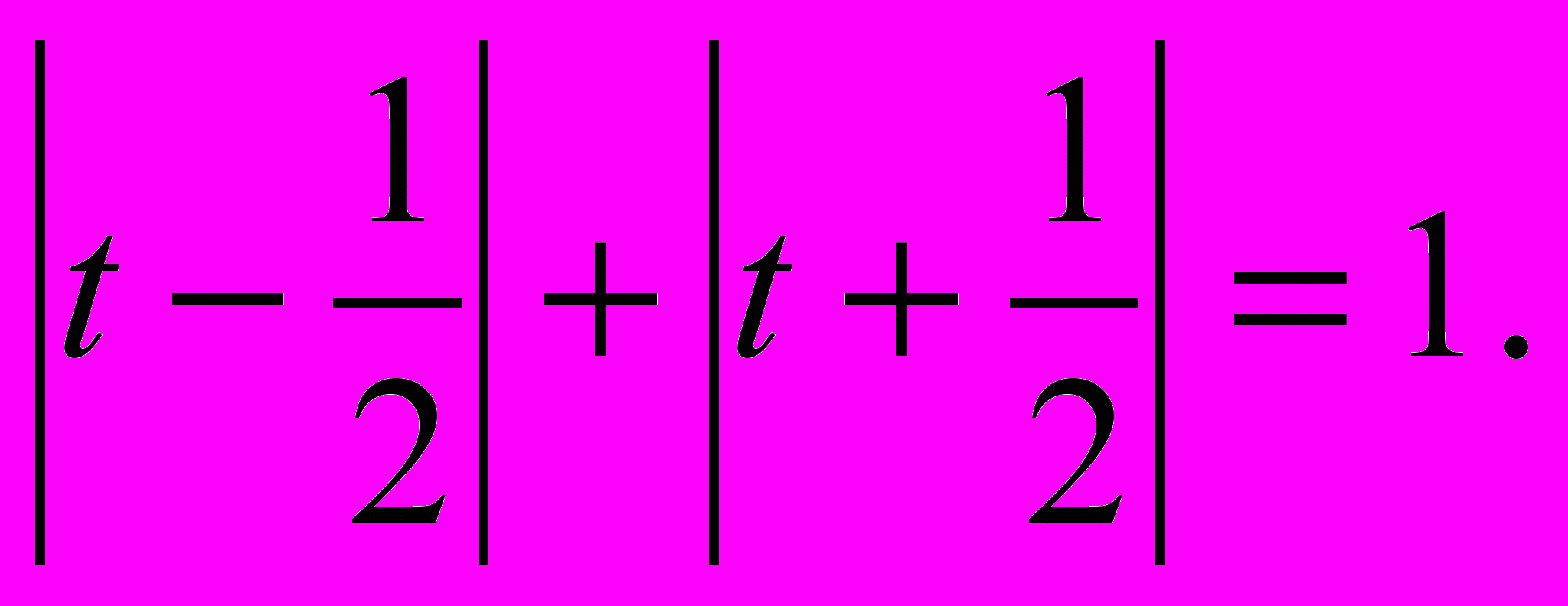
Выражения под знаком модуля обращаются в ноль при
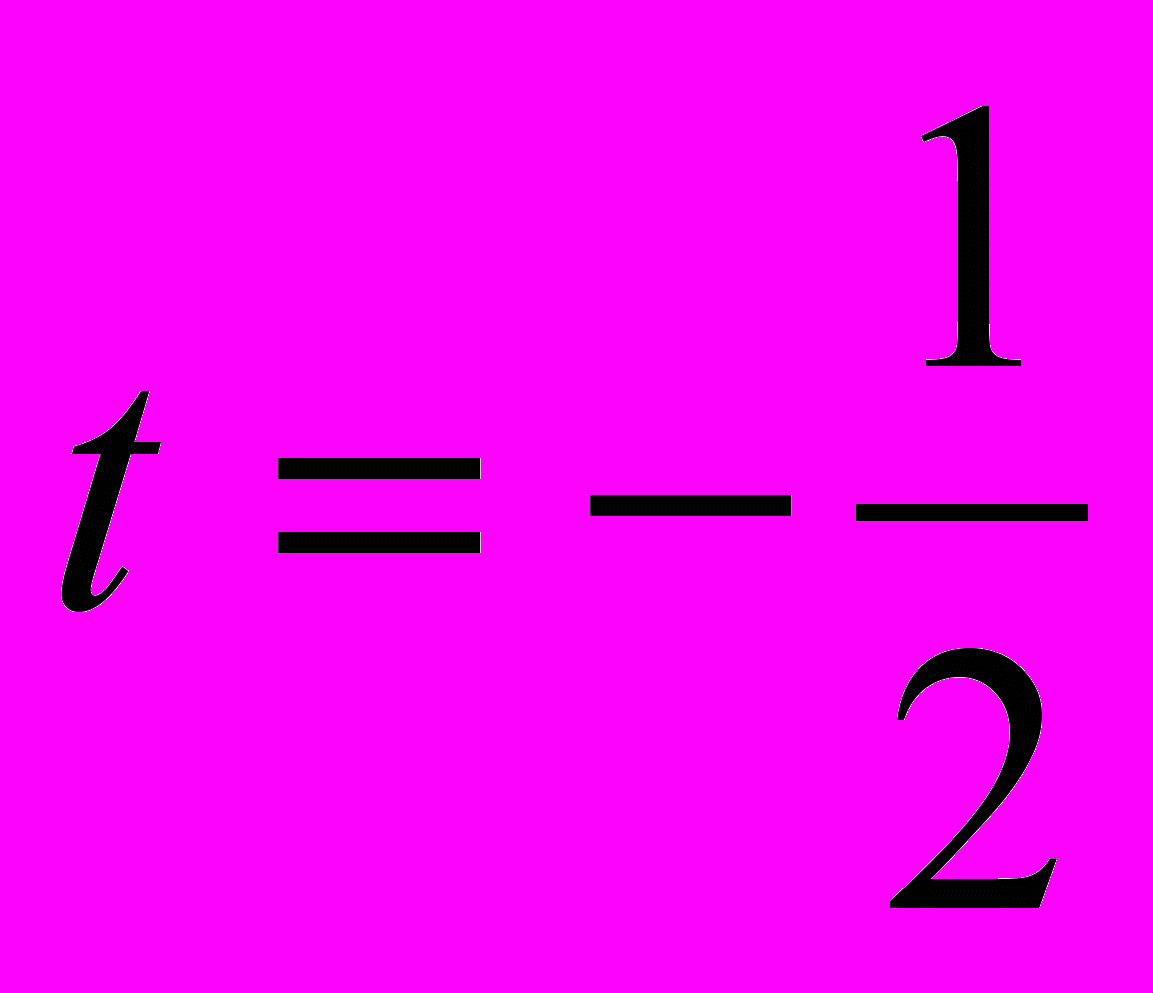 и
и 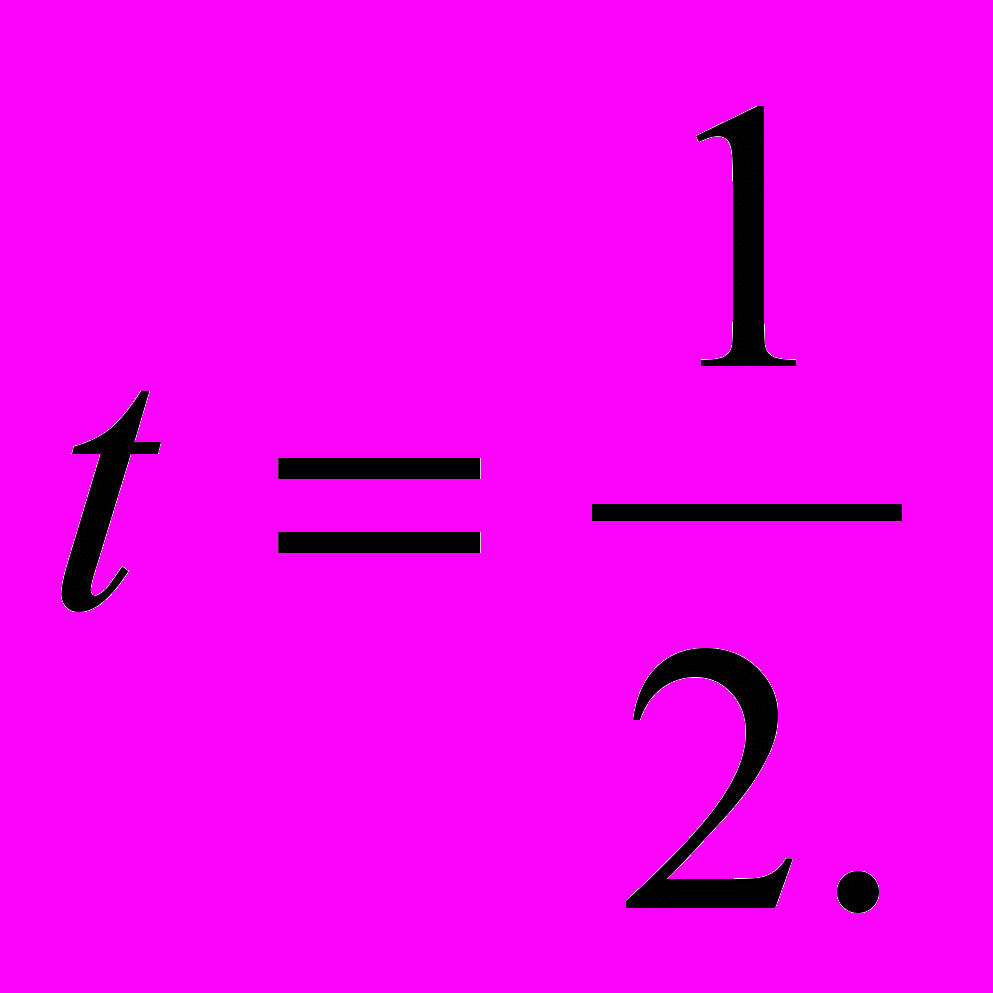
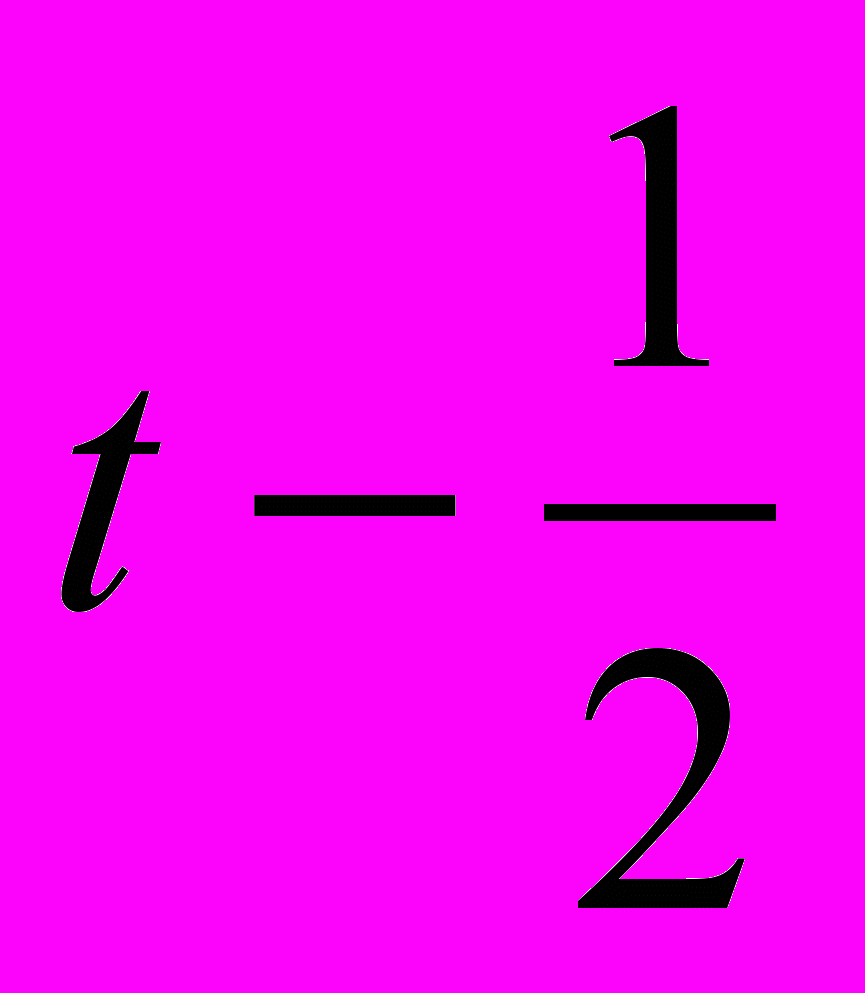 - - +
- - +  . . . .
. . . .-1 -
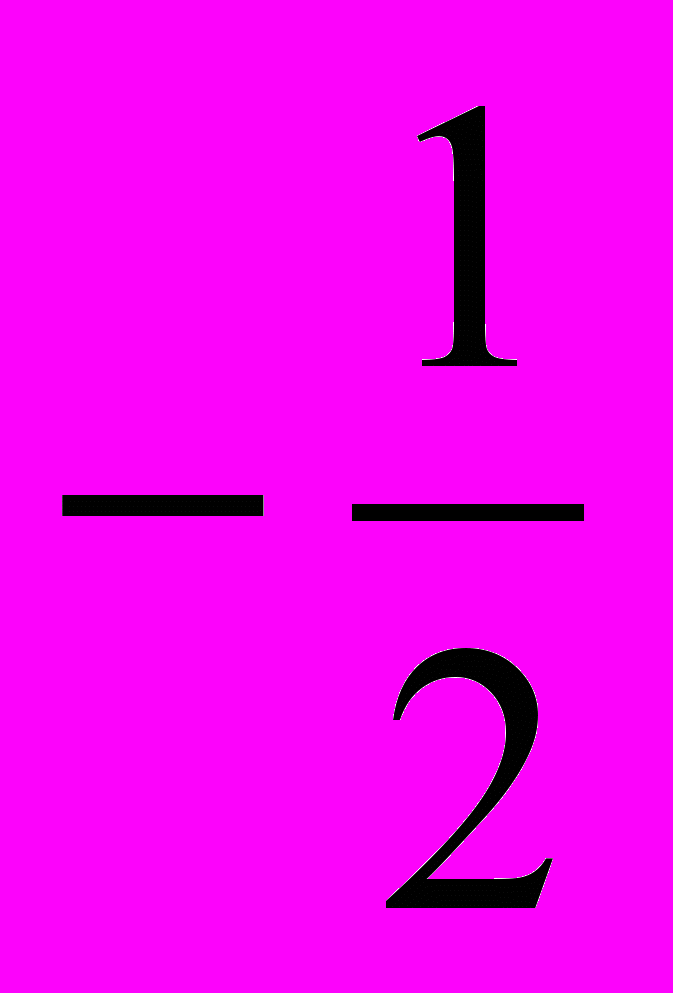 +
+ 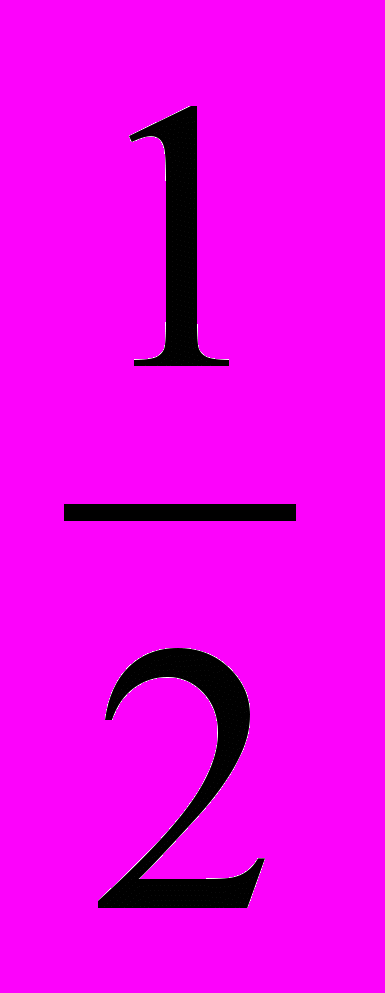 +
+ 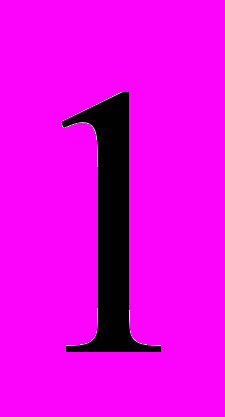 t
t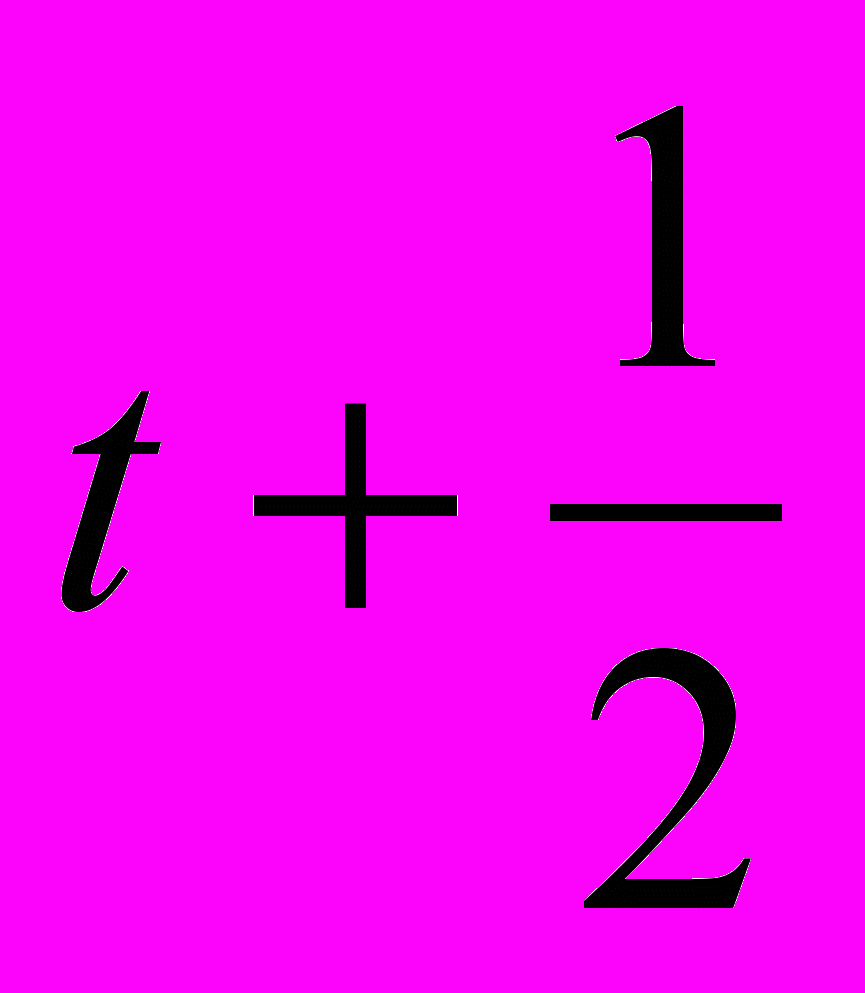
1)
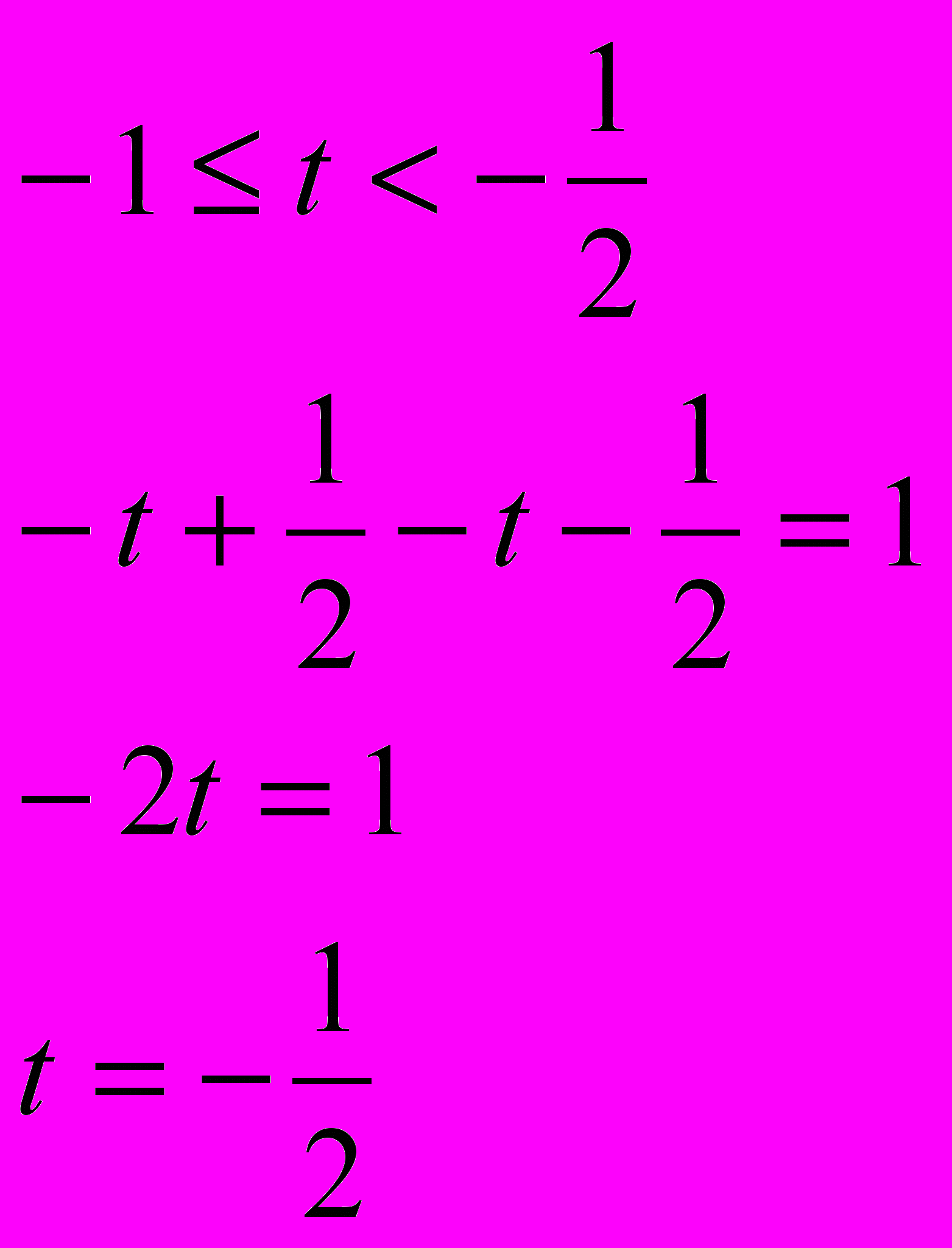
- не удовл. условию.
2)
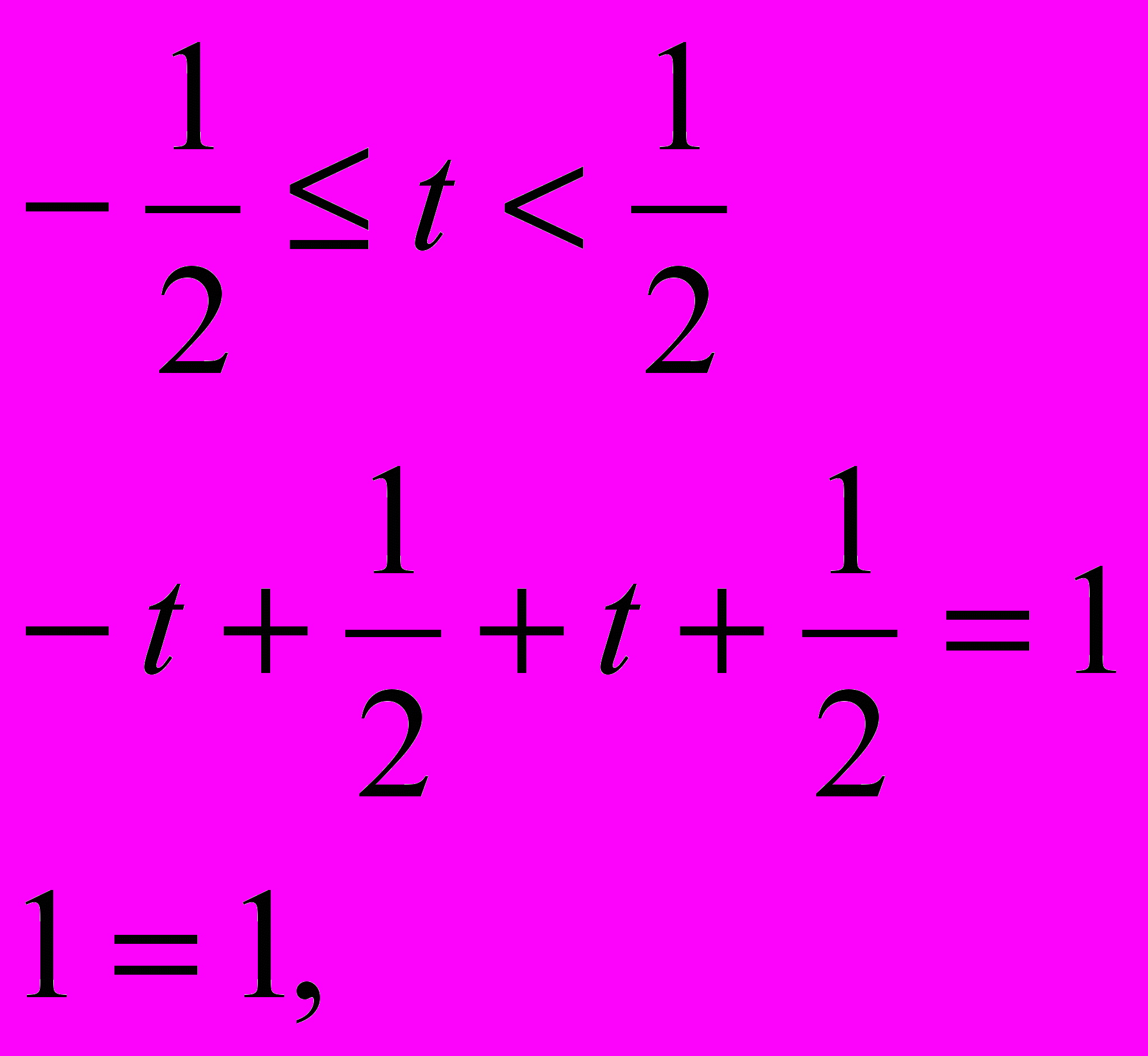
значит
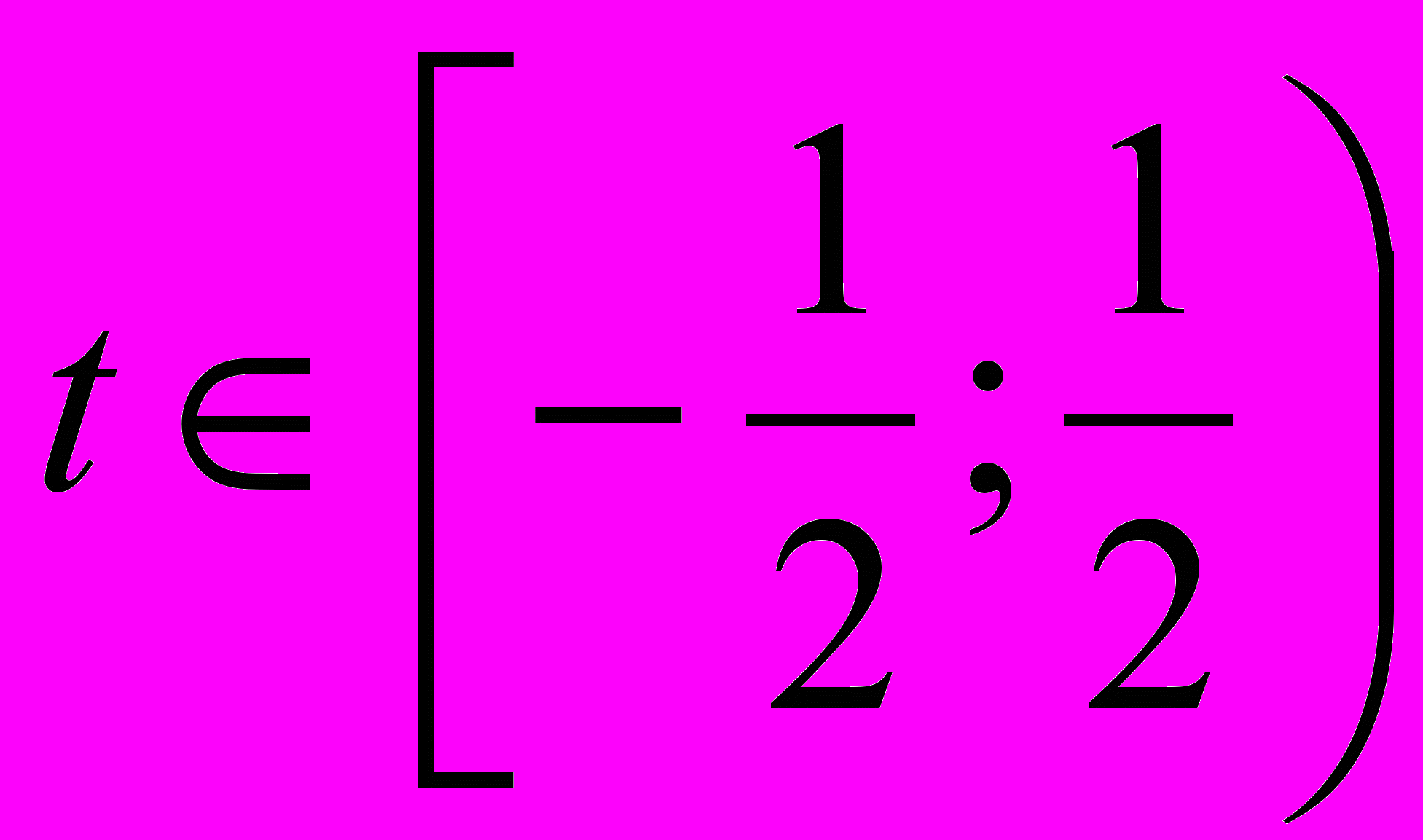 .
.3)
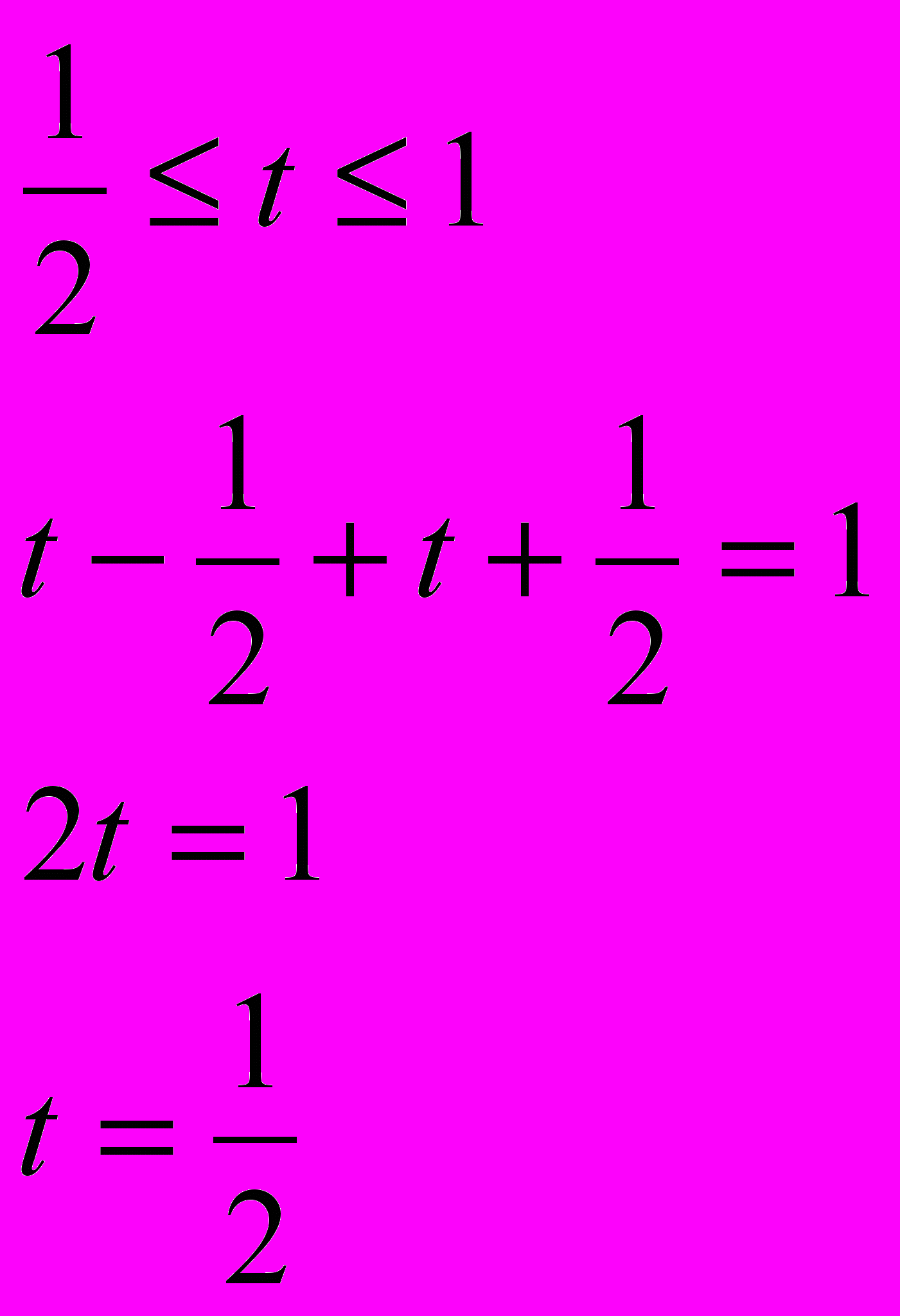
- является корнем.
Решением уравнения является отрезок
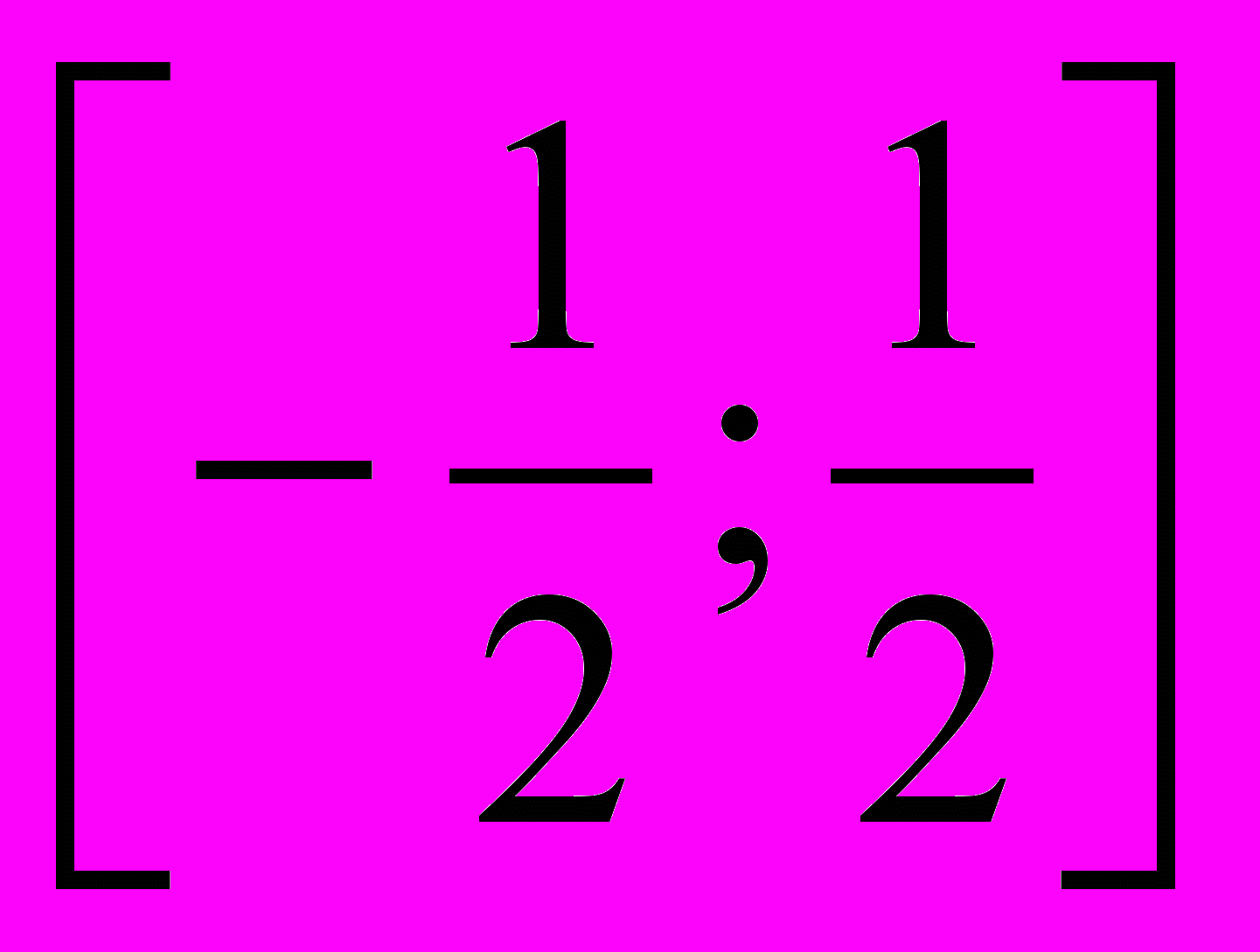 .
.Вернемся к замене.
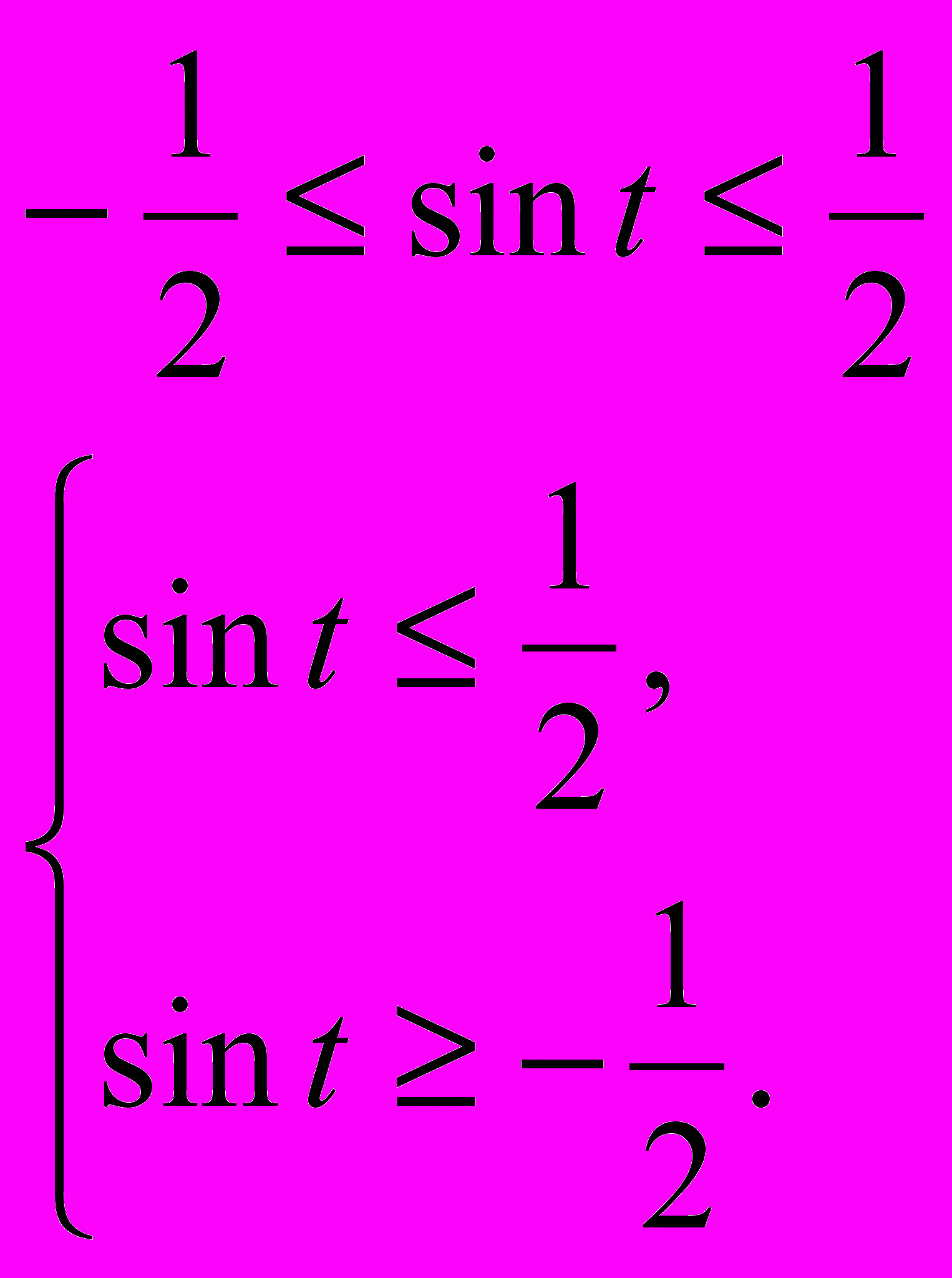
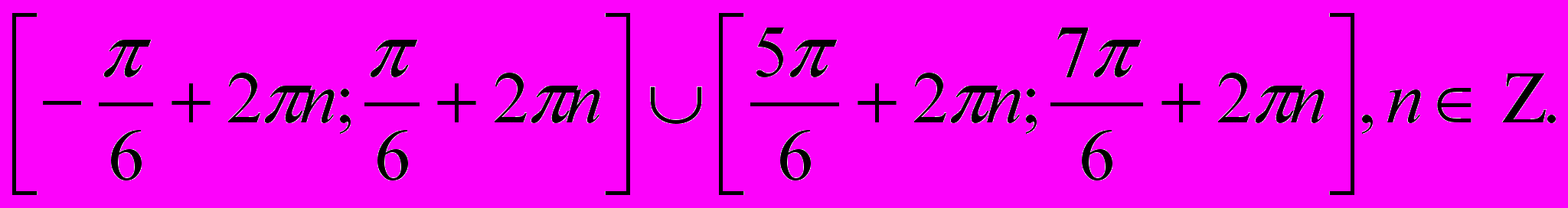
Ответ:
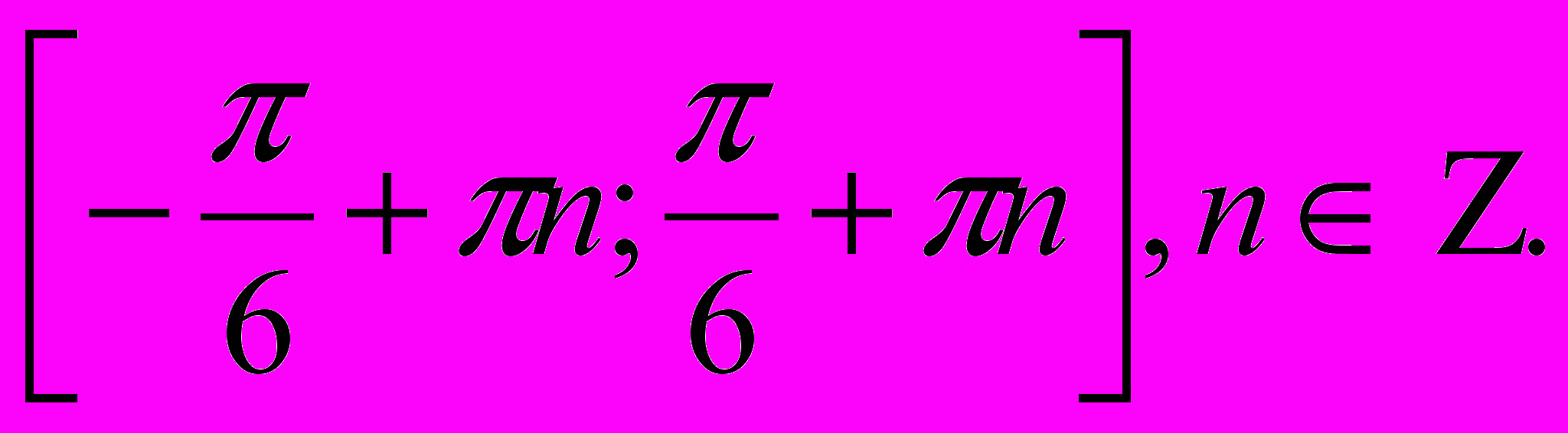
3).
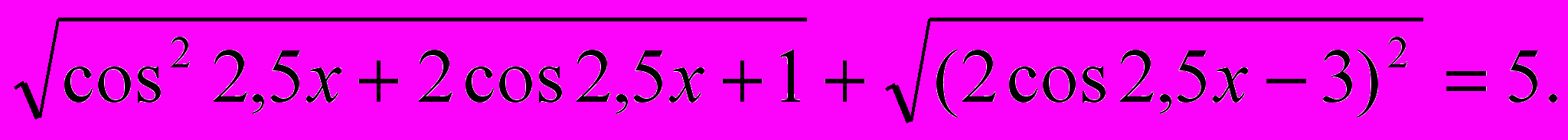
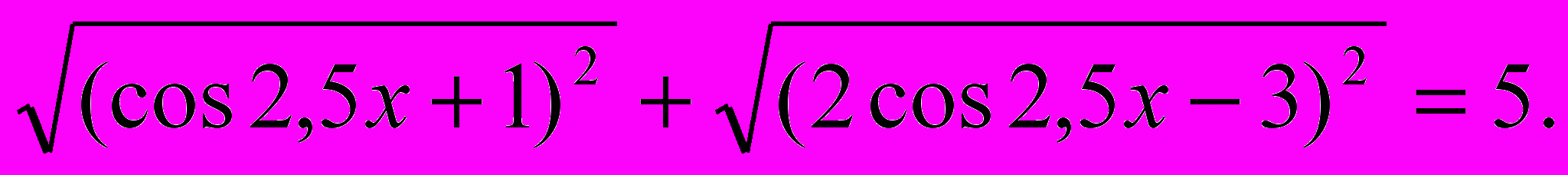
Так как
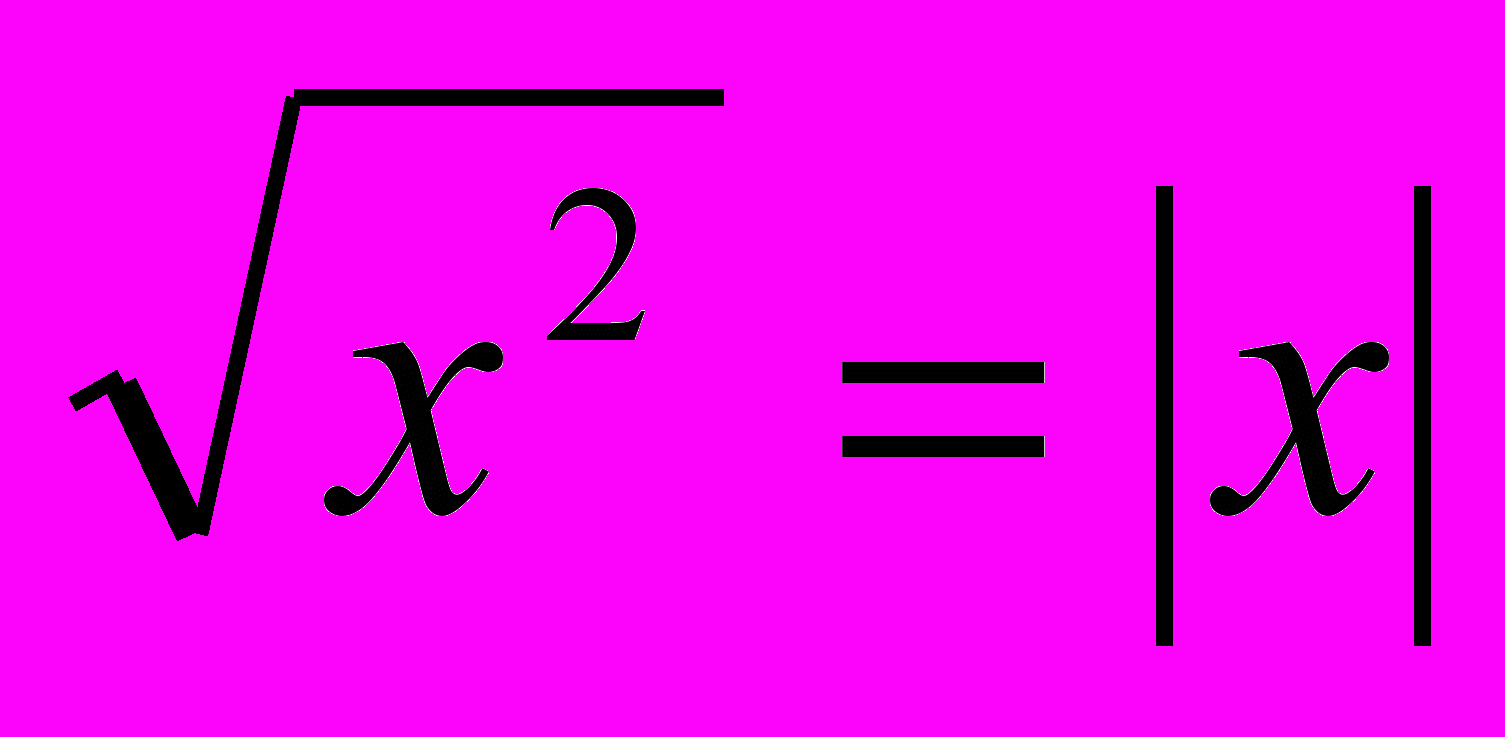 , то
, то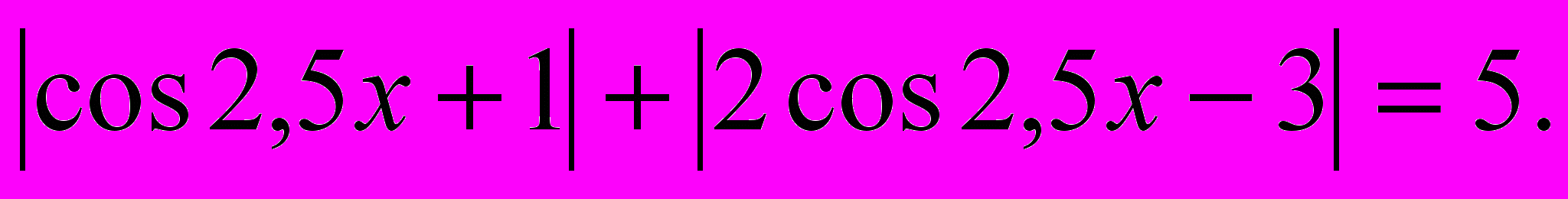
Так как
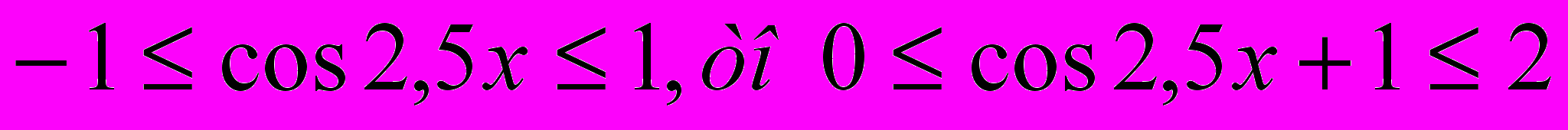 , значит
, значит 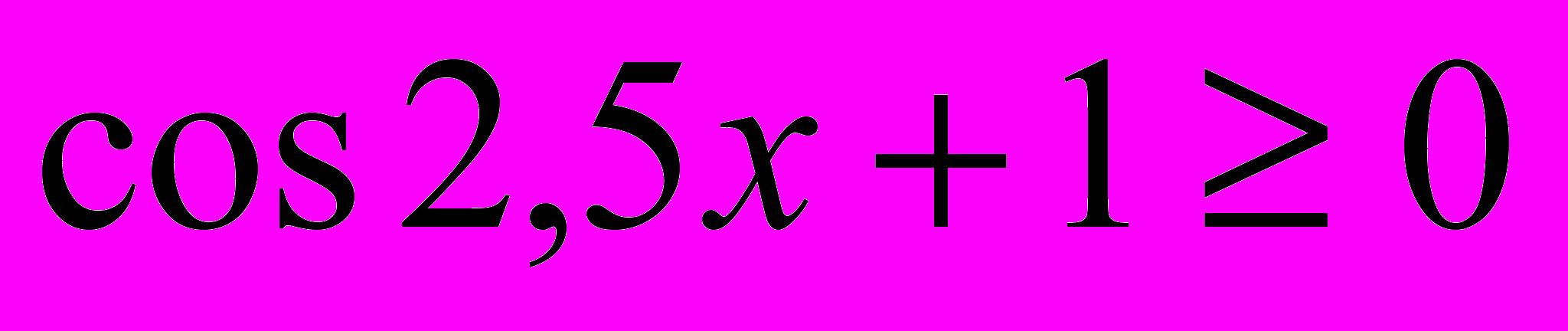 при любом x, следовательно
при любом x, следовательно 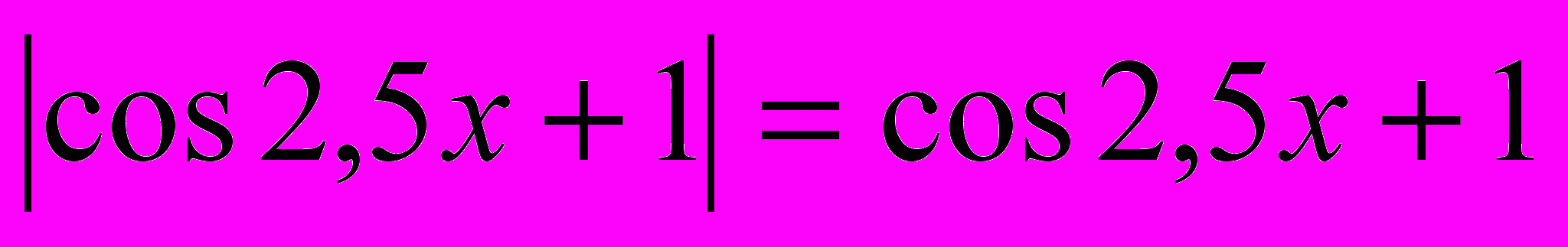 .
.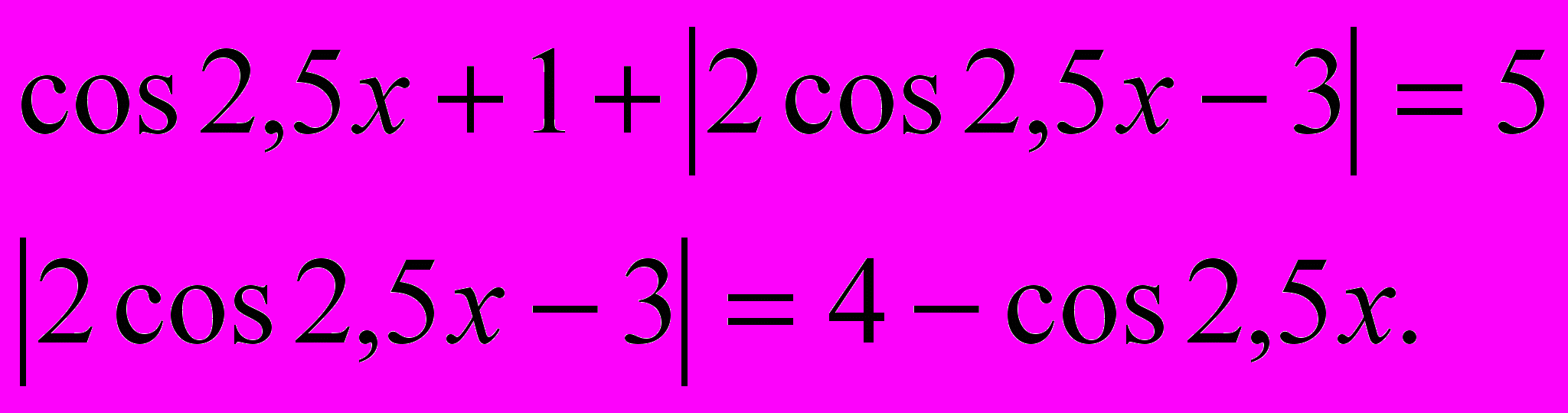
Пусть
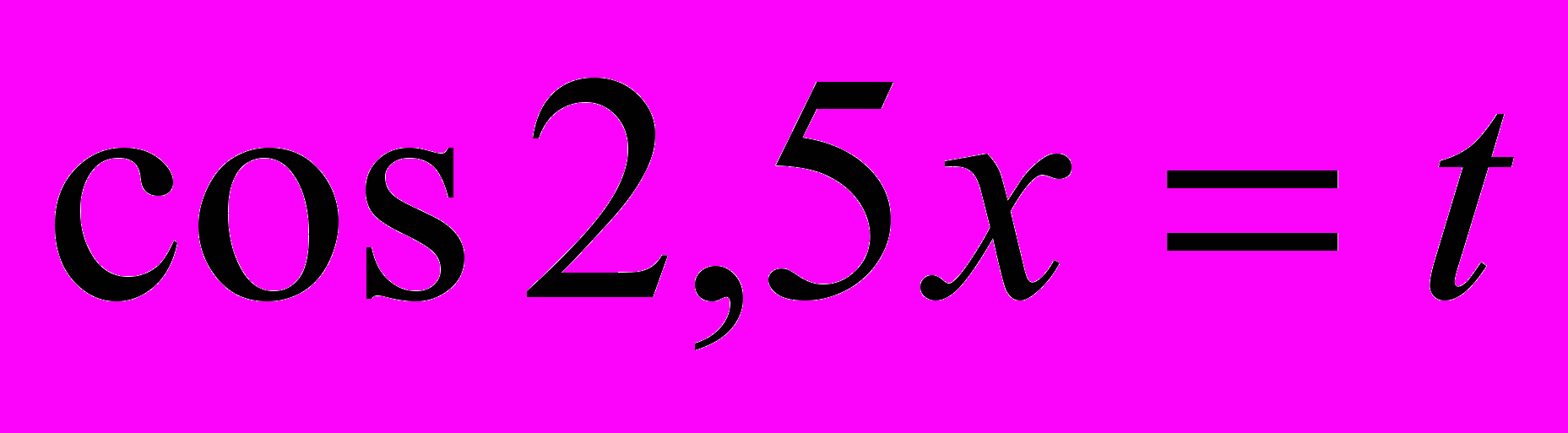 , тогда уравнение равносильно системе:
, тогда уравнение равносильно системе: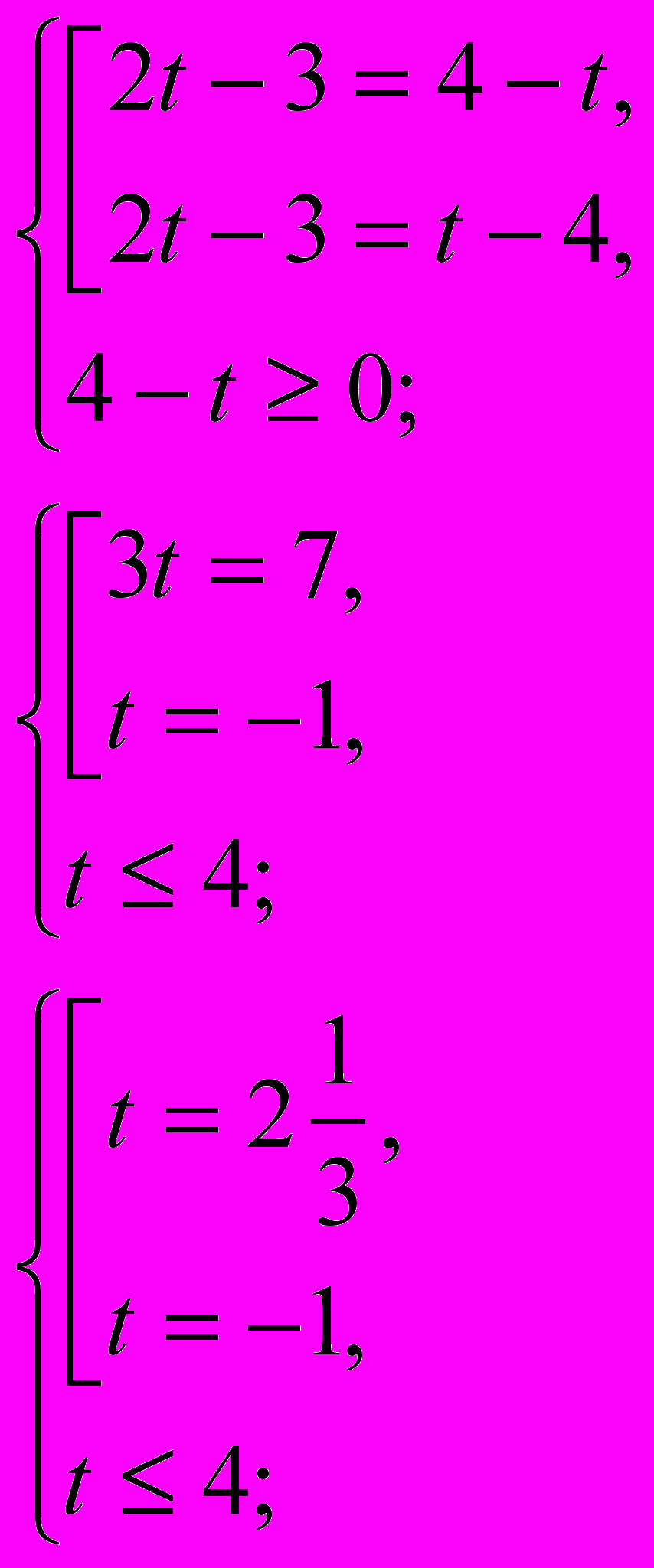
Вернемся к замене.
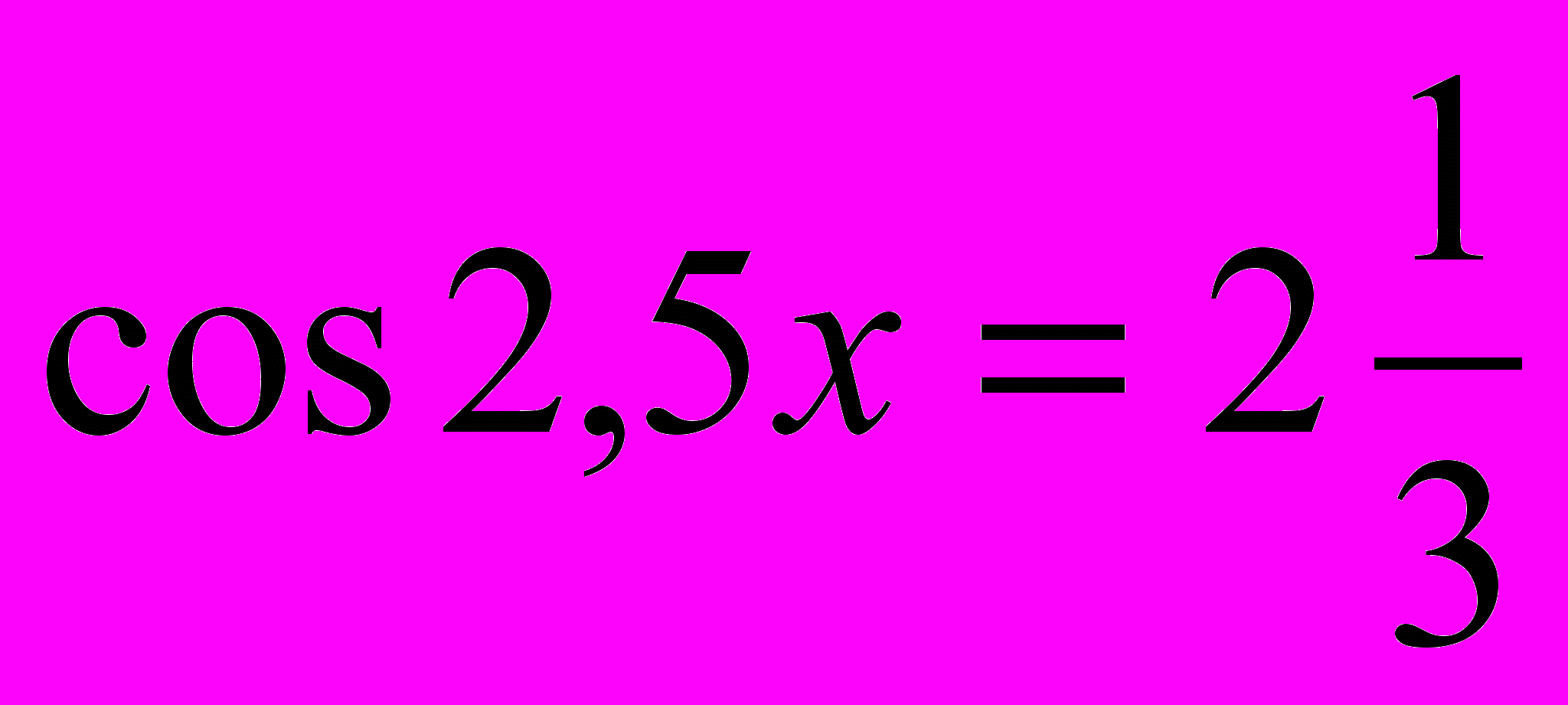 или
или 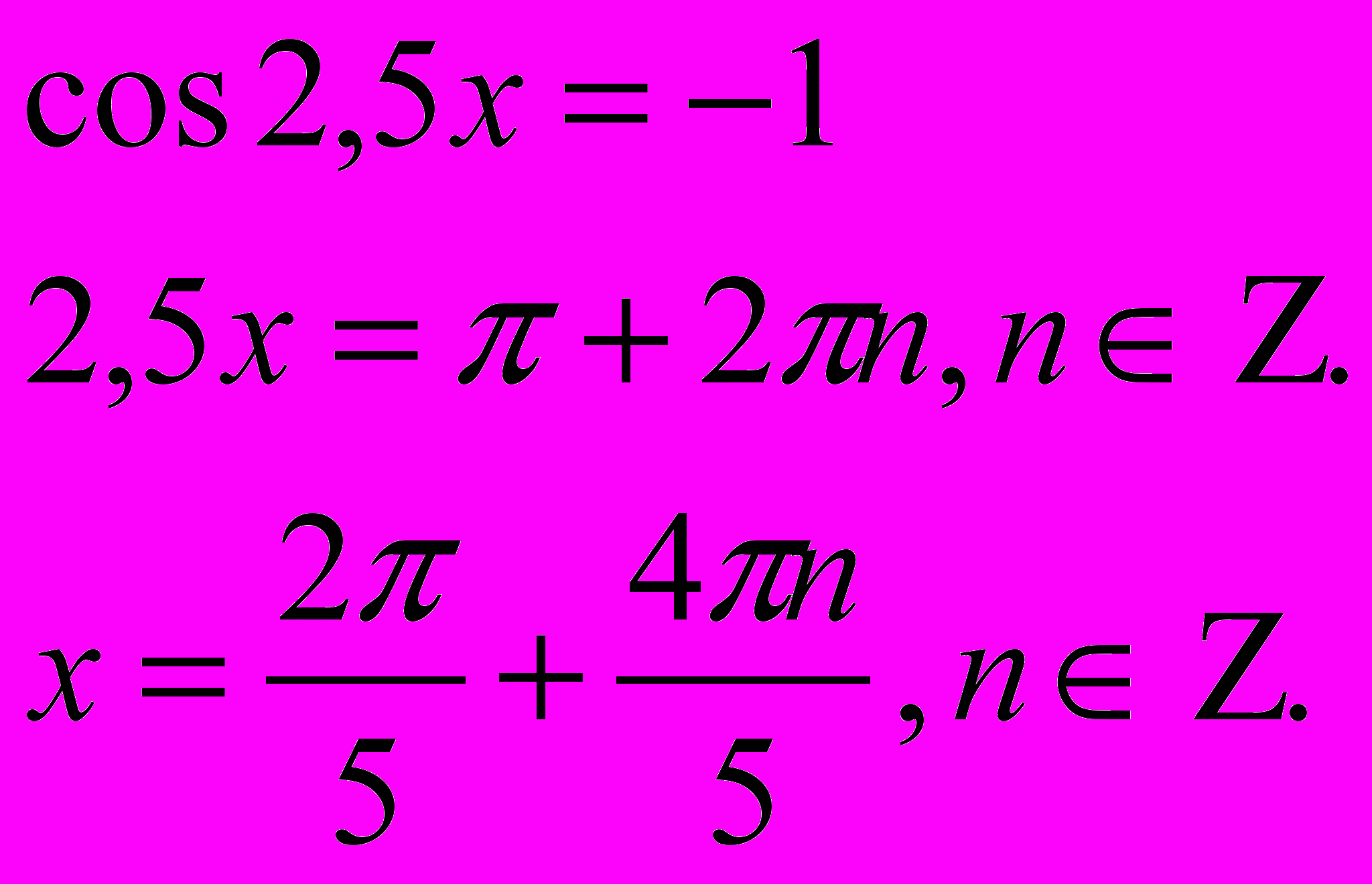
- нет решений.
Ответ:
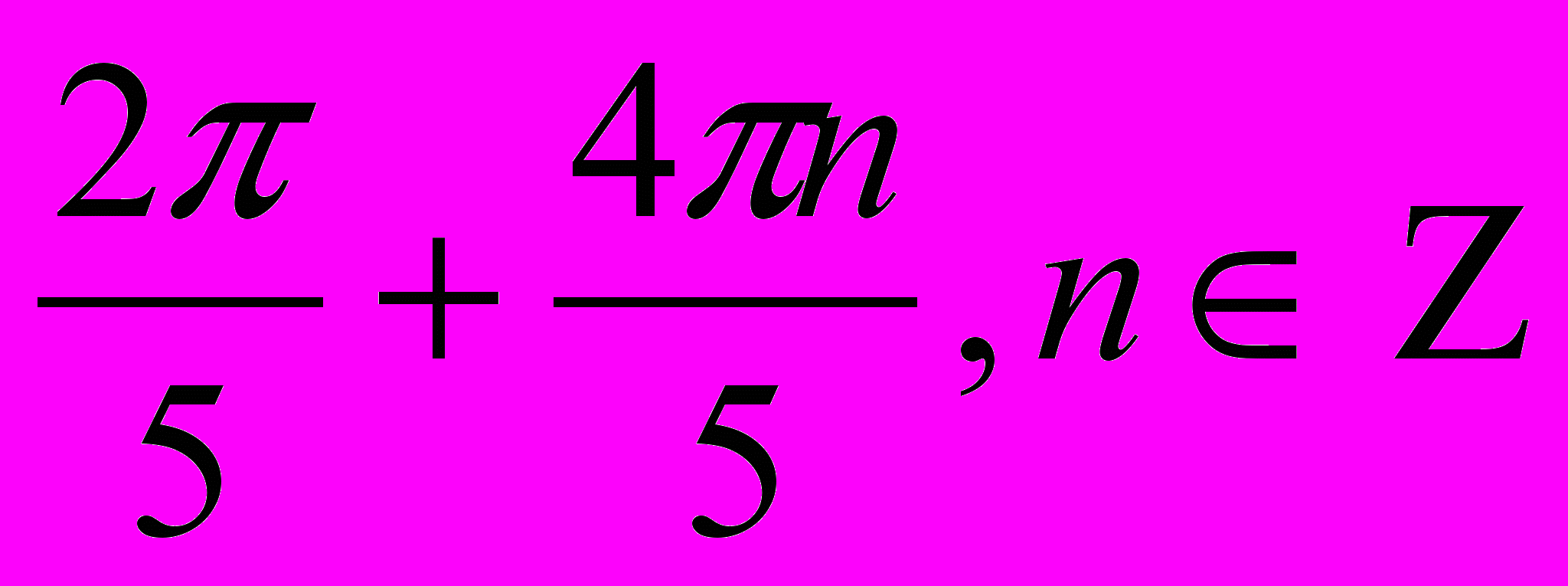 .
.- Заключение
Сегодня на занятии мы протянули нить между алгебраическими уравнениями с модулем к тригонометрическим уравнениям. Зная схему решения уравнений с модулем ее можно применить не только в тригонометрии, но и любой ьтеме начал анализа. Но необходимо не только знать схему решения, но и критически оценивать полученные результаты, объединять корни.
Сегодня мы продвинулись еще на один шаг в подготовке к ЕГЭ.
Д/з: с. 57, 58 – сборник.
