Ролі етапу актуалізації знань та способів дій в навчанні математики вцілому та в структурі уроку

Вид материала

Урок

Подобный материал:

• Схема поглибленого аналізу уроку іноземної мови, 33.13kb.
• Опис власного методичного досвіду, з актуалізації опорних знань та вмінь учнів в процесі, 366.74kb.
• Розділ передумови вдосконалення методики проведення етапу закріплення знань та формування, 442.2kb.
• Навчально-виховний комплекс №6 «Перспектива» виховання творчої особистості в умовах, 116.55kb.
• Політичний аспект мовної проблеми на дузі „Москва Київ- тель-Авів, 786.75kb.
• Політичний аспект мовної проблеми на дузі „Москва Київ- тель-Авів, 797.75kb.
• Орієнтовний план проведення уроку I. Організаційна частина. II. Актуалізація опорних, 45.38kb.
• Тема уроку: “ Вітаміни – це здоров’я та спосіб життя”. Цілі уроку, 57.35kb.
• Тема уроку: Здоров’я. Планування подальших дій І змін індивідуального способу життя, 121.25kb.
• Про графічний спосіб розв’язання математичних задач, 262.98kb.

Урок 7. Розкладання квадратного тричлена на лінійні множники

Мета. Формування вміння розкладання квадратного тричлена на лінійні множники

Тип. Урок вивчення нового матеріалу

Актуалізація опорних знань виконується усно. Проводимо фронтальну бесіду, в процесі якої повторюється означення квадратного тричлена, його коренів, пряма та обернена теореми Вієта.


Урок 8. Розкладання квадратного тричлена на лінійні множники

Мета. Формування вміння розкладання квадратного тричлена на лінійні множники

Тип. Урок закріплення вивченого

Актуалізація опорних знань – тест " Квадратний тричлен ".

П.р.

1.Які з даних виразів є квадратними тричленами:

а) х²+3х -1; б) х³ -х +2; в) 4 - х²; г) х² +х +1/х.

2.Які з тричленів набувають числового значення, рівного 2, при х = - 1:

а) х²-4х -7; б) 3 - х²; в) х² +х + 2; г) 3х²- х -2.

3. Коренями тричлена х² + х – 6 є числа:

а) -2 і 3; б) 2 і -6; в) -3 і 2; г) -3 і 1.

С.р.

4. Які з квадратних тричленів не мають дійсних коренів:

а) х² +х +1; б) х² +х -1; в) х² +5; г) х² -4.

5. Тричлен х²-4х +1:

а) не має дійсних коренів;

б) має один корінь;

в) має два корені.

6. Добуток (2х+3)(х-1) є розкладом на множники квадратного тричлена:

а) 2х² +5х -3; б) х² +х -3; в) 2х² +х +3; г) 2х² +х -3.

Д.р.

7. Не можна розкласти на лінійні множники квадратні тричлени:

а) х² -х +2; б) х² +х -2; в) х² -2х +4; г) х² -4.

8.Тричлен 2х² + х + р розкладається на множники 2(х+1)(х-1/2), якщо р має числове значення:

а)1; б) -2; в) -1; г) 2.

9. Тричлен х² -2х -8 розкладається на множники (х-4)(х-к), де к має значення:

а) -2; б) 2; в) 1; г) 4.

В.р.

10.При скороченні дробу (6х² +х -2)/(3х+2) одержимо:

а) 2х -1; б) 1- 2х; в) 2х +1; г) дріб нескоротний.

11. Для того, щоб дріб (х²-5х+р)(х-2) можна було скоротити, числове значення р має дорівнювати:

а) -6; б) 4; в) 6; г) 8.

12. Не можна скоротити дроби:

а)(х²+х+1)/(х+1); б)(х²+2х+1)/(х+1); в)(х²+х-2)(х+1).


Урок 9. Виділення квадрата двочлена з квадратного тричлена

Мета. Формування вміння виділяти квадрат двочлена

Тип. Комбінований урок

Інтерактивна вправа "Обери позицію"

-У чому полягає спосіб розв’язування квадратних рівнянь виділенням квадрата двочлена?

- Як вивести формулу коренів квадратного рівняння?

- З якого тричлена при цьому виділяється квадрат двочлена?

- Квадрат якого двочлена виділяється?

- Навести приклади


Урок 10. Найбільше і найменше значення квадратного тричлена

Мета. Формування вміння знаходити найменше чи найбільше значення квадратного тричлена

Тип. Комбінований урок

1. Фронтальне опитування (інтерактивна вправа "Мікрофон"):

- Що таке квадратний тричлен?

- Як знайти значення квадратного тричлена при заданому значенні х?

- Обчислити значення тричленів х²-6х+5 та -х² +4х-1 при х рівному 0;1;2;3;4. Розв'язки оформити у вигляді таблиці (двоє учнів працюють біля дошки)

х	0	1	2	3	4
х²-6х+5	5	0	-3	-4	-3

х	0	1	2	3	4
-х²+4х-1	5	0	-3	-4	-3

2. Інтерактивна вправа "Обери позицію":

Запитання до першого учня:

- Яке найменше значення тричлена на заданій множині?

- Чи може він набувати значень, менших за -4, при інших значеннях х?

Запитання до другого учня:

- Яке найбільше значення тричлена на заданій множині?

- Чи може він набувати значень, більших за 5?

На друге запитання учні можуть відповісти по-різному. Відповідь "не знаю" приймається з метою мотивації вивчення нового матеріалу.


Більшість уроків з алгебри - комбіновані. Тому актуалізація опорних знань на алгебрі відбувається як перевірка д/з. У цьому випадку добре працює різнорівневий підхід до навчання, адже кожна з диференційованих груп одержує своє д/з.

Від учнів початкового та середнього рівня оволодіння знаннями не слід вимагати виведення формул, розв’язування складних вправ, досить обмежитися знанням основних принципів та безпосереднього застосування теорії.

Учням достатнього та високого рівнів засвоєння знань доречно показати нестандартні методи чи способи розв’язання та уміти застосовувати ці знання при розв’язуванні складніших, багатокрокових вправ.


2.1.2. Особливості актуалізації знань з геометрії

( на матеріалі теми " Розв’язування трикутників",

за підручником Погорєлова О. В. Геометрія, 7-9).

Витяг із тематичного плану

(подано орієнтовну кількість годин)

Номер уроку	Тема уроку	Кількість годин
1	Теорема косинусів	1
2	Наслідки з теореми косинусів	1
3	Розв’язування задач із застосуванням теореми косинусів і наслідків з неї	1
4	Теорема синусів	1
5	Співвідношення між кутами і протилежними сторонами трикутника	1
6	Розв’язування задач	1
7 – 9	Розв’язування трикутників	3
10	Тематичне оцінювання. Контрольна робота "Розв’язування трикутників"	1

Урок 1. Теорема косинусів

Мета. Познайомити учнів з теоремою косинусів і наслідком з неї

Тип. Урок ознайомлення з новим матеріалом

Необхідні знання на уроці:

1)прямокутний трикутник, теорема Піфагора;

2)додавання і віднімання векторів.

Актуалізацію проводимо так:

1.Перевірка д/з

Попередньою була тема "Вектори на площині". Викликаємо до дошки учнів із середнім рівнем засвоєння знань.

2. Поки вони готуються, вчитель працює з іншими учнями. Іде повторення знань про прямокутний трикутник шляхом усного та напівусного розв’язування задач типу:

В прямокутному трикутнику дано:

а) довжина катетів 3см і 4см. Знайти довжину гіпотенузи.

б) довжина гіпотенузи 13см, катета- 3см. Знайти довжину іншого катета.

в) величина одного з кутів 45°, довжина прилеглого до нього катета 1 дм. Знайти довжину гіпотенузи та іншого катета.

3. Після розв’язування задач весь клас слухає пояснення д/з. У кінці вчитель задає питання про додавання та віднімання двох векторів за правилом трикутника; про скалярний добуток векторів; піднесення вектора до квадрату.

Якщо виникають труднощі у відповідях, то вчитель звертається до всього класу.

4. Розв’язати задачу у.в.р. за мал.1: АВС - довільний трикутник

В


2 ?


А 30 3 С мал.1

3√3

Далі вчитель ставить проблему: чи можна визначити довжину сторони у довільному трикутнику, якщо відомі довжини двох інших сторін і величина кута між ними?

І переходить до пояснення нового матеріалу про теорему косинусів.


Урок 2. Наслідки з теореми косинусів

Мета. Вивести наслідки теореми косинусів. Закріпити теорему косинусів і наслідки з неї, шляхом розв’язування задач.

Тип. Урок закріплення вивченого

Актуалізацію проводимо у формі перевірки д/з на засвоєння теореми косинусів:

1. Один із учнів високого рівня володіння знаннями доводить теорему біля дошки.
   
2. Поки він готується, перевірити:
   

а) виконання д/з;

б) формулювання теореми косинусів;

в) за малюнком 2 знайти невідому сторону трикутника:




?

2

а b

5 мал. 2.1. мал. 2.2.



. а




мал. 2.3.


Учителю слід приділити максимум уваги учням початкового та середнього рівнів засвоєння знань.

3.Прослухати доведення теореми косинусів.

4. Розв’язати задачу за мал.3 ( біля дошки працює у.с.р. )

В С


A 10 D

мал. 3

Потім пропонуємо задачу про суму квадратів діагоналей паралелограма, що слідує з теореми косинусів. Далі – розв’язування вправ.


Урок 3. Розв’язування задач із застосуванням теореми косинусів і наслідків з неї

Мета. Закріплення навичок використання теореми косинусів для розв’язування задач; перевірка засвоєння теми

Тип. Урок закріплення вивченого

Запитання до розв’язання д/з

До задачі 2 §12

● Як записати теорему косинусів для знаходження шуканої сторони? ( х² = 5² + 6² - 2 5 6 cos α )

● Як знайти cos α ? Яким числом може бути значення cos α ? (cos ²α +sin²α =1,отже cos ²α =0,64, cos α =+-0,8. cos α ‹ 0,якщо кут тупий, cos α › 0,якщо кут гострий. У задачі дві відповіді.)

До задачі 4 § 12

● Яким може бути кут між діагоналями паралелограма? (Гострим або тупим. Задача має два розвязки.)

До задачі 6 § 12

4 5

х 6 - х

мал. 4

● Знайдіть проекції сторін 4 і 5 м на сторону 6 м даного трикутника ( мал.4 ). ( 4² - х² = 5² - ( 6 – х )² ,

де х – проекція сторони 4 м на сторону 6 м, а 6 – х – проекція сторони 5 м на сторону 6 м.)

До задачі № 8 §12

● Як знайти висоту трикутника, проведеного до сторони 6 м? ( Знаходимо проекції двох інших сторін на сторону 6 м, як це було зроблено в задачі 6, а потім за теоремою Піфагора – шукану висоту даного трикутника ).

● Сформулюйте наслідки теореми косинусів.


Урок 4. Теорема синусів

Мета. Засвоєння учнями змісту й доведення теореми синусів і використання її для розв’язування задач

Тип. Комбінований урок

З метою актуалізації знань учням пропонуються завдання, які потрібно виконати на чернетках. На вимогу вчителя одержані відповіді учні пишуть на індивідуальних дошках і показують учителеві. Умови задач і малюнки до них поміщено на дошці.

Завдання класу

● У трикутнику АВС АС = b, кут А = α. Знайдіть висоту трикутника h, якщо: а) α – гострий кут;

б) α – тупий кут.


● Дано: ab = mn ( a, b, m, n – числа, відмінні від нуля ). Складіть із цих чисел пропорцію. Чи завжди задача має розв'язок.

● Як знайти довжину сторони ВС у трикутнику АВС, якщо АВ = 3 см, АС = 4 см, кут ВАС = 30°?

● Як знайти кути трикутника АВС, якщо АВ = 3 см, ВС = 4см, АС = 2см?


Урок 5. Співвідношення між кутами і протилежними сторонами трикутника

Мета. Ознайомлення учнів зі змістом і доведенням наслідку теореми синусів

Тип. Урок закріплення вивченого

Перевірка д/з й актуалізація знань учнів

Двоє учнів біля дошки готують розв’язання домашніх задач № 9,13. Наведемо розв’язання однієї з них.

Задача 9 §12. Нехай у трикутнику АВС проведено медіану АО, що дорівнює х (х>0) (мал. 5). Відкладемо на промені АО від точки О відрізок ОД, який дорівнює відрізку АО. Тоді чотирикутник АВСД - паралелограм. За властивістю діагоналей паралелограма (наслідок із теореми косинусів) (2х)²+ВС²=2 АВ²+2 АС². Звідси 4х²+5²=2 6²+2 7², тобто х²=145/4, х=√145/2.Відповідь.√145/2 м.

Д С


6 О


А 6 В

мал. 5


Запитання до класу

● Як читається і записується теорема синусів для задачі 12§12, якщо припустити, що АВ=с, АС=b, а

sin ß =3/4?(с/sin γ=b/sin ß,15/sin γ=10/sin ß, 3/sin γ=2 4/3/)

● Чому дорівнює sinγ в цій задачі? Чи можливо це? (sin γ=9/8. Це неможливо, тому що синус кута не може бути більший від 1. Тому sin ß=3/4.)


Урок 6. Розв’язування трикутників

Мета. Розв’язування задач з використанням теорем синусів і косинусів та їх наслідків

Тип. Урок закріплення вивченого

Перевірка д/з й актуалізація знань учнів

Опитування учнів за картками ( у.в.р. )

Картка 1. Відповісти на контрольне запитання 4 §12

Картка 2. Довести властивість бісектриси кута трикутника

Поки викликані учні готуються до відповіді, клас намічає хід розв’язування задачі 14 §12 за заздалегідь підготовленим малюнком (мал. 6).

Розв’язання:

1. За теоремою косинусів ( а² = в² + с² - 2вс соs α ) знаходимо соs α.
   
2. За формулою sin² α + cos² α = 1 знаходимо sin α.
   
3. а/ sin α = 2R ( на підставі опорної задачі 13 §12 ).
   

Тоді R = а/2 sin α.





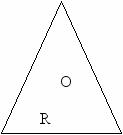
α

с в


а

мал.6


Наведемо приблизний зразок запису розв’язання задачі на властивість бісектриси кута трикутника.

Розв’язання:

Застосуємо теорему синусів до трикутників АВС і СВD. АD/sin ß = АВ/sin α; СD/sin ß =

= ВС/ sin( 180° - α ) = ВС/sin α. Якщо першу рівність розділити на другу, то дістанемо АD/СD =

= АВ/ВС, що й було потрібно довести.


Урок 7. Розв’язування трикутників

Мета. Формування умінь учнів розв’язування задач з даної теми

Тип. Урок узагальнення і систематизації вивченого матеріалу

Учитель зазначає, що на цьому уроці буде систематизовано знання учнів з теми "Розв’язування трикутників"; виділено основні типи задач, розглянуто їх. Нагадує учням зміст основних задач на розв’язування прямокутних трикутників. Підкреслює, що розв’язування цих задач ґрунтується на теоремі Піфагора й означеннях понять sin α, cos α, tg α, де α-гострий кут прямокутного трикутника.


Урок 8. Розв’язування трикутників

Мета. Формування умінь учнів розв’язування задач з даної теми

Тип. Урок узагальнення і систематизації вивченого матеріалу

Перевірка д/з й актуалізація знань учнів

1. Викликані до дошки учні середнього рівня засвоєння знань пояснюють розв’язування задач №15,28(2-4) §12.
   
2. Решта учнів виконують завдання математичного диктанту.
   

Математичний диктант

а) Якщо в трикутнику АВС відомі дві сторони b і c та кут між ними А, то третя сторона дорівнює … .

б) Якщо в трикутнику відома сторона а і два прилеглі до неї кути В і С, то дві інші сторони можна знайти так: … .

в) У трикутнику АВС АВ=4см, ВС=5см, АС=6см. Найбільший кут у трикутнику АВС- це кут … .

г) У трикутнику проти сторони а лежить кут α. Тоді радіус R кола, описаного навколо трикутника, можна знайти за формулою: … .

Після виконання завдань математичного диктанту учні звіряють ті відповіді, що дістали, з відповідями, записаними раніше вчителем на відкидній дошці, аналізують помилки. Так відбувається повторення основних властивостей, які застосовуються для розв’язування трикутників ( теореми синусів і косинусів, наслідки з них).

Урок 9. Розв’язування трикутників

Мета. Перевірка знань і умінь учнів розв’язування задач з даної теми, підготовка до к/р

Тип. Урок перевірки знань, умінь і навичок

1. Перевірка д/з .
   
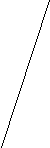
2. Усно розв’язати трикутники за малюнками (типу малюнка 7):
   

а) б)


а ? ? ?


в а с

в)

а в


с

мал.7


3. Розв’язати задачу:

3.1. У.п.р. та у.с.р. працюють самостійно над індивідуальною задачею на безпосереднє застосування теореми синусів чи косинусів типу:

Довжини сторін трикутника 2 см і 5 см, кут між ними 135°. Знайти третю сторону.

3.2. У.д.р. та у.в.р. розв’язують задачу типу:

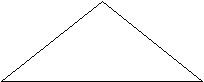
У рівнобічній трапеції довжина більшої основи a=3см, величина прилеглого до неї кута 60°, а довжина діагоналі d=6см. Знайти довжину бічної сторони трапеції.

Пояснення до задачі (дивись малюнок 8):





?

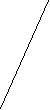
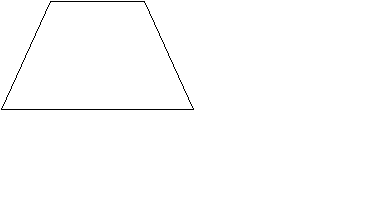
? ? ? d

a





a a

мал. 8


4. Підвести підсумок розв’язання задач; вказати окремим учням на необхідність допрацювати той чи інший матеріал під час підготовки до к/р.


Підготовку до к/р також можна провести у нетрадиційній формі, наприклад, як роботу в групах. В цьому випадку актуалізацію опорних знань проводимо у формі фронтального опитування.


Особливість організації актуалізації знань з геометрії полягає в тому, що від учнів початкового та середнього рівнів засвоєння навчального матеріалу не слід вимагати вміння доводити теореми, досить обмежитись вмінням чітко формулювати її і безпосередньо застосовувати під час розв’язування типових задач. Учні ж вищих рівнів оволодіння знаннями повинні доводити теореми, робити висновки з них і застосовувати набуті знання у багатокрокових задачах, які вимагають знань не лише з теми, що вивчається, а і з вивченого раніше матеріалу.


Ще хотілося б наголосити, що етапом актуалізації знань і вмінь не можна нехтувати, особливо у 9-му класі, адже це останній клас основної школи. Учні високого та достатнього рівнів засвоєння знань будуть продовжувати навчання у 10-12 класах, решта – підуть навчатися у середні спеціальні заклади. І першим, і другим необхідні міцні знання, до того ж знання, зведені у струнку систему. Цього можна досягти, працюючи поурочно на етапі актуалізації опорних знань, умінь і навичок.


2.2. Структурне представлення викладу даної теми


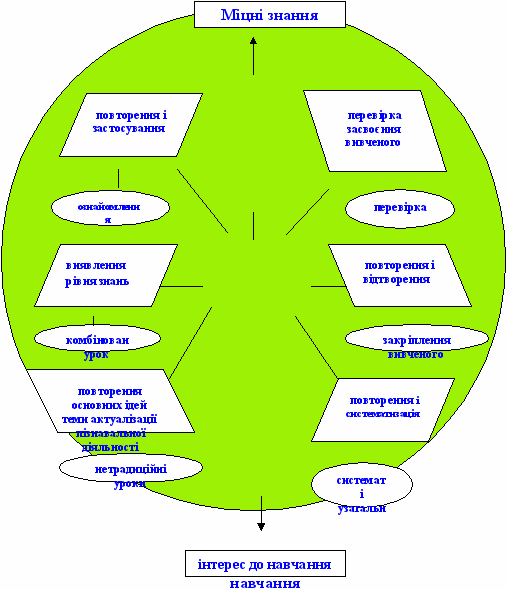
У даному пункті цього розділу за допомогою схем висвітлюються основні ідеї даної роботи, а саме дається мотивація актуалізації опорних вмінь та навичок (схема 15); демонструється доцільність застосування різнорівневого підходу до актуалізації знань, як етапу уроку математики (схема 16); пропонуються форми організації початку уроку згідно основної дидактичної мети уроку (схема 17).


Актуалізацію опорних вмінь та навичок необхідно проводити на кожному уроці, підбираючи систему запитань чи вправ так, щоб полегшити просування учнів уперед, а також з метою повторення і узагальнення знань дітей. Це, в свою чергу, полегшить навчання, зацікавить дітей, а там, де є інтерес до навчання, будуть і міцні знання. Це ілюструє схема 15.


Але необхідно пам’ятати, що різним дітям потрібні різні знання. З цією метою слід використовувати методику диференційованого навчання.

Пропонується схема 16 використання диференційованого підходу на уроках математики під час актуалізації опорних вмінь та навичок. Суцільна лінія показує, на яких уроках доцільно проводити актуалізацію знань з використанням диференційованого підходу; пунктиром – уроки, на яких диференційований підхід до навчання на етапі актуалізації знань і умінь можна застосовувати частково.

Так, диференціація навчання застосовна на етапі актуалізації опорних знань на уроках закріплення вивченого та комбінованих уроках; проведення нетрадиційних уроків повністю базується на різнорівневому підході до навчання. Урок перевірки вивченого, різні його види вимагають по-різному використовувати диференційований підхід: залік має бути класичним прикладом диференціації навчання. Що стосується самостійної чи контрольної робіт, то тут відбувається, так би мовити, внутрішня актуалізація знань, вона взагалі проводиться індивідуально: кожен учень напередодні уроку самостійно готується до письмової роботи. На уроках ознайомлення з новим матеріалом під час вивчення теми диференційований підхід не працює на початку уроку, адже всім учням необхідні певні знання для сприйняття нового. Якщо ж це уроки в межах певної теми чи розділу, то диференційований підхід до вивчення матеріалу, при повторенні на етапі актуалізації, можна повністю використовувати.

Схема 17 пропонує форми організації етапу актуалізації знань і вмінь в умовах різнорівневого навчання. Нею можна користуватися у методичному плані з двох сторін: по-перше, виходячи з типу уроку відносно основної дидактичної мети, користуючись схемою 17, можна спланувати форми проведення початкового етапу відповідного уроку. Так, початок уроку ознайомлення з новим матеріалом можна організувати як перевірку д/з (декілька учнів) чи фронтального опитування класу в залежності від структури і мети уроку, або провести актуалізацію так, щоб вона прямо підводила дітей до проблеми даного уроку. Актуалізація знань і умінь, організована у формі гри, або так, щоб діти нібито самі виділили необхідні знання, характерна для нетрадиційних уроків. По-друге, при наявностіі бажання урізноманітніти структуру уроку, а

саме - його початок. За допомогою даної схеми можна вибрати форми проведення актуалізації знань та їх комбінації, які є найдоцільнішими при проведенні того чи іншого уроку.


Висновки


Вивчення стану проблеми через опрацювання психолого-педагогічної та науково-методичної літератури і аналіз викладання математики в середній школі дало змогу з'ясувати і виділити теоретичні аспекти даної проблеми; обґрунтувати необхідність етапу актуалізації опорних знань, умінь та навичок, а саме урізноманітнення форм його проведення в умовах різнорівневого підходу до навчання математики.

Нерозробленість цього питання спонукала до організації розрізнених даних у певну систему. Цьому присвячений розділ 1 даної розробки, а також пункт "Структурне представлення викладу даної проблеми" розділу 2.

Теоретичні основи проблеми дали змогу обґрунтувати власну точку зору на формування, організацію роботи на початковому етапі уроку математики. Конкретне представлення використання цієї методики дається на прикладі тем "Розв’язування трикутників" з геометрії та "Квадратична функція" з алгебри.

Всі представлені ідеї перевірялися у процесі проведення уроків математики. Практика показала, що дана методика зручна тим, що кожен урок з теми, що вивчається, повинен бути спланованованим і відрізнятись від попереднього своїм ходом. Це сприяє активізації розумової діяльності школярів. Безумовно, кожен урок повинен починатися з актуалізації знань, умінь та навичок учнів. Особливо ефективним застосування даної методики виявилося на уроках ознайомлення з новим матеріалом. Так, у процесі подачі теореми косинусів, повторивши властивості векторів, учні, майже самі, довели дану теорему.

Подані у роботі схеми висвітлюють основні ідеї даної проблеми. Схема 15 дає обґрунтування етапу актуалізації знань, умінь та навичок і вказує мету його проведення. Схема 16 встановлює відповідність між типом уроку щодо основної дидактичної мети і застосуванням диференційованого підходу до початкового етапу уроку. Схема 17 узгоджує вибір форми організації етапу актуалізації знань і вмінь відносно вибраного типу уроку і навпаки.

Написання роботи дало змогу краще зрозуміти питання, розрізнені у психолого-педагогічній та методичній літературі і узагальнити знання з проблеми диференційованого підходу до навчання математики.

Результати проведеної роботи можуть використовуватися вчителями з метою більш раціонального використання часу на уроці і вдалого вибору форм роботи на початку уроку відносно його типу будь-якої теми шкільного курсу математики.


Схема 15. Мотивація етапу актуалізації знань

у відповідності з типом обраного уроку