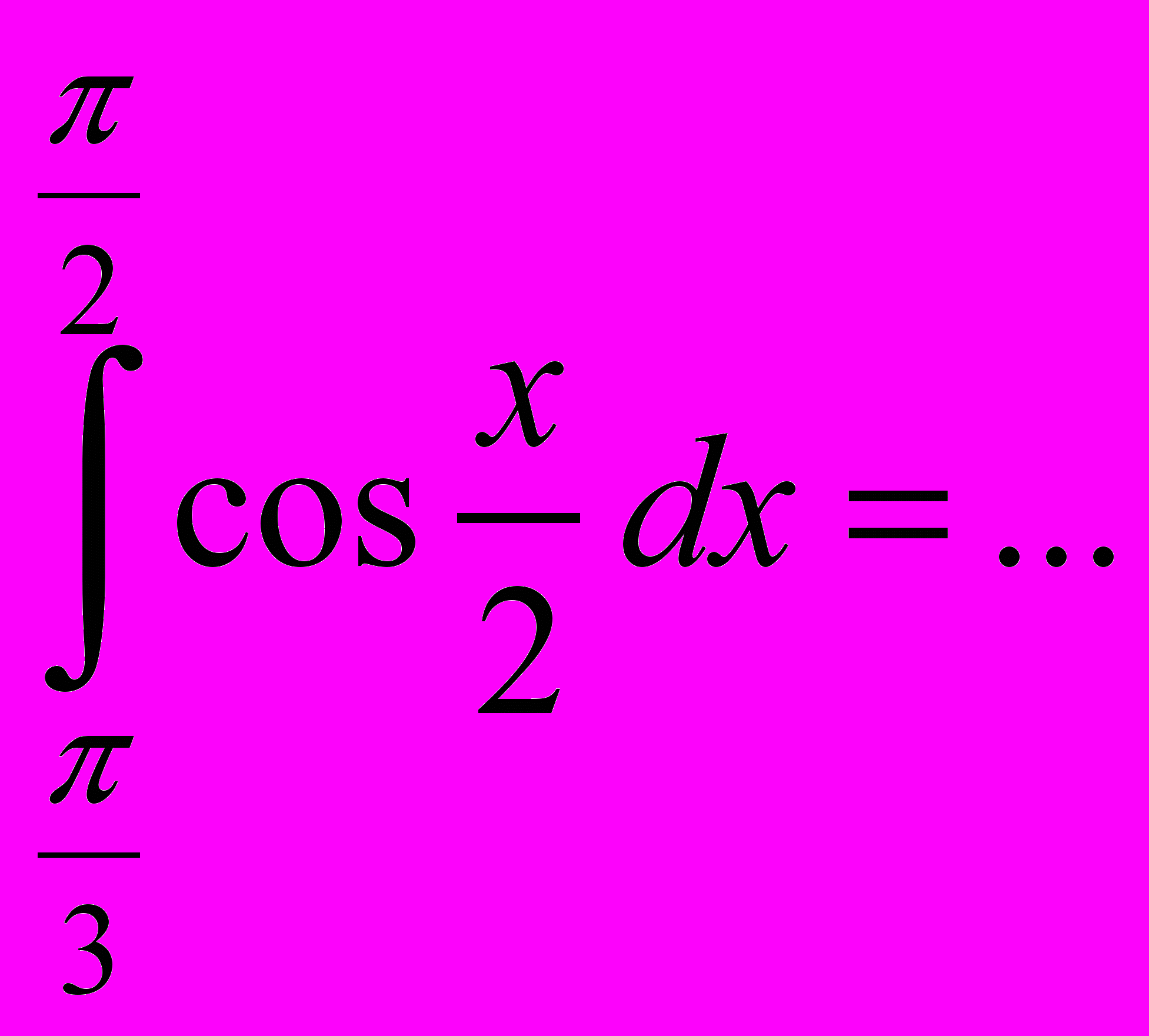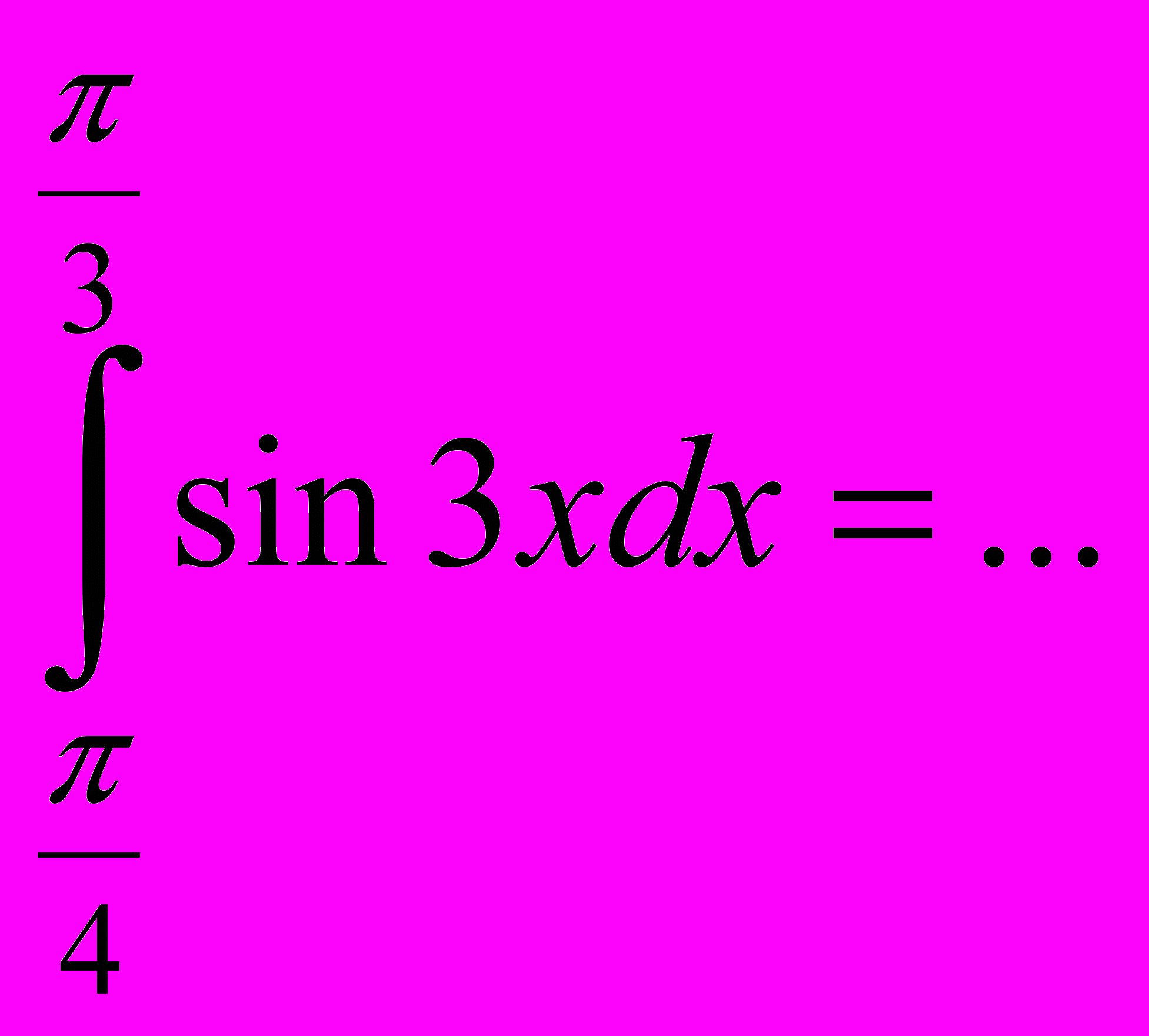Навчально-виховний комплекс №6 «Перспектива» виховання творчої особистості в умовах інтегрованого уроку розробка інтегрованого уроку з математики-інформатики
| Вид материала | Урок |
СодержаниеВиховання творчої особистості Мета уроку. Тип уроку. 1.Організаційний момент. 3.Актуалізація опорних знань 4.Розв’язування вправ 5. Вчитель інформатики Advanced Grapher 6. Підсумок уроку. |
- План Урок. Елементи уроку Взаємозв'язок типу І структури уроку Форми роботи на уроці, 186.36kb.
- Тема уроку. Панас Мирний. Життєвий І творчий шлях письменника. Мета уроку, 87.23kb.
- Тема уроку, 255.23kb.
- План уроку: Загальна тема №2: «Музика виражає та зображує», 77.38kb.
- Навчально-виховний комплекс №16 Методична розробка циклу уроків з теми, 229.79kb.
- Устатті подаються методичні рекомендації щодо проведення бінарного інтегрованого уроку, 201.48kb.
- Програма виховання учнів 1-12 класів (проект), 733.12kb.
- Програма виховання учнів 1-12 класів (проект), 735.28kb.
- Програма виховання учнів 1-12 класів (проект), 726.18kb.
- Устатті розглядаються особистісно орієнтовані технології навчання майбутніх учителів, 129.69kb.
М
 іністерство освіти і науки України
іністерство освіти і науки УкраїниГоловне управління освіти і науки
Дніпропетровський обласний інститут післядипломної педагогічної освіти
Відділ освіти виконкому Жовтоводської міської ради
Комунальний заклад освіти
навчально-виховний комплекс № 6 «Перспектива»
ВИХОВАННЯ ТВОРЧОЇ ОСОБИСТОСТІ
В УМОВАХ ІНТЕГРОВАНОГО УРОКУ
Розробка інтегрованого уроку з математики-інформатики
«Застосування інтеграла до обчислення площ плоских фігур»
Вчитель математики
Ковальчук Наталія Аркадіївна
Вчитель інформатики
Лапченко Світлана Сергіївна
м.Жовті Води - 2011
Ковальчук Н.А.
вчитель математики вищої кваліфікаційної категорії
НВК №6 «Перспектива»
Лапченко С.С.
вчитель математики та інформатики вищої кваліфікаційної категорії
НВК №6 «Перспектива»
Сучасна педагогічна наука стверджує, що для продуктивного засвоєння учнем знань і для його інтелектуального розвитку важливо встановити широкі зв’язки як між різними розділами курсу, що вивчається, так і між різними дисциплінами в цілому ( внутрішньопредметна і міжпредметна інтеграція). Метою проведення інтегрованого уроку з математики-інформатики в 11 класі є розв’язання задач геометричного змісту на знаходження площ плоских фігур та оформлення їх розв’язання з використанням можливостей прикладної програми Advanced Grapher.
Виховання творчої особистості
в умовах інтегрованого уроку.
“Той, хто серйозно прямує до пізнання істини, не повинен займатись якоюсь однією наукою, бо всі науки взаємопов’язані”
Р. Декарт
“Творчість – це здатність дивувати і пізнавати, вміння знаходити рішення в нестандартних ситуаціях…”
Творчість – це діяльність людини, спрямована на створення духовних і матеріальних цінностей – прагнення до гармонії, до рефлексії, до духовного.
Саме цими ознаками характеризується і дитяча творчість. Для дитини, створені нею продукти є суб’єктивним, новими та оригінальними, вони потребують пошуку, думки, є відкриттям. У такому розумінні, творчою – є така діяльність, яка дає дитині задоволення, збуджує інтерес і є для неї надзвичайно значущою.
Розвивати творчість – це навчати дитину розуміти сутність незрозумілого, адже нова ідея виникає лише тоді, коли людина має певний набір знань і за рахунок уже відомого має можливість осягнути незрозуміле. Тобто в неї виникає бажання знайти правильне пояснення того чи іншого явища. Результатом такої діяльності є відкриття. Хоча б для маленького відкриття потрібно творчо мислити, мати добре розвинуті творчі здібності, для розвитку яких необхідні умови, що випереджають розвиток; свобода у виборі знань; не виконувати за дитину те, що вона може зробити сама.
Щоб розвивати творче мислення – ті розумові здібності, що необхідні для успішного навчання в школі, необхідно розвивати пам’ять, увагу, образне мислення, логічне мислення ( вміння порівнювати, доводити, аналізувати, узагальнювати); творчі здібності, фантазію, уяву; конструктивне мислення.
Саме математика дає широкі можливості для інтелектуального розвитку, розвитку логічного мислення, уяви. Досвід показує, що інтегроване навчання математики, за якого матеріал доповнюється відомостями з інших предметів та повторюється, дає набагато кращий результат. Учні повинні сприймати світ у цілому, а не лише з точки зору окремого предмета.
Так, у 5-6 класах на уроках математики вивчаються дії з раціональними числами. Вміння виконувати ці дії необхідні при розв’язанні задач на уроках фізики, хімії. Тому я вважаю доцільним вже в 5-6 класах проводити підготовчу роботу, направлену на знайомство з такими предметами як фізика, біологія, хімія, географія, що такі науки взагалі існують, що саме вони вивчають, що їх об’єднує.
При вивченні теми ”Відсотки” розв’язуючи слідуючи задачі:
- 3 500 зерен жита, зійшло 400. Визначити відсоток схожості насіння.
- Тіло сома містить 6,5 % жирів. Скільки треба взяти риби, щоб дістати 2,5 кг жирів.
слід сказати, що наука про живу природу, про велике розмаїття живих істот, їх будову, виникнення та розвиток називається біологією.
Ідеї інтеграції знаходять своє відбиття і в концепції сучасної шкільної освіти. Їх актуальність зумовила нові соціальні запити, адресовані школі: оновлення змісту навчання; математизація науки; диференціація та інтеграція наук про природу, створення інтегрованих курсів; виховання творчих працівників, які здатні після закінчення школи включитися в різні сфери людської діяльності, які знають історію культури рідного краю, є патріотами своєї Батьківщини.
Сучасна педагогічна наука стверджує, що для продуктивного засвоєння учнем знань і для його інтелектуального розвитку важливо встановити широкі зв’язки як між різними розділами курсу, що вивчається, так і між різними дисциплінами в цілому ( внутрішньопредметна і між предметна інтеграція).
Ідеї інтеграції будуть дуже корисними та ефективними на заключному етапі вивчення будь-якої теми. Вони допоможуть знання сучасних учнів, які, на жаль, являють собою так звану “клаптикову ковдру” зробити більш цілісними.
Одним із засобів реалізації цих ідей є інтегровані уроки математики з іншими предметами.
Інтегрований урок – це урок, який проводиться з метою розкриття загальних закономірностей, законів, ідей, теорій, відображення у різних науках та відповідних навчальних предметах. Це уроки інтегрованих зв’язків декількох предметів. Такі уроки дають можливість формування і яскравішого уявлення навколишнього, взаємозв’язків і явищ. Основний акцент припадає не стільки на засвоєння певних знань, скільки на розвиток освітнього мислення.
Структура таких уроків відрізняється чіткістю, компактністю, стислістю, логічною взаємообумовленістю навчального матеріалу на кожному етапі уроку, великою інформативністю, об’ємністю матеріалу. Інтегровані уроки передбачають обов’язковий розвиток творчої активності учнів, розподіл навантаження за рахунок переключення на різноманітні види діяльності; підвищують пізнавальний інтерес, сприяють розвитку у школярів мислення, уваги, пам’яті, мовлення, уяви.
Отже інтегровані уроки сприяють:
- більш повному осмисленню учнями навчального матеріалу, різні аспекти якого не можуть бути розкриті засобами якогось одного навчального предмета;
- формуванню умінь переносити знання з однієї галузі науки чи мистецтва в іншу;
- стимулюванню аналітико-синтетичної діяльності учнів, розвитку потреби в системному підході до об’єкта пізнання, аналізу та порівнянню процесів та явищ;
- розвитку творчих здібностей учнів: уяви, фантазії, образного мислення, інтелекту та емоційної сфери.
На таких уроках яскраво виражена прикладна спрямованість, тому вони викликають незаперечний пізнавальний інтерес учнів. Вони допомагають формувати науковий світогляд, сприяють встановленню логічних зв’язків між поняттями. Для їх проведення доцільно об’єднувати зусилля декількох учителів. Для прикладу пропонуємо розробку інтегрованого уроку з алгебри та початків аналізу і інформатики “Застосування інтеграла до обчислення площ плоских фігур”.
«Ми ніколи не станемо математиками, навіть знаючи на пам’ять усі чужі доведення, якщо наш розум не здатний самостійно розв’язувати які б то не було проблеми»
Р.Декарт
Тема уроку. Застосування інтеграла до обчислення площ плоских фігур.
Мета уроку. Формувати уміння застосовувати інтеграл до обчислення площ фігур; розвивати пізнавальний інтерес учнів; сприяти виробленню умінь використовувати свої знання в нових ситуаціях; сприяти розширенню кругозору; виховувати вміння раціонально використовувати робочий час.
Тип уроку. Інтегрований урок.
Обладнання: плакати, малюнки, дидактичні матеріали, схеми алгоритмів, комп’ютерні програми обчислення, визначений інтеграл, комп’ютери.
Хід уроку
1.Організаційний момент.
2.Перевірка домашнього завдання.
Перевіряється наявність домашнього завдання, а вкінці уроку кожен перевіряє правильність виконання за допомогою комп’ютерної програми.
3.Актуалізація опорних знань:
1.Фронтальне опитування:
- визначення первісної;
- властивості первісної;
- означення інтеграла;
- обчислення визначеного інтеграла;
- формула Ньютона – Лейбніца;
- яка відмінність між загальним видом первісної (невизначеним інтегралом) і визначеним інтегралом?( Невизначений інтеграл – це функція, а визначений - число).
- яка фігура називається криволінійною трапецією?
- як знайти координати точок перетину графіків функцій f(х) і q(х)?
2.В той час, коли проходить фронтальне опитування, учні на дошці будують графіки наступних функцій:
- y=kx+b, коли k>0 та k<0;
y=kx;
y=b, x=a;
2)
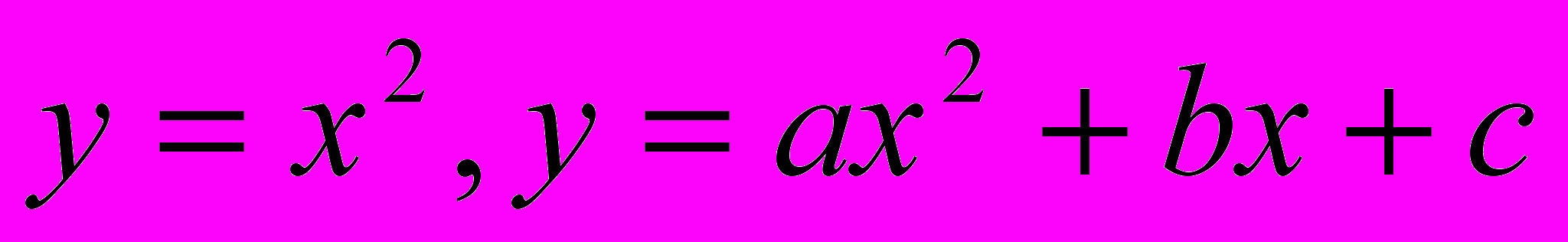 , коли a>0, a<0;
, коли a>0, a<0;3)
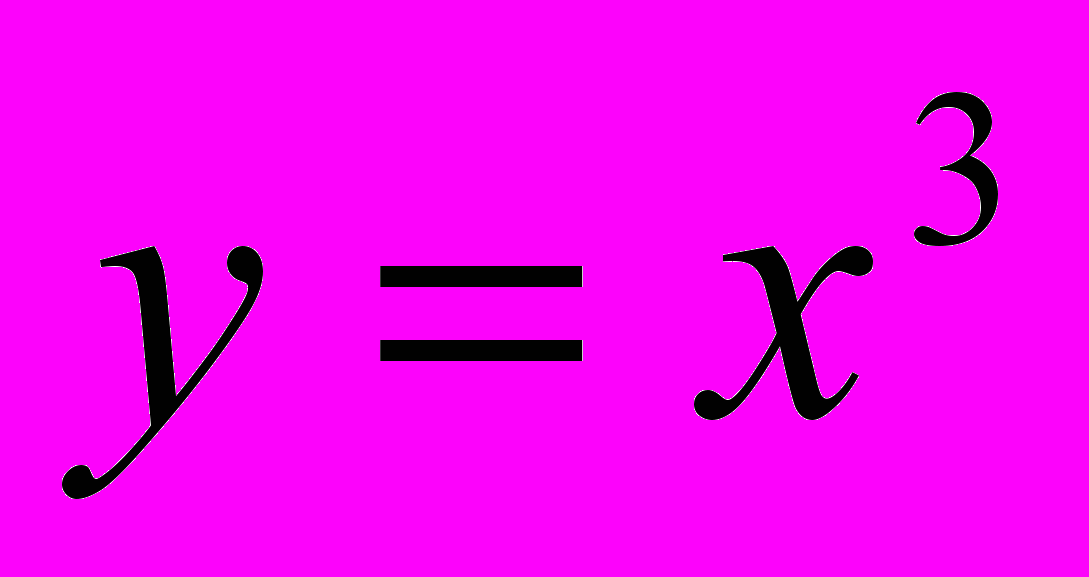 ;
;4)
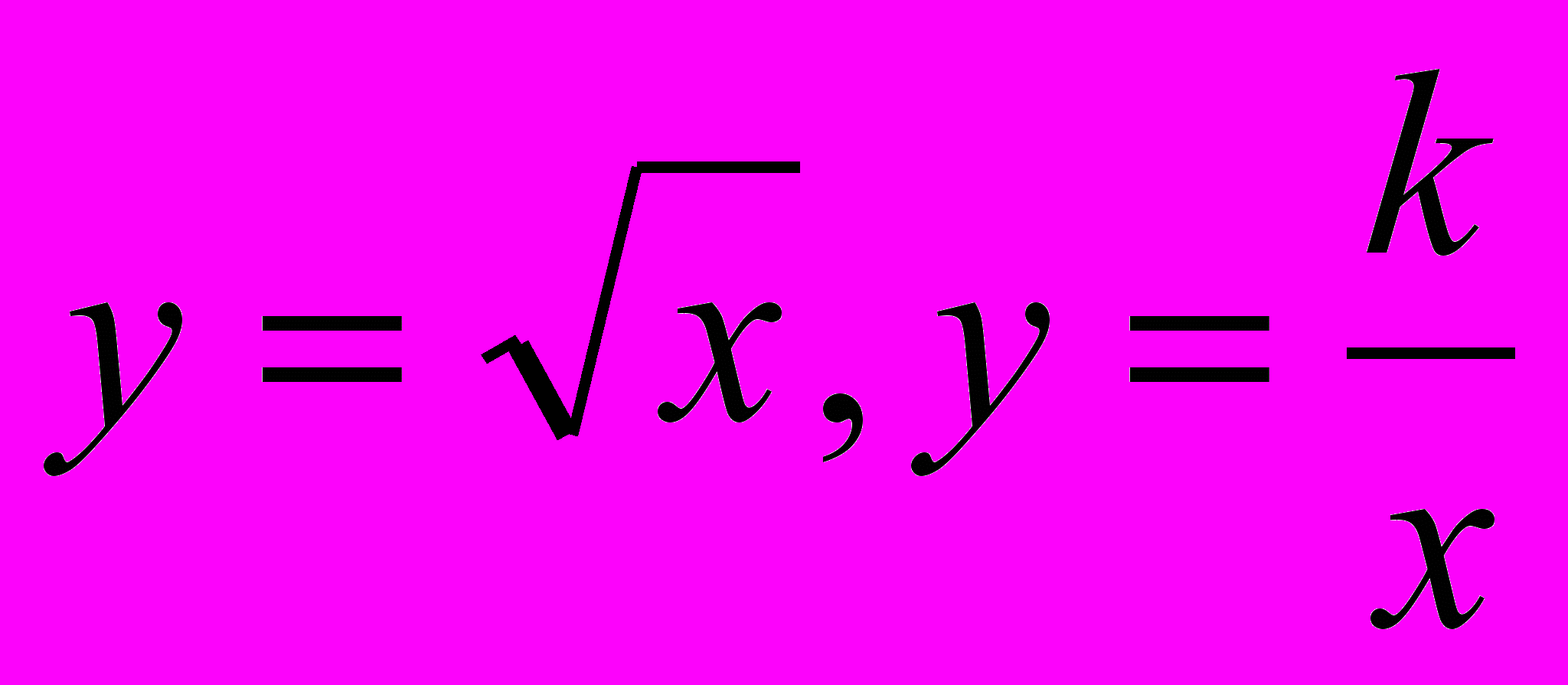 ;
;5)
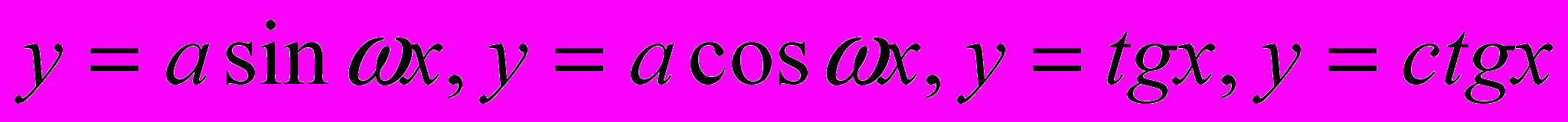 ;
;6)
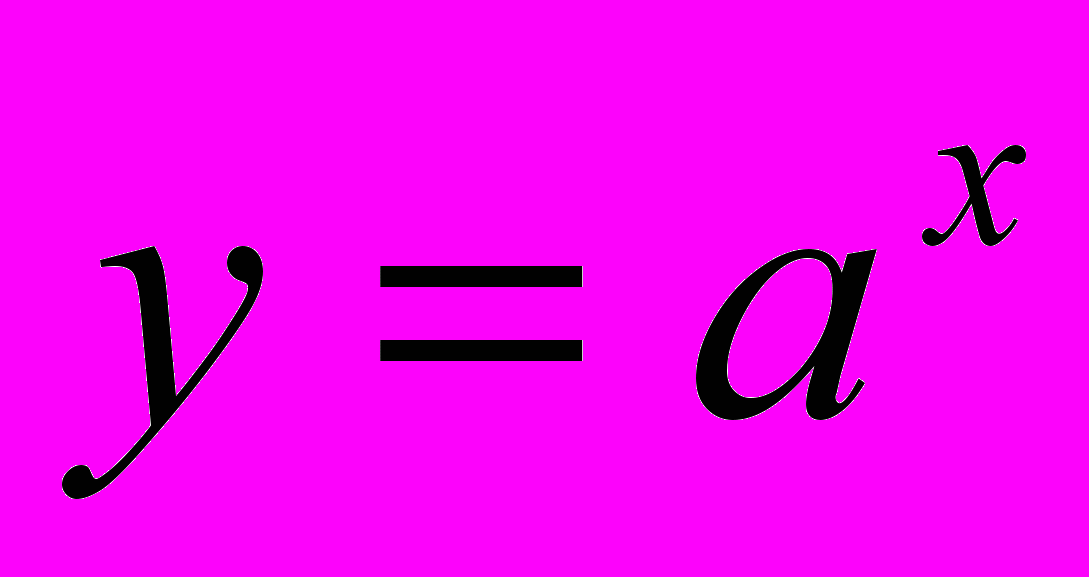 , коли 0
, коли 0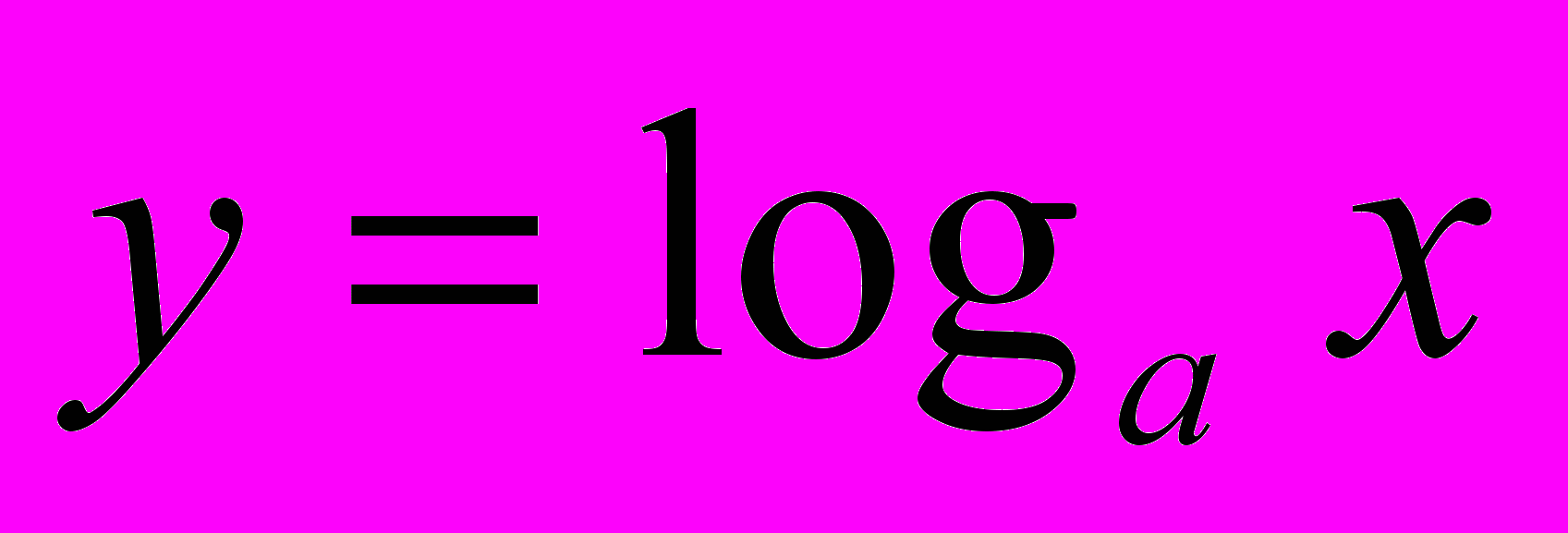 , коли 0
, коли 0Побудова графіків даних функцій повинна бути відпрацьована до автоматизму.
3.Обчислити визначений інтеграл:
На дошці зашифровано вислів:

16 40
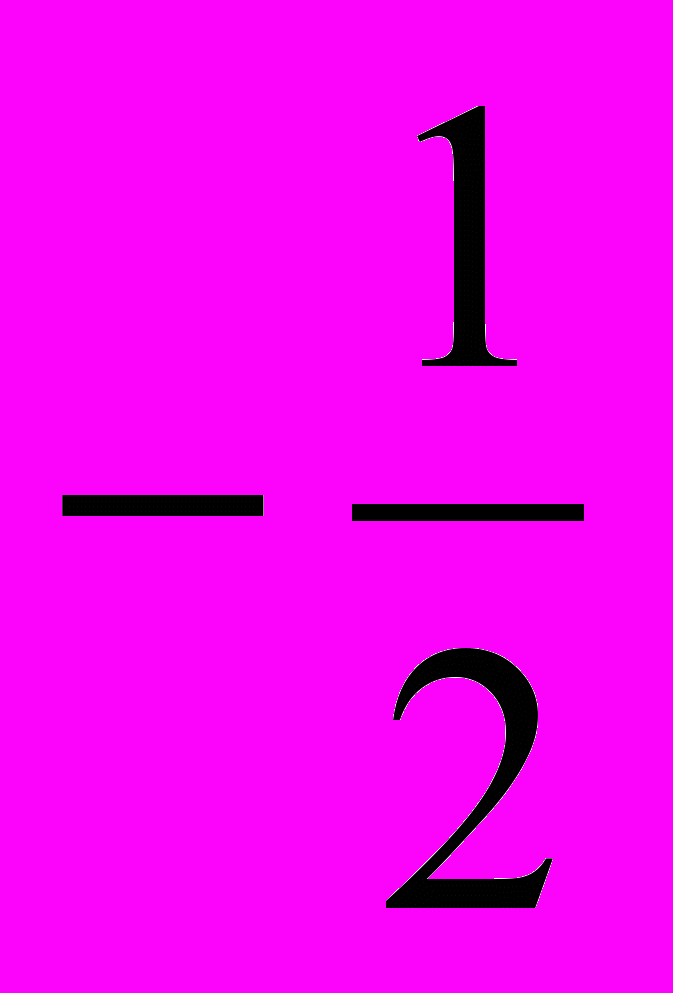 192 8
192 8 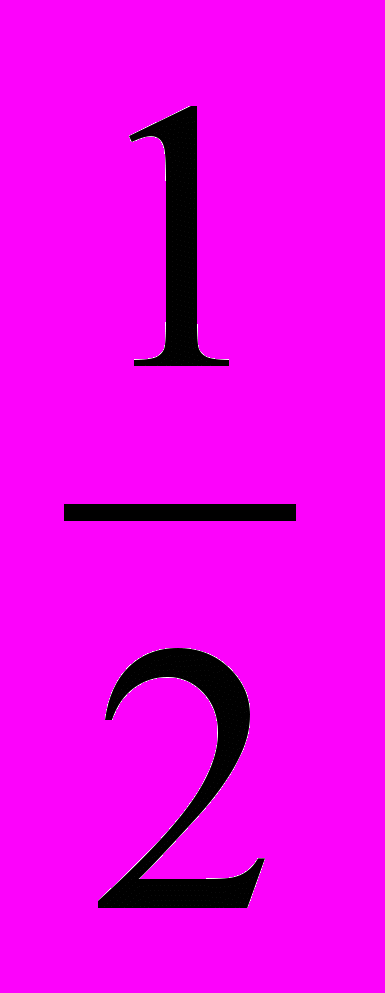
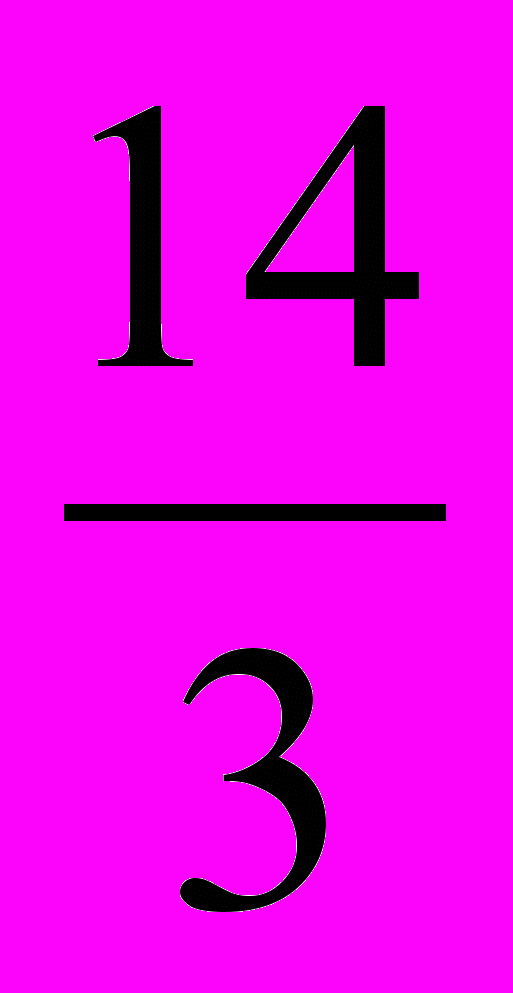
1
 )
) 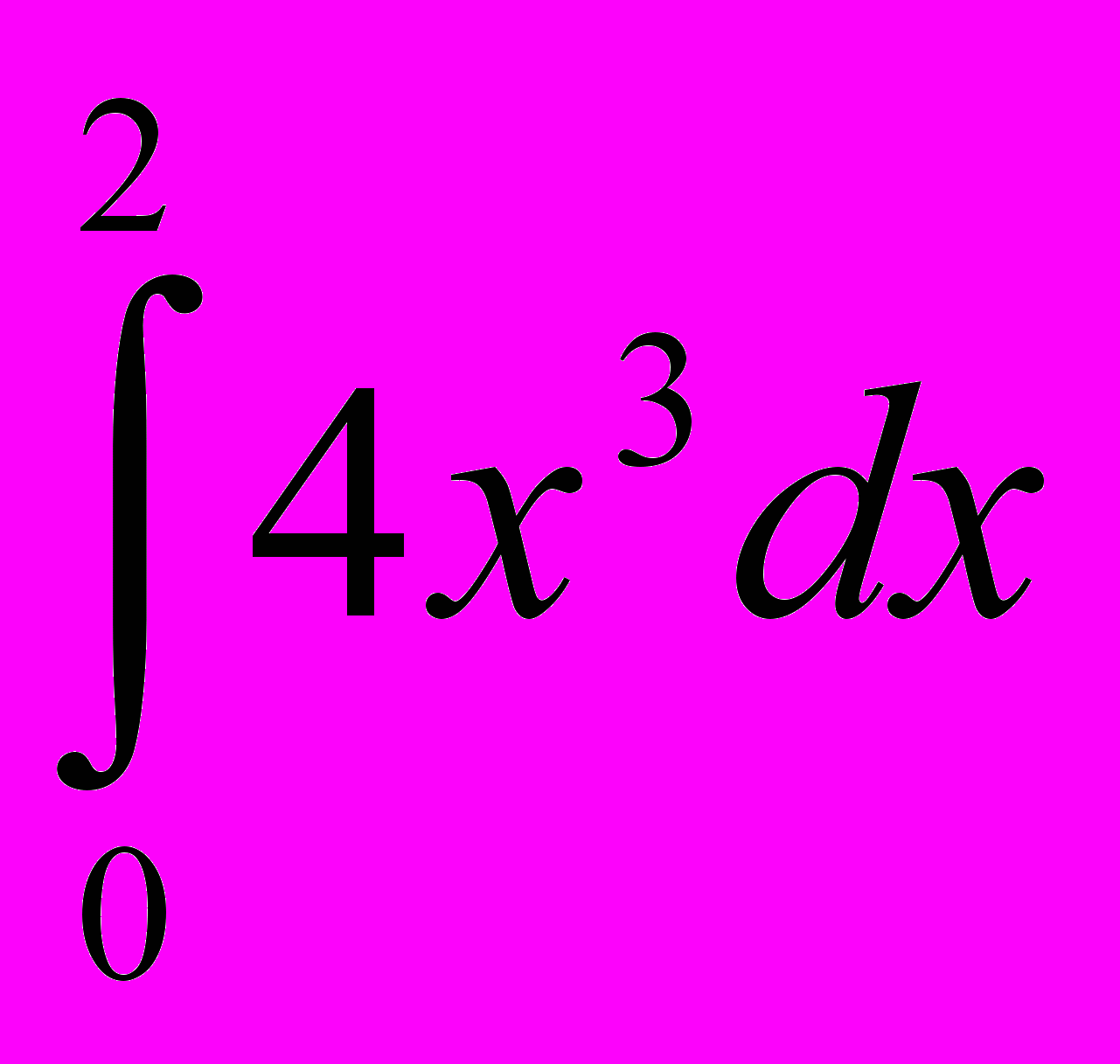 ; 2)
; 2) 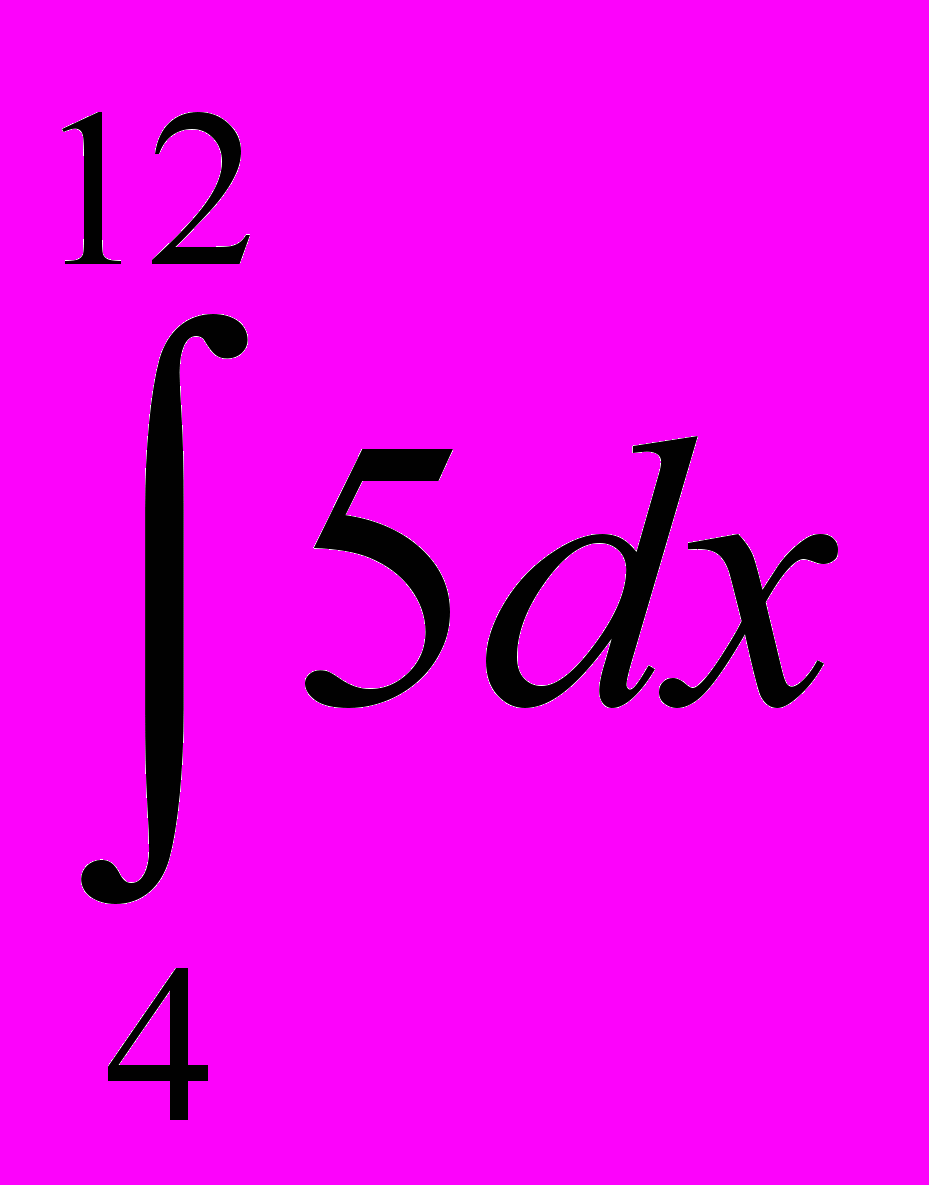 ; 3)
; 3) 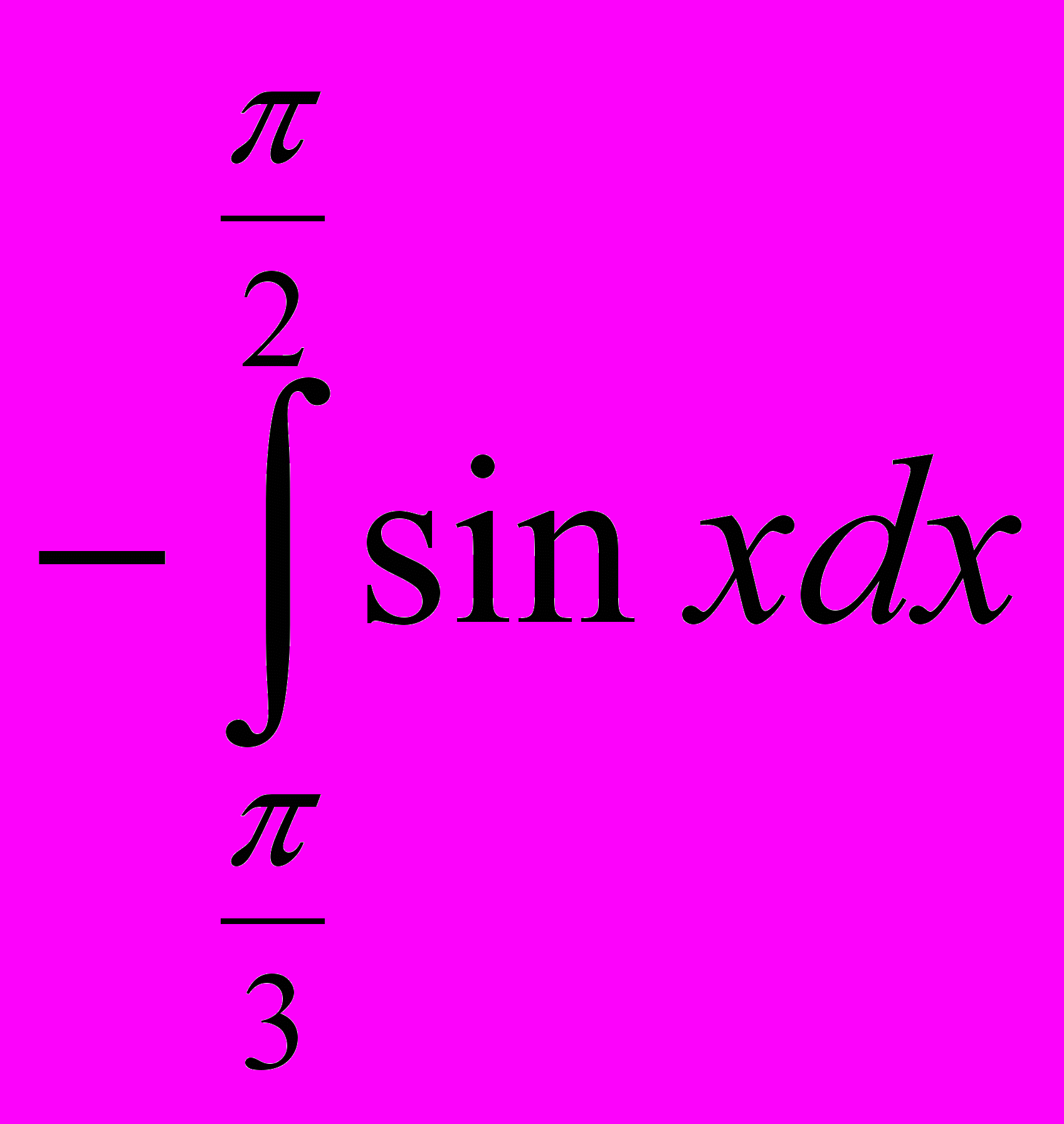 ;
; 4)
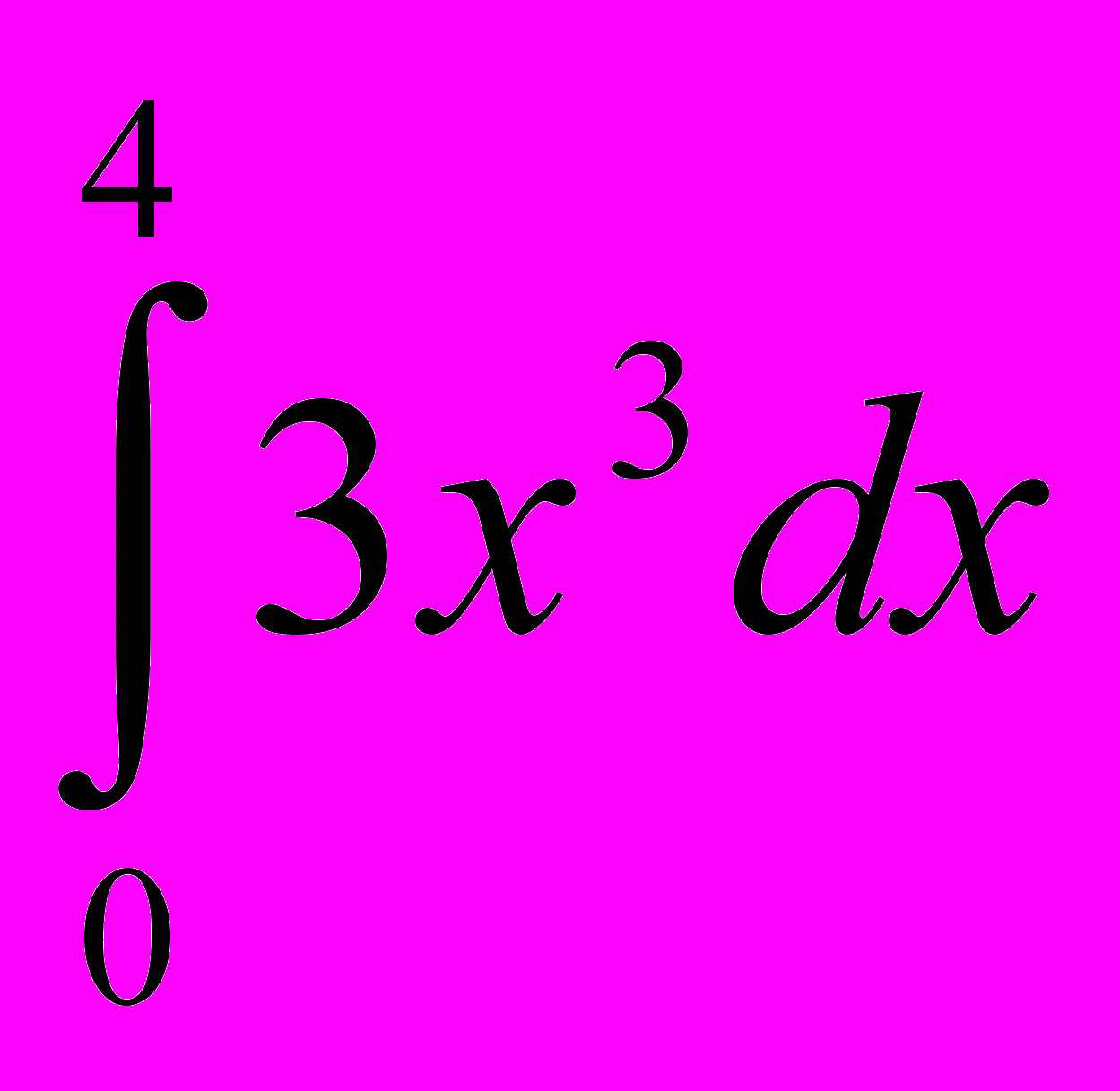 ; 5)
; 5) 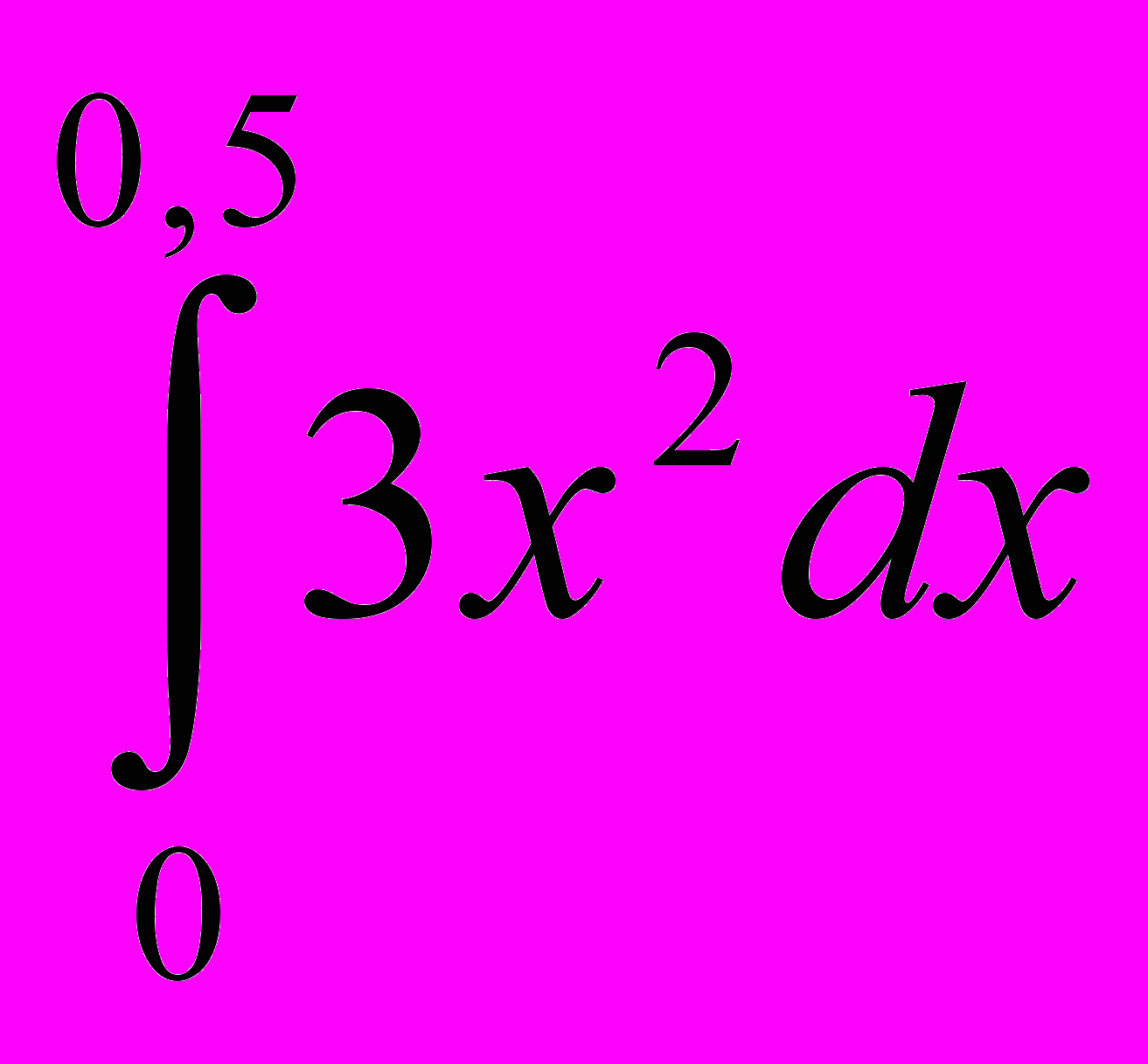 +
+ 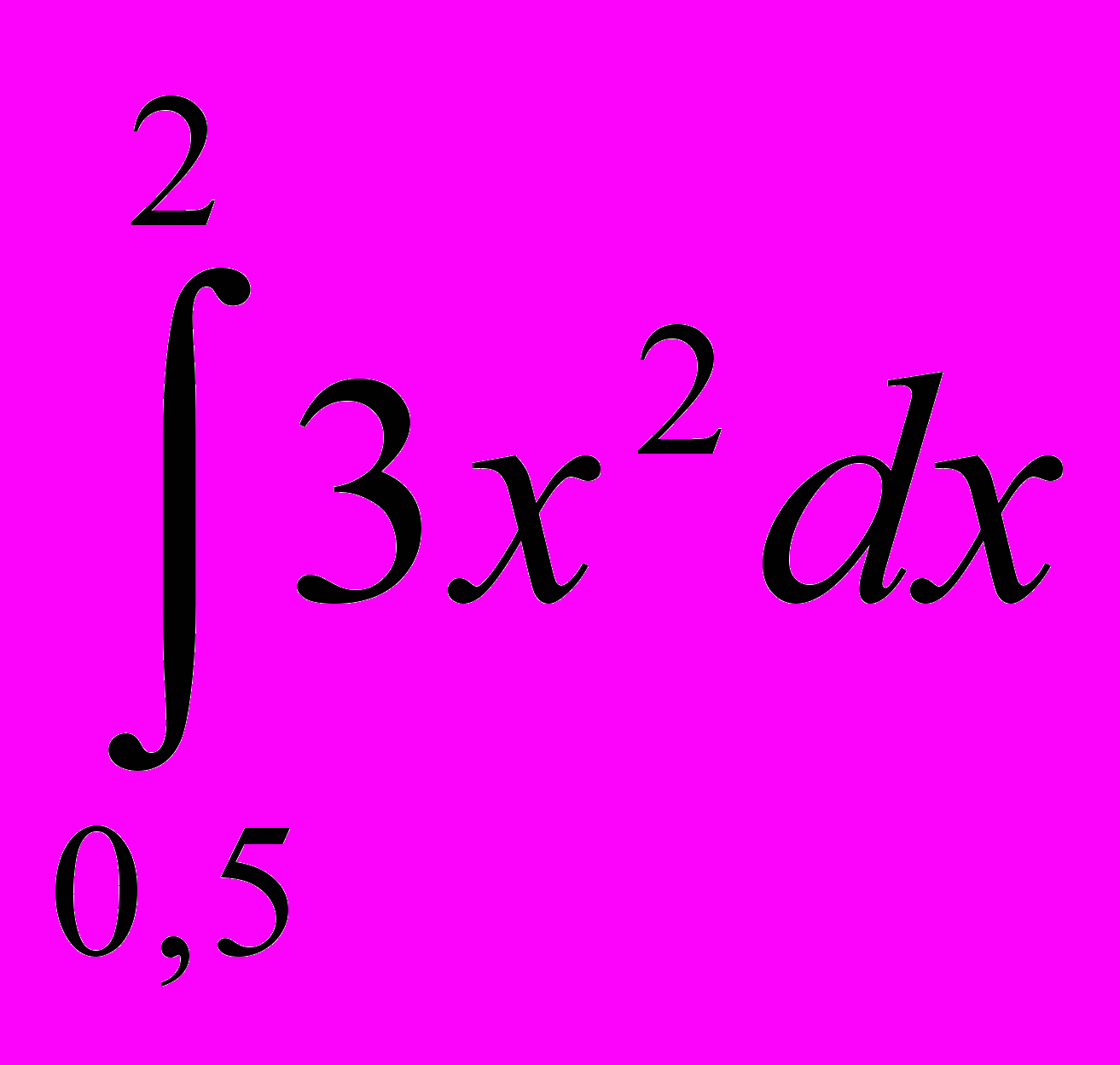 ;
;6)
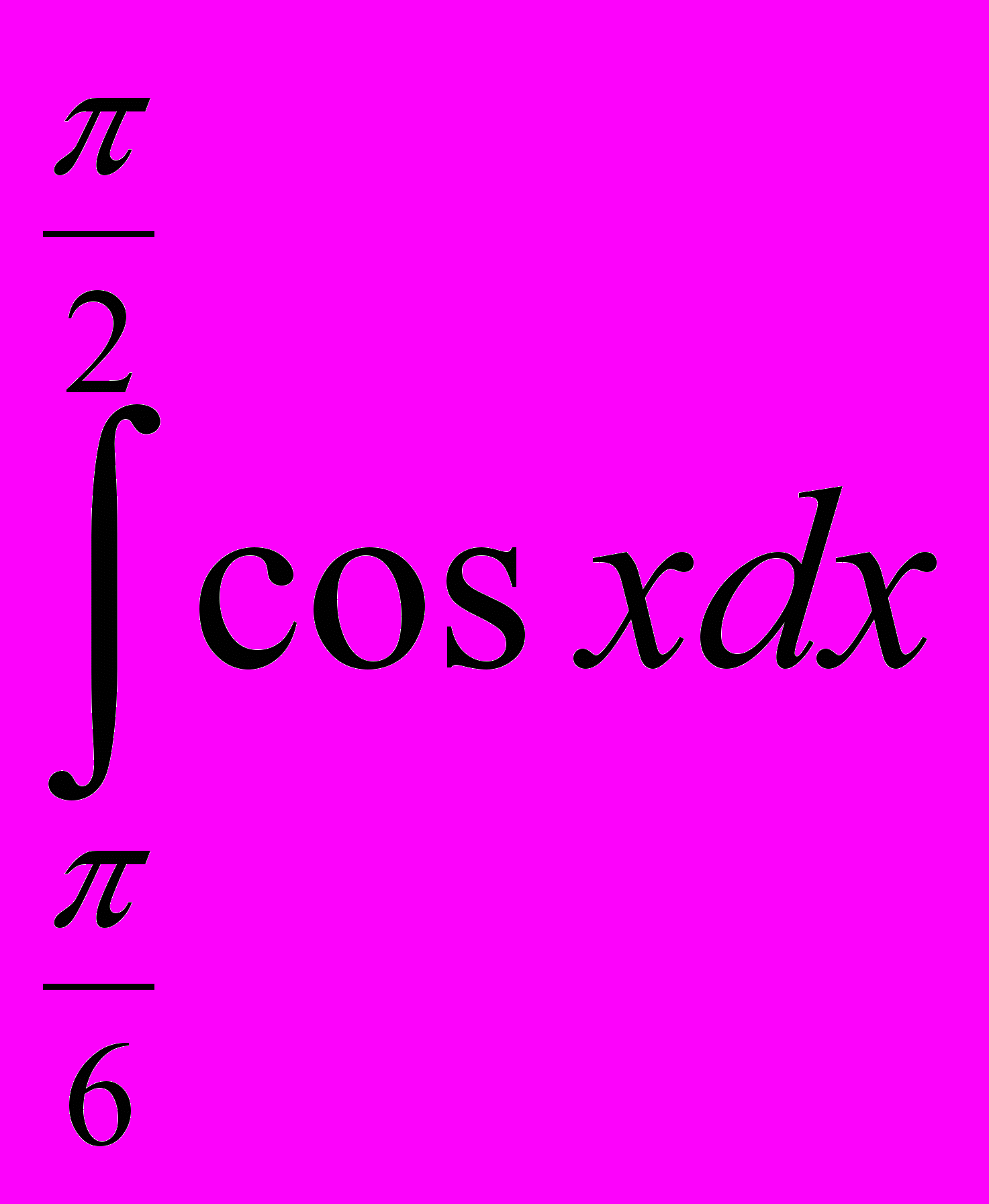 ; 7)
; 7) 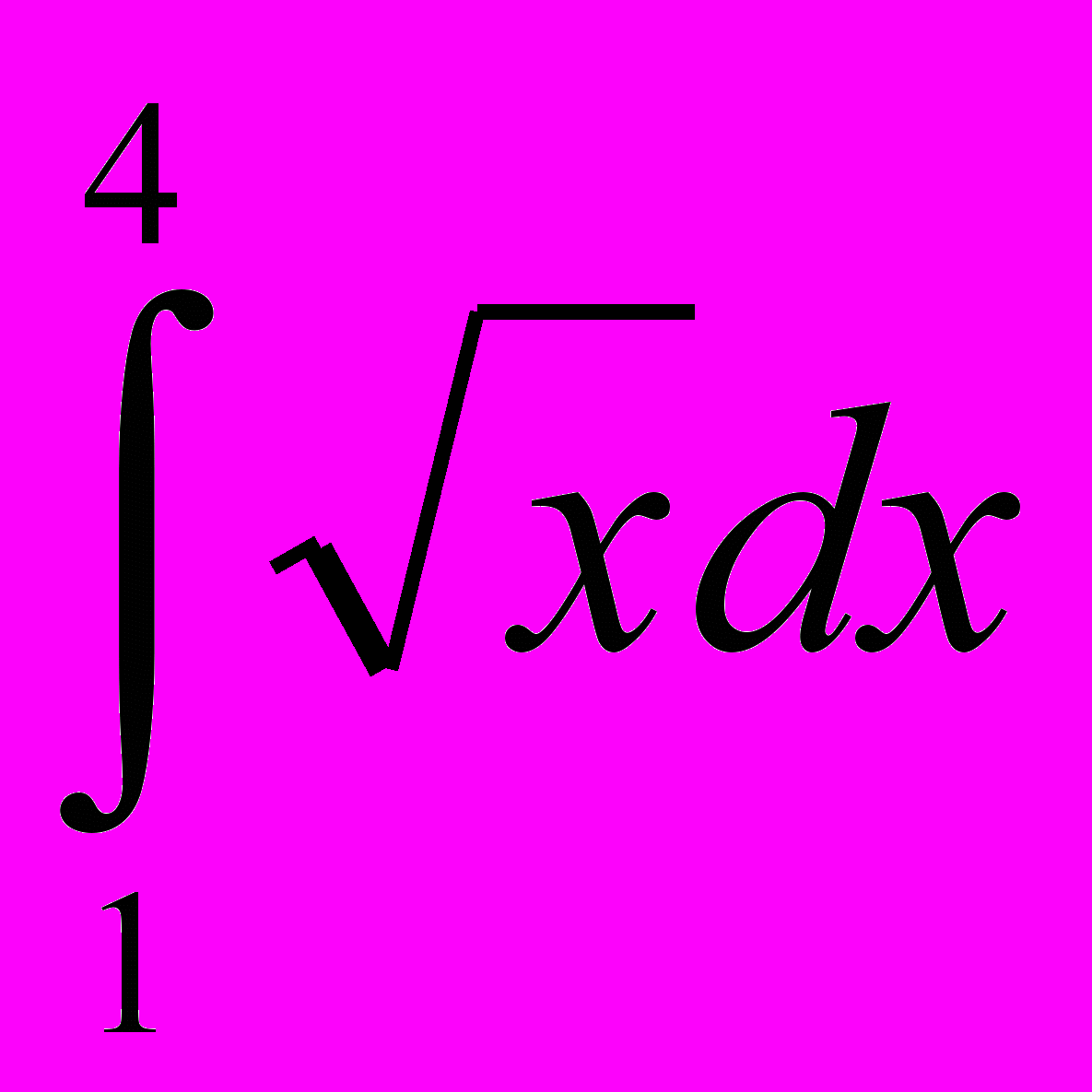 .
.4.Розв’язування вправ
На попередніх уроках ми обчислювали площі криволінійних трапецій. Але на практиці часто доводиться обчислювати площі фігур, які не є криволінійними трапеціями.
Якщо треба обчислювати площу фігури, обмеженої декількома лініями, то знаходять криволінійні трапеції, перерізом або об’єднанням яких є дана фігура, обчислюють площу кожної з них, і знаходять різницю або суму площ цих криволінійних трапецій.
Виконаємо вправи для формування умінь і навичок обчислення площі плоскої
фігури.
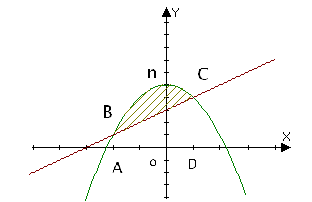
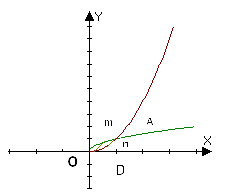
1.Записати площі заштрихованих фігур як суму або різницю площ криволінійних трапецій, обмежених графіками відомих функцій:
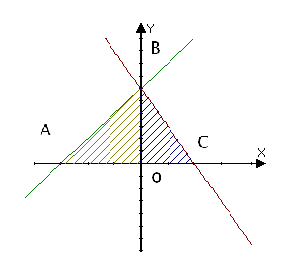
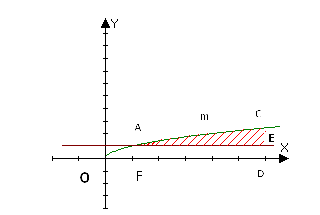
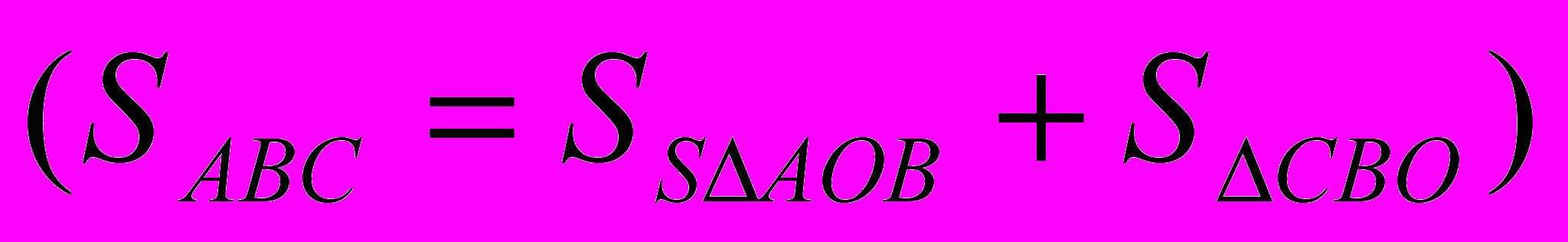
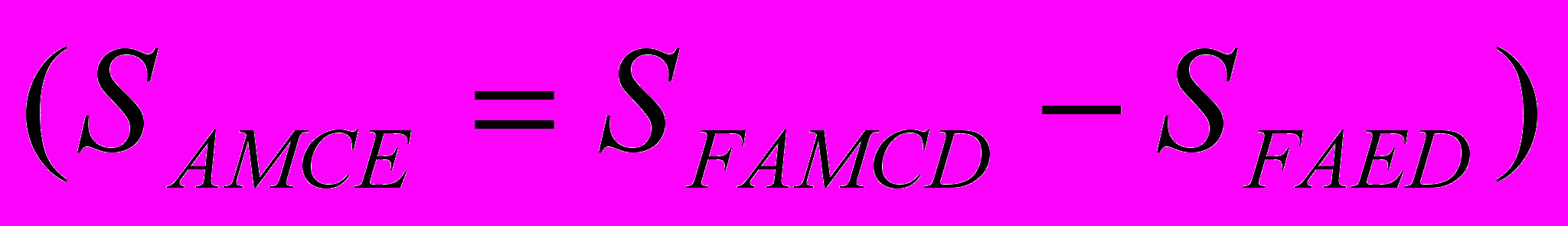
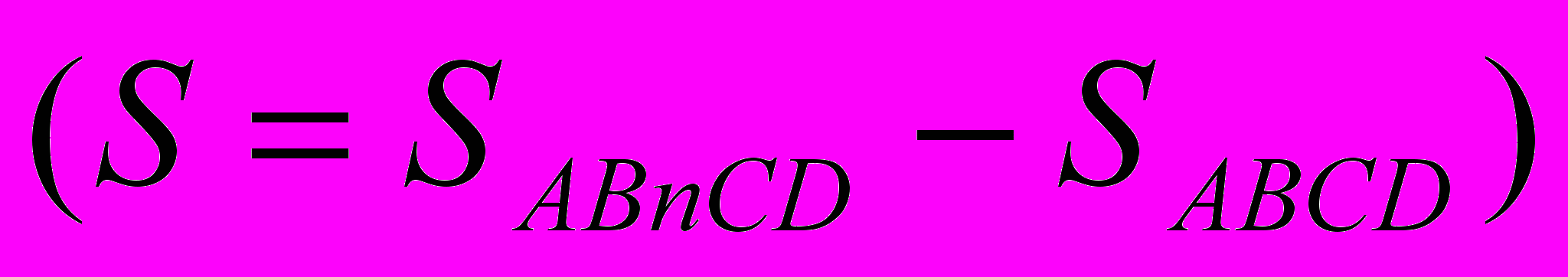
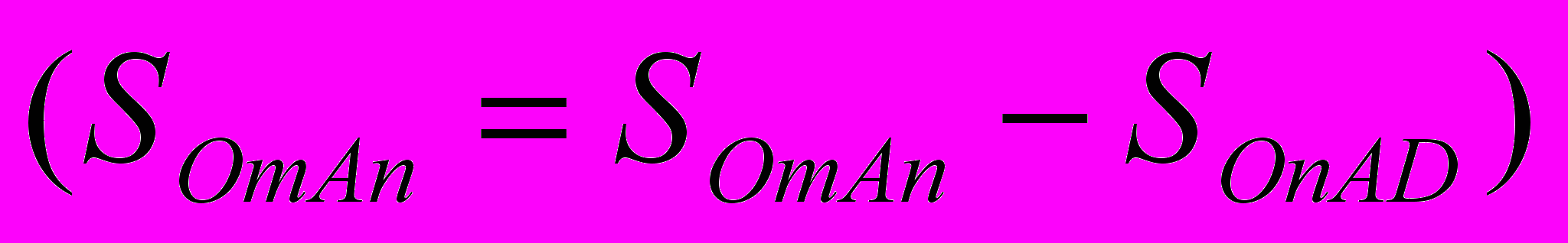
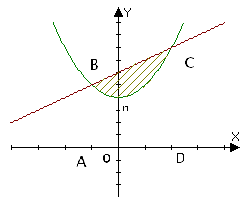
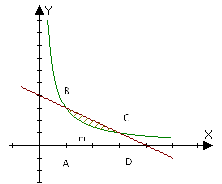
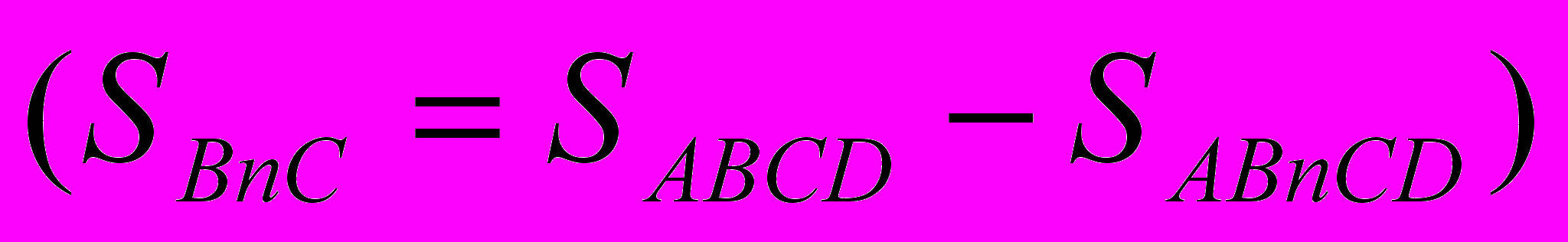
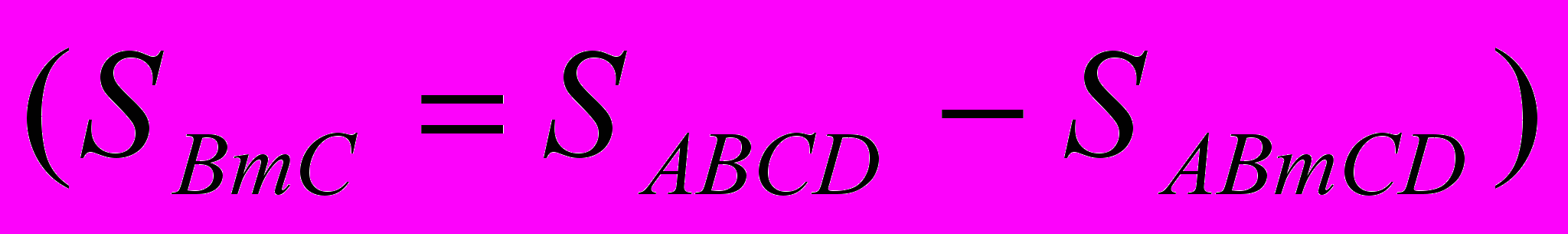
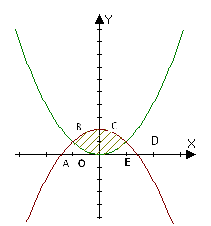
2.Обчислити площу фігури обмеженої лініями
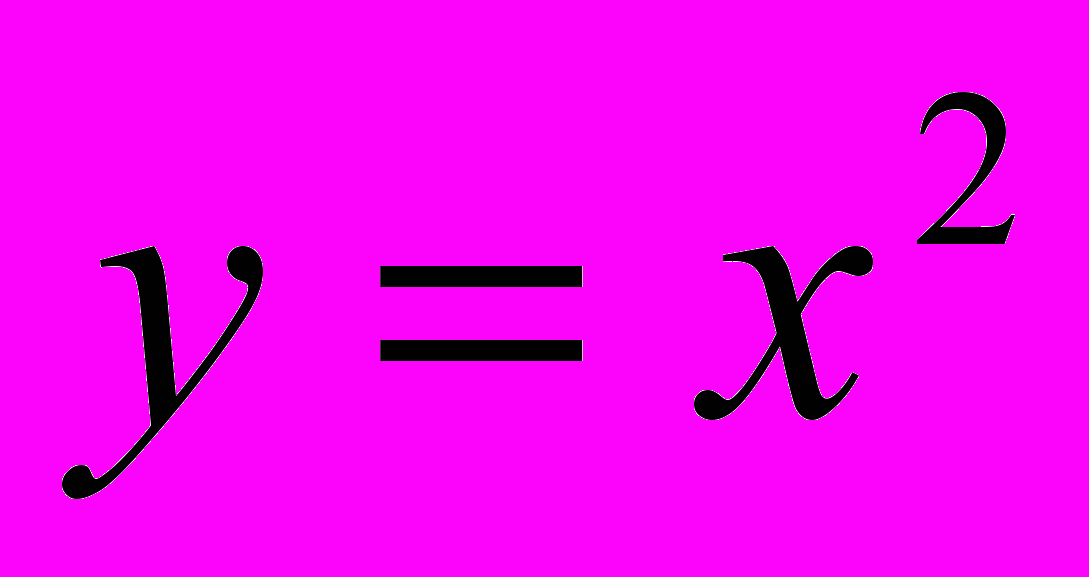 ,
, 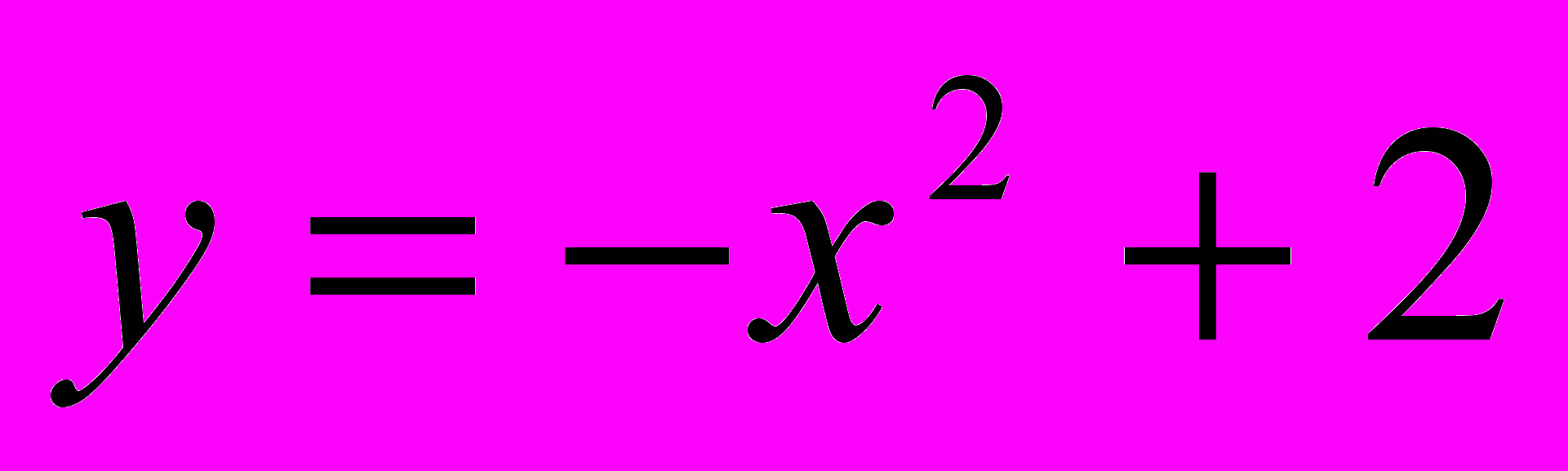
Розв’язання:
Будуємо графіки функцій
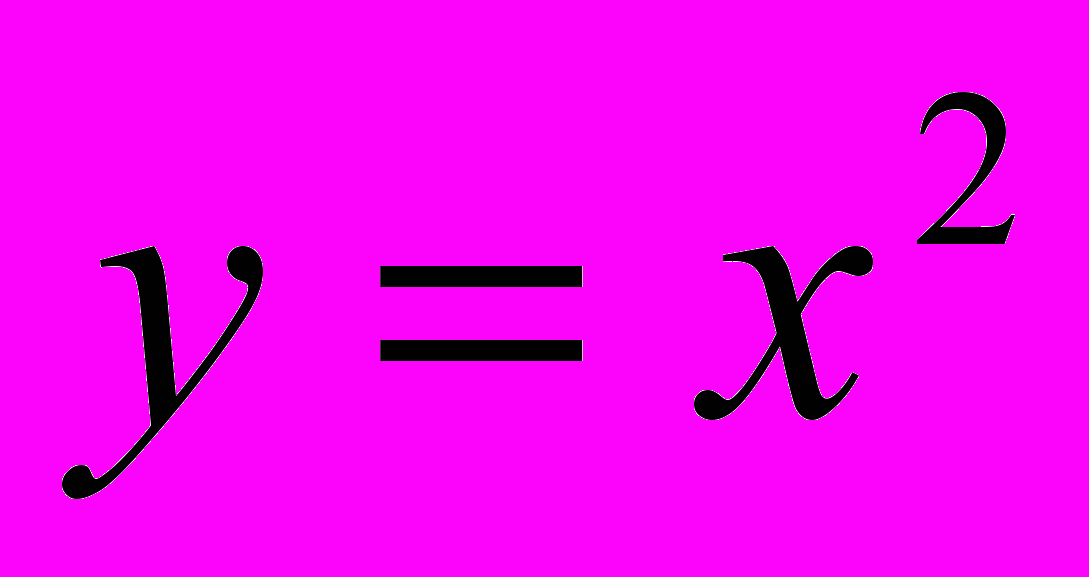 ;
; 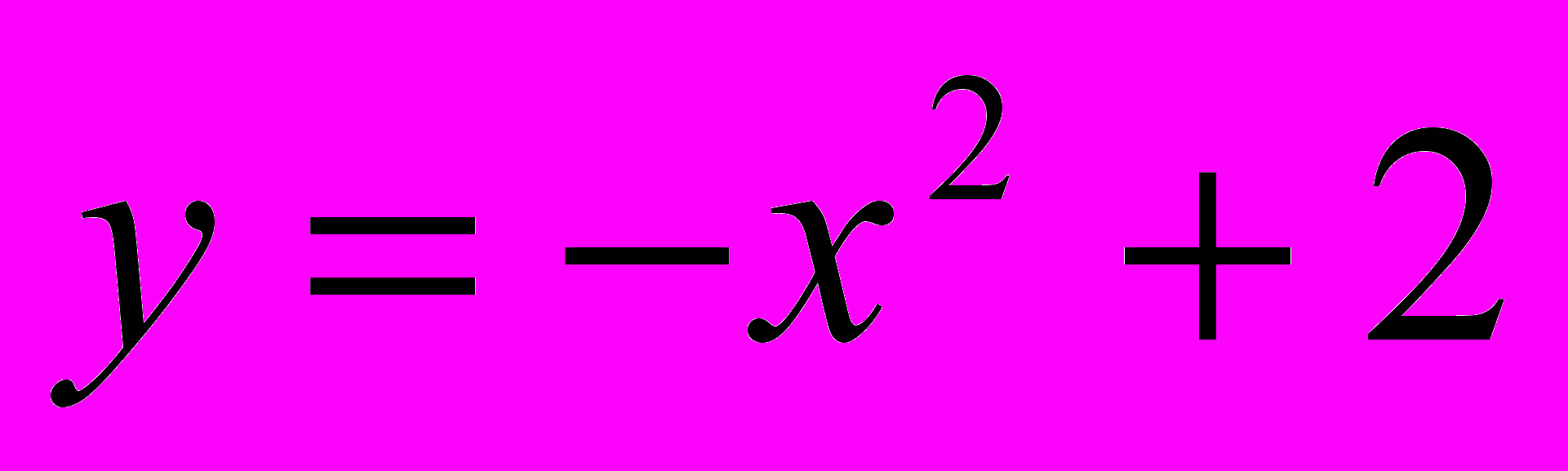
Знайдемо абсциси точок перетину графіків:
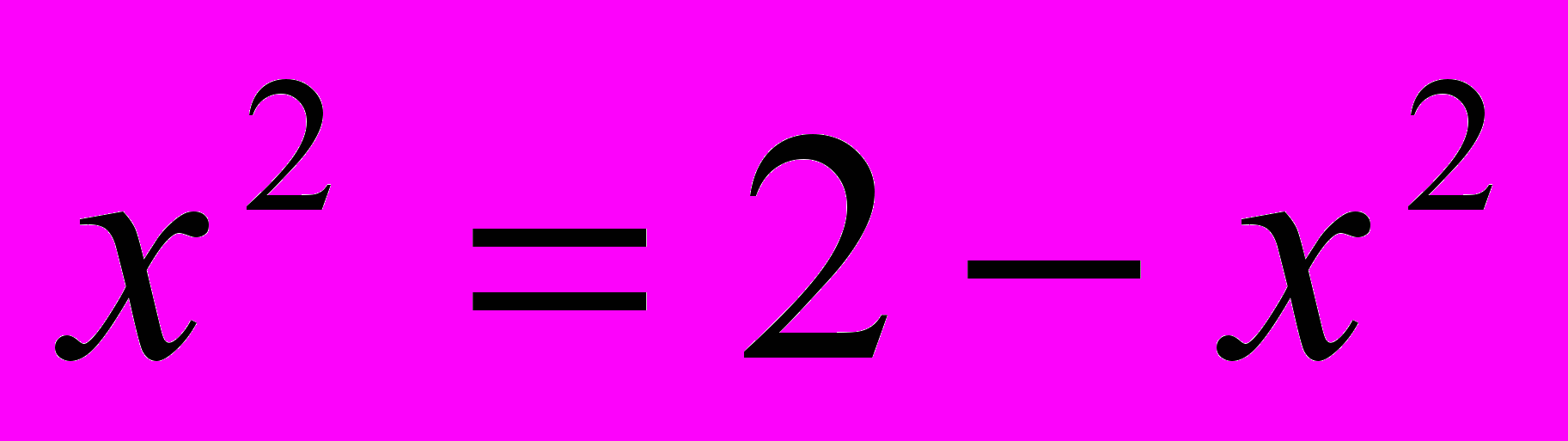
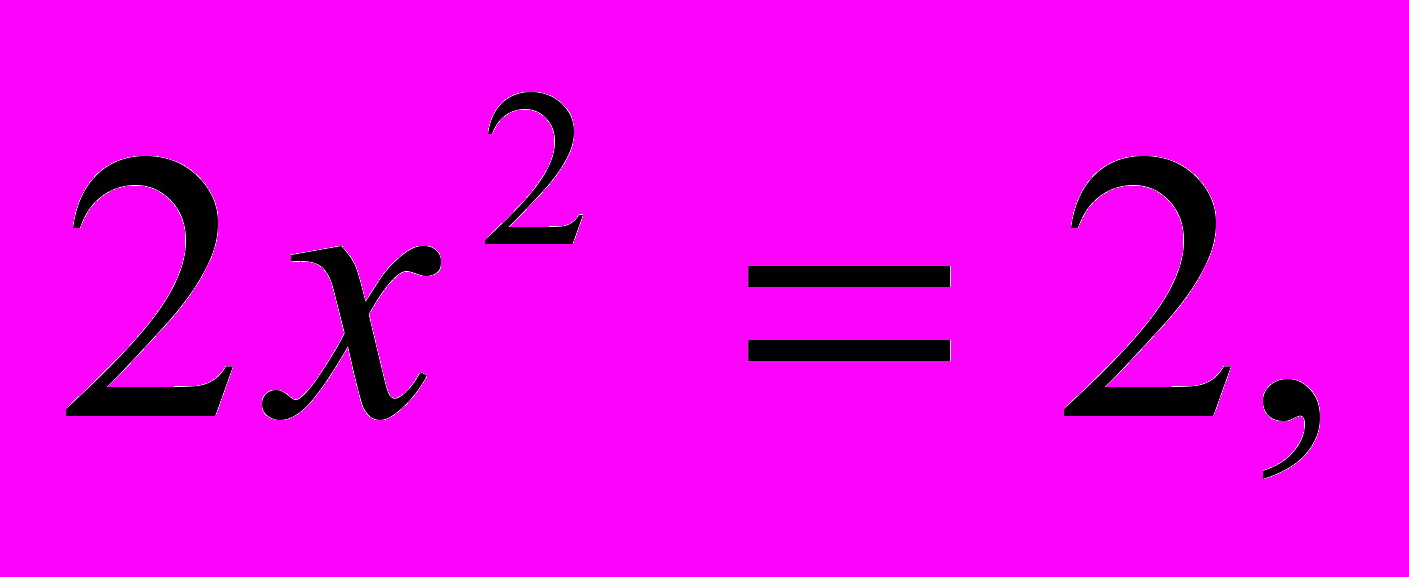
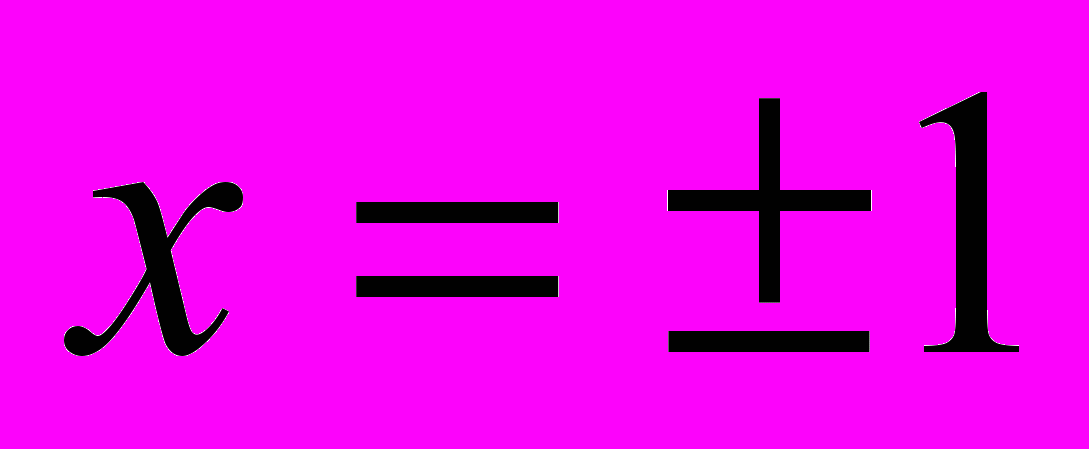
Шукана площа обмежена кривими BCD і BOD. Ця площа дорівнює різниці площ криволінійних трапецій ABCDE і BAOED.
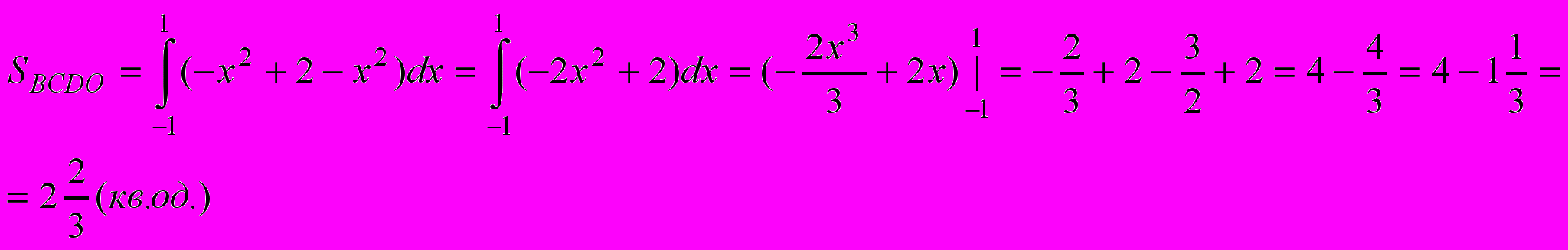
5. Вчитель інформатики:
А зараз ми цю задачу розв’яжемо за допомогою програми Advanced Grapher.
Виконаємо наступний алгоритм дій.
1. Запускаємо програму Advanced Grapher.
2. Будуємо в системі координат відповідні графіки функцій. Для цього заходимо в розділ «Побудова», вибираємо «Додати графік» та вписуємо формулу першої функції.
Аналогічно будуємо графік другої функції.
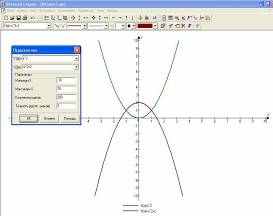
3. Визначаємо фігуру, площу якої треба знайти, та визначаємо межі інтегрування. Для цього заходимо в розділ «Обчислення», обираємо «Перетин», вводимо формули даних функцій та натискуємо клавішу «ОК». У з’явившомуся вікні визначаємо межі інтегрування а = 1, b = -1 (див. рисунок).
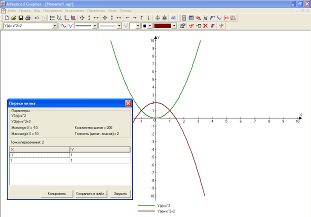
4. Заходимо в розділ «Обчислити», вибираємо «Інтегрування» та вказуємо основні лінії.
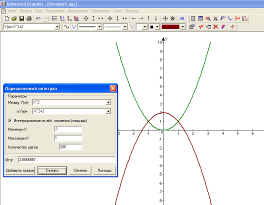
5. Дістаємо шукану площу S даної фігури (як видно з рисунка, S =2,(6) кв.од). Для того щоб одержати візуально заштриховану область фігури, необхідно виконати такі дії: натиснути клавіші «Додати графік» та «ОК».
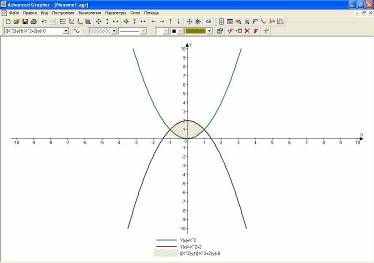
Отже, ми з вами познайомилися з програмним забезпеченням Advanced Grapher - робота з графіками і функціями. Це досить потужна, але легка у використанні програма, призначена для побудови графіків, креслення кривих і обчислення функцій. Advanced Grapher допоможе вам побудувати різні графіки і провести їхній аналіз. Можливості обчислення: регресійний аналіз; нулі та екстремуми функцій, перетинань, похідних; рівняння тангенсів і нормалей; чисельне інтегрування. Ця програма стане вам в нагоді не тільки в школі, а й при навчанні у вищому навчальному закладі. Варто для глибшого засвоєння матеріалу паралельно розв’язувати його як в зошиті, так і на комп’ютері.
А тепер перевірте правильність виконання домашнього завдання на комп’ютері за допомогою програми Advanced Grapher.


6. Підсумок уроку.
7. Домашнє завдання.
Домашня контрольна робота
Варіант 1
- Обчисліть інтеграл
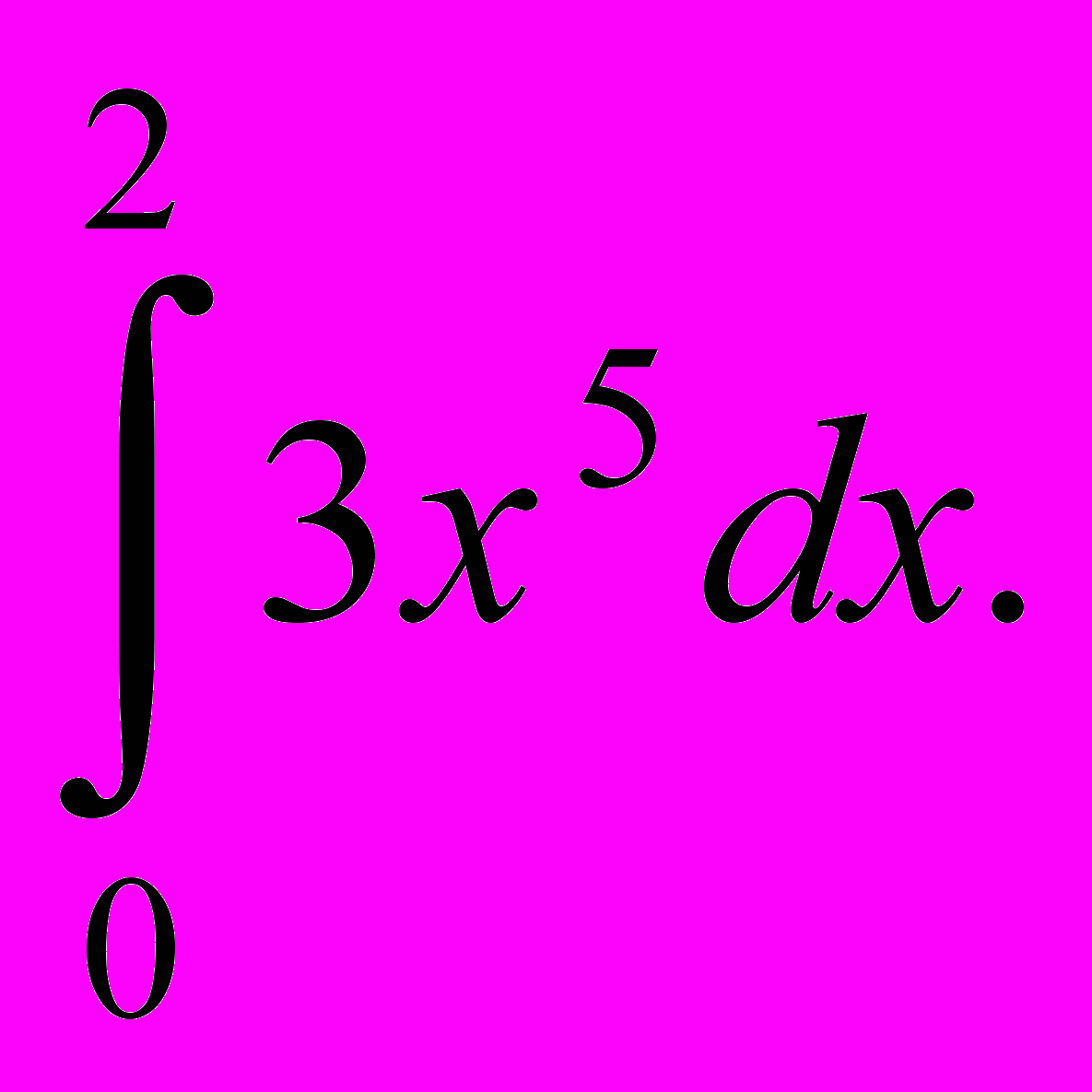
а) 64; б) 32; в) 160; г) 320.
- Обчисліть інтеграл
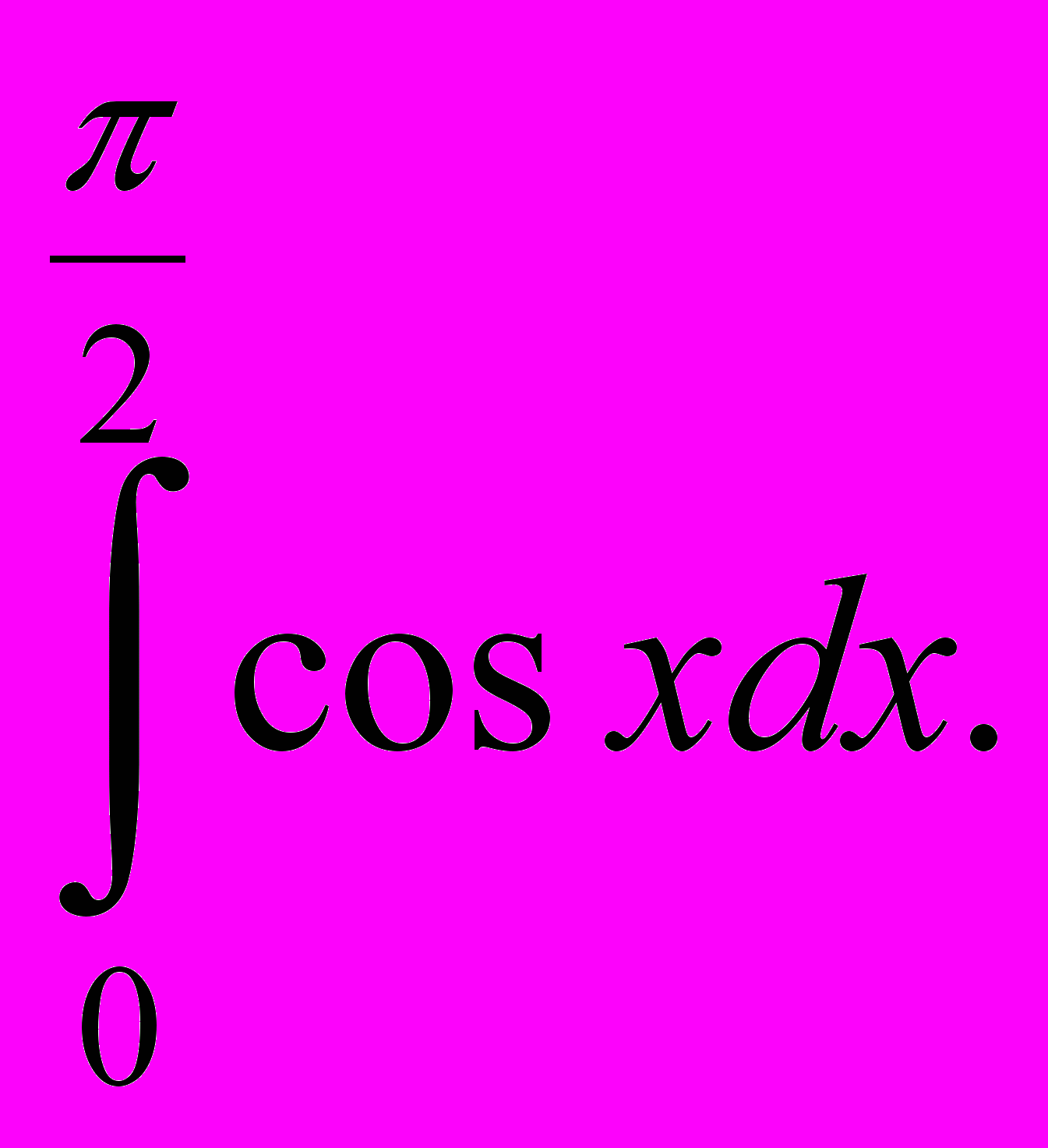
а) 0; б) 1; в) 2; г) -1.
- Яка з фігур не є криволінійною трапецією?
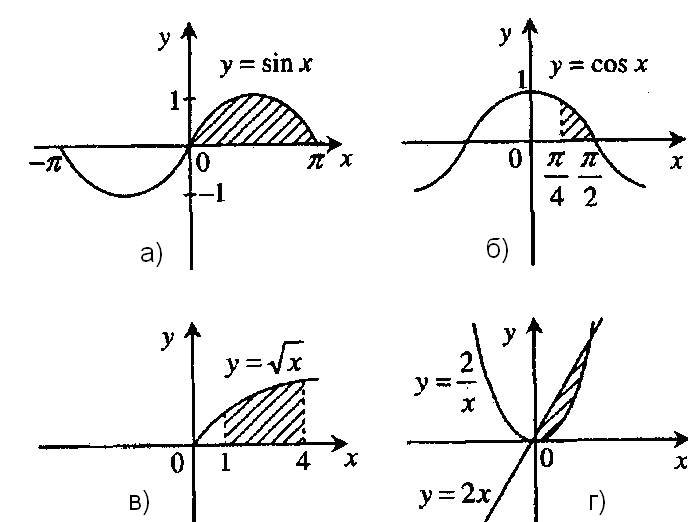
- Обчисліть інтеграл
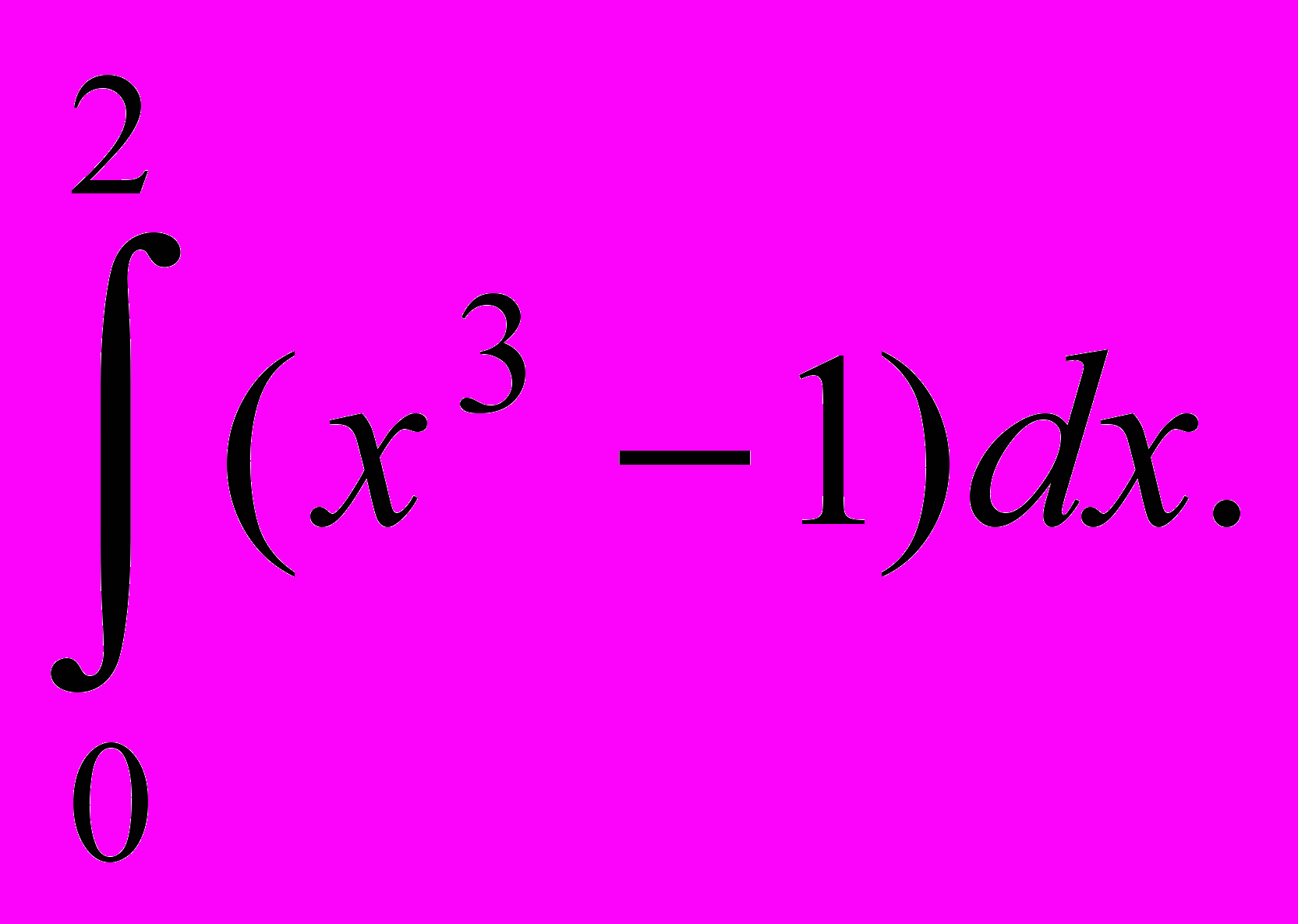
а) 1; б) 4; в) -1; г) 2.
- Площа фігури, зображеної на мал. а), дорівнює:
а)
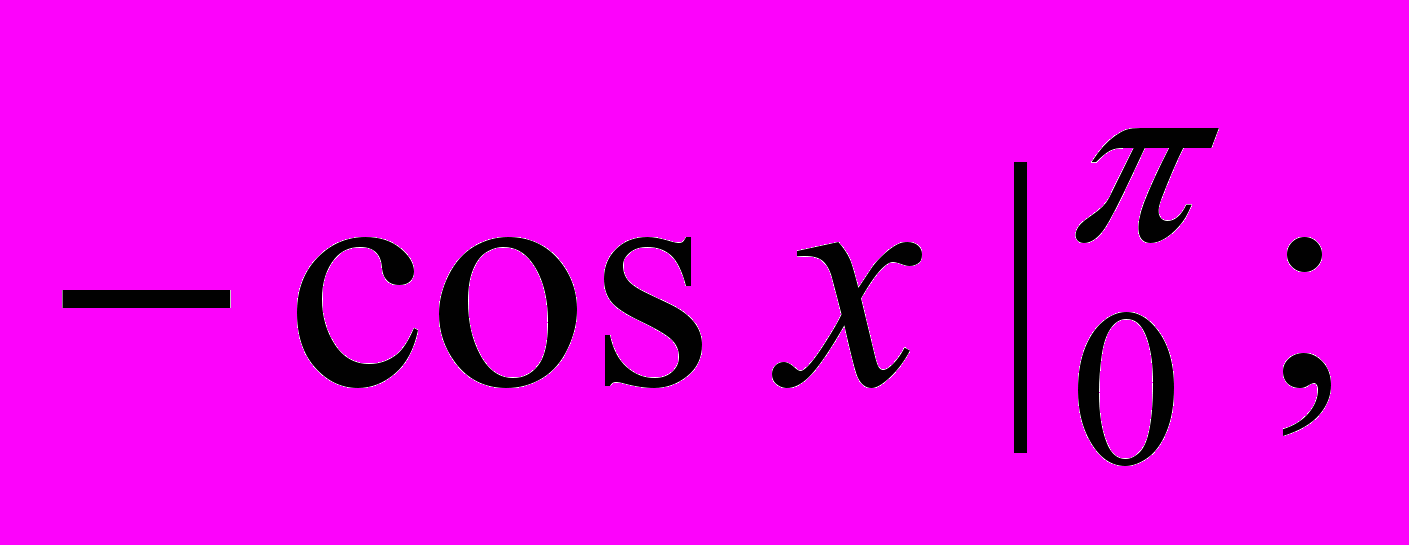 б)
б) 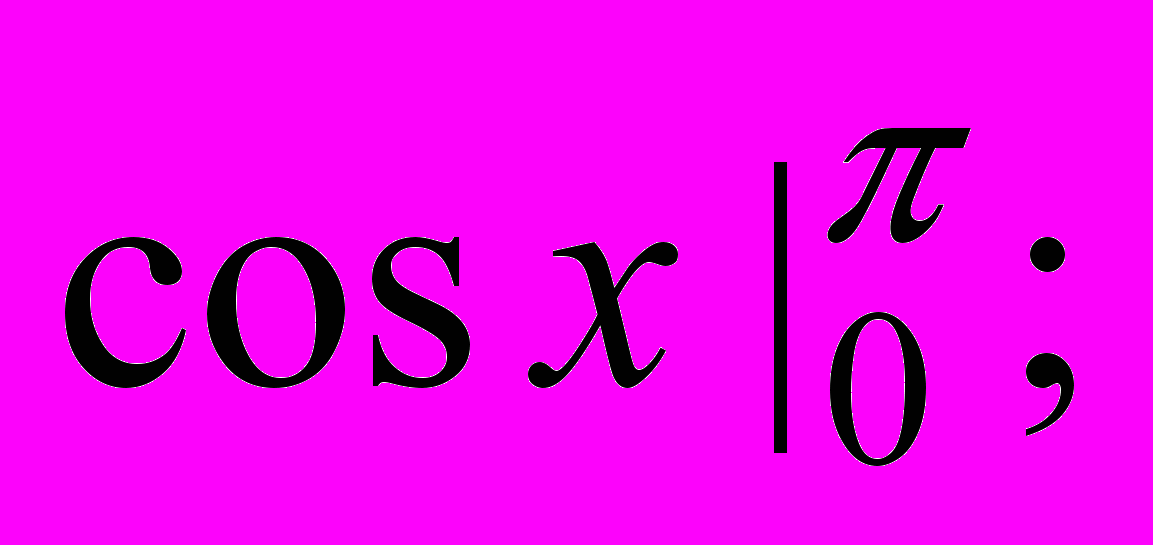 в)
в) 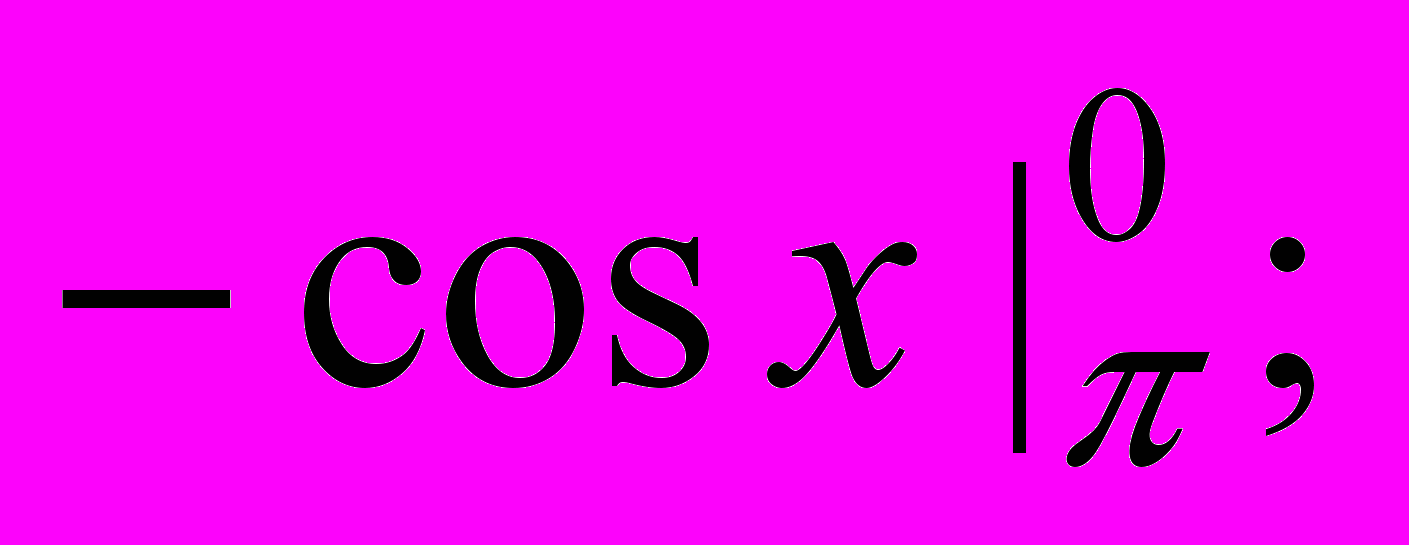 г)
г) 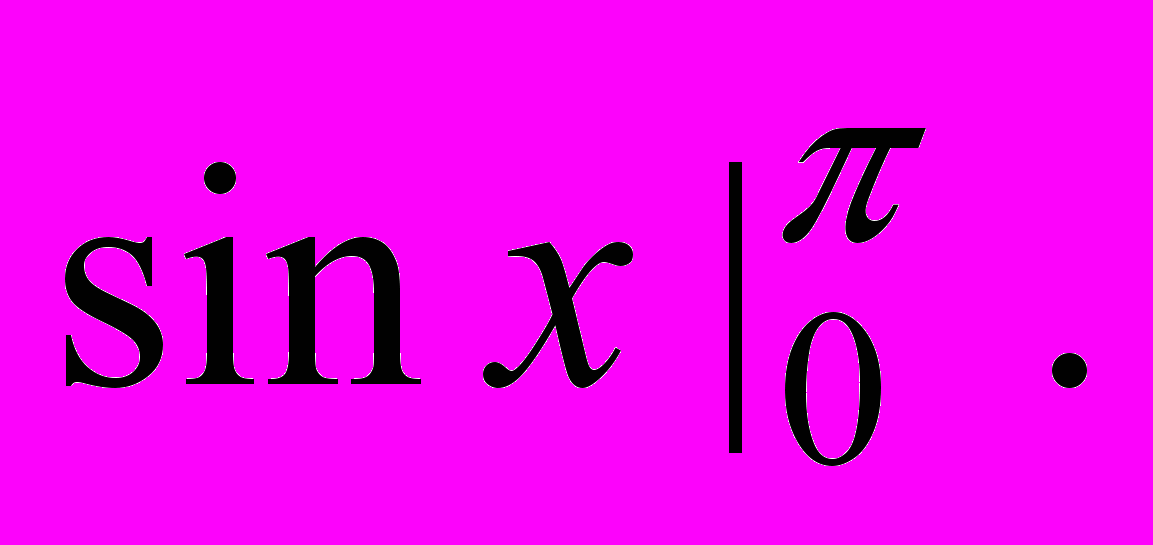
а)
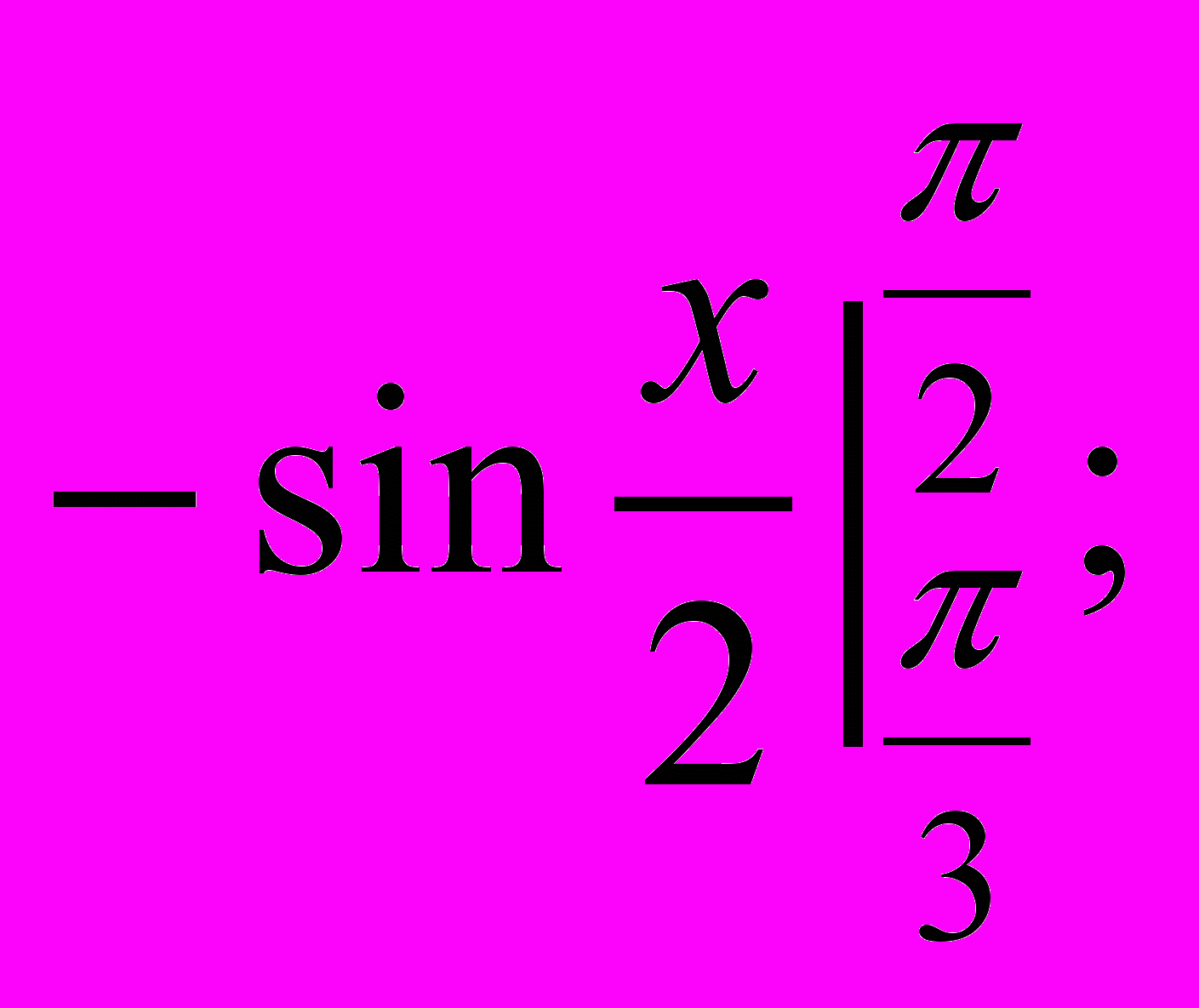 б)
б) 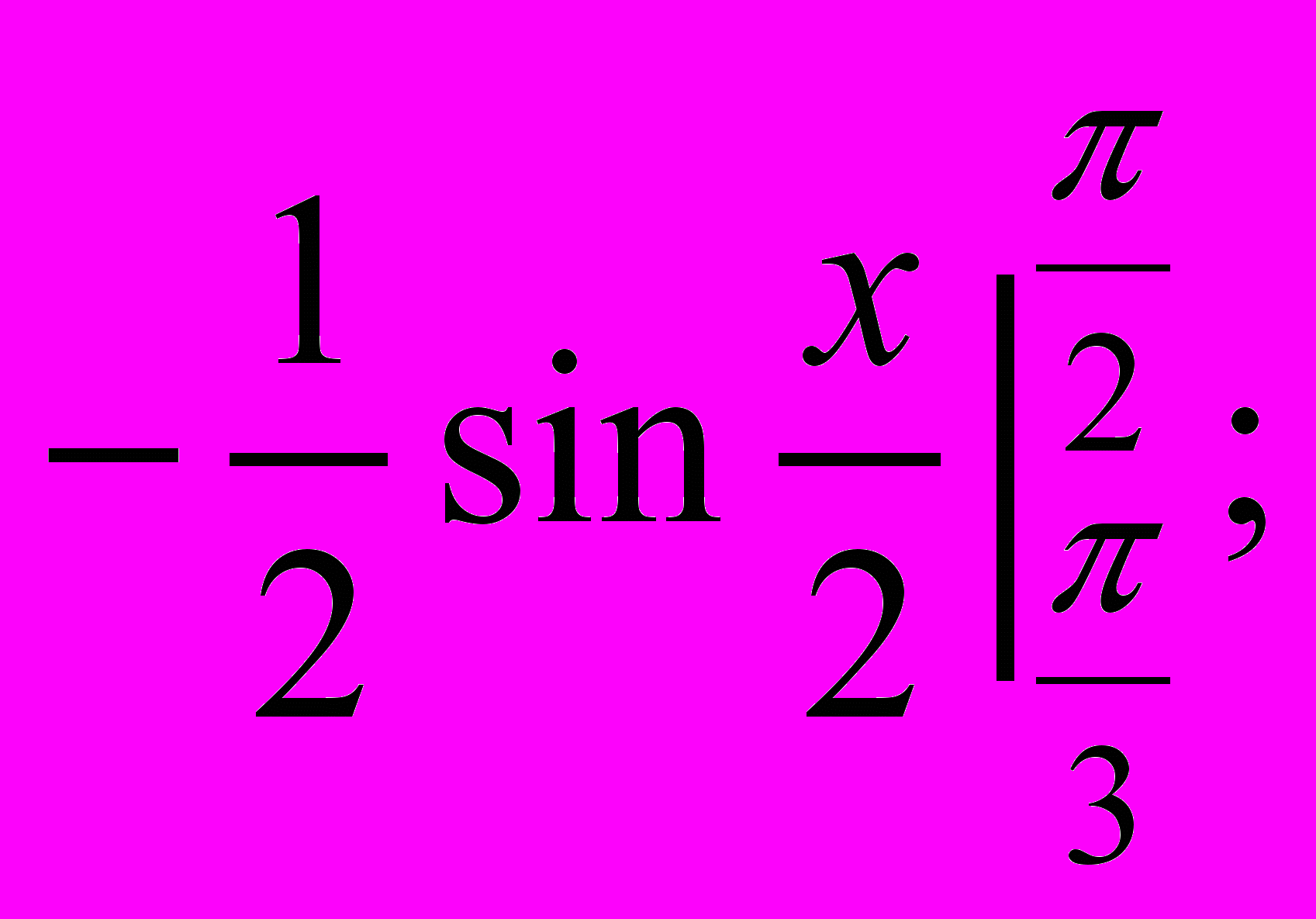 в)
в) 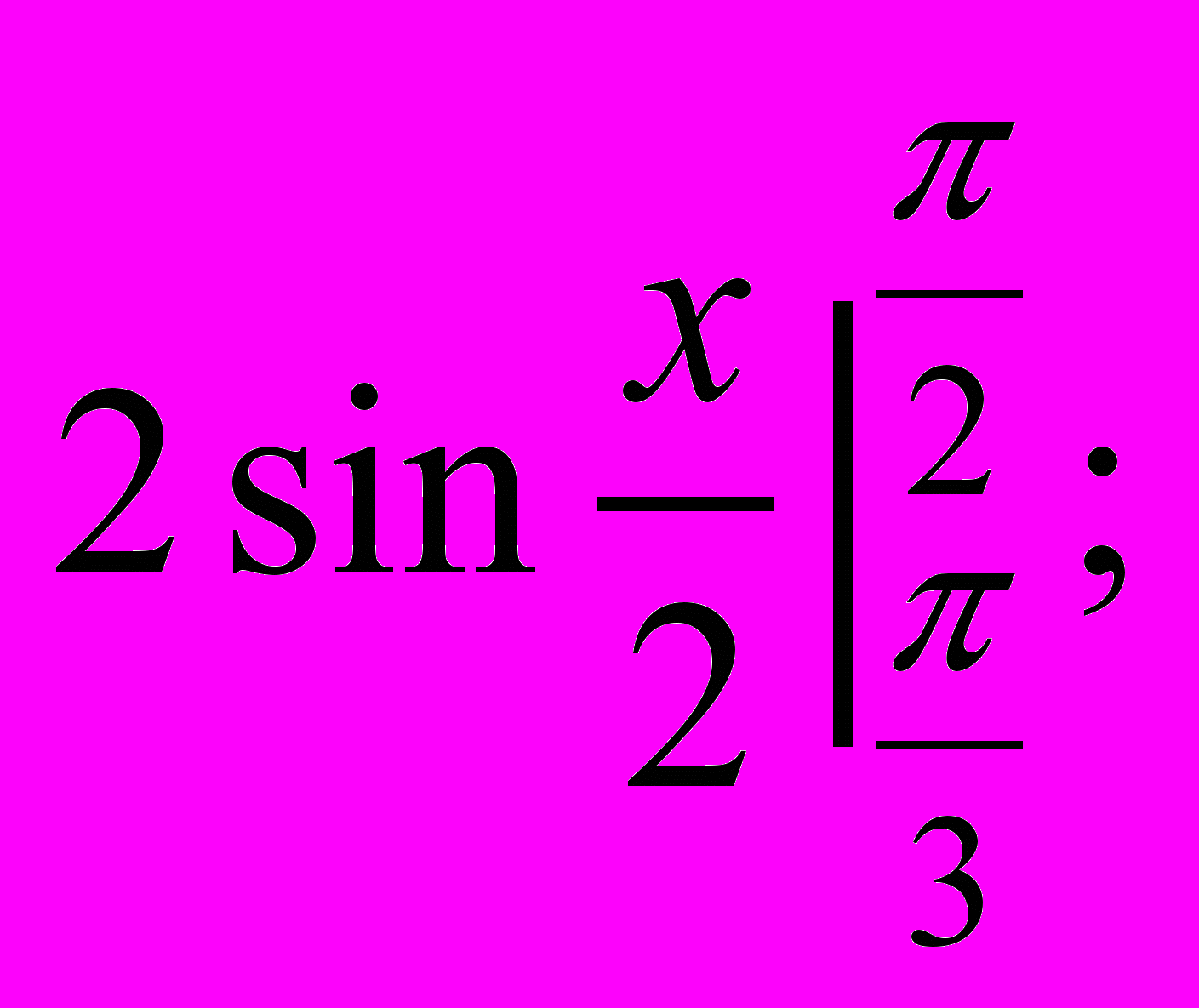 г)
г) 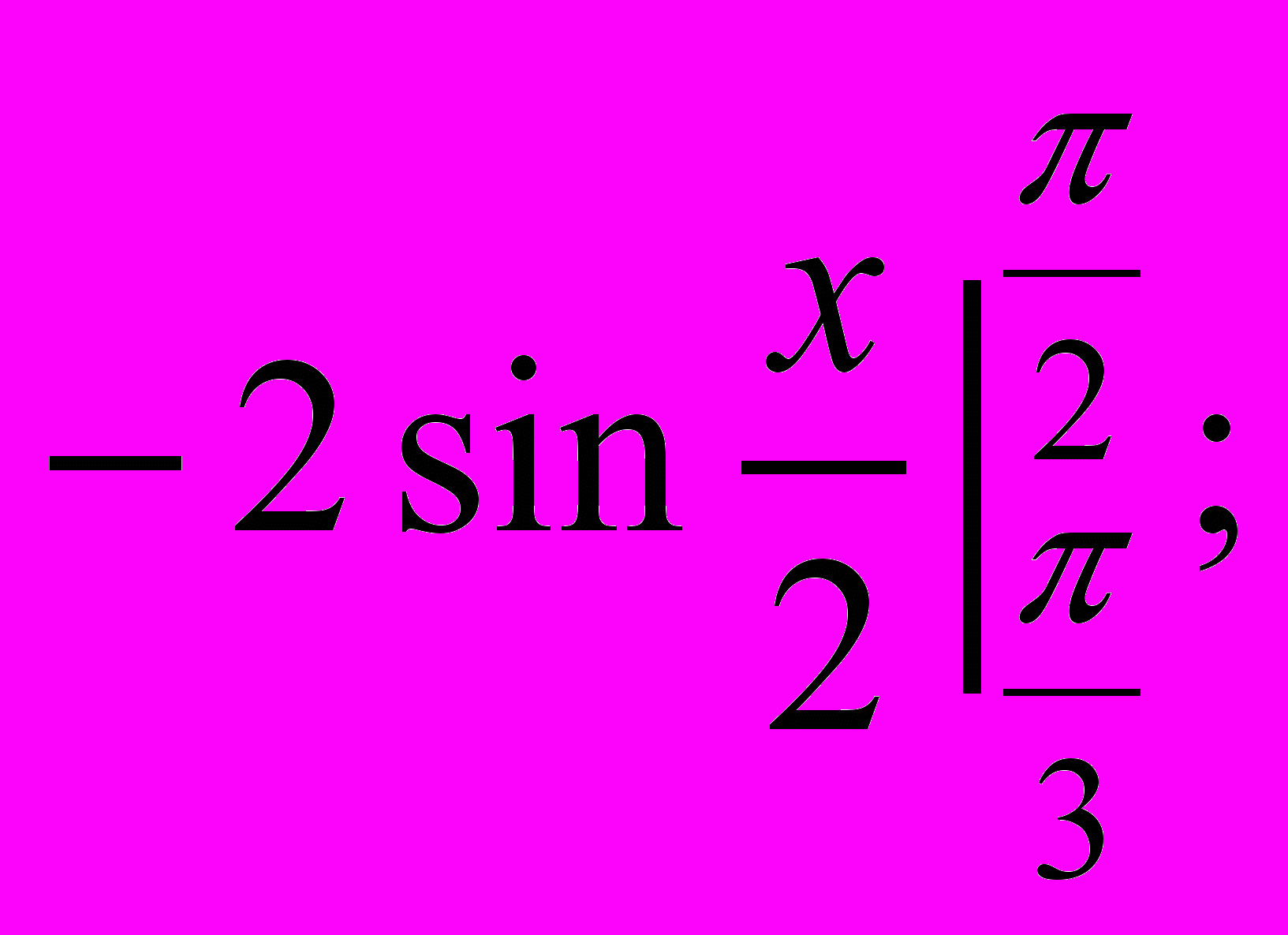
- Обчисліть площу заштрихованої фігури на малюнку в).
Варіант 2
- Обчисліть інтеграл
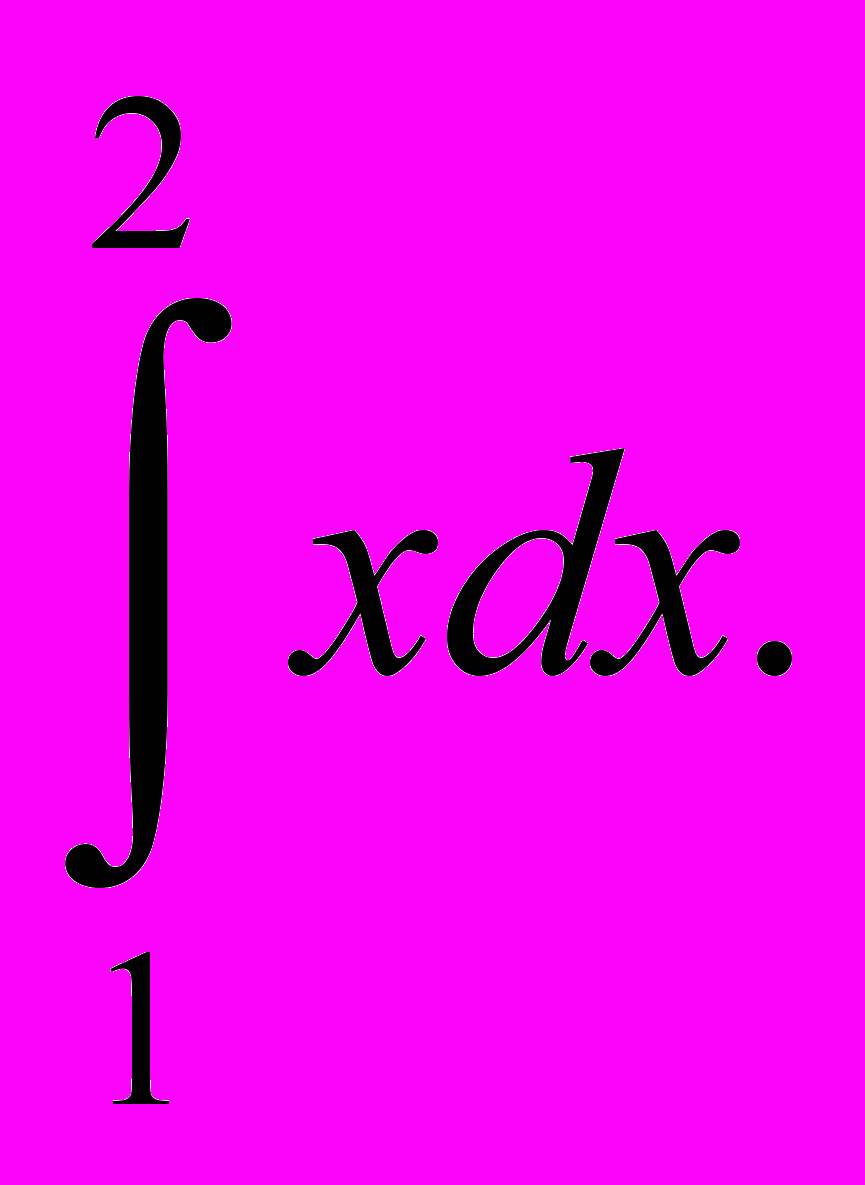
а)
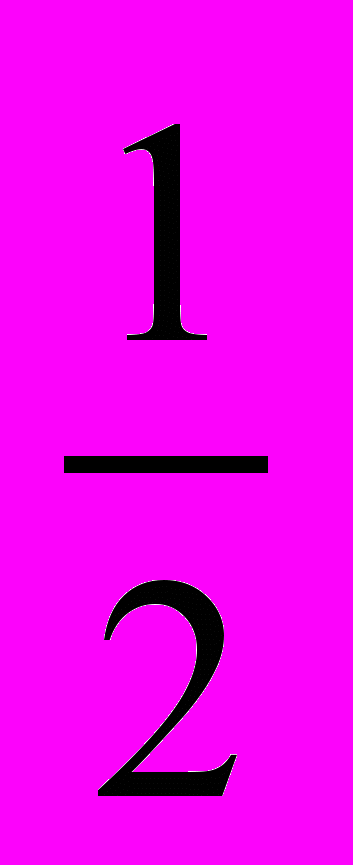 ; б)
; б) 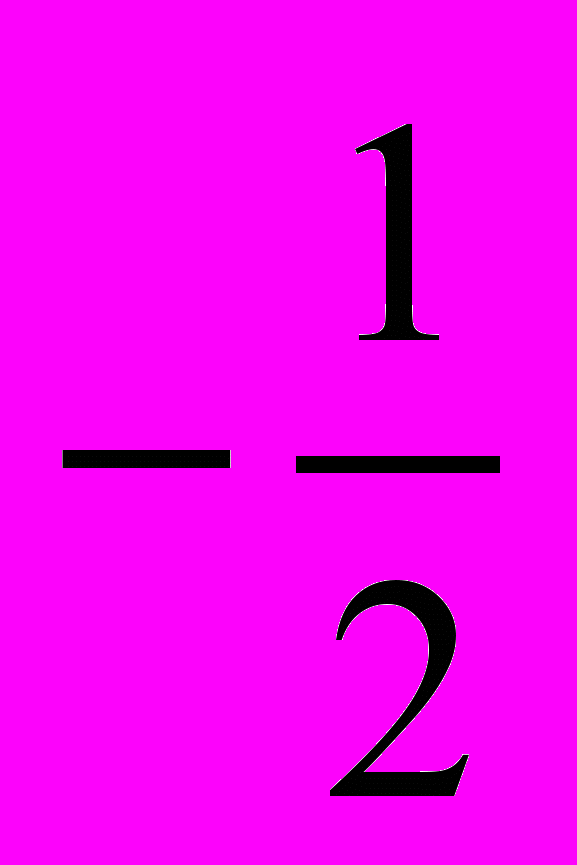 ; в)
; в) 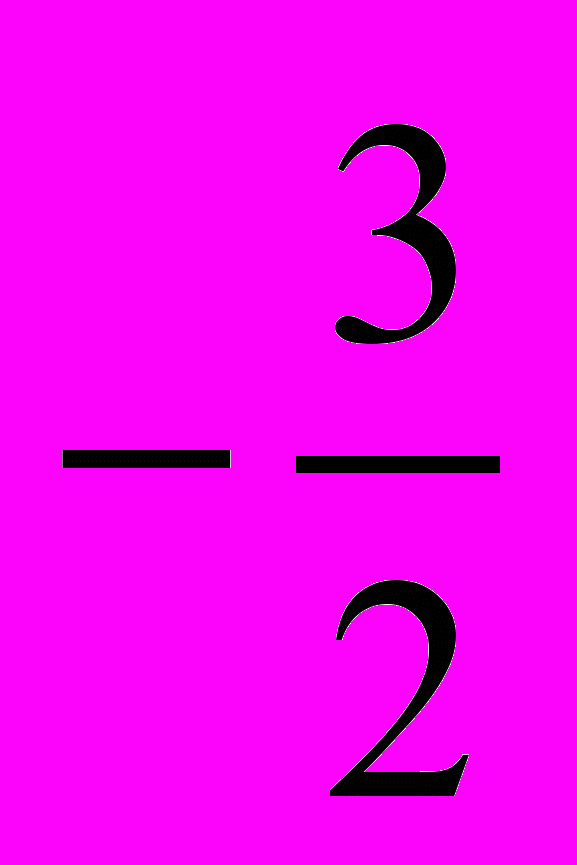 ; г)
; г) 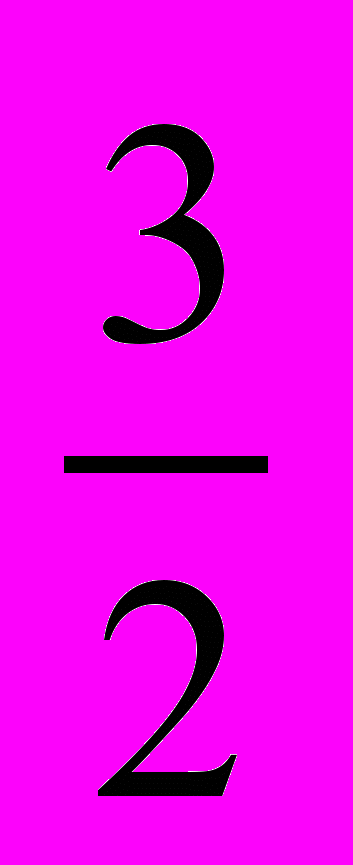 .
.- Обчисліть інтеграл
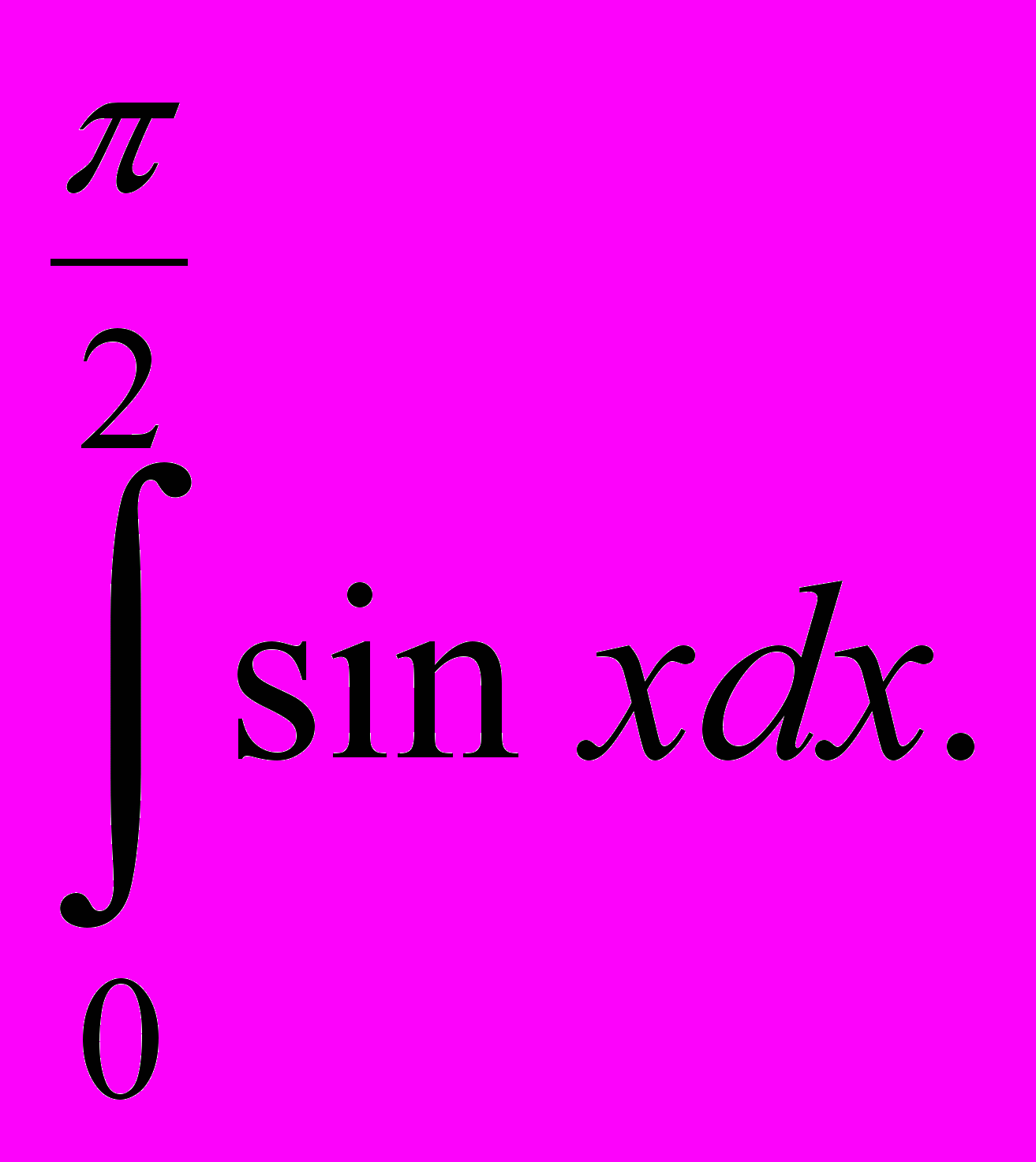
а) 0; б) -1; в) 1; г) 2.
- Яка з фігур не є криволінійною трапецією?
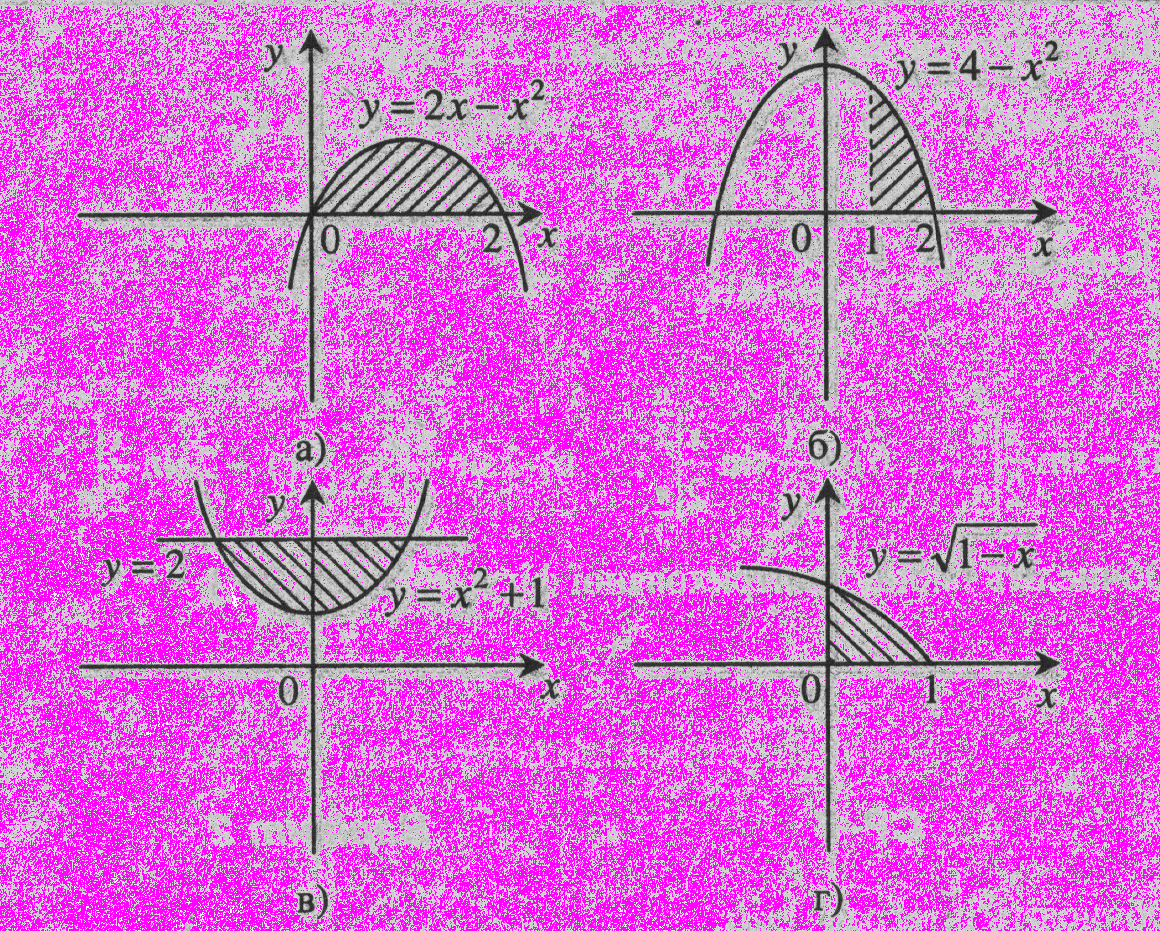
- Обчисліть інтеграл
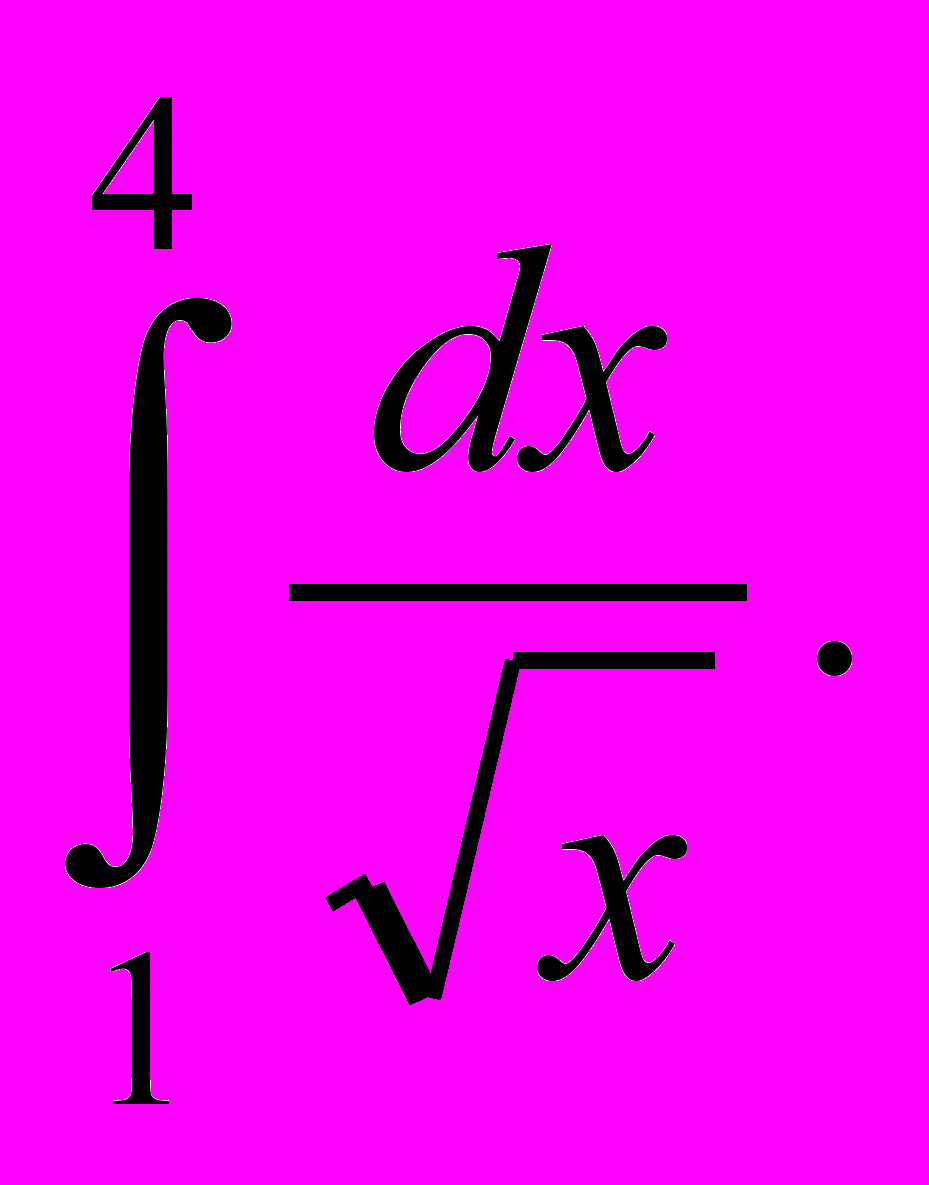
а) 1; б) 2; в) 3; г) 4.
- Площа фігури, зображеної на мал. б), дорівнює:
а)
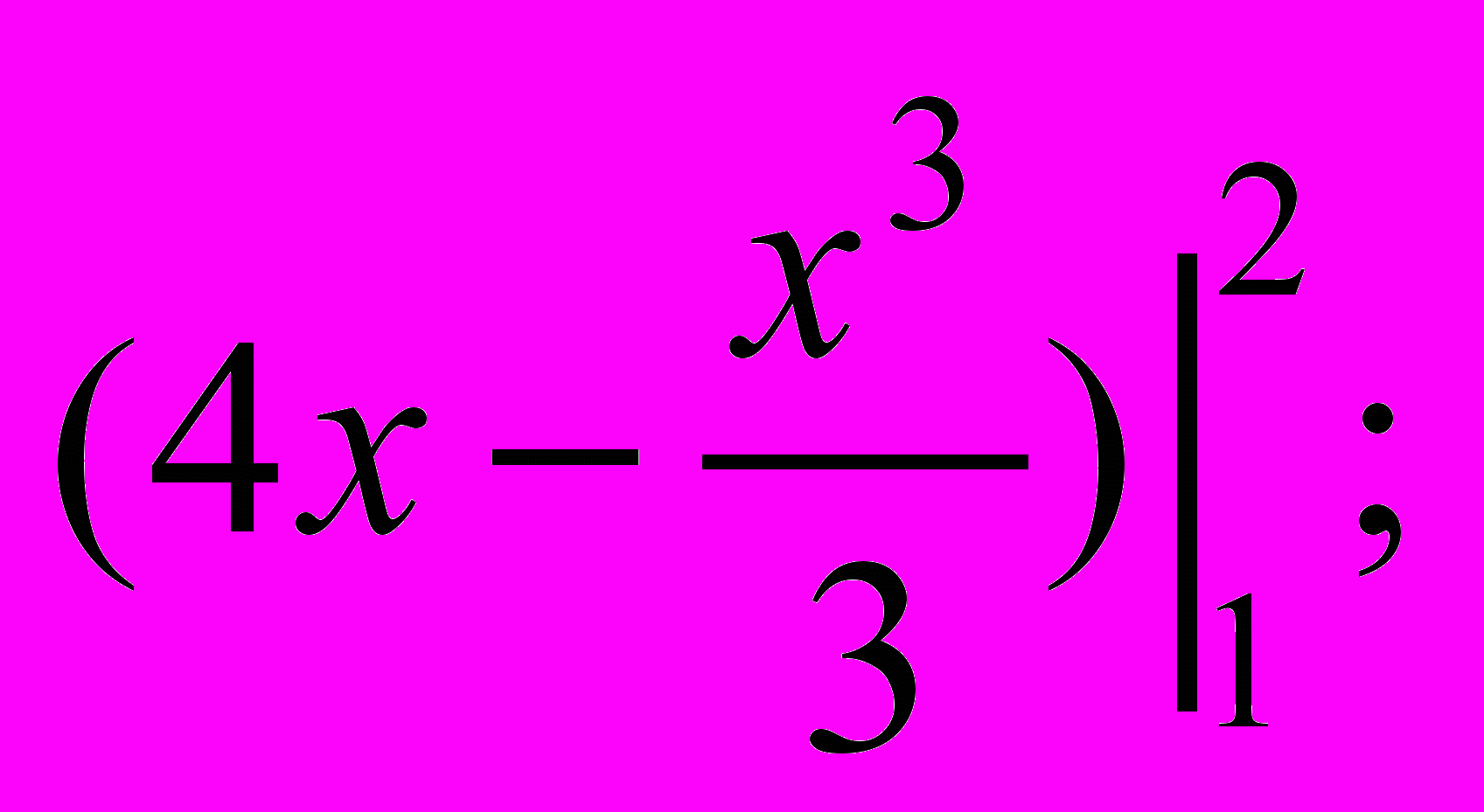 б)
б) 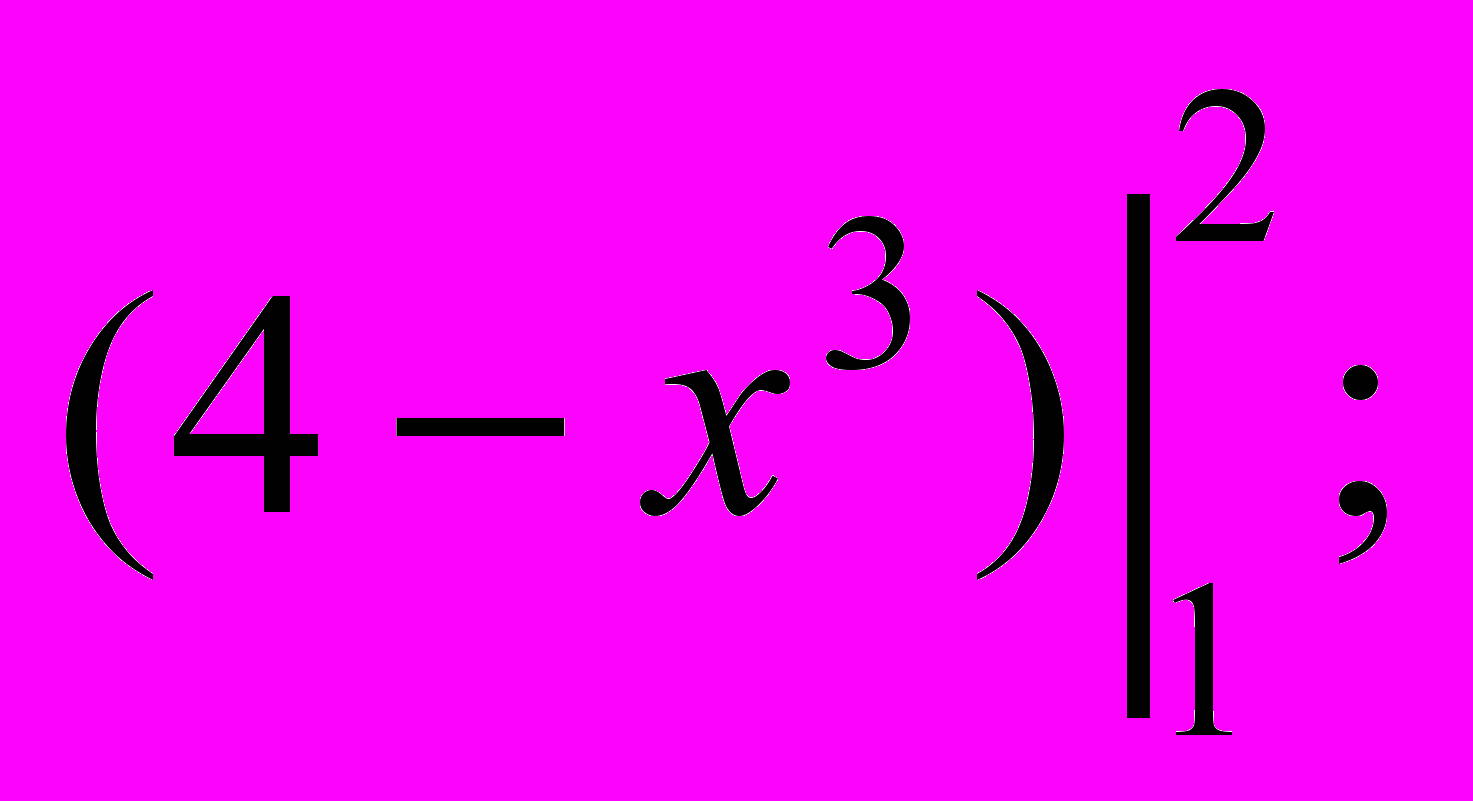 в)
в) 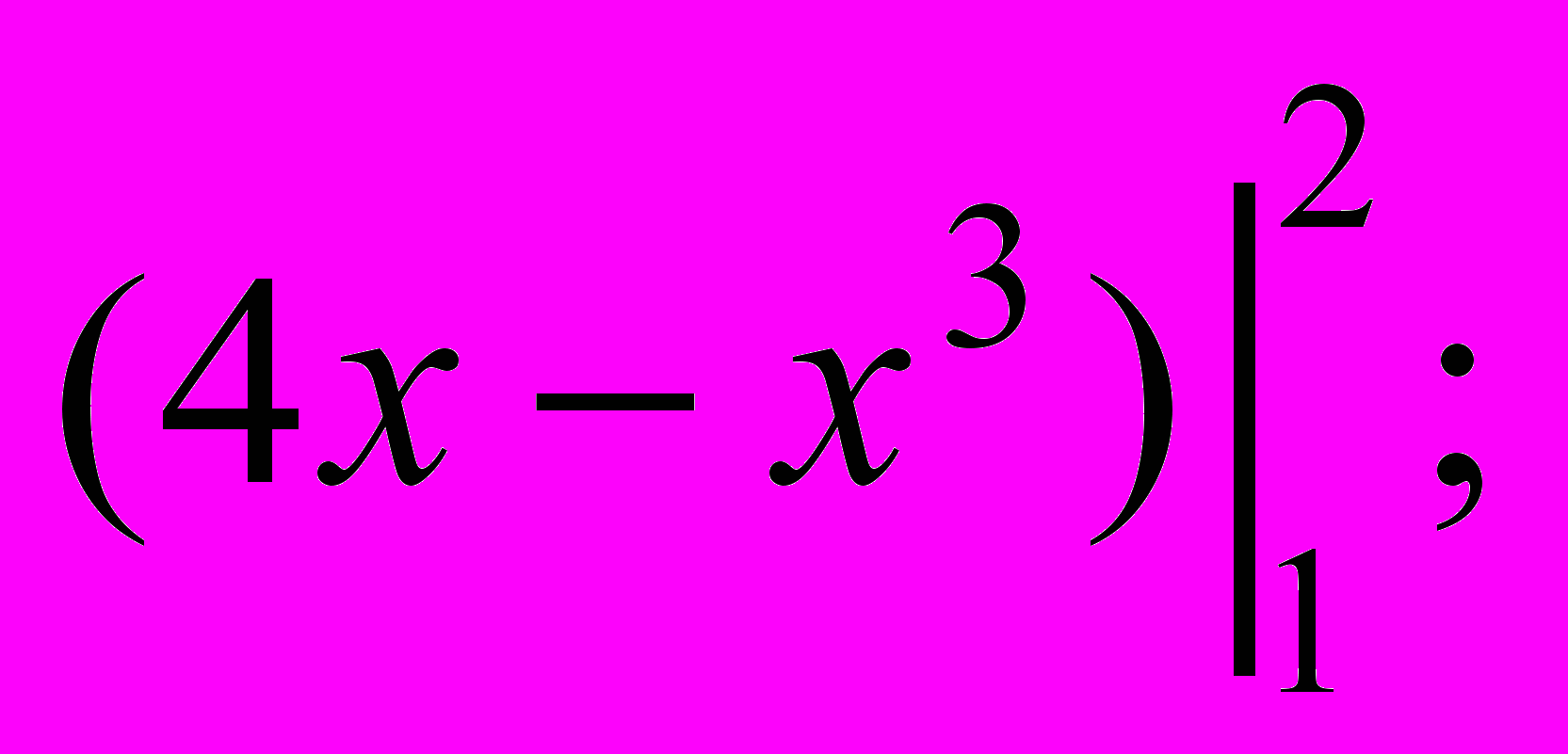 г)
г) 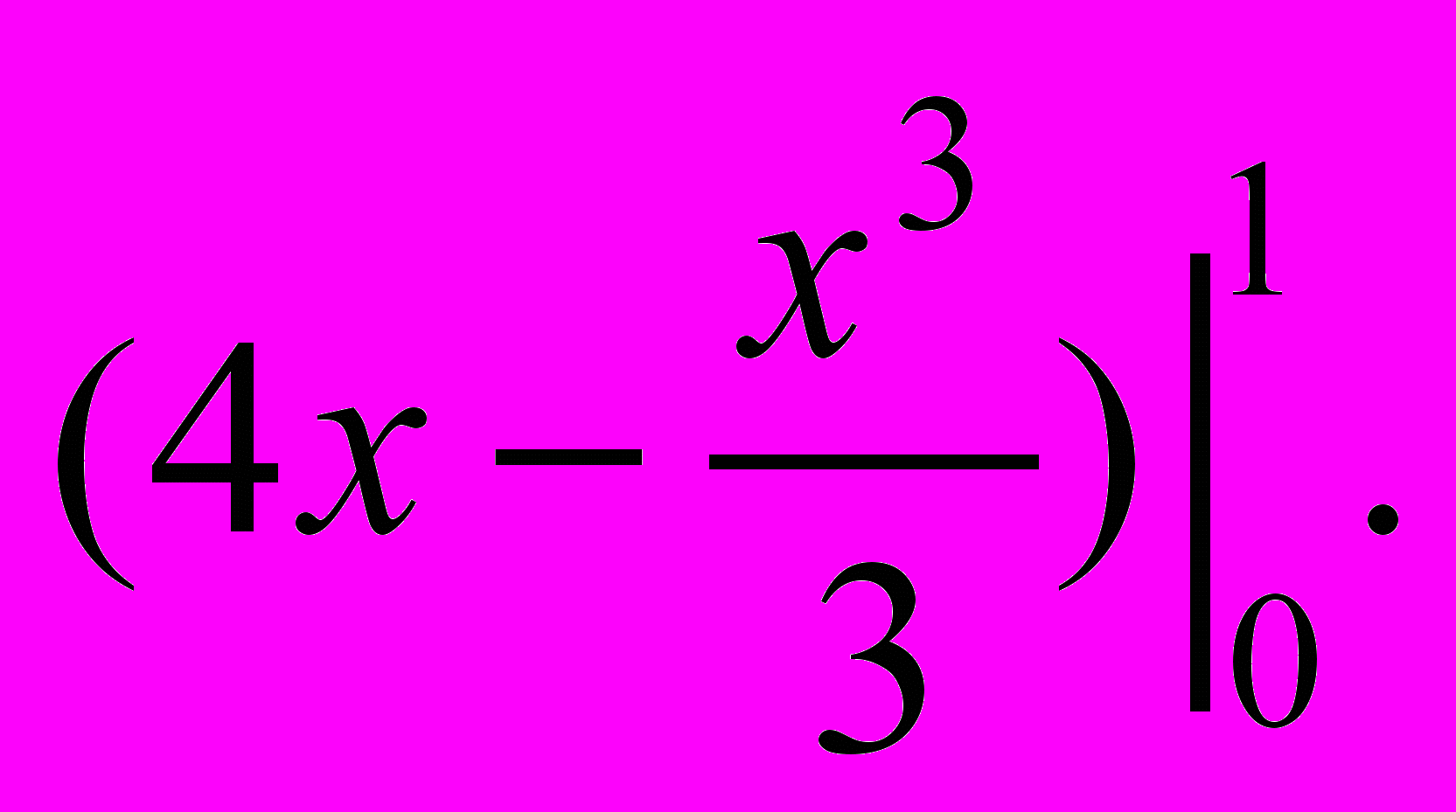
а)
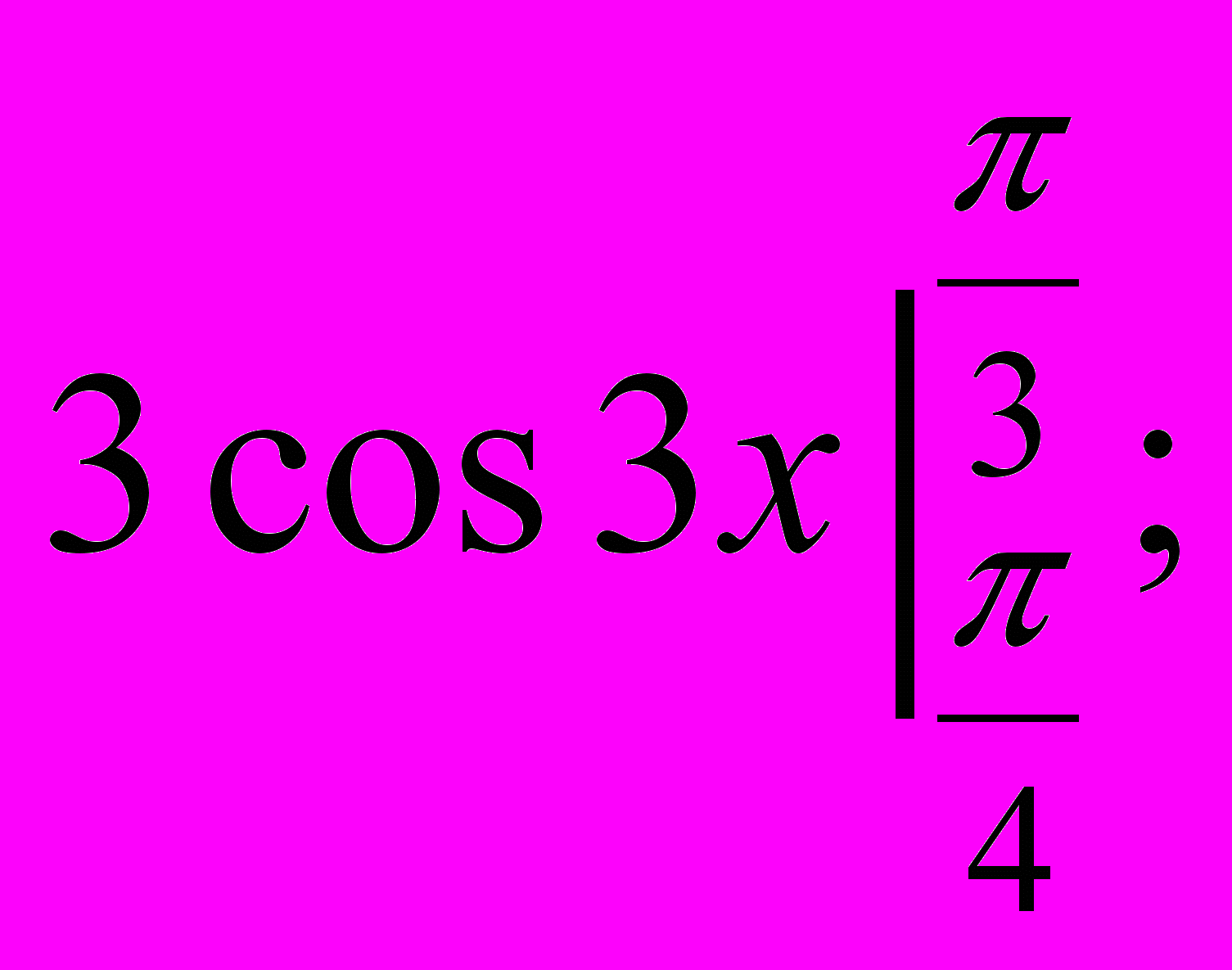 б)
б) 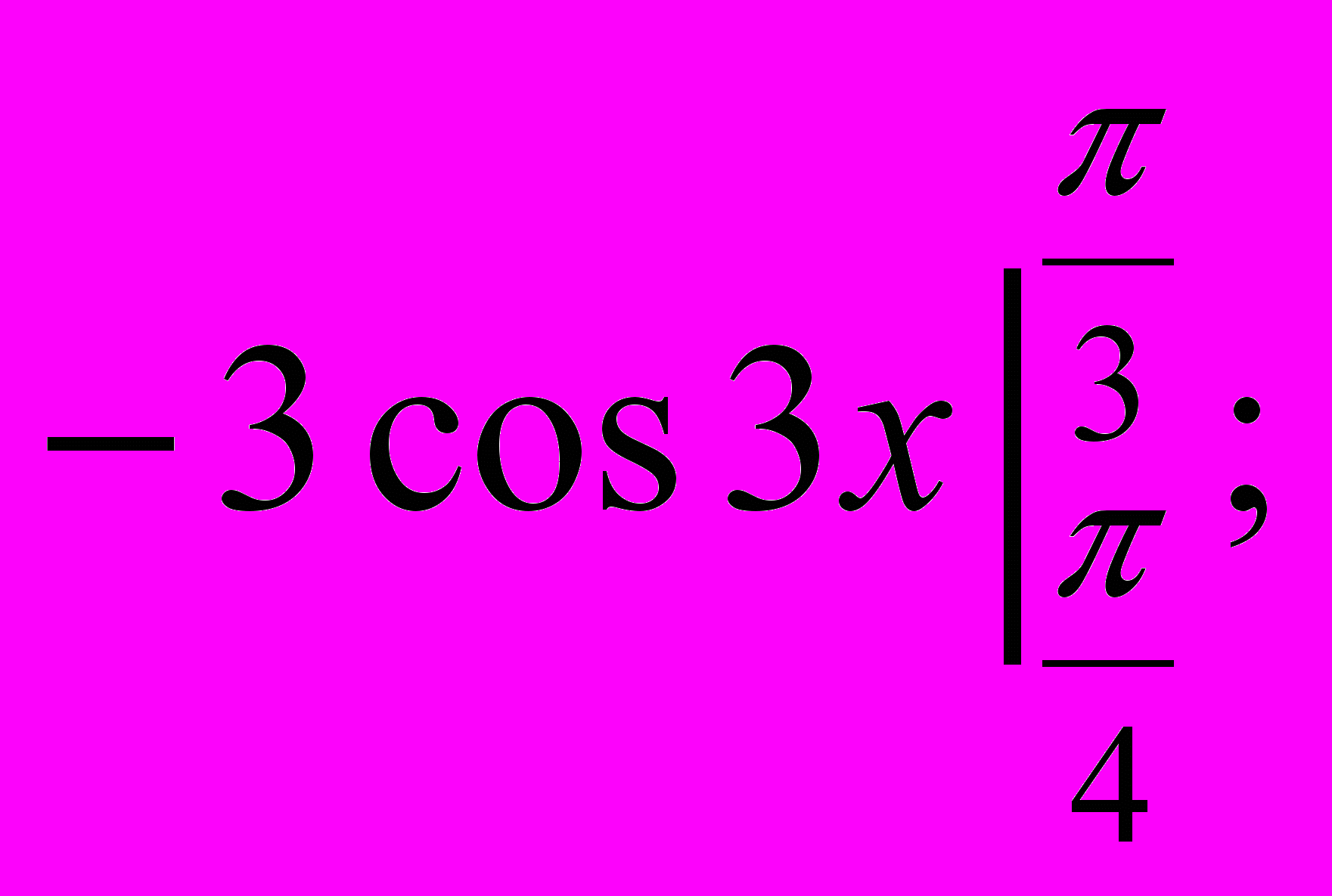 в)
в) 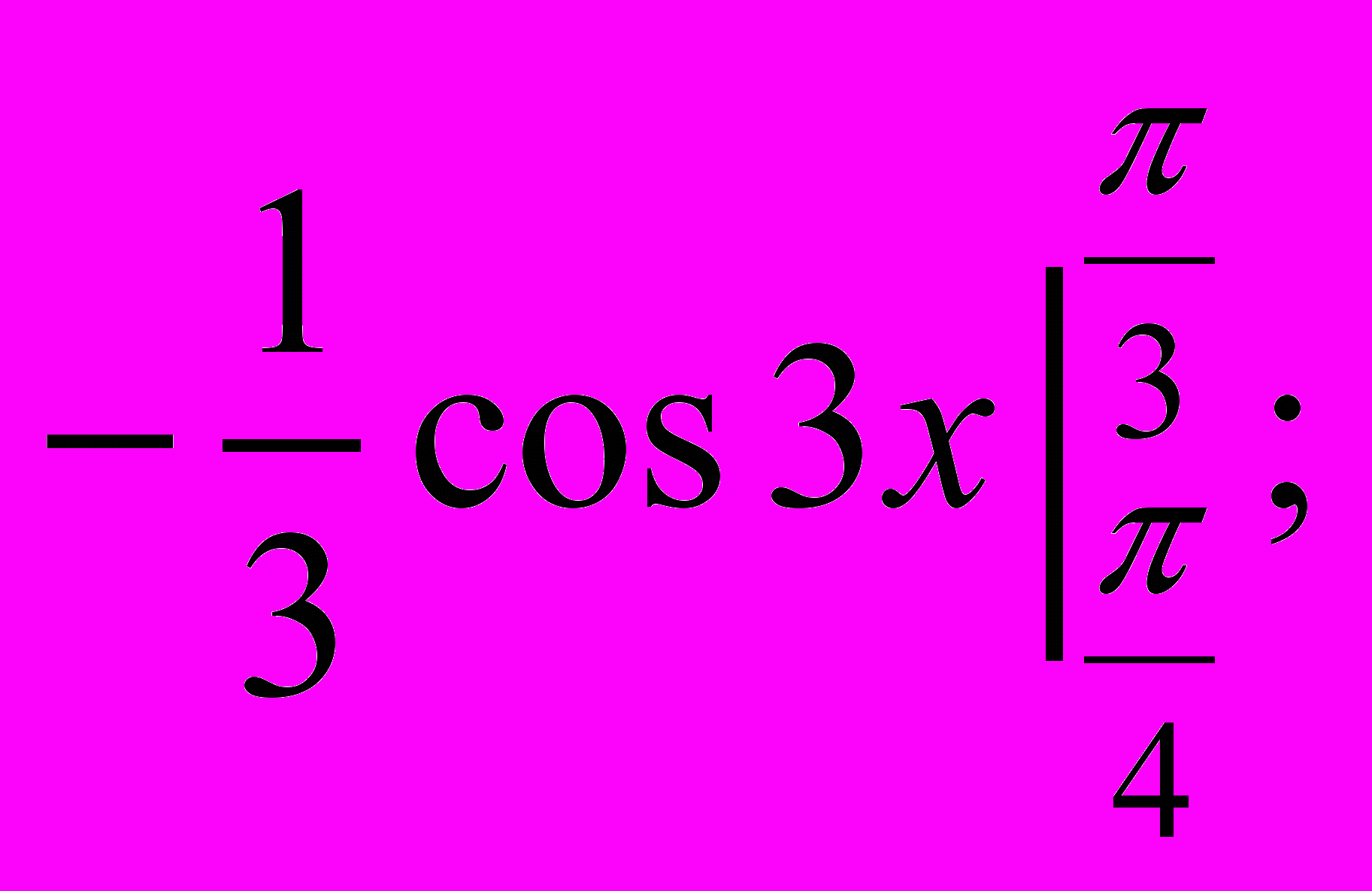 г)
г) 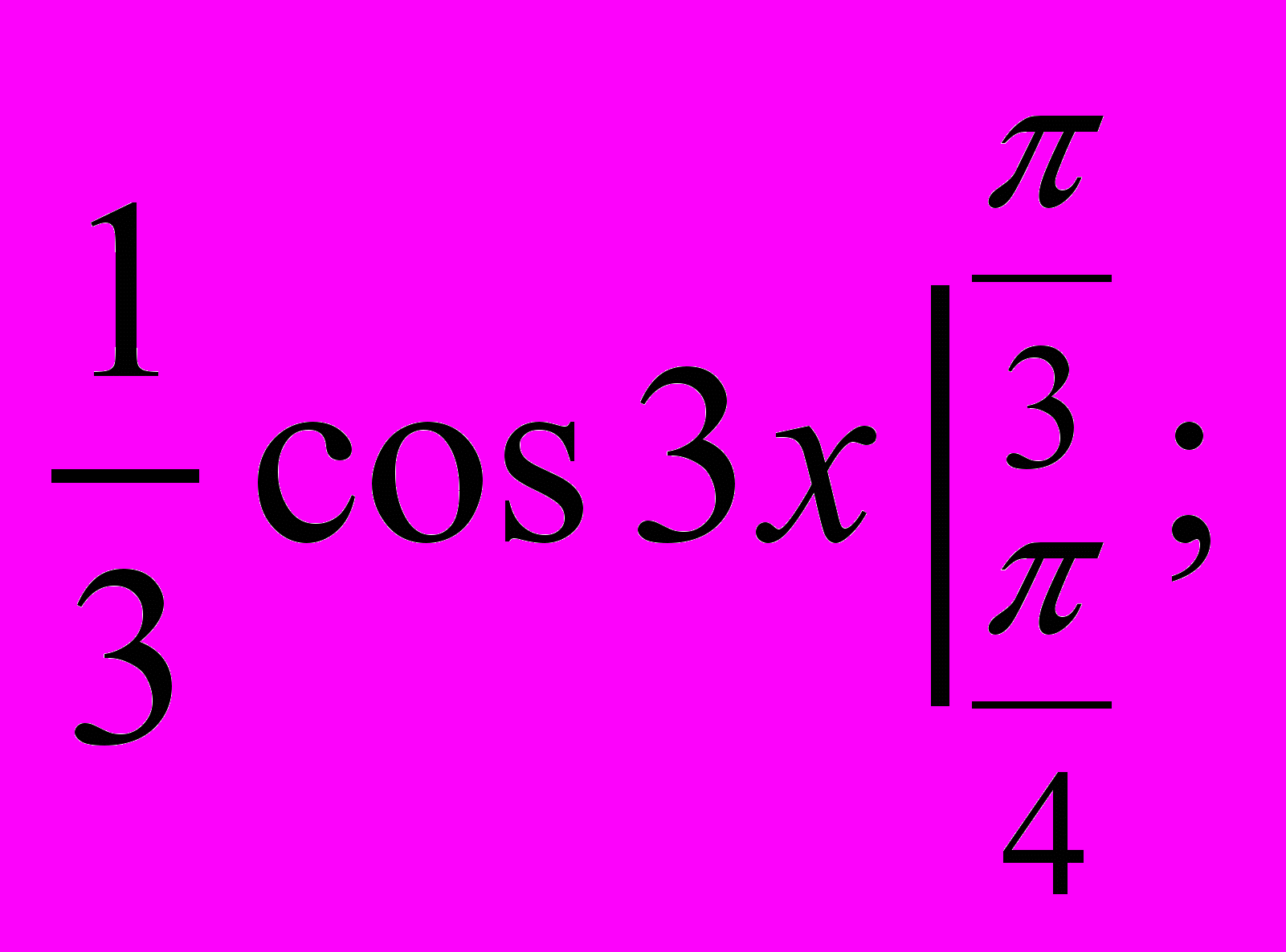
- Обчисліть площу заштрихованої фігури на малюнку в).
Література
Гін В.І. Прийоми педагогічної техніки. Харків «Ранок», 2007
Панішева О.В. Інтеграція у шкільному курсі. Математика у школах України, №13 2005
Семчишин Я.С. Контрольні та самостійні роботи з математики 11 клас. Тернопіль «Астон»,2006
Седенко Л. М., Седенко О. М. Побудова графіків функцій та виконання математичних завдань… Харків Видавнича група «Основа», 2007
Старова О.О. Реалізація між предметних зв’язків на уроках математики. Математика у школах України, №3 2004
Страннікова С.В. Інтегрований урок з геометрії та інформатики. Математика у школах України, №5 2006