Ролі етапу актуалізації знань та способів дій в навчанні математики вцілому та в структурі уроку
| Вид материала | Урок |
СодержаниеАктуалізація опорних знань за видами діяльності учнів Вимоги програми Систематична (основна) актуалізація опорних знань |
- Схема поглибленого аналізу уроку іноземної мови, 33.13kb.
- Опис власного методичного досвіду, з актуалізації опорних знань та вмінь учнів в процесі, 366.74kb.
- Розділ передумови вдосконалення методики проведення етапу закріплення знань та формування, 442.2kb.
- Навчально-виховний комплекс №6 «Перспектива» виховання творчої особистості в умовах, 116.55kb.
- Політичний аспект мовної проблеми на дузі „Москва Київ- тель-Авів, 786.75kb.
- Політичний аспект мовної проблеми на дузі „Москва Київ- тель-Авів, 797.75kb.
- Орієнтовний план проведення уроку I. Організаційна частина. II. Актуалізація опорних, 45.38kb.
- Тема уроку: “ Вітаміни – це здоров’я та спосіб життя”. Цілі уроку, 57.35kb.
- Тема уроку: Здоров’я. Планування подальших дій І змін індивідуального способу життя, 121.25kb.
- Про графічний спосіб розв’язання математичних задач, 262.98kb.
Схема 11.2.
Наприклад, урок вивчення нового матеріалу не завжди доцільно починати з актуалізації опорних знань. Доречним буде виклад нового матеріалу шляхом пояснення вчителем або створення проблемної ситуації, чи висунення пропозицій про спосіб розв’язання раніше поставленої проблеми. Тоді допоміжна актуалізація може знадобитись в ході доведення висунутої гіпотези, чи в ході вирішення проблемної ситуації. Або навпаки, випереджальна актуалізація проводиться на початку уроку і базується на знаннях отриманих на попередніх уроках необхідних для засвоєння нового матеріалу.
Отож, щоб уникнути плутанини, та полегшити засвоєння нового матеріалу, треба актуалізувати та систематизувати набуті знання, бо тільки система як зазначав К.Д. Ушинський, дає цілковиту владу над знаннями. "Голова, наповнена уривчастими, непов’язаними знаннями, схожа на комору, в якій все без ладу, і де сам хазяїн нічого не знайде." Інакше кажучи, це означає що в процесі навчання має бути реалізований принцип повторення та систематичності. Для цього при проведенні актуалізації опорних знань учнів можна використовувати пам’ятки, опори, таблиці, схеми, алгоритми, зразки міркувань.
Актуалізація – це більш широке поняття, ніж просто опитування. В неї входить і контроль учителя за станом знань учнів. Вона повинна проводитись в різних не стандартних формах, треба намагатися використовувати їх комплексно, щоб уникнути монотонності і одноманітності. Тоді учень сам приходить до думки, що одне і теж завдання можна розв’язати різними шляхами, так формується варіативність мислення учнів.
Форми та методи проведення актуалізації опорних знань і способів дій обираємо в залежності від складності матеріалу. На уроках геометрії де програмовий матеріал вимагає від учнів більшого уявлення і порівняння, актуалізації зазвичай відводиться менше часу ніж на уроках алгебри.
Не організувавши відповідну підготовку учнів до вивчення нового матеріалу не можна мати високих якісних показників у вивченні математики. Тому треба враховувати не тільки зміст матеріалу, а й рівень готовності школярів до засвоєння. Необхідно при цьому розглядати локальну (вміння розв’язувати конкретне завдання) і загальну готовність учнів до вивчення нового матеріалу.
Актуалізація опорних знань за видами діяльності учнів
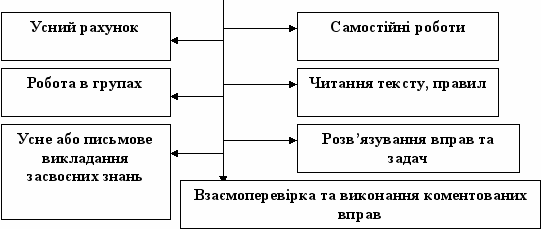
Схема 12. Актуалізація опорних знань за видами діяльності учнів
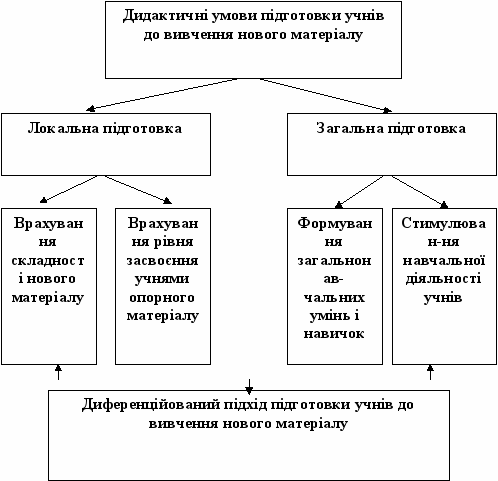
Схема 13. Дидактичні умови підготовки учнів до вивчення нового матеріалу
Недостатня сформованість в учнів базових знань є однією з болючих проблем сьогодні. У міру зростання об'єктивних і суб’єктивних факторів (велика кількість нових інформаційних потоків, об’єм матеріалу, тощо) учневі стає все важче "утримувати" той комплекс необхідних знань, які обумовлює подальші успіхи у навчанні. Здебільшого виявляється проблематичним відпрацювати необхідні навички та вміння на належному рівні в межах тієї кількості годин, що відводиться програмою на вивчення даної теми, вивчення будь якого нового матеріалу неодмінно потребує опори на попередньо сформовані в учня знання (Вимоги програми-------Систематична (основна) актуалізація опорних знань------Результативність) (схема 14)
| Вимоги програми | |
| 5 клас | Розв’язувати вправи, що передбачають знаходження дробу від числа; перетворення, порівняння, округлення, додавання, віднімання, множення, ділення дробів; Знаходження відсотків, розв’язування текстових задач. |
| 6 клас | Розв’язувати вправи, що передбачають використання ознак подільності; скорочення і зведення дробів до спільного знаменника, знаходження відношень; знаходження модуля; додавання, віднімання, множення, ділення раціональних чисел; розкриття дужок; знаходження координат точок. |
| 7 клас | Розв’язувати лінійні рівняння з однією змінною, системи двох лінійних рівнянь, задачі за допомогою рівнянь, обчислення значень виразів із змінними, розкладання многочленів на множники способом винесення спільного множника за дужки, та за формулами скороченого множення. |
| 8 клас | Розв’язувати вправи, що передбачають скорочення та зведення дробів; знаходження суми, різниці, добутку, частки дробів; застосування поняття арифметичного квадратного кореня, перетворення виразів, знаходження коренів квадратного рівняння, складання і розв’язування квадратних рівнянь. |
| 9 клас | Розв’язувати вправи, що передбачають розв’язування лінійних нерівностей з однією змінною та систем двох лінійних нерівностей, побудова графіків, знаходження розв’язків систем двох рівнянь другого степеня з двома змінними, обчислення членів прогресій, використання формул загальних членів і сум прогресій для знаходження невідомих елементів прогресій. |
| 10 клас | Знаходити значення функцій при заданих значеннях аргументу, досліджувати властивості функцій, встановлювати за графіком функції її найважливіші властивості, розв’язувати найпростіші тригонометричні рівняння, будувати графіки тригонометричних функцій. |
| 11 клас | Розв’язувати найпростіші показникові та логарифмічні рівняння і нерівності, обчислювати інтеграл за допомогою основних властивостей і формул Ньютона-Лейбніца, знаходити площі криволінійних трапецій. |
| | |
| Систематична (основна) актуалізація опорних знань | |
| 5 клас | Розв’язування вправ на додавання, віднімання, множення і ділення натуральних чисел, розв’язування рівнянь, уявлення про окремі геометричні фігури, знаходження периметрів цих фігур |
| 6 клас | Розв’язування вправ на всі дії з натуральними та дробовими числами, перетворення дробів, знаходження числа за його дробом та дробу від числа, відсоткові розрахунки. |
| 7 клас | Вправи на всі дії з раціональними числами, знаходження модуля числа, розкриття дужок, зведення подібних доданків, розв’язування рівнянь з використанням основних властивостей рівнянь. |
| 8 клас | Вправи на всі дії з раціональними числами, знаходження модуля числа, розкриття дужок, зведення подібних доданків, використання формул скороченого множення. |
| 9 клас | Вправи на всі дії з раціональними числами, знаходження модуля числа, розкриття дужок, зведення подібних доданків, використання формул скороченого множення, вправи на застосування поняття арифметичного квадратного кореня, розв’язування квадратних рівнянь |
| 10 клас | Вправи на всі дії з раціональними числами, знаходження модуля числа, розкриття дужок, зведення подібних доданків, використання формул скороченого множення, вправи на застосування поняття арифметичного квадратного кореня, розв’язування квадратних рівнянь, розв’язування найпростіших тригонометричних рівнянь. |
| 11 клас | Вправи на всі дії з раціональними числами, знаходження модуля числа, розкриття дужок, зведення подібних доданків, використання формул скороченого множення, вправи на застосування поняття арифметичного квадратного кореня, розв’язування квадратних рівнянь, розв’язування найпростіших тригонометричних рівнянь. |
| | |
| Результативність | |
| 1 | Відтворення в пам'яті раніше засвоєних знань |
| 2 | Підвищення ефективності засвоєння нового матеріалу, стимулювання пізнавальної активності учнів |
| 3 | Систематичне застосування засвоєних знань в нових ситуаціях, в теоретичній і практичній навчальній діяльності учнів |
| 4 | Життєва компетентність |
Схема 14. Основні моменти актуалізації опорних знань
у відповідності із вимогами програми
Програми з математики хоч і складні, але доступні учням. Усі учні без винятку здатні оволодіти шкільною програмою на рівні своєї навченості. Для цього учителю просто необхідно звертатися до раніше вивченого матеріалу, тобто актуалізувати набуті знання.
Працюючи над даним проблемним питанням було помічено, що якщо під час формування знань учнів або узагальнення і систематизації знань, чи перед проведенням контролю знань було проведено актуалізацію опорних знань, то учні мають більш глибокі знання, кращі результати навченості. Тому актуалізація є невід'ємним етапом на більшості уроків і дає позитивні результати. Викладаючи математику в 9-му класі отримано результати навчання учнів:
| Бал | За 8 клас | За 9 клас, алгебра (після постійного проведення актуалізації) |
| 1 2 3 4 5 6 7 8 9 10 11 12 Коефіцієнт навченості | - - - - 1 8 7 8 5 - - 1 7,43 | - - - - - 5 11 8 3 1 - 2 7,73 |
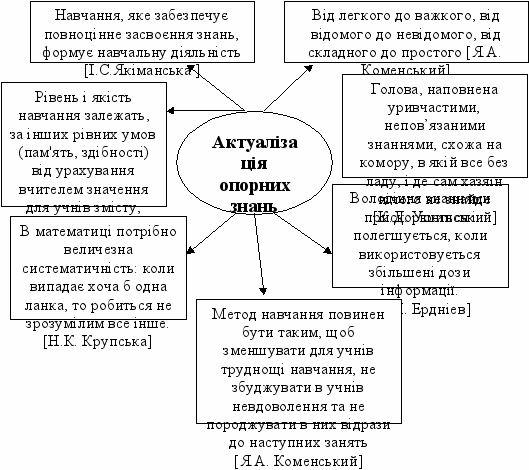
Таким чином "Рівень і якість навчання залежать, за інших рівних умов (пам'ять, здібності), від урахування вчителем значення для учнів змісту, який вони засвоюють" (І.Я. Лернер).
Важливим є не тільки факт наявності в учнів знань, але і характер процесу, в результаті якого вони сформовані, введення нових знань, як нового елементу в систему вже відомих положень математичної теорії. Важливу роль при цьому набуває актуалізація раніше засвоєних знань – відтворення їх в зв’язку з новими, пов’язаними з ними знаннями, які слід засвоїти на уроці.
У даному розділі розглядається система уроків з розділів "Розв’язування трикутників" (геометрія) та "Рівняння та системи рівнянь" (алгебра) 9-го класу, пропонується методика організації роботи з класом на початковому етапі уроку з математики при різнорівневому підході до навчання. У систему входять різні типи уроків, і, виходячи з доцільності проведення актуалізації знань та вмінь на уроці, показана схема проведення та форми організації роботи на даному етапі.
Нагадаємо, що на початку уроку треба зацікавити дітей, заохотити до навчання та створити робочу обстановку, сконцентрувати увагу дітей на тему чи проблему уроку. В умовах різнорівневого навчання вчитель працює з однією диференційованою групою, але працює на весь клас. Усі учні повинні повторити необхідний на даному уроці матеріал, уміти оперувати опорними знаннями та вміннями чи просто пояснити розв'язання домашнього завдання.
Запропонована методика дозволяє користуватися нею не тільки в умовах різнорівневого підходу до навчання, але й тоді, коли клас не поділений на різні диференційовані групи, адже у будь-якому класі є учні, що навчаються добре і посередньо.
2.1. Методика проведення етапу актуалізації знань
на уроках математики в 9-му класі
2.1.1. Специфіка актуалізації знань з алгебри
(на прикладі частини теми "Квадратична функція", за підручником Бевз Г.П. Алгебра,7-9)
Витяг з тематичного плану
(подано орієнтовну кількість годин)
| Номер уроку | Тема уроку | Кількість годин |
| 1 | Функції та їх властивості | 1 |
| 2 | Властивості функцій | 1 |
| 3-4 | Найпростіші перетворення графіків функцій | 2 |
| 5 | Графіки функцій, що містять знак модуля | 1 |
| 6 | Квадратний тричлен, його корені | 1 |
| 7-8 | Розкладання квадратного тричлена на лінійні множники | 2 |
| 9 | Виділення квадрата двочлена з квадратного тричлена | 1 |
| 10 | Найбільше і найменше значення квадратного тричлена | 1 |
| 11 | Тематичне оцінювання. Контрольна робота | 1 |
Урок 1. Функції та їх властивості
Мета. Узагальнити та розширити знання учнів про функції та їх властивості
Тип. Комбінований урок
Актуалізацію опорних знань спочатку проводимо у формі фронтального опитування.
1.Яка залежність між змінними називається функціональною або функцією?
2.Що таке аргумент(незалежна змінна)?
3.Наведіть приклади функцій.
4.Як знайти область визначення функції? область значень?
5.Які ви знаєте способи задання функції?
6.Що таке графік функції? Як його побудувати?
7.Які властивості функції легко побачити з її графіка?
8.Чи можна за графіком функції знайти її значення при заданому значенні аргументу? Як?
9.Чи кожна лінія в координатній площині задає функцію, тобто є графіком деякої функції?10.Як розпізнати графік функції?
Далі учні початкового (далі - у.п.р.) та середнього (у.с.р.) рівнів навчальних досягнень працюють з вчителем, розв’язуючи №№ 107, 108, 109(усно), 110(а, г, е)
Учні достатнього (у.д.р.) рівня підготовки працюють над №113, високого (у.в.р.) - №№116, 117 (по одному представнику на кожен № готуються біля дошки). Потім вони коментують розв’язання заданих вправ для учнів з іншим рівнем підготовки.
Урок 2. Властивості функцій
Мета. Закріпити знання учнів про функції та їх властивості
Тип. Урок закріплення вивченого
1. Перевірка д/з та опитування учнів
- Яка функція називається зростаючою? спадною? парною? непарною?
- Що таке область визначення функції? область значень?
2. №193(а) розв’язує вчитель з детальним поясненням
№193(б, в)- у.п.р. та у.с.р.
№194(а, б)- у.д.р. та у.в.р.
3. Тест " Функції та їх властивості"
П.р.
1. Функція у = ∫ (х) наз. зростаючою, якщо з того, що х ‹ х ,випливає, що
а) у › у ; б) у ≥ у ; в) у ‹ у .
2. Функція наз. парною, якщо її область визначення симетрична відносно нуля і :
а) ∫ (-х) = │∫ (х)│; б) ∫ (-х) = ∫ (х); в) ∫ (-х) = - ∫ (х).
3. Графік непарної функції симетричний відносно:
а) осі Ох; б) осі Оу; в) початку координат.
С.р.
4. Відомо,що функція у = ∫ (х) спадна на проміжку │-10;10│. Порівняти:
а) ∫ (4) і ∫ (5); б) ∫ (-3) і ∫ (-7).
5. На яких малюнках зображено графіки парних функцій:
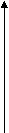
а) б) в) 
г) д) е)
ж)
є
) 
6. На яких малюнках зображено графіки спадних функцій?
Д.р.
7. Функція, графік якої зображено на малюнку е), зростає на:
а) (-4;0) і (1;3); б) на всій області визначення;
в) (-3;3); г) (0;4).
8. Областю визначення функції у = √ 5- 2х є проміжок:
а) │0;+∞); б) (-∞;2,5│; в) │2,5;+∞).
9. Які з даних функцій є непарними:
а) у = 3х + 1; б) у = 2/х; в) у = х - х; г) у = х + 4.
10. Які з даних функцій зростають на всій області визначення:
а) у = √ х + 1; б) у = х ; в) у = х – 2; г) у = 4 – 3х.
В.р.
11. Знайти найбільше значення функції у = х + 3 на проміжку │-5;-3 │.
12. Функція у = х - 3х зростає:
а) на всій осі; б) (0; ∞)
в) (-∞; -1) та ( 1; ∞); г) (-1; 1).
Урок 3. Найпростіші перетворення графіків функції
Мета. Формування вміння побудови графіків функцій у = а ∫ (х) за графіком функції у = ∫ (х)
Тип. Урок ознайомлення з новим матеріалом
Поки троє учнів біля дошки готують д/з ( по одному завданню з кожної вправи ), з класом проводиться бесіда, в якій повторюються означення функції, її властивості.
Далі розпочинається вивчення нового матеріалу.
Урок 4. Найпростіші перетворення графіків функції
Мета. Формування вміння побудови графіків шляхом перетворень
Тип. Комбінований урок
Фронтальне опитування (на дошці представлені малюнки, які треба співвідносити із запитаннями)
- Як розміщені графіки функції у = ∫ (х) та у = -∫ (х)?
- Як побудувати графік функції у = -∫ (х), маючи графік функції у = ∫ (х)?
- В якому випадку графік у = к ∫ (х) одержується розтягуванням графіка у = ∫ (х), а в якому – стисканням? Відносно якої осі ?
- Як з графіка функції у = ∫(х) одержати графік функції у = к∫(х) при к›│ 1│?, при к‹ │ 1│?
Урок 5. Графіки функцій, що містять знак модуля
Мета. Формування навичок побудови графіків функцій з модулями
Тип. Комбінований урок
Троє учнів (у.д.р. або у.в.р.) біля дошки виконують д/з – кожен по 2 графіка. Після побудови графіка вказують множину значень, корені (нулі), проміжки знакосталості, проміжки зростання і спадання функції.
З класом (у.с.р. та у.п.р.) тим часом повторити, коли графік функції зміщується вгору, вниз, вліво, вправо; як перетворити вираз ах² +вх +с, щоб графік квадратичної функції одержати з параболи у=х ².
Далі актуалізацію опорних знань проводимо для всіх учнів класу.
- Що наз. модулем числа?
- Чому дорівнює │х-а│? │-х│?
- Яких значень набуває вираз │х│?
Записи:
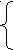
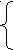х, якщо х≥0. х-а, якщо х≥а,│х│= │х-а│=
-х, якщо х‹0. а-х, якщо х‹а.
Урок 6. Квадратний тричлен, його корені
Мета. Формування поняття квадратного тричлена
Тип. Комбінований урок
Учні об’єднуються в групи за рівнем навчальних досягнень.
Побудувати графік функції.
І
група (у.с.р. та у.п.р.)3, х ≤ 3
а) у = │х - 3│ + х = 2х – 3, х > 3
б) Побудувати графік функції у = │х² - 4│.
Будується графік у = х² - 4 і нижня частина відбивається симетрично відносно ох.
ІІ група (у.д.р. та у.в.р.)
а) у = │х – 1│ +│х - 3│.
Вирази, що стоять під знаком модуля, перетворюються в нуль у точках 1 і 3.
1) х ≤ 1 │х - 1│ = 1 – х; │х - 3│ = 3 – х; у = 4 – 2х.2) 1 ≤ х ≤3 │х - 1│= х – 1;│х – 3│ = 3 – х; у = 2.
3) х > 3 │ х – 1│= х – 1; │х – 3 │= х – 3; у = 2х -4.Графік функції
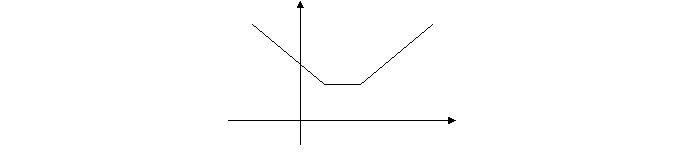
б) у = х² - 3│х│ + 2. Оскільки х² = │х│², то будується графік функції у= х² -3х +2 для х ≥0 і відбивається симетрично осі Оу.
Після роботи в групах, по 2 учні з кожної виходять до дошки і пояснюють порядок побудови запропонованих графіків.
Далі починаємо пояснення нового матеріалу.