Geum.ru

”Використання математичних пакетів при вивченні математики у вищій школі ”

Вид материалаДокументы

Содержание


Розв’язок задачі в пакеті Mathematica 4.1
Подобный материал:
1   2   3   4

Розв’язок задачі в пакеті Mathematica 4.1:

1. Вводимо початкові дані задачі і будуємо інтерполяційний многочлен:

data: {{0.11, 9.05421), (0.15, 6.61659}, {0.21, 4.6917},

{0.29, 3.35106}, {0.35, 2.73951},{0.4, 2.36522}}

twoInterpolation[data] InterpolatingFunction[{{0.11, 0.4}}, <>]

{funi[0.15], luni[0.314], find[0.4])

{6.61659, 3.07646, 2.36522}

2. Побудуємо графік табличний заданої функції:

gl:=PlotLaga, a, 0, 0.5

g2:=ListPlot 0.11 9.05421 0.15 6.61659

0.21 4.69170 0.29 3.35106 0.35 2.73951

0.4 2.36522, PlotStriePointSifle 02 Show[9l, g2, PlotHange-» {2, 10}];

3. Складемо функцію, що повертає значення в заданій точці з використанням інтерполяційного многочлена Лагранжа:

BeginPackege [" Lagrange ' Lagr'" ]

Begin["'Private'"]

s := 0

x:={0.11, 0.15, 0.21, 0.29, 0.35, 0.4}

у := (9.05421, 6.61659, 4.6911, 3.35106, 2.73951, 2.36522}

Do i := 1;

Do if j == i. Continued,

1 = 1* (a-Part[x, j])/[Part[x, i]-Part[x, j])],

1, 6}];

l = l>>Part[y, i];

s = s + l, (i, 1, 6}] Lag[a] = s End[] EndPackege[]

Мал. 3. Фрагмент документа в Mathematica розв’язку задачі інтерполяції за допомогою многочлена Лагранжа

Розв’язок задачі в пакеті MatLAB:

1. Введення початкових даних задачі:

X=[0.11,0.15,0.21,0.29,0.35,0.4];

Y=[9.05421,6.61659,4.69170,3.35106,2.73951,2.36522];

2. Побудова графіка функції, заданої таблично:



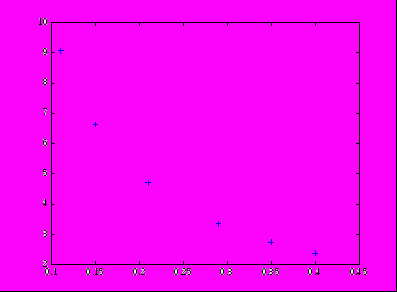
plot([0.11,0.15,0.21,0.29,0.35,0.4],[9.05421,6.61659,4.69170,3.35106,2.73951, 2.36522],'+')

3. Створення m-файла, реалізовуючого розв’язок задачі інтерполяції за допомогою многочлена Лагранжа:

function [C,L]=lagrang(X,Y)

Х=[0.11,0.15,0.21,0.29,0.35,0.4] % Вхід - X - вектор абсцис

Y=[9.05421,6.61659,4.69170,3.35106,2.73951,2.36522] % У - вектор ординат

% Вихід - матриця коефіцієнтів інтерполюючого полінома Лагранжа

% L - матриця коефіцієнтів полінома Лагранжа

w=length(X); n=w-l

L=zeros(w,w); % Формування коефіцієнтів полінома Лагранжа

For k=l: n+l

V=l;

For j=l: n+l

V=conv(V,poly(XG)))/(X(k)-X(j)); end end

L(k,:)=V; end

% Визначення коефіцієнтів інтерполюючого полінома

% Лагранжа C=Y*L;

4. Далі необхідно виконати наступну послідовність команд:

X=[0.11,0.15,0.21,0.29,0.35,0.4];

Y=[9.05421,6.61659,4.69170,3.35106 2.7395 1,2.36522];

lagrang(X,Y) % визначення коефіцієнтів многочлена Лагранжа

Х = Columns 1 through 5

0.1100 0.1500 0.2100 0.2900 0.3500 Column 6

0.4000 Y = Columns 1 through 5

9.0542 6.6166 4.6917 3.3511 2.7395 Column 6 2.3652 n = 5

ans = 1.0*Coluns 1 through 5

-0.7109 1.0734 -0.6521 0.2033 -0.0342 Column 60.0029

% Складений многочлен виглядатиме так:

-7109х5 +10734х4 -6521х3 +2033х2 -342х + 29

polyval(lagrang,0.314) % знаходження значення функції в точці 0,314 з допомогою складеного многочлена Лагранжа

Х = Columns I through 5

0.1100 0.1500 0.2100 0.2900 0.3500 Column 6

0.4000 Y = Columns 1 through 5

9.0542 6.6166 4.6917 3.3511 2.7395 Column 6

2.3652 n = 5

3.0735

5. Побудова графіка побудованого інтерполяційного многочленна Лагранжа

dd=lagrang;r=polyval(dd,X);plot(r,'+')

Мал. 6 . Фрагмент документа в MatLAB розв’язку задачі інтерполяції за допомогою многочлена Лагранжа

Розв’язок задачі в пакеті MathCAD:

Складемо функцію, що повертає значення функції у вказаній крапці



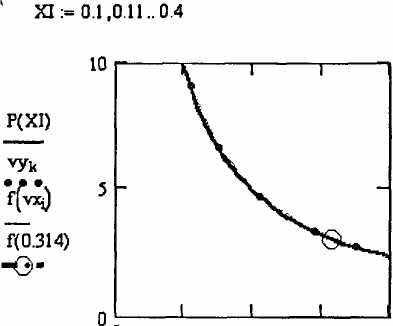
lagrang(vx,vy,0.3.14)=3.073 5

Вводимо матриці початкових даних:

Знаходимо величину n - показник ступеня многочлена:

n:= length(vx) - 1

Задаємо змінні:

i:=0..n j:=0..n

Побудуємо графіки многочлена f(x), отриманого по формулі Лагранжа, полінома Р(х) і даних значень табличний заданої функції vy :

Мал. 7 . Фрагмент документа в MathCAD розв’язку задачі інтерполяції за допомогою многочлена Лагранжа.

Порівняльний аналіз наведених вище фрагментів документів, створених в ході рішення розглянутої задачі за допомогою програмних засобів, дозволяє зробити наступні висновки:
  1. Написання програми на мові програмування вимагає від студента знання мови програмування, яке, як показує практика викладання, не завжди відповідає рівню, що вимагається, що істотно уповільнює процес розв’язку задачі.
  2. Mathematica, Maple, MatLAB, MathCAD об'єднали в собі велику кількість відомих математичних методів. Це привело до того, що список доступних команд і функцій більше тисячі, що з неминучістю утрудняє використовування математичних пакетів в навчальному процесі.
  3. В пакеті MathCAD достатньо проста вхідна мова, максимально наближена до звичайної математичної мови. Робочий лист пакету можна використовувати як звичайний робочий зошит.

Графічна візуалізація завдання і виведення результатів математичних обчислень робить перераховані пакети привабливим засобом для візуалізації розв’язку. Проте для вирішення задачі, наприклад в MatLAB, необхідно складати спеціальний файл, відкриваючи при цьому додаткове вікно.

Для зміни початкових даних (пакет MatLAB) команду необхідно скопіювати з вікна Command History, потім змінити значення і запустити на виконання.

Об'єм кожного пакету розрізнений. Наприклад, пакет MatLAB в п'ять і більш разів займає більше простору на жорсткому диску ніж Maple або MathCAD.

Мова пакетів Mathematica, MatLAB і Maple вимагає обов'язкової розстановки розділових знаків, без яких команда буде прочитана як неправильна або на екрані відображатимуться всі результати проміжних обчислень.

Таке систематичне застосування математичних пакетів у викладанні різних дисциплін дозволяє говорити про формування професійної компетентності майбутнього фахівця, у тому числі і його інформаційної компетентності.

Аналіз використаних програмних засобів показує, що найоптимальнішим засобом для реалізації різних вузівських курсів є пакет MathCAD з причини своєї відносної простоти освоєння і використовування, наявністю простого варіанту реалізації мови програмування, представлення даних на робочому листі (аналогічно робочому зошиту користувача) і наочного представлення інформації на екрані комп'ютера. Далі розглянемо питання наочності навчання студентів при вивченні математики більш детально.


ЛІТЕРАТУРА
  1. Абрамов Ю. Ф. Картина мира и информация (философские очерки). Иркутск: Изд-во Иркутск, ун-та, 1988. 162 с.
  2. Амосов А.А., Дубинский Ю.А., Копченова Н.В. Вычислительные методы для инженеров: Учеб пособие. М.: Высшая школа, 1994. 544 с.
  3. Апатова Н.В. Развитие школьного курса информатики. М., 1993. 132 с.
  4. Арнхейм Р. В защиту визуального мышления // Арнхейм Р. Новые очерки по психологии искусства: Пер. с англ. М.: Прометей, 1994. С.153-173.
  5. Арнхейм Р. Визуальное мышление //Зрительные образы: феноменология и эксперимент. Душанбе, 1971. С.45-49.
  6. Арнхейм Р. Искусство и визуальное восприятие. М.: Прогресс, 1974. 395 с.
  7. Архангельский СИ. Учебный процесс в высшей школе, его основные закономерности и методы. М.: Высшая школа, 1980. 389 с.
  8. Бабанский Ю. К. Оптимизация учебно-воспитательного процесса. М., 1988. 192 с.
  9. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. М.: Лаборатория базовых знаний, 2001. 632 с.
  10. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы: Учеб. пособие. М.: Наука, 1987. 463 с.
  11. Безрукова B.C. Словарь нового педагогического мышления. Екатеринбург, 1992. 93 с.
  12. Беленкова И.В. Наглядность и визуальное мышление в курсе «Численные методы» //Новые информационные технологии в университетском образовании: Тез. докл. Междунар. науч.-метод. конф. / Сиб. гос. ун-т телекоммуникаций и информатики. Новосибирск, 2003. С. 117-119.
  13. Беленкова И.В. Из истории парадигм образования //Повышение эффективности подготовки учителей физики и информатики в условиях модернизации Российского образования: Материалы Всерос. науч.-практ. конф. Екатеринбург, 2003. С. 459.
  1. Беленкова И.В. Изучение некоторых вопросов курса «Численные методы» на профильном уровне общеобразовательной школы в рамках факультатива // Инновационные технологии в школе: Тез. докл. гор. науч. конф. Н.Тагил, 2001. С. 49-52.
  2. Беленкова И.В. Использование информационных технологий на примере решения нелинейных уравнений в курсе «Численные методы» // Проблемы современного математического образования в педвузах и школах России: Тез. докл. 2-й межрегион, науч. конф. Киров, 2001. С. 170.
  3. Беленкова И.В. Математические пакеты при изучении курса «Численные методы» в вузе // Повышение эффективности подготовки учителей физики и информатики в современных условиях: Материалы Междунар. конф. Екатеринбург, 2002. С. 70-73.
  4. Беленкова И.В. Место технологии в общей структуре методической системы обучения численным методам // Информационные технологии в управлении и учебном процессе вуза: Материалы 4-ой Всерос. науч.-практ. конф., Владивосток, 15-17 окт. 2003 г. Владивосток, 2003. С.78-81.
  5. Беленкова И.В. Методика преподавания курса «Численные методы» на физико-математических факультетах педагогических вузов // Сб. науч. тр. аспирантов и соискателей НТГПИ / Нижнетаг. гос. пед. ин-т. Нижний Тагил, 2002. Вып. 4. С. 13-22.
  6. Беленкова И.В. Об использовании электронной таблицы Quattro Pro в преподавании курса «Численные методы» для студентов физико-математических факультетов педагогических вузов // Современные проблемы школьного и вузовского математического образования: Материалы регион, совещания-семинара преподавателей пед. вузов и учителей математики. Н. Тагил, 1996. С. 22-23.
  7. Беленкова И.В. Обзор методик преподавания курса «Численные методы» // О новых функциях преподавателей профессионального образования в современных условиях: Материалы регион, семинара, Красноярск, 23-24 сент. 2003 г. Красноярск, 2003. С.126-129.
  1. Беленкова И.В. Организационные формы обучения в курсе «Численные методы» // Рейтинговая система оценки успеваемости студентов: Сб. науч. тр. семинара. Владивосток, 2003. С.111-112.
  2. Беленкова И.В. Сравнительный анализ программных средств для интерполирования функций // Информатизация общего, профессионального и дополнительного образования: Материалы электр. науч.-практ. конф. Оренбург, 2003.
  3. Беленкова И.В. Сравнительный анализ программных средств для приближенного решения систем уравнений // Учен. зап. Нижнетаг. гос. пед. ин-та. Сер. Естеств. науки / Нижнетаг. гос. пед. ин-т. Нижний Тагил, 2002. Вып. 5. С. 46-51.
  4. Беленкова И.В. Сравнительный анализ программных средств для приближенного решения уравнений // Информатизация образования — 2003: Сб. тр. Всерос. науч.-метод. конф. /Под ред. СВ. Поршнева. Н. Тагил, 2002. С. 131-141.
  5. Беленкова И.В. Учебно-методические комплексы для высшего профессионального образования //Информатизация общего и педагогического образования - главное условие их модернизации: Тез.выступл. участников Всеросс. конф. Челябинск: Изд-во ЧГГТУ, 2004. С.64.
  6. Беленкова И.В. Формирование информационной компетентности учителя информатики на занятиях по курсу «Численные методы» //Повышение эффективности подготовки учителей физики и информатики в современных условиях: Материалы междунар. науч.-практ. конф. Екатеринбург: Урал. гос. пед. ун-т, 2004. С.38-40.
  7. Беленкова И.В. Численные методы: Учеб. материалы к выполнению лаб. работ по курсу «Численные методы» / Нижнетаг. гос. пед. ин-т. Н. Тагил, 1996. 131 с.
  1. Беленкова И.В. Численные методы: Учеб.-метод. Пособие / Нижнетаг. гос. соц.-пед. академия. Н. Тагил, 2003. 135 с.
  2. Беленкова И.В. Электронный учебник, как учебное средство нового типа //Информационные технологии и технические средства обучения в образовательном процессе: Материалы 1-й науч.-практ. конф. Н-Тагил: Изд-во НТГСПА, 2004. С.25-28.
  3. Беленкова И.В., Виноградов Д.В., Жигунова Е.В., Поршнев СВ. Системы компьютерного тестирования учебных достижений //Повышение эффективности подготовки учителей физики и информатики в современных условиях: Материалы Междунар. конф. Екатеринбург, 2002. С. 65-69.
  4. Беленкова И.В., Кадыров А.Р. Использование компьютерных информационных технологий в курсе «Численные методы» на физико-математических факультетах. //Регинформ — 99: Региональные проблемы информатизации образования: Материалы Всерос. науч.-практ. конф. Пермь, 1999. С. 101-102.
  5. Беленкова И.В., Поршнев СВ. Место компьютера и информационных технологий в современном вузовском образовании // Педагогическая информатика, 2003. №4. С.34-45.
  6. Беленкова И.В., Поршнев СВ. Методика организации учебного процесса при изучении курса «Численные методы» // Учен. зап. Нижнетаг. гос.пед.ин-та. Сер. Естеств. науки / Нижнетаг. гос. пед. ин-т.Нижний Тагил, 2003. Вып. 2. С12-23.
  7. Беленкова И.В., Поршнев СВ., Тяжельникова О.Ю. Методика использования пакета MathCAD для решения систем нелинейных уравнений методом Ньютона // Новые технологии в образовании: Сб. науч. тр. Междунар. электронной науч. конф. /Воронеж, гос. пед. ун-т. Воронеж, 2001. Вып.4. С. 60-62.
  1. Белова З.С. Визуальная наглядность в формировании реалистического мышления учащихся. Дис. ... канд. пед. наук. Чебоксары, 1997. 182 с.
  2. Березин В.Н. Методические функции наглядности в обучении математике: Дис. ... канд. пед. наук. М., 1976. 156 с.
  3. Березин И.С., Жидков Н.П. Методы вычислений. Т.1, 2. М.: Физ-матгиз, 1962. 794 с.
  4. Беспалько В.П. Слагаемые педагогической технологии. М.: Педагогика, 1989. 192 с.
  5. Богословский В.И., Извозчиков В.А., Потемкин М.Н. Информационно-образовательное пространство как информационно-образовательный хронотоп // Наука и школа, 2000. №5. С.41-46.
  6. Болтянский В.Г. Формула наглядности: изоморфизм плюс простота //Советская педагогика. 1970, №5. С.46-60.
  7. Бондаревская Е.В. Гуманистическая парадигма личностно-ориентированного образования // Педагогика. 1997. №4. С. 11-17.
  8. Брадис В.М. Четырехзначные математические таблицы. М.: Учпедгиз, 1964. 64 с.
  9. Брановский Ю.С. Введение в педагогическую информатику: Учебное пособие для студентов педвузов. Ставрополь, 1995. 206 с.
  10. Бронштейн И.Н., Семендяев К.А. Справочник по математике. М.: Наука, 1965.268 с.
  11. Брушлинский А.В. Субъект: мышление, учение, воображение. Воронеж, 1996.265 с.
  12. Быстрицкий Е.К. Научное познание и проблема понимания. Киев, 1986.63 с.
  13. Валицкая А.П. Культуротворческая школа: концепция и модель образовательного процесса // Педагогика. № 4. С. 12-18.
  14. Васильков Ю.В., Боровков А.В. Электронный учебник по численным методам оптимизации. РосАПО №960181 20.05.96.
  1. Васильков Ю.В., Василькова Н.Н. Компьютерные технологии вычислений в математическом моделировании: Учеб. пособие. М.: Финансы и статистика, 2002. 256 с.
  2. Вержбицкий В.М. Основы численных методов: Учеб. пособие для вузов. М.: Высшая школа, 2002. 705 с.
  3. Вержбицкий В.М. Численные методы (линейная алгебра и нелинейные уравнения): Учеб пособие для вузов. М.: Высшая школа, 2000. 266 с.
  4. Вержбицкий В.М. Численные методы (математический анализ и обыкновенные дифференциальные уравнения).: Учеб. пособие для вузов. М.: Высшая школа, 2001. 382 с.
  5. Возрастные и индивидуальные способности образного мышления учащихся / Под ред. И.С. Якиманской. М.: Педагогика, 1989.
  6. Воробьева Г.Н., Данилова А.Н. Практикум по вычислительной математике: Учеб. пособие для техникумов. 2-е изд. перераб. и доп. М.: Высшая школа, 1990. 208 с.
  7. Вычислительная математика: Учеб. пособие для техникумов /Данилина Н.И., Дубровская Н.С., Кваша О.П., Смирнов Г.Л. М.: Высшая школа, 1985.239 с.
  8. Вычислительный практикум. Свердловск, 1986. 96 с.
  9. Гальперин П.Я., Эльконин Д.Б. К анализу теории Пиаже о развитии детского мышления. В кн.: Флейвен Д.Х. Генетическая психология Жана Пиаже. М., 1967. 164 с.
  10. Гамезо Н.В. Знаки и знаковое моделирование познавательной деятельности. Автореф. дис ... д-ра психол. наук. М., 1977. 37 с.
  11. Гаркунов В.П. О типах наглядности и видах изображений // Советская педагогика, 1983. №8. С. 141-142.
  12. Гершунский Б. С. Компьютеризация в сфере образования: Проблемы и перспективы. М.: Педагогика, 1987. 264 с.
  1. Гершунский Б.С. Философия образования для XXI века. (В поисках практико-ориентированных образовательных концепций). М.: Изд-во «Совершенство», 1998. 608 с.
  2. Гинецинский В.И. Предмет психологии. Дидактический аспект. М.: Логос, 1994. 293 с.
  3. Говорухин В.Н., Цибулин В.Г. Введение в Maple. Математический пакет для всех. М.: Мир, 1997. 278 с.
  4. Говорухин В.Н., Цибулин В.Г. Компьютер в математическом исследовании. Учебный курс. СПб.: Питер, 2001. 368 с.
  5. Государственный образовательный стандарт высшего профессионального образования. Специальность 030100. М.: МО РФ, 2000. 26 с.
  6. Государственный стандарт высшего профессионального образования. М.: Гос. ком. РФ по высш. обр-ю, 1995. 383 с.
  7. Грегори Р.Л. Глаз и мозг. Психология зрительного восприятия: Перс англ. /Предисл. и общ. ред. А.Р. Лурия, В.П. Зинченко. М.: Прогресс, 1970. 271 с.
  1. Груздев В., Груздева В. Педагогическая технология эвристического типа // Высшее образование в России, 1996. № 1. С 117-121.
  2. Гузеев В.В. Планирование результатов образования и образовательная технология М., 1999. 147 с.
  3. Гурова Л.Л. Развитие мышления в процессе овладения компьютерной грамотностью: Психологические проблемы создания и использования ЭВМ. М., 1985. 165 с.
  4. Давыдов В.В. Виды обобщения в обучении. М.: Педагогика, 2000. 423 с.
  5. Данилов М.А., Есипов Б.П. Дидактика / Под ред. Б.П. Есипова. М., 1957.246 с.
  6. Демидович Б.П., Марон И.А. Основы вычислительной математики. М.: Физматлит, I960. 659 с.
  1. Демидович Б.П., Марон И.А., Шувалова Э.В. Численные методы анализа. Приближение функций, дифференциальные уравнения / Под ред. Б.П. Демидовича. М.: Физматлит, 1962. 367 с.
  2. Денисова А.Л. Теория и методика профессиональной подготовки студентов на основе информационных технологий: Дис. ... д-ра пед. наук. М., 1994. 445 с.
  3. Долинер Л.И. Киборгизация как один из принципов построения учебного процесса в условиях информатизации образования // Образование и наука: Известия УрО РАО. Екатеринбург: Изд-во Урал. гос. проф.-пед. ун-та, 2001. №4 (10). С.57-66.
  4. Дьяконов В. MATLAB: Учебный курс. СПб: Питер, 2001. 432 с.
  5. Дьяконов В.П. Компьютерная математика. Теория и практика. М.: Нолидж, 1999. 1296 с.
  6. Дьяконов В.П. Справочник по MAthCAD 7.0 PRO. М.: СК-ПРЕСС, 1998. 785 с.
  7. Дьяконов В.П. Справочник по MathCAD PLUS 6/0/ PRO. M.: СК-ПРЕСС, 1997. 765 с.
  8. Дьяконов В.П. Справочник по математической системе Mathematica. M.: СК-ПРЕСС, 1998.
  9. Дьяконов В.П., Абраменкова И.В. Mathcad 7.0 в математике, в физике и Internet. M.: Нолидж, 1999. 169 с.
  10. Дьяченко С.А. Использование интегрированной символьной системы Mathematica при изучении курса высшей математики в вузе: Дис. ... канд. пед. наук. Орел, 2000. 164 с.
  11. Егорова Ю.Н. Использование информационных технологий в учебном процессе технического университета // Информатизация образования -2002: Сб. тр. Всерос. науч.-метод, конф. Нижний Тагил, 7-10 октября 2002 г. / Под ред. СВ. Поршнева. Нижний Тагил, 2002. 408 с.
  1. Ермилова Е.Б. Визуализация обучения как средство формирования учебных способностей: Дис. ... канд. пед. наук. Казань, 1999. 194 с.
  2. Ершов А.П. Компьютеризация школы и математическое образование. // Математика в школе. 1989. № 1. С. 14-31.
  3. Жданов С.А. Применение информационных технологий в учебном процессе педагогического института и педагогических исследованиях: Дис. ... канд. пед. наук, в форме науч. докл. М., 1992. 36 с.
  4. Заболотный В. П. Философские проблемы информатизации // Про­
    блемы информатизации. 1999. № 1. 129 с.
  5. Заварыкин В.М. и др. Техника вычислений и алгоритмизация:
    Вводный курс: Учеб. пособие для студентов пед. ин-тов по физ.-мат. спец.
    М.: Просвещение, 1987. 158 с.
  6. Заварыкин В.М. и др. Численные методы: Учеб. пособие для сту­
    дентов физ.-мат. спец. пед ин-тов /В.М. Заварыкин, В.Г. Житомирский, М.П.
    Лапчик. М.: Просвещение, 1991. 176 с.
  7. Заварыкин В.М., Житомирский В.Г., Лапчик М.П. Вычислительная
    математика. Учебное пособие для студентов физико-математических факуль­
    тетов пединститутов. Свердловск: СГПИ, 1985. 76 с.
  8. Заварыкин В.М., Житомирский В.Г., Лапчик М.П. Вычислительная