Силовой расчет механизмов

Вид материала

Документы

Содержание Результаты силового расчета Исходные данные

Подобный материал:

• Краткое содержание: Виброзащита машин и механизмов. Методы виброзащиты. Взаимодействие, 294.78kb.
• Темы курсового проекта по дисциплине «Теория механизмов и машин», 69.21kb.
• Расчётно-пояснительная записка к курсовому проекту по дисциплине: "Теория механизмов, 22.29kb.
• Курс Семестр Трудоемкость (в зачетных единицах), 33.22kb.
• Концепция специальной силовой подготовленности, 63.68kb.
• О повышении эффективности работы машин при помощи уточненного динамического расчета, 26.88kb.
• Пояснительная записка содержит: 5 рис., 4 источника, 22 стр, 223.14kb.
• Реферат пояснительная записка содержит: 5 рис., 4 источника, 22 стр, 222.54kb.
• Рабочей программы дисциплины Теория механизмов и машин по направлению подготовки 190100, 33.66kb.
• Задачи кинематического анализа и синтеза механизмов. Передаточные функции и отношения., 55.01kb.

Из решения этой системы уравнений определяются реакции в КП и движущий момент М_д3.

9. Силовой расчет сложных зубчатых механизмов.

Сложные зубчатые механизмы подразделяются на рядные и плане­тарные. Кроме того, по числу силовых или энергетических потоков они де­лятся на механизмы с одним силовым потоком и многопоточные механизмы. В механиз­мах с одним силовым потоком звенья или типовые механизмы образуют ки­нематические цепи с последовательным соединением, кинематические цепи в многопоточных механизмах имеют параллельное или последовательно-па­раллельное соединение элементов. Рассмотрим силовой расчет сложных зуб­чатых механизмов на простейших примерах: двухступенчатого цилиндричес­кого редуктора и трех поточного однорядного планетарного редуктора.

9.1. Силовой расчет двухступенчатого цилиндрического

редуктора.

Двухступенчатый цилиндрический редуктор представляет собой после­довательное соединение двух простейших зубчатых передач. Он состоит из трех подвижных звеньев: входного или быстроходного вала с шестерней первой ступени, промежуточного вала, на котором размещается колесо первой сту­пени и шестерня второй, и выходного или тихоходного вала с колесом второй ступени. Расчетная схема механизма изображена на рис.36 .







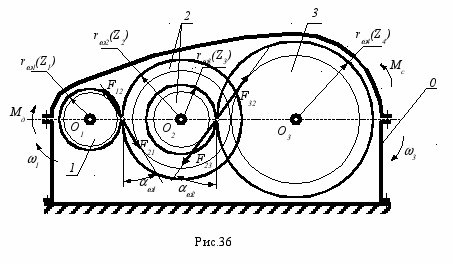
При силовом расчете зубчатых механизмов необходимо знать геометрические параметры зубчатой передачи: радиусы основных окружностей колес и углы зацепле­ния. Кроме того, должны быть известны: массы и моменты инерции подвижных звеньев (валов и зубчатых колес), ускорения центров масс и угловые ускорения звеньев, момент нагрузки на выходном валу или движущий момент на входном валу. Неизвестными в сило­вом расчете являются величины и направления реакций в КП и уравновеши­вающий момент (движущий или сопротивления). Число неизвестных в силовом расчете редуктора при плоском представлении механизма равно числу свя­зей в кинематических парах плюс число основных подвижностей механизма.

n_s = S + W = 6 + 1 = 7.

Для определения семи неизвестных необходимо составить семь урав­нений кинетостатики. Так как для каждого рассматриваемого элемента можно составить только три независимых уравнения, то необходимо расс­мотреть равновесие трех элементов нашей системы. Перед составлением уравнений равновесия необходимо определить силы веса и главные векто­ры и главные моменты сил инерции. Так как в зубчатых колесах центр масс обычно расположен на оси вращения колеса, то главные вектора сил инерции равны нулю. Поэтому необходимо определить только главные мо­менты сил инерции. Последовательно рассматриваем следующие элементы системы (считаем, что задан момент сопротивления на выходном валу):

• выходной вал с зубчатым колесом второй ступени
  

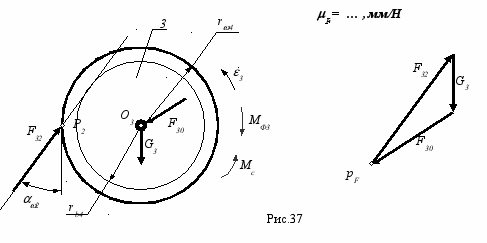
Составляется уравнение моментов относительно центра колеса и находится величина реакции в зацеплении второй ступени (направление реакции известно - по нормали к контактирующим профилям);

 M₀₃⁽³⁾=0  F₂₃ = ( M_c - M_Ф3 )/ r_b4

Из решения векторного уравнения сил для выходного вала определяется величина и направление реакции в кинематической паре, соединяющей вал с корпусом

_{__ __ __ __}

 F⁽³⁾=0  G₃ + F₃₂ + F₃₀= 0 .

^??

Примечание: Необходимо отметить, что в реальных конструкциях редукто­ров вращательная пара опоры вала соответствует двум подшипникам. Для определения нагрузки на каждый из подшипников необходимо рассмотреть редуктор как пространственный механизм.

• промежуточный вал
  

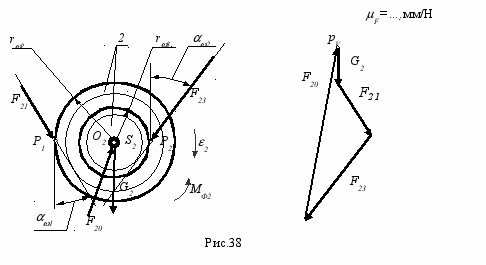
По уравнению моментов относительно оси вала опре­деляем величину реакции в зацеплении колес первой ступени F₂₁ (направление реакции известно - по нормали к контактирующим профилям)

 M₀₂⁽²⁾=0  F₂₁ = ( F₂₃  r_w3 - M_Ф3 )/ r_b2..

Из векторного уравнения сил для промежуточного вала опре­деляем величину и направление реакции F₂₀ в кинематической паре, соединяю­щей промежуточный вал с корпусом

_{__ __ __ __ __}

 F⁽²⁾=0  G₂ + F₂₃ + F₂₁ + F₂₀= 0.

^??

выходной вал с шестерней первой ступени









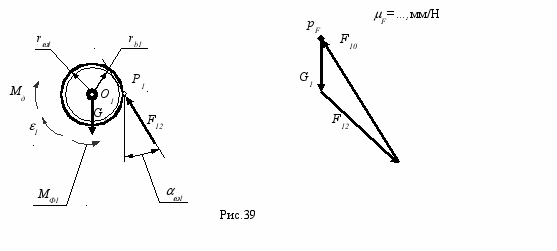
Уравнение моментов относительно оси вала дает возможность опре­делить величину движущего момента на входном валу


 M₀₁⁽¹⁾=0  М_д = M_Ф1 + F₁₂  r_b1 .

Из векторного уравнение сил для входного вала определяем величину и направление реакции в кинематической паре, соединяющей вал с корпусом

_{__ __ __ __}

 F⁽¹⁾=0  G₁ + F₁₂ + F₁₀= 0 .

^??

В общем случае зубчатые колеса в цилиндрической передаче могут быть выполнены косозубыми (с винтовой линией зуба). Для таких механиз­мов силовой расчет нужно проводить, рассматривая механизм как пространственный. На практике часто используют комбинированный метод при котором реакции в зацеплении раскладываются по взаимно перпендикулярным направлениям на три составляющих: тангенциальную или окружную, радиальную и осевую. Тангенциальная составляющая равна суммарному мо­менту, действующему на колесо, деленному на радиус начальной окружности и направлена перпендикулярно линии центров. Радиальная равна произве­дению тангенциальной составляющей на тангенс угла зацепления и направ­лена по линии центров. Осевая составляющая равна тангенциальной сос­тавляющей деленной на тангенс угла наклона линии зуба и направлена па­раллельно осям колес. Геометрическая сумма радиальной и тангенциальной составляющих определяет проекцию реакции в зацепления на торцевую или расчетную плоскость зубчатой передачи. Для первого колеса рассматриваемого редуктора составляющие можно записать так:

окружная или тангенциальная F ^t₁₂ = F₁₂  cos _w1 ,

радиальная F ^r₁₂ = F₁₂  sin _w1 = F ^t₁₂  tg _w1 ,

осевая F ^z₁₂ = F ^t₁₂  tg  , где  - угол наклона линии зуба.

Анализ составляющих широко ис­пользуется при расчете зубчатых колес и подшипников редукторов. На принципе разложения реакций на составляющие основаны существующие стандартные методы прочностных расчетов.

9.2. Силовой расчет однорядного планетарного редуктора.

Рассмотрим статический силовой расчет однорядного планетарного механизма с числом сателлитов равным трем (см. рис. 40). В этом механизме установленное на входном валу солнечное зубчатое колесо одновременно зацепляется с тремя сателлитами, каждый из которых образует с колесом с внутренними зубьями (или эпициклом) внут­реннее зацепление. Энергетический поток, поступающий на входной вал, разделяется на три части (по числу сателлитов), а затем суммируется на валу водила. В идеальном механизме разделение потока должно происхо­дить равномерно. В реальных механизмах из-за погрешностей изготовления и сборки распределение нагрузки между сателлитами будет неравномерным. В расчетной практике величиной неравномерности распределения нагрузки задаются, вводя в расчет коэффициент неравномерности k = 1 ... 1,2. В этом примере будем считать заданным движущий момент на первом звене. Число неизвестных в силовом расчете опре­делится суммой числа связей в кинематических парах и числа основных подвижностей механизма.

n_S = S + W = 16 + 1 = 17.













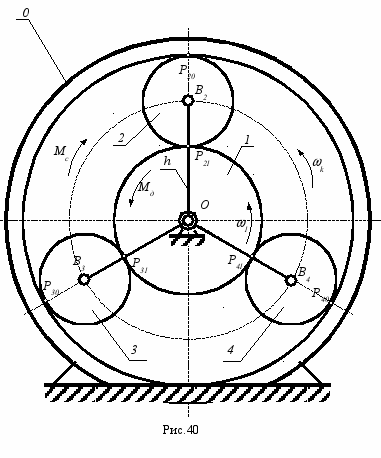
Для определения семнадцати неизвестных необходимо составить сем­надцать уравнений. Из них пятнадцать будут уравнениями статики плюс два дополнительных уравнения, учитывающих неравномерность распределения нагрузки между сателлитами. Так как для каждого рассматриваемого элемента системы можно составить только три независимых уравнения, то необ­ходимо рассмотреть равновесие пяти элементов нашей системы: входного вала с солнечным колесом, трех сателлитов и водила.

1. Солнечное колесо или входное звено 1 ( рис. 41а )
   

Из уравнения моментов относительно точки 0₁, которое решешается совместно с уравнениями неравномерности распределения нагрузки между сателлитами, определяются реакции в зонах зацепления


 M₀₁⁽¹⁾=0  М_д = ( F₁₂ + F₁₃ + F₁₄ )  r_b1 ,

F₁₃ = F₁₂  k₂₃ , F₁₄ = F₁₂  k₂₄

Из векторного уравнение сил определяется по величине и направлению реакция в опоре 0<sub>1

_ _ _ _ _</sub>

 F⁽¹⁾=0  F₁₂ + F₁₄ + F₁₃ + F₁₀= 0 .

^??

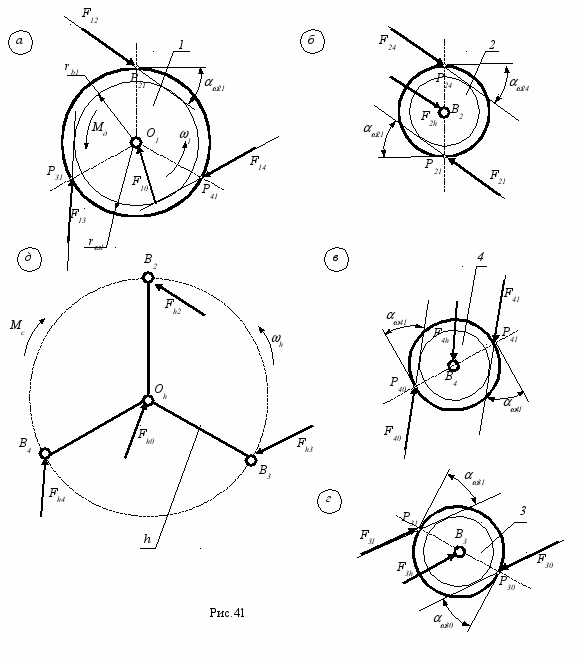
2. Сателлиты (звенья 2,3 и 4 - рис. 41б,в и г)
   

Реакции в зонах зацепления определяются из уравнения моментов относительно точек В_i

 M_Bi⁽ⁱ⁾=0  F_i0  r_bi = - F_i1  r_bi , F_i0 = - F_i1 .

Реакции в опорах В_i по величине и направлению находятся из векторных уравнений сил

_{_ _ _ _}

 F⁽ⁱ⁾=0  F_i1 + F_i4 + F_ih= 0 .

^??

3. Водило ( входное звено 1 - рис. 41д )
   

Из уравнения моментов относительно точки 0_h определяется момент сопротивления на водиле М_с

 M_0h^(h)=0  М_с = ( F_h2 + F_h3 + F_h4 )  a_w20 ,

где a_w20 - межосевое расстояние в зацеплении сателлита и колеса с внутренними зубьями z₀.

Реакция в опоре 0_h по величине и направлению определяется из векторного уравнения

_{_ _ _ _ _}

 F^(h)=0  F_h2 + F_h4 + F_h3 + F_h0= 0 .

^??


10. Применение компьютеров при решении задач

силового расчета механизмов

При решении задач силового расчета механизмов можно либо разрабатывать оригинальную программу для решения конкретной задачи, либо использовать существующие универсальные программы для силового расчета механизма. На кафедре ТММ МГТУ им. Н.Э.Баумана при участии студентов и преподавателей разработано большое количество программ для силового расчета различных механизмов. Рассмотрим программы, предназначенные для решения задач кинематического и силового расчета механизмов при выполнении домашних заданий и курсовых проектов.

10.1. Силовой расчет по программе PR 1.

Программа предназначена для кинетостатического силового расчета четырехзвенного кривошипно-ползунного механизма . Расчетная схема механизма дана на рис. 42 .

Механизм состоит из кривошипа 1, шатуна 2, ползуна (поршня) 3 и стойки 4. Внешняя сила F₃, приложенная к звену 3, в зависимости от назначения механизма может быть или силой сопротивления, или движущей силой. В поршневых машинах эта сила определяется давлением в цилиндре и вычисляется по индикаторной диаграмме. Центр вращения кривошипа (рис. 42) совпадает с началом системы координат х₀Ау₀; ось х₀ направлена горизонтально, а направление оси у₀ соответствует правой системе координат. Кинематические параметры механизма задаются в системе координат хАу повернутой относительно системы х₀Ау₀ на угол . Внешняя нагрузка задается массивом значений силы F₃, при этом сила считается положительной если она совпадает по направлению с осью х.

Исходные данные для силового расчета: № варианта задания, число позиций в цикле N, угол наклона оси ползуна , длина кривошипа l₁, относительная длина шатуна ₂= l₂/l₁, относительная координата центра масс шатуна _S2= l_BS2/l_BC , относительная внеосность _e= e/l₁, начальная угловая координата ₁, моменты инерции I_1S, I_2S звеньев 1 и 2 относительно их центров масс S₁ и S₂, массы m₁, m₂ и m₃ звеньев 1, 2 и 3, массив значений угловых скоростей ₃ звена 3 за время поворота, массив внешней силы F₃.















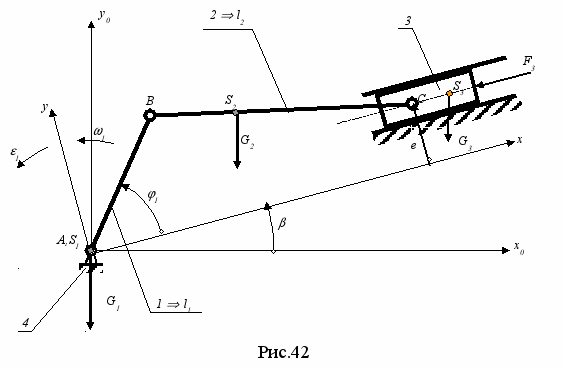
Результаты силового расчета – массивы значений модулей векторов сил в кинематических парах и их угловые координаты в зависимости от угла поворота ₁: F₄₁ и ₄₁ - в шарнире A, F₃₂ и ₃₂ - в шарнире C, F₁₂ и ₁₂ - в шарнире B, F₃₄ - в поступательной паре D . Более подробно программа PR1 описана в учебном пособии [ 3 ].

10.2. Силовой расчет по программе PR 3050.

Программа предназначена для кинетостатического силового расчета четырехзвенного кулисного механизма (механизм гидроподъемника). Расчетная схема механизма дана на рис.43 .

Механизм состоит из гидроцилиндра 1, штока с поршнем 2, поворотной платформы 3 и стойки 4. Сила F₂, создаваемая давлением масла в гидроцилиндре и приложенная к звену 2, вызывает относительное перемещение звеньев 2 и 1 и поворот коромысла 3 с угловой скоростью ₃. Схема (рис.43) дана в правой системе координат хСу; ось Х на- правлена от оси С вращения коромысла 3 к оси поворота цилиндра 1, а направление оси у соответствует вращению против часовой стрелки звена 3, принятого за начальное. Отсчет всех угловых координат ведется от оси Х в направлении против часовой стрелки.












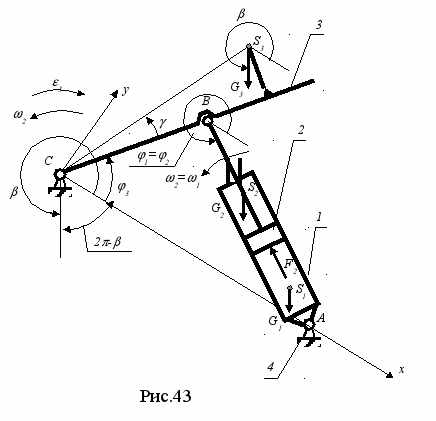
Исходные данные для силового расчета: межосевое расстояние l_CA, длина коромысла l_CB, начальная угловая координата _3н звена 3, угловая координата _3ж звена 3 в конце поворота, угловая координата  центра масс S₃ звена 3, расстояние l_CS3 от оси С до центра массы S₃, расстояние l_BS2 от шарнира В до центра массы S₂, расстояние l_S1A от центра масс S₁ до оси А, угловая координата  сил тяжести G₁, G₂ и G₃, моменты инерции I_1S, I_2S, I_3S звеньев 1, 2 и 3 относительно их центров масс S₁, S₂ и S₃, массы m₁, m₂ и m₃ звеньев 1, 2 и 3, массив значений угловых скоростей ₃ звена 3 за время поворота, массив значений угловых ускорений ₃ звена 3, число