О повышении эффективности работы машин при помощи уточненного динамического расчета кулачково-рычажных механизмов е. В. Булатников, В. А. Перов
| Вид материала | Документы |
- Закономерности проектирования механизмов для передачи и преобразования, 19.17kb.
- Рабочая программа по дисциплине опд. Ф. 04 Теория механизмов и машин для направления, 252.07kb.
- С. В. Фёдоров, Н. А. Середа Обосновывается теоретико-расчётный метод определения, 90.27kb.
- Задачи изучения дисциплины, 26.06kb.
- Программа дисциплины по кафедре Детали машин детали машин и механизмов, 575.22kb.
- Памятка для студентов группы пкм- по изучению дисциплины " Теория механизмов и машин, 72.92kb.
- Задачи кинематического анализа и синтеза механизмов. Передаточные функции и отношения., 55.01kb.
- Является воздействие на потерпевших движущихся, разлетающихся, вращающихся предметов,, 56.73kb.
- Курс 3 (3) Лекции 34 (34) часа Семестр 5 (6) Лаб занятия 17 (17) часов Часов в неделю, 183.64kb.
- Примерная программа дисциплины теория механизмов и машин Рекомендуется Минобразованием, 326.52kb.
УДК 631.311
О ПОВЫШЕНИИ ЭФФЕКТИВНОСТИ РАБОТЫ МАШИН ПРИ ПОМОЩИ
УТОЧНЕННОГО ДИНАМИЧЕСКОГО РАСЧЕТА КУЛАЧКОВО-РЫЧАЖНЫХ
МЕХАНИЗМОВ
Е.В. Булатников, В.А. Перов
ФГОУ ВПО МГУП, г. Москва, Россия
Рычажно-кулачковые механизмы достаточно широко применяются в современных машинах, в том числе и в мелиоративных [1]. В частности, рычажно-кулачковым механизмом можно считать механизм уклона дренажных трубоукладочных машин [2]. Уточненный динамический расчет этих механизмов с учетом упругости элементов и стохастического характера нагрузки приведет к повышению эффективности их работы, а также к повышению эффективности работы всей мелиоративной машины.
В качестве примера уточненного динамического расчета рычажно-кулачкового механизма мелиоративной машины приведем расчет кулачкового механизма с учетом упругости элементов и стохастического характера нагрузки.
Дифференциальное уравнение движения кулачкового механизма с упругим толкателем имеет следующий вид:
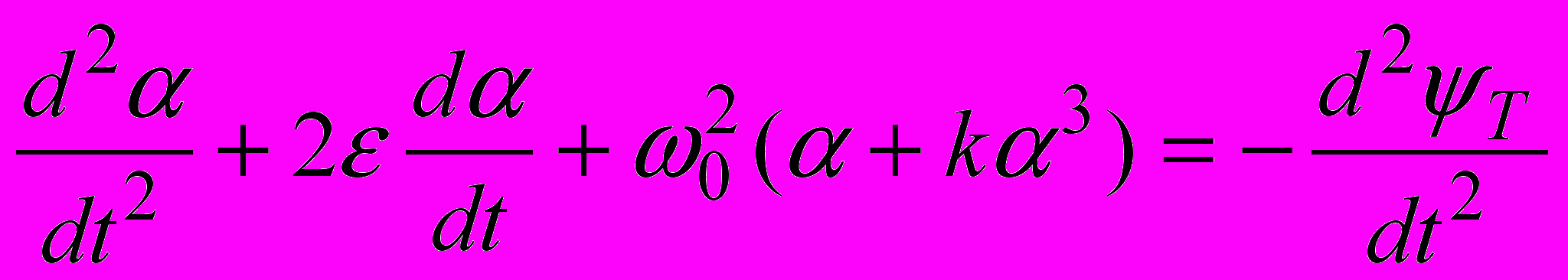. (1)Здесь
, 
, 
, 
, 
, 
,
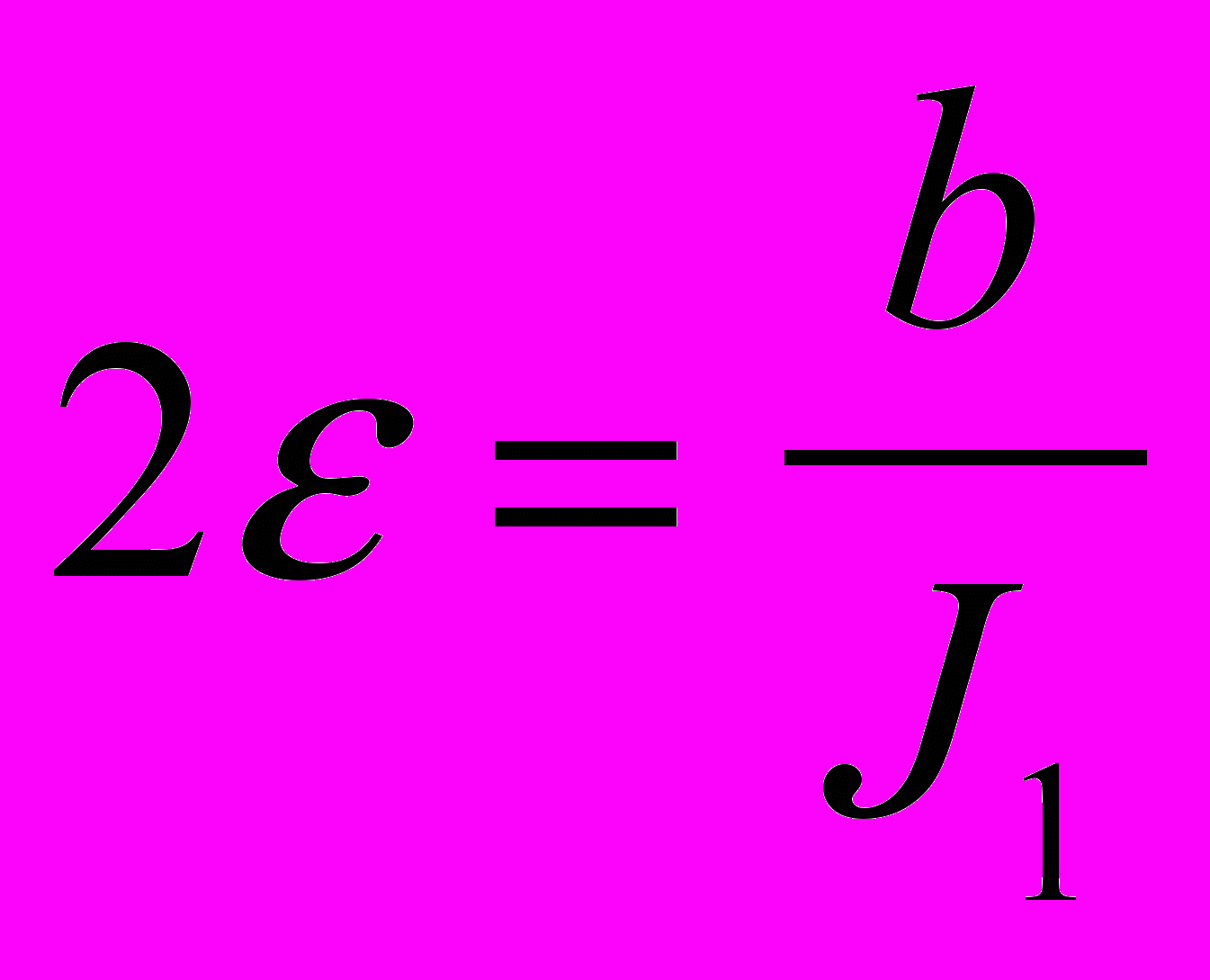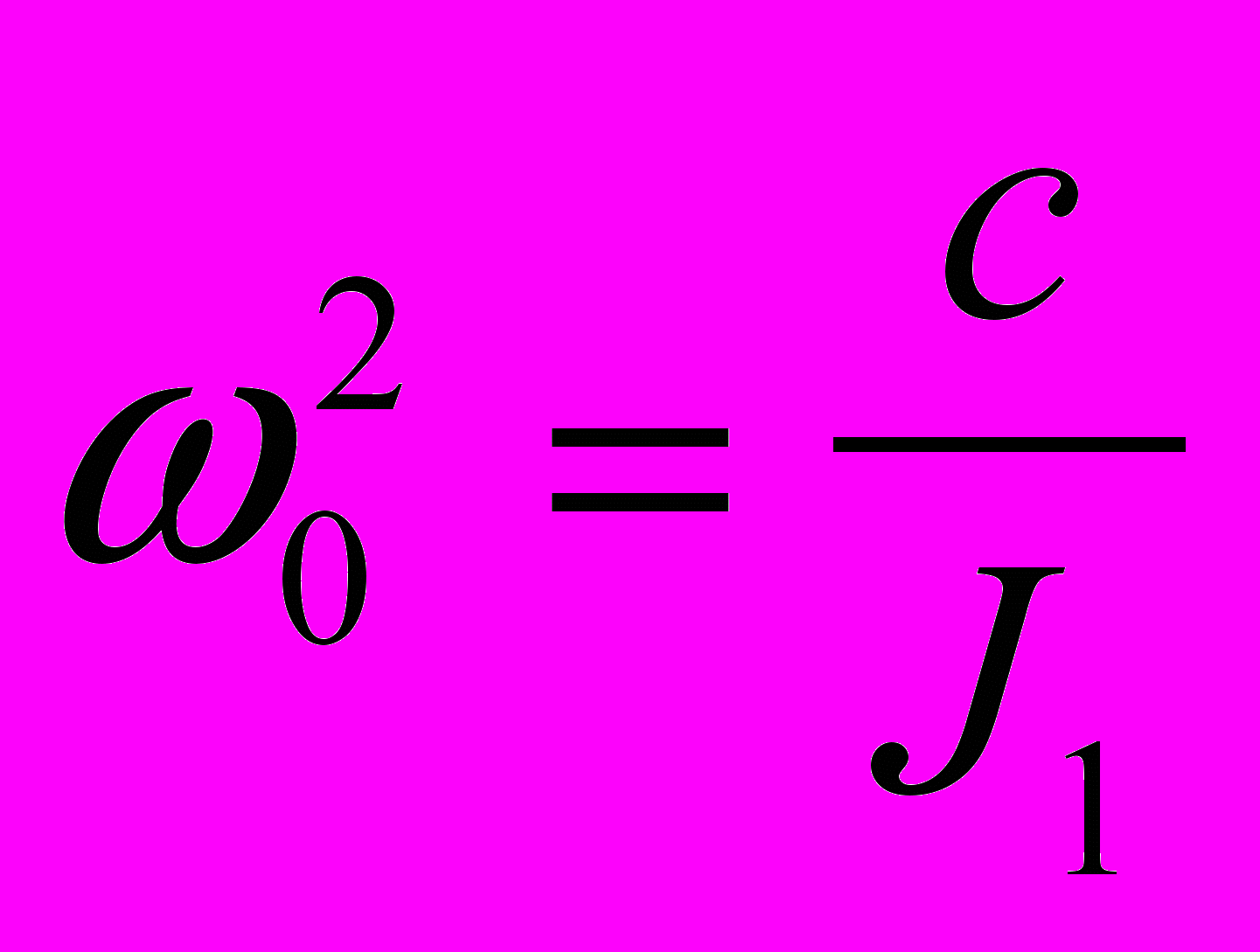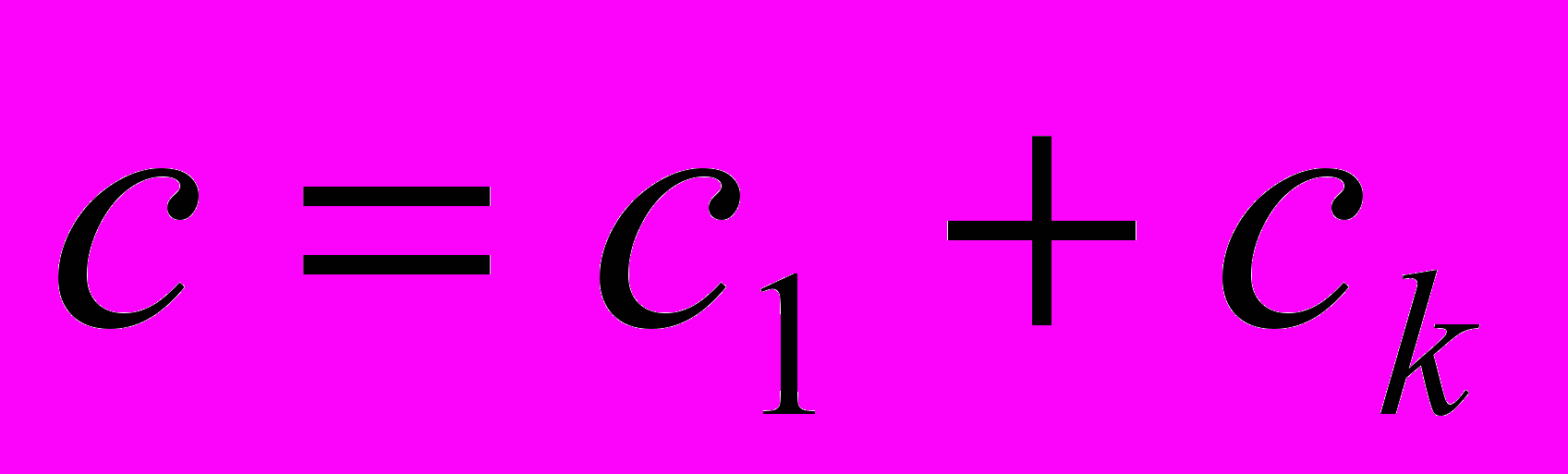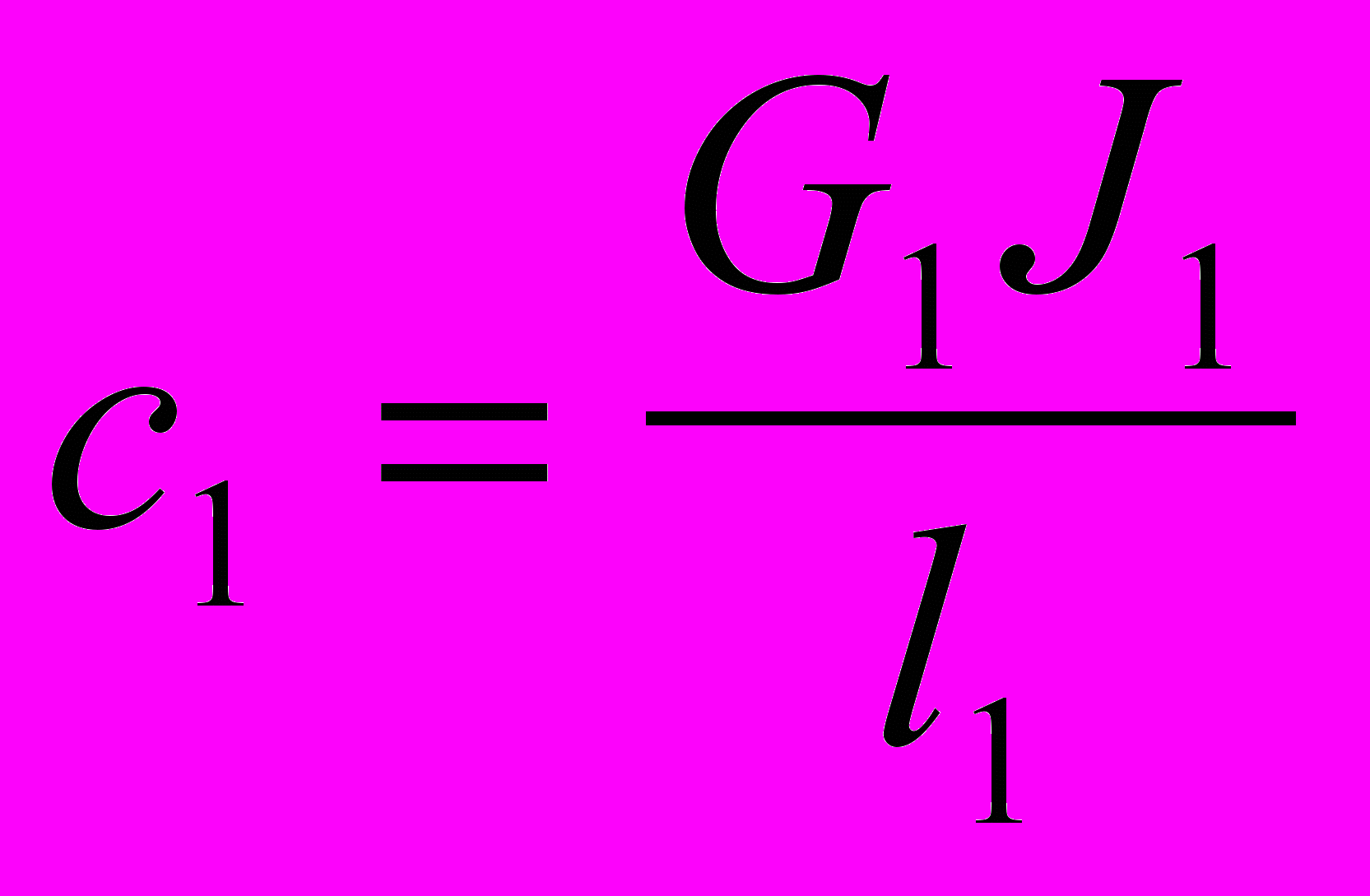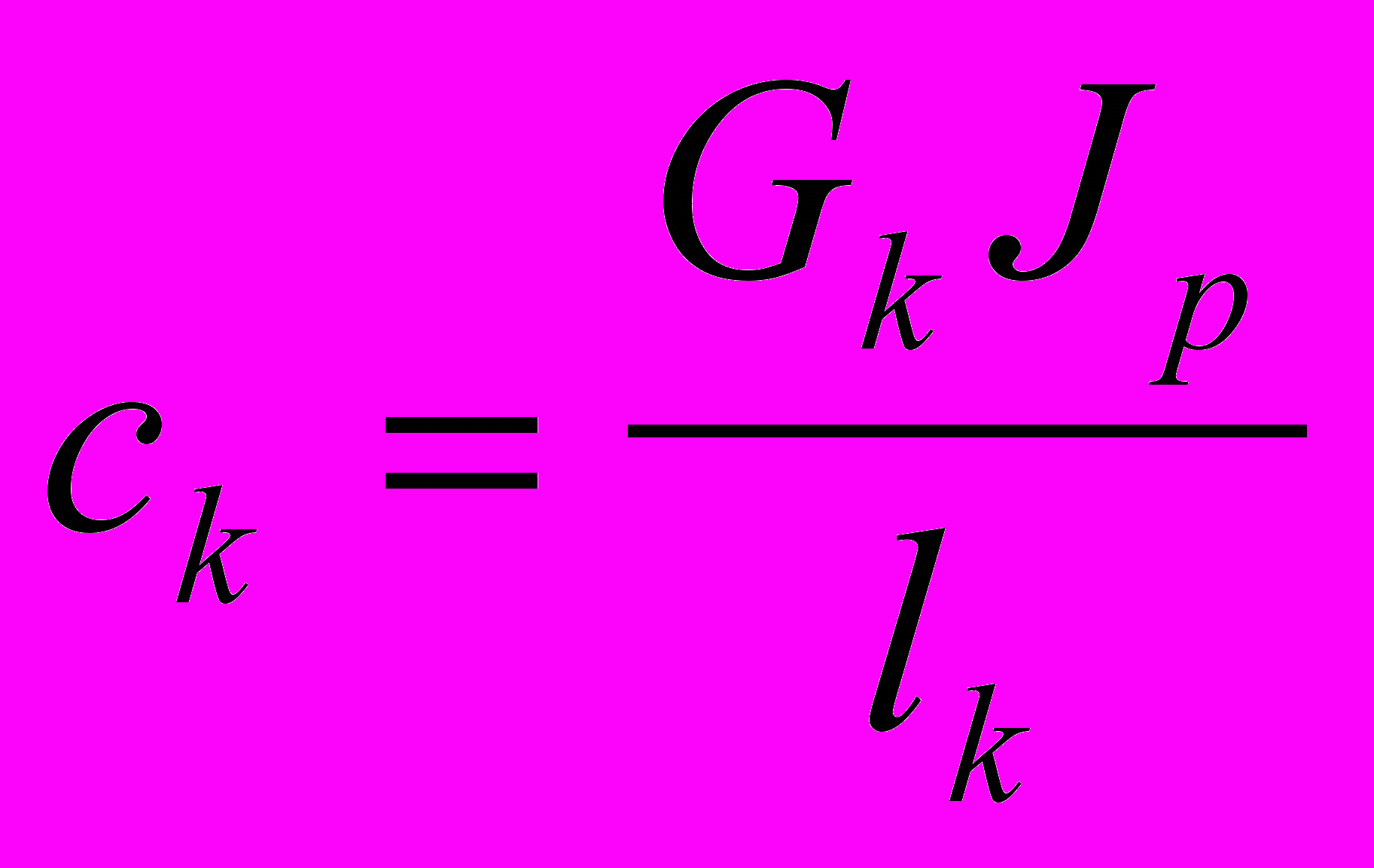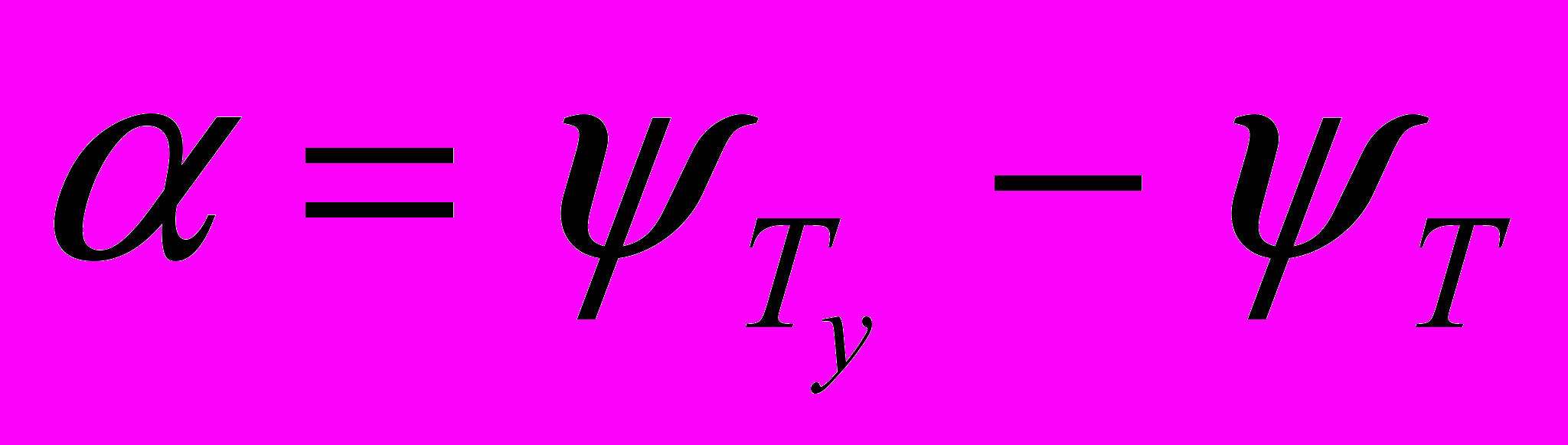- обобщенная координата;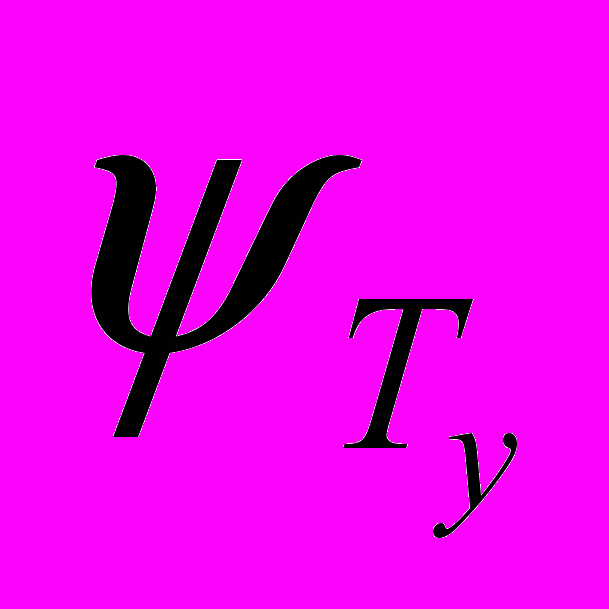 
- угол поворота упругого коромысла (толкателя); 
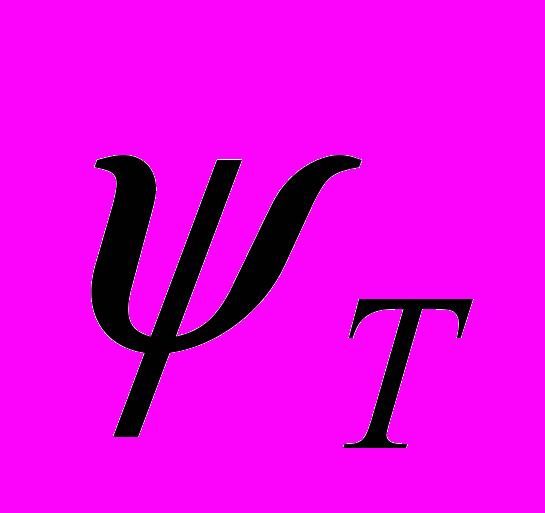- угол поворота жесткого толкателя; b, c – коэффициент сопротивления и коэффициент жесткости толкателя (
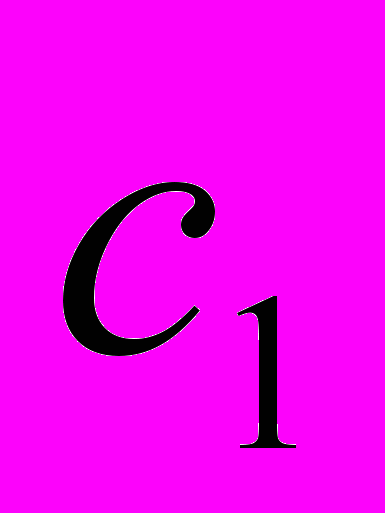) и вала (
), 
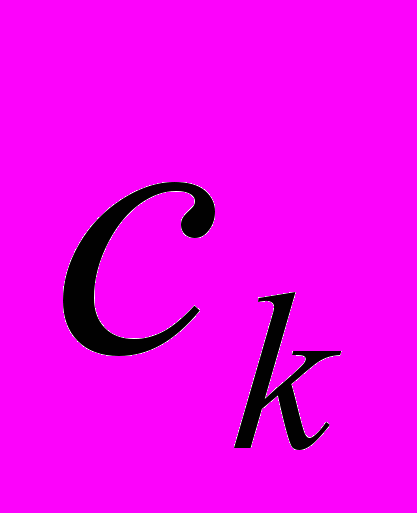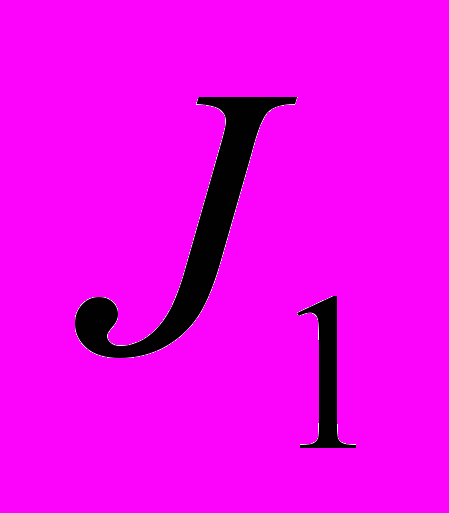- момент инерции толкателя относительно оси вращения 
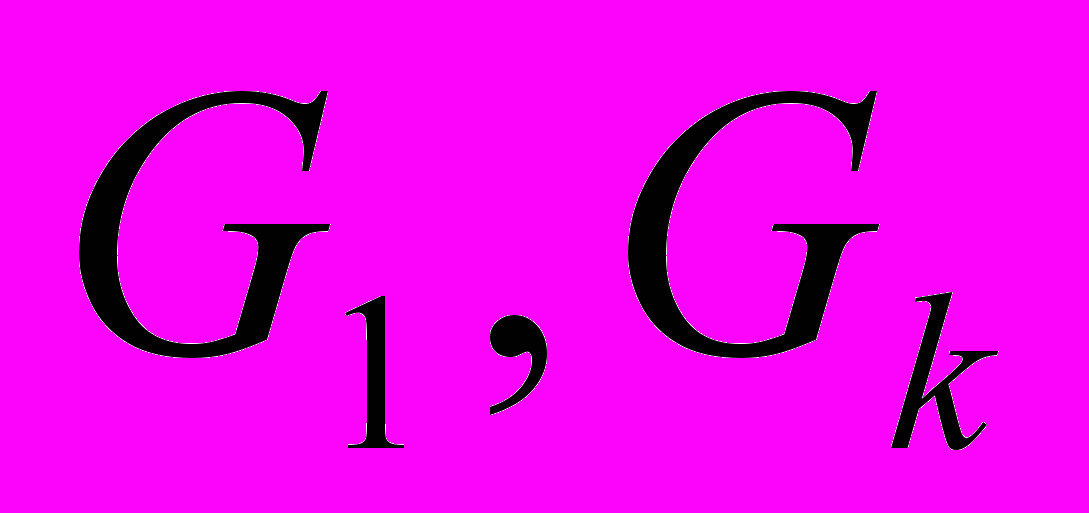- модули сдвига материалов толкателя и кулачкового вала.Если принять, что
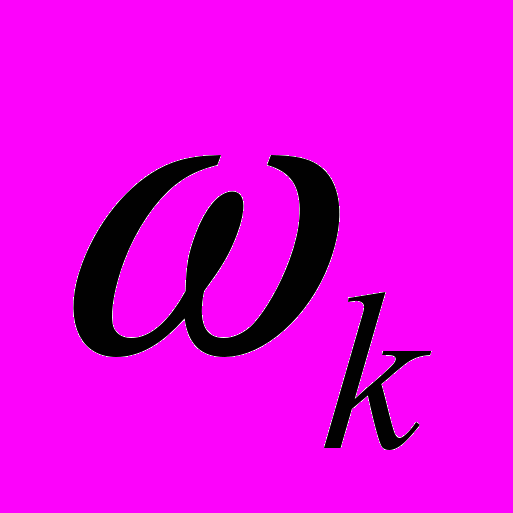- угловая скорость вращения кулачка, то можно от уравнения (1) перейти к следующему уравнению
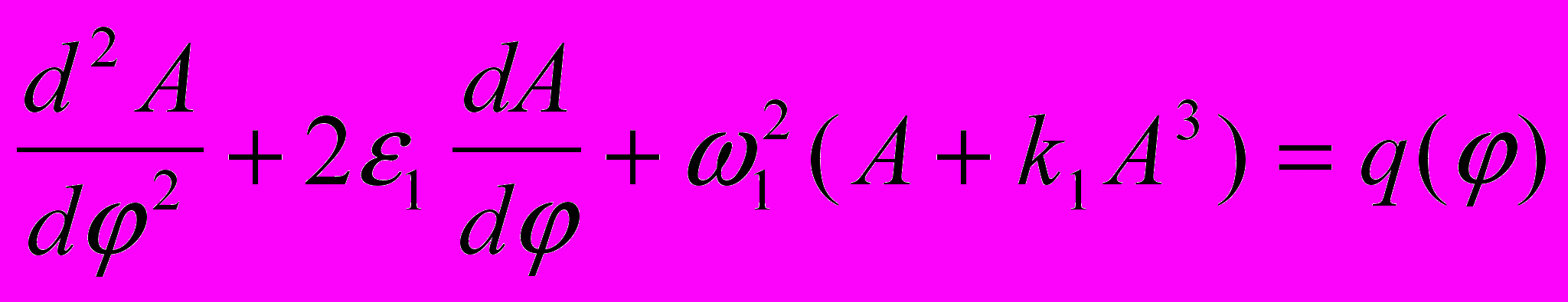, (2)где введены обозначения
, 
, 
, 
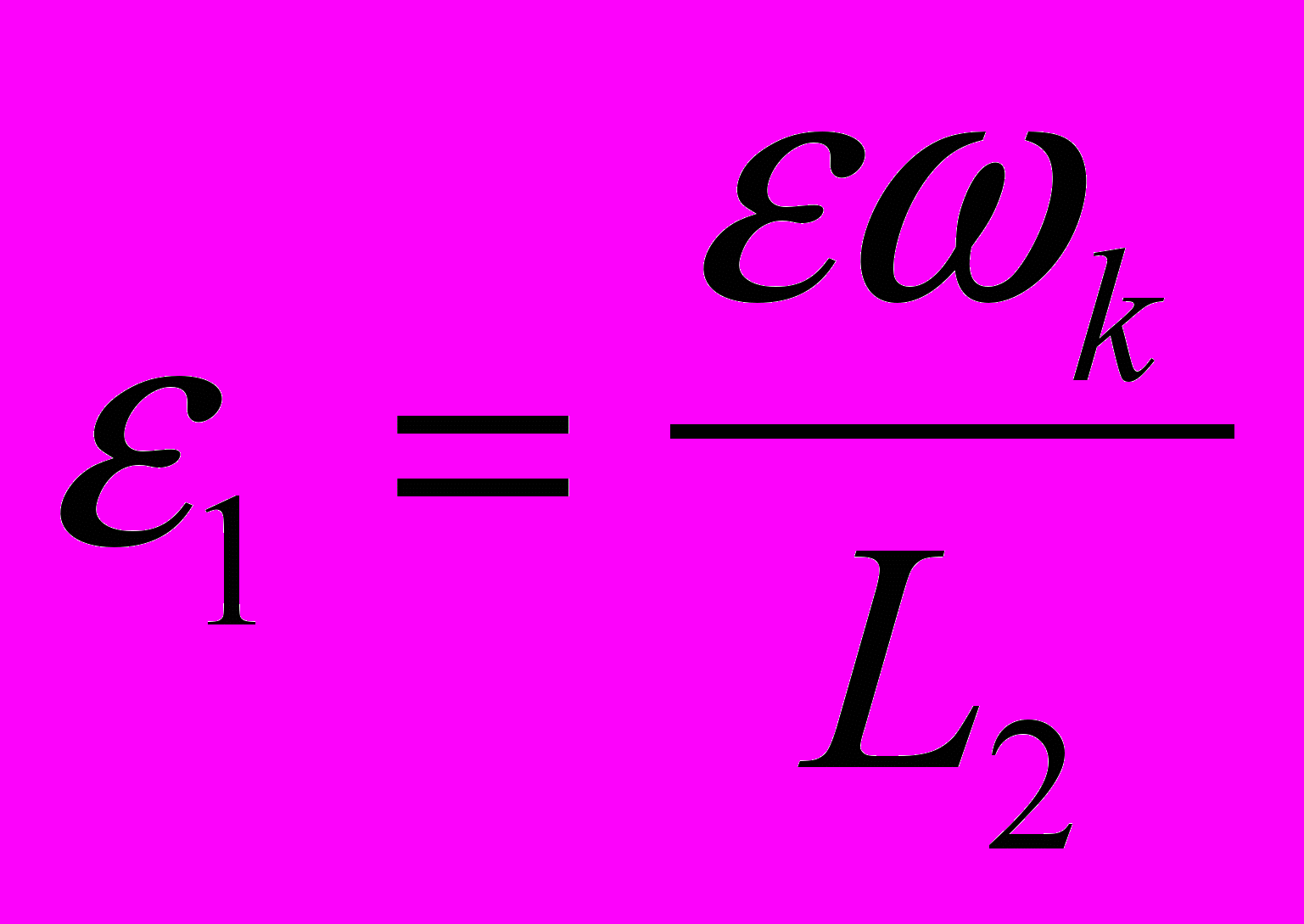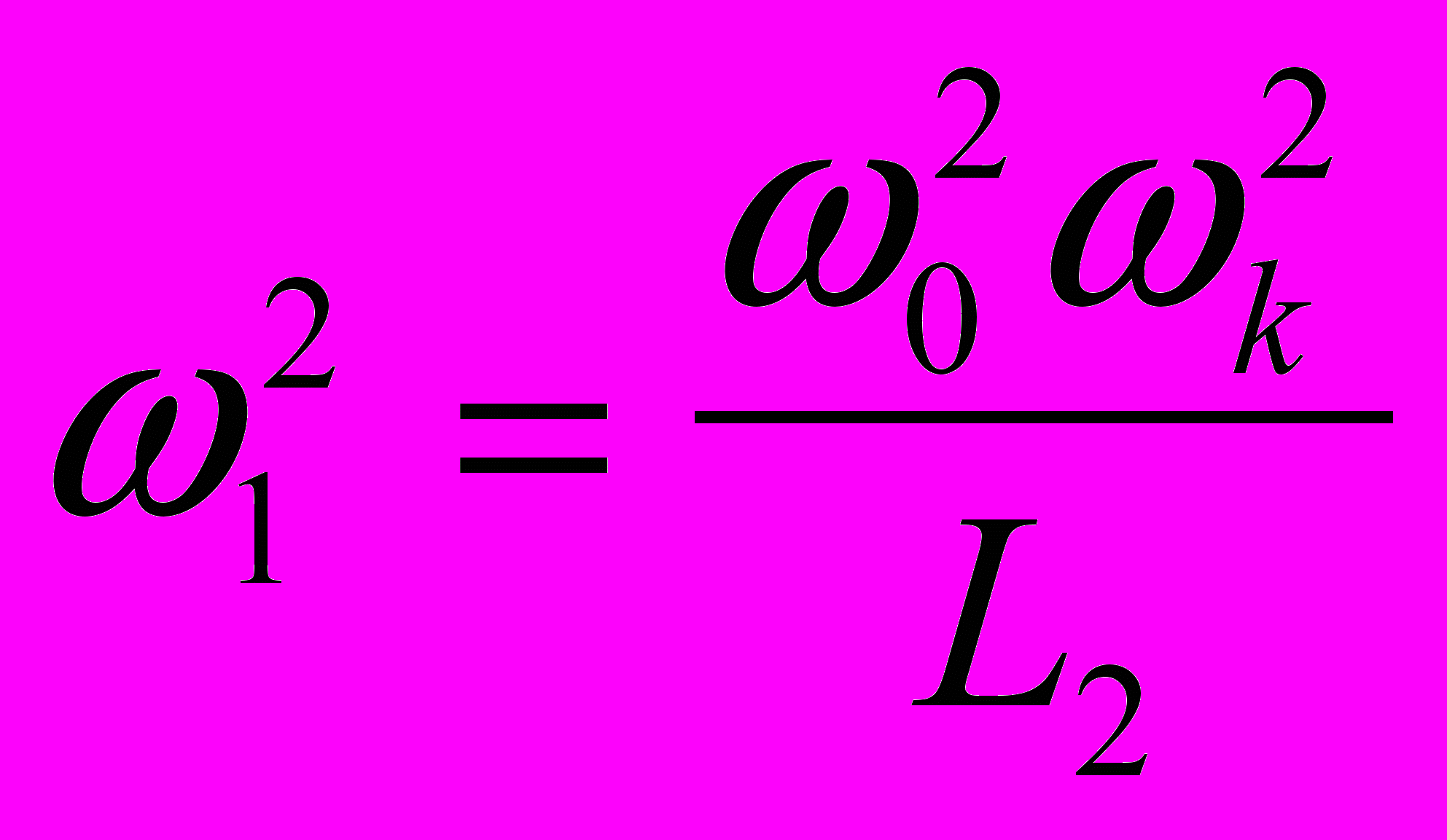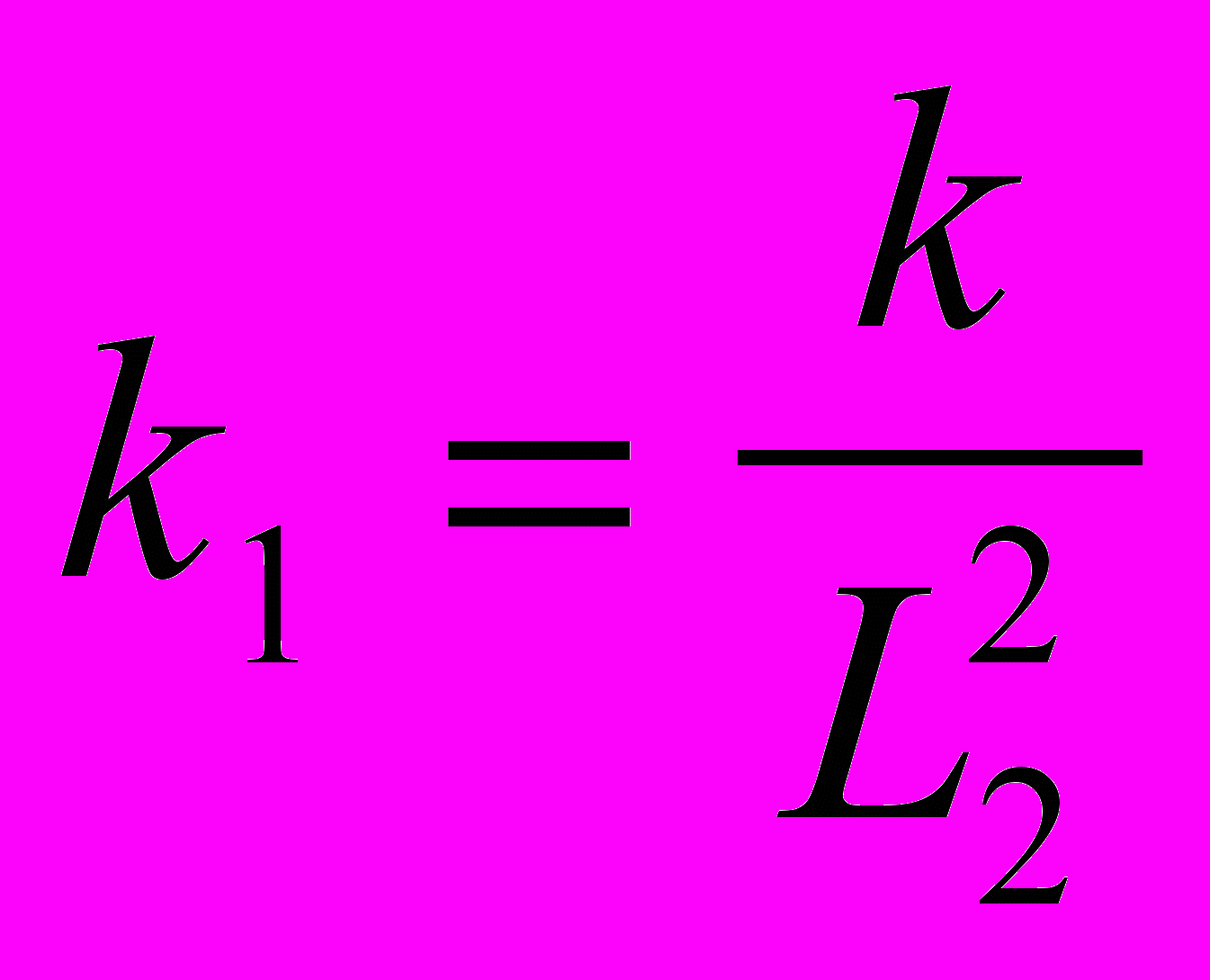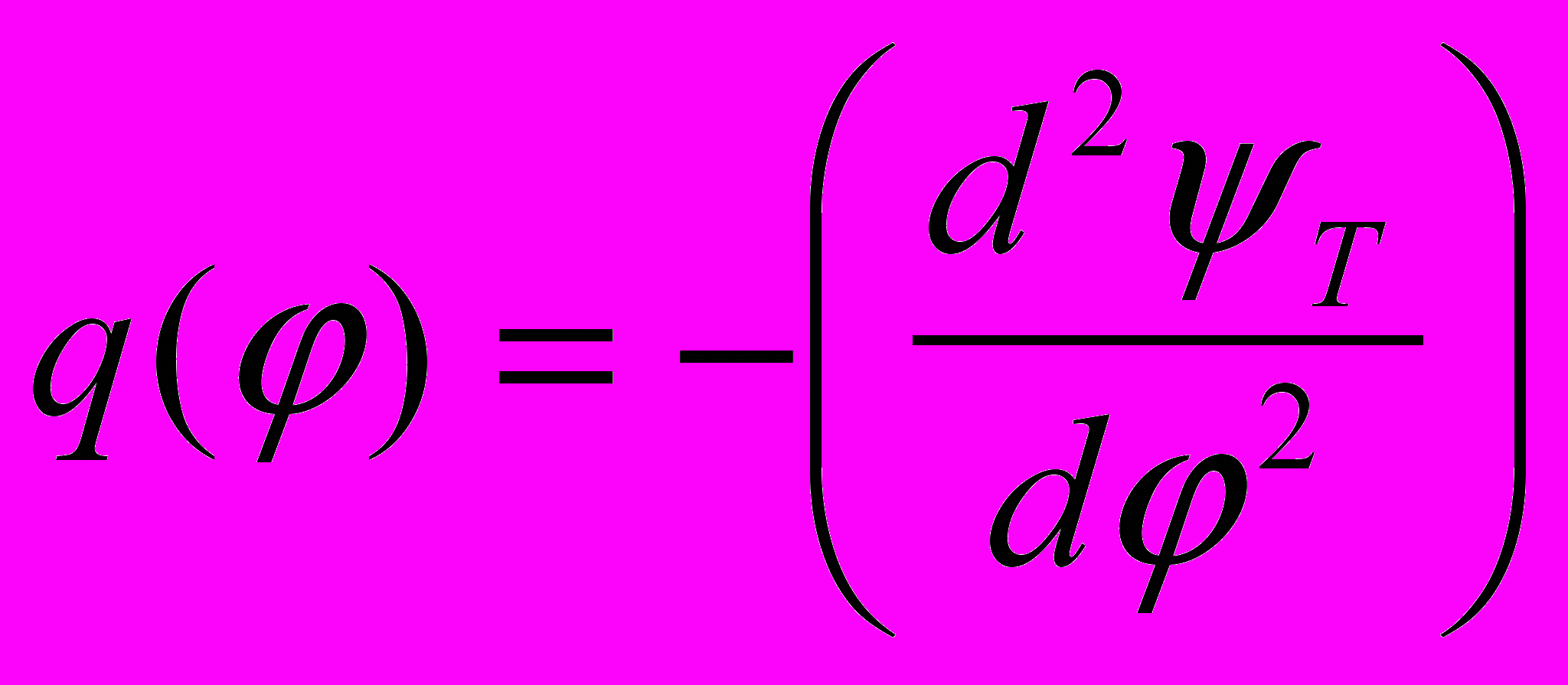. Представим функцию нагрузки
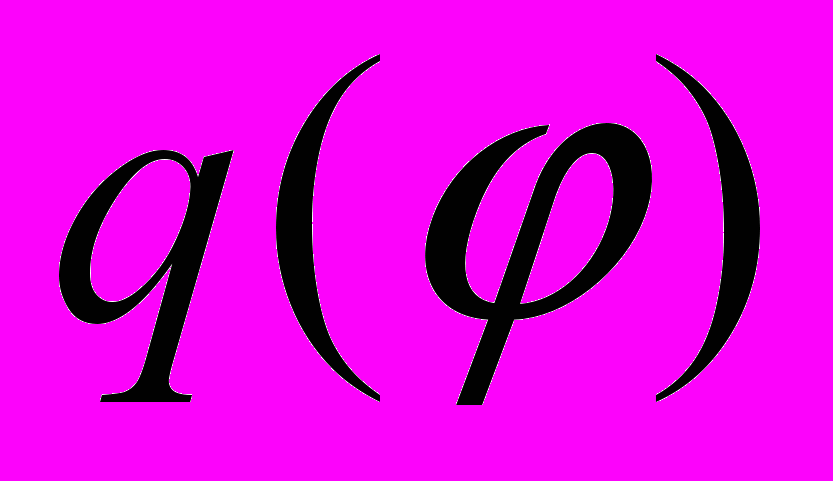в виде
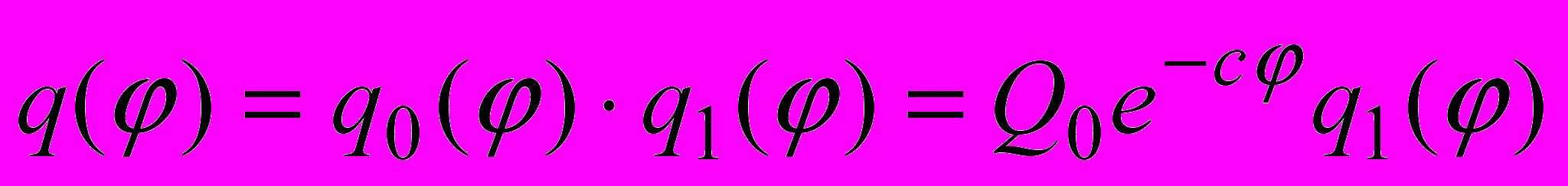. (3)Здесь
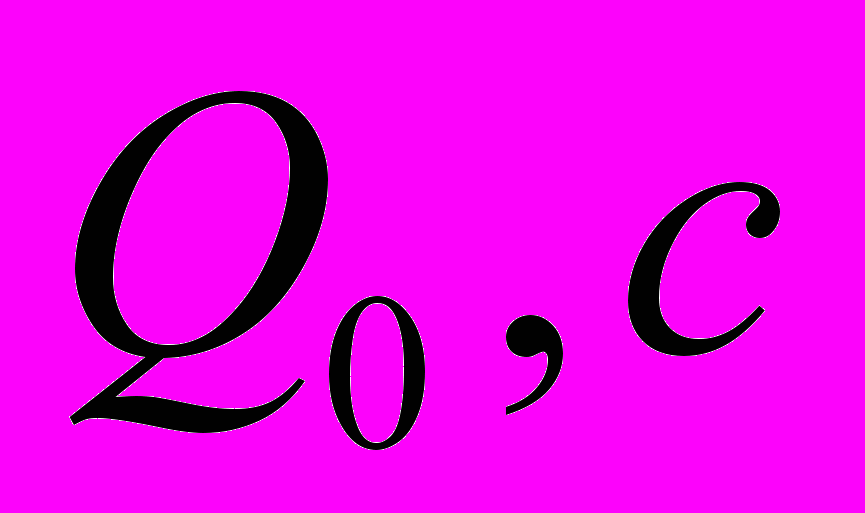- заданные постоянные, которые можно получить из аппроксимации экспериментальных данных 2. Стационарную случайную функцию 
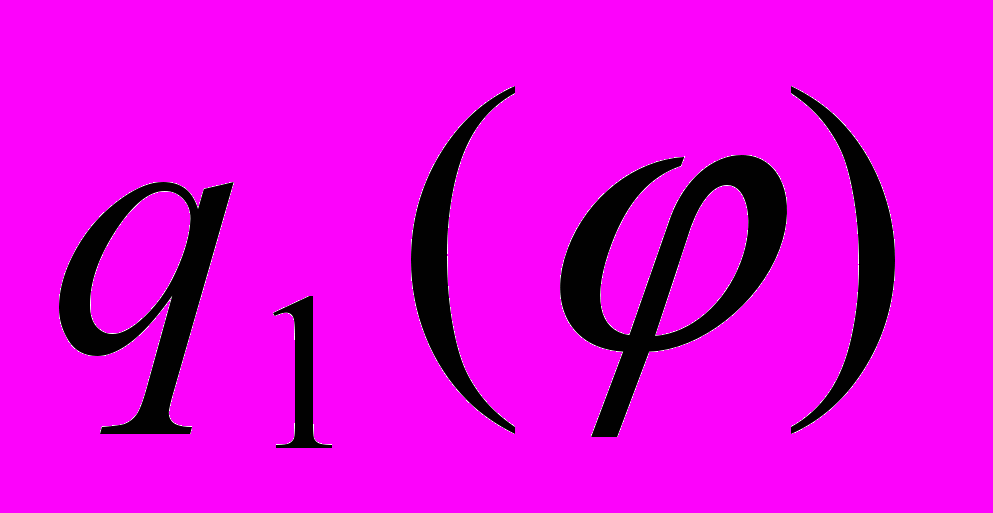берем с известной спектральной плотностью
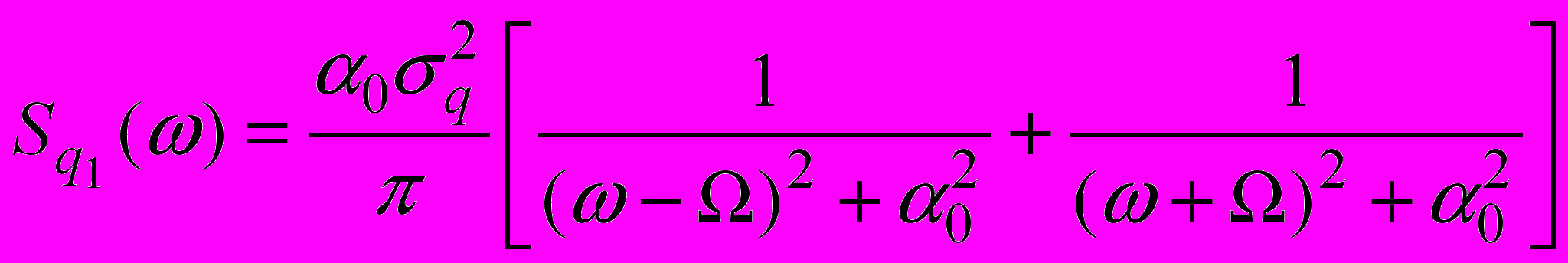, (4)где
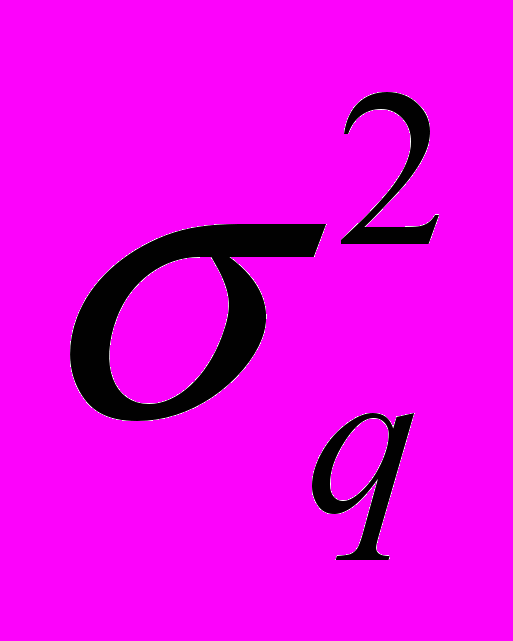- дисперсия; 
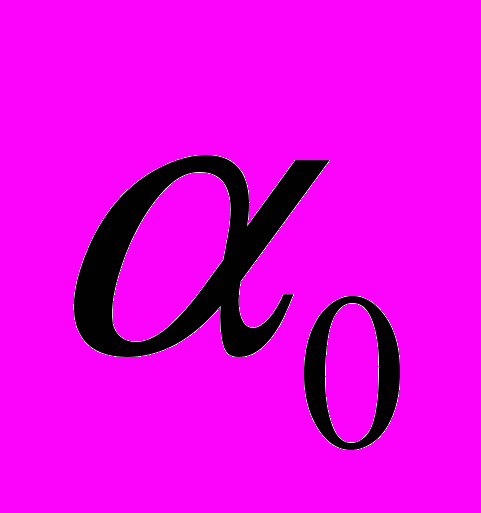- коэффициент корреляции; 
- преобладающая частота воздействия.Для уравнения (2) получаем импульсную переходную функцию системы в виде
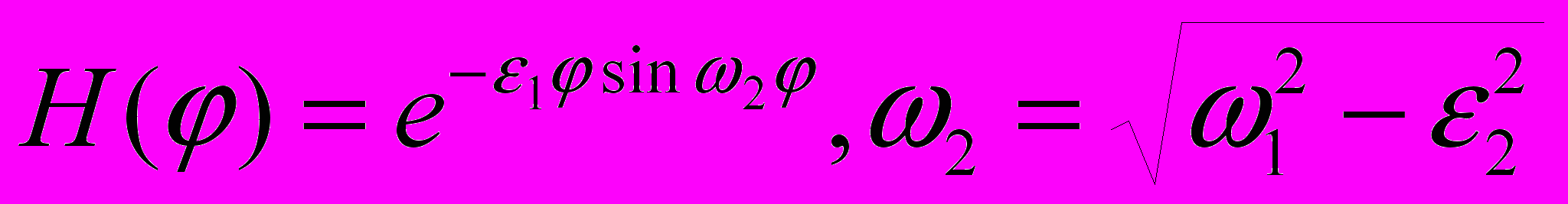. (5)Если воспользоваться методикой определения стохастических характеристик ударных случайных процессов в рассматриваемой системе, то получим при
; 
, 
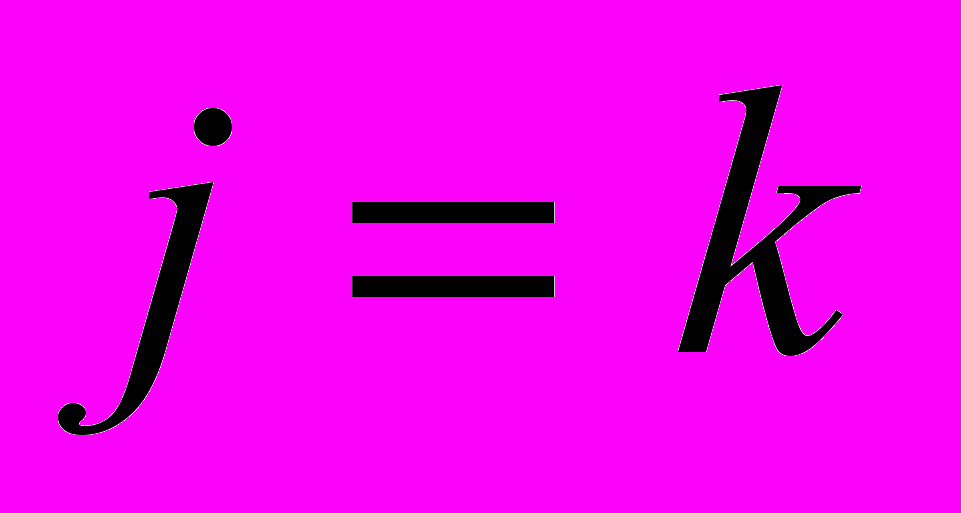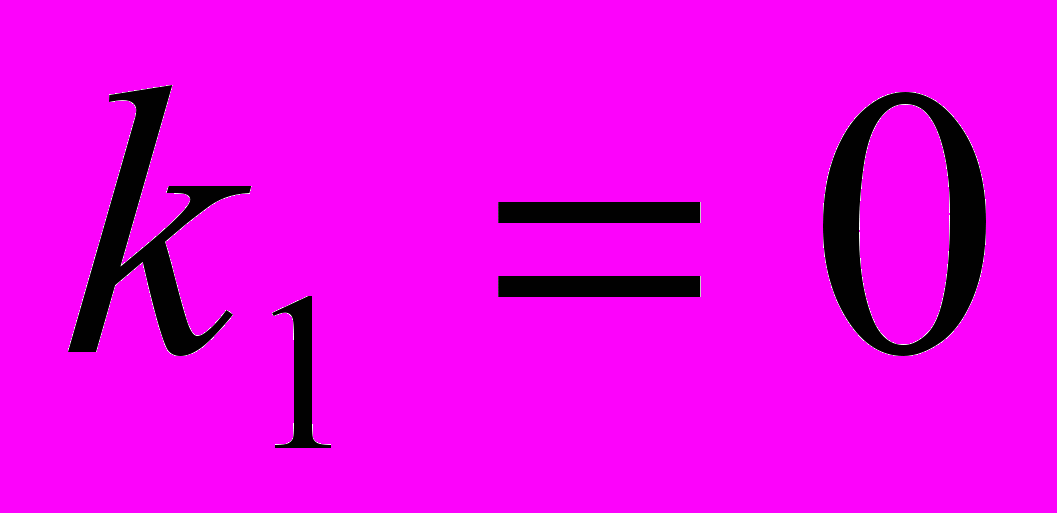
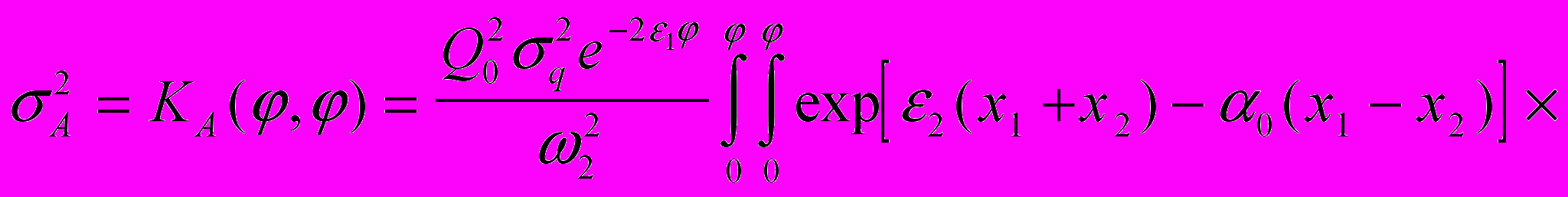
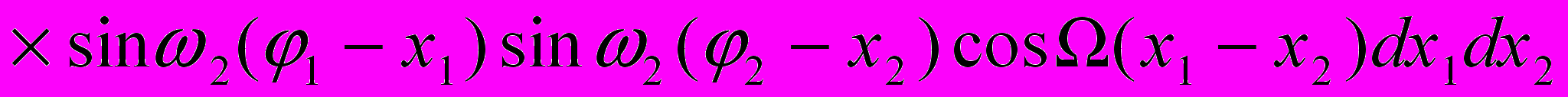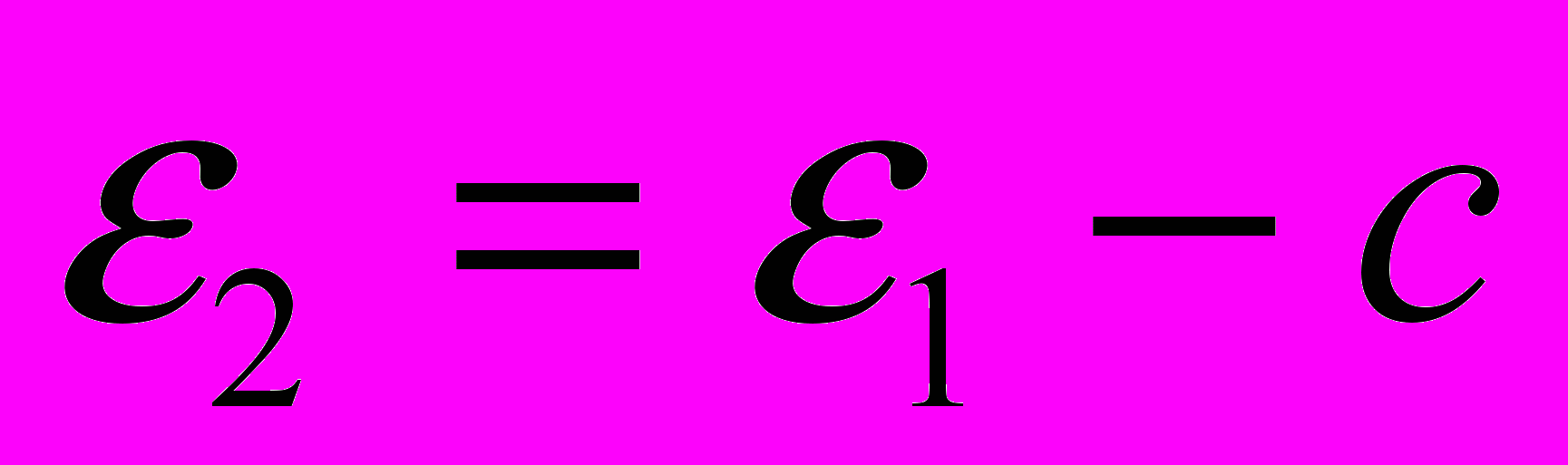. (6)Если для упрощения принять, что
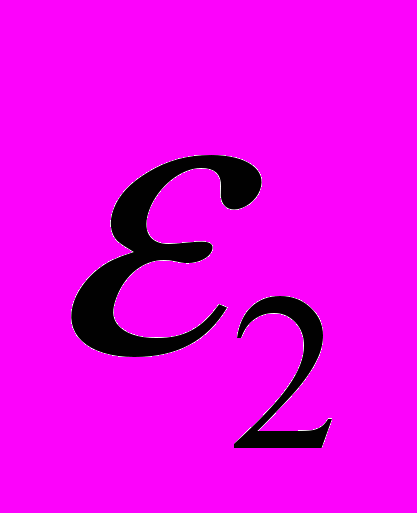
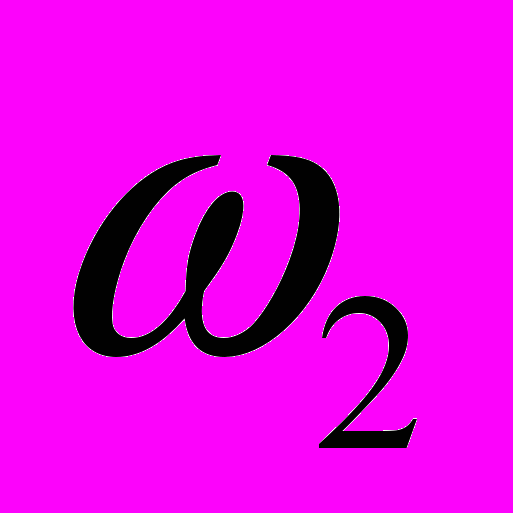, то получаем приближенную формулу для стохастической характеристики виброупругого перемещения А:
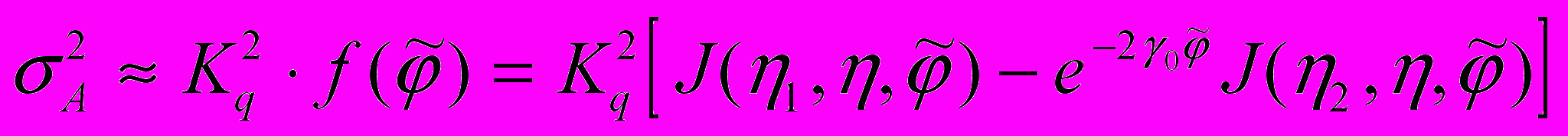(7)Здесь введены обозначения:
, 
, 
, 
, 
.
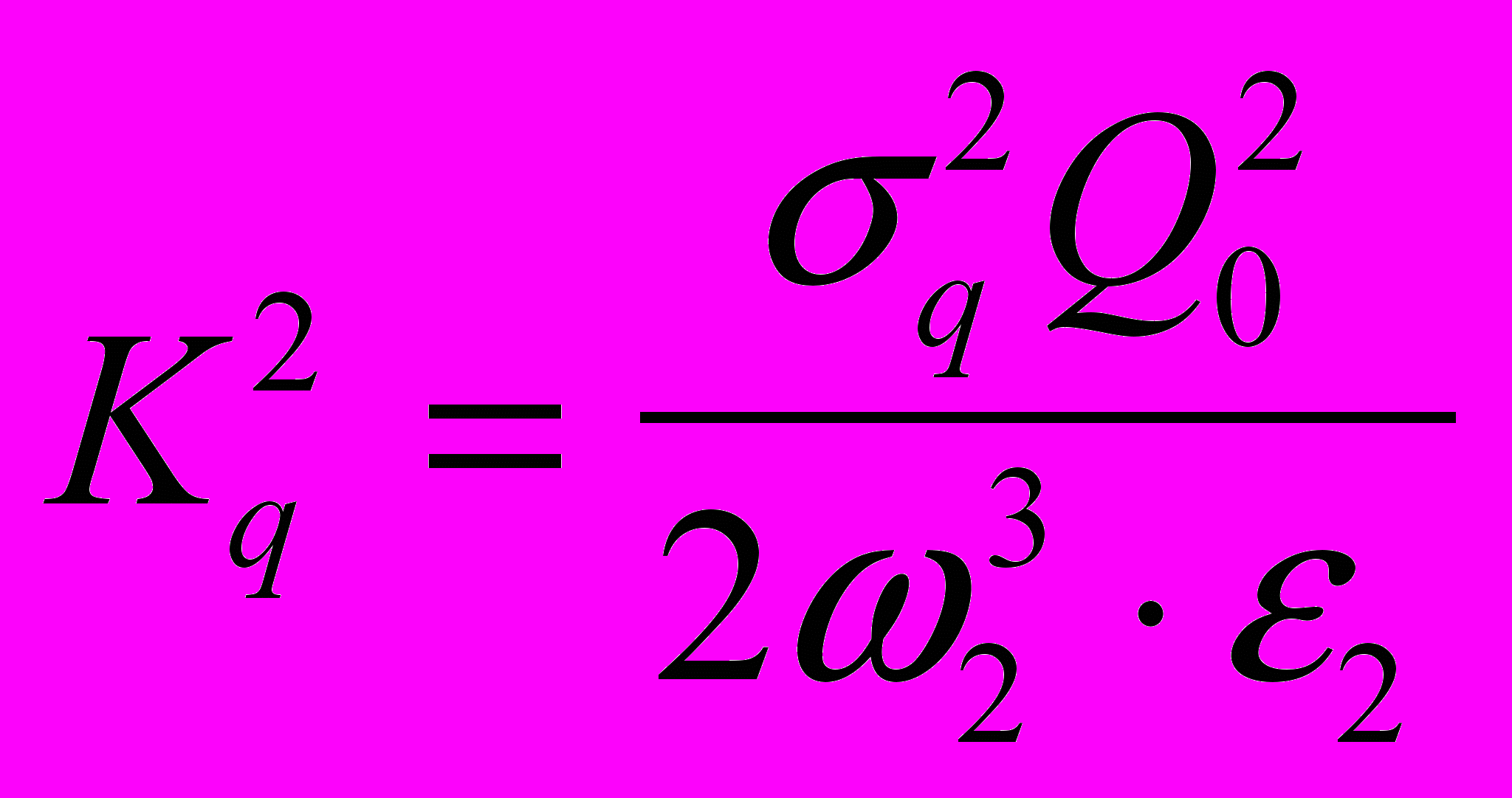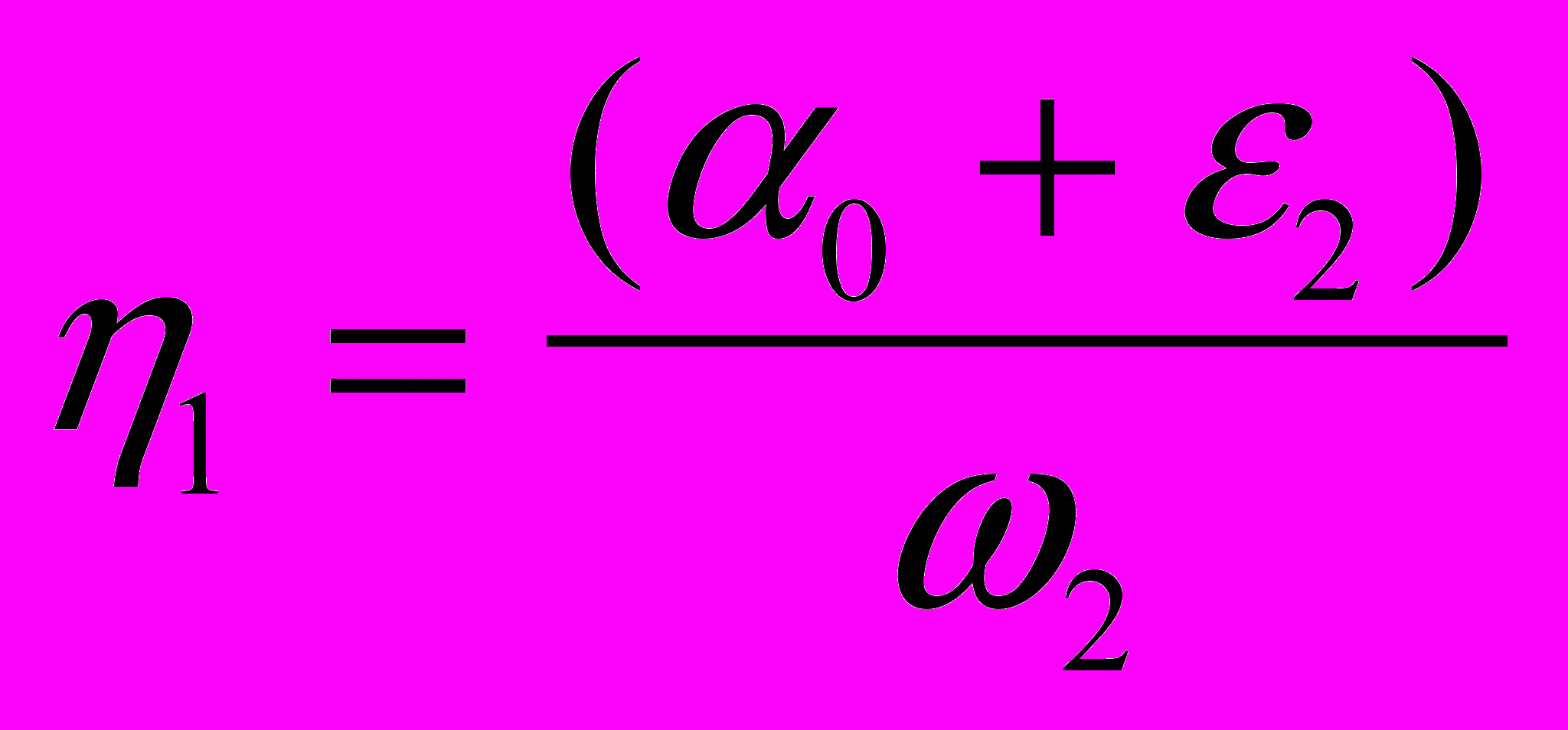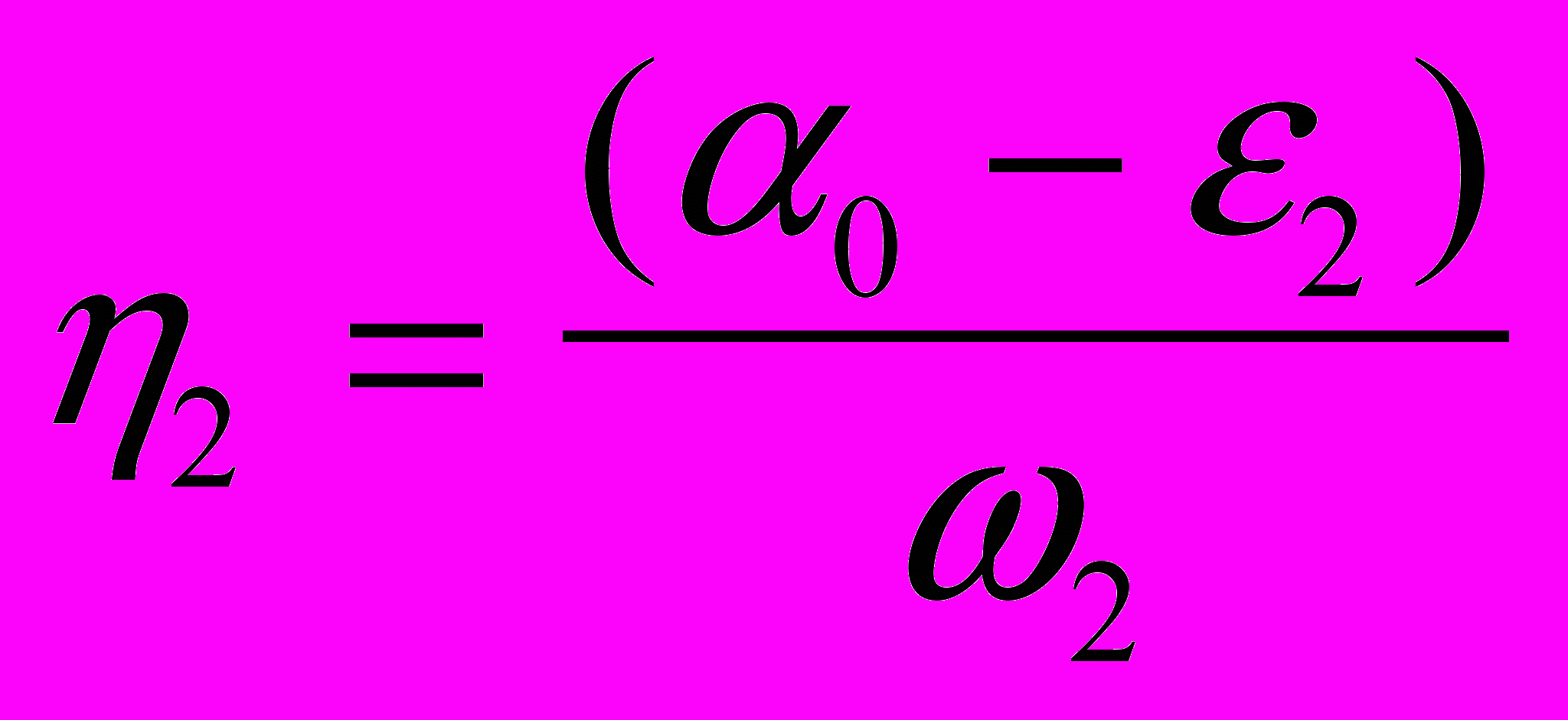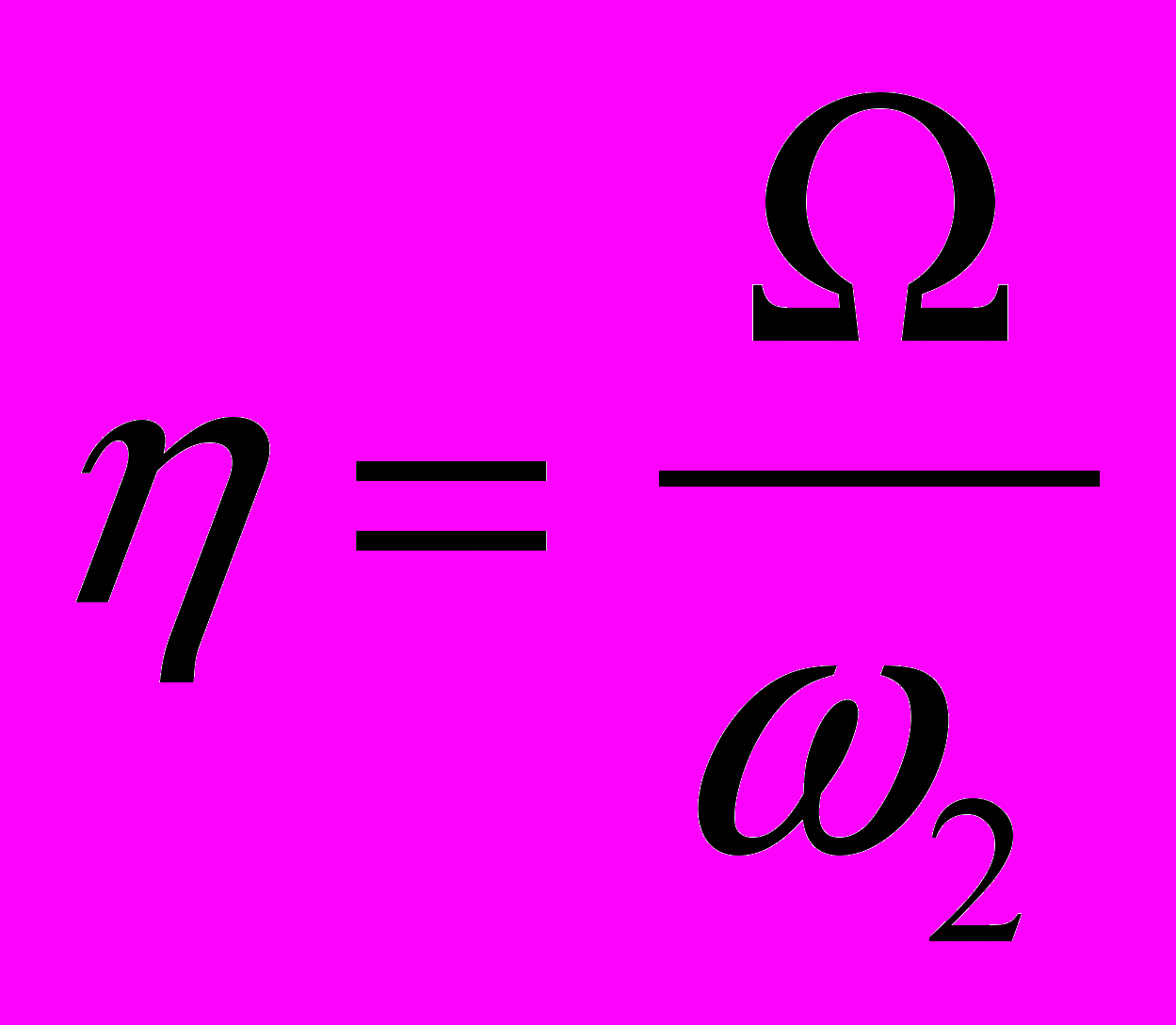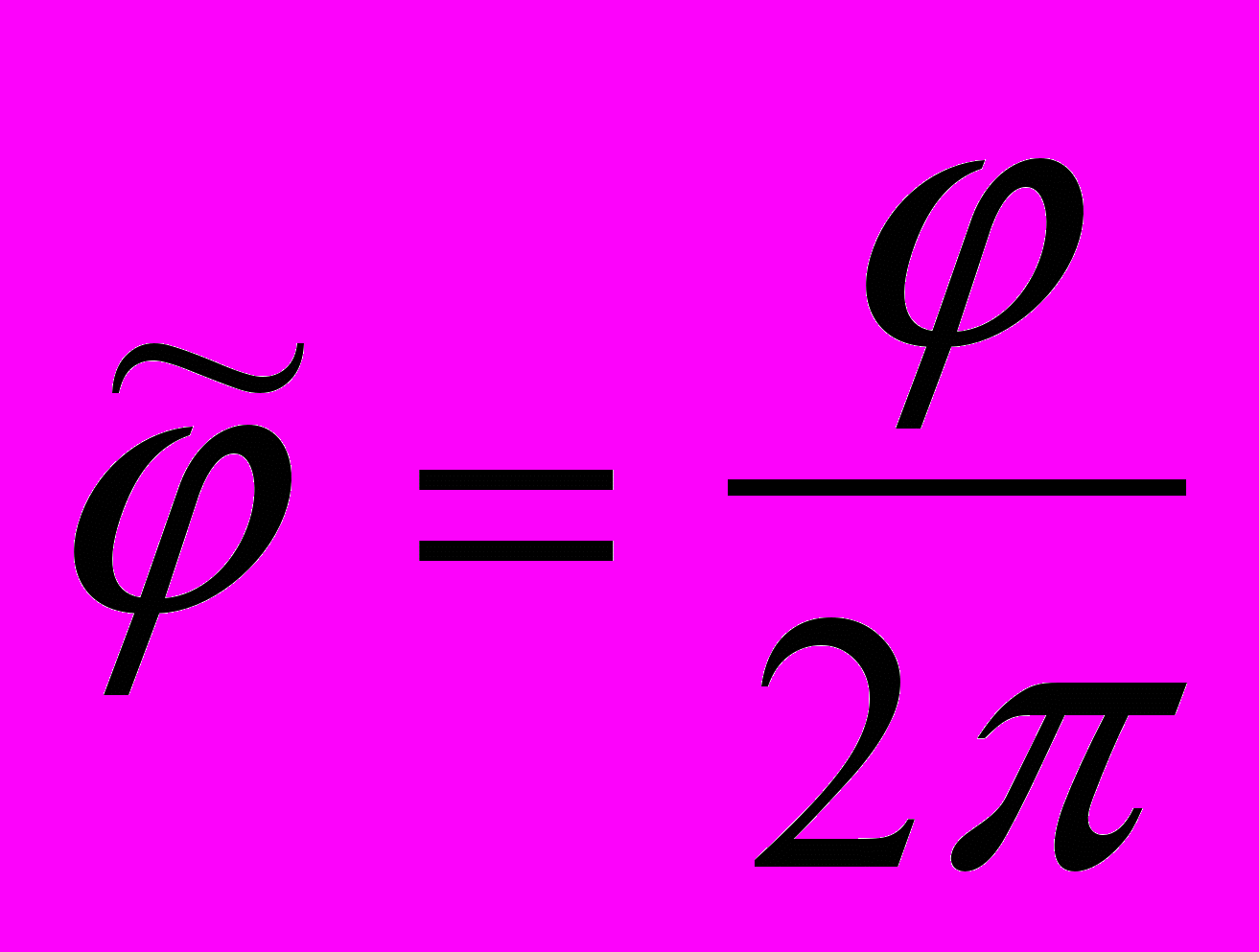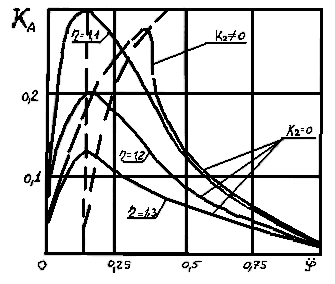
График зависимости безразмерной дисперсии виброупругого
перемещения от относительного угла поворота кулачкового вала
Для некоторых численных данных:
, 
, 
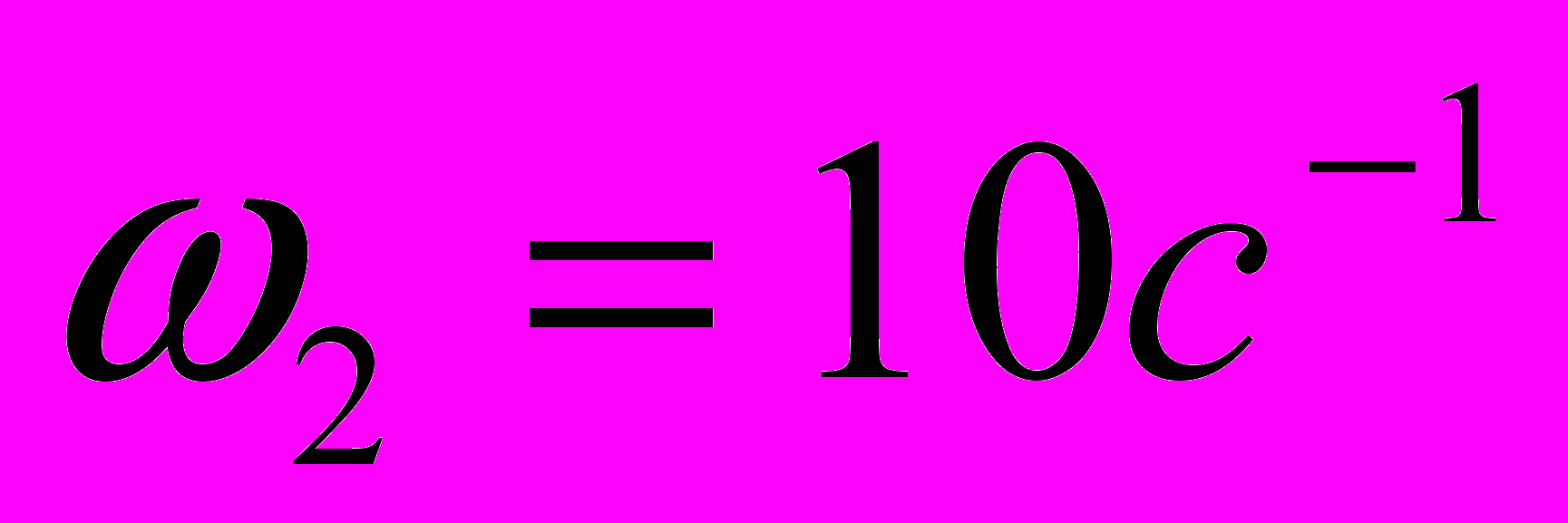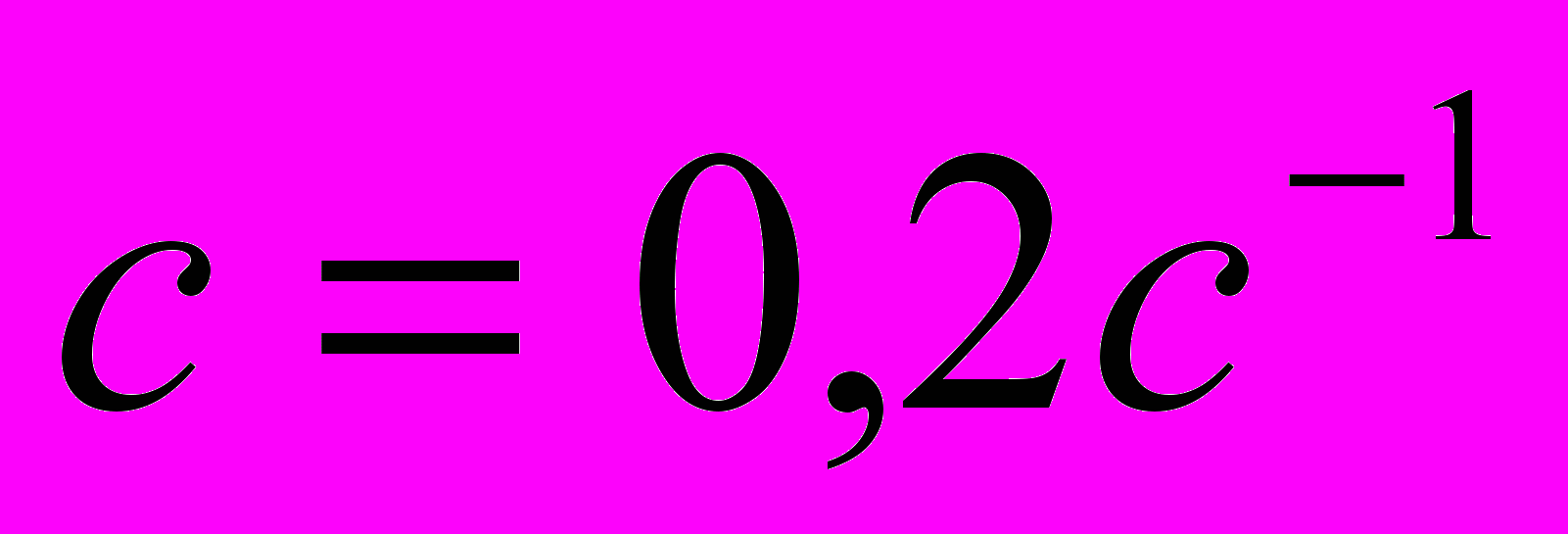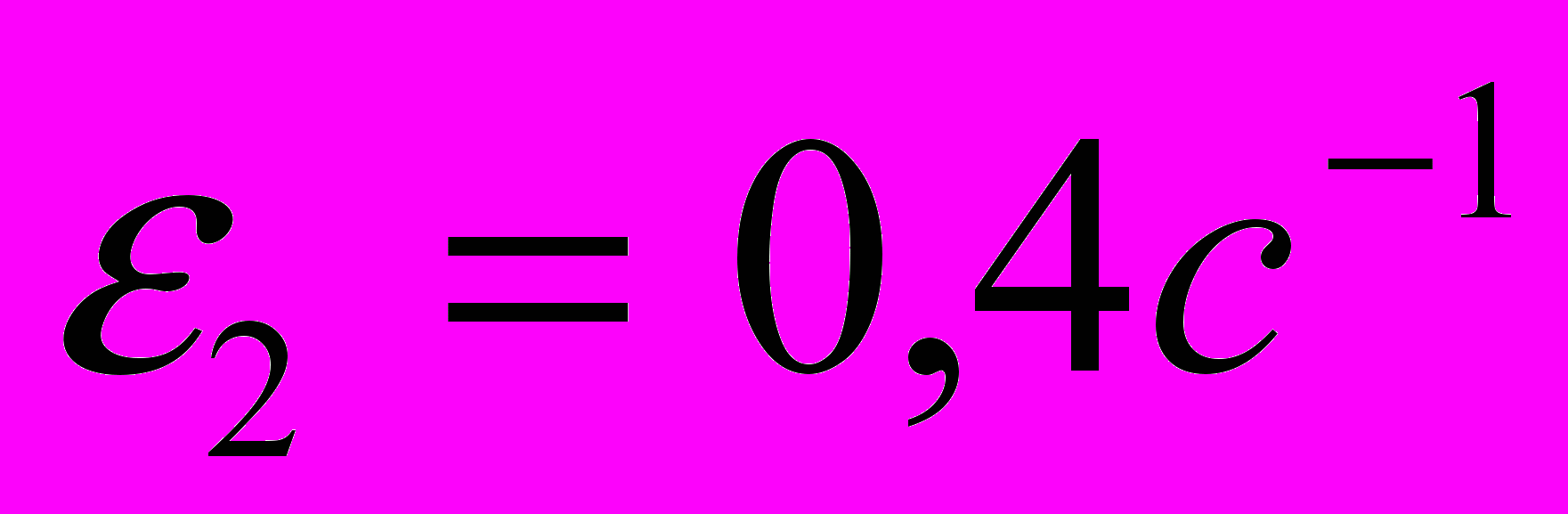был построен график безразмерной дисперсии виброупругого смещения 
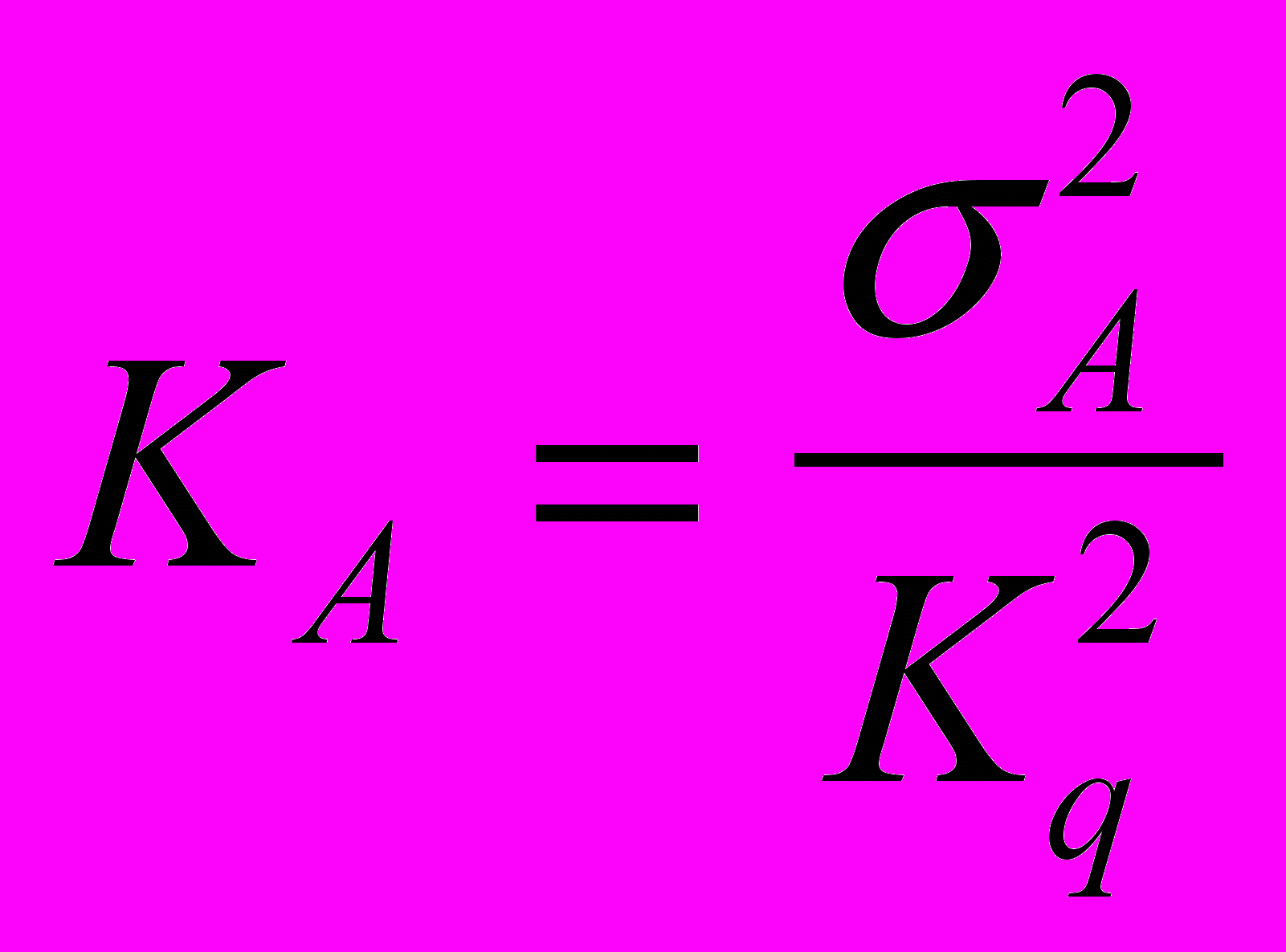, который представлен на рисунке при значениях параметра нелинейност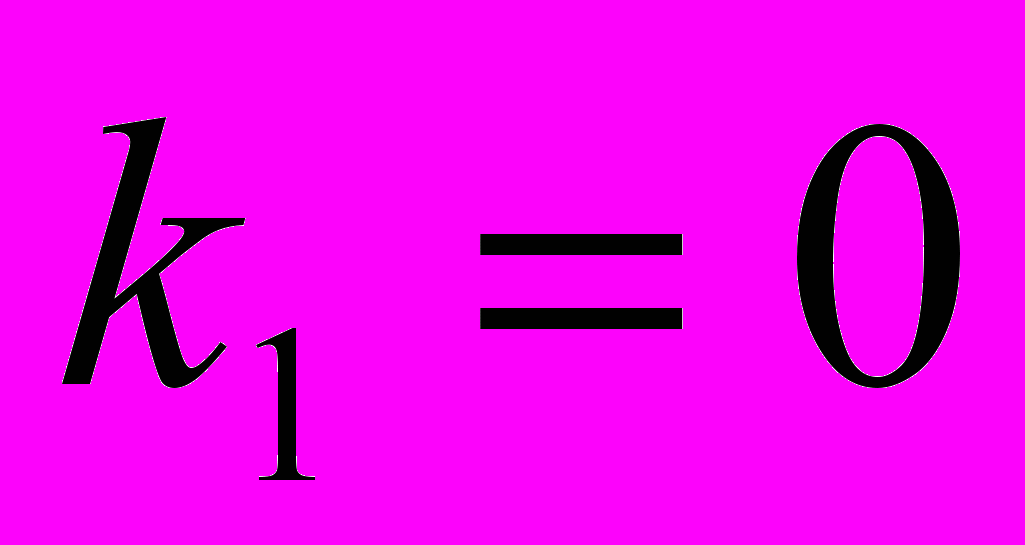и 
и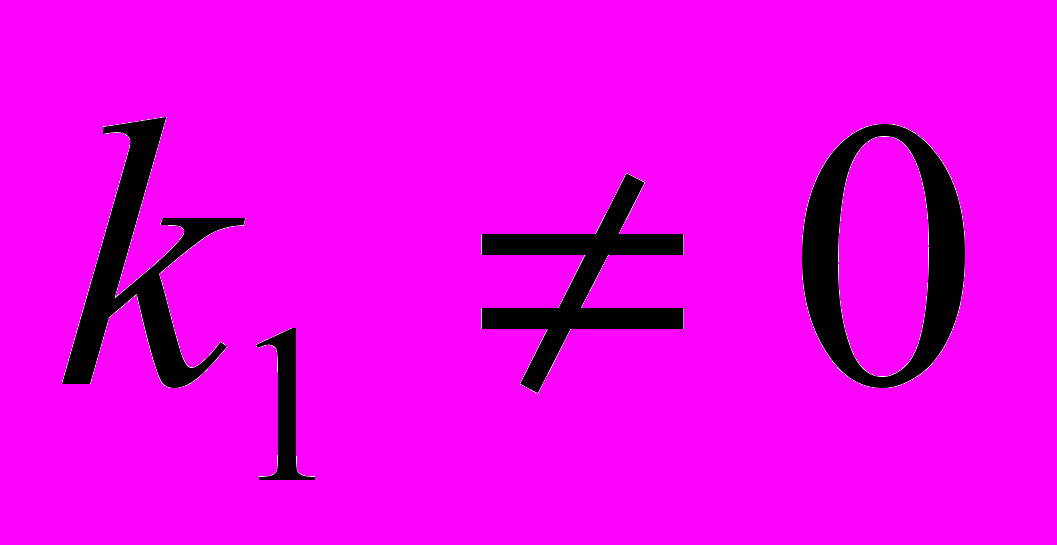 
(пунктирная линия) и трех значений параметра отношения частот . Из анализа графиков видно, что максимальная величина KA уменьшается с увеличением величины отношения частот . Это дает уменьшение среднеквадратичной амплитуды виброупругого смещения, что в свою очередь, повышает эффективность работы механизма и машины.Библиографический список
- Горецкий С.С., Мер И.И. Современные мелиоративные и строительные машины. М.: Колос, 1970. 200 с.
- Строительные машины для механизации гидромелиоративных работ. /Под ред. Сурикова В.В.. М.: Агропромиздат, 1985. 351 с.