С. В. Фёдоров, Н. А. Середа Обосновывается теоретико-расчётный метод определения и подбора коэффициентов трения в шарнирах рычажных механизмов пищевых машин
| Вид материала | Документы |
СодержаниеСписок использованных литературных источников |
- Содержатся предложения по определению числовых значений коэффициентов трения в стадии, 58.42kb.
- Задачи кинематического анализа и синтеза механизмов. Передаточные функции и отношения., 55.01kb.
- Краткое содержание: Виброзащита машин и механизмов. Методы виброзащиты. Взаимодействие, 294.78kb.
- Памятка для студентов группы пкм- по изучению дисциплины " Теория механизмов и машин, 72.92kb.
- О повышении эффективности работы машин при помощи уточненного динамического расчета, 26.88kb.
- Димитрюк Сергей Олегович, доцент кафедры «Теория механизмов и машин» к т. н., доцент, 37.69kb.
- Закономерности проектирования механизмов для передачи и преобразования, 19.17kb.
- Примерная программа дисциплины теория механизмов и машин Рекомендуется Минобразованием, 326.52kb.
- Рабочая программа по дисциплине опд. Ф. 04 Теория механизмов и машин для направления, 252.07kb.
- Оптимизационный кинематический синтез плоских рычажных механизмов IV класса с приближенным, 314.16kb.
УДК 621.891 (06)
МЕТОД ОЦЕНКИ И ПОДБОРА КОЭФФИЦИЕНТОВ ТРЕНИЯ В ПАРАХ
ТРЕНИЯ РЫЧАЖНЫХ МЕХАНИЗМОВ ПИЩЕВЫХ МАШИН
С.В. Фёдоров, Н.А. Середа
Обосновывается теоретико-расчётный метод определения и подбора коэффициентов трения в шарнирах рычажных механизмов пищевых машин. Метод обладает свойством логически последовательного анализа трения.
коэффициент трения, шарнир, номинальная трибосистема, узел трения
В современной расчётной практике [1-4] нет чёткого инженерного метода подбора значений коэффициентов трения для пар трения рычажных механизмов. Параметры трения подбираются либо на основе физического эксперимента, как правило, из принципа минимальности, либо на основании опыта эксплуатации типовых пар трения.
Определённый научный и практический интерес представляет разработка строгих теоретических моделей трения, а также основанных на них расчётных методик.
Современные методы определения параметров трения основаны на так называемом силовом анализе кинематической цепи механизма с учётом трения. Существо метода заключается в определении реакций в кинематических парах механизма в предположении, что трение в парах отсутствует. Далее в уравнения моментов сил движущих и сил сопротивления вводятся принудительно величины коэффициентов трения. Таким образом, задача оценки трения становится разрешимой.
В материалах [5-7] изложен метод силового анализа кинематических цепей механизмов с последующим определением истинных значений коэффициентов трения. В соответствии с данным методом определяются равнодействующие силы в кинематических парах как нормальные силы в парах трения; составляется условие равновесия моментов в шарнире вращения для сил движущих (
) и сил сопротивления (
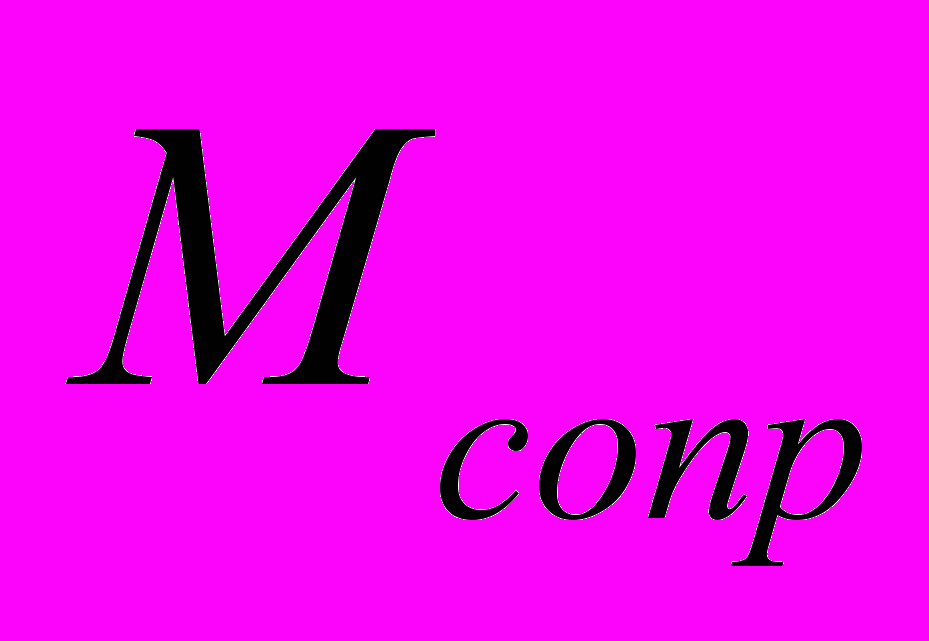), и при этом вводится значение расчётного диаметра вала шарнира. Последний определяют, используя упрощённый метод оценки диаметра вала из условия действия, например, напряжения кручения по следующей формуле [8]: 
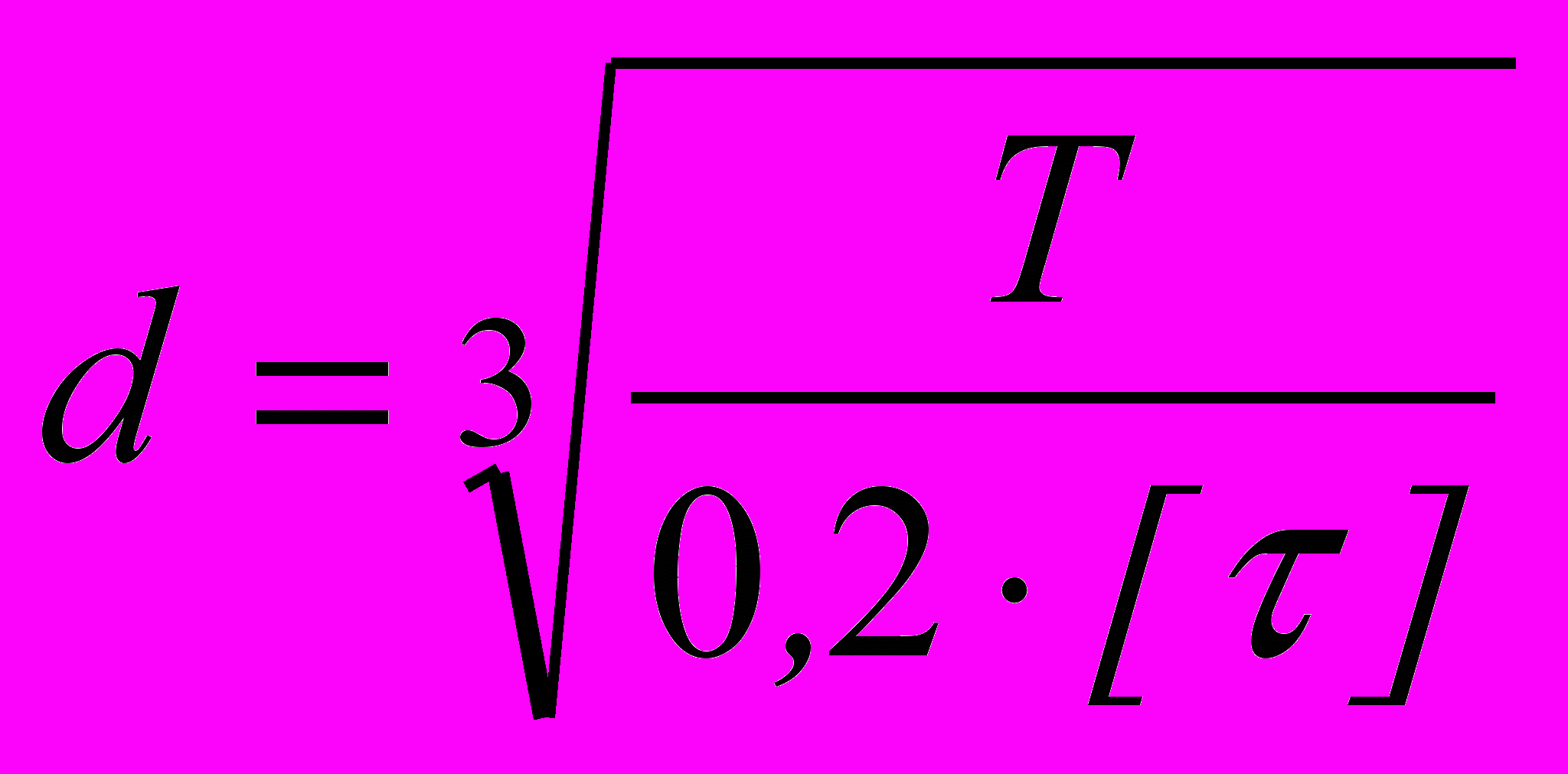, (1)где T – крутящий момент;
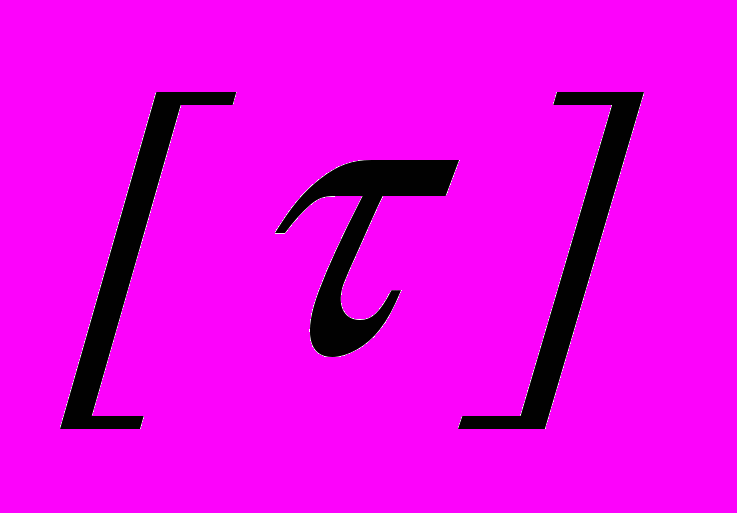– напряжение кручения. 
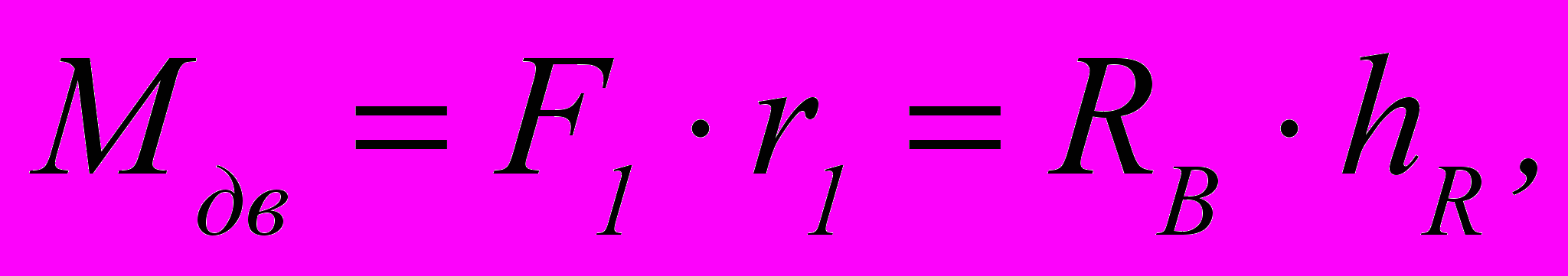(2)где
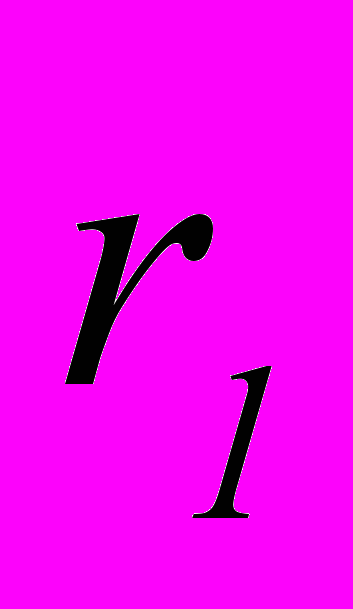– длина кривошипа.
. (3)Решая совместно уравнения (2) и (3), получим формулу для определения силы трения
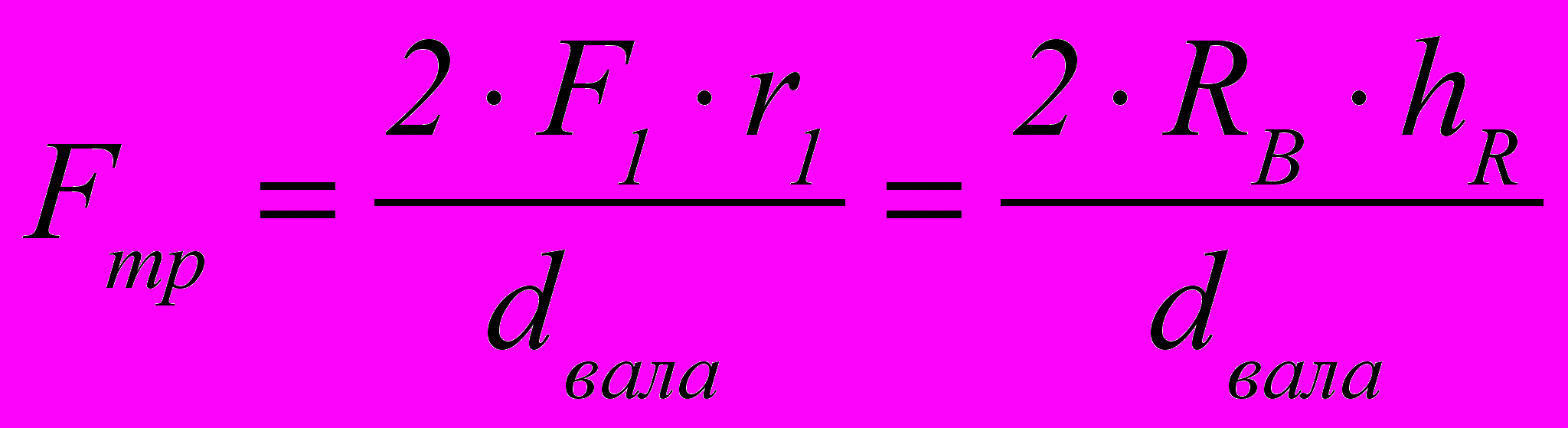. (4)Расчётный коэффициент трения определим по формуле
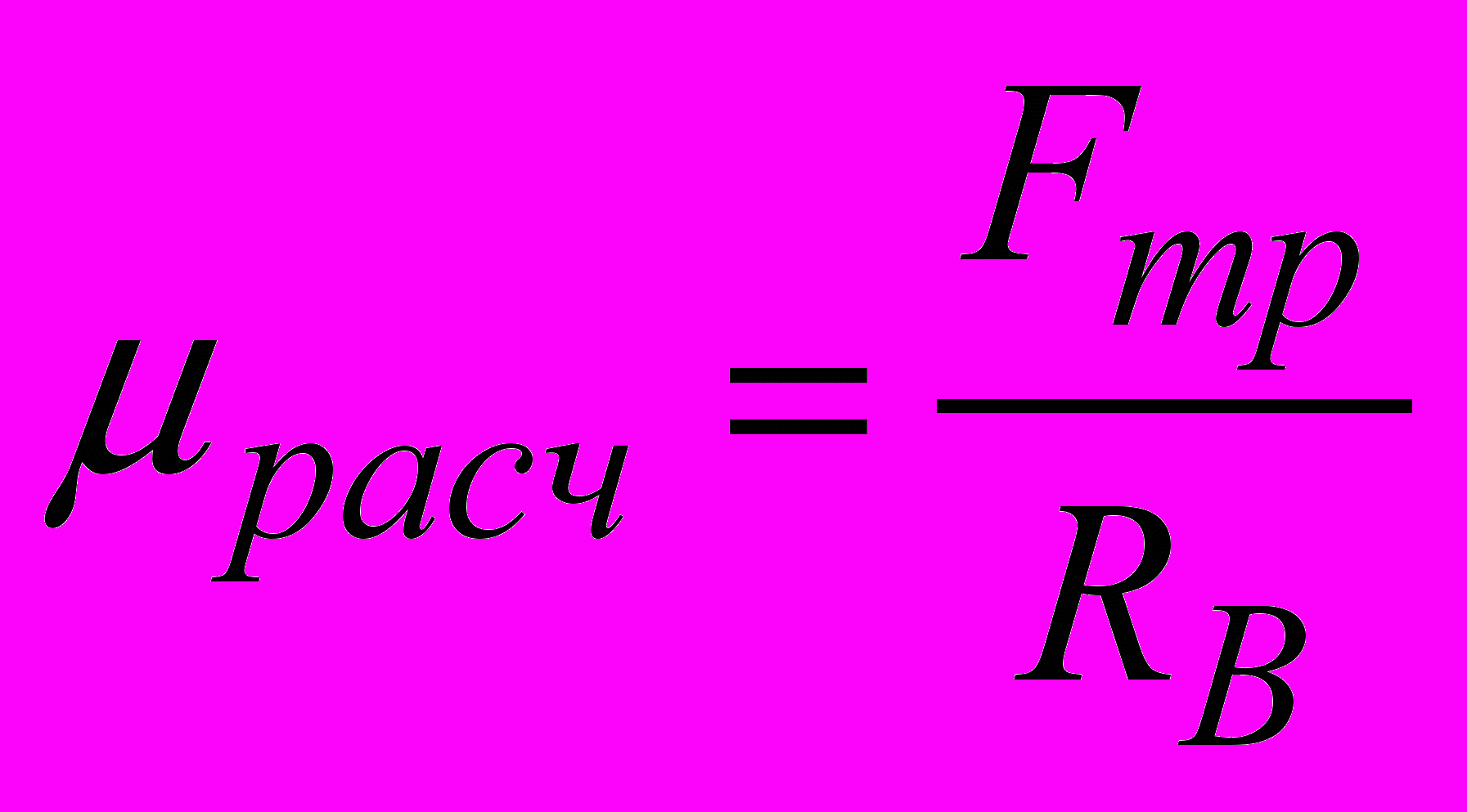. (5)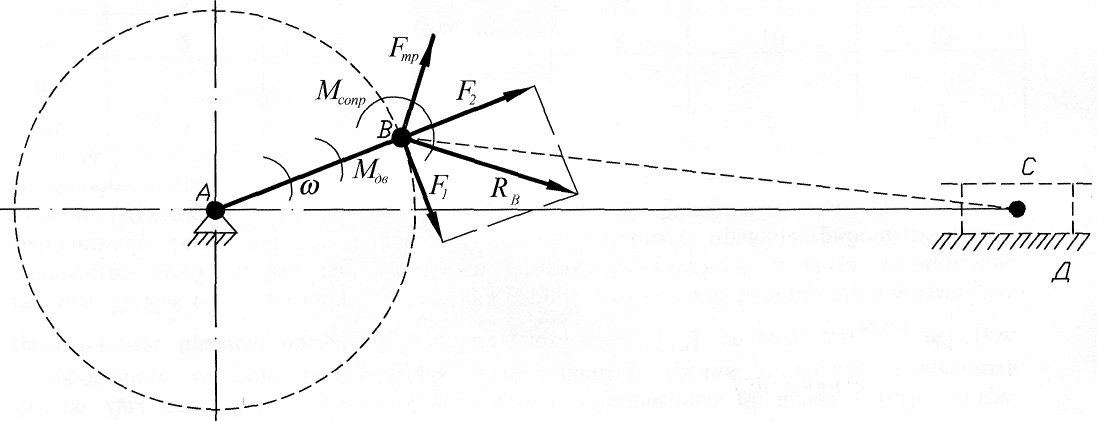
На рис. 1 представлена схема, иллюстрирующая предложенные формулы (2)-(5).Рис. 1. Схема к определению коэффициента трения в шарнире вращения
Fig. 1. The Scheme to determination of friction coefficient into rotation joint
Выполненные нами расчёты [9] по данной модели показали, что величины коэффициентов трения в шарнирах механизмов имеют большие (
) значения. Данный результат вполне очевиден, так как, по существу, решалась задача силового расчёта именно с трением собственно одноимённых пар. Другого результата, по-видимому, не могло быть, поскольку схема просто кинематической цепи не несёт в себе смысла элемента (шарнира) как конструкции именно антифрикционной пары. Следовательно, силовой анализ кинематической цепи механизма с определением расчётных коэффициентов трения приводит к главному логическому выводу теории и практики трения – необходимости подбора элементов (шарниров) антифрикционного трения. Возникает вопрос: «Как выполнять это целенаправленно?». Здесь можно использовать один из основных выводов трибоэргодинамики [10]. Рассматривая принцип номинальных машин (механизмов), которые образованы из номинальных трибосистем, пришли к выводу, что величины коэффициентов трения номинальных трибосистем имеют строго определённые величины – квантовые уровни (см. табл. 1) [10].
Номинальную машину (механизм) следует образовывать из трибосистем с такими коэффициентами трения, чтобы их сумма была равна единице:
.Таблица 1. Возможный ряд трибосистем, образующих машину (трибонадсистему)
Table 1. Possible row of tribosystems which forming a machine (tribosupersystem)
 |  |  | | | |
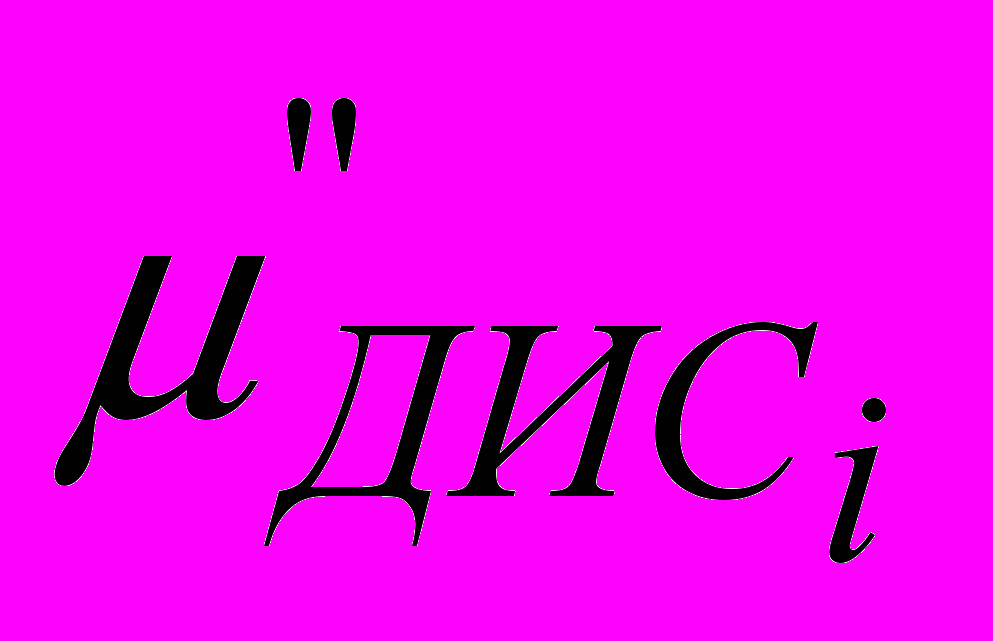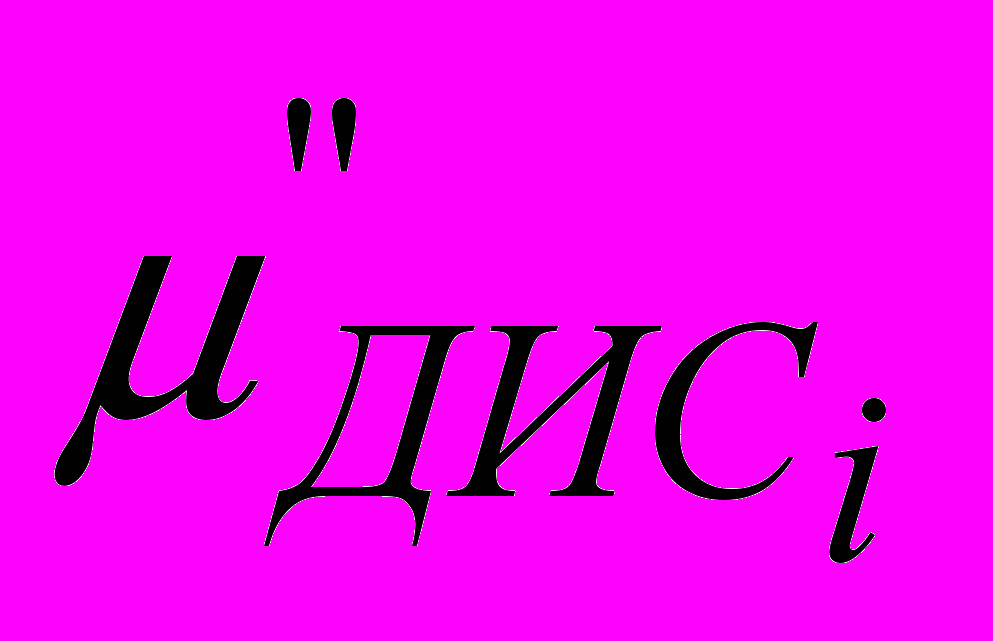| 0,5 | 0,5 | 2 | 0,005 | 0,995 | 200 |
| 0,25 | 0,75 | 4 | 0,0025 | 0,9975 | 400 |
| 0,2 | 0,8 | 5 | 0,002 | 0,998 | 500 |
| 0,1 | 0,9 | 10 | 0,001 | 0,999 | 1000 |
| 0,05 | 0,95 | 20 | 0,0005 | 0,9995 | 2000 |
| 0,025 | 0,975 | 40 | 0,00025 | 0,99975 | 4000 |
| 0,02 | 0,980 | 50 | 0,0002 | 0,9998 | 5000 |
| 0,01 | 0,990 | 100 | 0,0001 | 0,9999 | 10000… |
В табл. 1 приняты следующие обозначения:
– адаптивный коэффициент (Амонтона) трения; 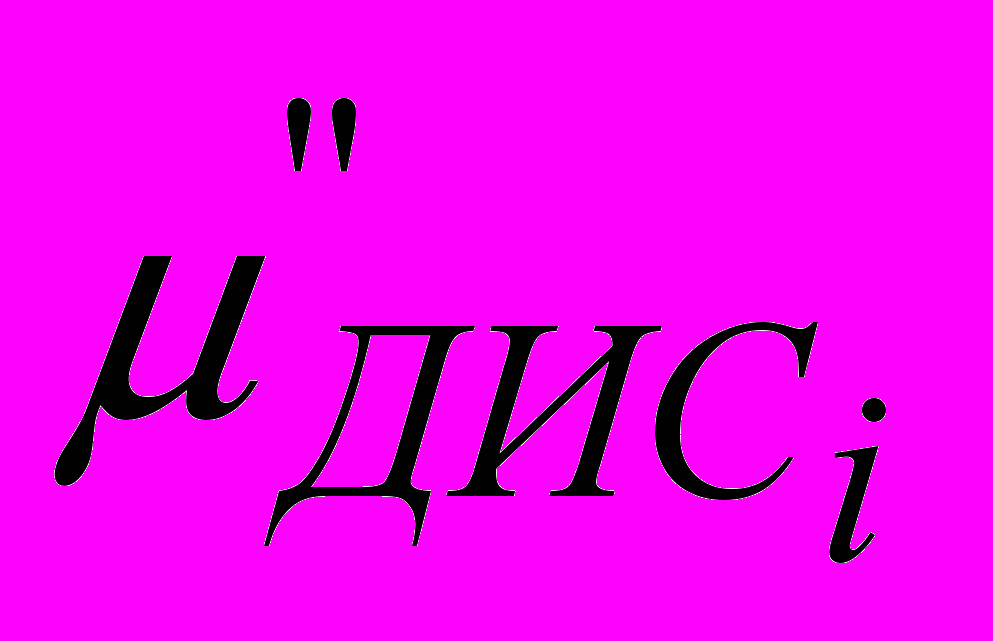– диссипативный коэффициент трения; 
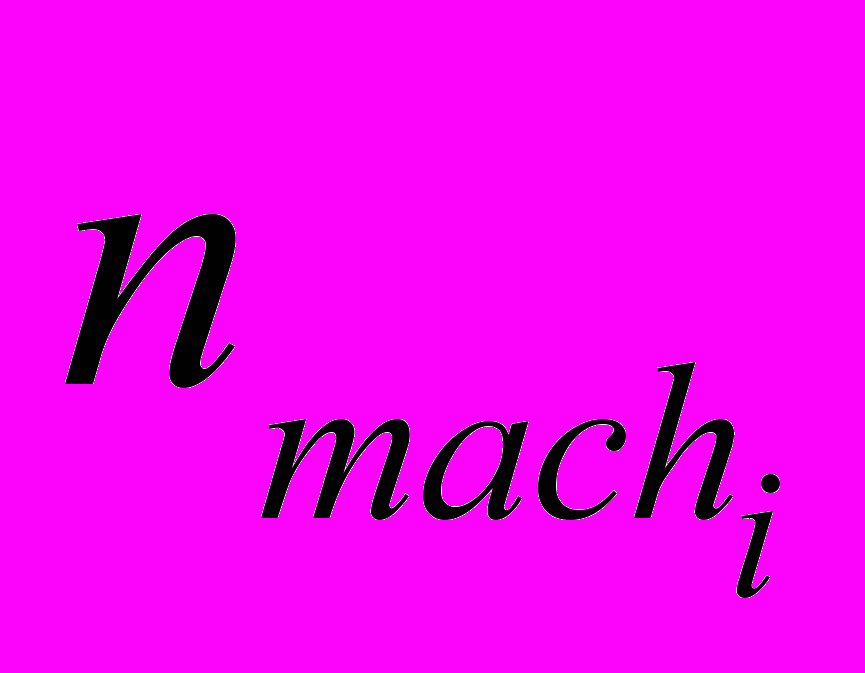– число машин (число трибосистем в машине) [10]. В рамках структурного анализа плоских механизмов [1-4] известно правило Л.В. Ассура, которое определяет количество звеньев и элементов в присоединяемых группах Л.В. Ассура, т. е. основной принцип образования механизмов. Для простейших рычажных механизмов, образованных по правилу Л.В. Ассура, использование величин номинальных коэффициентов трения (табл. 1) позволяет реализовать теоретическое правило идеальной (оптимальной) машины [11], т. е.
. Как видно из табл. 2, правило трибооптимальной машины (механизма) для количества трибосистем, получаемых в рамках структурного анализа механизмов, выполняется. Таким образом, подтверждается объективность правила трибооптимальной машины (механизма), предложенного в работе [10], и его практическая целесообразность.Таблица 2. Подбор коэффициентов трения в трибосистемах для плоских рычажных механизмов
Table 2. Selection of friction coefficients for flat lever mechanisms
| № п/п | 1 | 2 | 3 | 4 | 5 | 6 |
| n | 2 | 4 | 6 | 8 | 10 | 12 |
| p  | 3 | 6 | 9 | 12 | 15 | 18 |
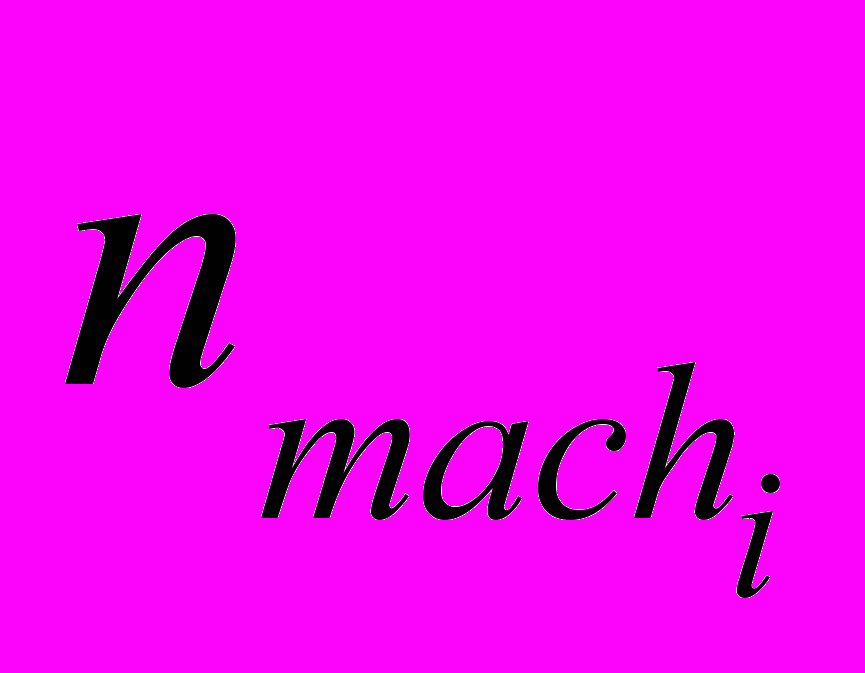| | 4 | 7 | 10 | 13 | 16 | 19 |
 | 0,25  4==1,0 | 0,05+0,25+ +(0,2 2)++(0,1 3)==1,0 | 0,1 10==1,0 | (0,05 8)++0,2+ +(0,1 4)==1,0 | (0,05 12)++(0,1 4)==1,0 | 0,1+ +(0,05 18)==1,0 |
В табл. 2 приняты следующие обозначения: n – число звеньев присоединяемой группы механизма;
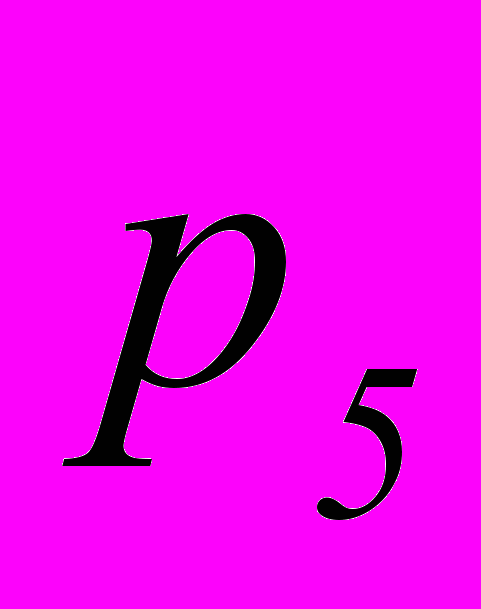– число кинематических пар пятого класса.К примеру, на рис. 1 представлена кинематическая схема кривошипно-ползунного механизма, который содержит четыре звена: кривошип, шатун, ползун и стойку. В соответствии с табл. 2 число трибосистем в механизме
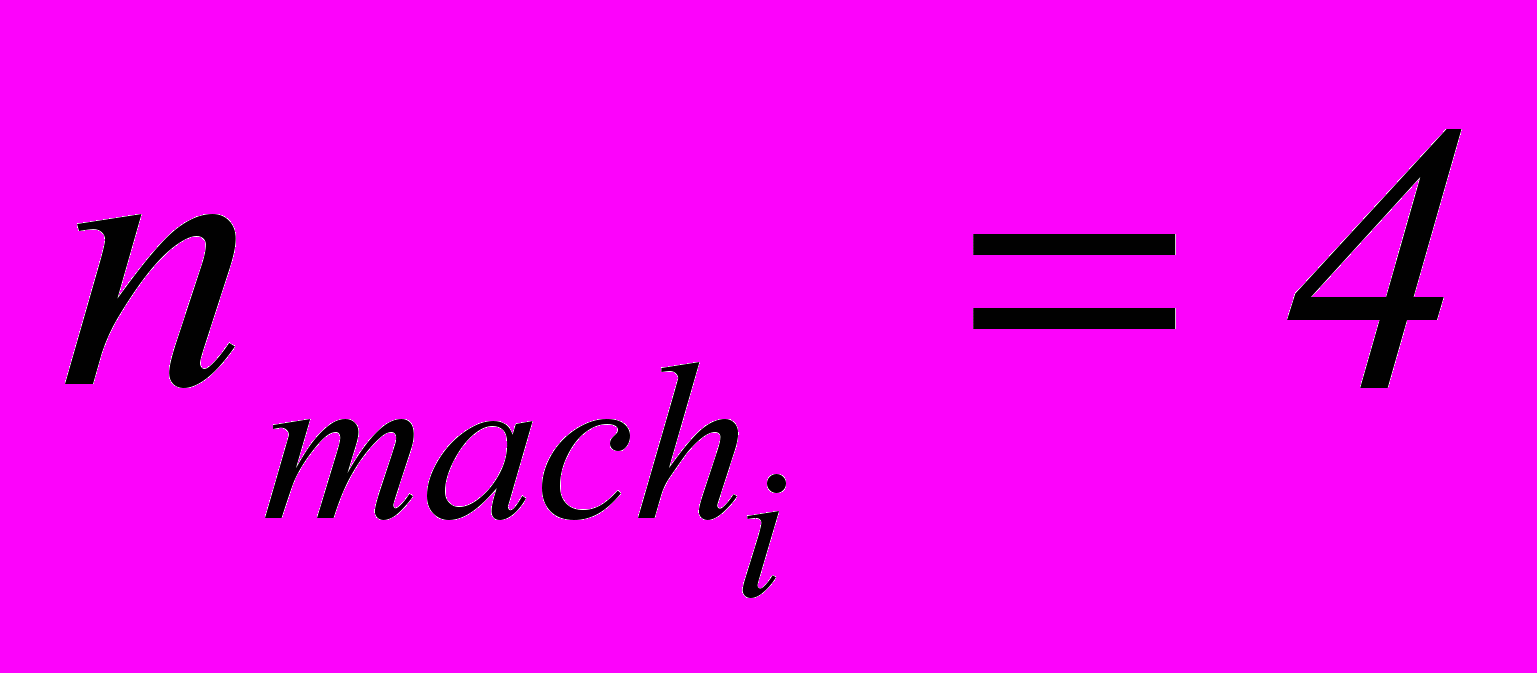, коэффициент трения во всех кинематических парах (оптимальных трибосистемах) равен 0,25. Таким образом, зная конкретные величины коэффициентов трения для трибопар механизма, далее необходимо обеспечить конструктивное исполнение данных пар. Здесь можно использовать современную информацию [12], которая определяет общий смазочно-конструктивный принцип уровней трения в зависимости от типа смазки на контакте трения (рис. 2).
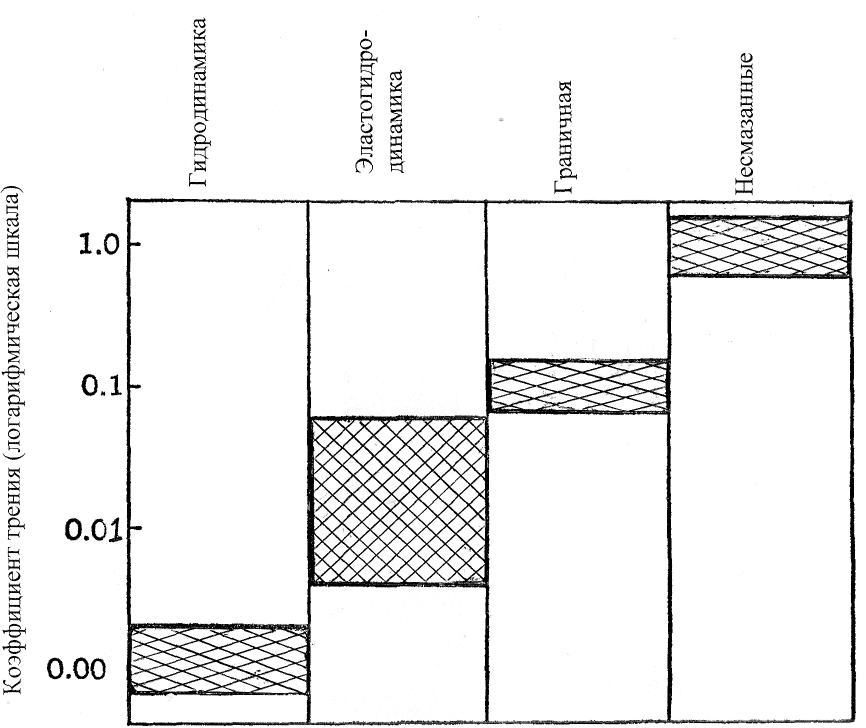
Рис. 2. Схематический рисунок, показывающий, как тип смазки меняется
от гидродинамики до эластогидродинамики и вплоть до граничной смазки
по мере того, как жесткость действующих условий увеличивается [12]
Fig. 2. Schematic drawing showing how the type of lubrication shifts from hydrodynamic to elasto-hydrodynamic to boundary lubrication as the severity of running
conditions is increased [12]
В итоге рассмотренная выше модель оптимизации инженерного принципа оценки коэффициентов трения для трибопар механизмов позволяет сделать следующие выводы:
1. Предложен расчётный метод оценки коэффициентов трения в кинематической паре механизма на стадии силового анализа.
2. Результат силового анализа механизмов с определением расчётных значений коэффициентов трения показывает наличие большого трения (высоких коэффициентов трения) в элементах кинематических цепей, не учитывающих трибоконструктивных принципов.
3. Для обеспечения внутреннего движения в механизмах элементы кинематических цепей должны создаваться и анализироваться с учётом современной задачи антифрикционности.
4. Выбор величин коэффициентов трения для элементов кинематических цепей простейших рычажных механизмов возможно осуществлять, используя величины коэффициентов трения для номинальной машины (см. табл. 1) и удовлетворяя условию
(см. табл. 2); 5. По величинам коэффициента трения (см. рис. 2) можно определять способ смазывания пары трения и соответственно назначать и оптимизировать конструкцию всего трибоузла пищевой машины.
СПИСОК ИСПОЛЬЗОВАННЫХ ЛИТЕРАТУРНЫХ ИСТОЧНИКОВ
1. Артоболевский И.И. Теория механизмов и машин. – М.: Наука, 1975. – 638 с.
2. Артоболевский С.И. Теория механизмов и машин. – М.: Высш. шк., 1968. – 364 с.
3. Колчин Н.И. Механика машин: в 2-х т. – М.-Л.: Машгиз, 1963. – Т. 2. – 534 с.
4. Теория механизмов и машин / под ред. К.В. Фролова. – М.: Высш. шк., 1987. – 496 с.
5. Фёдоров С.В., Середа Н.А. К определению коэффициентов трения в кинематических парах рычажных механизмов // Известия КГТУ. – 2010. – № 17. – С. 84-88.
6. Фёдоров С.В., Середа Н.А. Уточнение силового анализа кинематических цепей с учётом сил трения // Вестник РАЕН. – Калининград: ФГОУ ВПО «КГТУ», 2010. – С. 146-150.
7. Фёдоров С.В., Середа Н.А. Метод определения коэффициентов трения в кинематических парах рычажных механизмов // Известия КГТУ. – 2010. – №18. – С. 189-193.
8. Детали машин / под ред. В.А. Финогенова.–М.: Высш.шк., 1998.–382 с.
9. Калюжнов Д.А. Метод определения коэффициентов трения в кинематических парах рычажных механизмов // Студ. науч. конф. КГТУ: материалы. – Калининград, 2010. – С. 41-42.
10. Фёдоров С.В. Основы трибоэргодинамики и физико-химические предпосылки теории совместимости. – Калининград: КГТУ, 2003. – 415 с.
11. Фёдоров С.В. Трибоэнергетический и энтропийный анализ структуры машины // Инновации в науке и образовании – 2008: Междунар. науч. конф. (23-25 окт. 2008 г.): труды – Калининград, 2008. – Ч. 2. – С. 99-102.
12. Bowden F.P., Tabor D. Friction. An Introduction to Tribology. Anchor Books, Anchor Press / Doubleday, Garden City, New York, 1973, p. 178.
METHOD OF THE ESTIMATION AND SELECTION OF THE FRICTION
COEFFICIENTS FOR SIMPLEST LEVER FOOD MECHANISM
S.V. Fedorov, N.A. Sereda
Theoretical and estimation method of the friction coefficients determination and selection for simplest lever food mechanisms has motivated. This method has the logical order property for friction analyse.
friction coefficients, joint, nominal tribosystems, group of friction