Силовой расчет механизмов

Вид материала

Документы

Подобный материал:

• Краткое содержание: Виброзащита машин и механизмов. Методы виброзащиты. Взаимодействие, 294.78kb.
• Темы курсового проекта по дисциплине «Теория механизмов и машин», 69.21kb.
• Расчётно-пояснительная записка к курсовому проекту по дисциплине: "Теория механизмов, 22.29kb.
• Курс Семестр Трудоемкость (в зачетных единицах), 33.22kb.
• Концепция специальной силовой подготовленности, 63.68kb.
• О повышении эффективности работы машин при помощи уточненного динамического расчета, 26.88kb.
• Пояснительная записка содержит: 5 рис., 4 источника, 22 стр, 223.14kb.
• Реферат пояснительная записка содержит: 5 рис., 4 источника, 22 стр, 222.54kb.
• Рабочей программы дисциплины Теория механизмов и машин по направлению подготовки 190100, 33.66kb.
• Задачи кинематического анализа и синтеза механизмов. Передаточные функции и отношения., 55.01kb.

_2вп

F₂₁

G₂

2 n G₂

₂ _w

r_b2

Рис. 24 Рис. 25


В начале решается уравнение моментов и определяется величина силы F₂₁. Затем графически в масштабе _F, по векторному уравнению сил строится многоугольник сил (рис.25), из которого определяется величина и направление реакции F₂₀ .

2. Звено 1.

Расчетная схема для звена 1 приведена на рис. 26. Уравнения равновесия для звена 1:

векторное уравнение силового равновесия

_{_ _ _ _}

 F = 0; F₁₂ + G₁ + F₁₀ = 0;

^??

уравнение моментов относительно точки А


 M_А = 0; M_c1 - M_Ф1 + F₁₂ r_b1 = 0.


F₁₂

_F, мм/Н 1



n M_Ф1

p_F F₁₂ ₁ r_b1

F₁₀ S₁

P_2вп А_1в ₁

G₁ G₁ r_w1



_w n M_д1

F₁₀

Рис. 26 Рис. 27


Для звена 1 движущий момент M_д1 рассчитывается по уравнению моментов, а величина и направление реакции F₁₀ определяется графически (рис.27), построением плана сил в масштабе _F .

8.2. Кинетостатический расчет кулачкового механизма (метод планов сил).

При проведении расчета необходима информация о размерах и форме профиля кулачка, длине толкателя и радиусе ролика. По этим данным в масштабе изображается кинематическая схема кулачкового механизма, на которую наносятся все известные силы и моменты, а также главные вектора и главные моменты сил инерции




3

Дано: _{k =} f(₂), l_СE,

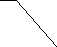
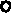r_p, I_si, m_i, _i, _i, M_c3 3 n c₃ 2

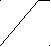
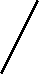
E_1в K_2вп

Определить: M_д2 , F_ij. M_c3

c₂ n ₂

S₃,C_1в ₃ B_1в ,S₂

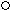
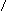
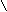
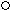
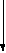M_д1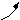



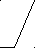
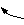
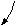M_и3 ₃ G₂

0 G₃ ₂




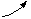
M_и3




Рис. 28

Определяется подвижность, число избыточных связей в механизме, а также число неизвестных в силовом расчете:


W_пл = 3 3 - 23 - 11 = 2, где W_о = 1, W_м = 1,


q_пл = 1 + 1 - 1 = 0, n_s = 23 + 11 + 1 = 8,

т.е. в данном кулачковом механизме неизвестно 8 компонент реакций, для решения задачи силового расчета необходимо составить 8 уравнений кинетостатики. Структурный анализ механизма показывает, что механизм состоит из одного первичного механизма (звено 2 и стойка) и структурной группы, состоящей из толкателя 3 и ролика 3. Особенность этой группы - местная подвижность ролика. В данном случае местная подвижность выполняет функцию замены в высшей паре трения скольжения трением качения. Положение ролика относительно толкателя не имеет значения, поэтому в паре с местной подвижностью нет уравновешивающего момента. Силовой расчет начнем с рассмотрения ролика.

1. Звено 3.

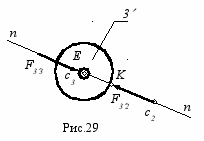
Расчетная схема для звена 3 приведена на рис. 29. Уравнение силового равновесия :

_{_ _ _}

 F = 0; F_32 + F_33 = 0;

^??

Из этого уравнения определяется направление вектора F_33 , которое в данном случае совпадает с контактной нормалью.





2. Звено 3 (толкатель).

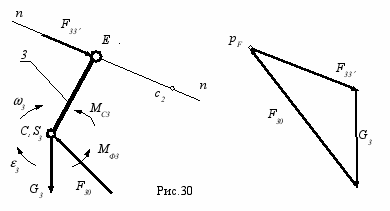
Затем рассматривается звено 3, расчетная схема для которого дана на рис.30. Из уравнения моментов относительно точки С

 M_С = 0; M_c3 + M_Ф3 - F_33  h_CF33 = 0,

определяется величина F_33 , а из векторного уравнения силового равновесия

_{_ _ _ _}

 F = 0; F₃₂ + G₃ + F_33 = 0,

^??

по построенному в масштабе _F плану сил, величина и направление вектора F_33 (см. рис. 30).







3. Звено 2 (кулачок).

Расчетная схема для звена 2 приведена на рис. 31. Уравнения равновесия для звена 2:

векторное уравнение силового равновесия

_{_ _ _ _}

 F = 0; F_32 + G₂ + F₂₀ = 0;

^??









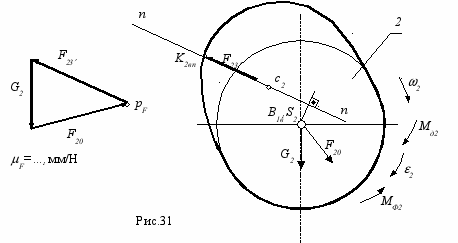уравнение моментов относительно точки В


 M_В = 0; - M_д2 + M_Ф2 + F_32  h_BF32 = 0.

Для звена 2 момент M_д2 рассчитывается по уравнению моментов, а величина и направление реакции F₂₀ определяется графически (рис. 31), построением плана сил в масштабе _F .

8.3. Кинетостатический расчет четырехшарнирного механизма (аналитический метод).

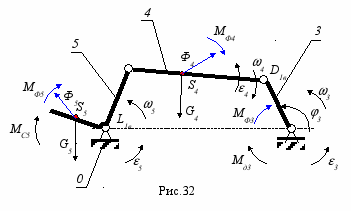Изобразим расчетную схему механизма и нанесем на нее все внешние силы и моменты (рис.32).








Постановка задачи. Дано: l_i, ₃, ₃, ₃, m_i, I_Si, M_c5.

_________________________

Определить: F_ij, M_д3.

1. Определим подвижность механизма, число избыточных связей в КП и число неизвестных в силовом расчете.

W_пл = 3 3 - 2 4 = 1, q_пл = 1 + 0 - 1 = 0, n_s = 2 4 + 1 = 9.

2. Определим скорости и ускорения звеньев и центров их масс.
   
3. Определим главные векторы и главные моменты сил инерции.
   

Ф_i = - m_i a_Si, M_Фi = I_Si_i .

4. 4. Кинетостатический расчет механизма.
   

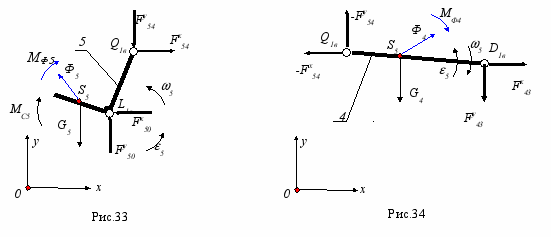
1. Звено 5 (рис. 33).
   

Уравнения силового равновесия в проекциях на оси координат

 F ^x₅ =0; - F ^x₅₄ + F ^x₅₀ - Ф^x₅ = 0;

 F ^y₅ =0; - F ^y₅₄ + F ^y₅₀ + Ф ^y₅ - G₅ = 0;

и сумма моментов сил относительно точки L


 M _L =0; - F ^y₅₄ x_Q + F^x₅₄y_Q - M_c5 - M_Ф5 + (-Ф ^y₅+ G₅)x_S5 + Ф ^x₅y_S5 = 0.

4. 
   
5. 4.2.Звено 4. (рис. 34).
   
6. 
   

Уравнения силового равновесия в проекциях на оси координат


 F ^x₄ =0; F ^x₅₄ + F ^x₄₃ + Ф ^x_и4 = 0;


 F ^y₅ =0; - F ^y₅₄ – F ^y₄₃ + Ф ^y_и4 - G₄ = 0;


и сумма моментов сил относительно точки Q


 M _Q =0;

- F ^y₄₃ x_D4 + F ^x₄₃y_D4 - M_Ф4 + (Ф ^y_и4- G₄)x_S4 + Ф^x_и4y_S4 = 0.

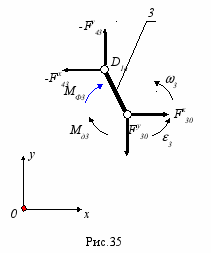
3. Звено 3. (рис. 35).
   

Уравнения силового равновесия в проекциях на оси координат

 F ^x₃ =0;

F ^x₃₀ + F ^x₄₃ = 0;

 F ^y₃ =0;

- F ^y₃₀ - F ^y₄₃ = 0;


и сумма моментов сил относительно точки C

 M _C =0; F ^y₄₃  x_D3 - F^x₄₃ y_D3 - M_Ф3 - M_д3 = 0.

Таким образом мы составили систему 9-и уравнение с 9-ю неизвестными. При составлении этой системы были учтены равенства действия и противодействия F_ij = - F_ji ( без учета этих равенств общее число неизвестных и уравнений системы 18 ). Составим матрицу этой системы:

F y50	F x50	F y54	F x54	F y43	F x43	F y30	F x30	Мд3
	1		-1						=	Ф x5
1		-1							=	-Ф y5 + G5
		- xQ	yQ						=	Mc5+MФ5+(Ф y5-G5)xS5 - -Ф x5 yS5
			1		1				=	-Ф x4
		-1		-1					=	-Ф y4 + G4
				-xD4	yD4					Mи4+(-Ф y4+G4)xS4-Ф x4  yS4
					1		1		=	0
				-1		-1			=	0
				xD3	-yD3			-1	=	MФ3