Силовой расчет механизмов

Вид материала

Документы

Содержание Механической характеристикой машины

Подобный материал:

• Краткое содержание: Виброзащита машин и механизмов. Методы виброзащиты. Взаимодействие, 294.78kb.
• Темы курсового проекта по дисциплине «Теория механизмов и машин», 69.21kb.
• Расчётно-пояснительная записка к курсовому проекту по дисциплине: "Теория механизмов, 22.29kb.
• Курс Семестр Трудоемкость (в зачетных единицах), 33.22kb.
• Концепция специальной силовой подготовленности, 63.68kb.
• О повышении эффективности работы машин при помощи уточненного динамического расчета, 26.88kb.
• Пояснительная записка содержит: 5 рис., 4 источника, 22 стр, 223.14kb.
• Реферат пояснительная записка содержит: 5 рис., 4 источника, 22 стр, 222.54kb.
• Рабочей программы дисциплины Теория механизмов и машин по направлению подготовки 190100, 33.66kb.
• Задачи кинематического анализа и синтеза механизмов. Передаточные функции и отношения., 55.01kb.

+  (H-i)p_i ,

ⁱ⁼¹

где n_s - число неизвестных в силовом расчете, Н - число степеней свободы твердого тела (на плоскости Н=3, в пространстве Н=6), i – число подвижностей в кинематической паре, p_i – число пар с i подвижностями.

5. Механические характеристики машин.

На этапе подготовки исходных данных необходимо определить внешние силы действующие на входные и выходные звенья машины. В машинах-двигателях, которые преобразуют любой вид энергии в механическую, закон изменения движущей силы определяется используемыми для этого преобразования физическими законами. Для электродвигателей – это законы электромагнитной индукции, для тепловых двигателей – законы термодинамики и т.д. На выходных звеньях рабочих машин силы сопротивления определяются законами взаимодействия рабочего органа с обрабатываемой деталью или с окружающей средой. В металлообрабатывающих станках это силы резания, в кузнечно-прессовых машинах – силы деформации заготовки, в транспортерах и конвейерах - силы трения и т.д. Законы изменения этих сил определяются экспериментально. Обобщение экспериментальных исследований используются в динамических расчетах машин в виде механических характеристик.


Механической характеристикой машины называется зависимость силы или момента на выходном валу или рабочем органе машины от скорости или перемещения точки или звена ее приложения.

То есть внешние силы действующие на механизмы зависят от скорости (а следовательно и от времени) или от положения. В студенческом курсе ТММ рассматриваются в основном силы зависящие от положения или позиционные.

Рассмотрим примеры механических характеристик различных машин.

1. Двигатели внутреннего сгорания (ДВС):
   

• четырехтактный ДВС
  

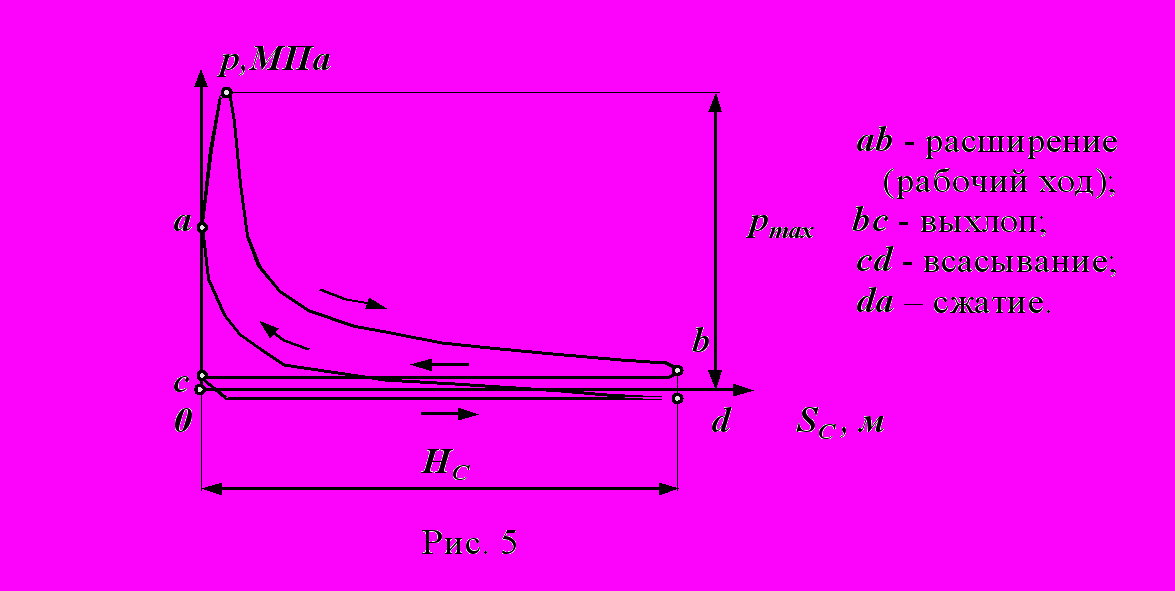
Индикаторная диаграмма - графическое изображение зависимости давления в цилиндре поршневой машины от хода поршня.

• двухтактный ДВС
  

2. Э
   лектродвигатели
   

• асинхронный электродвигатель переменного тока
  

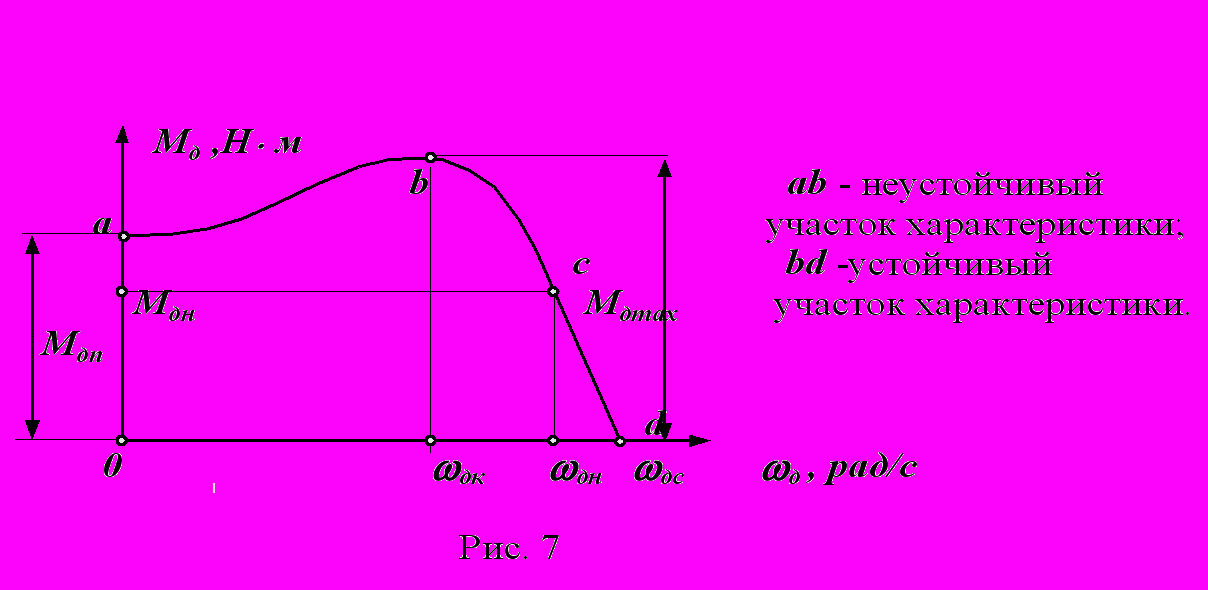
На диаграмме: М_дп - пусковой момент;

М_дн - номинальный крутящий момент;

М_дк или М_дmax - критический или максимальный момент;

_дн - номинальная круговая частота вращения вала двигателя;

_дхх или _дс - частота вращения вала двигателя холостого хода или синхронная.

Уравнение статической характеристики асинхронного электродвигателя на линеаризованном участке устойчивой части [2] имеет вид

М_д = b₁ + k₁_д ,

где М_д - движущий момент на валу двигателя,

_д - круговая частота вала двигателя ,

b₁ = М_дн  _д /(_дс - _дн ) , k₁ = - М_дн / (_дс - _дн ).

Статическая характеристика асинхронного двигателя, выражающая зависимость нагрузки от скольжения, определяется формулой Клосса

М_д = 2 М_дк  (S/S_к + S_к/S ),

где S = 1 - _д /_дс , S_к = 1 - _дк /_дс , _д >=_дс .

• д
  
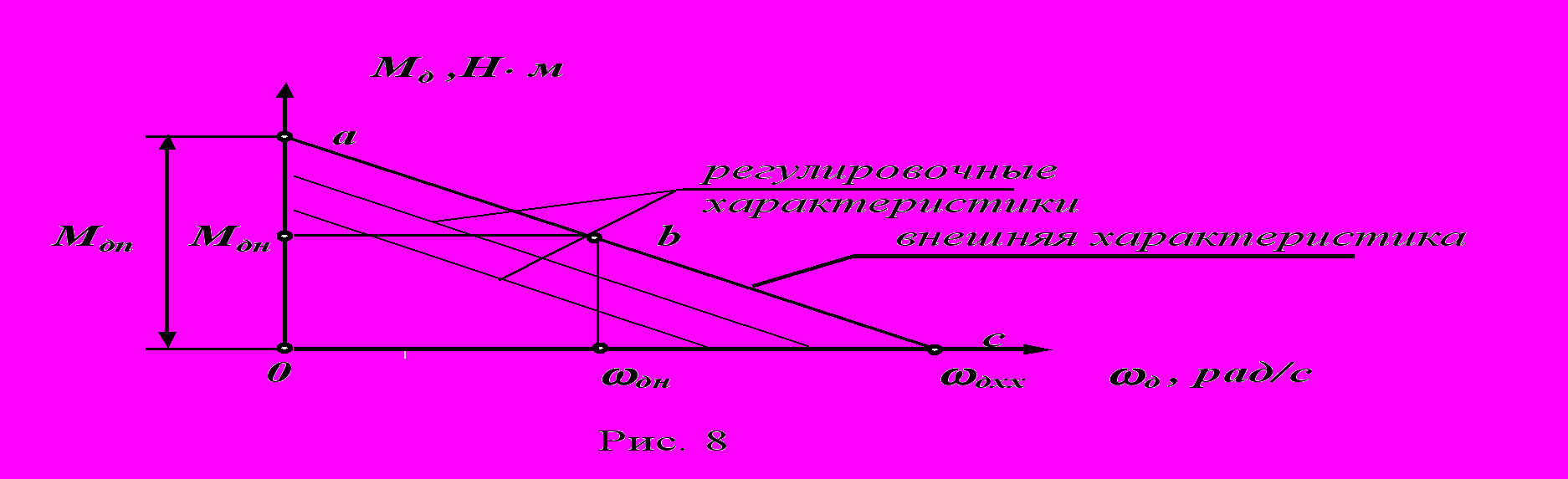
  вигатель постоянного тока с независимым возбуждением
  

Уравнение статической характеристики для двигателя постоянного тока с независимым возбуждением

М_д = M_дн + k (_дн - _д ) ,

где k = М_дн /(_дхх - _дн ).

3. Рабочие машины
   

• п
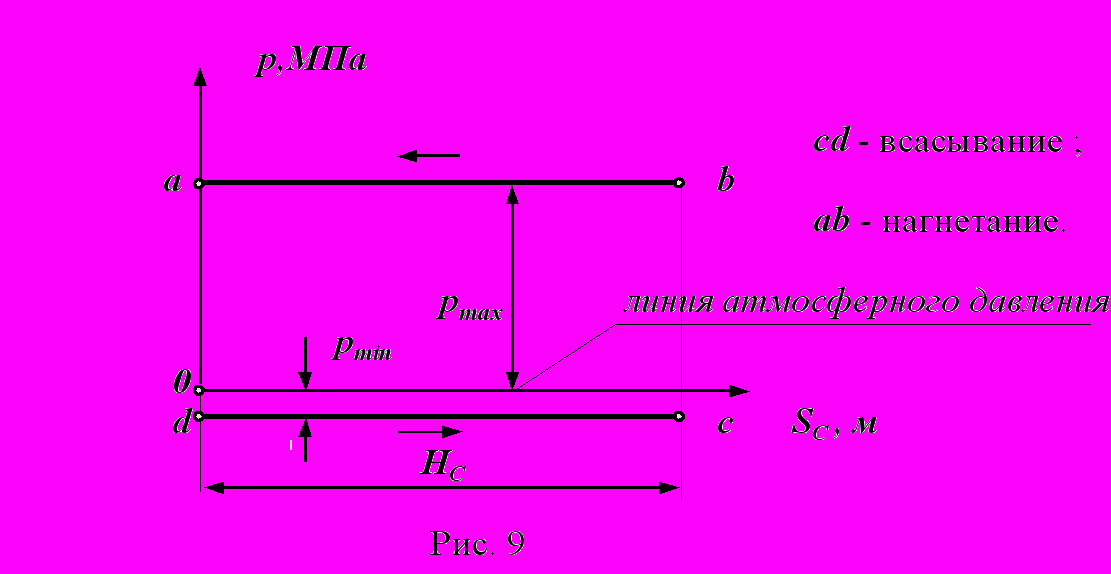
  оршневой насос
  

• п
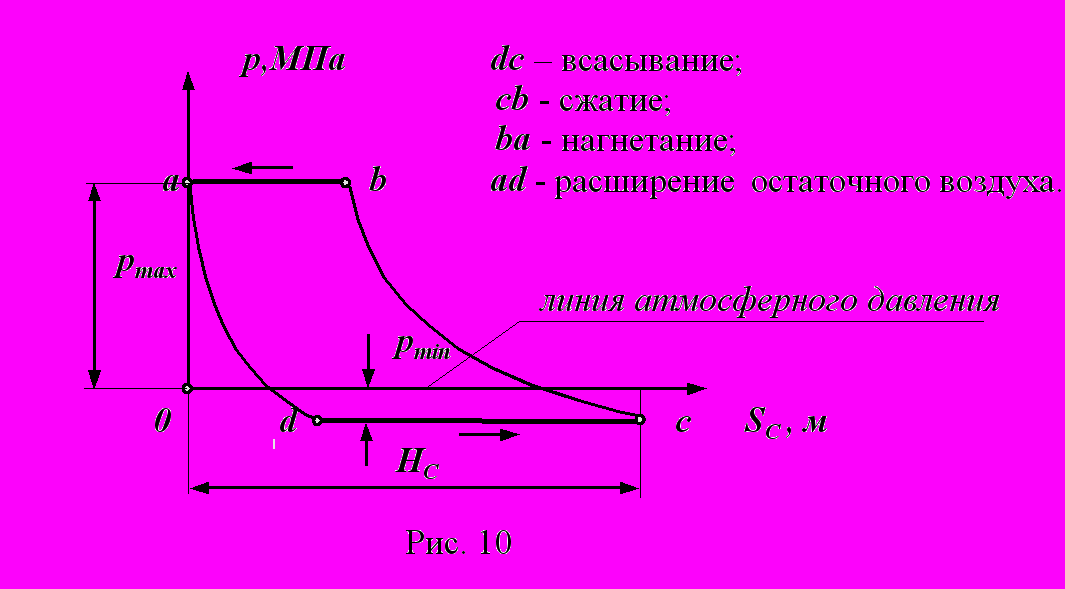
  оршневой компрессор
  

Линии cb и ad - линии сжатия и расширения газа (воздуха) определяются параметрами газа (объемом, давлением и температурой) и в общем виде описываются уравнением политропы p  Vⁿ = const , где n - показатель политропы.

• строгальный станок
  

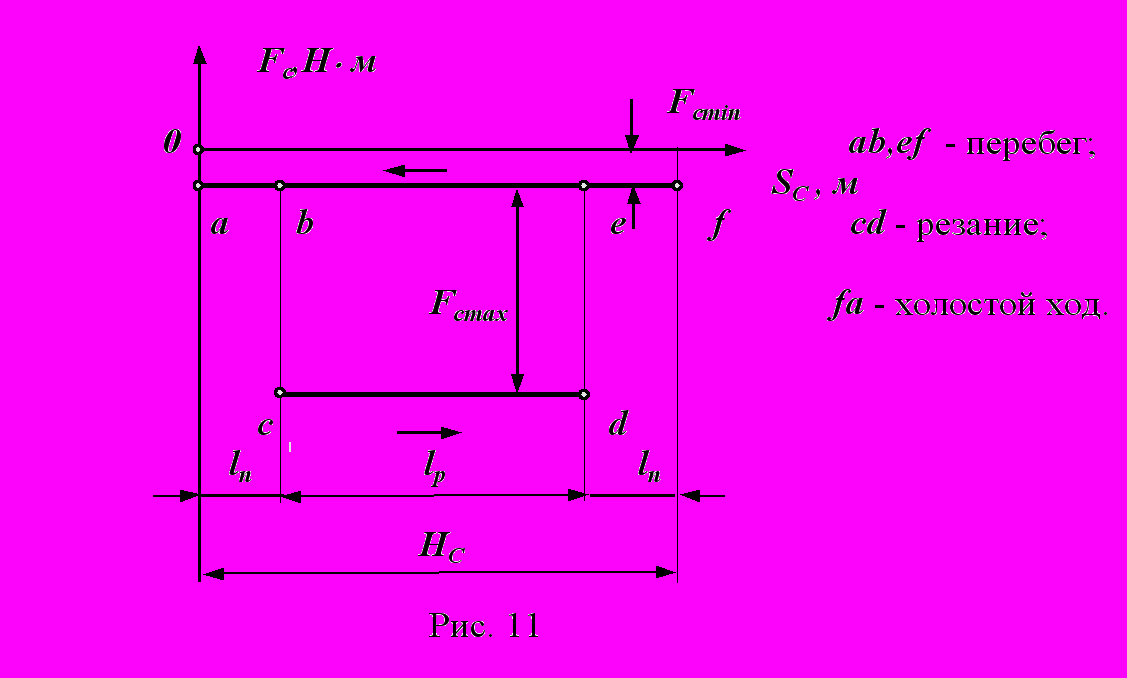
6. Этапы силового расчета механизмов.

В силовом расчете механизма можно выделить следующие этапы:

• структурный анализ механизма: определение числа звеньев, вида и класса КП, числа связей в КП механизма, числа основных и местных подвижностей, определение и устранение избыточных связей;
  
• определение всех внешних сил и моментов, включая силы веса, главные векторы и главные моменты сил инерции;
  
• декомпозиция механизма на звенья, группы или типовые механизмы, при этом число рассматриваемых подсистем или элементов должно быть равно числу неизвестных деленному на число уравнений статики для каждого рассматриваемого в силовом расчете элемента (для плоских механизмов – 3, для пространственных – 6);
  
• составление уравнений статики или кинетостатики для всех рассматриваемых элементов системы;
  
• решение полученной системы уравнений и определение неизвестных реакций (во вращательной КП по величине и направлению, в поступательной – определяется величина реакции и реактивный момент).
  

7. Силовой расчет рычажных механизмов по группам Ассура

Часто в качестве элементов системы при силовом расчете применяются структурные группы Ассура. Эти группы по определению являются статически определимыми. Поэтому система уравнений силового расчета распадается на подсистемы меньшего порядка по числу групп Ассура. При изучении курса ТММ в разделе силового расчета рассматриваются в основном простые рычажные механизмы, состоящие из простейших двухповодковых групп. Разновидностей двухповодковых групп всего пять. Рассмотрим алгоритмы решения задачи силового расчета для двухповодковых групп:

1. г
   руппа первого вида с тремя вращательными парами - ВВВ (рис. 12).
   

2. группа второго вида с двумя вращательными парами и одной поступательной - ВВП (рис. 13).
   

3. группа третьего вида с двумя вращательными парами и одной поступательной - ВПВ (рис. 14 ).
   

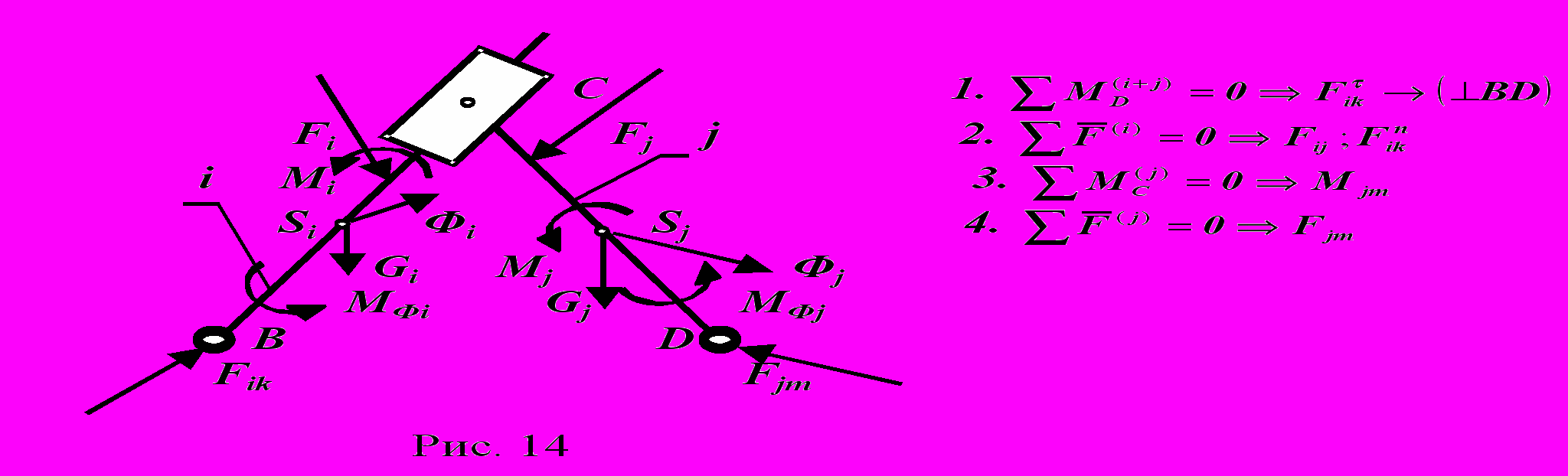
4. группа четвертого вида с двумя поступательными парами и одной вращательной - ПВП (рис. 15 ).
   

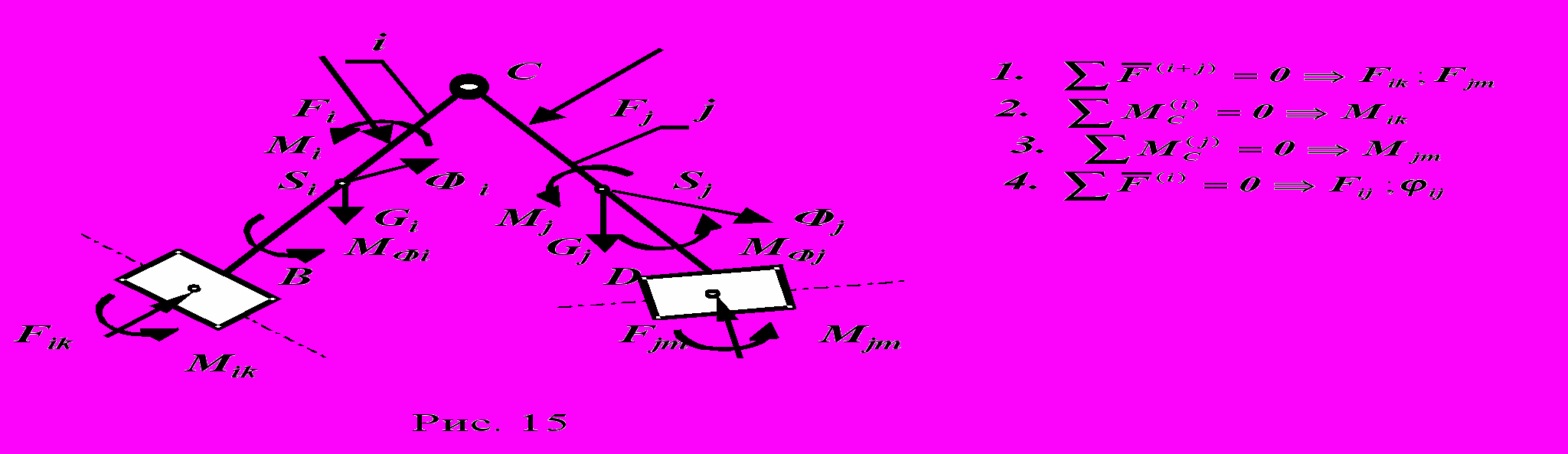
5. группа третьего вида с одной вращательной парой и двумя поступательными - ВПП (рис. 16 ).
   

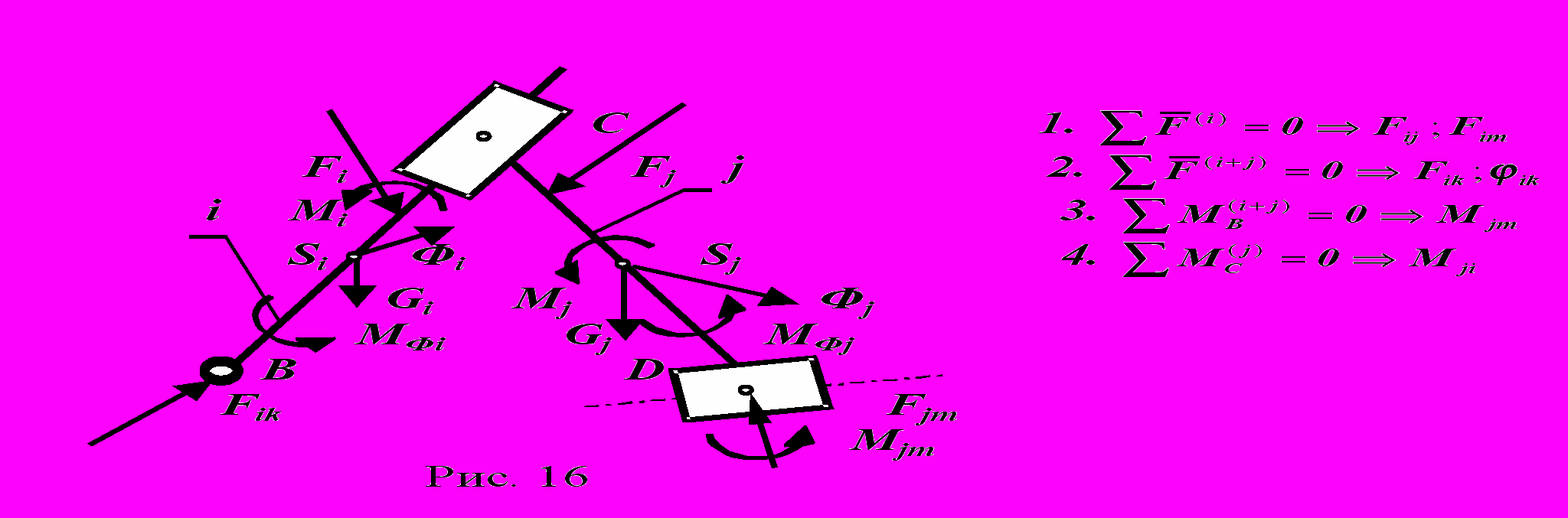
На заключительном этапе силового расчета рассматривается силовое равновесие подвижного звена 1 первичного механизма. Число возможных вариантов схем этого звена четыре:

1. з
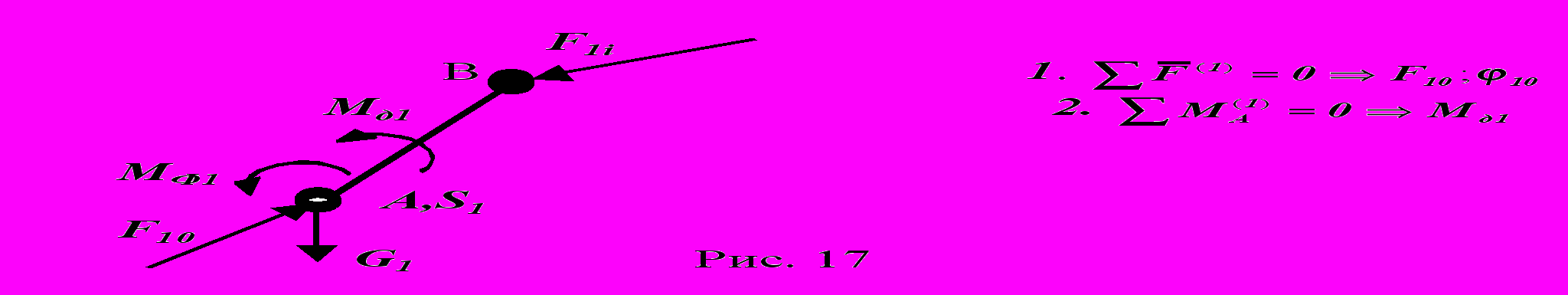
   вено 1 образует со стойкой и с подвижным звеном группы вращательные КП
   

2. з
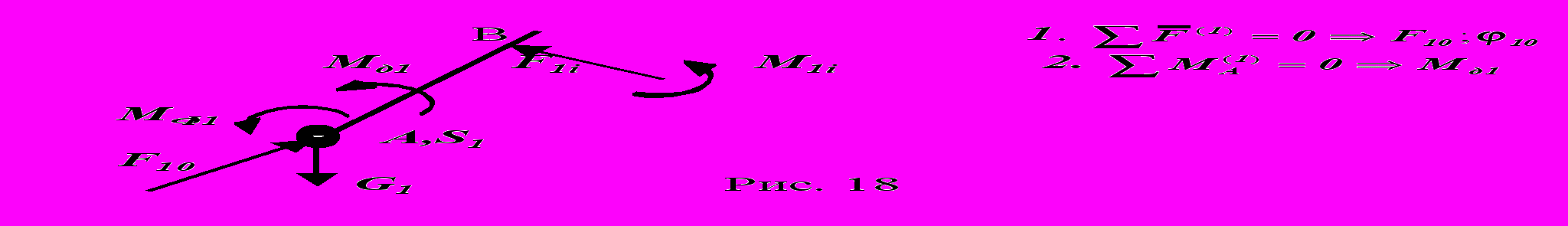
   вено 1 образует со стойкой вращательную КП, а с подвижным звеном группы поступательную КП
   

3. з
   вено 1 образует со стойкой поступательную КП, а с подвижным звеном группы вращательную КП
   

4. звено 1 образует со стойкой и с подвижным звеном группы поступательные КП
   

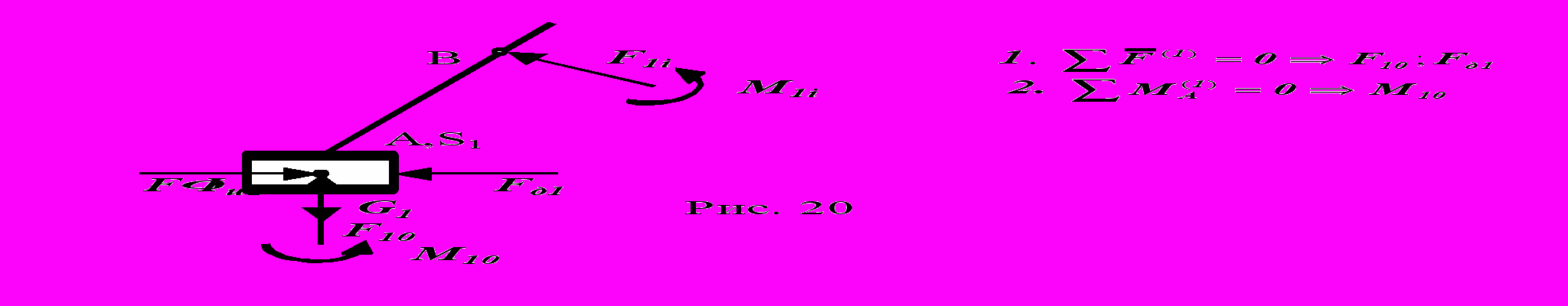
8. Кинетостатический силовой расчет типовых механизмов.

ассмотрим сложный механизм, состоящий из трех соединенных последовательно простых механизмов: зубчатой передачи, кулачкового механизма и четырехшарнирного рычажного механизма (рис. 21).


Рис. 21



M_c5 M_д1



Четырехшарнирный механизм Зубчатая передача




М_д3 = -М_с3 М_д2 = -М_с2




Кулачковый механизм
Представим этот механизм в виде комбинации типовых механизмов:


Рис. 22


8.1.Кинетостатический расчет зубчатой передачи (метод планов сил).

При проведении расчета нам необходима информация о размерах зубчатых колес и положении контактной нормали в высшей КП. Для эвольвентной передачи необходимо знать радиусы основных r_b1 ,r_b2 или начальных окружностей r_w1 , r_w2 и угол зацепления _w, т.к

r_bi = r_w1  cos _w .

По этим размерам в масштабе изображается кинематическая схема механизма, на которую наносятся все известные силы и моменты. Главные вектора и моменты сил инерции рассчитываются по формулам

Ф_i = - m_i a_Si, M_Фi = I_Si_i ,

так как кинематические параметры a_Si, _i механизма при кинетостатическом расчете заданы.

Примечание: Необходимо отметить, что определение линейных ускорений центров масс и угловых ускорений звеньев, расчет главных векторов и главных моментов сил инерции и расчет сил веса являются предварительными или подготовительными этапами в кинетостатическом силовом расчете. На этих этапах подготавливаются или преобразуются исходные данные. Результаты расчета на этих этапах не входят в результаты силового расчета.


2 r_w2 1

₂ Дано: r_i, _w , I_Si, m_i,

M_Ф2 n M_Ф1 ₁,₁, ₂,₂,

₁ r_b2 M_c2

B_1в ,S₂ P_2вп A_1в,S₁

₁ Определить: M_д1 , F_ij.

M_c2 r_w2

M_д1

0 ₂ _w n

r_b2


Рис. 23

Определим подвижность, число избыточных связей в механизме, а также число неизвестных в силовом расчете:


W_пл = 3 2 - 22 - 11 = 1, q_пл = 1 + 0 - 1 = 0, n_s = 22 + 11 + 1 = 6,

т.е. в нашем механизме неизвестно 6 компонент реакций, для решения задачи силового расчета необходимо составить 6 уравнений кинетостатики. Структурный анализ механизма показывает, что механизм состоит из одного первичного механизма (звено 1 и стойка) и монады (структурной группы, состоящей из одного звена 2). Анализ начнем со второго звена так, как к нему приложен заданный момент спротивления.

1. Звено 2.
   

Расчетная схема для звена 2 приведена на рис. 24. Уравнения равновесия для звена 2:

векторное уравнение силового равновесия

_{_ _ _ _}

 F = 0; F₂₁ + G₂ + F₂₀ = 0;

^??

уравнение моментов относительно точки В


 M_B = 0; M_c2 + M_Ф2 + F₂₁ r_b2 = 0.


r_w2

F₂₀ p_F _F , мм/Н

M_Ф2 n ₂ F₂₀

N₂

F₂₁

M_c2 B_1в S₂ P