Сценарий урока по теме "Решение квадратных неравенств"

Вид материала

Сценарий

Содержание Ситуация коммуникации.

Подобный материал:

• Урока алгебры и информатики «система счисления. Решение задач с помощью квадратных, 98.53kb.
• «Решение квадратных неравенств», 20.58kb.
• Сценарий урока №2 "Решение полных квадратных уравнений", 15.69kb.
• Решение квадратных уравнений Цели урока, 92.37kb.
• Методические рекомендации к проведению урока: «Методы решения уравнений и неравенств., 15.21kb.
• Решение неравенств. Равносильные неравенства, 46.71kb.
• Урок алгебры в 8 классе с применением информационных технологий по теме «Решение квадратных, 94.17kb.
• Программа элективного курса Рецензенты, 53.18kb.
• Элективный курс по математике, 37.2kb.
• Элективный курс «Решение уравнений и неравенств» Класс: 11 Профиль класса: общеобразовательный, 47.74kb.

Слепых М.В.

ГОУ СОШ №597

СЦЕНАРИЙ УРОКА

по теме

"Решение квадратных неравенств"

(алгебра, 9 класс, аналитический метод, приводящий к системе)

1. Знают:
   
   1. метод решения линейных неравенств с одной переменной;
      
   2. метод решения систем неравенств с одной переменной;
      
   3. разложение на множители квадратного трехчлена.
      
      
      
2. Тренировочные задания:
   
   1. ;
      
   2. ;
      
   3. .
      
      
      
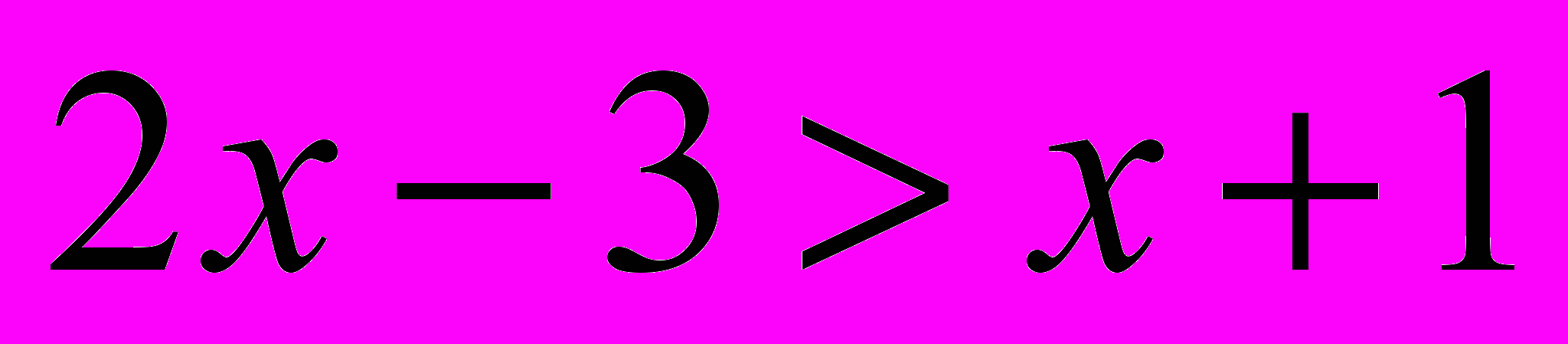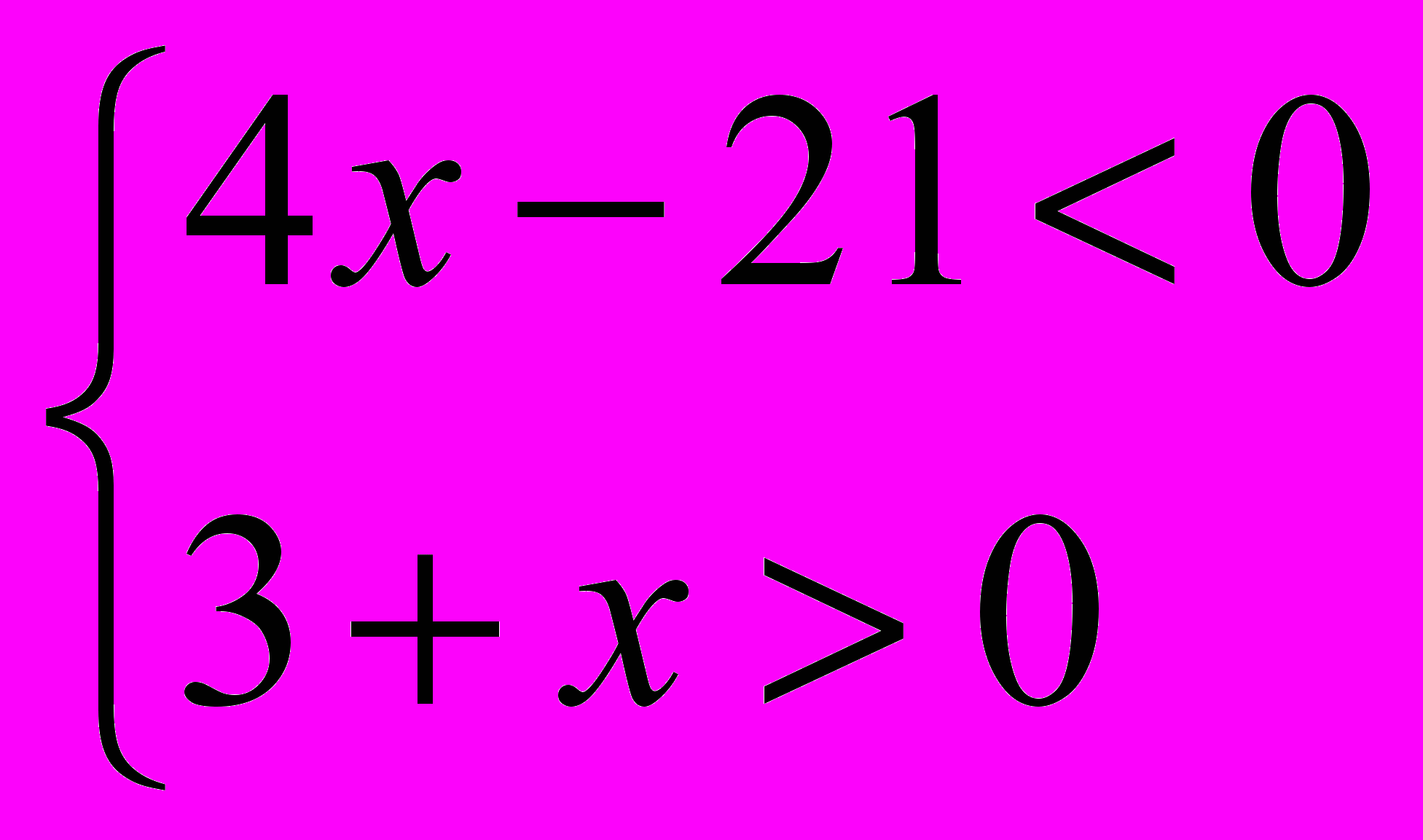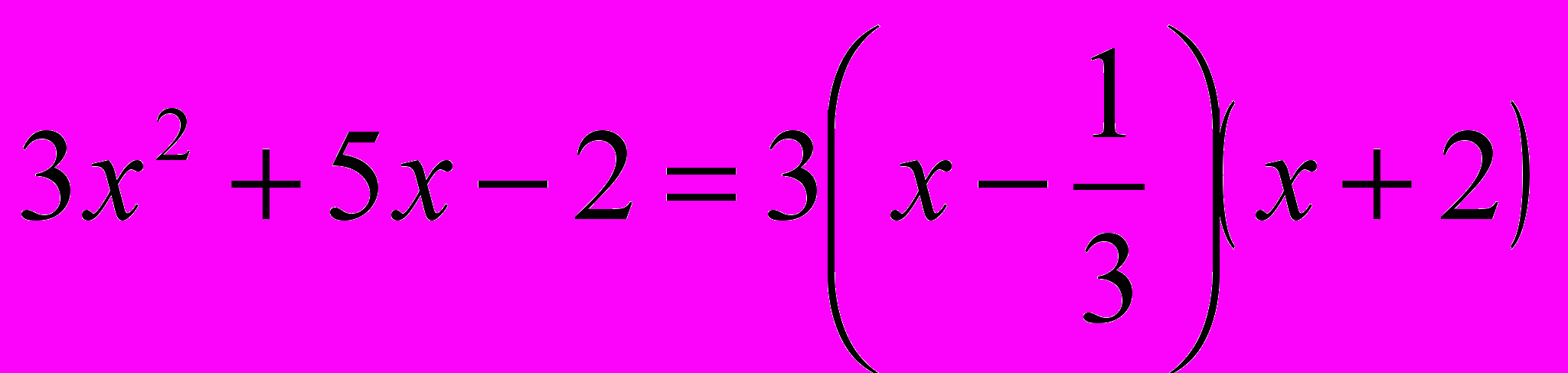3. Задание 1 (метод 1)
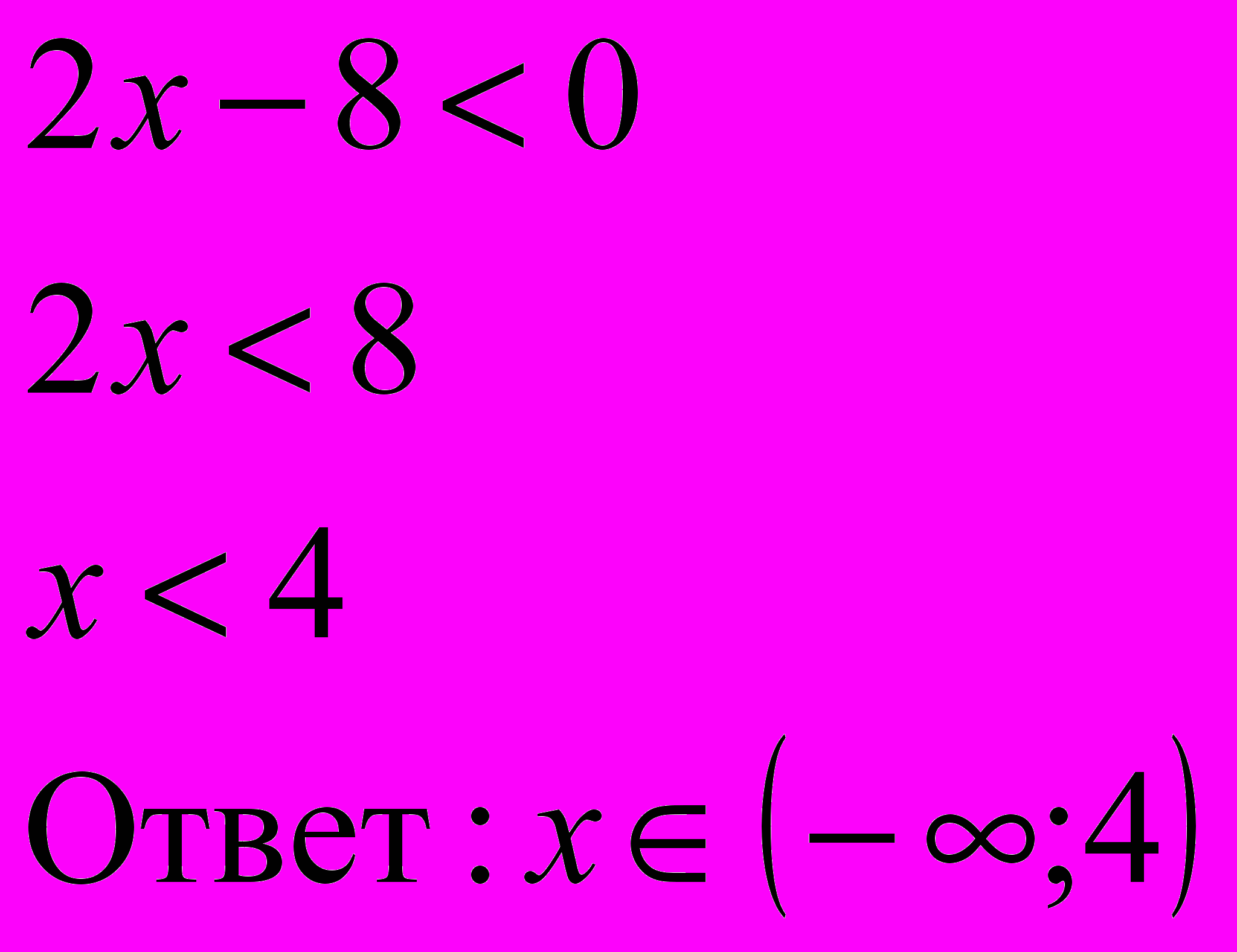   4
   Какие равносильные преобразования выполнили:
   
   1. прибавили к двум частям неравенства 8;
      
   2. разделили обе части неравенства на положительное число 2.
      
      
      

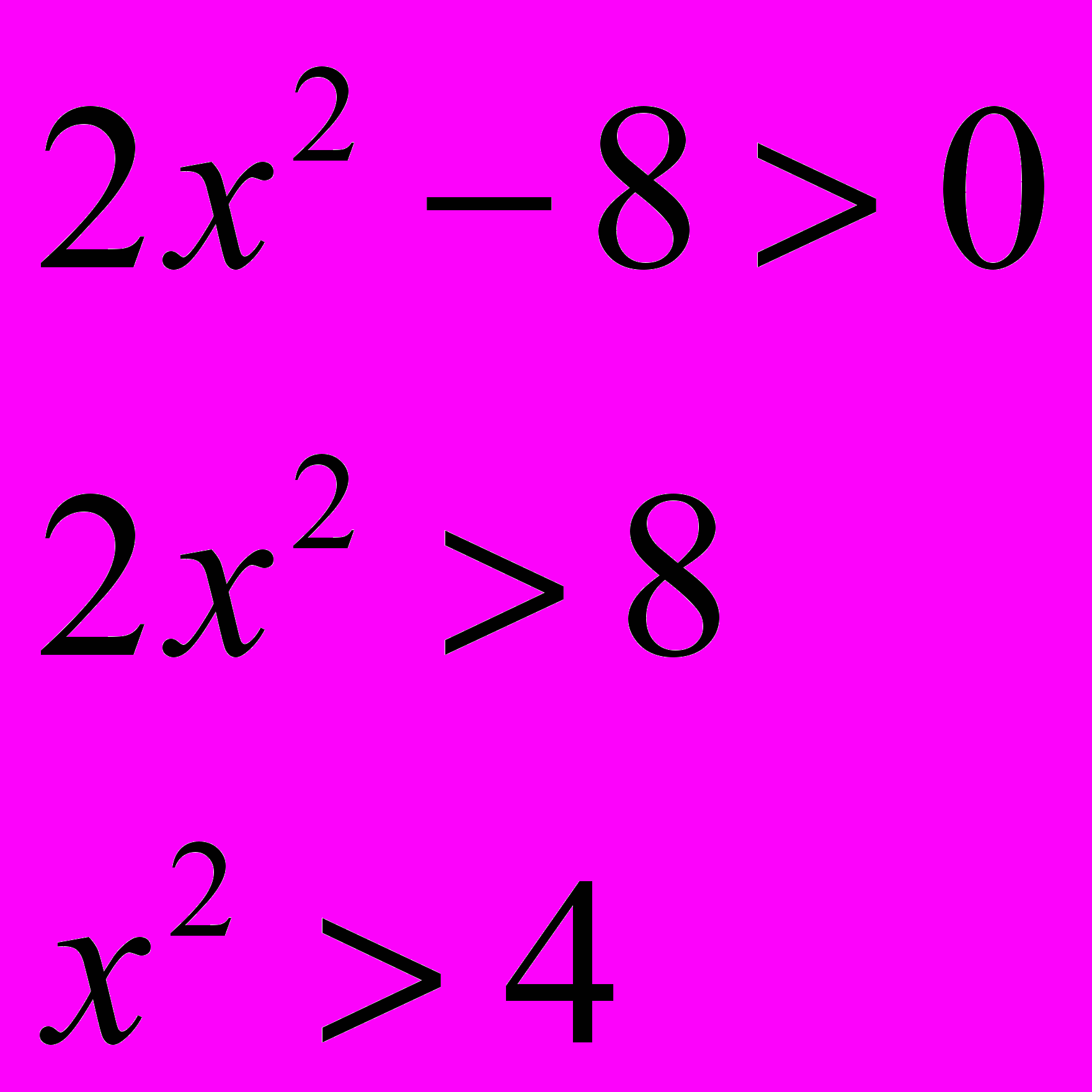
З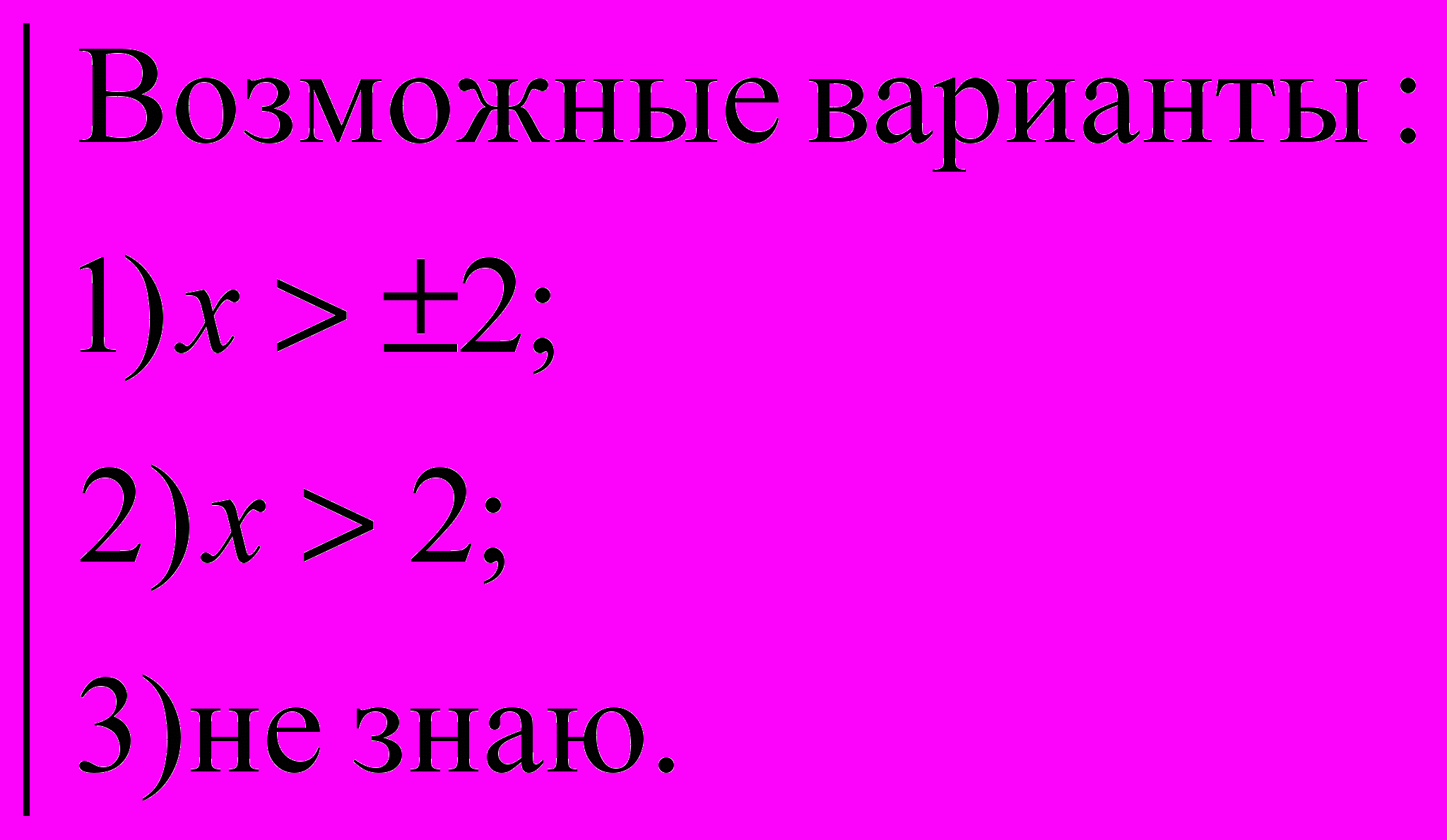адание 2 (метод 2)


Действия учителя:
Варианты 1, 2 отобразить решения на координатной прямой:

1. 
   -2 2
   
2. 
   2
   Выполнить проверку: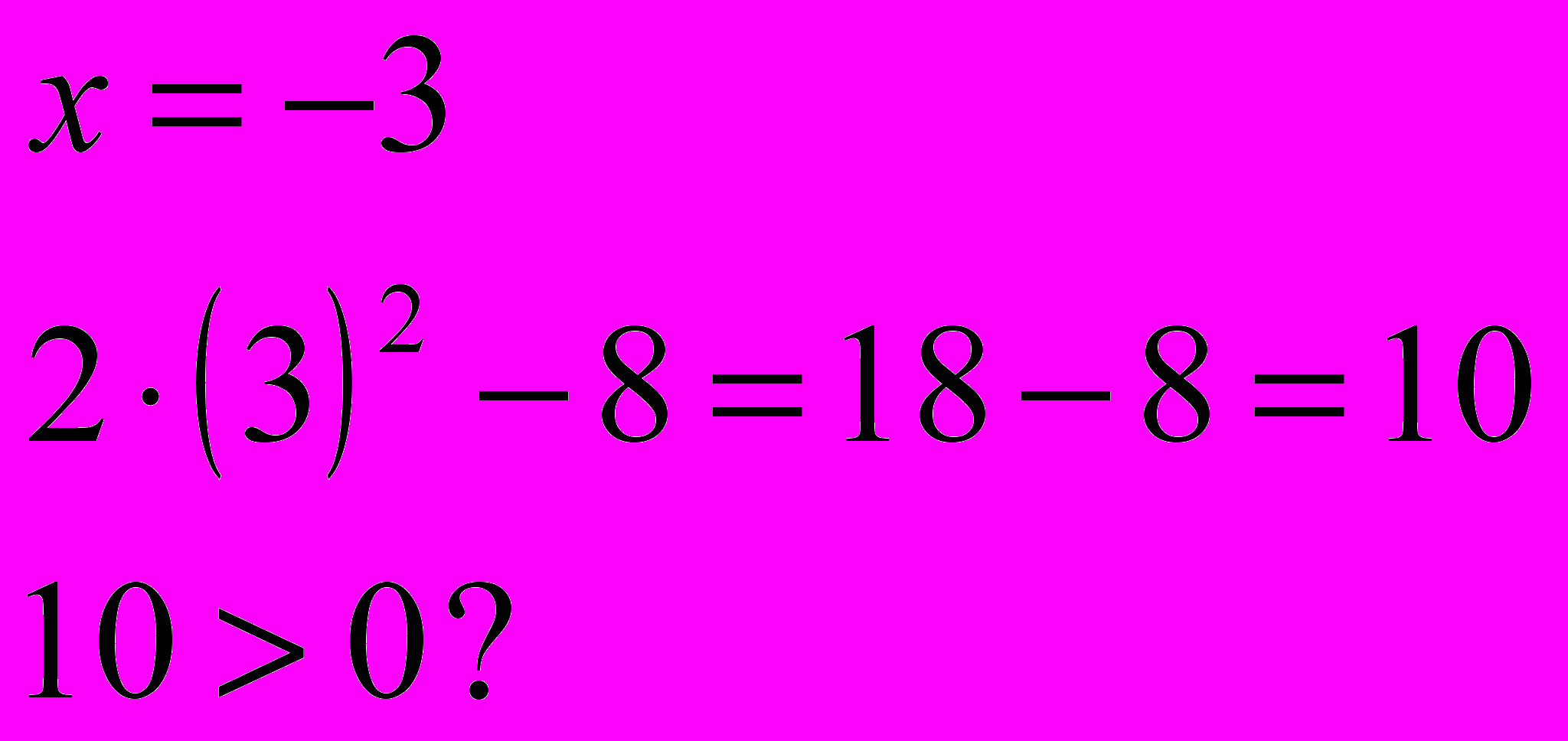
   
   Вернуться к решению и определить:
   
   1. какое дополнительное преобразование, по сравнению с предыдущим примером сделано (извлечение корня);
      
   2. можем ли мы выполнять такое преобразование в неравенствах.
      (Работа в группах по поиску выхода)
      

Предлагаемый выход из ситуации:



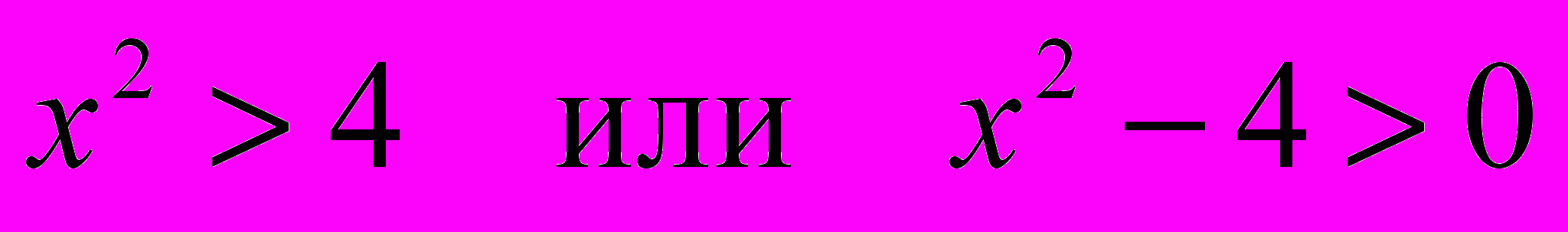
Какое преобразование можно сделать с левой частью неравенства?


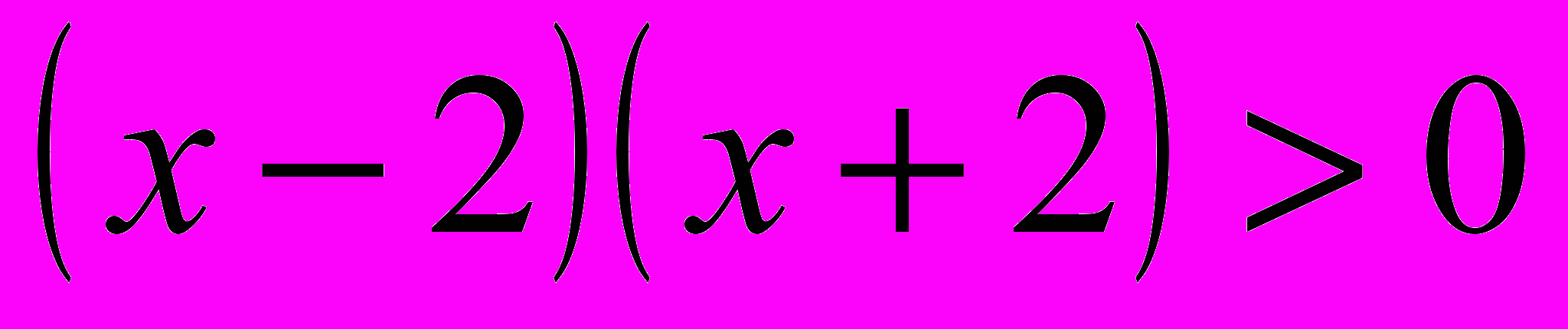
Когда произведение больше нуля? (Оформить данный вопрос должны учащиеся)






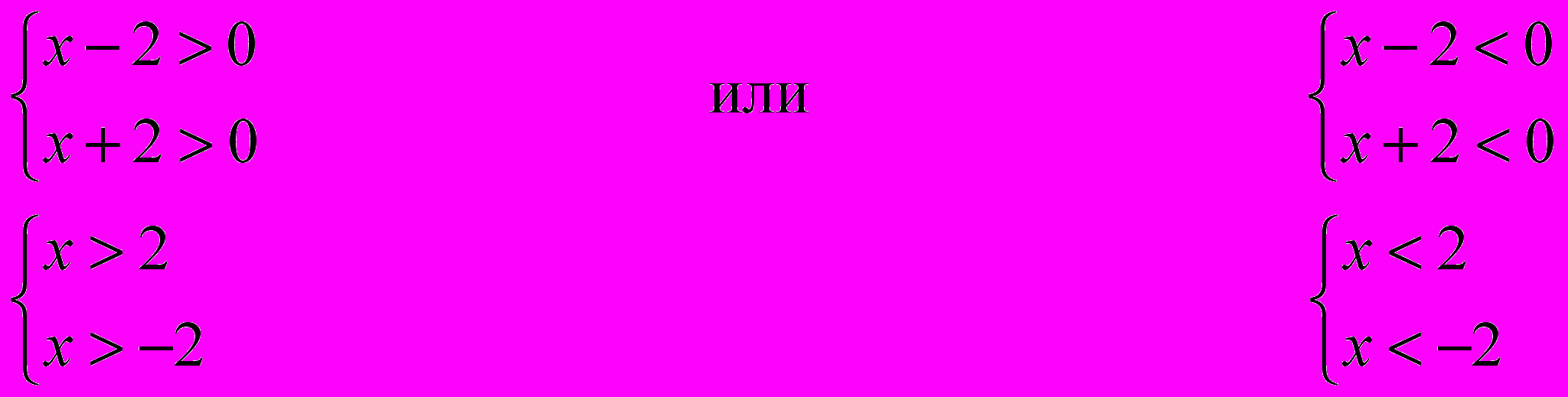
-2 2 - -2 2



Ответ: .

1. 
   
2. 
   
3. 
   
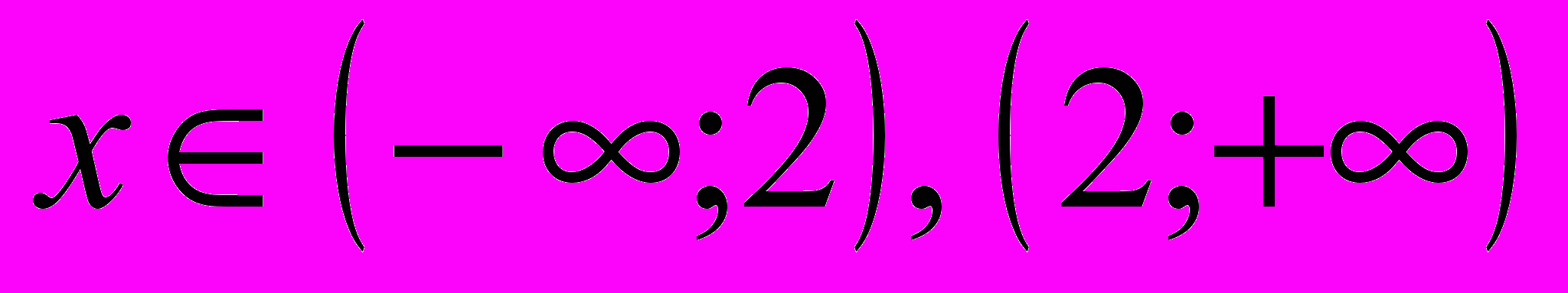4. Отработка метода 2.
   
   1. ;
      
   2. ;
      
   3. .
      
      
      
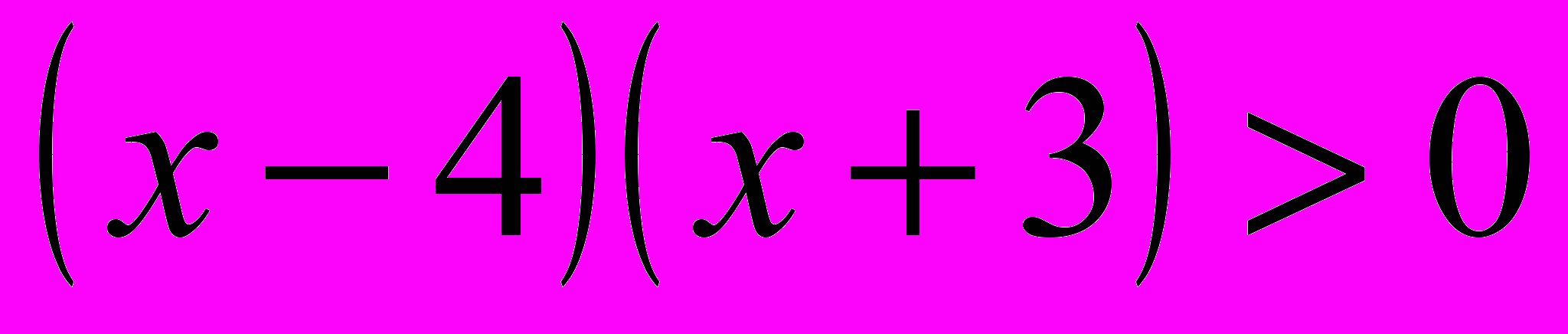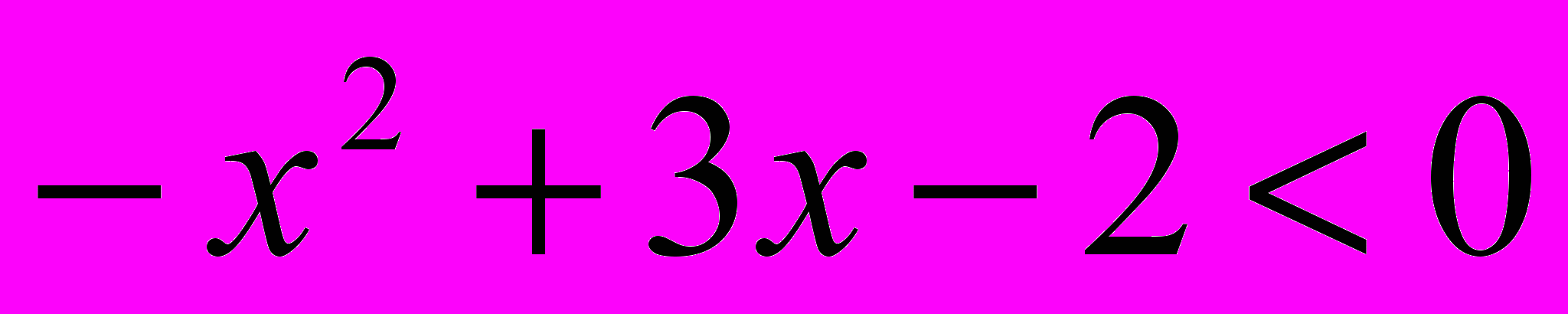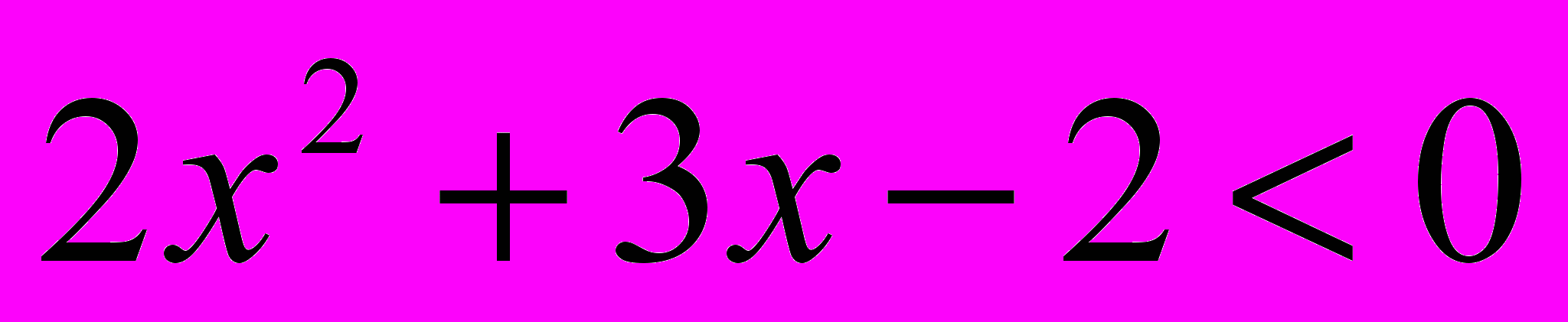5. Рефлексия.
   Метод 1 не применим, так как появилась необходимость новых преобразований, которые приводят к равносильному неравенству.
   

Ситуация коммуникации.

Занятие проводиться для конструирования учащимися методов решения квадратных неравенств. Имеется два способа решения квадратных неравенств – алгебраический, путем перехода от квадратного неравенства к двум системам линейных неравенств, и графический, основанный на построении графика квадратичной функции и определении интервалов положительного и отрицательного значения функции.

Наиболее распространенная ошибка при решении неполных квадратных неравенств детьми – перенос способов решения уравнений на неравенства.

В сценарии заложена работа по анализу такой ошибки, рефлексия метода решения, доказательство неправильности решения и выход на необходимость поиска нового решения.

Далее предполагается выход детей на конструирование одного их двух (или двух сразу) способов решения квадратных неравенств, однако логика повторения должна вывести их на метод составления систем неравенств.