2 Методы оптимизации в задачах концептуального проектирования и логистики

Вид материала

Задача

Содержание 1.Эвристические методы, основанные на правилах 2.Линейное целочисленное программирование. Методы локальной оптимизации. Методы сокращения интервалов и распространения ог­раничений Генетические алгоритмы

Подобный материал:

• Программа дисциплины " методы оптимизации " Направление, 59.57kb.
• Методическое пособие к курсу лекций "Логистика" (в схемах, таблицах, определениях), 1325.21kb.
• Оптимизация в задачах аналитической логистики, 87.71kb.
• Календарный план учебных занятий по дисциплине Компьютерный дизайн оптических наноструктур,, 39.38kb.
• Магистерская программа: Менеджмент в электроэнергетике Квалификация (степень) выпускника:, 133.56kb.
• Сибирский банковский учебный центр проводит, 87.42kb.
• Конспект лекций по Методам оптимизации для студентов, обучающихся по специальности, 41.05kb.
• Концепция системного подхода при проектировании сапр. Последовательный метод компоновки, 29.25kb.
• Учебной дисциплины «Методы оптимизации» для направления 010400. 62 «Прикладная математика, 40.12kb.
• Рабочая учебная программа по дисциплине «Методы оптимизации» Направление №230100 «Информатика, 129.28kb.

2.4.6. Методы оптимизации в задачах концептуального проектирования и логистики

Проблема представления данных в CALS-технологиях включа­ет не только вопросы грамматики единого языка описания объек­тов, в качестве которого в STEP используется язык Express, но и семантические аспекты представляемых данных, отраженные в настоящее время в интегрированных ресурсах и прикладных протоколах STEP. Выделение приложений для создания стан­дартных информационных моделей происходит или по предметной области проектируемых объектов (например, прикладные протоколы для электротехнической промышленности, литейного производства, автомобиле- и судостроения, строительства и др.), или по методам и процедурам оперирования данными на этапах жизненного цикла изделий (например, управление конфигурацией проектов, оформление документов, в том числе чертежей, взаимо­действие разных проектирующих систем и т.п.)

Очевидно, что на различных этапах жизненного цикла изделий наряду с информационными моделями часто необходимо использовать поведенческие имитационные модели и методы оптимизации процессов и изделий. В результате в некоторых приложениях появились методики и языки структурного и поведенческого моделирования, получившие статус международного стандарта. Примерами могут служить языки APT описания технологических процессов, методика функционального проектирования IDEFO или язык моделирования дискретных электронных устройств VHDL.

Однако в отношении процедур оптимизации и принятия решений желательная степень общности и унификации пока не достигнута. Интегрированные средства принятия решений, подобные разрабо­танным для моделирования с помощью метода конечных элемен­тов в стандарте ISO 10303-104, не созданы. Основная причина этого заключается в сложности как постановки многих задач проектиро­вания и управления, так и построения эффективных вычислитель­ных процедур оптимизации. В то же время практическая потреб­ность в методиках принятия обоснованных, близких к оптималь­ным решений довольно велика. Особая значимость придается ме­тодикам оптимизации на этапах концептуального проектирования и логистической поддержки производства сложной техники, так как именно на этих этапах материальные и временные потери от нера­циональных решений наиболее значительны.

Этот подраздел посвящен рассмотрению существующих под­ходов к оптимизации, обладающих повышенной степенью общнос­ти и ориентированных на применение к многомерным задачам структурного синтеза при проектировании, в информационной ло­гистике и управлении проектами. Сущность этих подходов выра­жают методы эволюционные и распространения ограничений.

Как отмечено выше, под информационной логистикой пони­мают раздел логистики, занимающийся вопросами организации и использования систем информационного обеспечения, планирова­ния и управления производственно-хозяйственными процессами на предприятии. Содержанием задач информационной логистики яв­ляется планирование работ, распределение ресурсов и управ­ление проектами. Значительное место в логистических системах занимают задачи транспортной логистики, нацеленные на опреде­ление во времени последовательности событий, совершаемых в процессе транспортировки грузов.

Методы структурного синтеза для многих практически важных приложений, включая концептуальное проектирование и логистику, могут быть созданы на базе генетических алгоритмов, к которым поэтому в настоящее время проявляется заметный интерес.

Важным и обширным множеством приложений, в которых для синтеза целесообразно применять генетические алгоритмы, явля­ется планирование производства и распределение ресурсов, вклю­чая задачи проектирования технологических процессов производ­ства изделий. Возникающие здесь задачи можно трактовать как задачи синтеза расписаний. Другими примерами приложений гене­тических методов синтеза могут служить компоновка и размеще­ние оборудования, диспетчирование потоков работ, распределение частот в радиоканалах сетей мобильной связи, проектирование подвески автомобиля и др.

В CALS-технологии первым шагом в формализации задач ана­лиза логистических процессов является построение функциональ­ной модели приложения по методике IDEFO. На их базе создаются имитационные модели, используемые для расчета длительности Т процессов. В имитационной модели должны быть отражены сле­дующие компоненты процесса.

1. Структура процесса, выражаемая совокупностью выполняе­
   мых операций (функций) с возможным их полным или частичным
   упорядочением. В IDEFO-моделях операции представлены блоками
   ICOM (см. рис. 2.5).
   
2. Входные потоки заявок (транзактов) с указанием их типов и
   моментов поступления на входы. Внутри системы, реализующей
   процесс, заявки могут разветвляться и объединяться. Заявка или
   ее часть, появляющаяся на входах I, С или выходе О блока ICOM,
   далее называется работой, а выполнение одной работы на одной
   операции - шагом процесса.
   
3. Ресурсы М для выполнения процесса. Ресурсы - компонен­ты обеспечения деятельности, включающие исполнителей, энергию, материалы, оборудование и т.д. Ресурсы могут быть неразделяе­мыми и разделяемыми. Каждая единица неразделяемого, иначе унарного (unary), ресурса, называемая далее сервером, может одновременно использоваться только одной работой, и работа не
   может использовать более одного сервера в одно и то же время.
   Разделяемый, иначе объемный (volumetric), ресурс может распре­деляться между работами в том или ином отношении.
   

Правила распределения ресурсов. В частном случае ресур­сы могут быть жестко закреплены за операциями. В общем случае выделение ресурсов некоторой операции зависит не только от ее типа, но и от характеристик входных потоков заявок. Поэтому распределение ресурсов между работами не может быть осуществ­лено до конкретизации входных потоков, заранее могут быть зада­ны лишь ограничения на ресурсы. Следовательно, распределение ресурсов должно быть частью моделирования. Под распределе­нием ресурсов при этом понимается порядок выбора работ из оче­редей на входах блоков ICOM для их обслуживания, назначение унарных ресурсов, выбор направления движения транзакта в не­однозначных ситуациях, размер объемных ресурсов, выделяемых на очередном шаге процесса.

Имитационные модели процессов в случае фиксированного рас­пределения ресурсов по операциям сравнительно просты. В каче­стве таких моделей часто используют цветные сети Петри, при этом функции исходных IDEFO-моделей преобразуются в перехо­ды, работы - в маркеры, очереди - в позиции. На рынке программ­ных продуктов имеются средства для преобразований IDEFO-моделей в имитационные, например, известная программа CPN/Design предназначена для представления IDEFO-моделей в виде цветных сетей Петри.

Распределение ресурсов необязательно непосредственно свя­зано с имитационным моделированием. Обычно оно является со­ставной частью задач планирования производственных процессов, перевозок грузов, учебных занятий и др. Особое место среди этих приложений отводится управлению проектами. Управление про­ектами (project management) - вид деятельности, включающий пла­нирование, контроль за выполнением работ и коррекцию плана пу­тем применения современных методов управления.

В логистических задачах оптимизации необходимо так распре­делить работы во времени и ограниченные ресурсы между рабо­тами, чтобы минимизировать целевую функцию, выражающую один или несколько различных критериев.

Таким образом, оптимизационные задачи рассматриваемого класса характеризуются следующими особенностями.

1. Широкие диапазоны размеров задач, причем в ряде случаев
управления проектами число работ может составлять десятки тысяч.

2. Наличие среди управляемых параметров величин разного типа
(действительных, целочисленных, булевых, лингвистических).

3. Известна модель приложения, с помощью которой можно
   оценивать качество альтернативы, т.е. вычислять значения крите­риев качества. Обычно число критериев оказывается более одно­го, т.е. имеет место многокритериальность.
   
4. Наличие ограничений, причем целевая функция и ограниче­ния в общем случае оказываются нелинейными.
   
5. Возможна декомпозиция исходной задачи на частные (локаль­ные) подзадачи, в которых последовательно определяются элементы множества управляемых параметров X, однако количествен­ные зависимости между сформулированной целевой функцией F(X) и частными целевыми функциями ψ_i(х_i) в подзадачах остаются неизвестными.
   

В этих условиях точные методы дискретной оптимизации ока­зываются неприменимыми. На практике используются декомпо­зиционные эвристические методы с применением субъективно выбираемых частных целевых функций ψ_i(х_i). К сожалению, сте­пень приближения к оптимальному результату при этом может ока­заться крайне низкой по следующим причинам.

Во-первых, априорный удачный выбор эвристики (частной це­левой функции) маловероятен и при этом апостериорная оценка точности результата невозможна.

Во-вторых, эффективность применения любой эвристики зави­сит от конкретной ситуации в процессе поиска, и поскольку ситуа­ции меняются, то и эвристики должны изменяться при переходе от одной подзадачи к другой. Однако в используемых эвристических методах это обстоятельство не учитывается.

Одним из основных условий успешной реализации задач струк­турного синтеза в САПР является наличие методов, обеспечива­ющих поиск решения, близкого к оптимальному, с приемлемыми затратами вычислительных ресурсов. В настоящее время для ре­шения оптимизационных задач концептуального проектирования и логистики используют следующие подходы.

1.Эвристические методы, основанные на правилах (rule based systems). Правила зачастую являются некоторым обобще­нием имеющегося опыта решения задач конкретного приложения и представлены в виде продукционной экспертной системы или семантической сети. По своей сути это не оптимизационные мето­ды, так как ставится задача найти любой приемлемый по предъяв­ленным требованиям вариант структуры. В этих методах обычно реализуется поиск в глубину и бектрекинг (backtracking), что мо­жет привести к полному перебору вариантов. Для малой размерно­
сти задач это вполне приемлемо. Однако с увеличением размерно­
сти задач нужно переходить к другим методам.

2.Линейное целочисленное программирование. Это эффек­тивный подход в случае непрерывных и целочисленных целевых функций и ограничений, являющихся линейными. Требование ли­нейности ограничивает возможности применения методов линей­ного программирования, поскольку во многих приложениях исполь­зуемые модели оказываются нелинейными.

3. Методы локальной оптимизации. Эти методы успешно
используются для поиска локальных экстремумов в метризован­ных пространствах. К сожалению, велика вероятность «застрева­ния» текущей точки на траектории поиска вдали от глобального экстремума. Чтобы уменьшить эту вероятность, применяют по­иск с запретами (tabu search), в котором запрещается переход в некоторые точки, в том числе в точки, пройденные на нескольких
последних итерациях поиска. Спуск происходит в лучшую из прой­денных на очередной итерации точек, даже если эта точка хуже
результата предыдущей итерации. Тем самым облегчается выход из локальных экстремумов.

Преимущественное применение для решения охарактеризован­ного выше класса задач получили методы следующих двух групп, иногда в сочетании с методами локальной оптимизации.

4. Методы сокращения интервалов и распространения ог­раничений (domain reduction and constraint propagation). Эти мето­ды могут применяться для задач с ограничениями и переменными различных типов. В них задаются некоторыми исходными интер­валами (domain) неизвестных, эти интервалы сокращают путем
   учета имеющихся ограничений. Сокращенные интервалы в явном
   виде определяют подмножество допустимых решений. Так, если управляемые параметры являются числовыми, то полученное допустимое подмножество определяется прямыми ограничения­ми вида x_min ≤ х_i ≤ х_max где
   х_i - управляемый параметр, х. и
   х — его предельно допустимые минимальное и максимальное
   значения. Распространение ограничений выражается в увеличении
   нижних х_{ю1л t} и в уменьшении верхних х_тк1. границ интервалов. При
   нечисловых управляемых параметрах распространение ограниче­
   ний приводит к сокращению списка возможных вариантов струк­
   туры. В том случае, когда требуется найти не подмножество допу­
   стимых вариантов структуры, а экстремальный вариант в этом
   подмножестве, нужно дополнительно сформулировать целевую
   функцию и использовать какой-либо метод поиска в сокращенном
   подмножестве структур.
   

Генетические алгоритмы и методы отжига. Генетичес­кие алгоритмы относятся к наиболее универсальным подходам к
решению сложных задач структурного синтеза и подробно обсуж­даются далее. Методы отжига можно рассматривать как реализа­цию идеи повышения вероятности определения глобального экст­ремума в других статистических методах оптимизации, таких, какгенетические или локальные методы поиска.

Рассмотрим идею отжига применительно к методу локальной оптимизации.

Собственно понятие «отжиг» в оптимизацию пришло из термо­динамики в связи с аналогией поиска экстремума и моделирова­ния процесса отжига металлов. При охлаждении жидкого металла переход термодинамической системы из состояния с энергией Е_} в состояние с энергией Е₂ происходит с вероятностью




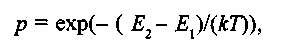
(2.1)

где k - постоянная Больцмана; Т - температура.

Чтобы достичь состояния с минимальной энергией, что соот­ветствует отжигу, нужно обеспечить возможность выхода из локаль­ных энергетических минимумов, что означает при Е₂> Е₁ увеличе­ние р и, следовательно, увеличение Т.

При оптимизации аналогом энергии является целевая функция и для увеличения вероятности выхода из областей притяжения локальных минимумов нужно, в отличие от базового метода локаль­ной оптимизации, разрешить переход в точки с худшим значением целевой функции с вероятностью p, определяемой по формуле (2.1). При этом Е₂ и Е₁- значения целевой функции в исследуемой и приня­той точках поиска, Т- параметр поиска.

Практически все реализуемые методы синтеза являются при­ближенными. Например, каждая эвристика, используемая для син­теза расписаний, включает несколько правил: одно - для выбора очередной работы, другие - для выделения этой работе на рас­сматриваемом шаге процесса определенных ресурсов.

Простейший подход основан на применении на всех шагах син­теза одной и той же эвристики. Так, при синтезе расписаний эвристика может включать выбор работы по правилу FIFO и выбор ресурсов, обеспечивающих наиболее быстрое завершение шага. Подобный моноэвристичный подход не требует заметных вычис­лительных затрат и сравнительно легко реализуем. Однако он оставляет без использования другие возможные эвристики, и поэто­му решение может оказаться вполне подходящим по одному критерию, но не удовлетворительным по другим показателям. Как показывают практические расчеты, моноэвристичный подход чаще всего приводит к заметным отличиям получающихся решений от оптимальных.

Получение расписаний, близких к оптимальным, возможно с помощью многоэвристичных методов, позволяющих на каждом шаге синтеза использовать ту эвристику из числа возможных, которая в наибольшей степени соответствует складывающейся кон­кретной ситуации. Такая постановка относится как к самостоятель­ным задачам синтеза оптимальных расписаний для производствен­ных и бизнес-процессов, так и ко многим другим логистическим задачам, в которых структурный синтез осуществляется посред­ством многократного моделирования процессов в CALS-средах. Многоэвристичный подход успешно реализован в методе комбини­рования эвристик, рассматриваемом далее.