Гармонический анализ периодических импульсных последовательностей
| Вид материала | Лабораторная работа |
- Календарный план учебных занятий по дисциплине «Математическое моделирование». Лектор, 35.95kb.
- Гармонический анализ и спектры некоторых периодических сигналов. Преобразование Фурье, 127.46kb.
- Программа вступительного испытания в магистратуру в форме экзамена по направлению 210400., 74.7kb.
- Убликация доклада(ов) Заказчика в сборнике докладов XV международной научной конференции, 48.75kb.
- Исполнение сольной программы Сольфеджио Исполнение сольной программы Поступающие должны, 286.73kb.
- Е. В. Коротков национальный исследовательский ядерный университет «мифи» исследование, 8.88kb.
- Влияние концентраторов напряжений на кинетику разрушения листовой нержавеющей стали, 75.78kb.
- Физические величины, измеряемые в аэрогидромеханике и теплофизическом эксперименте., 39.57kb.
- Программа курса лекций (3 курс, 6 сем., 32 ч., диф зачет) Профессор Киричук Валерий, 72.05kb.
- Моделирование периодических процессов на примере систем энергообеспечения, 43.92kb.
ЛАБОРАТОРНАЯ РАБОТА №1
Гармонический анализ периодических импульсных последовательностей.
- Основные теоретические положения и расчетные формулы.
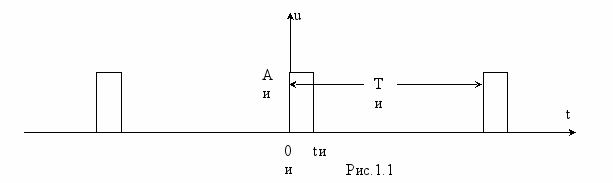
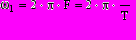 Периодическое колебание u(t), например последовательность прямоугольных импульсов с периодом T /рис1.1./ может быть представлено рядом Фурье как сумма гармонических составляющих с частотами, кратными “основной” частоте
Периодическое колебание u(t), например последовательность прямоугольных импульсов с периодом T /рис1.1./ может быть представлено рядом Фурье как сумма гармонических составляющих с частотами, кратными “основной” частоте этого колебания:
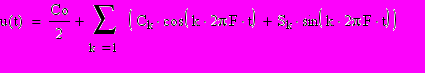
г
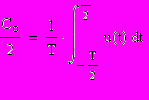 де: k=1,2,3… -коэффициенты кратности (номер гармоники),
де: k=1,2,3… -коэффициенты кратности (номер гармоники),-среднее значение колебания u(t) за период T, а коэффициенты Ck
и
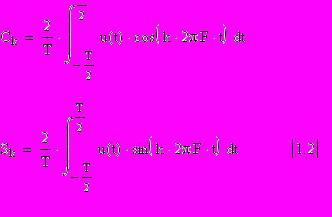 Sk определяются интегрированием u(t) с весовыми гармоническими функциями k-кратной частоты в пределах периода T /интервал ортогональности/:
Sk определяются интегрированием u(t) с весовыми гармоническими функциями k-кратной частоты в пределах периода T /интервал ортогональности/:При вычислении интегралов /1.2/ следует учитывать, что выбор “начала отсчета” t=0 на рис.1.1. для периодического сигнала является произвольным. При удачном выборе точки t = 0 в используемой системе координат иногда возможно значительное сокращение вычислений.
tи/2
Aи
t
-tи/2
-T/2
T/2
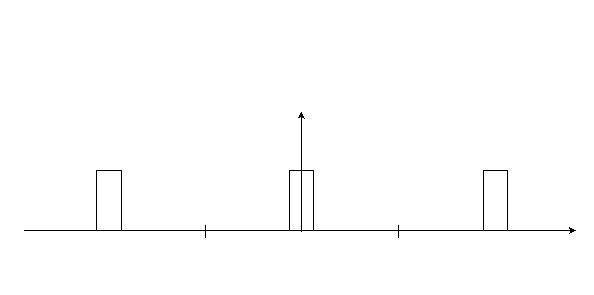
Рис.1.2
u
Так, на рис.1.2. начало отсчета t = 0 совмещено с серединой импульса в последовательности U(t). Тогда подинтегральные выражения в /1.2/ приобретают четный (Сk) и нечетный (Sk) характер соответственно, следовательно все коэффициенты Sk= 0, а величины Ск можно вычислить по формуле
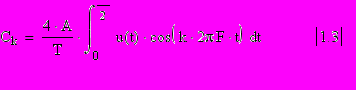
где интегрирование прямоугольного импульса с амплитудой А=const обеспечено соответствующим выбором пределов интеграла.
Для сопоставления с результатами эксперимента РЯД Фурье /1.1/ удобно представить в форме:
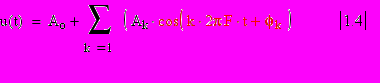
г
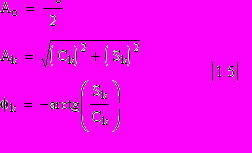 де:
де: Для прямоугольного импульса результаты вычисления по /1.3/ дают:
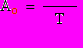
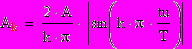
Экспериментальный анализ состоит в выделении из колебания U(t) гармонических составляющих /1.4/ с помощью колебательного контура, настроенного на соответствующую частоту, и измерении амплитуд, Ak и фаз φk этих гармоник. Совокупность { Ak }называется амплитудным, а { φk }- фазовым спектром колебания u(t).
В лабораторной работе измерение Ak и φk осуществляется по диграмме гармоники, наблюдаемой на экране электронного осциллографа.
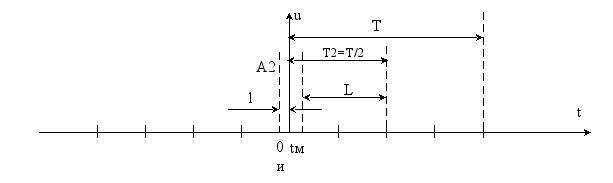
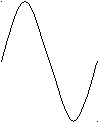
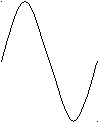
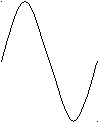
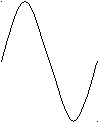
Рис.1.3
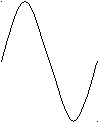
На рис.1.3 представлен пример такой диаграммы для второй гармоники входной последовательности импульсов. Номер гармоники k=2 можно определить сопоставлением периода Т основной частоты и периода Т2=T/2 данной гармоники. В лабораторной установке измерение временных соотношений меду последовательностью импульсов U(t) и максимумами гармоник возможно благодаря наличию специальных меток, соответствующих переднему и заднему фронтам импульсов входной последовательности U(t).
Амплитуда Ak любой гармоники определяется по амплитудной шкале электронного осциллографа безотносительно к временной шкале. В то же время измерение фазы φk гармонической составляющей
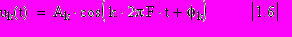
непосредственно определяется привязкой временной шкалы. Определить φk можно в точке максимума tм мгновенного значения UK(t) гармоники. Согласно
/1.6/ имеем:
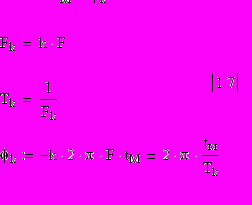
Таким образом фаза определяется отсчётом времени tM, соответствующим максимуму гармоники, а величина tM определяется в системе координат с произвольно выбираемым началом отсчета t=0. Например, если использовать систему отсчёта рис.1.2, то из диаграммы рис.1.3 определяем tM=0 и согласно /1.7/ имеем φ2 = 0.Однако, если для этого же колебания использовать систему координат рис.1.1 что представлено пунктирной осью на рис.1.3 то максимум гармоник оказывается сдвинутым на величину tM =l=tи/2 и согласно /1.7/ имеем:
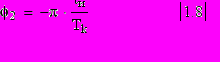
Связь изменения величины фазы с изменением отсчета временной шкалы является общим свойством фазовых измерений. При этом наиболее характерно, что согласно /1.7/ величина фазы является линейной функцией от произведения временного положения tM и частоты гармоники /номера k/.
 Ясно, что аналогичные изменения в фазовом спектре колебания происходят и вследствие изменения временного положения /запаздывания или опережения/ анализируемого колебания в условиях, когда шкала отсчета времени выбрана и неизменна. Появление линейно - зависящего от частоты фазового слагаемого спектра
Ясно, что аналогичные изменения в фазовом спектре колебания происходят и вследствие изменения временного положения /запаздывания или опережения/ анализируемого колебания в условиях, когда шкала отсчета времени выбрана и неизменна. Появление линейно - зависящего от частоты фазового слагаемого спектра вследствие задержки сигнала на время tз является одним из основных свойств преобразования Фурье.
1.2. Описание экспериментальной установки для гармонического анализа.
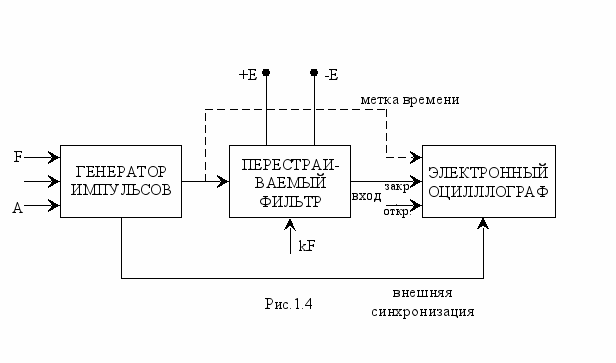
Для проведения измерений используется аппаратура согласно структурной схеме на рис.1.4.
tи
В качестве генератора импульсов используется прибор Г5-54, дающий последовательность прямоугольных импульсов с соответствующими заданию на работу параметрами
F - частота повторения, tи - длительность импульса, А - его амплитуда /см. рис.1.1/.
Импульсы измерительного генератора подаются на вход перестраиваемого по частоте колебательного контура /фильтра/, с помощью которого выделяется гармоника нужной частоты k•F. Перестройка контура осуществляется с помощью многооборотного потенциометра, что обеспечивает выделение гармоник с номерами вплоть до k=10. Следует иметь ввиду, что перестраиваемый фильтр представляет собой активное устройство, поэтому требует включения напряжения питания лабораторной установки +Е.
В
 ыходное напряжение фильтра подается на вход электронного осциллографа, с помощью которого определяется номер k выделенной гармоники и измеряется её амплитуда Ак и фаза .
ыходное напряжение фильтра подается на вход электронного осциллографа, с помощью которого определяется номер k выделенной гармоники и измеряется её амплитуда Ак и фаза .Для возможности измерения фазовых соотношений электронный осциллограф используется в режиме внешней синхронизации, что обеспечивает жесткую временную привязку /синхронность/ изображения на экране осциллографа и исследуемой последовательности импульсов, что позволяет фиксировать начало отсчёта времени как показано на рис.1.3.
Для удобства измерения временных соотношений в схеме рис. 1.4 предусмотрено формирование специальных временных меток, соответствующих фронту и спаду входных импульсов, и подача этих меток на экран осциллографа в смеси с напряжением выделяемой гармоники с выхода перестраиваемого фильтра.
1.3. РАСЧЕТНАЯ ЧАСТЬ
При подготовке к работе необходимо, используя соотношения(1.2 ,-1.5)
рассчитать амплитудный и фазовый спектры последовательности прямоугольных импульсов для k=1,2...10 при следующих исходных данных:
- частота повторения: F = 320±10 Гц,
- амплитуда: A = 5 В,
-длительности импульса: tи = 0.35 мс
Длительность импульса tи2 определяется из условия, чтобы k –ая гармоника Ak=0. Номер k приведён в таблице 1.
Таблица 1
| № рабочего места | 1 | 2 | 3 | 4 | 5 | 6 |
| k | 3 | 4 | 5 | 6 | 7 | 8 |
Результаты этой работы необходимо хранить для выполнения последующих работ.
Результаты расчетов представить в виде таблицы и изобразить точками , в системе координат "напряжение-частота" с соблюдением масштаба величин. Для наглядности можно на графике соединить расчетные точки плавной кривой ("огибающая спектра").
1.4. ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
1.Присоединить вход генератора импульсов ко входу электронного
осциллографа. Установить режим внешней синхронизации с использованием
отдельного провода согласно рис.1.4. Обеспечить на экране осциллографа
устойчивое изображение последовательности u(t) входных импульсов и
зарисовать их диаграммы с соблюдением масштабов осей напряжения и
врекени.
2.Произвести измерение величины А0 = С0 /2 (среднего значения напряжения u(t) за период Т) для двух длительностей импульса. Для этого переключить режим входа осциллографа из "закрытый" в "открытый" или
наоборот и измерить смещение изображения по оси напряжений. Пояснить
результат.
 3.Присоединить выход генератора импульсов ко входу перестраиваемого фильтра, а выход последнего - ко входу электронного осциллографа. Перестраивая фильтр с помощью многооборотного потенциометра, выделять последовательно гармоники входного напряжения для k=1,2,3… При настройке на максимум каждой гармоники измерить по диаграмме на экране осциллографа ее амплитуду Аk и фазу .
3.Присоединить выход генератора импульсов ко входу перестраиваемого фильтра, а выход последнего - ко входу электронного осциллографа. Перестраивая фильтр с помощью многооборотного потенциометра, выделять последовательно гармоники входного напряжения для k=1,2,3… При настройке на максимум каждой гармоники измерить по диаграмме на экране осциллографа ее амплитуду Аk и фазу .Для измерения фазы согласно рис.1.3. следует по экрану осциллографа определить временное смещение максимума гармоники относительно выбранного начала отсчёта t = 0 и рассчитать согласно (1.7) фазу как величину l в долях периода L данной гармоники:
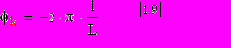
Для расчёта по формуле (1.9) величины l и L могут быть измерены по экрану осциллографа в единицах времени в соответствии с масштабом используемой шкалы или просто в единицах длины (числе клеток экрана).
Измерение фаз провести дважды: а) для начала отсчёта, совпадающего с серединой входного импульса и б) для начала отсчёта, совпадающего с передним фронтом импульса.
Результаты измерений спектров представить в общей системе координат с результатами расчетов. Результаты этой работы необходимо хранить для выполнения последующих работ.
При изображении фазового спектра иметь ввиду, что на фазовых диаграммах в следствие периодичности этого параметра можно прибавлять “скачки” фазы на
величину ±π.
Диаграммы гармоник с номерами k=1,2,3... следует зарисовать в системе координат, совмещенной по времени с диаграммами входных импульсов. Сделать выводы по работе.
1.5. СОДЕРЖАНИЕ ОТЧЕТА
Отчет должен содержать:
-структурную схему экспериментальной установки;
-расчеты амплитудного и фазового спектров (начало отсчета совпадает с серединой импульса и передним фронтом импульса), сведенные в таблицу;
-графики;
-экспериментальные данные, сведенные в таблицу;
-экспериментальные графики, совмещенные с расчетными;
-выводы по работе.
1.6. КОНТРОЛЬНЫЕ ВОПРОСЫ
1.Что такое спектр сигнала (амплитудный, фазовый, энергетический)?
2.Что такое ряд Фурье, какие сигналы могут быть представлены рядом Фурье?
3.Как определяются коэффициенты ряда Фурье?
4.Как отразится на спектре периодической последовательности прямоугольных импульсов изменение длительности импульса и периода повторения?
5.Как изменится спектр периодического сигнала, если длительность импульса устремить к нулю?
6.Как изменится спектр сигнала, если период повторения устремить в бесконечность?
7.Как влияет на амплитудный и фазовый спектры сигнала изменение начала отсчета времени?
8.Как зависит ширина спектра сигнала от длительности импульса?
ЛАБОРАТОРНАЯ РАБОТА №2
Частотные характеристики линейных радио-
технических цепей с постоянными параметрами.
2.1. Основные теоретические сведения и расчетные формулы.
Для представления характеристик линейных цепей в частотной области используется комплексная передаточная характеристика
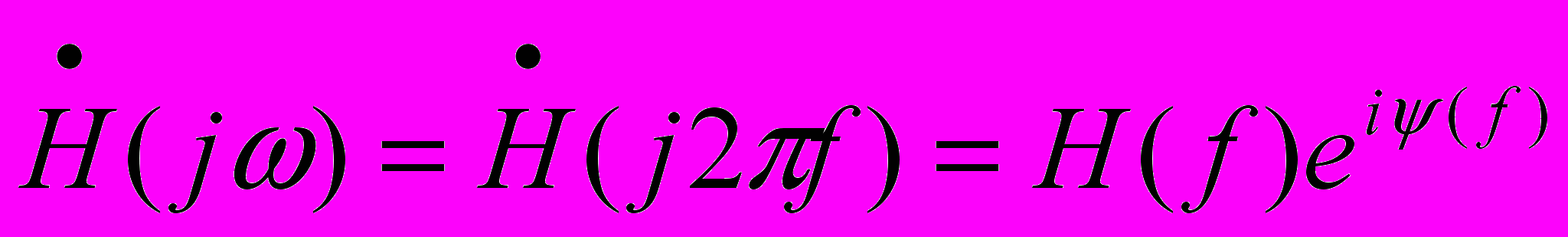 /2.1/
/2.1/
модуль H(f) и фаза которой называются амплитудно-частотной и фазо-частотной характеристиками и определяют отношение амплитуд и разность фаз гармонических сигналов частоты f на выходе и входе цепи.
Для расчета
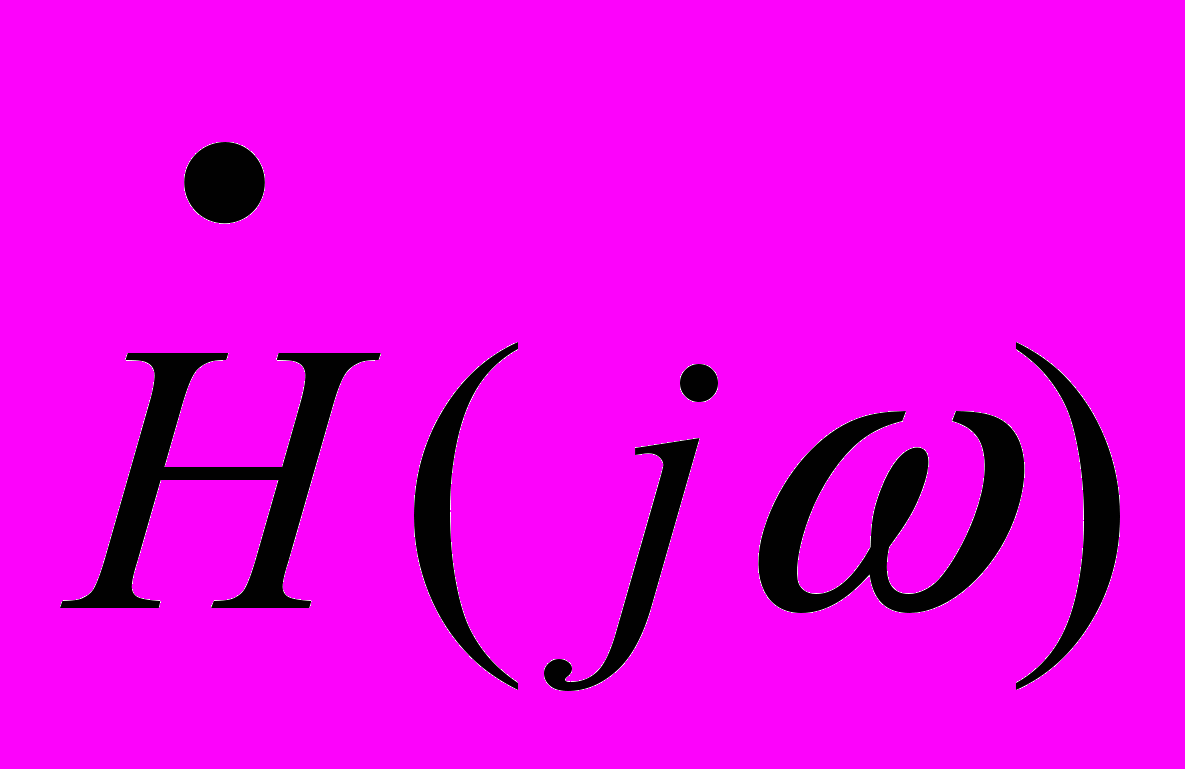 удобно использовать отношение изобретении по Лапласу выходного Uвых(p) и входного Uвх(p) сигналов:
удобно использовать отношение изобретении по Лапласу выходного Uвых(p) и входного Uвх(p) сигналов: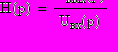
(2.2)
которое определяет передаточную характеристику (2.1) на мнимой оси плоскости p=jω.
В лабораторной работе исследуются широко распространенные RC - цепочки первого и второго порядков (рис.2.1 а, б, в).













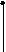


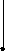



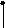




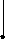




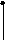




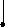


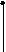


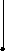
R1
C1
C2
R2
C3
R3
R4
Рис.2.1.
а
б
в
C4
Расчёт передаточных характеристик этих цепочек можно выполнить по обобщённой схеме рис.2.2.












I(p)
Z1(p)
Z2(p)
U2(p)
Рис.2.2.
U1(p)
В соответствии с правилами Кирхгофа для этой схемы имеем:

откуда:
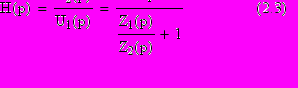
Е
 стественно, что передаточная характеристика цепи H(p) не зависит от вида входного сигнала и его изображения U1(p), хотя, как отмечалось, амплитудно-частотная H(f) и фазо-частотная характеристики в (2.1) могут рассматриваться как результаты измерения амплитуды и фазы гармонического сигнала частоты f.
стественно, что передаточная характеристика цепи H(p) не зависит от вида входного сигнала и его изображения U1(p), хотя, как отмечалось, амплитудно-частотная H(f) и фазо-частотная характеристики в (2.1) могут рассматриваться как результаты измерения амплитуды и фазы гармонического сигнала частоты f.Для цепочки рис.2.1 а:

и с помощью (2.3) легко получить
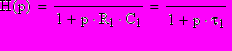
Полагая здесь
 , определяют передаточную характеристику
, определяют передаточную характеристику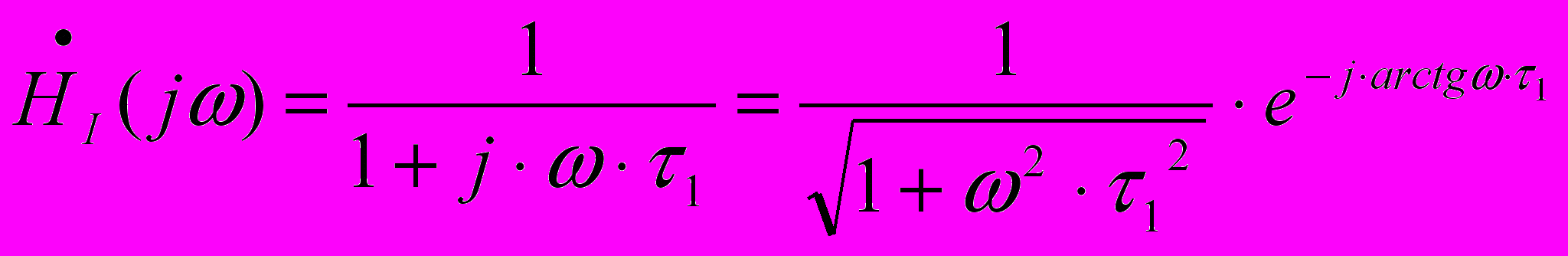 (2,4)
(2,4)Аналогично для цепи рис2.1б можно найти
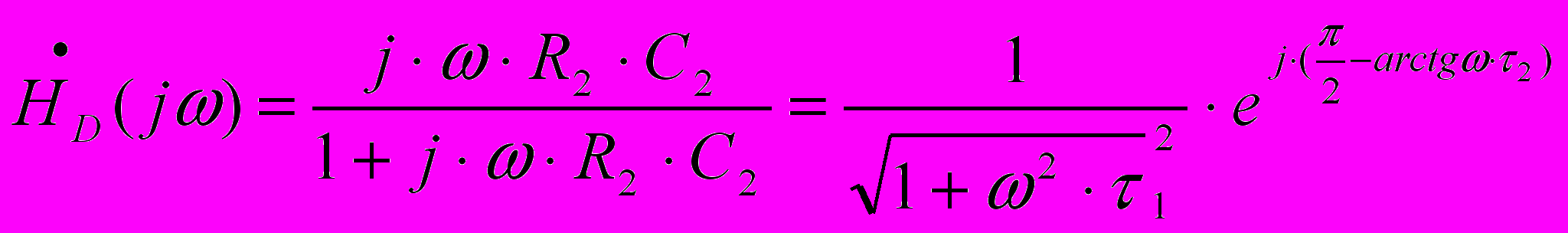 (2,5)
(2,5)Для цепи второго порядка (мост Вина,рис.2.1в) получается более сложное выражение, которое можно упростить, положив R3=R4, C3=C4 и RC=τ , тогда
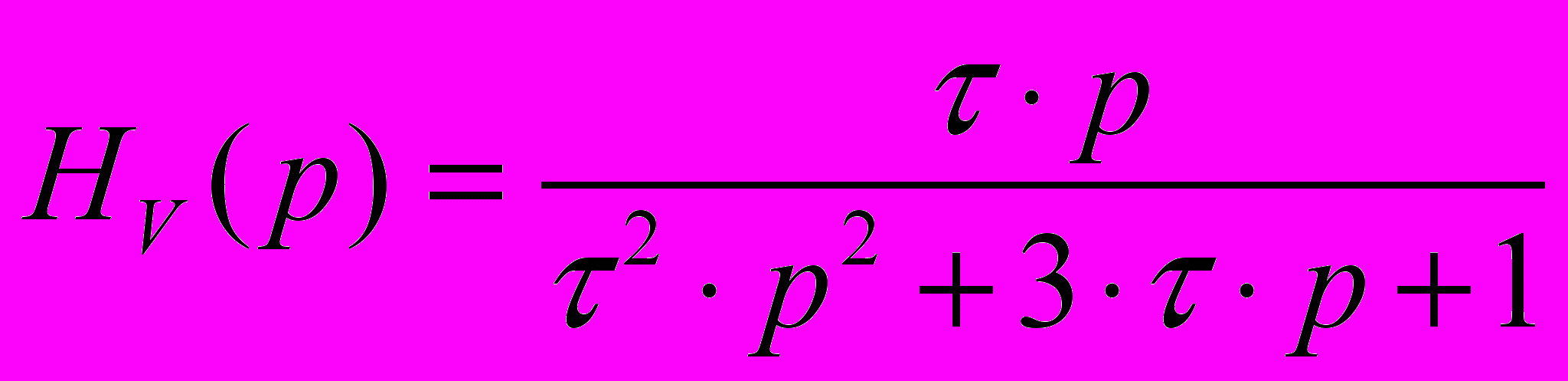
(2.6)
откуда легко найти:
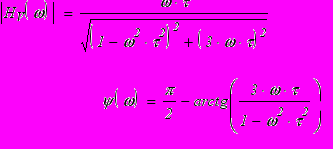
Модуль частотной характеристики такой цепочки имеет экстремум (максимум) при частоте ω0=1/τ , при этом
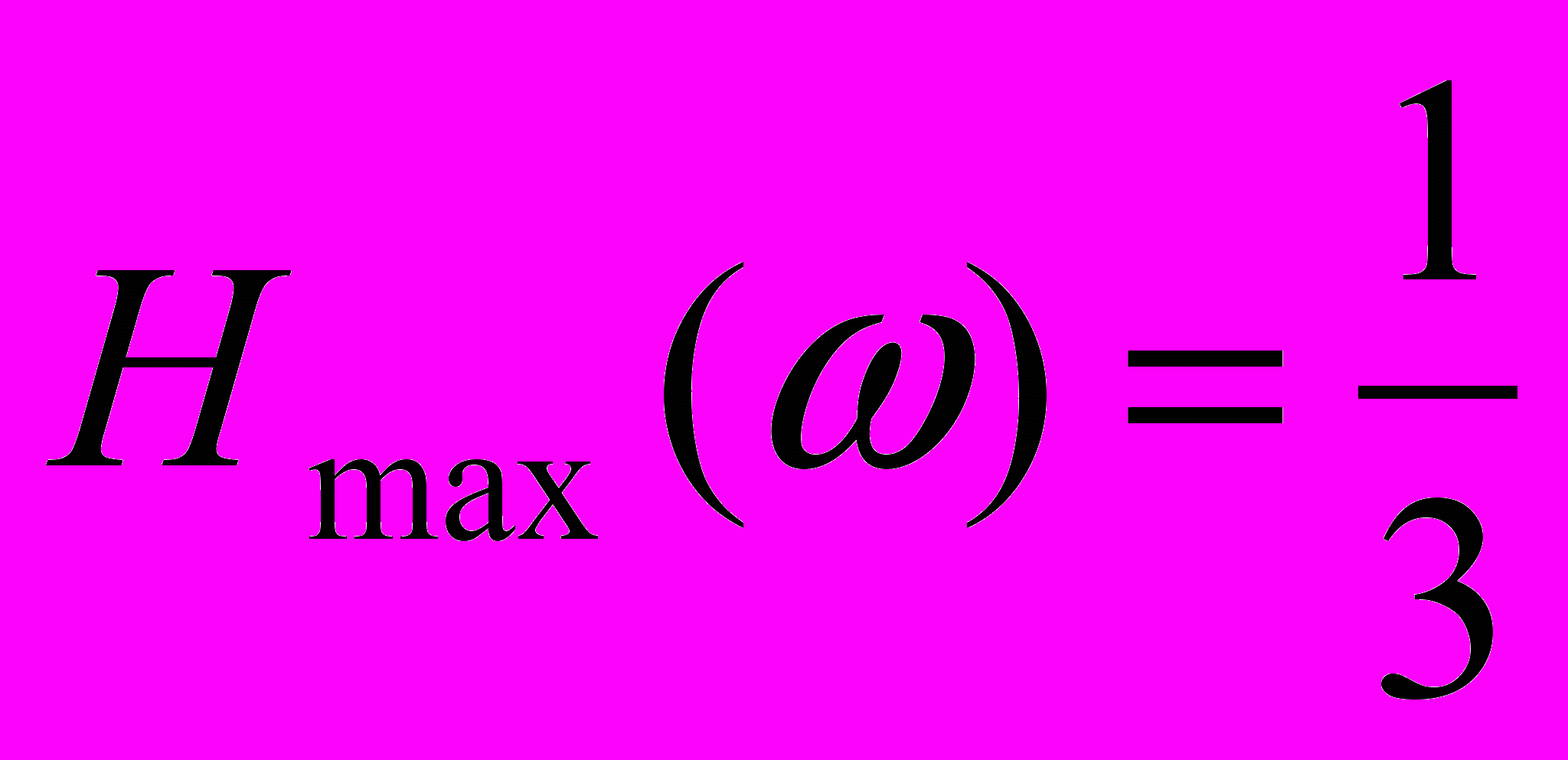 и
и 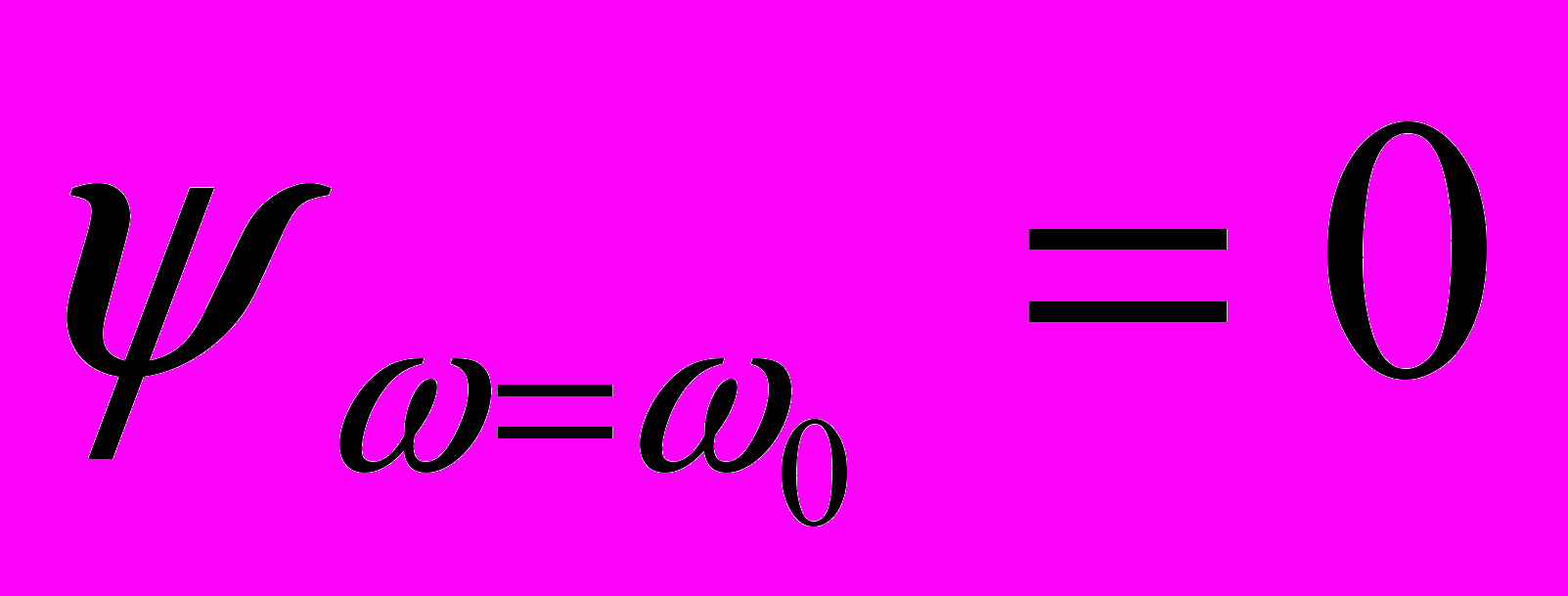
Значения аргументов
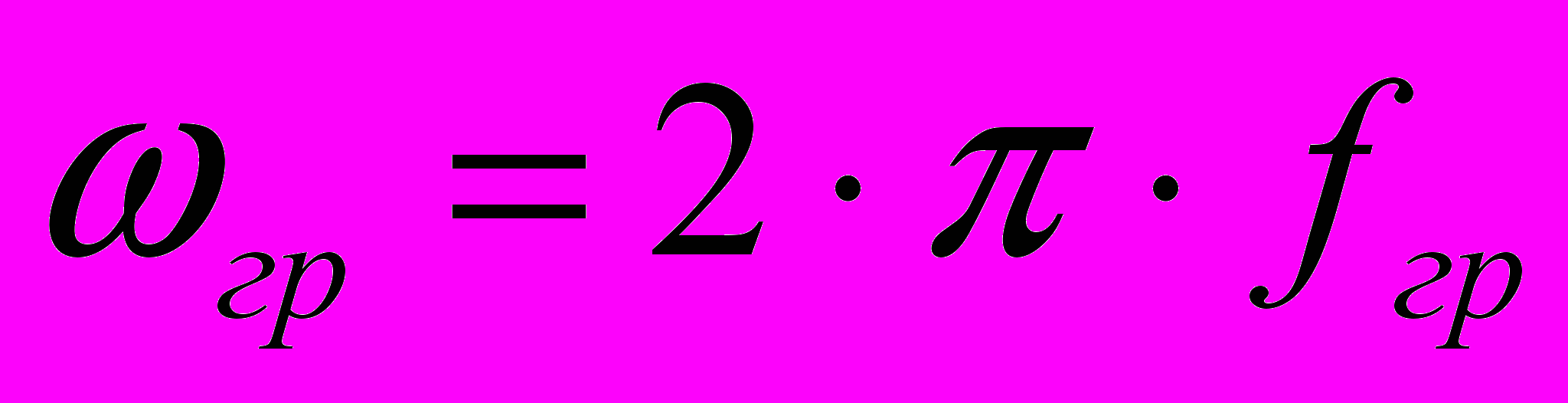 , при которых амплитудно-частотная характеристика уменьшается до 0,707 от максимума называются граничными частотами.
, при которых амплитудно-частотная характеристика уменьшается до 0,707 от максимума называются граничными частотами.При анализе частотных характеристик цепей всегда полезно рассматривать предельные значения частоты:
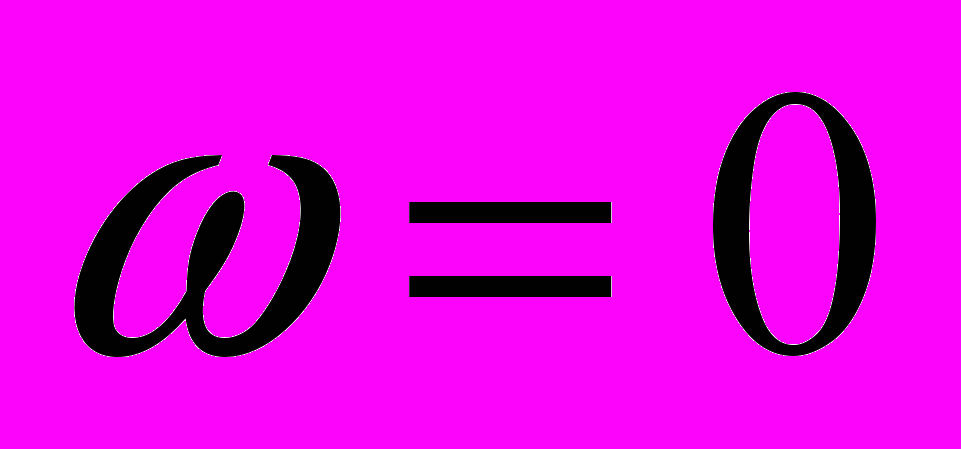 ,
,  .
.Например, для цепи рис.2.1а из (2,4) при
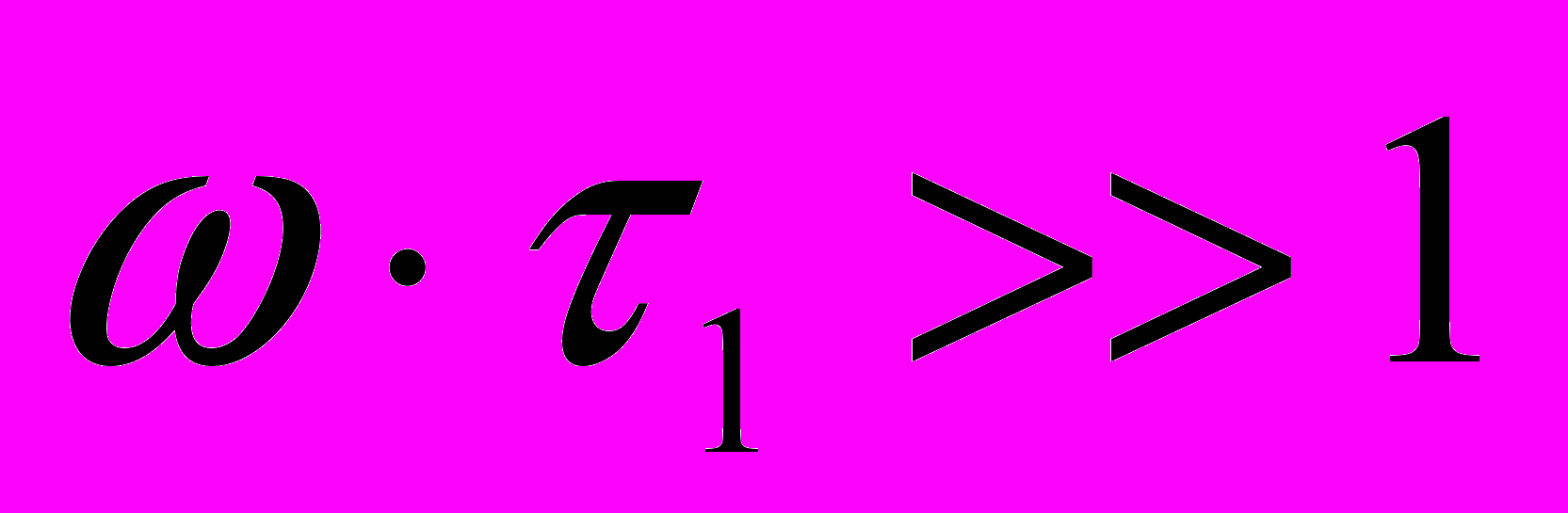 получаем
получаем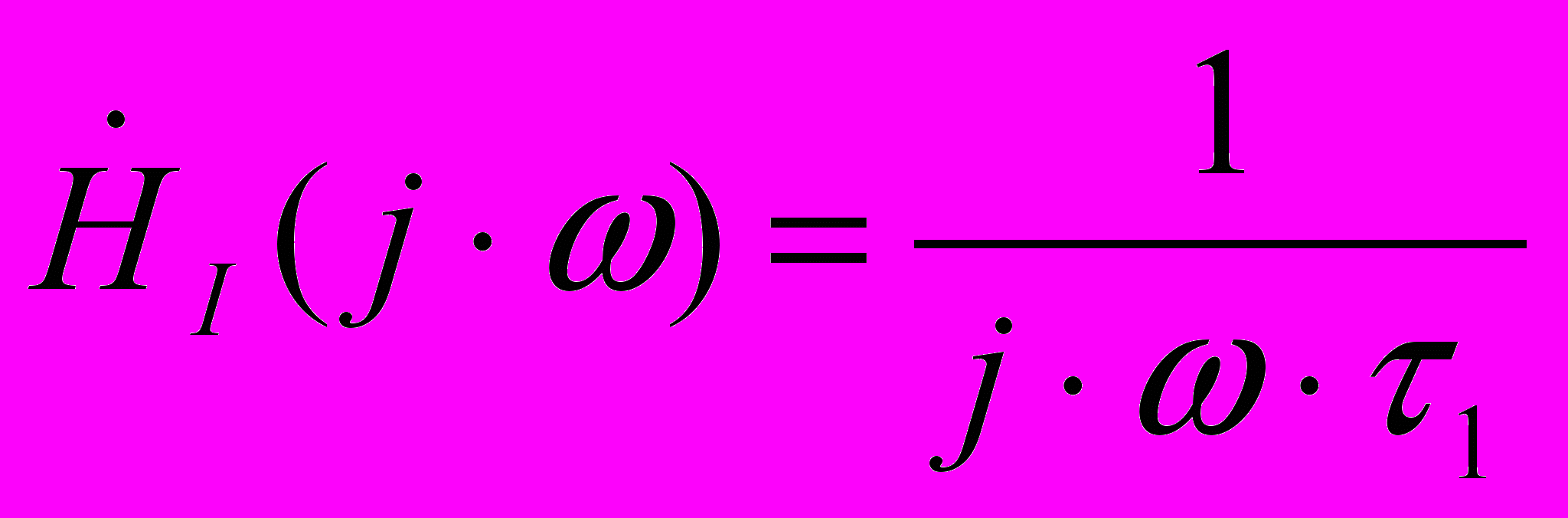 ,
,что в соответствии со свойствами преобразования Фурье является математически строгим выражением операции интегрирования и определяет использование для данной цепочки названия “интегрирующая”.В то же время при
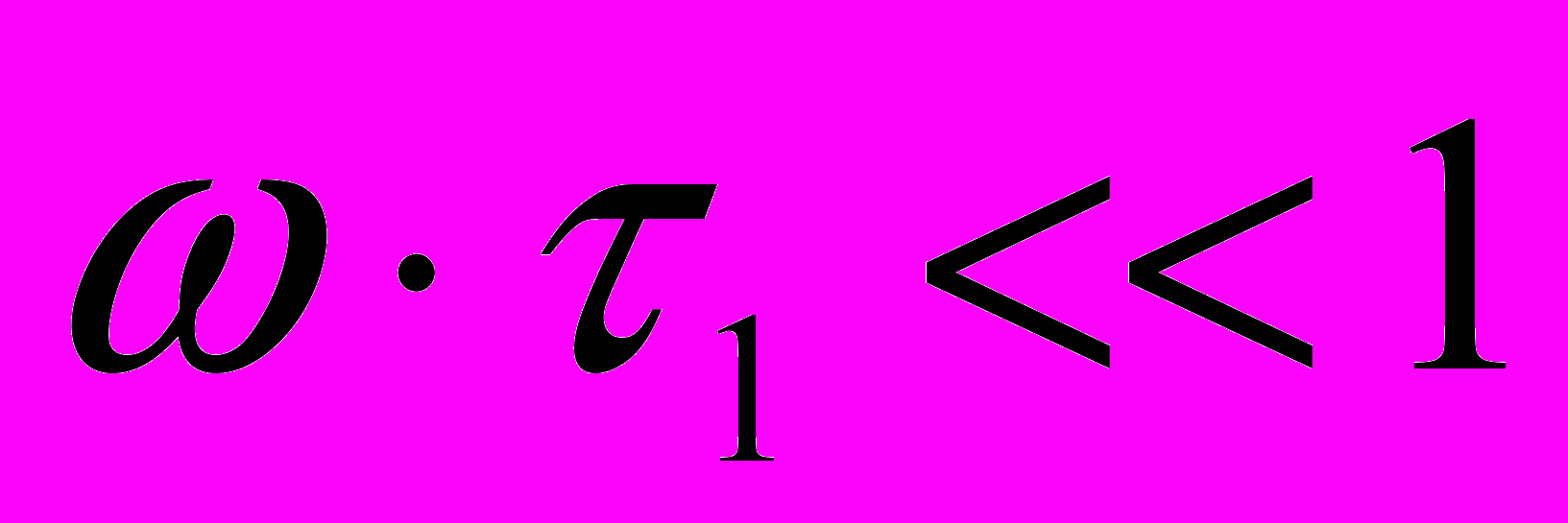 эта цепочка не оказывает никакого влияния на сигнал
эта цепочка не оказывает никакого влияния на сигнал 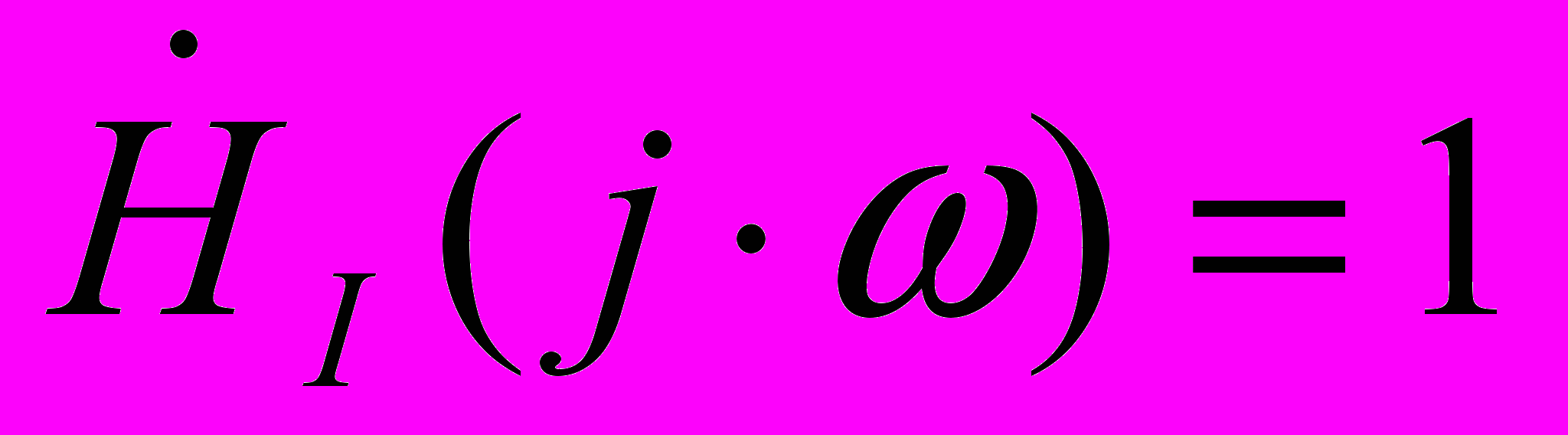 .
.Цепочка рис.2.1б на таких же основаниях называется “дифференцирующей”, что реализуется при
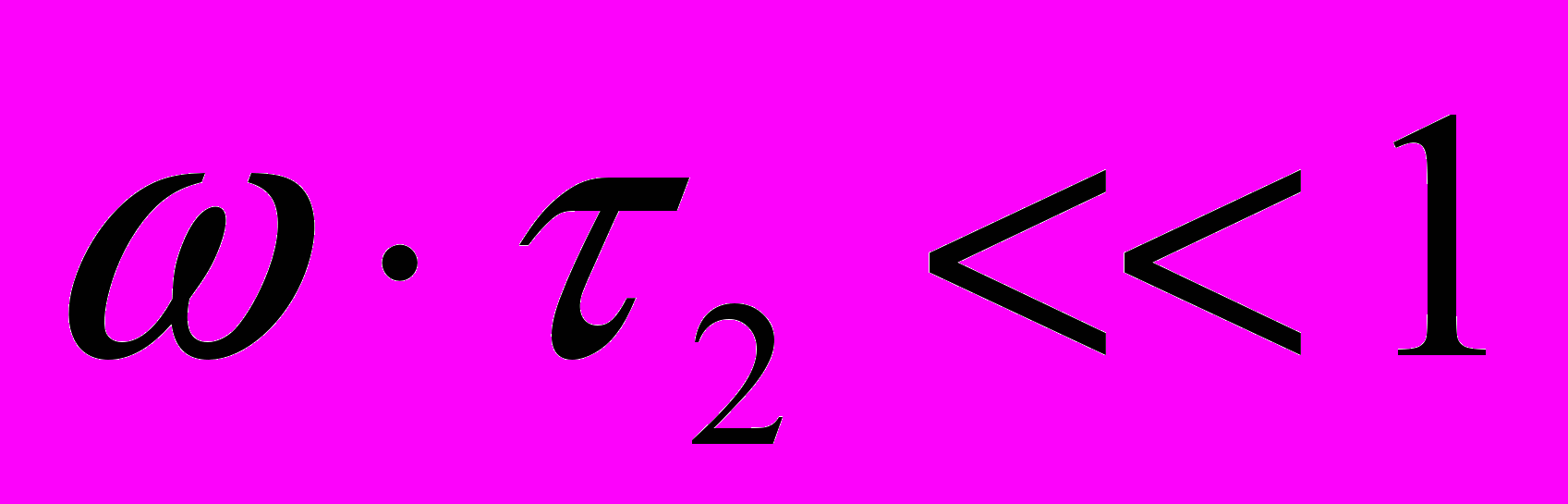 ; тогда
; тогда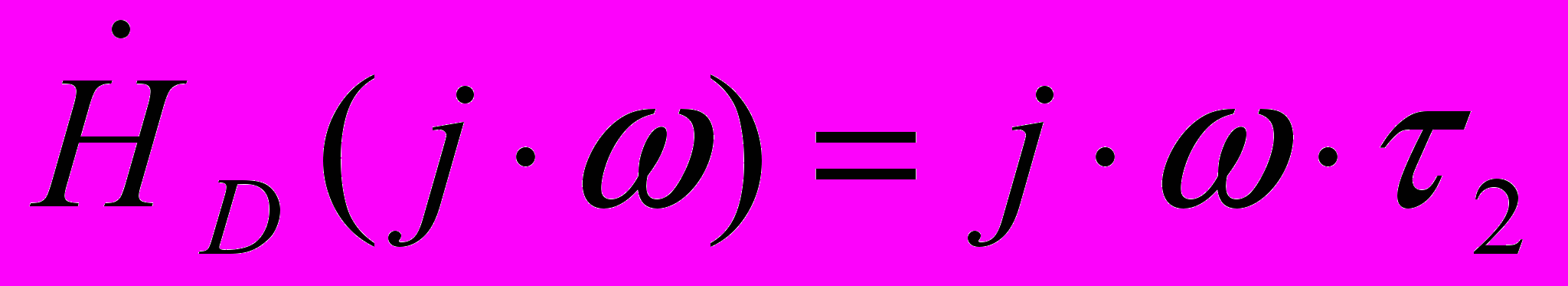 ,
,а при
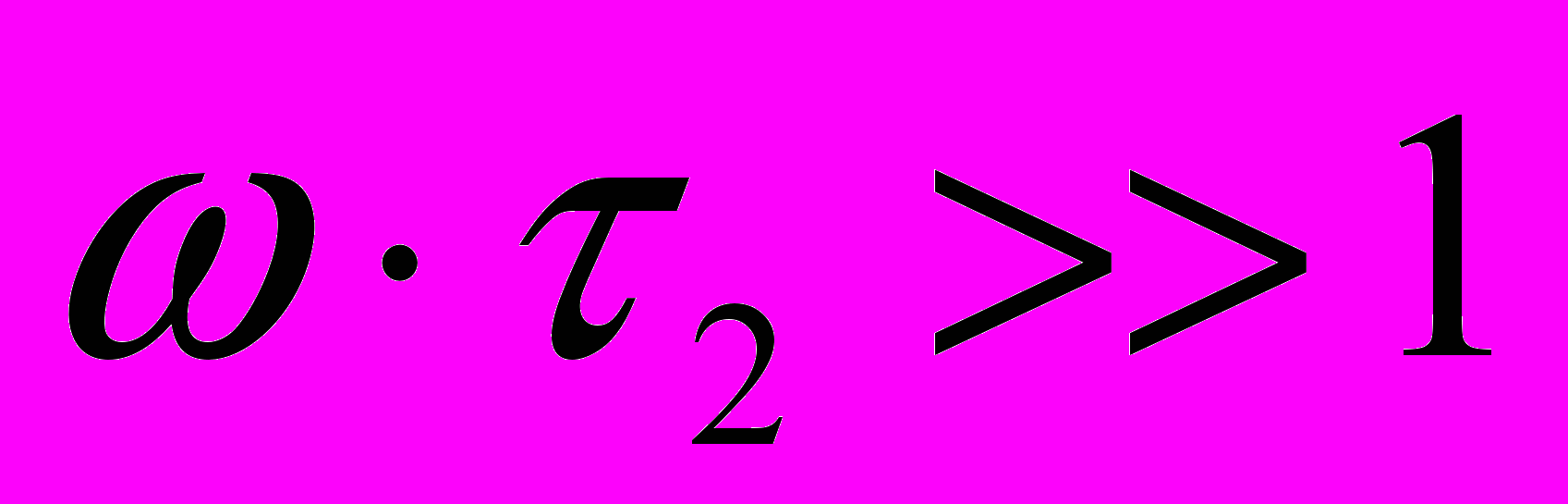 имеем
имеем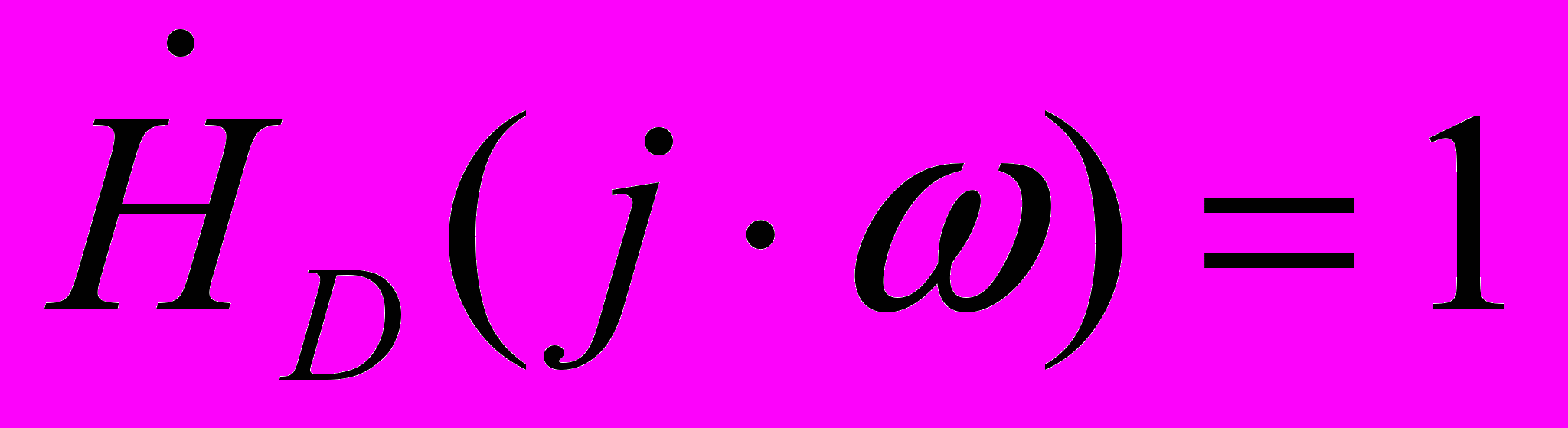 .
.Наконец, наличие экстремума частотной характеристики моста Вина (рис.2.1в) объясняется непропусканием низких частот
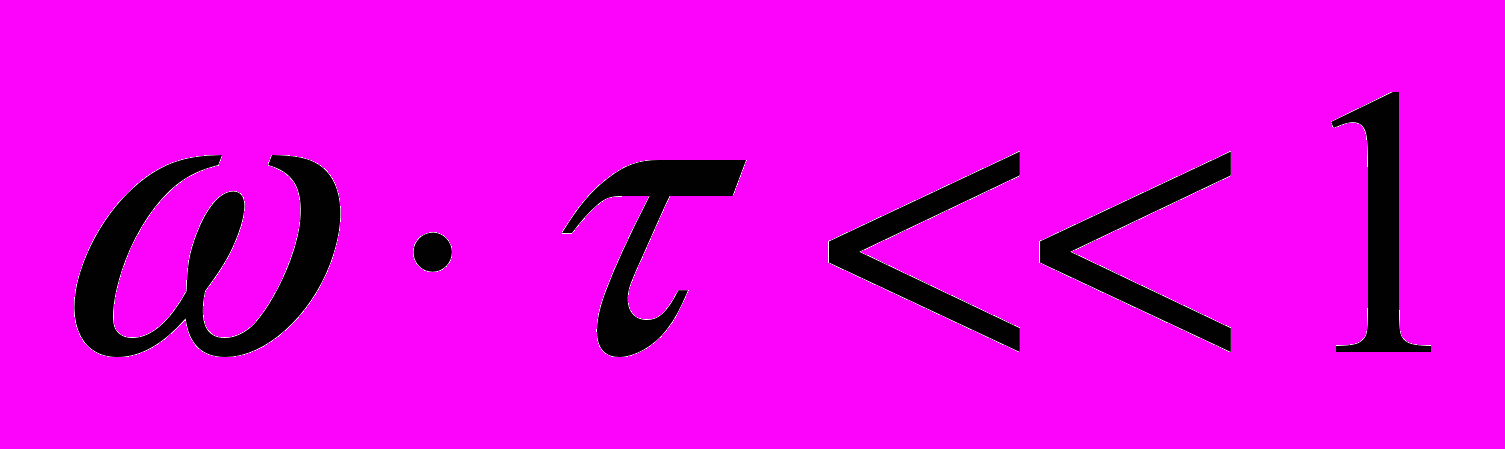 цепочкой C3R3 и шунтированием высоких частот
цепочкой C3R3 и шунтированием высоких частот 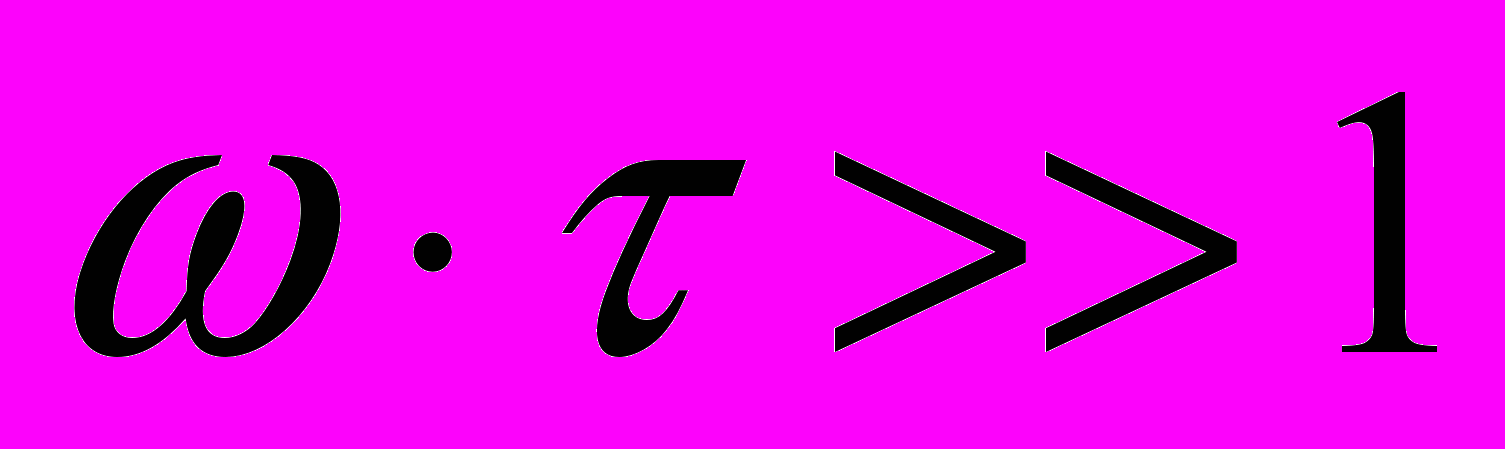 цепочкой C4R4.
цепочкой C4R4.Описание экспериментальной установки для измерения частотных характеристик цепей.
Для экспериментального измерения амплитудно - частотной характеристики в лабораторной работе используется измерительный генератор синусоидальных сигналов, напряжение с выхода которого подаётся на вход исследуемой цепи, а амплитуда выходного напряжения цепи измеряется по экрану осциллографа в требуемом диапазоне частоты f. .
Для измерения фазо - частотной характеристики электронный
осциллограф включается в режим наблюдения фигур Лиссажу. Для
этого, как показано на рис.2.3., напряжение измерительного
генератора подается на вход исследуемой цепи и на горизонтальноотклоняющие пластины осциллографа (Вход "X"). Напряжение с выхода цепи подается, как обычно, на вертикальноотклоняющие пластины "У".
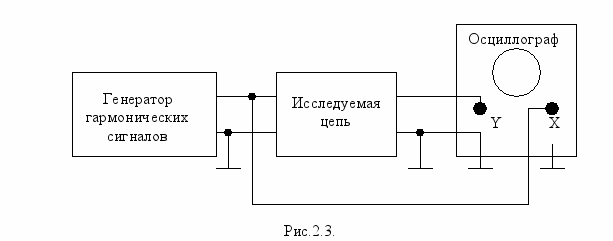
П
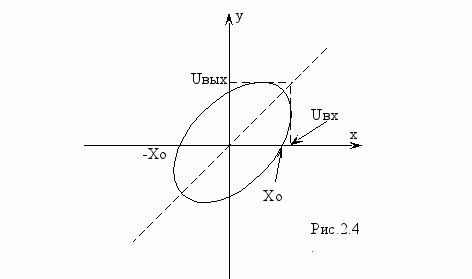 ри этом на экране осциллографа наблюдается эллипс с параметрами, показанными на рис.2.4.
ри этом на экране осциллографа наблюдается эллипс с параметрами, показанными на рис.2.4.Для гармонических колебаний на входе и выходе цепи:
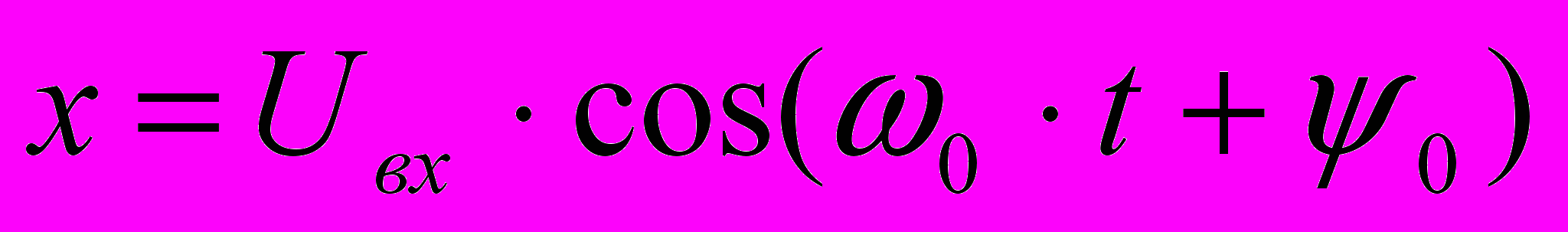 ,
,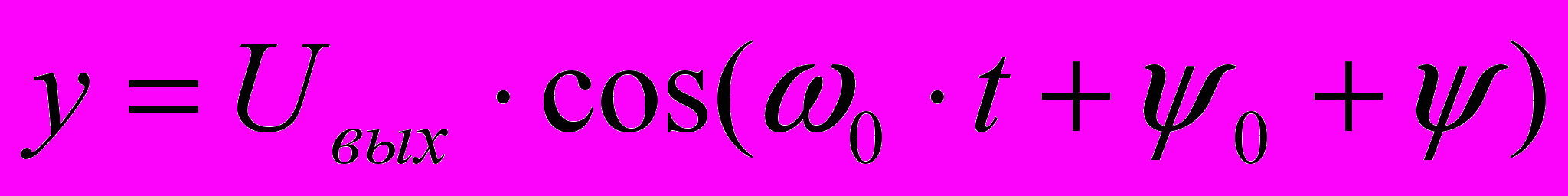 ,
,из условия y=0 получаем:
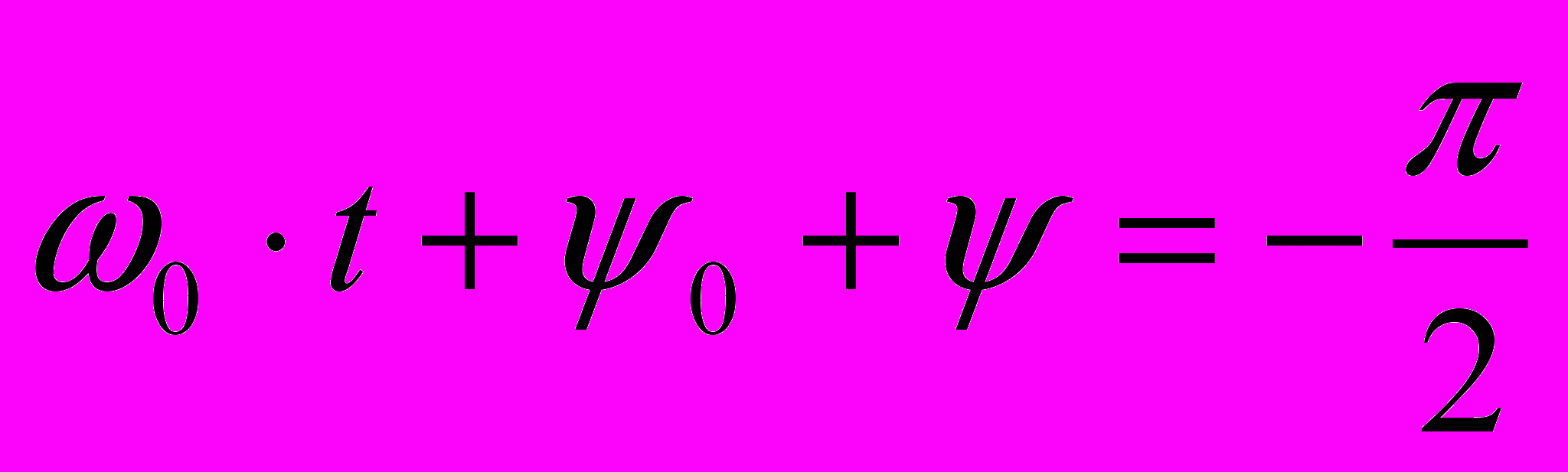 ,
,тогда
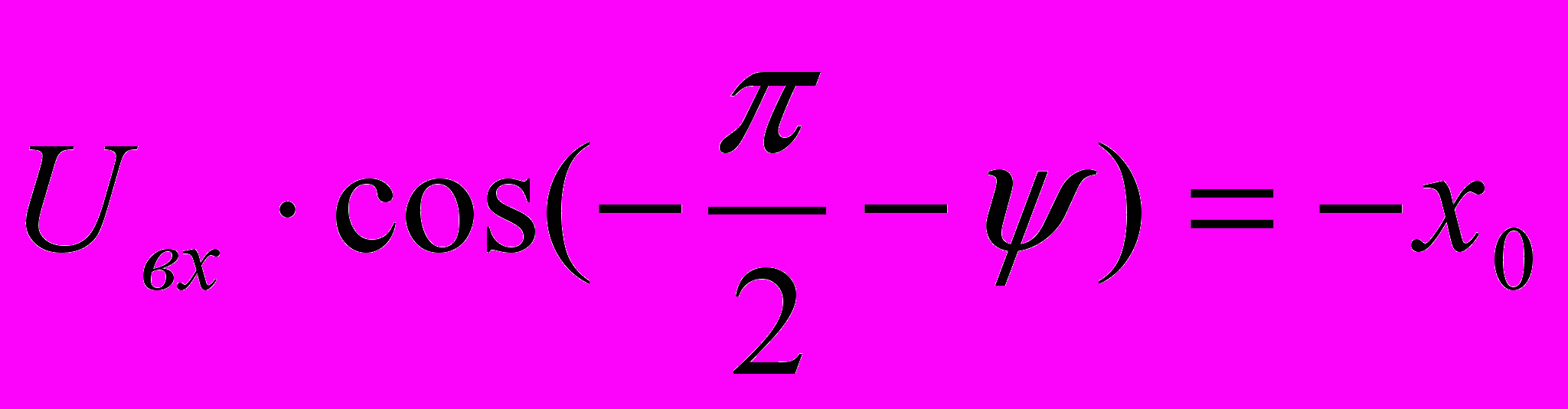 или
или  (2,7)
(2,7)Определяя по диаграммам рис.2.4 параметры
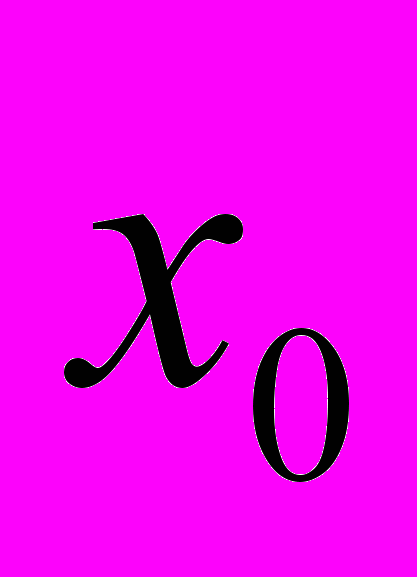 и
и 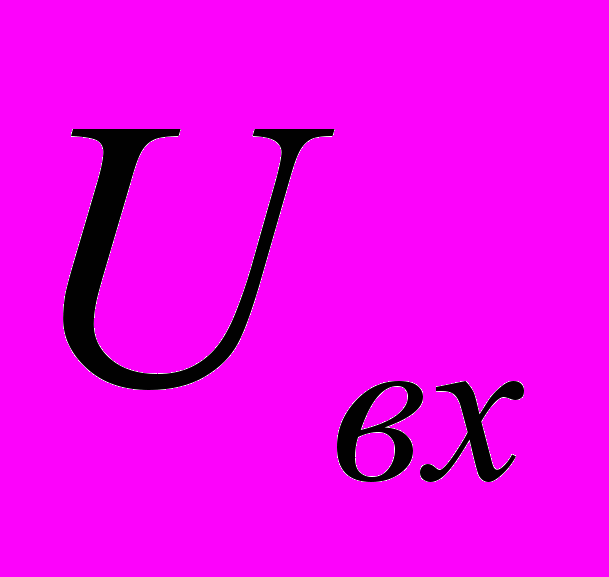 для различных частот по (2,7) рассчитывают фазо-частотную характеристику.
для различных частот по (2,7) рассчитывают фазо-частотную характеристику.2.3. РАСЧЕТНАЯ ЧАСТЬ
1. Рассчитать амплитудно-частотные и фазо-частотные характеристики для цепей рис. 2.1. при заданных параметрах:
R1= 3,3 kОм, С1= 72 нФ, R2= 3,0к0м, С2= ЗЗ нФ, R3=R4=2 кОм, С3=С4=72 нФ.
2. Рассчитать постоянные времени и граничные частоты fгр цепочек. Оценить требуемый для измерения диапазон изменения частоты f в каждом случае. Построить рассчитанные характеристики (2.1) в виде диаграмм H(f) ψ(f)
2.4. ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
Для проведения эксперимента по снятию АЧХ и ФЧХ линейных цепей необходимо собрать схему согласно рис. 2.3. Установить на входе амплитуду колебаний, равную 2В и поддерживать ее постоянной во время эксперимента. Изменяя частоту гармонических колебаний на входе и измеряя амплитуду колебаний на выходе цепи, найти значения АЧХ на соответствующих частотах .
Измерение ФЧХ осуществляется по фигурам Лиссажу, наблюдаемым на экране осциллографа.
2.5. СОДЕРЖАНИЕ ОТЧЕТА
Отчет должен содержать:
- структурную схему экспериментальной установки;
- расчеты АЧХ и ФЧХ для трех видов RC-цепей, сведенные в таблицу; графики;
- экспериментальные данные, сведенные в таблицу; графики АЧХ и ФЧХ совмещенные с расчетными;
- выводы по работе.
Данные отчета соранять для использования в лабораторной работе №3
2.6. КОНТРОЛЬНЫЕ ВОПРОСЫ
1.Что такое передаточная характеристика линейной цепи?
2.Что такое АЧХ, ФЧХ линейной цепи?
3.Как экспериментально снять АЧХ линейной цепи?
4.Как экспериментально снять ФЧХ линейной цепи?
5.Как выглядит АЧХ идеального фильтра низких частот, верхних частот и полосового фильтра?
6.Как выглядят АЧХ и ФЧХ интегрирующей RС-цепи?
7.Как выглядят АЧХ и ФЧХ идеального интегратора?
8.Как выглядят АЧХ и ФЧХ дифференцирующей RC-цепи?
9. Как выглядят АЧХ и ФЧХ идеальной дифференцирующей RC-цепи?
ЛАБОРАТОРНАЯ РАБОТА №3
Спектральный метод расчета выходных сигналов радиотехнических цепей.
3.1. Основные теоретические положения и расчетные формулы.
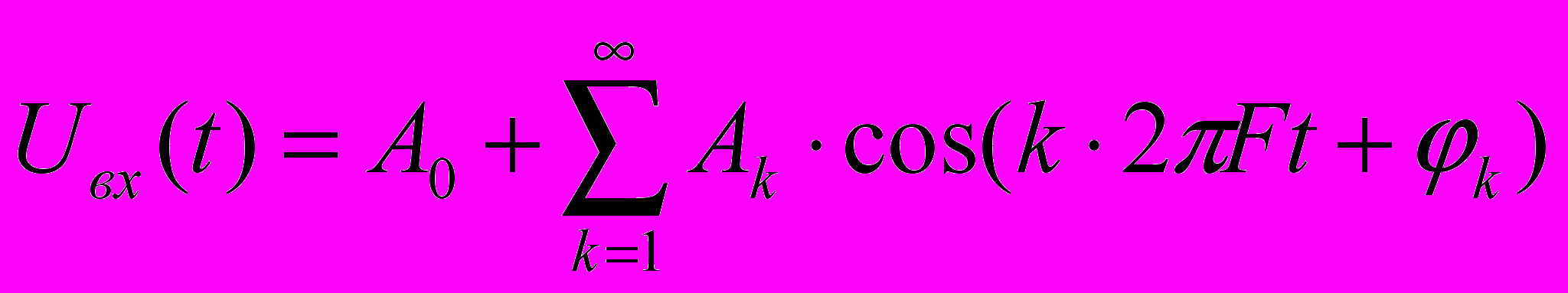 Спектральный метод расчета основан на возможности определения спектральной характеристики выходного сигнала радиотехнической цепи путем умножения спектральной характеристики входного сигнала на передаточную функцию цепи на каждой интересующей частоте. Для спектра периодического входного сигнала с частотой повторения F , исследованного в лабораторной работе №1 и представляемого суммой гармоник с дискретными частотами kF в форме
Спектральный метод расчета основан на возможности определения спектральной характеристики выходного сигнала радиотехнической цепи путем умножения спектральной характеристики входного сигнала на передаточную функцию цепи на каждой интересующей частоте. Для спектра периодического входного сигнала с частотой повторения F , исследованного в лабораторной работе №1 и представляемого суммой гармоник с дискретными частотами kF в форме
(3.1)
с
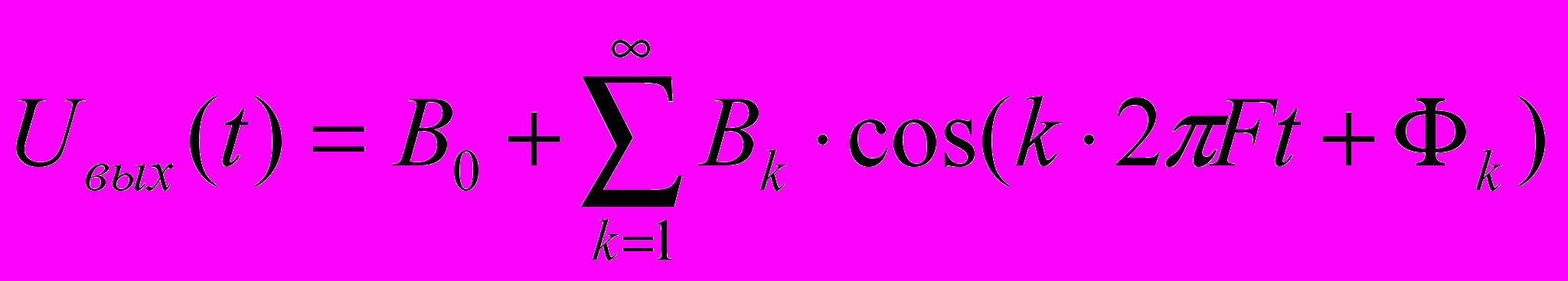 пектр выходного сигнала цепи также дискретен
пектр выходного сигнала цепи также дискретен(3.2)
где Bk и Фк определяются передаточной функцией цепи H(f)eiΨ(f) исследованной в лабораторной работе №2 как
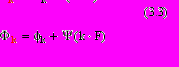
В общем случае для непрерывного спектра входного сигнала спектр выходного сигнала определяется умножением на комплексную передаточную функцию цепи:
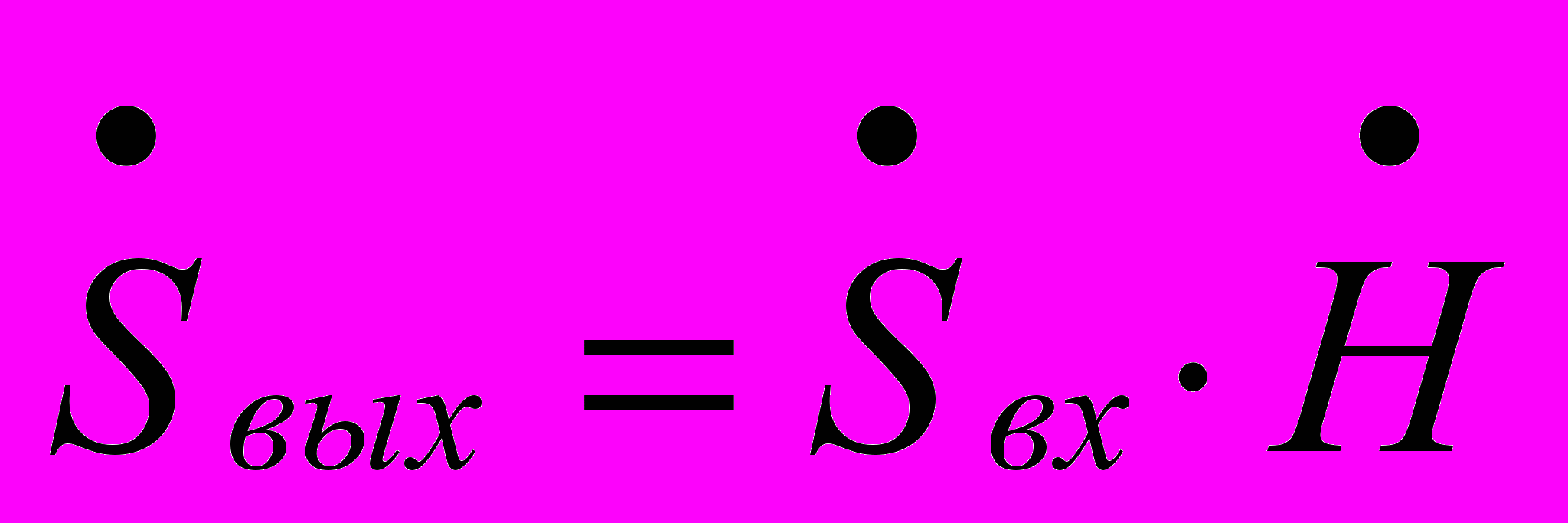
(3.4)
Простота алгоритмов (3.3) и (3.4), состоящая в отсутствии интегральных выражений, определяет широкое распространение спектральных методов в радиоэлектронике.
3.2. Описание экспериментальной установки.
Экспериментальные исследования производятся на той же лабораторной панели, что и лабораторные работы №1 и №2. Периодический сигнал импульсног генератора с параметрами, использованными в лабораторной работе №1, поочерёдно подаётся на входы цепочек рис.2.1 а, б, в, передаточные характеристики которых были исследованы в лабораторной работе №2. Спектральные характеристики выходного сигнала цепочек определяются с помощью перестраиваемого фильтра и электронного осциллографа, как в работе №1.
3.3. РАСЧЕТНАЯ ЧАСТЬ
При подготовке к работе, используя результаты работ №1 и №2, а также соотношение (3.3) рассчитать спектральные характеристики выходных сигналов для трех видов цепей. Представить исходные данные и результаты расчетов Вк и Фк в виде частотных диаграмм в совмещенных по оси частот координатах с соблюдением масштабов.
4. ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
Для проведения эксперимента задать на генераторе периодическую последовательность прямоугольных импульсов с заданными параметрами по методике, изложенной в лабораторной работе №1.
В соответствии с пунктом 3.2. провести измерение амплитуд и фаз гармоник выходного сигнала для трех типов RC-цепей.
3.5. СОДЕРЖАНИЕ ОТЧЕТА
Отчет должен содержать:
-структурную схему экспериментальной установки;
-расчеты амплитудного и фазового спектров выходного сигнала для
трех типов RC-цепей, сведенные в таблицы; графики;
-экспериментальные данные, сведенные в таблицу и графики, совмещенные с расчетными.
3.6. КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Как связаны между собой спектры сигналов на входе и выходе
линейной цепи?
2. Каков порядок расчета выходного сигнала линейной цепи
спектральным методом?
3. Как видоизменяется амплитудный спектр сигнала прошедший через
фильтр верхних частот?
4. Как видоизменяется амплитудный спектр сигнала прошедший через
фильтр нижних частот?
ЛАБОРАТОРНАЯ РАБОТА №4
Временные характеристики линейных радиотехнических цепей с постоянными параметрами.
4.1. Основные теоретические сведения и расчетные формулы.
Во временной области характеристиками линейных радиотехнических цепей являются их отклики на определённые 'тестовые воздействия. Наиболее распространены переходные и импульсные характеристики.
- Переходной характеристикой g(t) называется отклик цепи на тестовое воздействие в виде ступенчатой функции (единичного скачка) σ(t).
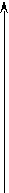







1.0
t
δ(t)
а)
tфр.и
tи
Рис.4.1.а
Для расчета переходной характеристики методом Лапласа следует найти изображение выходного напряжения цепи как произведение передаточной функции Н(р) цепи и изображения единичного скачка:
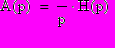
(4.1)
Обратное преобразование Лапласа от (4.1) дает переходную характеристику
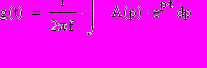
и может быть найдено с помощью теорег.ол о вычетах функции А(р). Однако, для простейших цепей типа рис.2.1. (лабораторная работа №2) целесообразно использовать непосредственное построение. переходного процесса на основе законов электротехники. Так, для цепи рис.2.1а переходный процесс состоит в заряде конденсатора С1 с постоянной времени τ1 от нулевого значения в момент t=o до асимптотического уровня I при t→∞. Построение переходной характеристики в этом случае иллюстрируется на рис.4.1.б


1.0
0.9


tфр.


0

τ1
t
б)
gI
Рис.4.1.б


В качестве параметра переходной характеристики
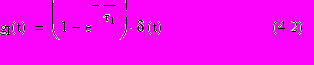
обычно используют длительность нарастания напряжения до уровня 0.9 от асимптотического (длительность фронта переходной характеристики tфр). Логарифмируя (4.2) легко найти
tфр=2.3τ1
Из рис.4.1. следует, что переходная характеристика (4.2) представляет результат интегрирования единичного скачка σ (t) , т.е. линейно возрастающую функцию лишь для малых интервалов времени t<<τ, т.е. операция интегрирования с помощью цепи рис.2.1.а осуществляется лишь приближенно. Этот вывод полезно сравнить с частотным описанием свойств "интегрирующей" цепи в лабораторной работе №2.
Переходная характеристика "дифференцирующей" цепи (рис.2.1б)
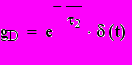
изображена на рис.4.2. Здесь заряд конденсатора С2 выражается в уменьшении выходного напряжения цепи с постоянной времени τ2
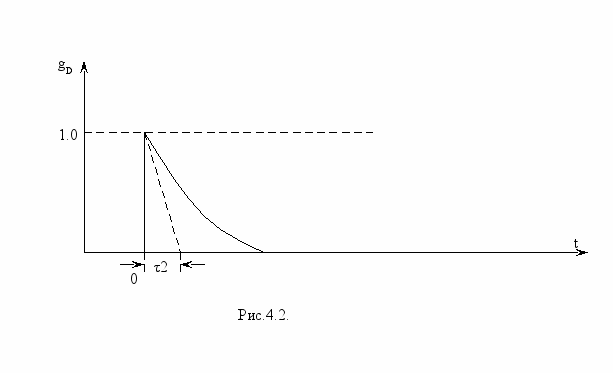
Ясно, что эта функция описывает операцию дифференцирования единичного скачка также лишь приближенно.
Переходная характеристика моста Вина выражается суммой двух
экспонент и приближенно может быть построена как на рис.4.3. при R3=R4=R, C3=C4=C, τ=RC, с использованием выражения:
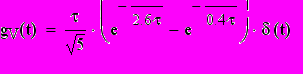
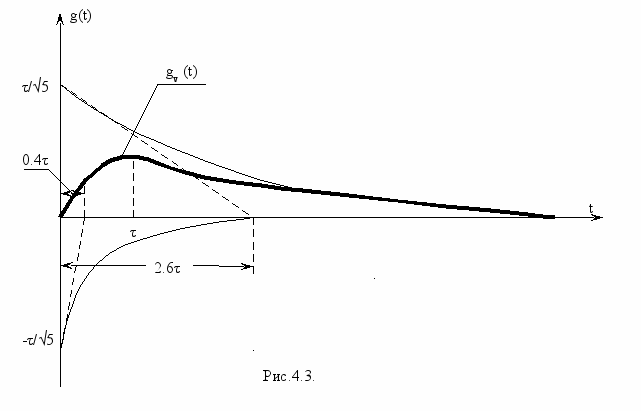
При экспериментальном измерении возникает ряд особенностей по сравнению с рассмотренной идеализированной схемой, поскольку используется не идеальный единичный скачок, а периодическая последовательность импульсов, что обеспечивает возможность наблюдения процессов на экране электронного осциллографа. Используемые импульсы имеют конечную длительность tи и конечное время нарастания/спада tфр.и, как показано на рис.4.1а пунктиром. Из этих диаграмм следует, что для точного измерения переходной характеристики эти параметры следует выбирать из условий:
tфр.и<<τ1
tи>>τ1 (4.3)
При этом следует учитывать, что спад испытательного импульса при t ≥tи вызывает в исследуемой цепи переходный процесс, являющийся переходной характеристикой с обратной полярностью. Наконец, периодическая последовательность импульсов длительностью tи, амплитудой А, с периодом Т имеет в своем спектральном составе (см.(1.4.) в лабораторной работе №1) постоянную составляющую
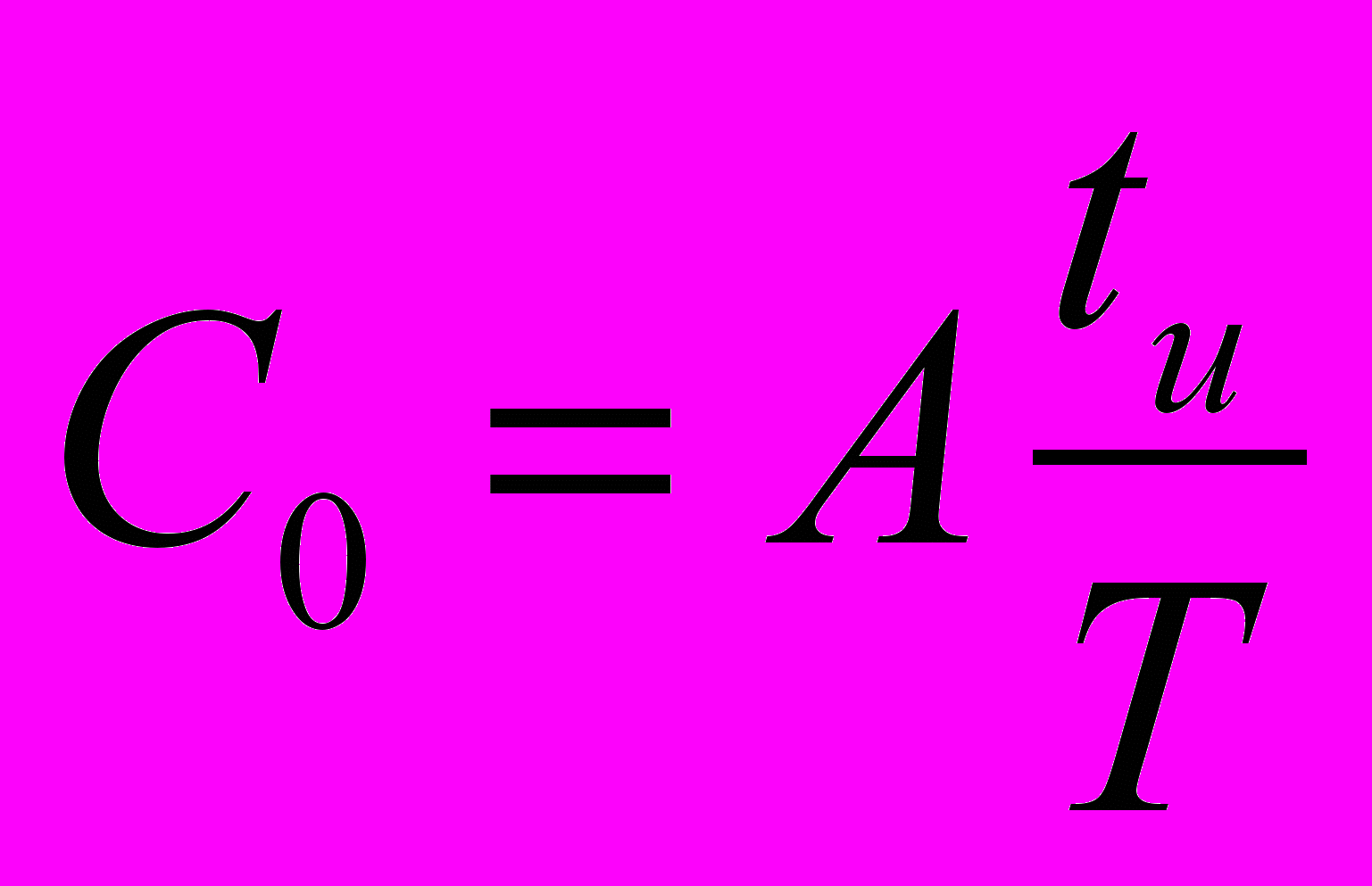
(4.4)
До этой величины напряжения постоянного тока заряжаются конденсаторы C1, C2, C3 в цепочках рис.2.1, что приводит к смещению уровня ноля на экране осциллографа. Уменьшение этого явления можно достичь, увеличивая период испытательных импульсов до величины:
T>>tи (4.5)
4.1.2. Вторым видом временных характеристик линейных радиотехнических цепей являются импульсные характеристики. Импульсной характеристикой h (t) называется отклик цепи на входное воздействие в виде δ - функции δ(t) . Поскольку формально δ(t) является производной от единичного скачка
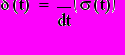
(4.5)
то в силу линейности рассматриваемых цепей и математических соотношений импульсные характеристики находятся дифференцированием переходных характеристик. Результаты такого дифференцирования для цепей рис.2.1.а, б, в приведены на рис.4.4а,б,в.
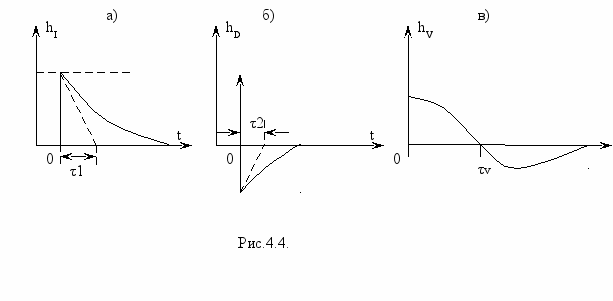
Для экспериментального измерения импульсных характеристик на вход цепи должен подаваться достаточно короткий импульс, который, строго говоря, никаким предельным переходе не сводится к δ-функции. Тем не менее, в соответствии с рис.4.4. при выборе длительности импульса из условия tи<<τ импульсные характеристики могут быть измерены с достаточной для практики точностью.
4.2. Описание экспериментальной установки для измерения временных характеристик линейных радиотехнических цепей.
В состав экспериментальной установки входит измерительный генератор импульсных сигналов, линейные радиотехнические цепи рис.2.1а,6,в и электронный осциллограф для наблюдения процессов на входе и выходе исследуемых цепей.
4.3. РАСЧЕТНАЯ ЧАСТЬ
При подготовке к работе (используя данные лаб. раб. №2) следует рассчитать постоянные времени исследуемых цепей и построить их переходные и импульсные характеристики. Оценить требуемые параметры импульсных сигналов при измерении переходных и импульсных характеристик.
4.4. ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
При выполнении работы подавать импульсные сигналы на вход исследуемых RC-цепей и при помощи осциллографа наблюдать переходные процессы на их выходах. Подобрать удобную для наблюдений амплитуду импульсов. Изменяя длительность входных импульсов, убедиться в правильности предварительного выбора этого параметра. Зарисовать осциллограммы переходных и импульсных характеристик.
4.5. СОДЕРЖАНИЕ ОТЧЕТА
Отчет должен содержать:
-структурную схему экспериментальной установки;
-расчеты переходных и импульсных характеристик исследуемых цепей
графики;
-осциллограммы переходных и импульсных характеристик;
-выводы по работе.
4.6. КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что такое импульсная характеристика линейной цепи?
2. Что такое переходная характеристика линейной цепи?
3. Как рассчитывается переходная характеристика линейной цепи
методом интеграла Лапласа?
4. Как экспериментально снять импульсную и переходную
характеристики линейной цепи?
5. Какие требования предъявляются к реальным тестовым сигналам при
экспериментальном измерении импульсной и переходной характеристик?
6. Как связаны между собой переходная и импульсная характеристики линейной цепи?
7. Как выглядят импульсные характеристики интегрирующей и дифференцирующей RC-цепей?
8. Как выглядят переходные характеристики интегрирующей и дифференцирующей RC-цепей?
9. Какие трудности возникают при экспериментальном измерении импульсной характеристики линейной цепи?
ЛАБОРАТОРНАЯ РАБОТА № 5
Временной метод расчета выходных сигналов линейных радиотехнических цепей.
5.1. Основные теоретические положения и расчетные формулы.
Временной метод расчета основан на определении выходного напряжения радиотехнической цепи Uвых(t) путем вычисления интеграла свёртки входного напряжения Uвх(t) и импульсной характеристики цепи h(t):
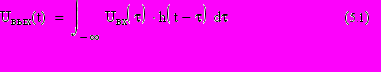
В простейших случаях интеграл (5.1) можно найти аналитически. Для импульсных входных сигналов длительностью tи при интегрировании в (5.1) необходимо выбирать соответствующие пределы интегрирования по τ. Однако, в силу справедливости принципа суперпозиции для линейных цепей входное действие в виде прямоугольного импульса можно заменить воздействием двух разнополярных скачков напряжения с соответствующим временным сдвигом (рис.5.1).
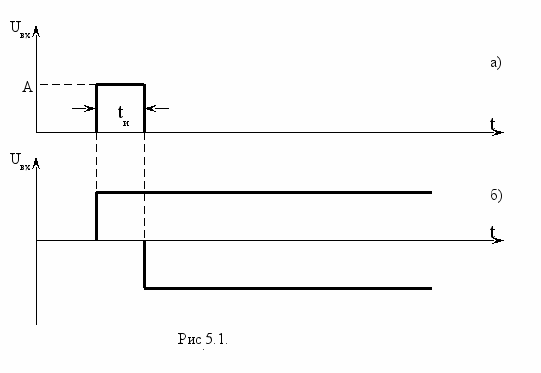
Тогда диаграмму выходного напряжения можно просто построить как разность переходных характеристик, сдвинутых на интервал tи.
На рис. 5.2. такое построение проведено для цепочки интегрирующего типа, переходная характеристика которой исследована в лабораторной работе №4 (рис.4.1.).
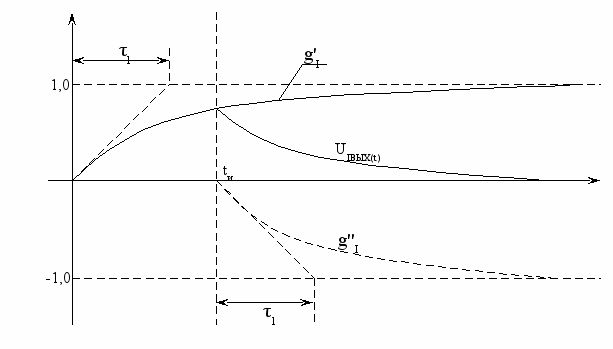
Рис.5.2.
Аналитически выходное напряжение определяется согласно с (5.1) различными выражениями на различных интервалах времени:
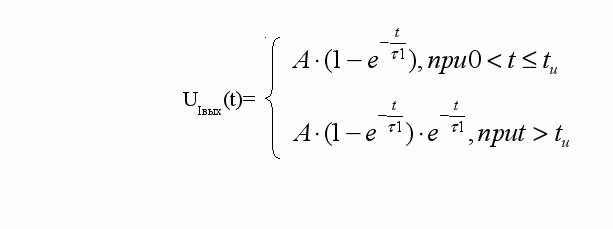
(5.2)
Из этих соотношений и интеграла (5.1) видно, что если длительность входного импульса много меньше постоянной времени цепи, то выходное напряжение Uвых(t) в каждый момент времени совпадает с формой импульсной характеристики цепи h(t), однако для измерения требуется значительное увеличение амплитуды входного воздействия A.
В другой предельной ситуации, когда длительность сигнала Uвх(t) много больше длительности импульсной характеристики, выражение (5.1)определяет совпадение формы входного и выходного напряжения цепи с учётом конечной длительности фронта и спада, как показано на рис.4.1.а. Эти соображения обосновывают способы измерения импульсных и переходных характеристик, использованные в лабораторной работе №4.
В общем случае, когда длительность входного сигнала сопоставима с постоянной времени цепи, т.е. длительностью её импульсной характеристики, форма сигнала на выходе цепи существенно отличается от формы входного сигнала.
Заметим, что вычисления Uвых(t) по (5.1) требуют числа умножений, пропорционального квадрату размерности массивов представления Uвых(t) и h(t), что ограничивает применение временных методов областью относительно коротких сигналов.
5.2. ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ
Для проведения измерений используется экспериментальная установка, состоящая из измерительного генератора периодических импульсных сигналов, линейных радиотехнических цепей рис. 2.1 а, б, в (лаб. раб. №2) и электронного осциллографа для наблюдения процессов на входах и выходах цепей.
5.3. РАСЧЕТНАЯ ЧАСТЬ
При подготовке к работе следует построить выходные напряжения цепочек, рис. 2.1 а, б, в для длительности входного импульса tи использованной в лабораторной работе №l в соответствии с номером рабочего места. При построении использовать переходные характеристики рис. 4.1., 4. 2., 4.3. – результаты лабораторной работы №4. Диаграммы напряжений построить с соблюдением масштабов осей времени и напряжения.
5.4. ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
При выполнении работы произвести осциллографические измерения рассчитанных напряжений и представить результаты в системах координат, совместных с расчетными. Для каждой цепи изменить в 1.5-2 раза длительность импульса в большую сторону и меньшую стороны, а также зарисовать диаграммы выходного напряжения. Объяснить полученные результаты. Сравнить их с результатами гармонического анализа (лабораторные работы №1,2,3)
5.5. СОДЕРЖАНИЕ ОТЧЕТА
Отчет должен содержать:
-структурную схему экспериментальной установки;
-расчеты выходных напряжений RC-цепей, графики;
-осциллограммы выходных напряжений;
-выводы по работе.
5.6. КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какими методами рассчитываются выходные сигналы линейных радиотехнических цепей?
2. Какой зависимостью во временной области связаны входные и выходные сигналы линейной радиотехнической цепи?
3. Описать порядок расчёта выходного сигнала линейной цепи временным методом.
4. Почему при вычислении выходного сигнала реальной радиотехнической цепи свёртка вычисляется только для неотрицательных времён?
5. В чём особенность расчёта выходного сигнала временным методом при входном воздействии в виде прямоугольного импульса?
ЛАБОРАТОРНАЯ РАБОТА № 6
Исследование преобразования гармонического колебания нелинейным элементом с кусочно-линейной амплитудной характеристикой.
6.1. Основные теоретические положения и расчетные формулы.
При воздействии синусоидального колебания с постоянной составляющей E0
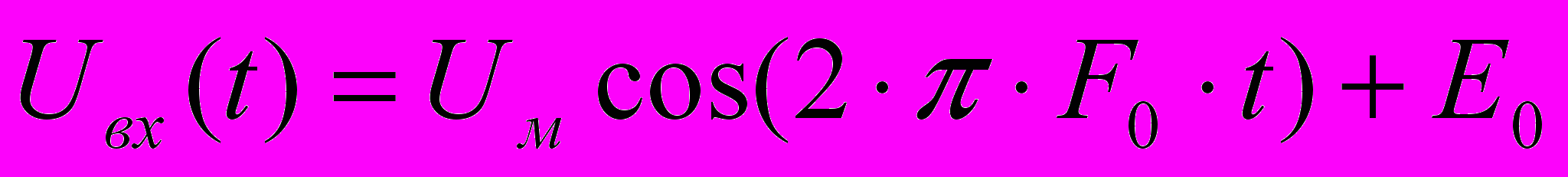 (6,1)
(6,1)б
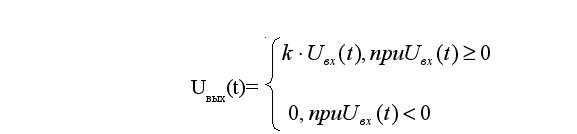 езынерционный нелинейный элемент, амплитудная характеристика которого допускает кусочно-линейную аппроксимацию
езынерционный нелинейный элемент, амплитудная характеристика которого допускает кусочно-линейную аппроксимацию(6,2)
на его выходе формируется периодическая последовательность импульсов, представляющих собой отрезки косинусоидального колебания (рис. 6.1.).Такие импульсы имеют спектральные составляющие основной F0 и кратных частот nF0 входного колебания (см. лабораторную работу №1). Нелинейное преобразование используется для оптимального выделения гармоник при n= 0,1,2,3 и т.д.
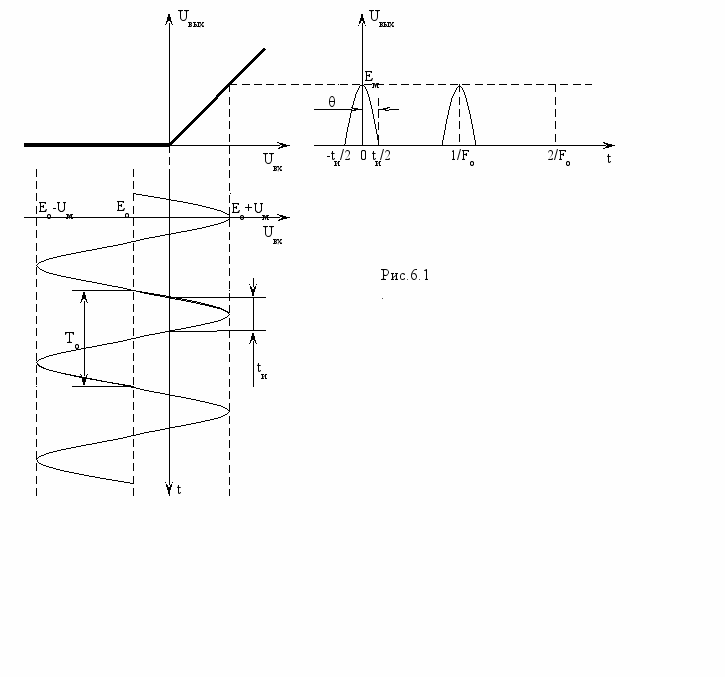
Академик Л.И.Берг показал, что амплитуда n-ой гармоники An в спектре косинусоидальных импульсов (при заданной в соответствии с рис.6.1. амплитуде выходного импульса Eм=K(E0+Uм) зависит только от угла отсечки θ, представляющего скважность формируемых импульсов:
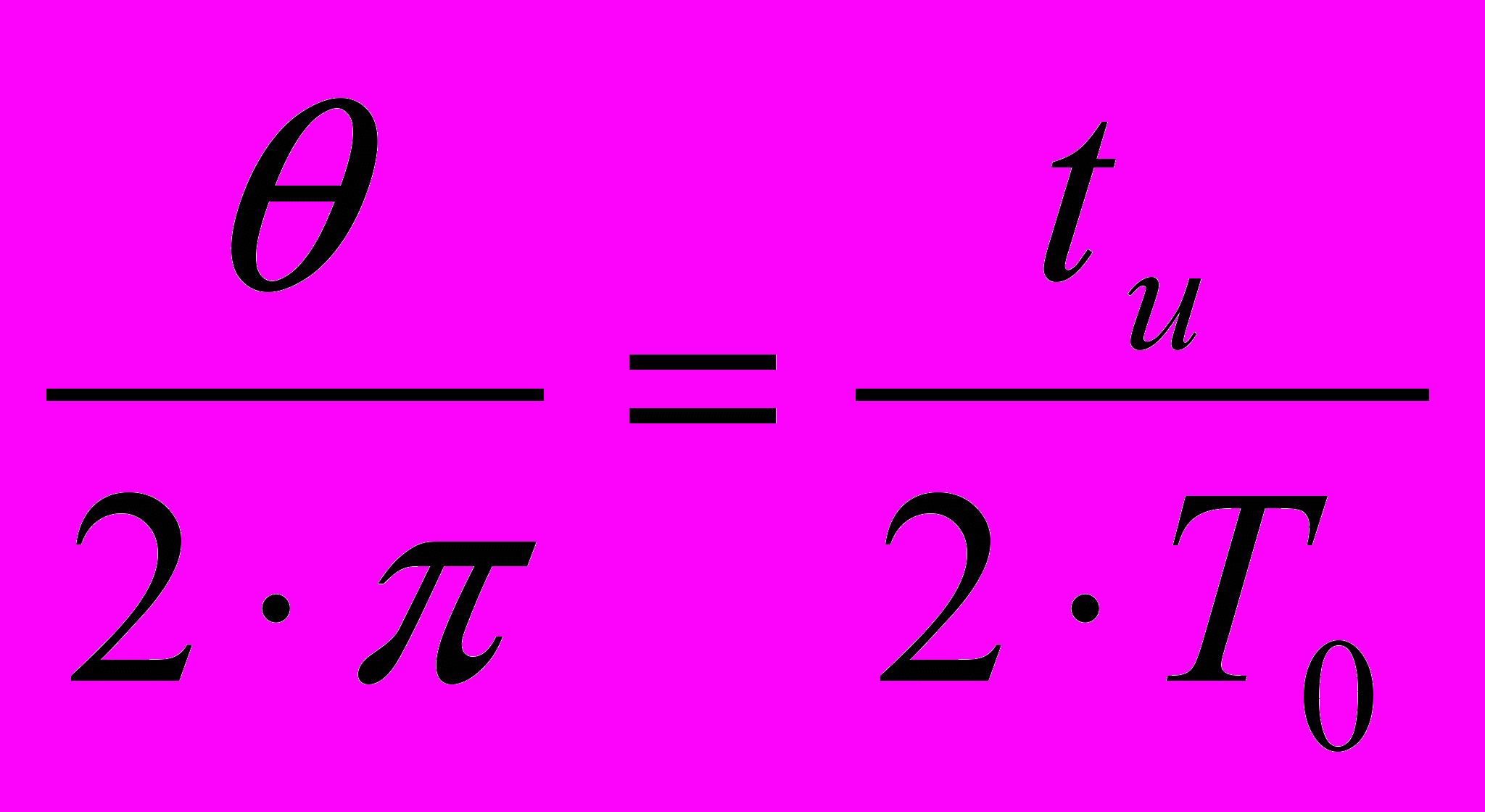 , где
, где 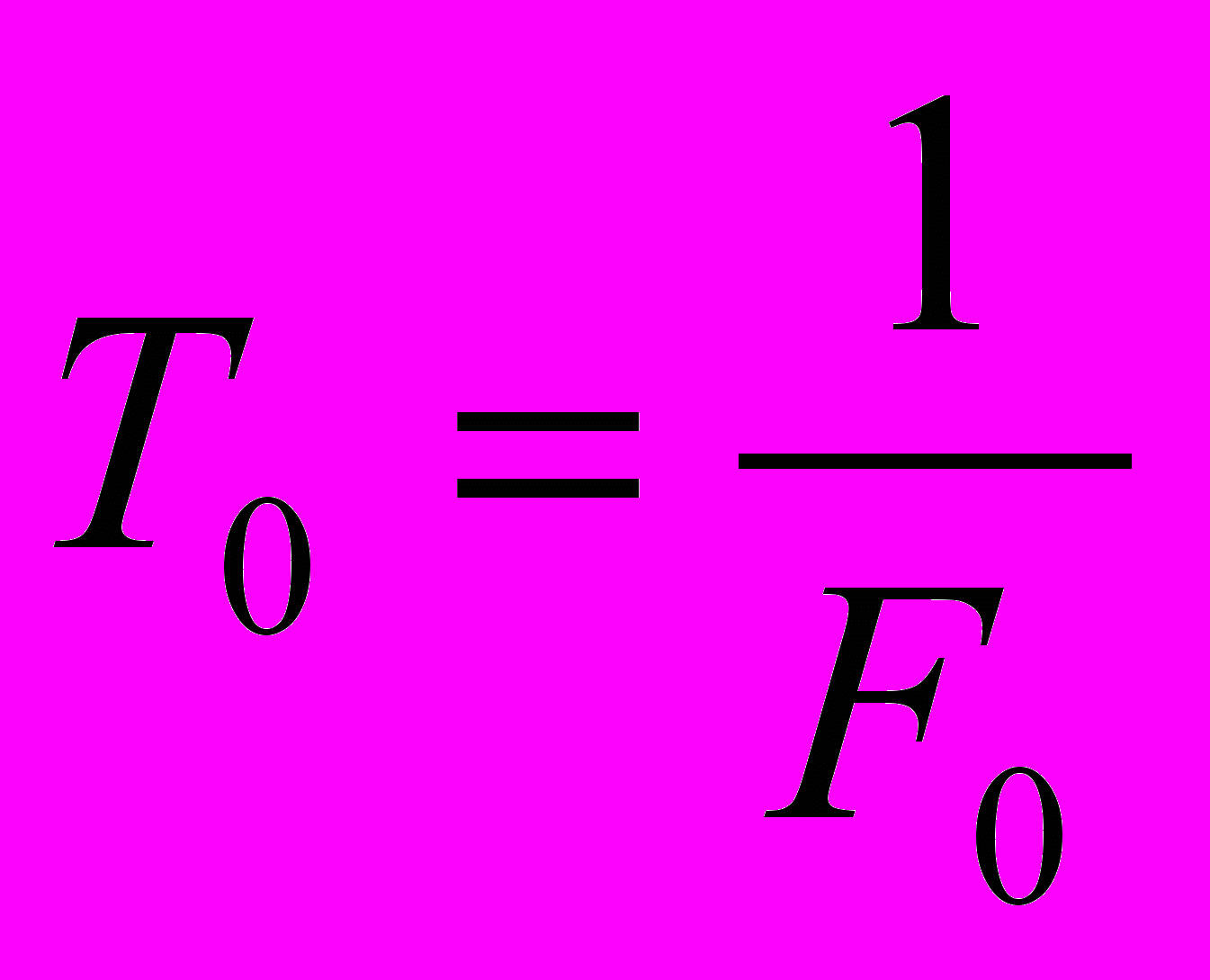 , т.е.
, т.е.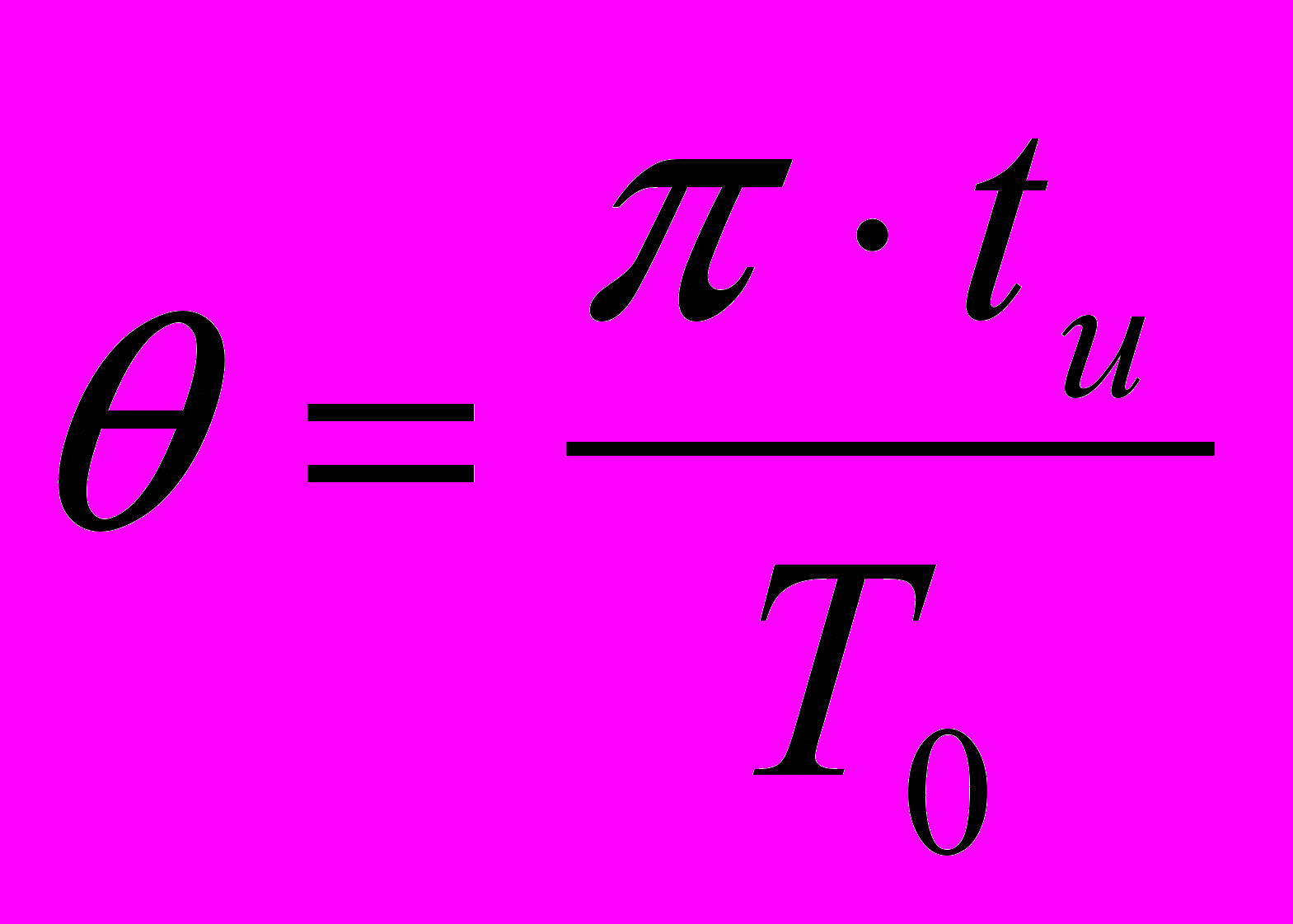 (6,3)
(6,3)Зависимости Аn (θ) обычно представляются в нормированной форме
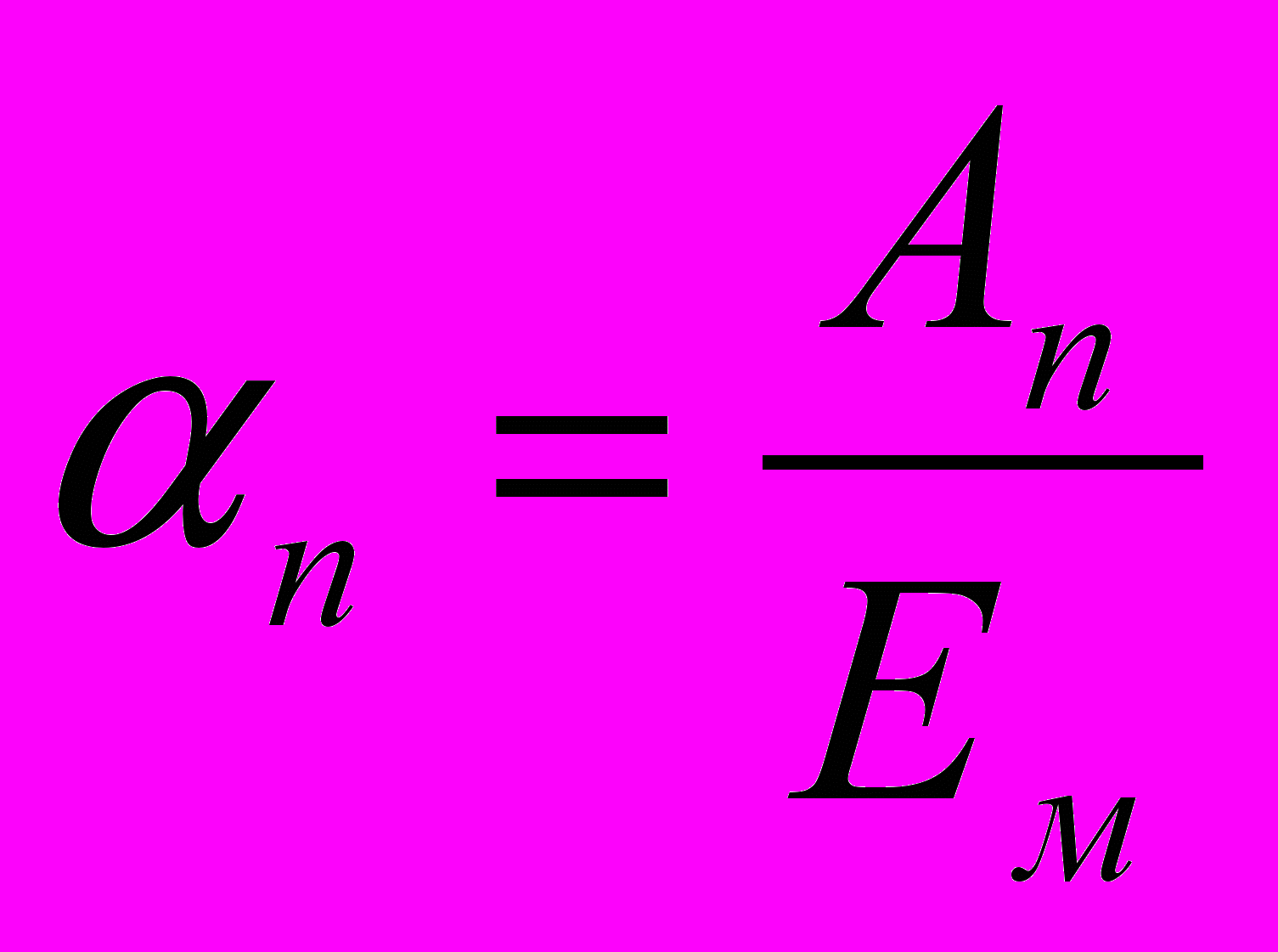 при n=0,1,2,3….и имеют вид
при n=0,1,2,3….и имеют вид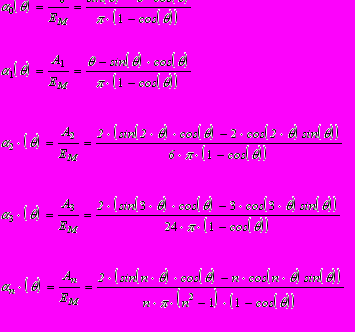 (6.4.)
(6.4.)Устройства, выделяющие вторую и третью гармоники, используются в умножителях частоты.
Выделение первой гармоники из состава косинусоидальных импульсов используется в мощных каскадах радиоустройств, поскольку при этом отношение
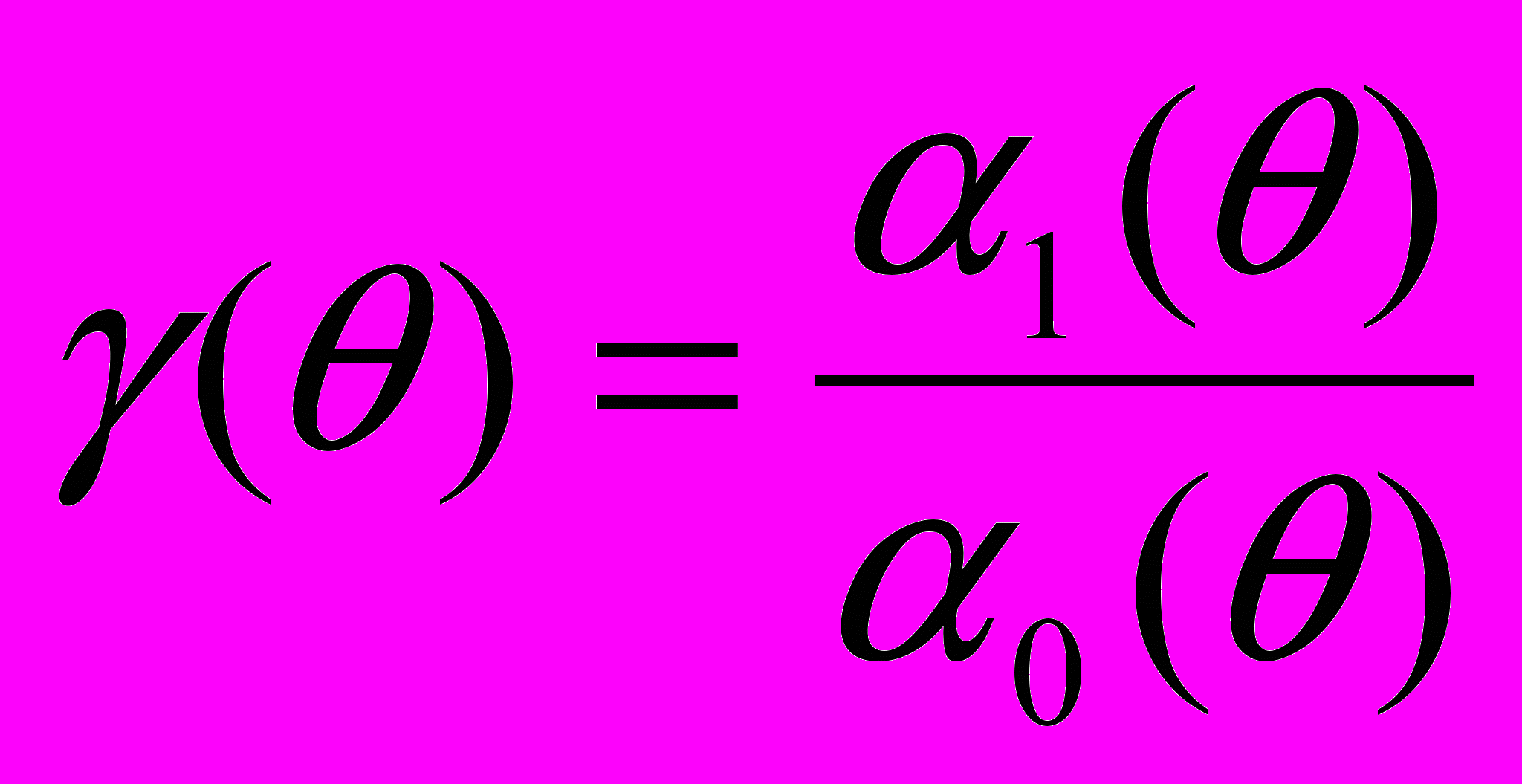 , определяющее к. п. д. нелинейной схемы, оказывается выше, чем для линейной. Типичной величиной при этом является θ = 90° (двухтактные схемы).
, определяющее к. п. д. нелинейной схемы, оказывается выше, чем для линейной. Типичной величиной при этом является θ = 90° (двухтактные схемы).Целью настоящей лабораторной работы является экспериментальное измерение зависимостей (6.4.).
6.2. ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ.
Лабораторная установка включает генератор гармонического сигнала, напряжение которого подается на вход нелинейного элемента использующего операционный усилитель и поэтому требующего включения напряжения питания установки. Выходное напряжение нелинейного элемента наблюдается на экране электронного осциллографа, с помощью которого определяется величина угла отсечки по соотношению (6.3.).
Гармонический анализ формируемых косинусоидальных импульсов производится
с помощью перестраиваемого фильтра как в лабораторной работе №1. В результате анализа определяют зависимости Аn(θ).
6.3. РАСЧЕТНАЯ ЧАСТЬ
При подготовке к работе с помощью соотношений (6.4) рассчитать зависимости Аn(θ) для n=0,1,2,3, а также отношение
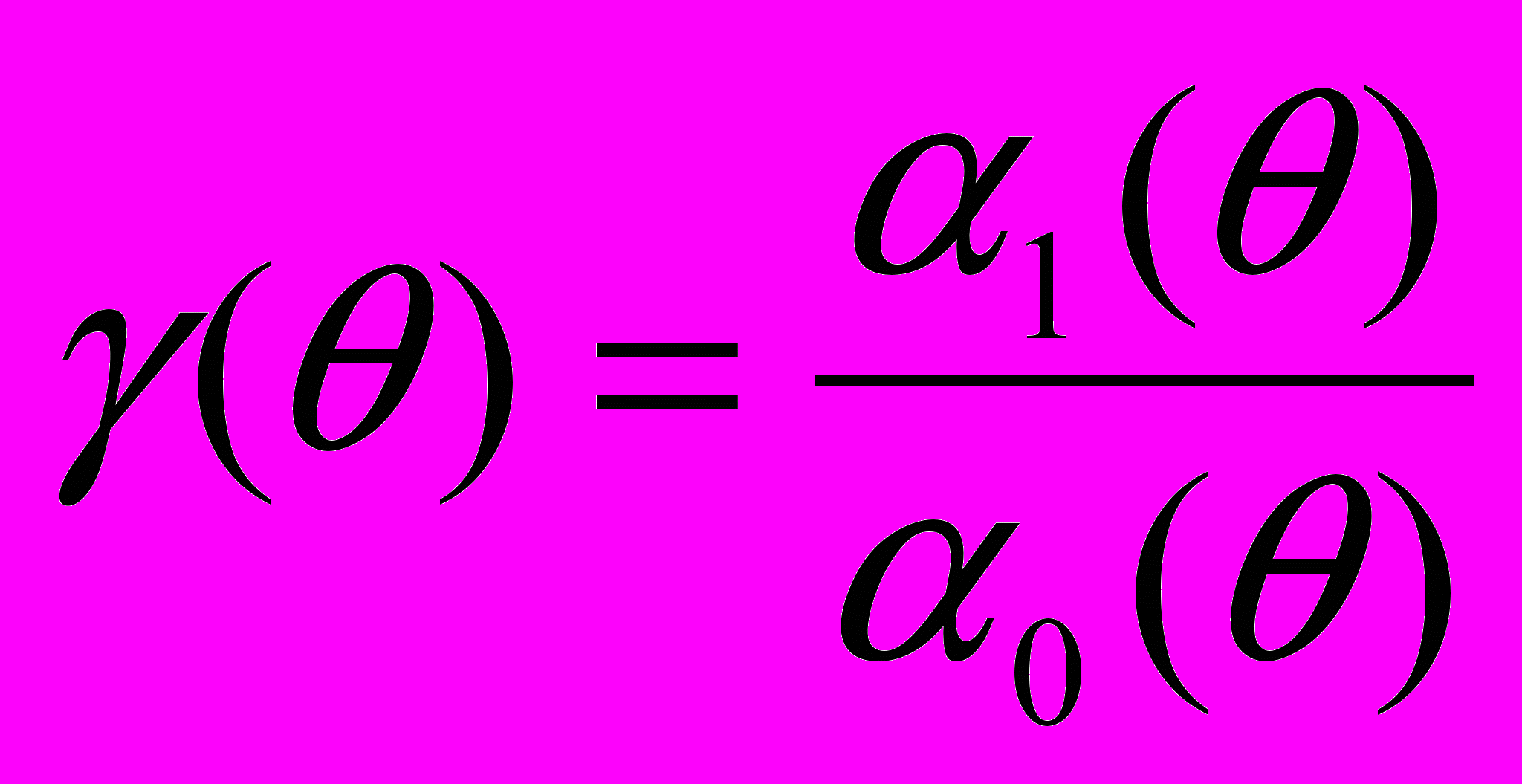 в диапазоне изменения углов от 0 до π с шагом π/8. Построить рассчитанные соотношения в совмещенной системе координат An(θ).
в диапазоне изменения углов от 0 до π с шагом π/8. Построить рассчитанные соотношения в совмещенной системе координат An(θ).6.4. ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
При выполнении работы установить входное напряжение с частотой, использованной в лабораторной работе №1. С помощью напряжения смещения Е нелинейного элемента установить угол отсечки =180°и определить в этих условиях максимально возможную амплитуду входного напряжения Uм , при которой отсутствуют нелинейные искажения в максимуме и минимуме гармонического напряжения на экране осциллографа. Эту амплитуду напряжения использовать в дальнейшей работе.
Изменяя напряжение Е0, обеспечить режим отсечки и определить соответствующее значение угла θ по экрану осциллографа. При каждом значении определить амплитуду гармоник An с помощью перестраиваемого фильтра. Использовать 8-10 отсчетных точек по θ, при этом строгое совпадение с величинами θ, использованными при предварительных расчетах не обязательно. Построить экспериментальные диаграммы в совмещенной системе координат с расчетными. Сделать выводы по работе. Обратить внимание на величину γ(θ) при =90°. Эта величина определяет к.п.д. усилителя.
6.5. ТРЕБОВАНИЯ К ОТЧЕТУ
Отчет должен содержать:
-структурную схему экспериментальной установки;
-расчеты зависимости Аn(θ) для n=0,1,2,3, γ(θ) ; графики;
-экспериментально снятые зависимости Аn(θ), сведенные в таблицу;
графики;
-выводы по работе.
6.6. КОНТРОЛЬНЫЕ ВОПРОСЫ
1.Что такое нелинейный безинерционный элемент?
2.Что такое угол отсечки, как он зависит от скважности формируемых
импульсов?
3. Каковы частоты гармонических составляющих выходного сигнала нелинейного безинерционного элемента с кусочно-линейной вольтамперной характеристикой, когда на его входе действует гармоническое колебание с частотой F0?
4.Что такое коэффициент Берга “n”-порядка?
5. При каком угле отсечки коэффициенты Берга первого порядка максимальны?
6.При каких углах отсечки максимальны коэффициенты Берга порядка выше первого?
7.Какова взаимосвязь коэффициента полезного действия усилителя с углом отсечки коллекторного тока и
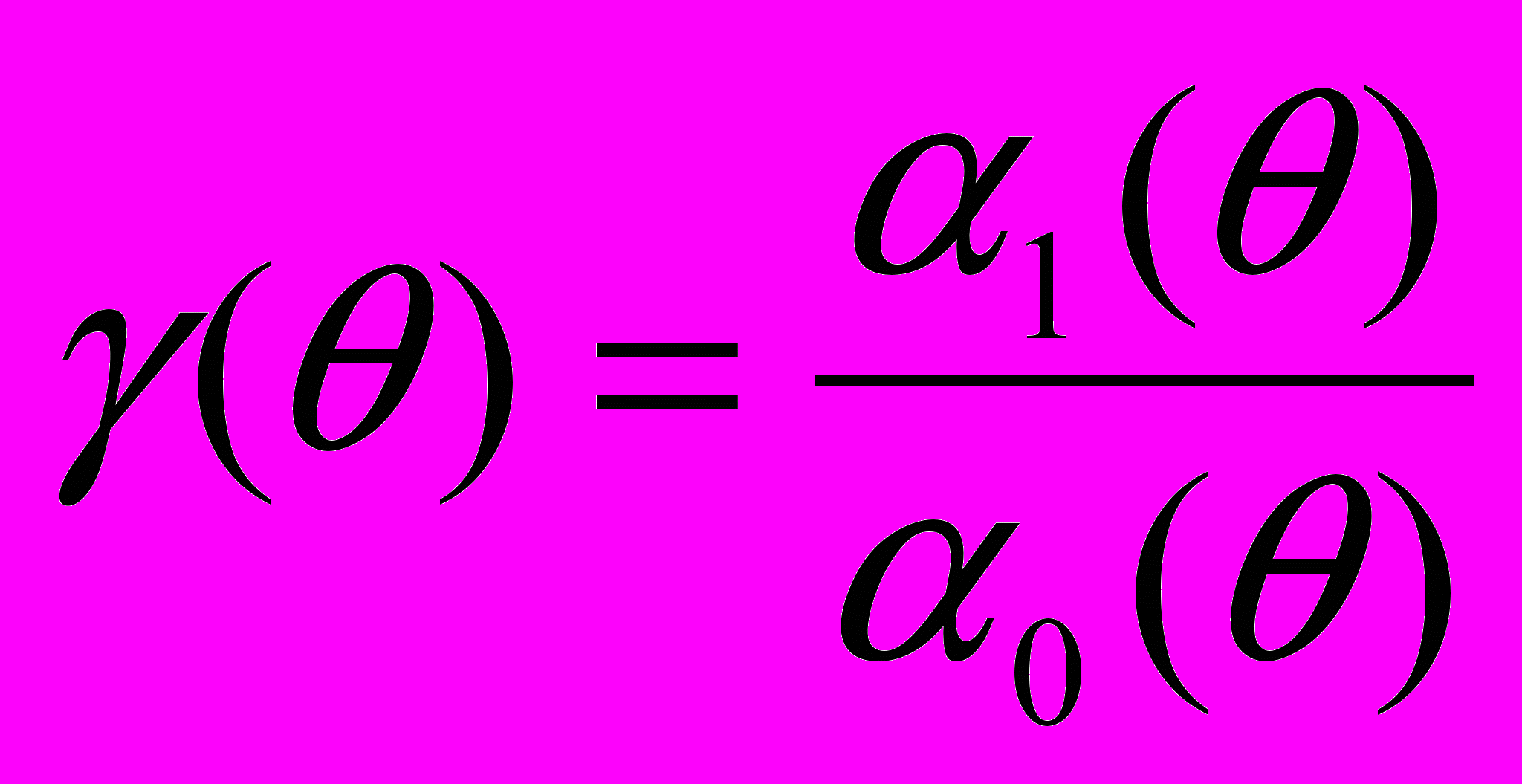 ?
?Балтийский Государственный Технический Университет “ВОЕНМЕХ” им.Д.Ф.Устинова
Астанин Л.Ю., Демин Ю.С., Кротов Н.А., Флёров А.Н.
Методические указания к лабораторным работам по дисциплине “Радиотехнические цепи и сигналы.”
ЧАСТЬ 1
Санкт-Петербург
2005г.
