Geum.ru

Программа курса лекций (3 курс, 6 сем., 32 ч., диф зачет) Профессор Киричук Валерий Сергеевич Доцент Косых Валерий Петрович

Вид материалаПрограмма курса
Подобный материал:

Обработка сигналов и изображений

Программа курса лекций
(3 курс, 6 сем., 32 ч., диф.зачет)


Профессор Киричук Валерий Сергеевич

Доцент Косых Валерий Петрович

Доцент Перетягин Георгий Иванович
  1. Классификация сигналов и способы их описания. Информативные характеристики детерминированных сигналов (энергия, мощность, моменты, автокорреляционная функция, спектральный состав). Гармонический анализ импульсной последовательности. Скважность, меандр, эффективная ширина спектра, база сигнала. Примеры.
  2. Процесс дискретизации сигналов (аналого-цифровое преобразование). Спектр дискретизованного сигнала. Восстановление аналогового сигнала по множеству отсчетов. Теорема Котельникова-Шеннона. Частота Найквиста. Эффект появления «ложных частот» (aliasing). Примеры.
  3. Дискретное преобразование Фурье (ДПФ). Основные свойства ДПФ. Использование ДПФ для восстановления исходного сигнала и для вычисления отсчетов «непрерывного» спектра (интерполяция спектра). Вычисление линейной свертки при помощи ДПФ. Эффект «растекания» спектра и весовые функции (окна). Алгоритмы быстрого преобразования Фурье (БПФ).
  4. Ограничения и недостатки преобразования Фурье. Проблемы частотно-временной локализации нестационарных сигналов. Оконное преобразование Фурье. Идея вейвлет-преобразования. Основы теории. Базисные функции непрерывного вейвлет – преобразования (WAVE -, MHAT -, DOG – вейвлеты). Примеры применения.
  5. Дискретный вейвлет-анализ. Кратномасштабное представление сигналов. Скейлинг-функция и материнский вейвлет. Вейвлеты Хаара и Добеши. Быстрое вейвлет-преобразование (алгоритм Малла). Примеры применения.
  6. Стохастическая модель сигналов и изображений (статистический ансамбль, совместное распределение, статистические моменты). Дискретные стационарные (однородные) случайные процессы и поля. Среднее, автокорреляция, автоковариация. Виды стационарности случайных процессов и полей. Спектральная плотность мощности (СПМ) случайных процессов. Взаимосвязь с автоковариационной последовательностью (АКП) – теорема Винера-Хинчина. Свойства АКП и СПМ стационарных случайных процессов.
  7. Некоторые модели случайных сигналов. Гармонический процесс со случайной фазой. Дискретный гауссовский случайный процесс. Марковское свойство. Винеровский процесс (броуновское движение) как пример гаусс-марковского случайного процесса. Случайный фототелеграфный сигнал (сканирование черно-белого изображения): вероятностная модель, автокорреляционная функция, спектральная плотность мощности.
  8. Эргодичность. Основные принципы теории оценок (несмещенность, состоятельность). Оценивание автокорреляции и взаимной корреляции. Свойства оценок. Коррелограммный метод оценки СПМ. Метод Блэкмана-Тьюки. Периодограммные оценки СПМ. Свойства оценок. Спектральные окна. Метод Уэлча.
  9. Линейные преобразования (фильтрация) стационарных случайных сигналов: свойства выходного сигнала (существование, моменты, автоковариационная функция). Описание фильтра в виде дискретной линейной системы: импульсная характеристика, частотная характеристика, фильтры с линейной фазовой характеристикой. Прямое Z-преобразование дискретных последовательностей. Область сходимости. Свойства Z-преобразования. Z-свертка последовательностей. Передаточная функция дискретной системы.
  10. Линейные разностные уравнения с постоянными коэффициентами как модели цифровых (рекурсивных) фильтров. Численное интегрирование как пример рекурсивной фильтрации. Бегущий усредняющий фильтр, авторегрессионный фильтр. Обратное Z-преобразование. Нули и полюсы дискретной системы, минимально-фазовое свойство. Авторегрессионная (параметрическая) модель стационарных случайных процессов как универсальная модель стохастических сигналов. Взаимосвязь параметров авторегрессионной (АР-) модели с автокорреляционной последовательностью. Нормальные уравнения Юла-Уолкера. СПМ авторегрессионного процесса.
  11. Оптимальный линейный прогноз стационарных случайных процессов. Принцип ортогональности. Разложение Вольда (регулярная и сингулярная составляющие случайного сигнала). Понятие «обновления». Алгоритм Левинсона рекуррентного оценивания параметров АР-модели. Спектральное оценивание. Характеристики АР-оценок СПМ.
  12. Оценивание случайного процесса по наблюдениям стохастически связанного с ним случайного сигнала (дискретное уравнение Винера-Хопфа). Метод восстановления дискретного (полезного) сигнала в линейной модели наблюдений на основе оптимального линейного фильтра Винера-Колмогорова. Ошибка восстановления сигнала в простейших вариантах.
  13. Аппроксимация (сглаживание) сигналов и метод наименьших квадратов (МНК). Алгебра и геометрия МНК. Нормальное решение. Метод псевдообратной матрицы. SVD-решение. Статистические свойства оценок МНК.
  14. Проверка гипотез при спецификации аппроксимирующей модели сигнала (основы проверки статистических гипотез). Проверка линейных гипотез. Критерии удаления (включения) переменных в описание сигнала.
  15. Модели дискретных систем в пространстве состояний (уравнение состояния системы, уравнение измерения). Пример на основе авторегрессионной схемы описания. Построение алгоритма рекуррентной фильтрации Калмана для дискретной линейной динамической системы: коэффициент усиления фильтра, оптимальный выбор параметров фильтрации. Двумерная дискретная фильтрация (примеры построения винеровского и калмановского фильтров). Сравнительный анализ.
  16. Распознавание образов (сигналов). Разделяющие функции. Алгоритмы классификации выборочных объектов. Байесовский метод распознавания. Дискриминантный анализ (распознавание) для двух многомерных нормальных выборок. Вероятности ошибок классификации. Виды и свойства оценок.
  17. Применение методов классификации в алгоритмах сегментации изображений двумерных сцен.

Задания


1. Вычислить коэффициенты ряда Фурье для последовательности прямоугольных импульсов. Охарактеризовать изменение спектра последовательности импульсов при увеличении периода их следования.

2. Вычислить спектр и автокорреляционную функцию гармонического сигнала 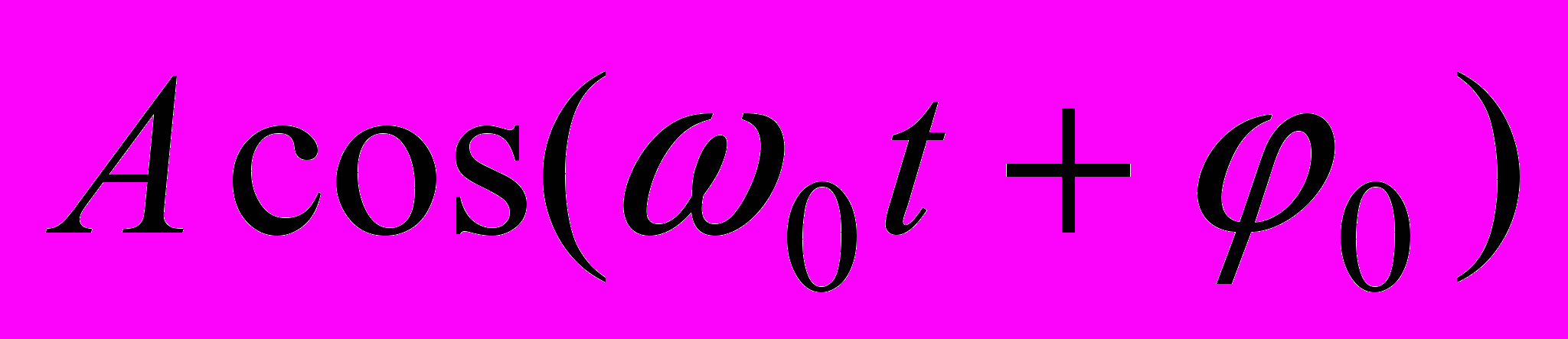, учитывая, что период такого сигнала равен .

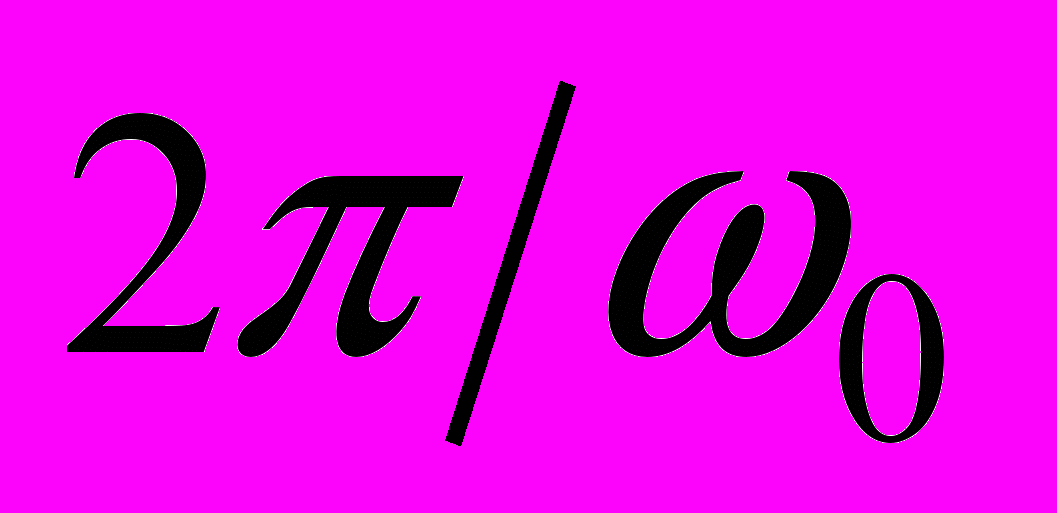3. Вывести взаимосвязь спектров аналогового сигнала и дискретной последовательности отсчетов этого сигнала. Как проявляется эффект «ложных частот».

4. Установить изменение спектра дискретного сигнала, состоящего из N отсчетов, при добавлении к нему N нулей.

5. Охарактеризовать суть эффекта «растекания» спектра и привести методы его уменьшения.

6. Как правильно вычислить линейную свертку с помощью БПФ?

7. Привлекая принцип неопределенности, определить вид частотно-временных окон Фурье и вейвлет базисов на плоскости время-частота.

8. Определить скейлинг-функцию и коэффициенты вейвлет-преобразования базиса Хаара.

9. Показать, что гармонический сигнал со случайной фазой является стационарным случайным процессом.

10. Вывести автокорреляционную функцию фототелеграфного сигнала.

11. Стационарная последовательность (дискретный сигнал) 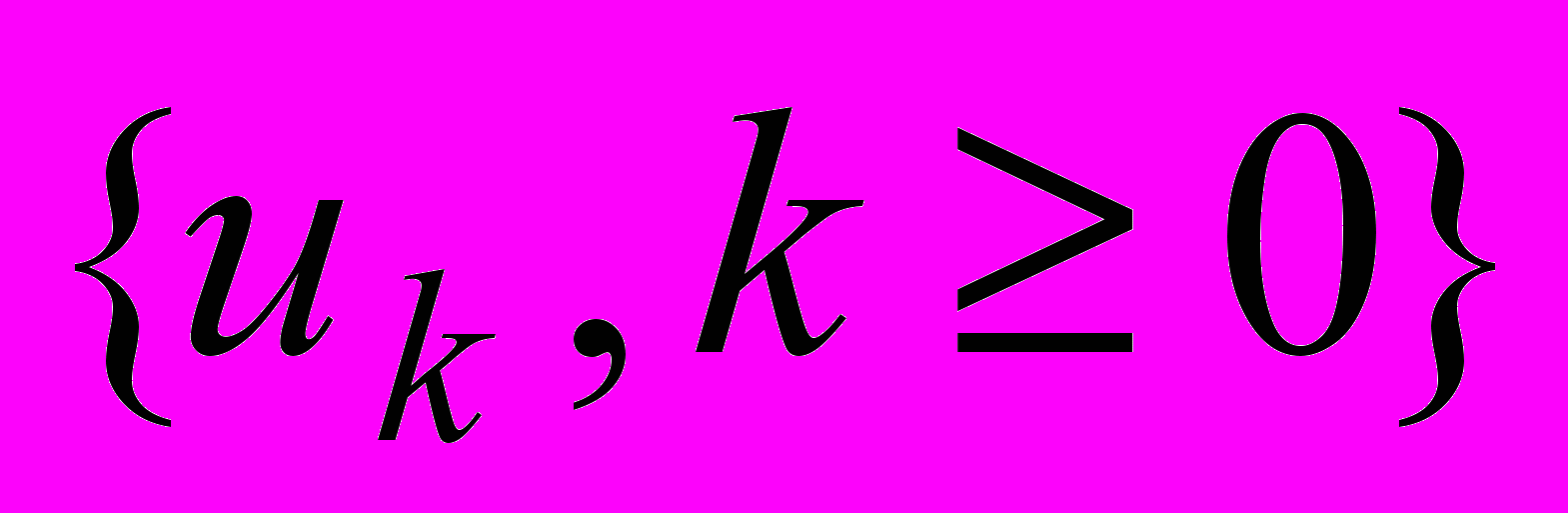определена соотношением 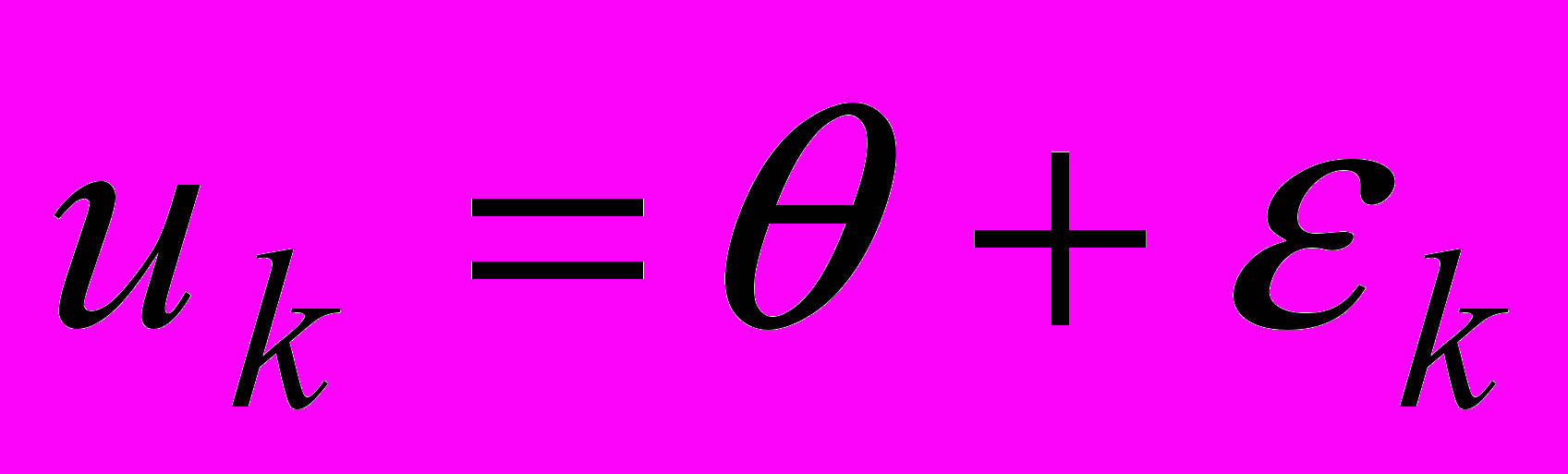, где - случайный параметр со средним значением 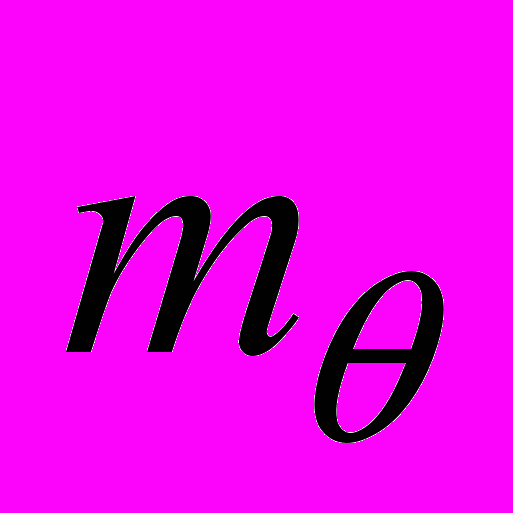и дисперсией 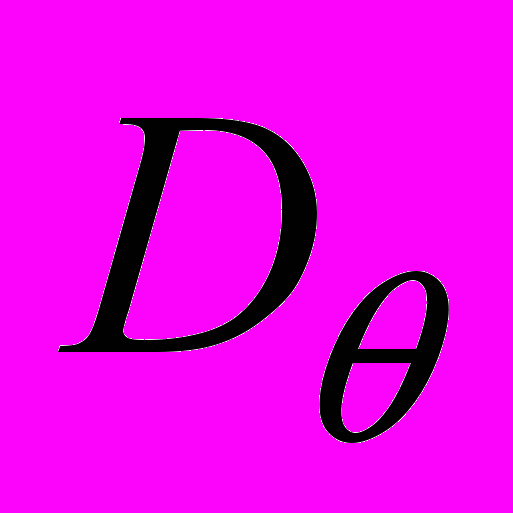, 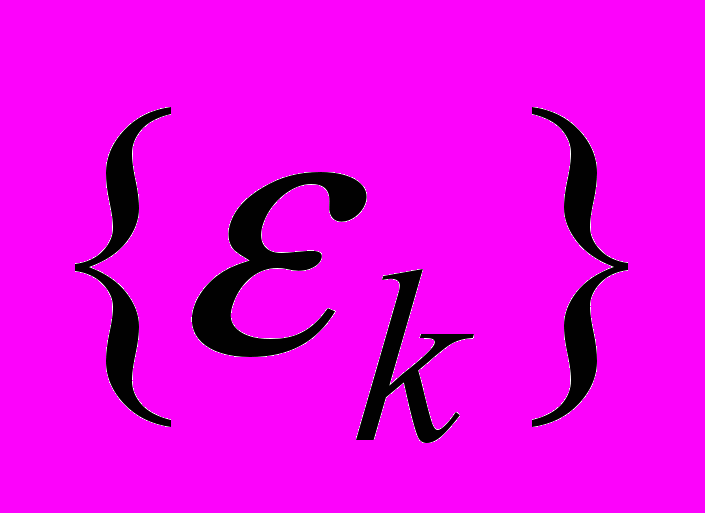- центрированный дискретный белый шум с дисперсией 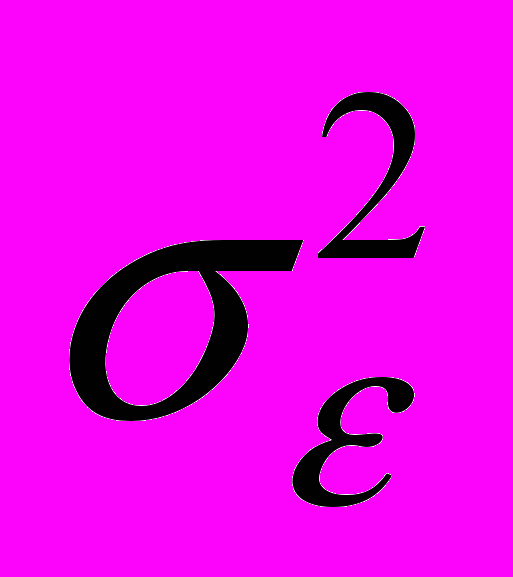, не коррелированный с .

Доказать, что среднее значение 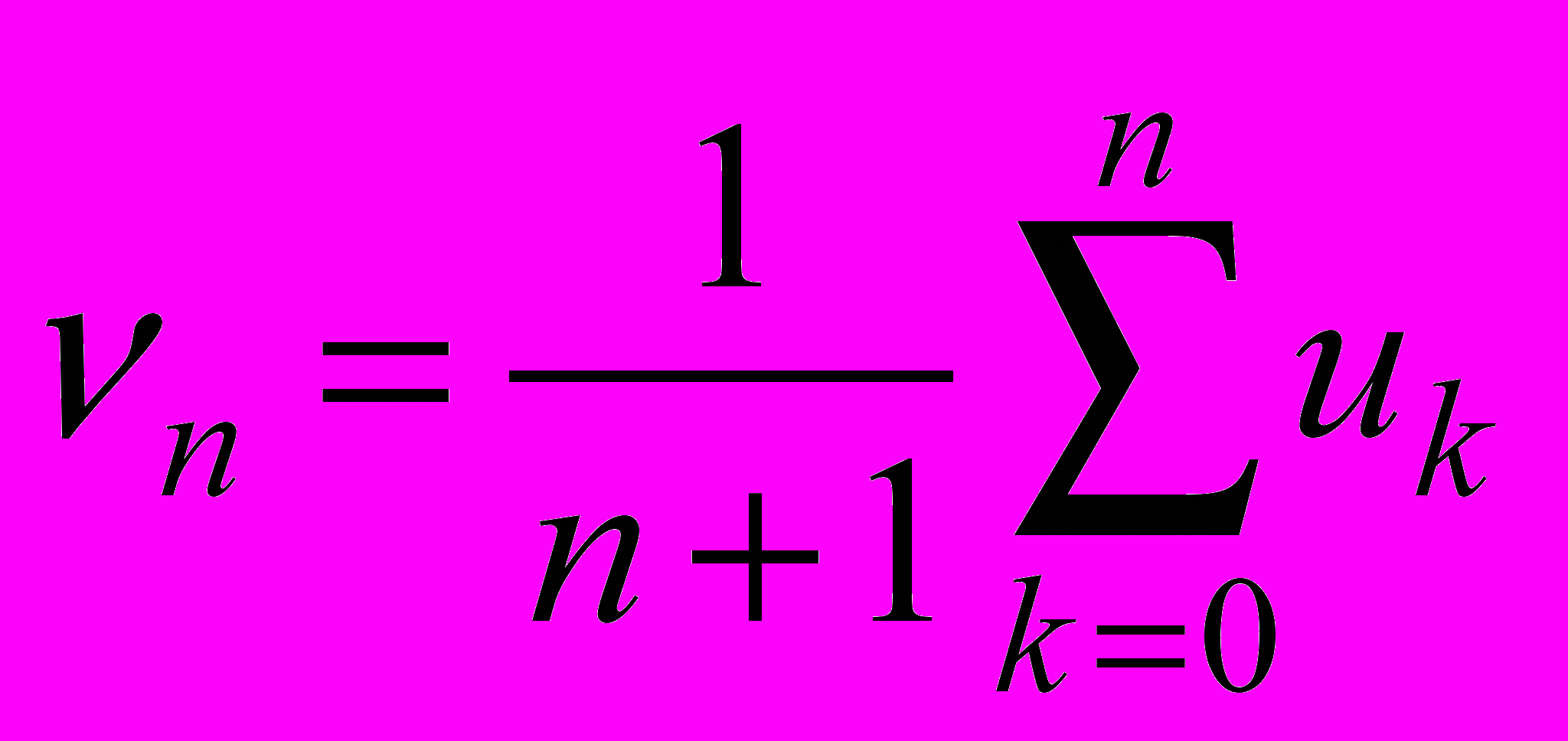, n>1, является несмещенной и состоятельной оценкой для .

12. Показать, что для оценки АКП 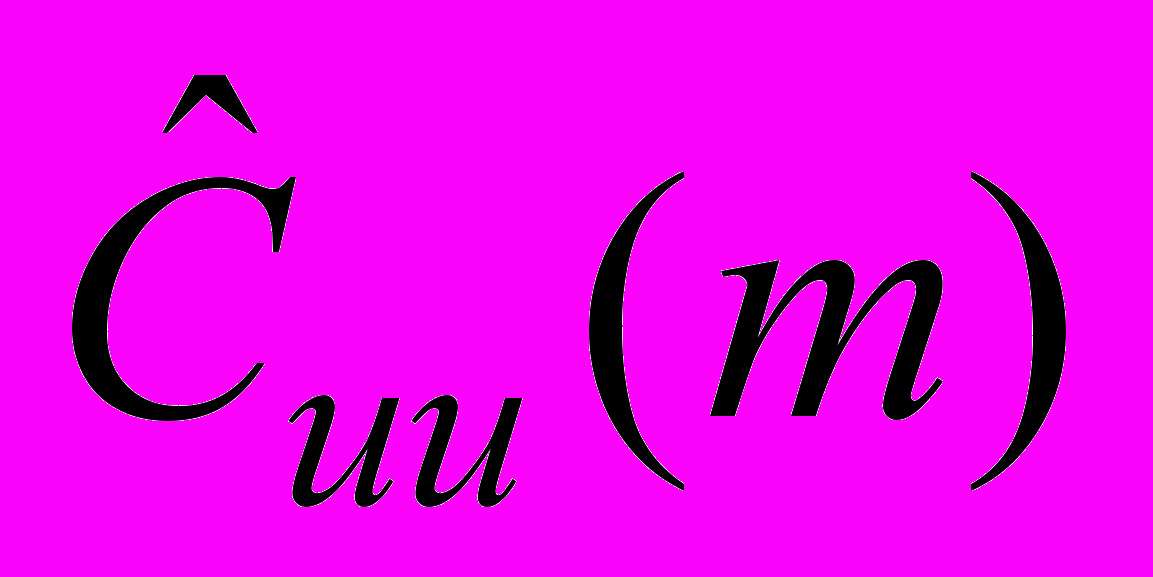оценка СПМ имеет вид

.

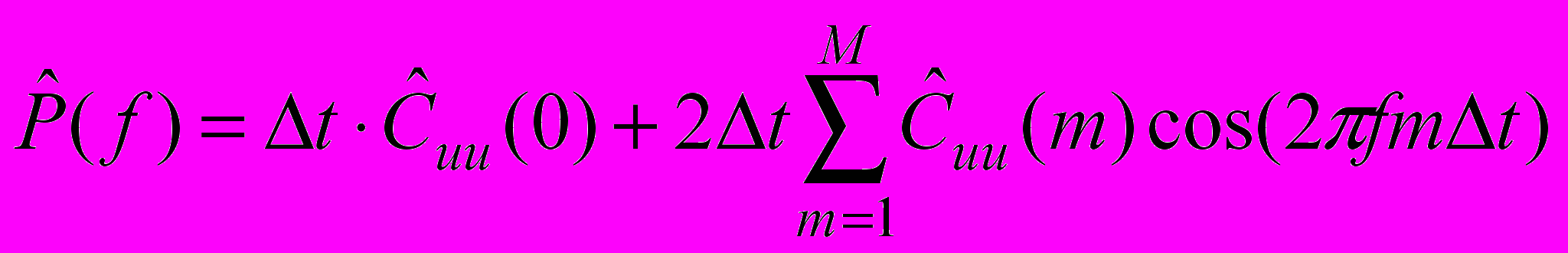13. Пусть дано N отсчетов данных 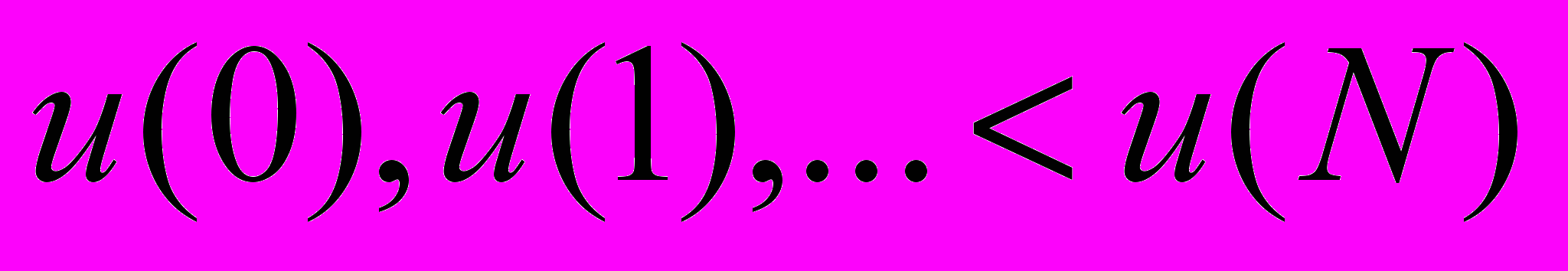. Показать, что коррелограммная оценка СПМ

,

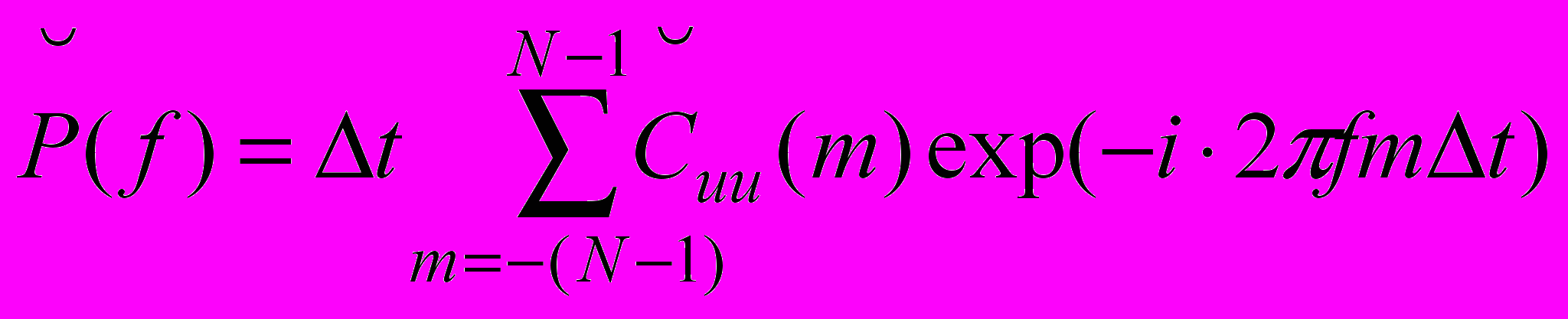в которой используется смещенная (альтернативная) оценка при максимальном числе возможных временных сдвигов, и выборочный энергетический спектр (периодограмма)

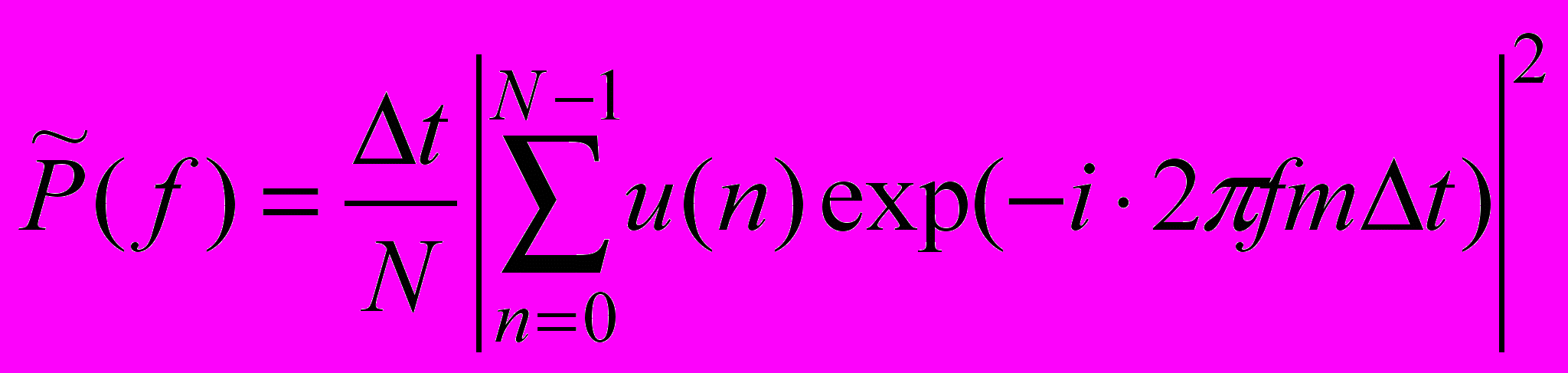, идентичны.

14. Процесс наблюдения формируется по следующей схеме: 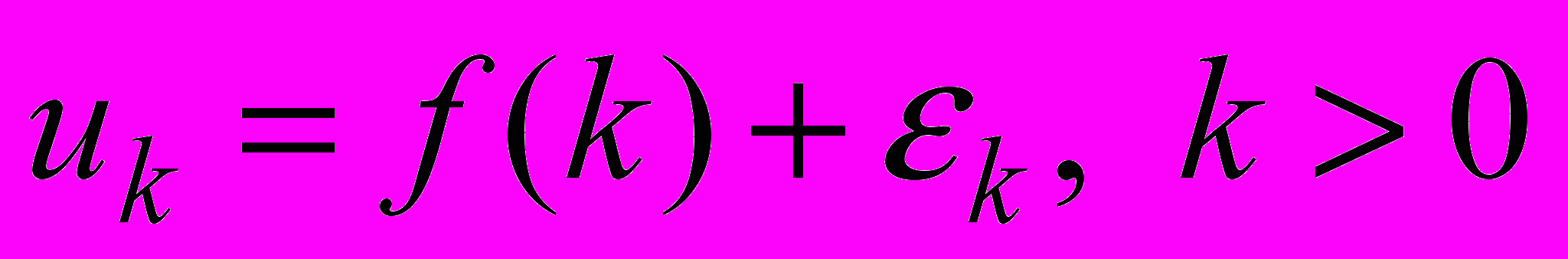, где f(k) – полезный нестационарный случайный сигнал, а 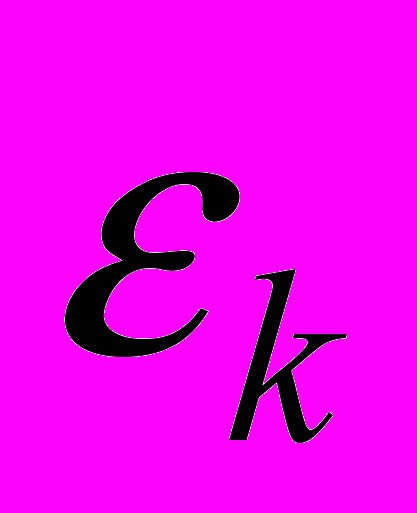- центрированный белый шум с дисперсией 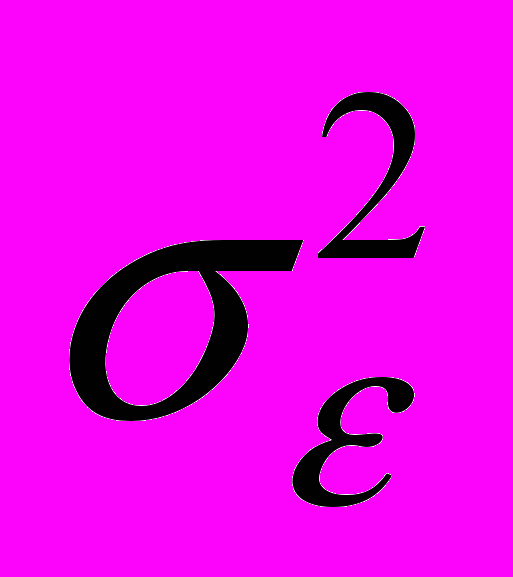. Для оценивания сигнала f(k) наблюдаемая последовательность подвергается преобразованию, которое называется фильтром экспоненциального сглаживания и имеет вид 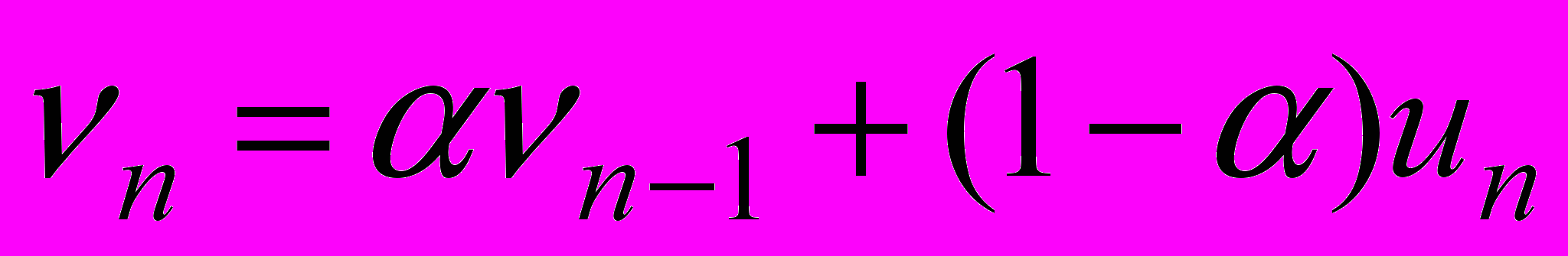, где 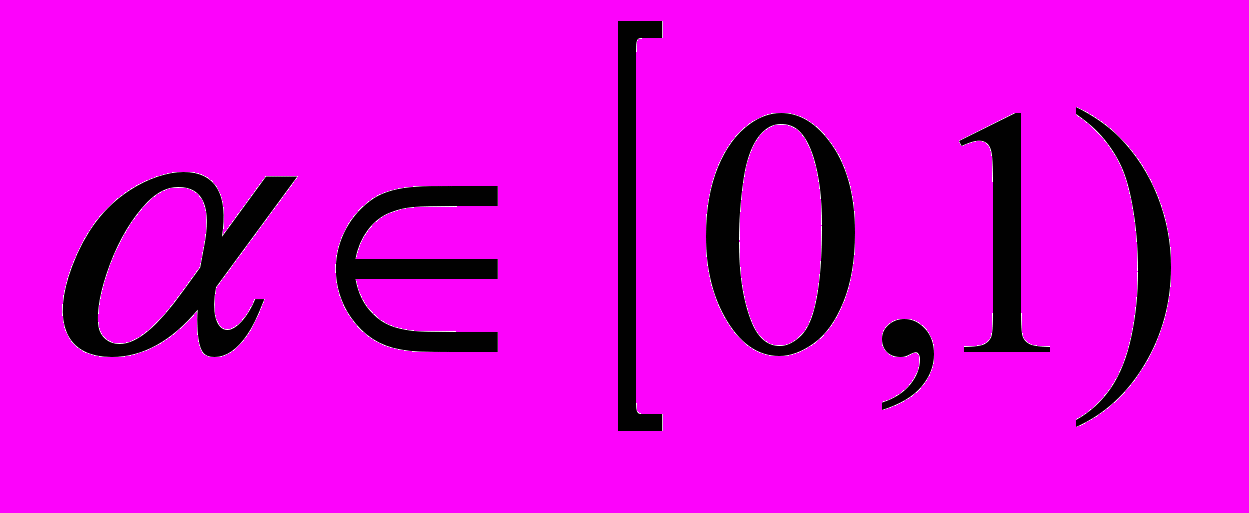- параметр фильтра. Показать, что данный фильтр является линейным преобразованием вида

.

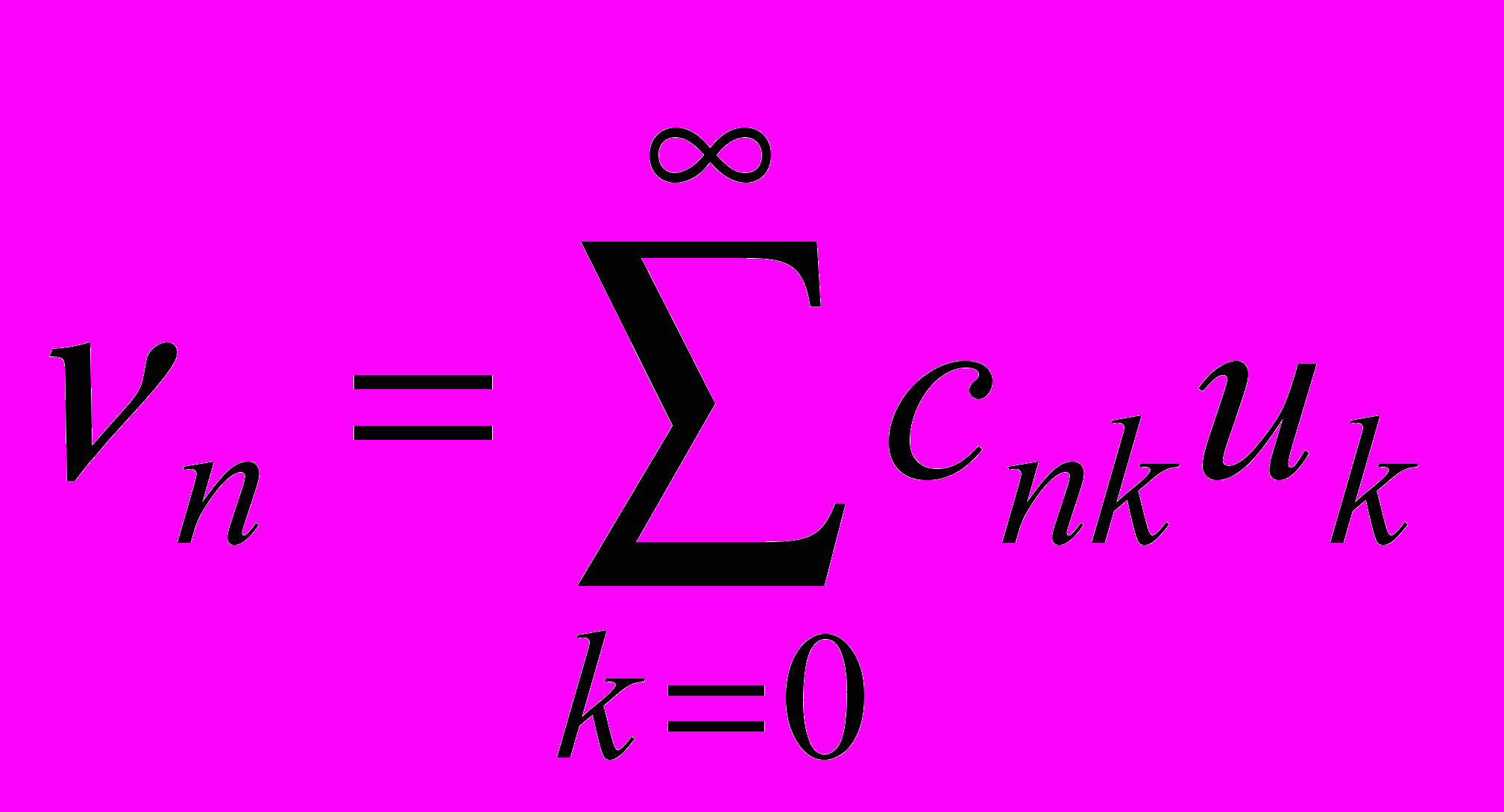15. Пусть при некотором 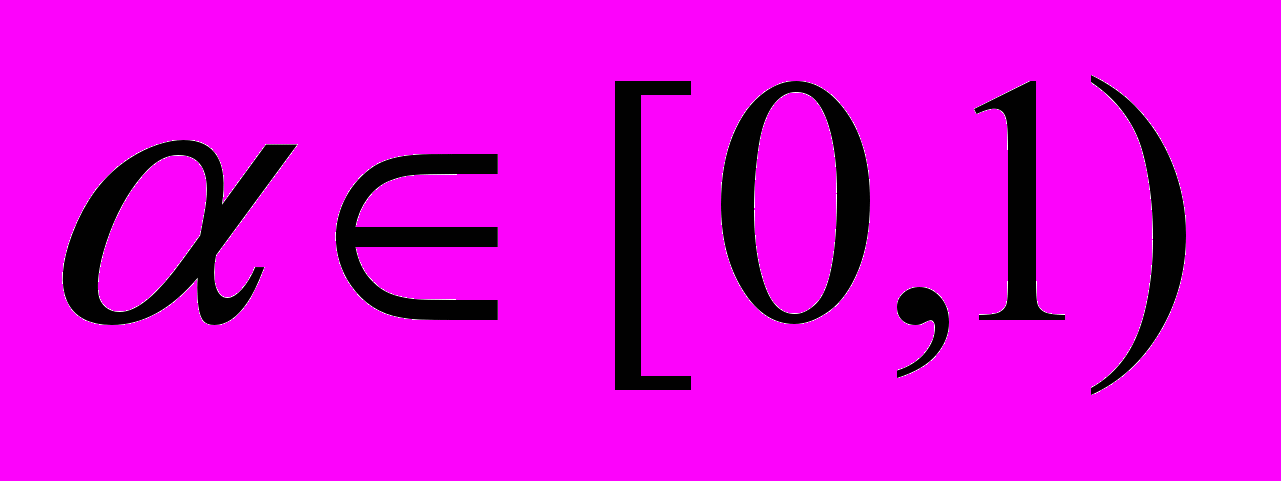последовательность 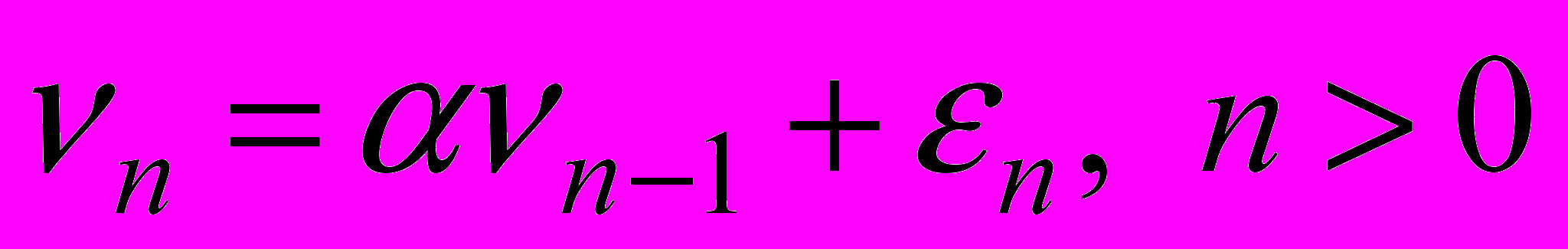. Показать, что данное соотношение является линейным стационарным фильтром, и найти среднее, дисперсию и автоковариационную функцию последовательности .

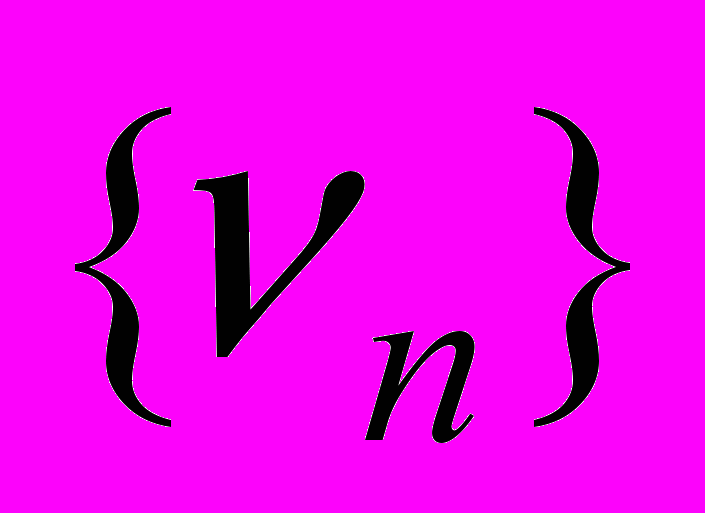16. Найти область сходимости Z-преобразования последовательности

.

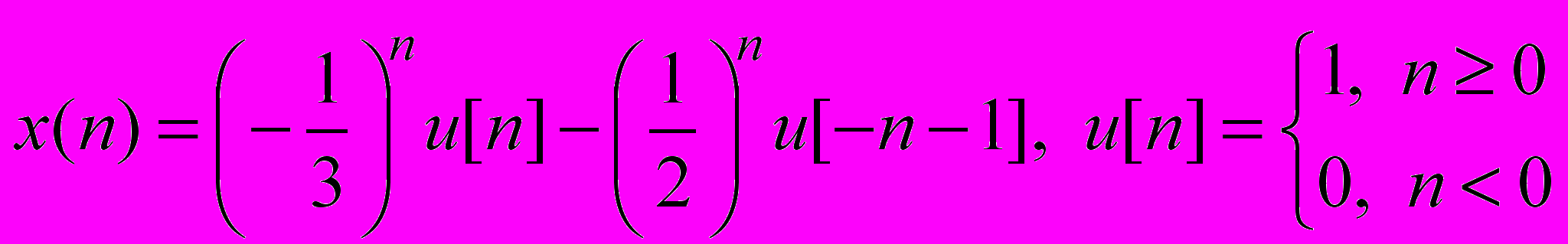17. Найти представление автоковариационной последовательности через последовательность авторегрессионных параметров.

18. Пусть в АР-модели первого порядка белый шум является стационарным. Найти математическое ожидание и дисперсию АР(1)-последовательности и показать ее стационарность.

19. Показать, что выход АР(p)-фильтра является регулярной последовательностью.

20. Охарактеризовать связь между фильтром линейного предсказания (прогноза) и АР – процессом.

21. Описать метод выбора порядка АР-модели в алгоритме Левинсона.

22. Дать геометрическую интерпретацию проблемы винеровской фильтрации.

23. Определить передаточную функцию фильтра Винера-Колмогорова.

24. Построить фильтр Калмана для скалярной модели наблюдений вида



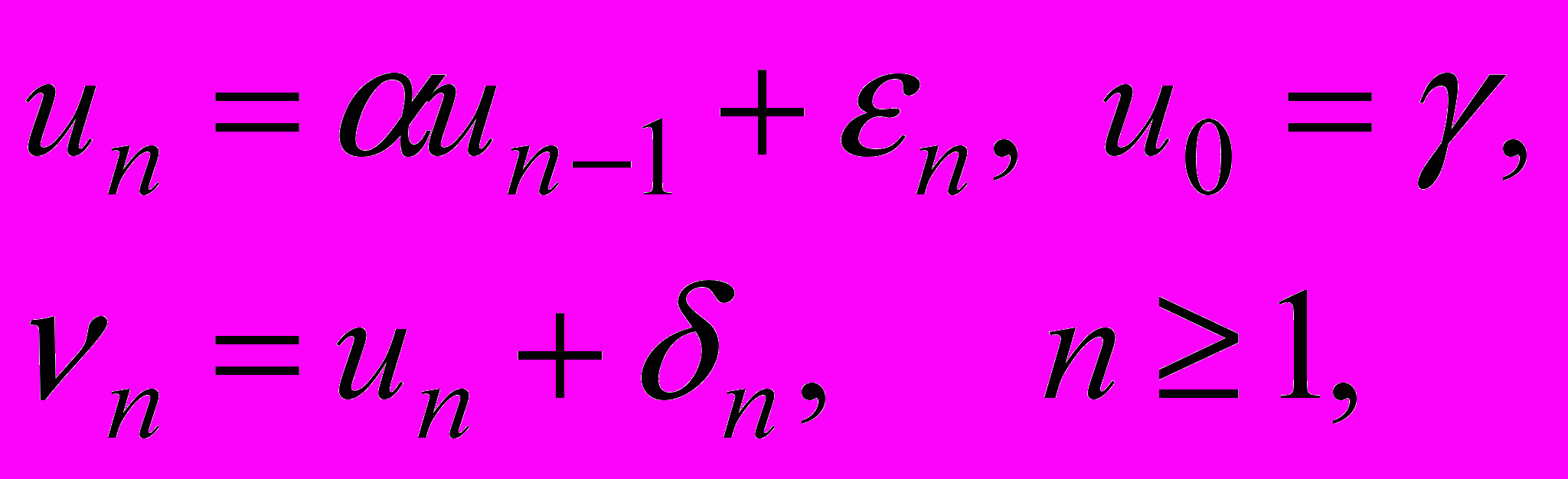
где 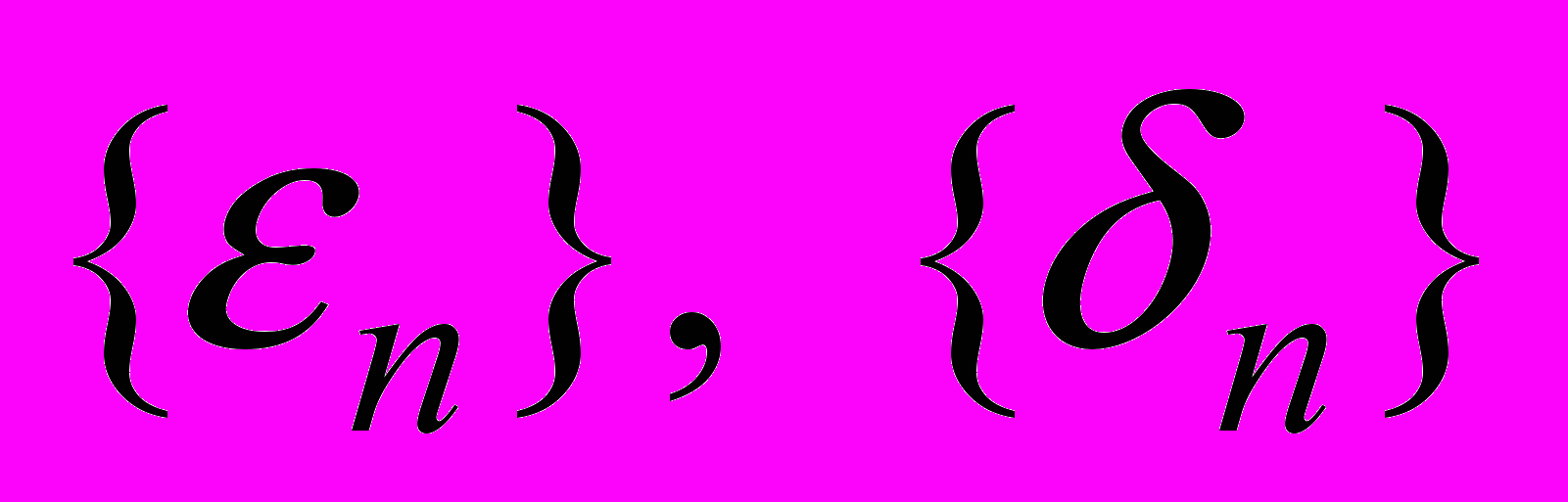- стационарные и центрированные белые шумы.

Литература

  1. Сергиенко А.Б. Цифровая обработка сигналов. – СПб.: Питер, 2002.
  2. Марпл-мл. С.Л. Цифровой спектральный анализ и его приложения. – М., Мир, 1990.
  3. Грузман И.С., Киричук В.С. и др. Цифровая обработка изображений в информационных системах. Учебное пособие. Новосибирск, 2001.
  4. Методы компьютерной обработки изображений. /Под ред. В.А.Сойфера. – М.: Физматлит, 2001.
  5. Н.М.Астафьева. Вейвлет-анализ: основы теории и примеры применения. //Успехи физических наук. Т.166, №11, 1996.
  6. Интернет-страничка «Теория и практика вейвлет-преобразования»: ссылка скрыта
  7. Дьяконов В., Абраменкова И. МАТЛАБ. Обработка сигналов и изображений. Специальный справочник. – СПб., Питер, 2002.
  8. Балакришнан А.В. Теория фильтрации Калмана. – М., Мир, 1988.
  9. Френкс Л. Теория сигналов.– М., Советское радио, 1974.
  10. Фукунага К. Введение в статистическую теорию распознавания образов. – М., Наука, 1979.