Компьютерная графика

Вид материала

Реферат

Содержание Рис 3.2 Эффект пикселизации при масштабировании растрового изображения 4.1 Средства создания векторных изображений 4.2 Особенности терминологии Объекты векторной графики

Подобный материал:

• Программа кружка «Компьютерная графика» (34 часа), 462.83kb.
• Элективный курс по информатике и икт компьютерная графика, 84.46kb.
• Трёхмерная компьютерная графика – пользовательский и алгоритмический подход, 72.66kb.
• Аннотация примерной программы дисциплины «Инженерная и компьютерная графика» Рекомендуется, 412.89kb.
• Программа дисциплины Компьютерная графика (цикл опд. Ф. 6): «Искусство интерьера»-052500, 165.78kb.
• Рабочая программа По дисциплине «Компьютерная графика» По специальности 230102., 250.33kb.
• Методическая разработка открытого урока по теме "Компьютерная графика", 96.49kb.
• Аннотации дисциплин, 456.29kb.
• Рабочая программа дисциплины «Компьютерная графика» для специальности 032401 «Реклама», 248.52kb.
• Реализация межпредметных связей математики и информатики на примере курса «инженерная, 227.3kb.

Рис 3.2 Эффект пикселизации при масштабировании растрового изображения

3.6 Преимущества и недостатки растровой графики

Одним из достоинств растровой графики является простота
и, как следствие, техническая реализуемость (автоматизация) ввода (оцифровки) изобразитель­ной информации. Существует развитая система внешних устройств ввода изо­бражений (к ним относятся сканеры, видеокамеры, цифровые фотокамеры, гра­фические планшеты).

Растровое изображение имеет преимущества при работе с фото­реалистичными объектами, например сценами природы или фотографиями людей. Наш мир создан как растровый. И его объекты трудно представить
в вектор­ном, то есть математическом, представлении. Фотореалистичность подразумева­ет, что в растровой программе можно получать живописные эффекты, например туман или дымку, добиваться тончайшей нюансировки цвета, создавать перспек­тивную глубину и не резкость, размытость и т. д.

Форматы файлов, предназначенные для сохранения точечных изображений, являются стандартными, поэтому не имеет решающего значения, в каком графическом редакторе создано то или иное изображение.

В растровой графике есть и недостатки. При первой же попытке что-нибудь нарисовать в программе точечной графики – например в Photoshop – она потребует принципиального ре­шения о разрешении (количестве точек на единицу длины) и о глубине цвета (количестве цветовых битов на пиксел). Ничего этого знать в векторной программе не нужно.

Объем файла точечной графики однозначно определяется произведением пло­щади изображения на разрешение и на глубину цвета (если они приведены
к единой размерности). При этом совершенно не важно, что отображено
на фото­графии: деревянный одноцветный столб или коллекция бабочек
с обилием цвета и форм. Если три параметра одинаковы, размер файла будет практически одинаковым.

Как только попытка отсканировать не очень большую фотографию
с максимальными разрешением и глубиной цвета, эта картинка потребует
для сохра­нения очень много дискового пространства.

При попытке слегка повернуть на небольшой угол изображение, например, с чет­кими тонкими вертикальными линиями, четкие линии превращаются в четкие «ступеньки». Любые трансформации (повороты, масштабирование, наклоны) в точечной графике не обходятся без искажений.

Невозможно увеличить рисунок для рассмотрения деталей. Поскольку изобра­жение состоит из точек, то его увеличение приводит только к тому,
что эти точки становятся крупнее. Никаких дополнительных деталей
при увеличении растрового изображения рассмотреть не удается. Более
того, увеличение точек растра визуально искажает иллюстрацию и делает
ее грубой (пикселизация).

До недавнего времени создание и редактирование текста в растровой графике было серьезной проблемой. Ранее в большинстве растровых программ редакти­ровать текст можно было только во время его создания. После окончания ввода текста и переходу к работе с другими инструментами печатные символы закреп­лялись там, где они были бы нанесены на холст. После этого отредакти­ровать уже набранный ранее текст (например, поместить курсор между двумя буквами, удалить одну из них и ввести новую) было нельзя. С этой проблемой можно столкнуться, например, в растровом графическом редакторе MS Paint. Кроме того, при большом разрешении файл растрового текста будет огромного размера.

Последние версии профессиональных растровых редакторов типа Adobe Photo­shop, Corel PHOTO-PAINT и Paint Shop Pro поддерживают возможность поме­щения введенного текста в специальные слои, которые сохраняют векторные свойства текста и, как следствие, возможность его редактирования даже после сохранения в виде файла (при условии использования родных форматов указанных редакторов).

Раздел 4 ВЕКТОРНАЯ ГРАФИКА


4.1 Средства создания векторных изображений

Векторные изображения можно создать в нескольких видах программ:

• в программах векторной графики;
  
• в программах САПР, типичным примером которых является AutoCAD. Её векторный формат – DXF (Dynamic Exchange Format) понимается многими современными программами;
  
• в специализированных программах конвертирования растровых изображений векторные. Одна их таких программ – CorelTrace 11, входящая
  в состав графического пакета Corel Graphics Suite 11. Другая известная программа этого класса – Adobe Streamline;
  
• к векторным объектам относятся также текст и PostScript- контуры вроде тех, которые можно найти также в файлах, созданных с помощью текстовых процессов типа MS Word или программ верстки, например PageMaker.
  

Рис. 4.1 Пример векторного изображения

На платформе Windows из программ векторной графики (рис. 4.1) наиболее распространен редактор CorelDRAW – мощный, удобный, но в тоже время требовательный к ресурсам. Со всеми входящими в него утилитами он займет не один десяток мегабайтов дискового пространства. Из других программ этого класса следует отметить Adobe Illustrator и Macromedia Freehand.

Среди компактных и универсальных программ векторной графики можно выделить Corel Xara и ее последнею версию Xara X. С помощью них можно создавать иллюстрации любого уровня сложности для веб-сайтов, полиграфии
и повседневных нужд любого офиса.

Векторные редакторы и программы САПР – наилучшее средство
для построения шрифтовых и высокоточных графических объектов, таких
как конструкторский чертежи. Для таких иллюстраций принципиальное значение имеет сохранение четких, ясных контуров независимо от размера изображения. Как правило, в векторном редакторе создается заготовка, затем
она масштабируется до нужного размера и переводится в необходимый
нам формат изображения.

4.2 Особенности терминологии

Каждый тип компьютерной графики имеет свою терминологию, математический аппарат и характерный для него набор инструментальных средств. Поэтому, несмотря на большое количество представленных на рынке векторных про­грамм, все они в той или иной мере содержат общий базовый набор инструмен­тальных средств.

Ситуация еще более осложняется при переходе к локализованным версиям оригинальных продуктов. Даже в случае локализа­ции различных версий одной и той же про­граммы ни переводчики, ни редакторы не заботятся о сохранении преемственности в терминологии. Поэтому для про­фессиональной работы с графикой важно составить представление об особен­ностях используемой терминологии и базовых примитивах векторной графики.

4.3 Математические основы векторной графики

Если основным элементом растровой графики является пиксел (точка),
то в векторной графике в роли базового элемента выступает линия. Это связано
с тем, что любой объект в ней состоит из набора линий, соединенных между собой уз­лами (рис. 4.2). Отдельная линия, соединяю­щая соседние узлы, называется сегментом (в геометрии ей соответствует отре­зок). Сегмент может быть задан с помощью уравнения прямой или уравнения кривой линии, требующих для своего описания разного количества параметров.





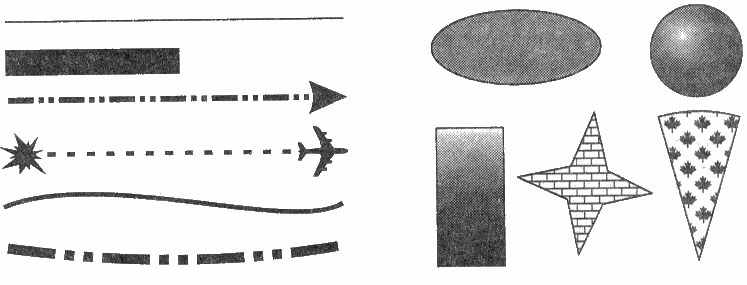
Рис. 4.2 Объекты векторной графики


Для более полного понимания механизма формирования векторных объектов рассматриваются способы представления основных элементов векторной графики: точки, прямой линии, отрезка прямой, кривой второго порядка, кривой третьего порядка, кривых Безье.

В векторной графике точке соответствует узел. На плоскости этот объект представляется двумя числами (X, Y), задающими его положение относительно на­чала координат.

Для описания прямой линии используется уравнение Y = аХ + b. Поэтому для построения данного объекта требуется задание всего двух параметров:
а и b. Результатом будет построение бесконечной прямой в декартовых координатах.

В отличие от прямой отрезок прямой требует для своего описания двух дополнительных параметров, соответствующих началу и концу отрезка (например, X1 и Х2).

К классу кривых второго порядка относятся параболы, гиперболы, эллипсы и окружности, то есть все линии, уравнения которых содержат переменные в степени не выше второй. В векторной графике эти кривые используются для построения базовых форм (примитивов) в виде эллипсов
и окружностей. Кривые второго порядка не имеют точек перегиба. Используемое для описания этих кривых классическое уравнение требует
для своего задания пяти параметров:

х² + a₁y² + а₂ху + а₃х + а₄у + а₅ = 0.

Для построения отрезка кривой требуется задать два дополнительных параметра.

В отличие от кривых второго порядка кривые третьего порядка (рис. 4.3) могут иметь точку перегиба. Прямые и кривые второго порядка являются частным случаем кривых третьего порядка.

Классическое уравнение, используемое для описания уравнения третьего порядка, требует для своего задания девяти параметров:

х³ + a₁y³ + а₂х²у + а₃ху² + а₄х² + а₅у² + а₆ху + а₇х + а₈у + а₉= 0.

Для описания отрезка кривой третьего порядка требуется на два параметра больше.




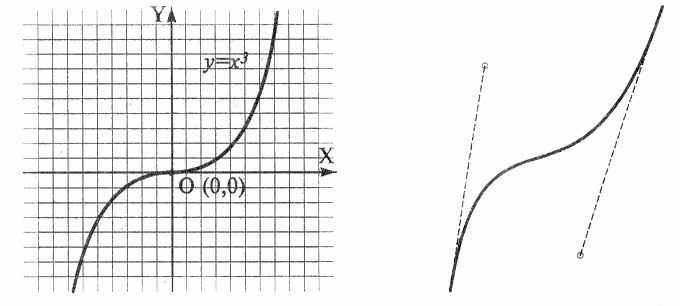
Рис 4.3 Кривая третьего порядка (слева) и кривая Безье (справа)


Кривые Безье – это частный вид кривых третьего порядка, требующий для своего описания меньшего количества параметров – восьми вместо одиннадцати (рис. 4.3). В основе построения кривых Безье лежит использование двух касательных, про­веденных к крайним точкам отрезка линии. На кривизну (форму) линии влияет угол наклона и длина отрезка касательной, значениями которых можно управлять в интерактивном режиме путем перетаскивания их концевых точек. Таким образом, касательные выполняют функции виртуальных рычагов, позволяющих управлять формой кривой.