Анализ среднего дисперсии и модель оценки финансовых активов

Вид материала

Анализ

Содержание 5.1 Применения среднего - дисперсии и модели CAMP в сегодняшнее время. 5.2 Суть анализа среднего дисперсии. Предположение, что инвесторы заботятся только о средней доходности и дисперсии. Предположение о том, что на финансовых рынках не возникает трений. 5.3. Эффективные границы и разделение ценных бумаг на два фонда. Пример 5.2: Расчёт отдельного граничного пакета акций 5.4 Касательный портфель и оптимальное инвестирование. Касательный актив и CML Уравнение CML. Эмпирическая оценка наклона CML. Алгебраический метод определения касательного портфеля Числовой пример, иллюстрирующий применение алгебраической формулы Сущность алгебраического метода Числовая иллюстрация достижения улучшения доходности и риска. 5.5 Нахождение эффективной границы для рисковых активов 5.6. Насколько полезен анализ среднего отклонения для нахождения эффективных портфелей? 5.7 Связь риска и ожидаемой отдачи Линия рынка ценных бумаг против диаграммы среднего стандартного отклонения. Контраст между бэтами и совместными изменениями Бэта против изменения в качестве меры риска ... Полное содержание

Подобный материал:

• Нка финансовых активов» является составной частью комплексного обучения специальности, 11.88kb.
• Тестирование методов оценки финансовых активов на российском рынке, 697.91kb.
• Примерная тематика рефератов по курсу, 16.99kb.
• Анализ и планирование безубыточности производства, расчет производственного и финансового, 210.52kb.
• 2. Анализ финансовых результатов коммерческой организации Модель формирования показателей, 38.32kb.
• Вопрос 4 Дисконтирование. Ставки дисконта. Метод калькулятивного построения. Оценка, 68.83kb.
• Встатье рассматривается принцип усовершенствования оценки нематериальных активов, 95.39kb.
• Конспект тема : Основные производственные фонды ( опф), 205.4kb.
• Темы курсовых работ по дисциплине «Анализ и диагностика финансово-хозяйственной деятельности, 58.19kb.
• Решение задач описательной статистики средствами ms excel содержание, 164.81kb.

Анализ среднего - дисперсии и модель оценки финансовых активов.

Цели изучения:

После прочтения этой главы, вы сможете:

1. 
   Понять важность графика среднего стандартного отклонения и узнаете эффективные границы расположения всех активов (кривая инвестиционных возможностей), эффективные границы рисковых активов, портфель с минимальным риском, максимально диверсифицируемый портфель, а также как использовать график для разных инвестиционных и корпоративных финансовых употреблений.
   
2. Вычисление максимально диверсифицируемого портфеля и определение эффективных границ рисковых активов.
   
3. Понять связь между изменениями эффективности и ожидаемым уровнем доходности.
   
4. Описать оценить данный портфель, оценить отдельные активы, входящие в портфель, а так же их соответствующие веса в этом портфеле.
   
5. Осмыслить что такое рыночный портфель, что необходимо предпринять для того, что бы рыночный портфель стал максимально диверсифицируемым портфелем- это для понимания модели оценки финансовых активов- и практические доказательства этой модели.
   

«First Quadrant», портфельная компания, нашла свою нишу в индустрии, предлагая клиентам международные портфельные стратегии. Одним из их продуктов является модель, полученная от BARRA, инвестиционная консалтинговая компания, которая занимается оценкой связи между фондовыми индексами в США, Японии, Великобритании и Канаде. Модель так же оценивает среднюю доходность от четырех фондовых индексов. В июле 19995, исходя из модели, была получена связь между фондовыми индексами четырех стран, данные модели приведены ниже:

		Связь с
	Япония	Великобритания	Канада
США	.0093	.0191	.0181
Япония		.0120	.0342
Великобритания			.0204

Анализ среднего и стандартного отклонений для фондовых индексов, связанных с четырьмя странами, показал следующее:

	США	Япония	Великобритания	Канада
Средняя	15,4%	11,3%	23,2%	13,2%
Стандартное отклонение	14,8	9,6	13,8	13,5

Основанные на этой модели и на этих данных, «First Quadrant» составляет портфели.


Когда большинство инвесторов обдумывают количественное измерение рисков портфеля, то они вычисляют дисперсию и среднее квадратическое отклонение доходности портфеля. Однако дисперсия это не единственный способ количественного измерения рисков, это самый широко используемый метод оценки рисков. В этой главе анализируется проблема, возникающая при выборе портфеля инвестором, который использует дисперсию как основной критерий оценки рисков, связанных с выбором того или иного портфеля. Другими словами, инвестор хочет выбрать портфель, у которого будет максимальная ожидаемая доходность при данной дисперсии. Для того, чтобы осуществить это он или она должны понимать компромиссный выбор между средней и дисперсией.

В четвертой главе представлен анализ такого компромиссного выбора, названный как «анализ средней дисперсии». Для того, что бы разобраться с такого рода проблемой, описанной в начальном, кратком изложении, необходимо более детально подойти к этому анализу. Например, основываясь на первоначальных данных, видно, что если инвестировать 54% портфеля в акции американской копании, 25% в акции японской компании, 15% в акции компании из Великобритании и 6% в акции канадской фирмы, то такую же среднюю доходность можно получить, если все 100% портфеля вложить в акции американской компании. В то же время, этот портфель, составленный из акций компаний разных стран, будет иметь среднее квадратическое отклонение около 13,5% в год, тогда как среднее квадратическое отклонение портфеля с акциями только американской компании составляет 14,8% в год. Задача отдельных частей этой главы заключается в необходимости понимания как выделить наиболее эффективные доли акций в портфеле в таких ситуациях.

Одними из основателей финансовой теории и анализа средней дисперсии, которых важно выделить, являются Джеймс Тобин и Гарри Маркович, получившие Нобелевскую награду в 1981 году и в 1990 году соответственно. Сама по себе средняя дисперсия является важным инструментом, но так же она косвенно явилась причиной третьей Нобелевской награды Вилльяма Шарпе в 1990 году, за его развитие модели оценки финансовых активов (CAMP), модель связывает риски с ожидаемым доходом. В этой главе мы изучим эту модель, которая напрямую выводится из анализа средней дисперсии.

Эта глава состоит из трех главных частей. После краткого введения применения анализа средней дисперсии и модели оценки финансовых активов в сегодняшней жизни, первая часть концентрируется на компромиссном выборе между средней и дисперсией, и использовании разработанных методов для составления оптимального портфеля. Во второй части рассматривается зависимость между рисками и доходностью, выведенная из анализа средней дисперсии, в виде модели оценки финансовых активов. Последняя часть исследует как выполняется CAMP и анализирует опытные доказательства этой модели.

5.1 Применения среднего - дисперсии и модели CAMP в сегодняшнее время.

Анализ средней дисперсии и модели оценки финансовых активов имеют практическое применение и для профессиональных инвесторов и для индивидуальных работников финансовых корпораций.

Инвестиционное применение анализа средней дисперсии и модели CAMP.

Как средство иллюстрирующее как добиться более высокой средней доходности с более низкими рискам, анализ средней дисперсии и модели CAMP регулярно используются брокерами, руководителями пенсионных фондов и консультантами, когда они разрабатывают инвестиционную стратегию и когда они дают советы в области финансов. Например, анализ средней дисперсии широко используется в принятии решений о распределении активов в различных странах. Также, когда инвестиционные банкиры предлагают руководителям пенсионных фондов инвестировать в недвижимость, то их представители часто базируют свои презентации на графике среднего квадратического отклонения.

Корпоративное использование анализа средней дисперсии и модели CAMP.

Понимание значения средней дисперсии и модели CAMP фирмой становится чрезвычайно важным для корпоративного менеджмента. В мире, где менеджеры компаний, с падающей ценой акций, могут потерять работу из-за поглощения или реструктуризации, должны осознавать всю важность необходимости правильной оценки определяющих факторов стоимости доли, и какие действия необходимо предпринять для того, чтобы увеличить эту долю в ответ на давление со стороны акционеров и директоров.

Например, корпорации могут использовать анализ средней дисперсии для страховки от рисков и диверсифицировать свои портфели для реальных инвестиционных проектов. Однако одним из выводов модели CAMP является то, что во время диверсификации, инвестиции могут уменьшить дисперсию цены акций компании, но это не уменьшает издержки финансирования, которые составляют средний уровень доходности, требуемый финансовым рынком для погашения долгов компании и для финансирования акции без фиксированного дивиденда. В результате, корпоративной диверсификации, стратегия может создать ценность для корпорации в том случае, если диверсификация увеличит ожидаемую доходность реального актива инвестируемого компанией.

Корпорации также используют модель CAMP и среднее значение дисперсии для оценки капитальных расходов. Финансовые менеджеры используют модель CAMP и анализ среднего значения дисперсии не только для того, чтобы сделать важные выводы по поводу того, как оценивать реальные активы, но также и для понимания как долговое финансирование влияет на риски и требуемый уровень доходности доли акций.

5.2 Суть анализа среднего дисперсии.

Для того, чтобы понять как правильно использовать график среднего квадратического отклонения, сначала надо понять где располагаются на графике все возможные ценные бумаги. В первый подразделе рассматривается, что график подразумевает под допустимым стандартным отклонением итога, который может быть достигнут благодаря портфелю. Во втором подразделе анализируется допущения средней дисперсии и обсуждается, какие итоговые стандартные отклонения желательны.



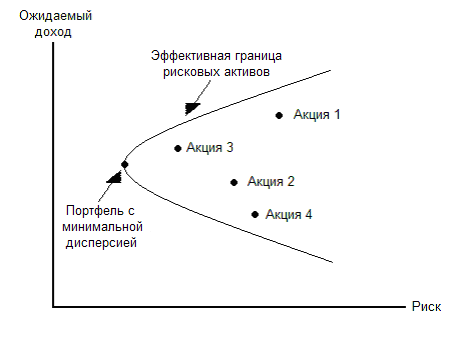
Возможный портфель.

График возможной совокупности среднего стандартного отклонения – это совокупность результатов среднего и стандартного отклонений, которые могут быть достигнуты составлением всевозможных портфелей, построенный таким образом, что средняя доходность откладывается по вертикальной оси, а среднее стандартное отклонение - по горизонтальной.

Для упрощения объяснения, предположим, что возможный портфель может быть составлен только из четырех акции, на графике это четыре точки, расположенные внутри гиперболической фигуры. Гиперболическая форма появляется тогда, когда безрисковая ценная бумага или портфель не могут быть использованы. В этом и некоторых других подразделах анализируется проблема оптимальных инвестиций, когда инвестиции в безрисковые активы возможны, и когда такие инвестиции не возможны.

В четвертой главе было отмечено, что доходность и дисперсия портфеля полностью определяются тремя характеристиками каждой акции, входящей в портфель.

• Средняя доходность каждой ценной бумаги, также ее называют ожидаемая доходность.
  
• Дисперсия доходности каждой ценной бумаги.
  
• Связь между доходностью ценной бумаги и доходностью других ценных бумаг, которые входят в данный портфель.
  

Следовательно, знание средних значений, дисперсий, и зависимости для группы инвестиций – это все, что необходимо для получения графика, который нарисован выше.

Как видно на графике инвесторы достигают самой высокой доходности и более низких дисперсий «двигаясь на северо-запад», или в верхний левый угол, при этом оставаясь внутри допустимых портфелей. Одной из целей этой главы является научиться определять доли активов в портфеле, двигаясь к левой верхней границе, или «на северо-запад», оставаясь при этом в рамках портфелей. Такие портфели являются наиболее эффективными.

Предположения анализа средней дисперсии.

Определение доле активов в портфелях на левых верхних границах, необходимо только тогда, когда инвестор предпочитает находиться на «северо-западе» и когда нет никаких трений или препятствий для составления таких портфелей. Таким образом, следующие два предположения анализа средней дисперсии не должны быть удивительными:

• Принимая решения об инвестициях сегодня, инвесторы думают только о средней доходности и дисперсии их портфелей за определенный период (например, следующая неделя, месяц, или год). Их предпочтения – это высокая доходность и низкие риски.
  
• Финансовые рынки свободны от трений.
  

Эти предположения анализа средней дисперсии позволяют нам использовать график среднего квадратического отклонения для того, чтобы сделать выводы какие портфели лучше. В качестве средства в изучении оптимальных инвестиций, график помогает исключить преобладающие портфели, которые расположены на графике в виде точек ниже и правее (на «юго-востоке»). Над этими портфелями доминируют другие возможные портфели, в том смысле, что они имеют более высокую доходность и более низкие риски, и поэтому лучше.

Предположение, что инвесторы заботятся только о средней доходности и дисперсии. Первое предположение анализа средней дисперсии – инвесторы тщательно относятся только к доходности и среднему квадратическому отклонению доходности своих портфелей, и предпочитают портфели с высокой доходностью и низкими рисками – основано на том, что инвесторы предпочитают те портфели, которые генерируют большее богатство при самых низких рисках. Анализ средней дисперсии предполагает, что ожидаемые риски, или неопределенность, которыми озабочены инвесторы, могут быть полностью суммированы дисперсией доходности. Инвесторы предпочитают высокий уровень ожидаемого дохода потому что, это означает, что в среднем, их уровень благосостояния повысится. Более низкая дисперсия предпочтительнее, так как это означает меньший разброс значений ожидаемого дохода. Считается, что инвесторы в основном не склонны к риску, это значит они не любят большой разброс значений ожидаемых результатов.

Статистка показала, что дисперсия полностью суммирует разброс любого нормально распределенного дохода. Мотивацией для использования дисперсии, как подходящего метода оценки для анализа инвестиционных рисков, является тесная связь между показательным распределением многих доходов портфелей и нормальным распределением.

Предположение о том, что на финансовых рынках не возникает трений.

Второе предположение анализа средней дисперсии – существование свободных от трений финансовых рынков – вообще-то, набор допущений, которые призваны упростить вычисление возможных портфелей. На свободных от трений рынках, все инвестиции продаются по любым ценам, не только по 1/8 или 1/32, и в любом количестве, как положительные так и отрицательные ( не существует ограничений на продажу в короткую). В добавление, нет трансакционных издержек, регулирований, или налогов, связанных с покупкой или продажей активов.

Насколько ограничительными являются допущения анализа средней дисперсии?

Так как эти два допущения очень важны, необходимо сделать какие-либо упрощения, которые будут связаны с определенными издержками. Например, Фама (1976) отметил, что большинство доходов от ценных бумаг распределены не по нормальному закону. Более того, инвесторы могут получать доходы, которые отчетливо не будут иметь нормальный закон распределения, например, покупая индексный опцион или используя страхование инвестиционного портфеля, основанного на опционе. Выбирая из двух стратегий страхования инвестиционного портфеля с одинаковой средней дисперсией, инвестор, который в основном заботится о больших потерях, выберет инвестиции с гарантией максимально низких потерь. Дисперсия не включает в себя именно тот риск, которого инвесторы хотят избежать.

Еще одним возражением к анализу средней дисперсии, которое возникает даже если доходы распределены по нормальному закону, является то, что инвесторы не рассматривают доходность своих портфелей, как они есть, как предлагает теория. Большинство инвесторов думает о том, как структура их портфельных доходов соотносится с экономикой в целом, и с факторами влияющими на их материальное благосостояние. Некоторые инвесторы, например, могут предпочесть портфель с высокой доходностью, в середине спада, когда дополнительные средства могут понадобиться, такому же портфелю, но с более высокой доходностью на подъеме экономического цикла. Предыдущие инвестиции будут выступать в качестве страховки от возможной безработицы. Подобным образом, пенсионер живущий за счет процентных ставок по сберегательным счетам, может предпочесть инвестиции, которые будут приносить доход, если короткосрочные ставки снизятся.

Так как это набор допущений, предположение о рынках свободных от трений может быть, а может и не быть важным, в зависимости от того на чем заостряется внимание. Смягчение частей этих допущений часто приводит к таким же результатам, но с более сложной структурой издержек. В других случаях, смягчение допущений приводит к другим результатам. В большинстве случаев, однако, основные идеи этой главы остаются неизменными: портфели преобладают над индивидуальными активами, зависимость намного важнее дисперсии между рисками и доходами, и оптимальный портфель может быть составлен с помощью анализа средней дисперсии, если известны вклады.

5.3. Эффективные границы и разделение ценных бумаг на два фонда.

Верхнюю часть графика иногда называют эффективной границей рисковых активов. Эффективная граница показывает доходность и среднее квадратическое отклонение эффективных портфелей. Эффективная граница – это самая эффективная возможность выбора между доходностью и дисперсией. Для сравнения, неэффективный портфель, такой как 100% инвестиции в акции американской компании, уменьшает риск путем неувеличения доходности по риску, содержащейся в этом портфеле. Наиболее эффективная схема составления портфеля позволяет достигнуть более высокой доходности при таких же значениях риска (или наоборот, такой же доходности, при более низких рисках).

Поиски святого Грааля: оптимальные портфели.

Основанные на допущениях последней части главы, можно сказать, что эффективная граница – это «святой Грааль», то есть та граница, на которой хочет находится инвестор. Конечно же, на этих границах находится большое количество различных портфелей, инвесторы в зависимости от своего собственного решения выбирают определенную связь между доходностью и дисперсией. Например, конечной точкой этой границы является точка V, которая характеризует среднее и стандартное отклонение портфеля с минимальной дисперсией. Этот портфель привлечет только тех инвесторов, которым не нравится размах настолько, что они будут отказываться от существенного среднего дохода, чтобы минимизировать дисперсию. Другие инвесторы, которые хотят испытать более высокую дисперсию в обмен на более высокий средний доход, выберут портфели, лежащие на эффективной границе, ниже точки V (приложение 5.1.).

В главе 4 говорится о том, что точка V, портфель с минимальной дисперсией, это уникальный портфель, взвешенный путем решения набора уравнений. В большинстве случаев, каждая точка

стандартной средней дисперсии на границе достигается уникальным портфелем акций. Во внутренней стороне допустимого портфеля, многие комбинации акций могут достичь результата данного среднего стандартного отклонения.

Т.к. инвесторы, которые обращаются с дисперсией как с первоначальной мерой измерения риска, хотят выбрать портфели со стандартной средней дисперсией, то для инвесторов оказывается полезным научиться их строить. Задача определения таких портфелей существенно упрощена изучением важности такого свойства, качества или характеристики, как «разделение ценных бумаг на два фонда»

«Разделение ценных бумаг на два фонда»

Разделение ценных бумаг на два фонда означает, что представляется возможным разделить доходы всех портфели со стандартной средней дисперсией на средние взвешенные доходов двух портфелей. Если двигаться по эффективной границе, веса могут меняться, а два разделяющих портфеля останутся неизменными.

Это вытекает из обобщенного результата:

Результат 5.1

Все портфели на границе со средней стандартной дисперсией могут быть сформированы средней взвешанной двух любых портфелей на этой границе.


Результат 5.1. может быть еще более обобщен. Два фонда не только образуют северо-западную границу эффективных портфелей, но и все портфели на границе допустимых портфелей: северо-запад плюс юго-запад (нижняя левая граница). Это значит, что если любые два портфеля на границе определены, можно создать все остальные эффективные средние дисперсные портфели исходя их этих 2-х портфелей.

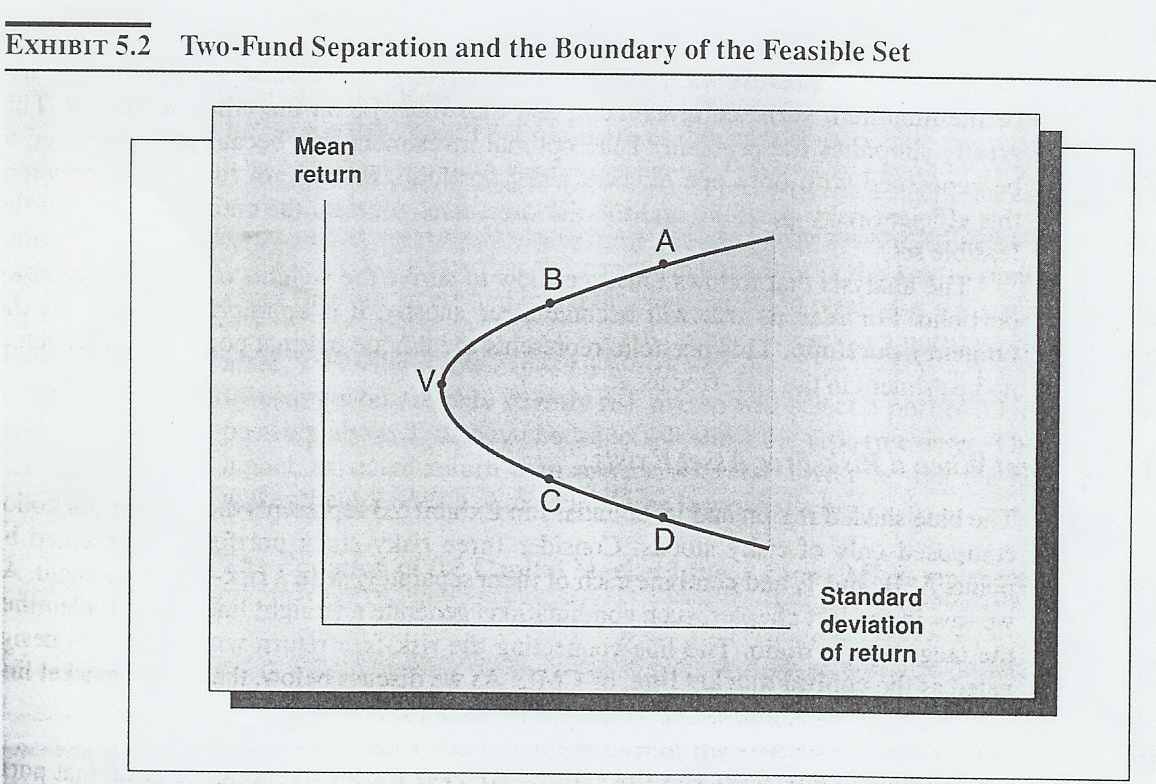
Приложение 5.2. выделяет 4 пограничных портфеля, A, B, C, D и портфель с минимальной дисперсией, V. Все портфели лежат на западной (левой) границе доступного портфеля являются средними взвешенными портфелей A и B, так же как и средние C и D, Bи D или B и V, и так далее. Более того, любая средняя взвешенная двух портфелей, лежащих на границе сама лежит на этой границе.


Пример 5.2: Расчёт отдельного граничного пакета акций

Каковы доли ценных бумаг 1, 2, 4, 5 в портфеле, если доля ценной бумаги 3 равна -0,1?

Из уравнения для ценной бумаги 3 найдём значение w: 1w + 0,2(1-w) = -0,1 => w = 3. Подставив w в уравнения для остальных ценных бумаг, найдём, как распределяются доли остальных ценных бумаг в данном портфеле. Портфель ценных бумаг будет иметь следующее соотношение ценных бумаг: 0,2, 0,5, -,01, -,01, 0,5.



Из примеров 5.1 и 5.2 следует, что, если какая-то ценная бумага имеет одинаковый вес в двух граничных портфелях акций (как ценная бумага 1 в наших примерах), то она будет иметь точно такой же вес во всех граничных портфелях ценных бумаг. Также следует отметить, что существуют ценные бумаги, чей вес в граничных портфелях растёт с увеличением w. Вес остальных ценных бумаг с ростом w падает.

Данные следствия помогают охарактеризовать граничные портфели ценных бумаг, но они не позволяют точно оценить веса двух портфелей на границе. К этому вопросу мы обратимся в следующей главе, после того как разберём влияние безрискового актива на анализ.

5.4 Касательный портфель и оптимальное инвестирование.

Выше рассматривалось инвестирование с помощью рисковых ценных бумаг. Как правило, как только дополнительный актив добавлен к набору ценных бумаг, которые могут быть включены в портфель ценных бумаг, увеличивается разброс отклонений. Безрисковый актив не является исключением, однако следует обратить внимание на то, как он изменяет форму множества доступных активов и границу эффективности.

В главе 4 говорилось, что на графике доходность – стандартное отклонение портфели безрискового актива и рискового актива лежат на прямой линии. Благодаря этому добавление безрискового актива не только расширяет множество доступных активов, но также изменяет форму границы эффективности, делая её прямой линией, а не гиперболой, что значительно облегчает поиск оптимального портфеля.

В данной главе будет показано, что при наличии безрискового актива в силу действия принципа разделения денег на два портфеля (говорящим, что граница эффективности может быть сформирована только из двух портфелей) требуется найти только один «ключевой» портфель. Это было наглядно показано в предыдущем разделе, в котором, так как существование безрискового актива исключалось, два портфеля, формировавшие границу эффективности, были всегда рисковые и имели положительные значения стандартных отклонений. Безрисковый же актив, если он существует, будет иметь наименьшее отклонение и, следовательно, будет лежать на границе эффективности. Это значительно упрощает проблему оптимального инвестирования, так как теперь требуется определить только один эффективный рисковый портфель. Благодаря принципу разделения денег на два портфеля, эффективный рисковый портфель и безрисковый актив формируют полностью границу множества доступных активов. Последующее исследование описывает, как найти доли ценных бумаг в эффективном рисковом портфеле. Данный портфель будем называть касательным портфелем (причины этого скоро станут ясны). Данный портфель представляет собой уникальный оптимальный портфель, не включающий инвестирование в безрисковый актив.

Оптимальное инвестирование в условиях существования безрискового актива

Закрашенная голубым область, а также её граница (на рисунке 5.3) представляют собой множество всех возможных портфелей, составленных только из рисковых активов. Рассмотрим три рисовых актива, обозначенные буквами А, В и Т и соединим их каждый по отдельности с безрисковым активом. Как мы видели в предыдущей главе, эти комбинации представляют собой прямые линии. В точке Т находится касательный портфель. Линия, соединяющая доходность от безрискового актива и с точкой Т называется CML (capital market line). Выше уже упоминалось, что CML она представляет собой множество портфелей, оптимально сочетающих в себе все вложения.

Касательный актив и CML

Очевидно, что портфель Т предпочтительнее среди трёх портфелей ценных бумаг, так как CML, проходящая через него, находится выше.



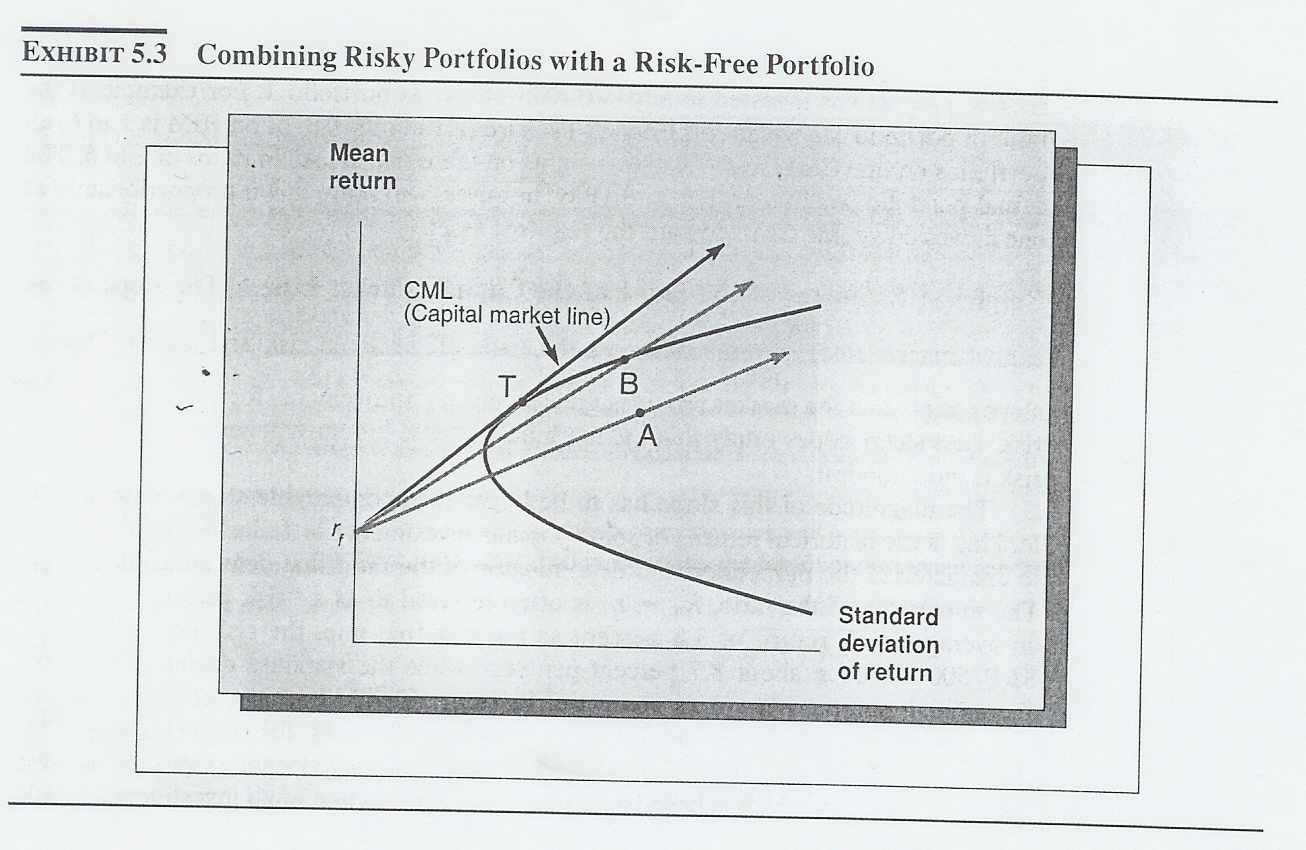
Можно сделать и более общий вывод: линия, проходящая через точу Т, является касательной к границе эффективности рисковых активов. В результате портфель лежит в левой верхней части графика. Инвесторы стремятся инвестировать в портфели с большей отдачей и меньшим риском и пытаются найти наилучшее для себя сочетание этих показателей. Все такие портфели лежат на CML.

Следовательно, можно сделать вывод, что с учётом предпосылок и допуская существование безрискового актива, все инвесторы выберут портфели, лежащие на CML. Чем менее инвестор расположен к риску, чем ближе будет расположен его оптимальный портфель к безрисковому активу, и наоборот, чем более инвестор предрасположен к риску, тем выше на линии CML будет располагаться оптимальный для него портфель ценных бумаг. Последние будут получать больший доход, однако вероятные убытки также будут выше.

Уравнение CML.

CML записывается следующим уравнением:



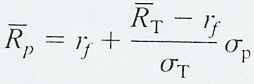
Где R_T и s_T соответственно среднее и стандартное отклонения доходности касательного портфеля, а r_f - доходность безрискового актива. Когда линия, соединяющая безрисковый актив с каким-либо рисковым активом, принимает свой максимально возможный наклон, CML показывает набор наиболее эффективных портфелей, который можно составить из рисковых ценных бумаг и безрискового актива. Во всех портфелях, лежащих на СML выше r_f, так как они являются составными из портфеля Т и безрискового актива, два каких-либо рисковых актива будут находиться в той же пропорции, в какой они есть в портфеле Т. Например, если доля ценных бумаг Hewlett Packard (HP) в портфеле Т относится к доли ценных бумаг IBM в том же портфеле Т как 1 к 6, то в любом портфеле, лежащем на CML, отношение долей этих ценных бумаг будет равно 1/6. Точные же значения долей будут пропорционально снижаться при приближении по линии CML к безрисковому активу.

Эмпирическая оценка наклона CML.

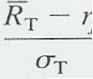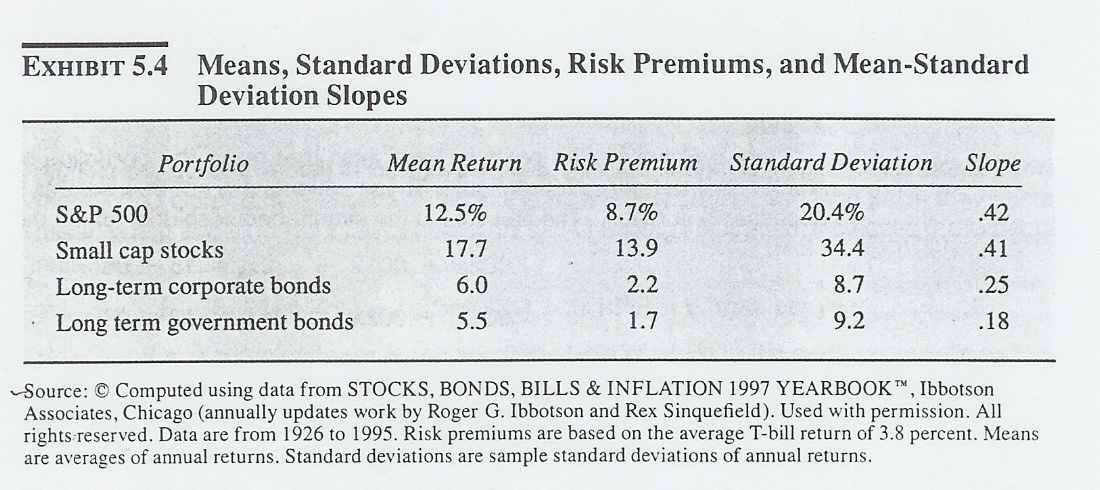
Наклон линии CML, , измеряет соотношение между риском и доходностью. Более крутой наклон означает, что рынок предоставляет больший доход за некоторые увеличения риска. Более пологий наклон означает меньшую предельную доходность при увеличении риска.

Угол наклона должен быть сравнительно больше, чем значения наклонов, исторически полученных от доходов некоторых наиболее популярных портфелей. Из примера 5.4 можно вычислить числитель и знаменатель коэффициента, определяющего угол наклона. Числитель коэффициента, R_T - r_f, часто называют «премией за риск». Используя среднюю доходность казначейского векселя, равную 3,8% в год, в качестве доходности безрискового актива, премия за риск при вложении в SMP 500 примерно равна 8,7% в год, а стандартное отклонение равняется примерно 20,4% в год. Таким образом, получается, что наклон равен 0,42. Для портфеля ценных бумаг компаний с малой капитализацией наклон равен 0,41. Для портфелей долгосрочных ценных бумаг корпораций наклон равен 0,25. Для портфелей некоторых других ценных бумаг наклон линии, соединяющей их доходность и доходность безрискового актива, и того меньше. Таким образом, наклон CML, состоящий из оптимальных портфелей для инвестирования, буден не меньше 0,42. Другими словами, для портфелей, лежащих на CML, увеличение стандартного отклонения с 10% до 20% в год принесёт не менее 4,2% в год прироста к доходности.

В примере 5.4 большинство портфелей с большей доходностью обладают большим стандартным отклонением. Однако это не верно для всех портфелей. К примеру, портфель, составленный из государственных облигаций, обладает меньшей доходностью и большим стандартным отклонением, чем портфель, составленный из долгосрочных ценных бумаг корпораций. В целом, можно сказать, что четкой зависимости между доходностью портфеля и соответствующим ему стандартным отклонением нет. Портфели, с одинаковым стандартным отклонением могут обладать различной доходностью. А следовательно необходимо выбрать оптимальный портфель, который будет давать максимальный доход при заданном стандартном отклонению.

Но если стандартное отклонение не влияет на среднюю доходность, чем же тогда определяется доходность портфеля? Далее у нашего исследования касательного портфеля становится две задачи: с одной стороны, мы должны найти оптимальный портфель, с другой, определить факторы, влияющие на среднюю доходность портфеля.



Определение касательного портфеля

Касательный портфель является уникальной комбинацией ценных бумаг. Определение долей различных ценных бумаг в составе касательного портфеля важно и необходимо, так как, зная их, можно будет найти любой портфель, лежащий на CML.

Алгебраический метод определения касательного портфеля

Для любого портфеля, как лежащего на CML, так и не лежащего на ней, справедливо следующее замечание: отношение премии за риск от вложения в ценную бумагу или портфель к его ковариации с касательным портфелем одинаково для любой ценной бумаги (формула 5.3):



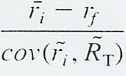
В этом заключается алгебраический способ определения касательного портфеля. Данный способ очень похож на способ, использовавшийся для нахождения портфеля с наименьшим стандартным отклонением. Вспомним, что, для того, чтобы найти портфель с минимальным стандартным отклонением, необходимо найти портфель, обладающий одинаковой ковариацией с каждой ценной бумагой. Для определения касательного портфеля, найдём портфель, который обладает ковариацией с каждой ценной бумагой и находится в строгой пропорции с премией за риск. Эта пропорция пока не известна, однако она равна для всех ценных бумаг, и независимо от её величины сумма долей внутри портфеля будет равна 1. Таким образом, чтобы определить доли ценных бумаг в касательном портфеле, надо:

1) Найти веса (в отличие от долей их сумма может быть не равна 1), при которых ковариация между доходностью от каждой акции и доходностью портфеля, составленного с этими весами, будет равна премии за риск.

2) Перевести веса в доли (сохранить пропорции между весами, но изменить их так, чтоб их сумма была равна 1).

Числовой пример, иллюстрирующий применение алгебраической формулы

Пример 5.3 показывает, как использовать написанную выше формулу для расчёта долей в касательном портфеле.

Пример 5.3: Определение касательного портфеля

Amalgamate Bottlers из примера 4.23 ищет касательный портфель капитальных инвестиций из франшизы в трёх менее развитых странах: Индии (актив 1), России (актив 2), Китае (актив 3). Значения ковариаций с этими активами приведены в таблице:



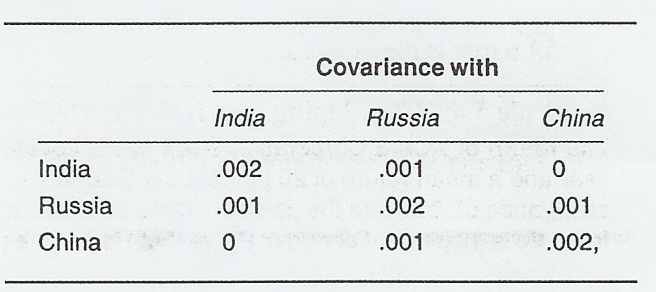
Найти касательный актив из трёх активов, если ожидаемая доходность этих активов равна 15, 17 и 17% в год соответственно, а доходность безрискового актива равна 6% в год.

Решение:

Шаг 1: Найдём веса, которые уравняют ковариацию портфеля с каждой акцией и премию за риск.

0,002x₁ + 0,001x₂ + 0x₃ = 0,15 – 0,06

0,001x₁ + 0,002x₂ + 0,001x₃ = 0,17 – 0,06

0x₁ + 0,001x₂ + 0,003x₃ = 0,17 – 0,06

В левой части первого уравнения записана ковариация портфеля с весами x₁, x₂, x₃ и активом 1. Из этого уравнения следует, что данная ковариация равна 0,9. Из двух других уравнений аналогичным образом получаем значения для двух других ковариаций. Из первого и последнего уравнений получаем:

x₁ = 45 – 0,5x2

x₃ = 55 – 0,5x2

Поставив их во второе уравнение, найдём x₂:

0,001 x₂ = 0,01

x₂ = 10

Тогда:

x₁ = 40

x₃ = 50

Шаг 2: Переведём эти веса в доли. Тогда касательный портфель запишется так:

x₁ = 0,4 x₂ = 0,1 x₃ = 0,5

Сущность алгебраического метода

Почему же отношение премии за риск к ковариации так важно? Рассмотрим случай, когда отношение премии за риск к ковариации с этой ценной бумаги с предполагаемым касательным портфелем различно для различных ценных бумаг. В этом случае с помощью незначительного изменения долей ценных бумаг внутри портфеля можно увеличить доходность и одновременно снизить риск (стандартное отклонение) этой акции. Это может быть достигнуто небольшим повышением доли ценной бумаги с высоким отношением премии за риск к предельному стандартному отклонению и одновременным снижением доли ценной бумаги с низким отношением и изменением доли безрисового актива так, что бы сумма долей была равна 1. Выполнение данных действий предполагает то, что предполагаемый касательный портфель изначально не лежал на CML.

Числовая иллюстрация достижения улучшения доходности и риска.

Пример 5.4 показывает, как может быть достигнуто улучшение доходности и риска с помощью создания нового портфеля лучшего, чем портфель, для которого нарушено условие, задаваемое формулой 5.3.

ПриПример 5.4: Создание улучшенного портфеля в условиях невыполнения условия 5.1

Доходность акции корпорации ACME обладает ковариацией с портфелем Генри, равную 0,001 в год и доходностью 20% в год. А ценная бумага корпорации ACYOU обладает ковариацией с тем же портфелем, равной 0,002 и доходностью 40 % в год. Доходность безрискового актива равна 10% в год. Докажите, что Генри выбрал не касательный портфель.

Решение:

Создадим самофинансируемый (то есть с нулевыми издержками) актив из ACME, ACYOU и безрискового актива, который обладает отрицательным предельным стандартным отклонением и положительной предельной доходностью. Добавляя такой актив в портфель Генри, получаем новый портфель с большей ожидаемой доходностью и меньшим риском (стандартным отклонением). Допустим m – небольшое количество денег ($), инвестируемое в портфель Генри. Тогда данный самофинансируемый портфель будет состоять из: долгосрочного инвестирования $0,99m в ценные бумаги корпорации ACYOU, краткосрочного инвестирования $1,99m в ценные бумаги корпорации ACME и долгосрочного инвестирования $m в безрисковый актив. Добавленный к портфелю Генри, данный актив увеличит доходность портфеля на:

0,99m(40%) – 1,99m(20%) + m(10%) = 9,8m% в год

Если m достаточно мало, то добавление такого портфеля к существующему уменьшает вариацию доходности, так как ковариация самофинансируемого портфеля, состоящего из трёх активов, и портфеля Генри равна:

0,99m(0,002) – 1,99m(0,001) = - 0,00001m

Отрицательное значение ковариации означает отрицательное предельное стандартное отклонение в случае, если добавленный портфель достаточно мал.




Отношение премии за риск к ковариации (формула 5.3) должно быть одинаковым, если отношение посчитано для отдельных ценных бумаг, проектов, которые содержат инвестирование в реальные активы или портфели. Например, если использовать касательный портфель вместо ценной бумаги i, отношение премии за риск касательного портфеля к его корреляции с самим собой должно быть рано формуле 5.3:



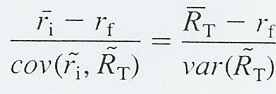
5.5 Нахождение эффективной границы для рисковых активов

Кто-то может поспорить, сказав, что безрискового актива не существует. Не смотря на то, что безопасные от невыполнения обязательств векселя казначейства США доступны для инвесторов, даже одномесячный казначейский вексель непредсказуемо меняет свою стоимость каждый день. Таким образом, если период меньше месяца, то данный актив не является безрисковым. К тому же, иностранные инвесторы не рассматривают векселя казначейства США в качестве безрискового актива. Итальянский инвестор, например, не рассматривает вексель казначейства США в качестве безрискового актива, так как доход нужно будет ещё перевести из долларов в итальянскую лиру (теперь в евро) согласно изменчивому обменному курсу. Даже для инвестора из США при периоде 1 месяц важна ещё и покупательная способность актива, а не только его номинальная стоимость. Таким образом, привязанные к инфляции доходности казначейских векселей связаны с риском, даже, когда выплаты посчитаны полностью. Во многих других ситуациях также может не существовать безрискового актива. К примеру, некоторые инвестиционные и корпоративные проблемы препятствуют инвестированию в безрисковый актив. Поэтому важно уметь посчитать все портфеля, находящиеся на границе (параболе) доступного множества активов, рисунок 5.1. Этот раздел использует выводы раздела 5.4 для того, чтобы найти эту границу.

Благодаря принципа разделения денег на два портфеля, определение любых двух портфелей, лежащих на границе достаточно для поиска всех рисковых портфелей с минимальным риском (стандартным отклонением) при заданном уровне доходности. Воспользуемся портфелем с минимальным риском в качестве одного из двух портфелей, так как для него проще рассчитать доли ценных бумаг. Для нахождения второго портфеля сперва отметим, что возможно нарисовать касательную линию из любой точки вертикальной оси на графике доходность - стандартное отклонение к гиперболической линии границы. Обозначим точку касания как «предположительную точку касательного портфеля». Следовательно:

1. 
   Выберите любую доходность, которая меньше, чем ожидаемый доход от портфеля ценных бумаг с минимальным расхождением.
   
2. Высчитайте самый эффективный портфель ценных бумаг представляя, что отдача в первом шаге является безрисковой отдачей, даже, если безрисковый актив не существует.
   
3. Возьмите среднюю взвешенную портфеля ценных бумаг с минимальным расхождением и эффективного портфеля ценных бумаг, полученного во втором шаге, чтобы объединить их в полный комплект рыночных портфелей, имеющих самую высокую ожидаемую доходность при данной дисперсии. Вес портфеля ценных бумаг с минимальным расхождением должен быть меньше, чем единица, чтобы находиться на верхней половине кривой эффективности.