Анализ среднего дисперсии и модель оценки финансовых активов
| Вид материала | Анализ |
- Нка финансовых активов» является составной частью комплексного обучения специальности, 11.88kb.
- Тестирование методов оценки финансовых активов на российском рынке, 697.91kb.
- Примерная тематика рефератов по курсу, 16.99kb.
- Анализ и планирование безубыточности производства, расчет производственного и финансового, 210.52kb.
- 2. Анализ финансовых результатов коммерческой организации Модель формирования показателей, 38.32kb.
- Вопрос 4 Дисконтирование. Ставки дисконта. Метод калькулятивного построения. Оценка, 68.83kb.
- Встатье рассматривается принцип усовершенствования оценки нематериальных активов, 95.39kb.
- Конспект тема : Основные производственные фонды ( опф), 205.4kb.
- Темы курсовых работ по дисциплине «Анализ и диагностика финансово-хозяйственной деятельности, 58.19kb.
- Решение задач описательной статистики средствами ms excel содержание, 164.81kb.
Корректировка Блумберга (Bloomberg)
Блумберг, корректирует оценки , по следующей формуле:
Скорректированная =0,66 х (не скорректированная ) + 0,34
Регулирующая формула Блумберг занижает , превышающие 1, и увеличивает , которые меньше 1. Приложение 5.10 показывает скорректированные и не скорректированные десяти хорошо известных акций. Блумберг корректировка, приведенная в приложении 5.10, применена одинаковым способом ко всем акциям. Однако, оценки могут быть улучшены, корректируя некоторые ценные бумаги сильнее относительно других. Например, можно было бы ожидать, что погрешность для маленьких фирм должна быть слегка больше, чем для больших фирм, что предполагает, что фирмы, которые меньше должны иметь больший регулирующий фактор. К тому же, лучшие оценки могут быть результатом сжатия не скорректированных оценок средней индустриальной (индустриальный индекс) сильнее, чем рыночного индекса. Дальнейшие корректировки берут в расчет коэффициент капитализации фирмы и другие характеристики, связанные с , которые также улучшают точность ее оценки.
Корректировка BARRA.
Большое число служб обработки данных обеспечивает урегулирования β. Возможно самая известная из них это фирма BARRA, которая была основана создателем Калифорнийского Университета и Berkeley, финансовым профессором, Баром Розенбергом, который был одним из первых кто разработал способы улучшения оценки . Розенберг и др. в 1985 году показали, что использование β за длительный период, в качестве предсказателей будущих β было намного менее эффективно, чем использование альтернативных методов предсказания β. Розенберг сначала использовал коэффициент сокращения подобный тому, что сейчас использует Bloomberg. Розенберг позже очистил свой метод предсказания, чтобы включить основные переменные - переменную промышленности и множество других характеристик компании.
Корректировка замедленной реакции цен акций маленькой компании на доходность от рыночного портфеля.
Так же может быть необходимо, сделать дополнительную корректировку для β(бет) ценных бумаг маленьких фирм, т.к. доходность от этих ценных бумаг имеет тенденцию реагировать на рыночные отдачи с опозданием. Эта замедленная реакция создает отклонения в меньшую сторону в оценке β(бет) акций с меньшей капитализацией, т.к. только часть эффекта оживления на рынке доходности от этих ценных бумаг поглощена их одновременными ковариациями. Смещение может быть значительным, если оценивать β от ежедневных доходностей от ценных бумаг. По этой причине, аналитики должны избежать использование ежедневных доходностей от ценных бумаг и вместо этого оценить беты с еженедельными или ежемесячными отдачами, где эффект замедленной реакции становится менее серьезным.
Однако, в статье Хонда, Котари и Васлей, написанной в 1989 году, предполагается, что ежемесячные β(беты) ценных бумаг с малой капитализацией также могут быть недооценены по сравнению с ежегодными β(бетами).
Следующий простой способ корректировки β(бет) ценных бумаг с меньшей капитализацией может скомпенсировать отстающую регулировку: добавьте задержанную рыночную отдачу как дополнительную переменную с правой стороны в уравнении регрессии, оценивающей β.
Затем сложите два коэффициента наклона регрессии – коэффициент наклона рыночной доходности, которая возникла одновременно с доходностью от ценной бумаги и коэффициент наклона задержанной рыночной доходности – чтобы посчитать скорректированную β. Дальше можно улучшать эту скорректированную β при помощи моделей Bloomberg или BARRA.
Подведение итога корректировки β.
β (беты), оцененные по стандартному уравнению регрессии могут не обеспечивать лучших оценок β(бет). Лучшие оценки могут быть получены, если учитывать опережающий или запаздывающий эффекты в отдачах от ценных бумаг и тот факт, что относительно высокая оценка β, скорее всего, переоценена, а относительно низкая оценка β недооценена.
Оценка рыночной премии за риск.
Если знать состав рыночного портфеля, выводя среднюю доходность из длинного динамического ряда, чтобы посчитать ожидаемую рентабельность рыночного портфеля, которая имеет преимущество делать статистические оценки лучше, если ожидаемая доходность рыночного портфеля также стабильна во времени. Хотя некоторые эмпирические свидетельства предполагают, что средняя доходность от портфелей, например S&P 500 изменяется со временем, тем самым, обеспечивая аргументами, использование более коротких временных рядов, хотя четыре года использованные в примере 5.11 может быть слишком коротким периодом. В дополнение, изменения в ожидаемой доходности рыночного актива являются прогнозируемыми от переменных таких, как уровень ставки процента, суммарные дивидендные мощности, и полученная рыночная отдача за предыдущие три или пять лет. В пределах этого, модель предсказывающая ожидаемую рыночную доходность точна и сохраняется в течении долгого времени. Нужно оценить пределы этой модели с таким количеством данных за длительный период времени, с каким только возможно, а затем использовать текущие уровни переменных предсказателей, чтобы произвести прогноз ожидаемой рыночной доходности.
Что бы посчитать премию за риск рыночного портфеля, вычтите безрисковую (или при β равной нулю) доходность из ожидаемой оценки доходности. Также возможно оценить премию за риск, непосредственно выводя среднюю для чрезмерных доходов от рыночного портфеля за длительный период времени. (Чрезмерные доходы - это доходы от рыночного портфеля, превышающие доходы от безрискового актива). Однако, это разумно, только если премия за риск устойчива в течение долгого времени. Эмпирические данные указывают на то, что средний ожидаемый рыночный доход сам по себе более устойчивый, чем средний избыточный доход. Следовательно, мы не рекомендуем использовать среднюю для чрезмерных доходов за длительный период времени, чтобы оценивать премию за риск.
Определяя рыночный пакет активов.
Конечно, полный анализ в данной ситуации предполагает, что аналитик может определить веса рыночного пакета. Ранее наше обсуждение сосредотачивалось на некоторых общих оценках рыночного портфеля, которые были отобраны потому что, как и рыночный пакет, они являлись ценностно-взвешенными пакетами. Однако, они составляют лишь маленькую долю мировых активов. Поэтому необходимо помнить, что это лишь оценки, и что полезность модели CAPM зависит от того, верны ли эти оценки или нет. В следующем параграфе обсуждается доказательство того, как хорошо эти оценки выступают в роли кандидатов на портфель.
5.11 Эмпирические тесты Модели Определении Стоимости Капитальных активов.
В 3ей части этого текста модель определения стоимости капитальных активов используется как способ получения требуемых норм доходности для оценки корпоративных инвестиционных проектов. Значимость применения модели определяется способностью теории безошибочно предсказывать эти нормы. Определив важность этой темы, финансовые экономисты провели сотни изучений, в которых рассматривается степень, с которой ожидаемая отдача, предсказанная с помощью модели CAPM, соответствует действительности. В данном параграфе приведены результаты этих изучений.
Согласно эмпирическим тестам модели определения стоимости капитальных активов (CAPM), отдача от акций с низким уровнем риска более предсказуема, нежели от акций с высоким уровнем риска. Не мене важно то, что ряд характеристик акций намного лучше объясняет среднюю величину отдач, чем величина beta модели CAPM. К таким характеристикам относятся совокупная рыночная стоимость выпущенных фирмой акций; отношение рыночной цены фирмы к реальной величине капитала, соответствующей массе выпущенных акций, или коэффициент рыночной балансовой стоимости; и доходность – отдача акций за предыдущие 6 месяцев. Интересно, инвестиционные фонды существуют с целью продвижения этих трех характеристик на рынок. Например, Dimensional Fund Advisors вероятно самый известный фонд в продвижении, который стал известен как незначительный эффект фирмы. Текущее истолкование результатов, полученных эмпириками, тщательно обсужденное ниже, заключается в том, что модель определения стоимости капитальных активов должным образом не описывает зависимость между риском и ожидаемой отдачей.
Может ли модель CAPM быть реально проверена?
Применение и проверка модели САРМ требуют использования рыночных оценок, таких как индекс S&P 500, поскольку, как было замечено ранее, точная структура рыночного портфеля незаметна. В статье Roll (1977) замечено, что незаметность рыночного портфеля делает модель САРМ неудобной для тестирования. По существу, предыдущие проверки , в которых использовались рыночные оценки не свидетельствовали ни о чем, что могло бы подвести кого-либо к принятию или отказу от модели САРМ. Логика Roll заключается в следующем:
- Свойством портфеля является то, что ожидаемые отдачи от всех ценных бумаг линейно зависят от индекса S&P 500, рассчитанного для данного портфеля. (Уравнение 5.4 показывает, что это фактор среднего отклонения или совокупный портфель).
- Даже в случае, если теория неверна, портфель, использовавшийся как рыночная оценка, может оказаться фактором среднего отклонения, в случае чего, тесты неверно подкрепляют теорию.
- В качестве альтернативы, оценка может не являться фактором среднего отклонения, даже если теория верна, в результате чего теория неверно не принята.
Применение модели САРМ в корпоративном финансировании и управлении портфелем ценных бумаг разделяют данную проблему с тестами. Допустимо ли применять модели, если они не могут быть протестированы, и невозможно пронаблюдать за их наиболее значительными компонентами?
Несмотря на обсуждения учеными, связанными с тем, возможно ли проверить модель САРМ, не давших никаких результатов, модели применяются практиками, используя разнообразные портфели и оценки на рынке. В таком применении, соответствующие ожидаемые отдачи получаются от любого рыночной оценки, которая является сомножителем среднего отклонения. Следовательно, правомерность разнообразного применения модели САРМ основывается не на том, имеет ли силу модель САРМ, а на том, являются ли индекс S&P 500 сомножителем среднего отклонения или какая-либо рыночная оценка применяет САРМ. Тесты модели, в которых использовались рыночные оценки, по сути, являются тестами среднего отклонения оценок и представляют интерес именно по этой причине.
Подведем итоги вышесказанного:
Результат 5.9 Тестирование модели определения стоимости капитальных активов может быть проблематично, так как рыночный портфель не поддается прямому наблюдению. Применение теорий использует различные оценки рынка. Несмотря на то, что результаты эмпирического теста модели САРМ, которая использует эти оценки, не могут быть рассмотрены как определяющие, они предоставляют ценное представление о справедливости теории, реализованной на специальных оценках, использованных в исследованиях.
Многие тесты модели САРМ использовали ценностно-взвешенный портфель из акций нью-йоркской и американской фондовых бирж как оценку рыночного пакета. Данный взвешенный по стоимости портфель сильно связан с индексом S&P 500, описанным ранее. В случае, если эмпирические исследования строго отвергают среднее отклонение ценностно-взвешенного портфеля (например, индекс S&P 500), для подсчета ожидаемой доходности, необходимо скептически отнестись к случаям, использующим подобные портфели. Тем не менее, если эти тесты поддерживают модель, вы можете свободно использовать индекс S&P 500.
Наш взгляд на эти обсуждения следующий, если объективная картина заключается в том, что портфель, использующийся как рыночная оценка, является средним отклонением, даже если теория неверна – как в ситуации с Roll – мы можем отбросить модель САРМ и использовать оценку даже, если отсутствует теоретическое подтверждение необходимости ее использования. Опасность заключается в том, что поиски среднего отклонения оценки, которая основана на соответствии эмпирическим требованиям, а не на оправданных теоретических основаниях, вряд ли будет иметь такое же соответствие в будущем. Тем не менее, лучшее из того, что мы можем сделать – это достигнуть некоего равновесия между теорией и подбором.
Is the value-weighted market index mean-variance efficient?
Чтобы понять характер разнообразных показателей модели САРМ , полезно сперва сопоставить модель с эмпирическими критериями, использующими данные за длительный период времени. Модель определения стоимости капитальных активов предусматривает прогноз о том, как ожидаемые нормы доходности ценных бумаг связаны с их бета величинами. К сожалению, аналитики не обнаруживают экспериментально ни ожидаемые доходности, ни бета величины. Показатели предполагают, что в больших объемах выборки средние доходности за длительный период времени каждой акции приближенно равняются их ожидаемой доходности и вычисленные бета величины приближенно равны их истинным значениям. Конечно, САРМ не точно не совпадет с вычисленными бета величинами и ожидаемыми доходностями. Исследование модели САРМ определяет статистические показатели, для определения, произошли ли измеренные отклонения от модели в результате ошибки в оценке (например, средние фактические доходности могли сильно отличаться от ожидаемых доходностей) или из-за неправильности модели.
Охватывающий разные стороны тест модели САРМ
В 70ые годы 20 века, проводились обширные испытания для определения совместимости модели САРМ с размещением доходностей акций нью-йоркской фондовой биржи. Один из наиболее ранних методов исследования САРМ включал двухстадийный подход, разработанный Фомой и Макбетом (1973). Сначала, бета величины вычислялись с серией регрессии временных рядов, каждый для отдельной ценной бумаги. (В регрессии временных рядов данные наблюдения соответствуют данным во времени; например, доходность и индекс S&P 500 акции IBM в январе 1997 должны быть соответствующими дебетом и кредитом для каждого отдельного наблюдения). Каждая из этих регрессий, одна для каждой ценной бумаги j, может быть отражена в уравнении:
rjt =
,где
= разрыв регрессии
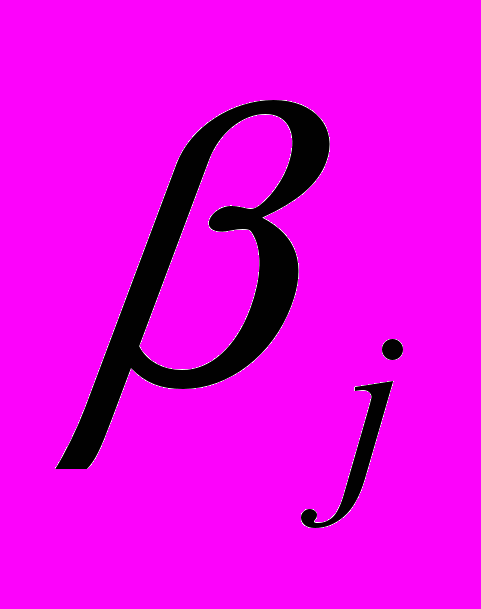= коэффициент наклона регрессии
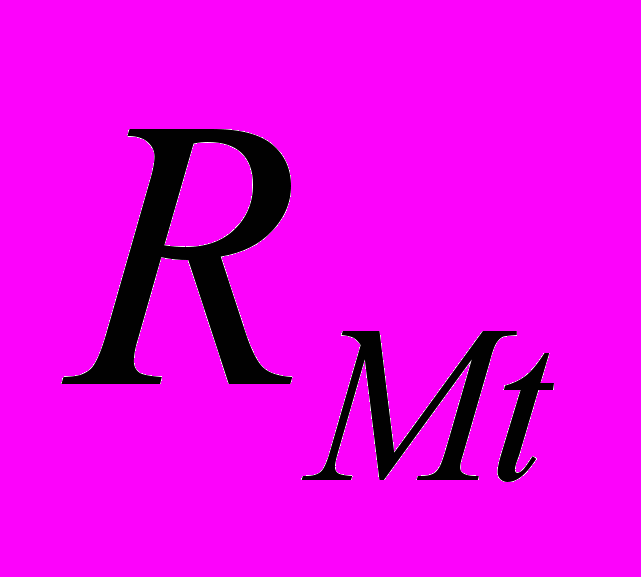= доходность t-го месяца взвешенного по стоимости портфеля акций американской и нью-йоркской фондовых бирж.
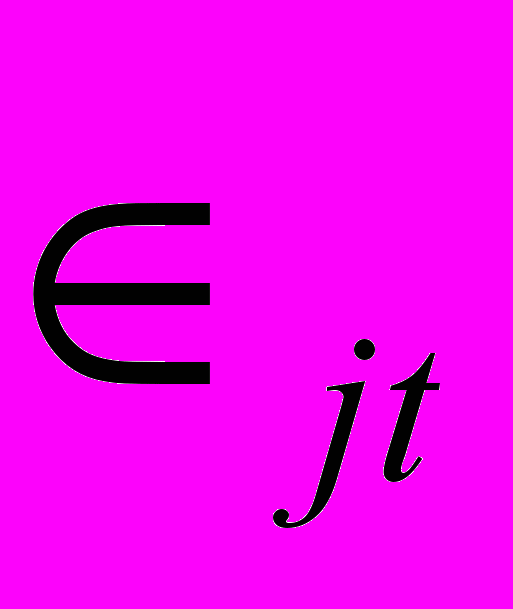= регрессия t-го месяца остаточная для акции jВ приложение 5.11 на странице 180 графически приведены данные и линия наибольшего соответствия для бета регрессии, описывающие доходность акции Dell Computer, используя ежеквартальные данные с конца 1991по конец 1995 годов (см. пример 5.11). величина бета – это наклон линии наибольшего соответствия.
Следующий шаг содержит возможные значения разрыва и коэффициента наклона поперечной регрессии, в которой каждое значение показателя соответствует ценной бумаге. (Например, средняя доходность и величина бета компании IBM должны быть соответствующими дебетом и кредитом для каждого отдельного наблюдения). Это уравнение может быть представлено алгебраически:
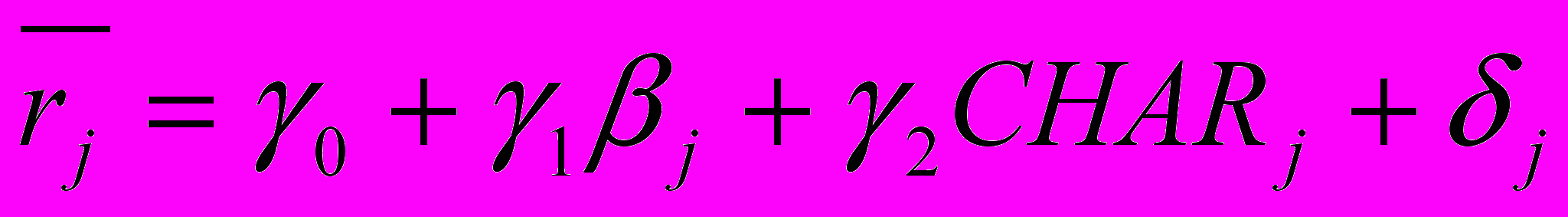
Приложение 5.11 Dell Computer: ежеквартальные доходности (31 Дек., 1991-29 Дек 1995)
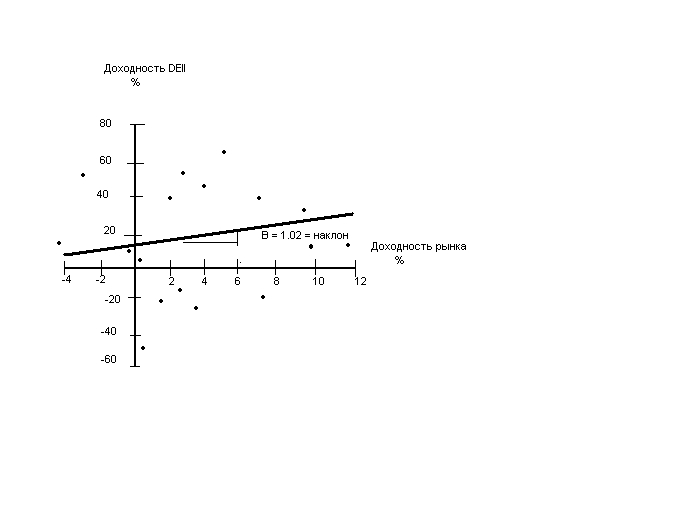
где
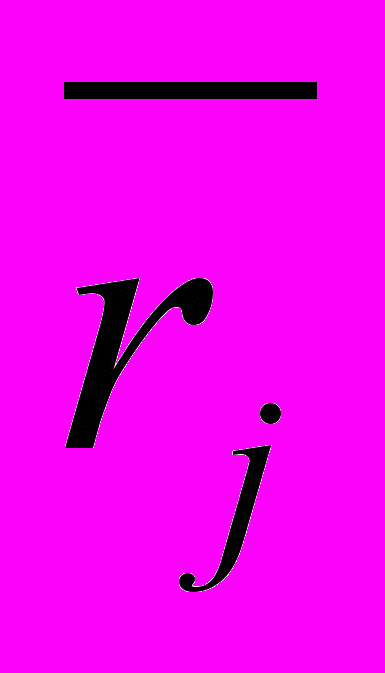= среднемесячная доходность ценной бумаги, j – ценная бумага нью-йоркской фондовой биржи 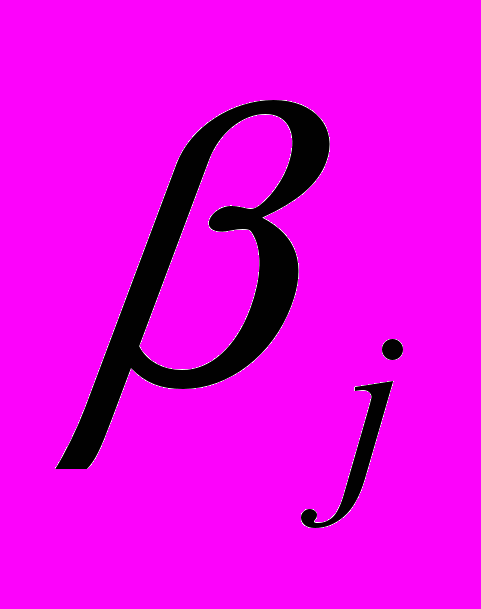= вычисленный коэффициент наклона из регрессии временных рядов, описанной в уравнении 5.9CHARj = характеристика jой ценой бумаги, несвязанная с САРМ, как размер фирмы
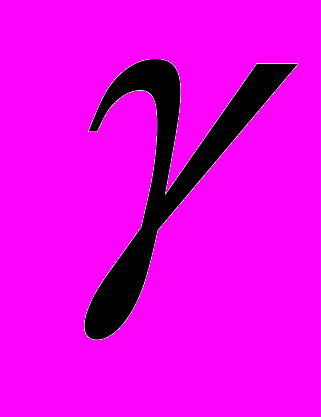’s = разрыв и коэффициент наклона регрессии
= разность регрессии jой ценной бумагиЕсли САРМ верна, то второй шаг регрессии, уравнение 5.10 должно иметь следующие особенности:
Отрезок на оси,
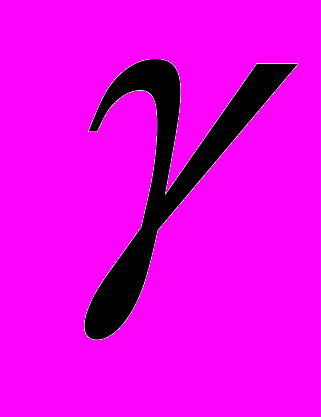0 должна быть устойчивая доходность.Наклон,
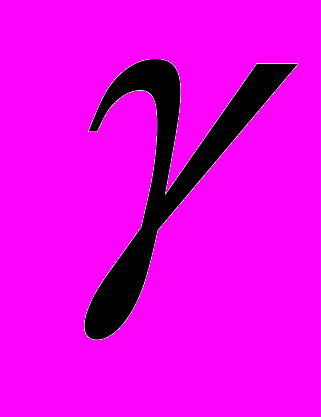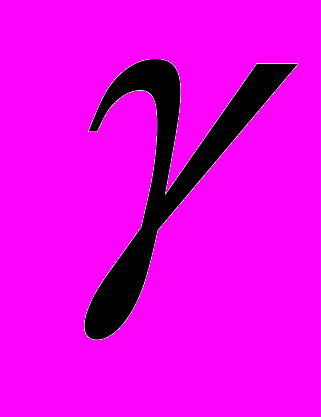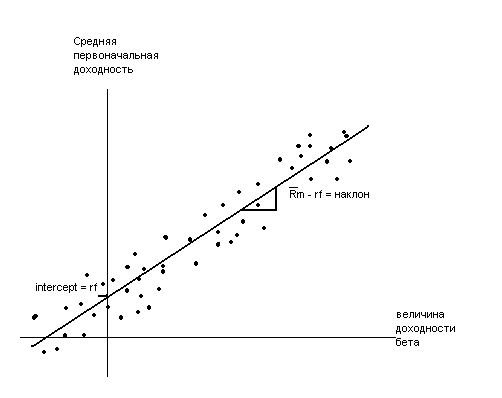
1 должна быть премия за риск рыночного портфеля.2 должна равняться нулю, так как является переменной, в отличие от величины бета (например, среднее отклонение доходности фирмы), CHARj не должна описывать средний ожидаемый доход, который учтен в коэффициенте бета. Приложение 5.12,которое иллюстрирует предположительные значения и соответствие поперечной регрессии, показывает на значение, соответствующее модели САРМ.
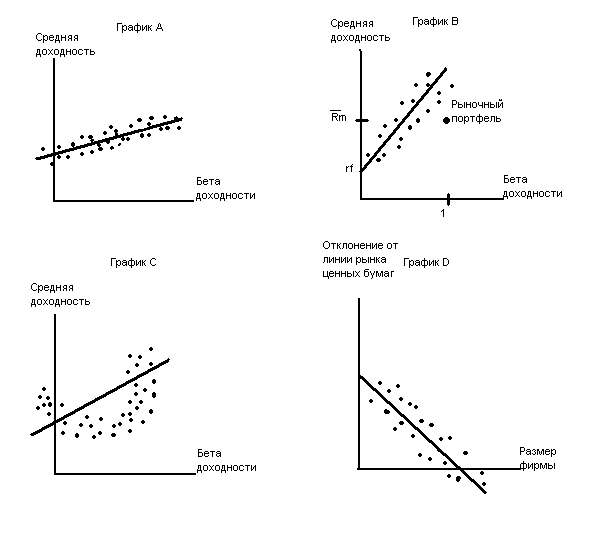
В частности, отрезок – это устойчивая доходность, а наклон – премия за риск рыночного пакета. В отличие от этого, четыре графика, в приложении 5.13, изображают значения, противоречащие теории. На графике А отрезок неверен, на графике В неверен наклон, на графике С ценные бумаги лежат скорее на окружности, нежели на прямой, на графике D отклонения средней ожидаемой доходности от линии рынка ценных бумаг изображены в зависимости от размера фирмы. Очевидность зависимости между доходностью (после расчета величины бета) и размером фирмы подразумевает отказ от модели САРМ.
Приложение 5.12 second step regression data соответствующее модели САРМ
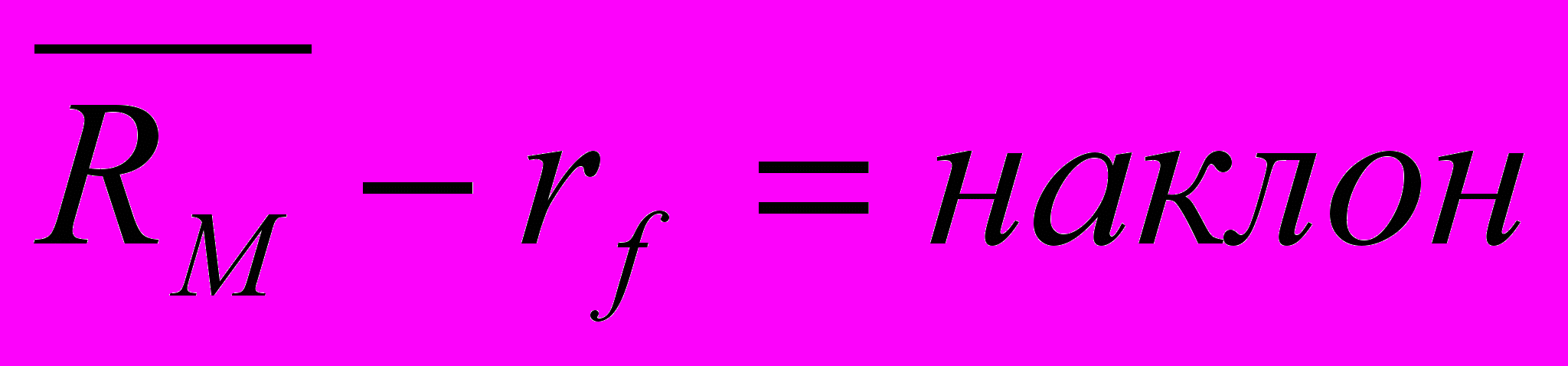
Приложение 5.13 second step regression data несоответствующее модели САРМ
Исследования временного ряда модели САРМ
При повторном исследовании модели САРМ, представленном Блэком, Дженсеном и Скоулзом (1972), были рассмотрены ограничения отрезка временного ряда рыночной модели регрессии. Рассмотрим регрессию:
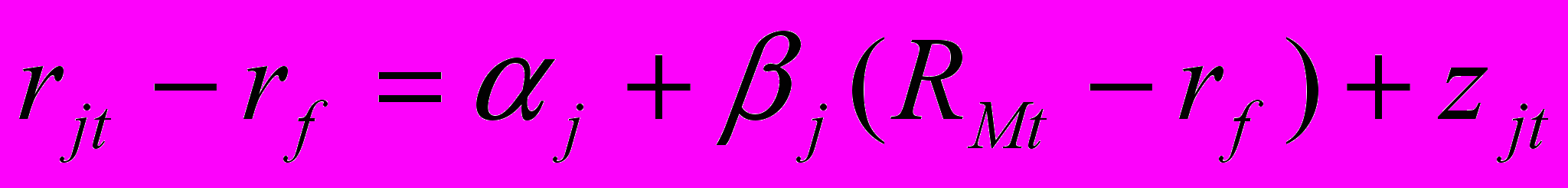
В основном она идентична регрессии из формулы 5.9 , за исключением того, что вместо доходностей используются избыточные доходности. САРМ подразумевает, что в формуле 5.11 отрезок ,
равен нулю для любой ценной бумаги или портфеля. Исследователи изучили модель с точки зрения данного подхода, используя доходность портфеля , сформированную из таких характеристик, как предыдущее значение величины бета ценной бумаги, размер фирмы, отношение рыночной цены ценной бумаги к ее реальной стоимости, для расчета коэффициентов в уравнении (5.11). Например, можно протестировать САРМ, регрессируя избыток доходности портфеля, состоящего из 100 облигаций на нью-йоркской фондовой бирже с минимальной капитализацией по избытку оценки рынка. САРМ предсказывает, что отрезок подобной регрессии будет равняться нулю. Тем не менее, если САРМ недооценит доходность слабокапитализированных ценных бумаг, отрезки в регрессии, включающие в себя ценные бумаги мелких компаний, будут положительны.Результаты поперечного и временного анализа: размер, отношение рыночной стоимости к ее бухгалтерской оценки и доходность.
Как поперечный так и временной анализы предоставляют факты, не поддерживающие модель САРМ. Ниже представлены заслуживающие внимания «нарушения» модели СРАМ:
- Связь между подсчитанной величиной бета и средней доходностью намного слабее, чем предполагается в модели. Некоторые ученые вообще не обнаружили связи между бетой и средней доходностью.
- Рыночная цена компании или размер фирмы являются параметром, предсказывающим ее среднюю доходность (см. приложение 5.15). Эта связь не может быть учтена, в силу того факта, что ценные бумаги с низким уровнем капитализации имеют тенденцию обладать большей величиной бета.
- Ценные бумаги с низким коэффициентом рыночной балансовой стоимости, как правило, имеют более высокую доходность, нежели бумаги с высоким коэффициентом рыночной балансовой стоимости (см. приложение 5.15) . И снова, различия в величине бета не объясняют эту разницу.
- Ценные бумаги, которые были эффективны на протяжении последних 6 месяцев, имеют склонность к высокой ожидаемой доходности в последующие 6 месяцев (см. приложение 5.16 на стр. 184).
С ожидаемой доходностью связано еще несколько дополнительных характеристик ценных бумаг:
- Соотношение цен/коэффициент доходности ( фирмы с высоким коэффициентом доходности имеют низкую доходность ценных бумаг).
- Дивидендный доход ( ценные бумаги с высоким дивидендным доходом обладают более высокой доходностью)
Приложение 5.14 Среднегодовая доходность, величина бета, и размер фирмы для взвешенных по ценности портфелей акций американской и нью-йоркской фондовых бирж
Сформированные на основе рыночной капитализации (Апрель 1951- Декабрь 1989)
| Размер портфеля | Среднегодовая доходность (в процентах) | Величина бета | Рыночная капитализация ( млн. долл.) |
| Минимальный | 19.8% | 1.17 | 9.7 |
| 2 | 17.8 | 1.19 | 23.2 |
| 3 | 16.1 | 1.15 | 41.4 |
| 4 | 15.4 | 1.17 | 68.0 |
| 5 | 16.0 | 1.11 | 109.8 |
| 6 | 14.5 | 1.05 | 178.9 |
| 7 | 14.4 | 1.04 | 291.4 |
| 8 | 14.8 | 1.03 | 502.3 |
| 9 | 13.0 | 1.01 | 902.1 |
| Наибольший | 11.9 | 0.95 | 3983.0 |
Приложение 5.15 Среднегодовая доходность, отношение рыночной цены акции к ее бухгалтерской оценке (МЕ/ВЕ), величина бета, и размер фирмы для взвешенных по ценности портфелей акций американской и нью-йоркской фондовых бирж
Сформированные на основе отношения рыночного курса ценных бумаг к цене по торговой книге.
( Апрель 1962 – Декабрь 1989)
| МЕ/ВЕ портфель | Среднегодовая доходность (в процентах) | Величина бета | Рыночная капитализация ( млн. долл.) |
| Отрицательный | 19.9 % | 1.29 | 118.6 |
| Наименьший > 0 | 17.9 | 1.04 | 260.5 |
| 2 | 17.5 | 0.95 | 401.2 |
| 3 | 13.0 | 0.90 | 619.5 |
| 4 | 13.4 | 0.83 | 667.1 |
| 5 | 11.5 | 0.90 | 641.1 |
| 6 | 9.8 | 0.91 | 834.6 |
| 7 | 10.3 | 0.98 | 752.3 |
| 8 | 11.2 | 1.02 | 813.0 |
| 9 | 10.2 | 1.11 | 1000.8 |
| Наибольший | 10.9 | 1.05 | 1429.8 |
- Долгосрочные стратегии инвестора, действующего вопреки тенденции рынка ( DeBondt и Thaler (1985) обнаружили, что ценные бумаги, неудачно выступавшие на рынке на протяжении трех-пяти месячного периода особенно сильно растут вплоть до 5 лет в будущем.
Приложение 5.16 Средняя годовая доходность портфелей, удерживаемых в течение шести месяцев, сгруппированная по шестимесячной доходности ( Июль 1965-Дек.1989)
| Портфель, ранжированный по доходности (по децилям) | Средняя годовая отдача (в процентах) |
| Портфель 1 (минимальная доходность) | 9.48% |
| Портфель 2 | 13.44 |
| Портфель 3 | 15.00 |
| Портфель 4 | 14.88 |
| Портфель 5 | 15.36 |
| Портфель 6 | 16.08 |
| Портфель 7 | 16.32 |
| Портфель 8 | 17.16 |
| Портфель 9 | 18.36 . |
| Портфель 10 (максимальная доходность) | 20.88 |
| Портфель 10 минус Портфель 1 | 11.40 |
Фама и Френч (1992) заявили, что после расчета ожидаемой доходности, основанной рыночных ценах акций, коэффициенте «рыночная - балансовая» цена, бете акций, и других характеристиках - мультипликатор цена/доход и долгосрочные прошлые доходности - практически не имеют возможности объяснить ожидаемую доходность акций.
Действительно, возможна отрицательная зависимость между бетой и доходностью акций компаний большего размера (а именно, капитализации). Верхний ряд Приложения 5.17 показывает доходность трех портфелей:
- портфель, взвешенный по капитализации всех акций (левая колонка)
- взвешенный портфель акций, ранжированных по бете в нижнем дециле (средняя колонка),
- портфель акций, ранжированных по бете в нижнем дециле (правая колонка).
Значения, представленные в этом ряду, показывают, что портфели акций с низкими бетами имели доходности, которые были несколько выше доходностей акций с высокими бетами. Когда портфели включают в себя только акции компаний с низкой капитализацией (средний ряд), результаты в основном такие же, т.е. низкие беты заключают в себе только доходность, которая не намного выше. Однако, для акций компаний с высокой капитализацией (нижний ряд), существует большая потеря доходности, связанная с бетой. Акции компаний с высокой капитализацией с высокими бетами показали очень низкую доходность за период с 1963-1990 года.
Приложение 5.17. Средне годовая доходность, основанная группировке по размеру и бете (Июль 1963-Дек.1990)
| | Все фирмы (%) | Низкие беты (%) | Высокие беты (%) |
| Все фирмы | 15.0% | 16.1% | 13.7% |
| Фирмы с низкой капитализацией | 18.2 | 20.5 | 17.0 |
| Фирмы с высокой капитализацией | 10.7 | 12.1 | 6.7 |
Приложение 5.18. Средне годовая доходность (%) отсортированная по размеру и ME/BE (Июль 1963-Дек.1990)
| | Все фирмы (%) | Высокие ME/BE (%) | Низкие ME/BE (%) |
| Все фирмы | 14.8% | 7.7% | 19.6% |
| Фирмы с низкой капитализацией | 17.6 | 8.4 | 23.0 |
| Фирмы с высокой капитализацией | 10.7 | 11.2 | 14.2 |
Приложение 5.18 показывает ежемесячную доходность девяти портфелей, образованную на основе капитализации и (ME/BE). Просматривая первый ряд, один увидит, что для примера всех фирм, низкая ME/BE показала гораздо большую доходность, чем высокая ME/BE. Однако, два нижних ряда показывают, что эффект ME/BE на доходность акций значительно сильнее для компаний с низкой капитализацией. Что приложение 5.18 показывает, так это то, что инвестор, который купил и удержал акции копании с низкой капитализацией и с низкой ME/BE, получит ежегодную доходность примерно в 23%.С учетом компаундирования , инвестиция в $1000 сделанная в начале 1963 года, выросла бы по 23% годовых до $267000 к концу 1989.
Вывод 5.10 суммирует все выводы этого пункта: