Анализ среднего дисперсии и модель оценки финансовых активов
| Вид материала | Анализ |
- Нка финансовых активов» является составной частью комплексного обучения специальности, 11.88kb.
- Тестирование методов оценки финансовых активов на российском рынке, 697.91kb.
- Примерная тематика рефератов по курсу, 16.99kb.
- Анализ и планирование безубыточности производства, расчет производственного и финансового, 210.52kb.
- 2. Анализ финансовых результатов коммерческой организации Модель формирования показателей, 38.32kb.
- Вопрос 4 Дисконтирование. Ставки дисконта. Метод калькулятивного построения. Оценка, 68.83kb.
- Встатье рассматривается принцип усовершенствования оценки нематериальных активов, 95.39kb.
- Конспект тема : Основные производственные фонды ( опф), 205.4kb.
- Темы курсовых работ по дисциплине «Анализ и диагностика финансово-хозяйственной деятельности, 58.19kb.
- Решение задач описательной статистики средствами ms excel содержание, 164.81kb.
5.6. Насколько полезен анализ среднего отклонения для нахождения эффективных портфелей?
Единственная трудность в применении анализа среднего отклонения для нахождения комплекта рыночных портфелей, имеющих самую высокую ожидаемую доходность при данной дисперсии, состоит в том, что средние и совместные изменения обычно не очевидны. Так как для выбора есть огромное количество акций и других бумаг, в которые можно вложить деньги, полное проведение анализа среднего отклонения для управления портфелями является ограниченным. Во-первых, подсчет необходимых вкладов является, чуть ли не героическим замыслом, учитывая, что только на американском рынке торгуют около десятью тысячами акций. Кроме того, оценка среднего значения и ковариация будут отличаться от реальных оценок и ковариаций, в сущности, для всех этих ценных бумаг.
Эти рассуждения не обязательно ограничивают применимость анализа среднего отклонения для более узких задач, таких как: распределение наличных средств по классам активов (то есть, на какую долю денег инвестора будут куплены акции, на какую облигации, какая доля останется в наличных деньгах и т.д.) , по странам (то есть, какая доля денег инвестора будет в Китае, какая в Европе, какая в Америке и т.д.) и по отраслям. За достижением этих простых целей легче следить, когда все рассчитано заранее и приблизительно оценены ковариация и произведена оценка их реальной ценности, потому что основные активы, в таком случае являются портфелями, лежащими на кривой эффективности в отличие от частных акций. Эти рассуждения также не ограничивают использования анализа среднего отклонения для ограниченных корпоративных финансов.
Эти трудности в применении анализа среднего отклонения для определения эффективности портфелей индивидуальных ценных бумаг могут быть преодолимы, если мы введем несколько допущений. Эти допущения, добавленные к уже имеющимся в анализе среднего отклонения, дают возможность аналитику выследить эффективные портфели нежели высчитывать их, исходя из ковариации и исторических способов. ( В этой главе мы обсудим модель CAPM, основанную на дополнительных допущениях)
5.7 Связь риска и ожидаемой отдачи
Вторичная выгода от идентификации комплекта рыночных портфелей, имеющих самую высокую ожидаемую доходность при данной дисперсии, состоит в том, что она обобщает стабилизацию, которая относится к рискам активов относительно их будущей доходности. Зная, что связь между риском и ожидаемой отдачей имеет огромное количество факторов, среди которых: оценка работы инвестиционных менеджеров, определение желаемых ставок доходности в качестве установленных справедливых ставок для регулируемых облигаций и оценка корпоративных инвестиционных проектов.
Пример последнего утверждения: предположим, что Dell Computer хочет расширения путем развития заводов на Дальнем Востоке. Эта компания оценила стоимость будущих работ и будущий поток наличности от такого вложения денег. Для того, чтобы определить увеличивает ли такое расширении ценность фирмы, ожидаемые в будущем денежные потоки от расширения должны быть переведены и оценены в долларовом эквиваленте сегодня. Dell Computer может вычислить это путем дисконтирования ожидаемых денежных потоков по норме прибыли, требуемой финансовыми рынками от инвесторов с таким же риском.
Распространенным предположением в оценке требуемой нормы прибыли является то, что проект по расширению имеет ту же требуемую доходность, что и непривилегированные акции Dell Computer. Как часто бывает, было бы глупо со стороны Dell Computer оценивать требуемую норму прибыли, взяв среднюю доходность своих акций за время существования. Так как было бы очень необычно для такого невероятного достижения, если бы оно повторилось. Другими словами, из-за своего знаменательного достижения в первые семь лет в качестве открытой торговой компании , средняя доходность акций за всю историю существования компании превышает ожидаемую норму прибыли , требуемую инвесторами.
Из-за того, что доходность акций имеет такое большое колебание, проблема Dell Computer часто возникает и у других компаний. Если данные за длительный период времени предоставляют надежные оценки действительной ожидаемой нормы прибыли от акций закрытых корпораций, то как эти компании получают эти оценки? К счастью, трудность в методах оценки не зависит от видов рисков. По этой причине точные оценки риска могут быть получены , если известен рыночный портфель. В таком случае, теория относительно колебаний, которые трудно предугадать (то есть ожидаемые отдачи от частных компаний) могла бы быть полезной для компаний типа Dell Computer.
Относительный риск и эффективные портфели
Когда существует безрисковый актив, связь между существенным риском инвестирования и его доходностью, может быть установлена прямо из уравнения 5.2. Уравнение же 5.3 получено путем перемещения премии за риск инвестирования в правую часть уравнения 5.2:
r - rf = cov (r, RT)* (RT – rf)
var (RT) 5.3
(Для простоты изображения мы опустили индекс i)
Уравнение 5.3 описывает связь между ожидаемой доходностью инвестиций и мерой риска этих инвестиций. В таком случае, относительной мерой риска является совместное изменение рыночного портфеля и инвестиций.
Бэты
Первый элемент в правой части уравнения 5.3 обычно называется бэтой и пишется как греческая буква b:
b = cov (r, RT)
var (RT)
Это обозначение вводится, потому что правая часть уравнения 5.3 также является формулой для нахождения угла наклона регрессии, которая обычно использует b для обозначения наклона. После ввода такого обозначения, уравнение приобретает вид:
r - rf = b (RT – rf)
Линия рынка ценных бумаг против диаграммы среднего стандартного отклонения.
Часть А рисунка 5.5 на странице 160 изображает знакомую диаграмму среднего стандартного отклонения. Для того же финансового рынка , часть Б, справа, изображает то, что обычно подразумевают под линией рынка ценных бумаг. Линия рынка ценных бумаг – это линия, связывающая два важных свойства всех инвестиций на рынке ценных бумаг. В уравнении 5.4 это графическое изображение противостояния бэты и средней. Четыре ценные бумаги, отображенные на обеих частях рисунка, и рыночный портфель одинаковы на обеих диаграммах.
Обратите внимание, что на рисунке Б бэта рыночного портфеля равна единице, потому что числитель и знаменатель дроби, вычислявшие бэту, идентичны для такого портфеля. У безрискового актива бэта всегда равна нулю, так как, являясь неизменной, его отдача не подвержена совместным изменениям. Каждый портфель на линии рынка капитала, средневзвешенная рыночного портфеля и безрискового портфеля, имеет свое место на линии рынка ценных бумаг, найденное путем взятия тех же средневзвешенных точек рыночного портфеля и безрискового актива. Что является особенностью линии рынка ценных бумаг, так это то, что все инвестиции из части А лежат на этой линии: и эффективные портфели, лежащие на линии рынка капитала и инвестиции справа от линии капитала.
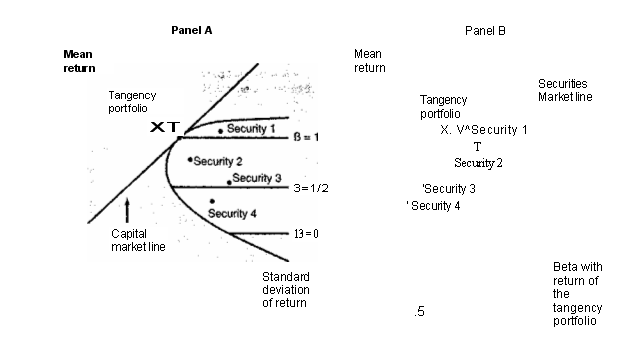





Рис 5.5
Panel A – часть А
Mean return – средняя доходность
Tangency portfolio – эффективный портфель
Security 1,2,3,4 – Ценные бумаги 1,2,3,4
Capital market line – линия рынка капитала
Standard deviation of return – стандартное отклонение доходности
Securities market line – линия рынка ценных бумаг
Beta with return of the tangency portfolio – Бэта доходности рыночного портфеля
На рисунке5.5 с целью иллюстрации критического отличия между линией рынка ценных бумаг и диаграммы среднего стандартного отклонения, они обе помещаются рядом. Разница между диаграммами на части А и части Б отражена на горизонтальной оси. Часть А показывает стандартное отклонение отдачи на этой оси, в то время как на части Б , показана бэта с отдачей от рыночного портфеля, которая пропорциональна предельной дисперсии. Таким образом, пока инвестиции с постоянной средней величиной могут показывать разные средние отклонения , как показано на части А, они должны иметь одинаковую бэту, как показано на части Б. Например, на части А все точки на серой линии, лежащие справа от точки Т, названной «b=1», это портфели с бэтой, равной бэте рыночного портфеля. На части В все портфели, даже несмотря на то, что они отличаются весами портфелей и стандартными отклонениями, отображаются в той же точке, что и рыночный портфель. По той же причине все точки, лежащие на серой горизонтальной прямой справа от безрисковых активов на диаграмме среднего стандартного отклонения, названные «b=0», являются портфелями с бэтой, равной нулю, даже несмотря на то, что они имеют разные стандартные отклонения. На диаграмме среднего стандартного отклонения, которая отображает линию рынка ценных бумаг на части Б, эти портфели изображены в той же точке, что и rf .
Контраст между бэтами и совместными изменениями
Обратите внимание на то, что бэты и совместные изменения обычно имеют одинаковую предельную дисперсию. Бэта – это просто совместное изменение, поделенное на одинаковую константу для каждой акции. По исторически сложившимся причинам так же как и простота оценки с регрессией , бэта стала более распространенным измерителем маргинальной дисперсии. В принципе, обе они одинаково хороши в качестве измерителей предельного риска.
Предельная дисперсия против общей дисперсии
До этого в тексте риск портфеля был определен как вариация его отдачи. Как это обычно бывает, для определения ожидаемой нормы прибыли от инвестиций существенный риск обозначается бэтой (или совместное изменение), вычисленной относительно рыночного портфеля.
Бэта против изменения в качестве меры риска
Почему именно бэта, а не изменение является относительной мерой риска? Аналогия с экономикой может пролить на это свет. Основным принципом экономики является то, что рыночные цены на товар равны предельным издержкам производства еще одной единицы продукции. Таким образом, общие издержки производства или средние издержки производства не влияют на цену – влияют только предельные издержки. В финансовом деле, предельное изменение (то есть, совместное изменение инвестиций, измеренное относительно оптимального портфеля инвестора) определяет возрастающий риск от добавления небольшого количества инвестиций в портфель. Следовательно, нет ничего удивительного в том, что требуемая норма прибыли от рисковых инвестиций определяется их предельным изменением.
Использование сущности предельного изменения для понимания уравнения, описывающего доходность ожидаемого риска.
Теперь обратим внимание на ситуацию, которая расширяет подход к рассмотрению предельного изменения, проанализированному в четвертой главе. Начнем с рыночного портфеля с доходностью RT. Добавим в этот портфель k акций на сумму m $ на каждый доллар, инвестированный в этот портфель. Как это обычно бывает, вместо финансирования этой покупки с позиции безрискового актива, мы покупаем их в короткую позицию, это мы будем называть «отслеживающий портфель акций k».
Отслеживающий портфель – это средняя взвешенная рыночного портфеля с весом b и безрискового актива. Новый портфель содержит:
1. рыночный портфель
2. небольшое дополнительное количество акций k
3. Акции k, принадлежащие рыночному портфелю, купленные в короткую позицию, того же объема, что и дополнительные акции k в пункте 2.
Доходность от нового портфеля, выражается формулой:
R = RT + m { rk - [b RT + (1 – b ) rf)]} = RT + m [(rk - rf) – b (Rr - rf)]
А его ожидаемая доходность:
R = RT + m{ rk - [b RT+ (1 — b ) rf)]} = RT + m [(rk - rf) – b (Rr - rf)]
Давайте обозначим
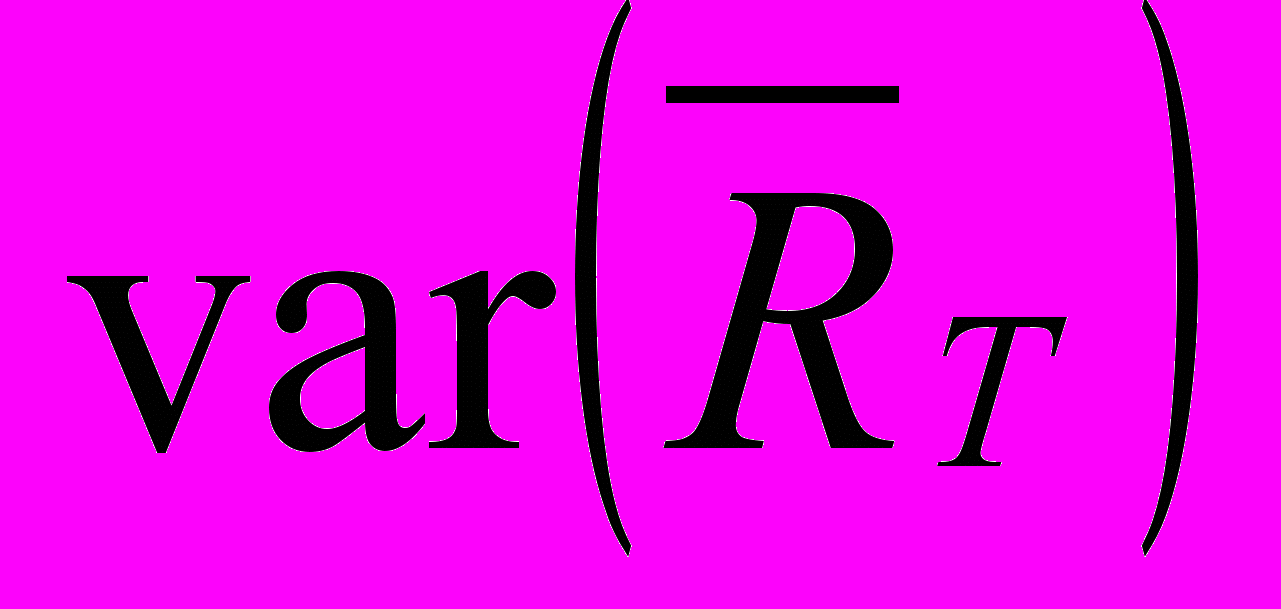 через
через 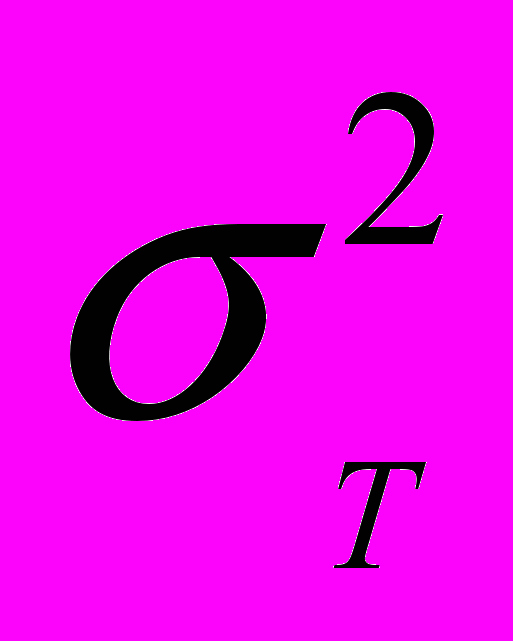 и
и 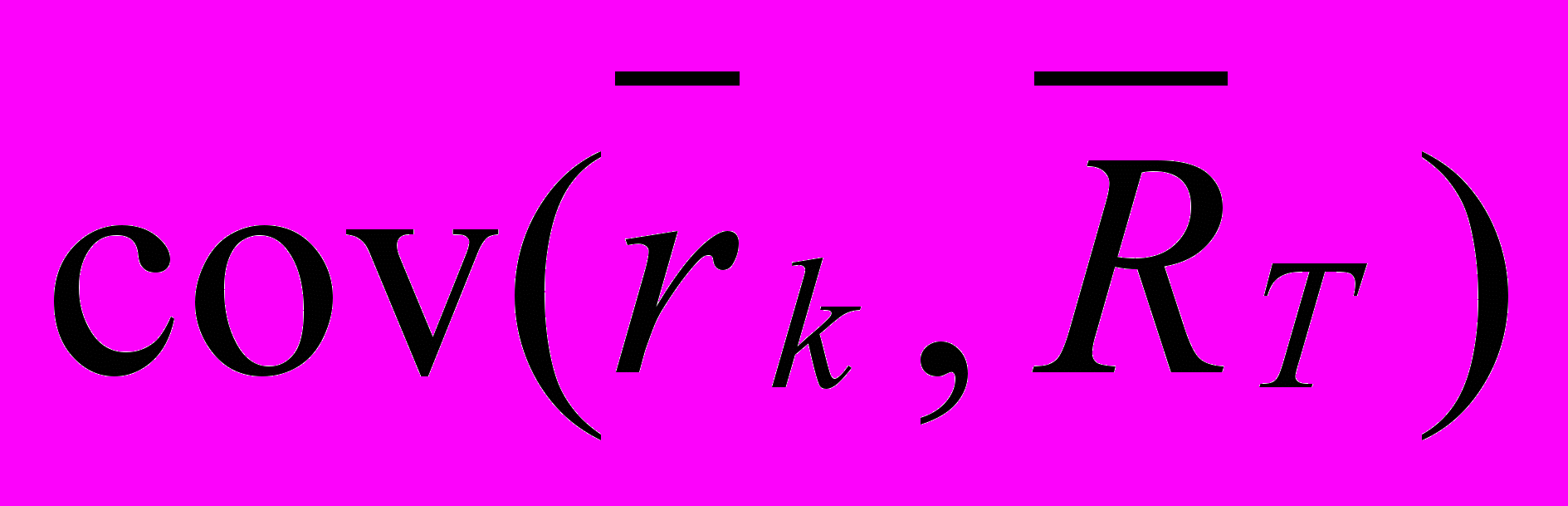 через
через  , дисперсия нового портфеля,
, дисперсия нового портфеля,  , есть:
, есть: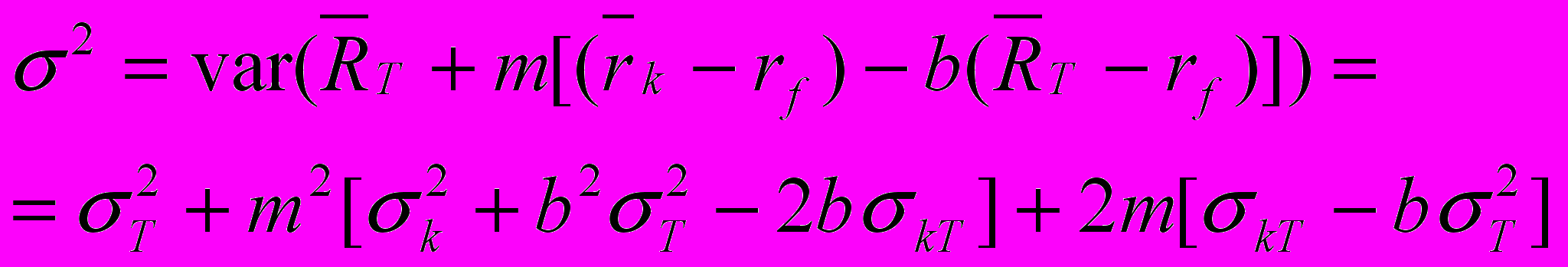
Последнюю строку можно получить, взяв портфельную дисперсию и формулы ковариации, уравнение (4.9а) и результаты 4.4. и 4.5. Производная этой дисперсии по m:
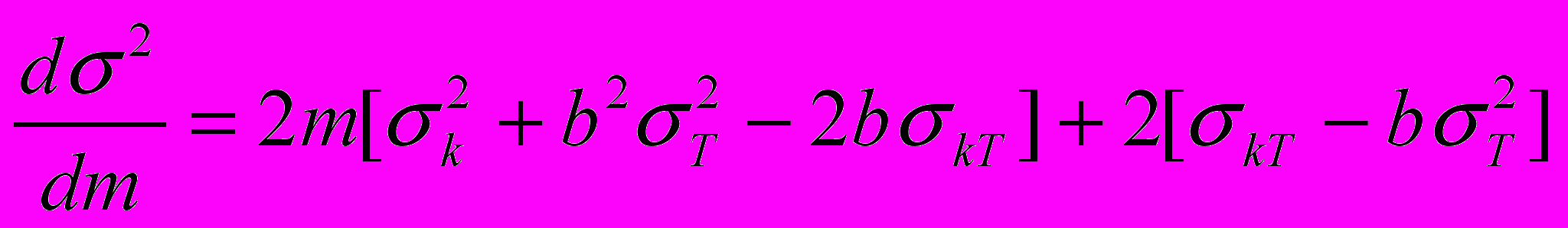
при m=0
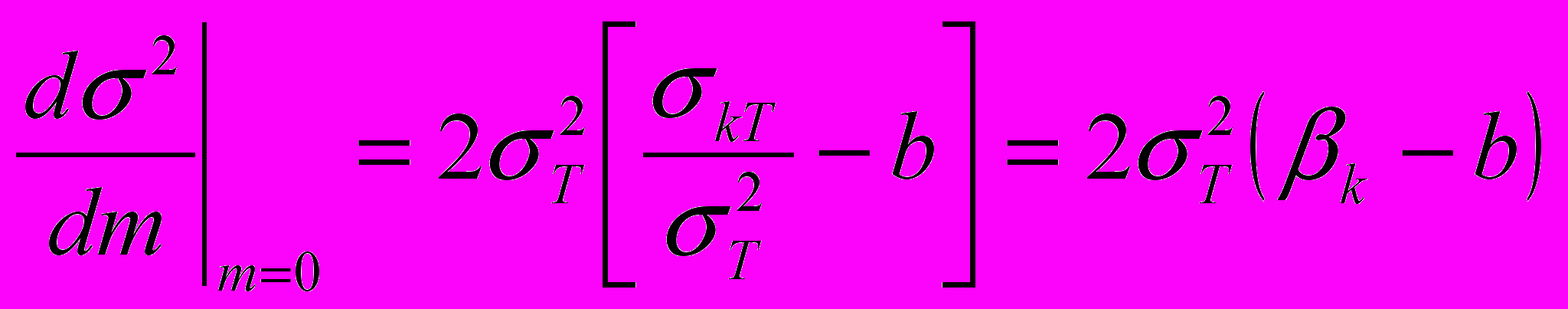 (5.5)
(5.5)Уравнение (5.5) подразумевает, что добавление небольшого количества акций k портфелю касания (рыночному портфелю, если судить по лекциям)(tangency portfolio), финансируемому так, как описано выше, приведет к:
1. увеличению дисперсии, если
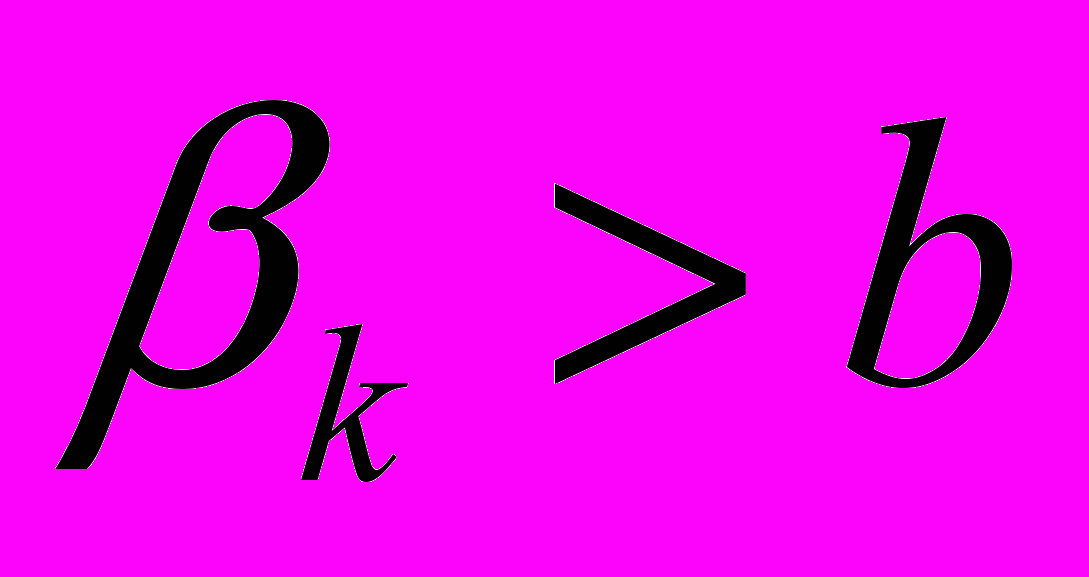
2. уменьшению дисперсии, если
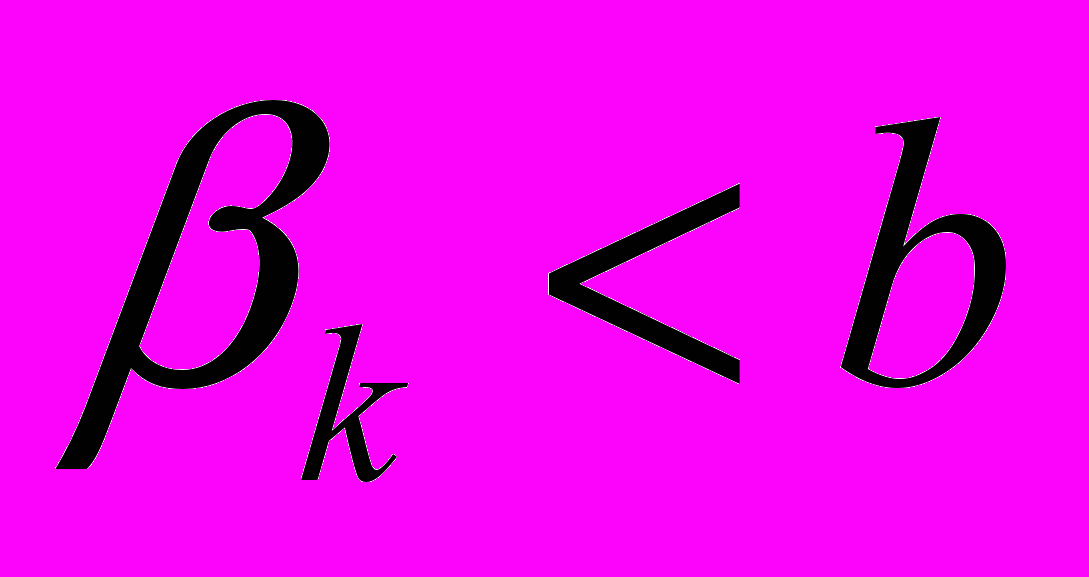
3. не изменит дисперсию (для бесконечно малого m), если
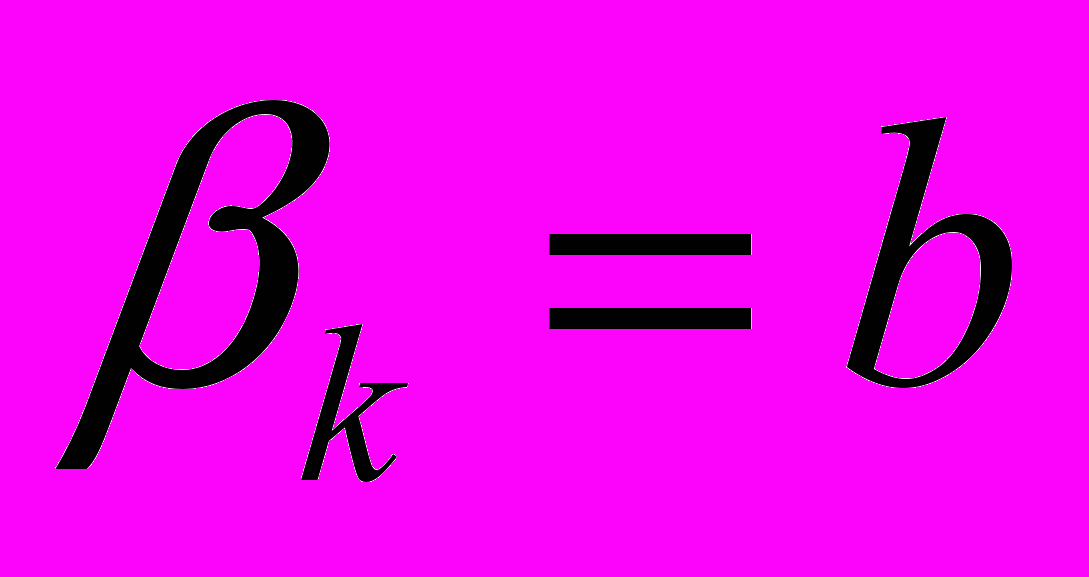 .
. Эти три случая положительной, отрицательной и нулевой предельной дисперсии в указанном порядке соответствуют бета акции k,
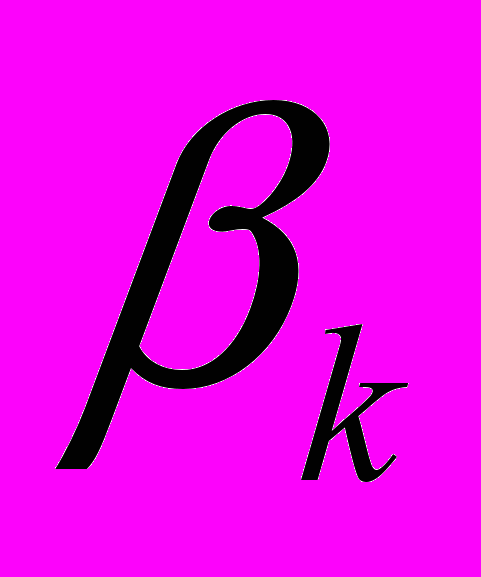 , больше, меньше, или равны бета отслеживающего портфеля (tracking portfolio), т.е. b.
, больше, меньше, или равны бета отслеживающего портфеля (tracking portfolio), т.е. b.Давайте разберем случай нулевой предельной дисперсии, случай 3, для которого отслеживающий портфель построен так, чтобы иметь такой же предельный риск как у акции k. Предположим, что в этом случае, когда
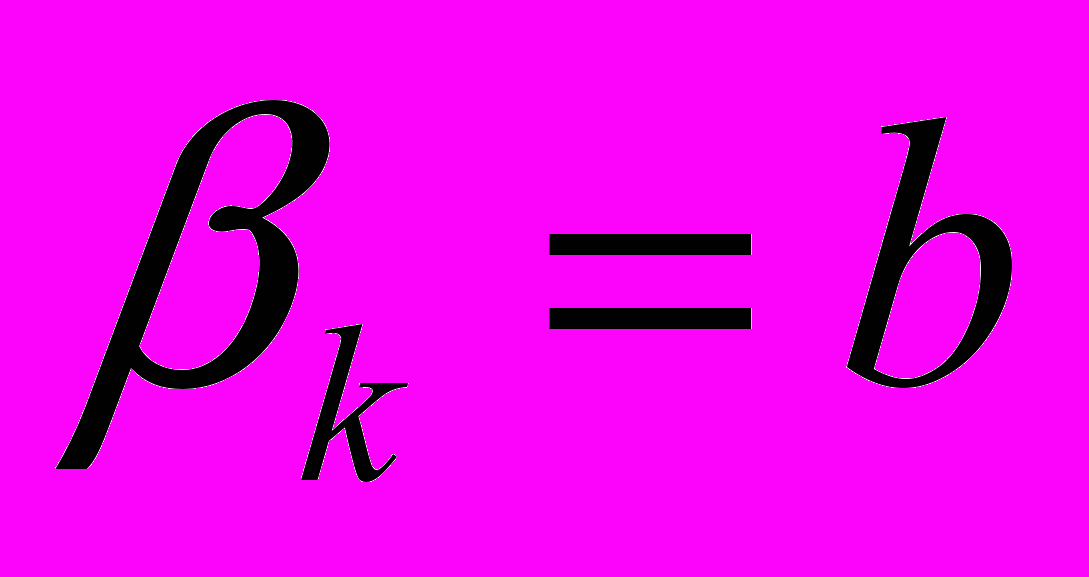 , премия за риск акции k превысила премию за риск отслеживающего портфеля.
, премия за риск акции k превысила премию за риск отслеживающего портфеля.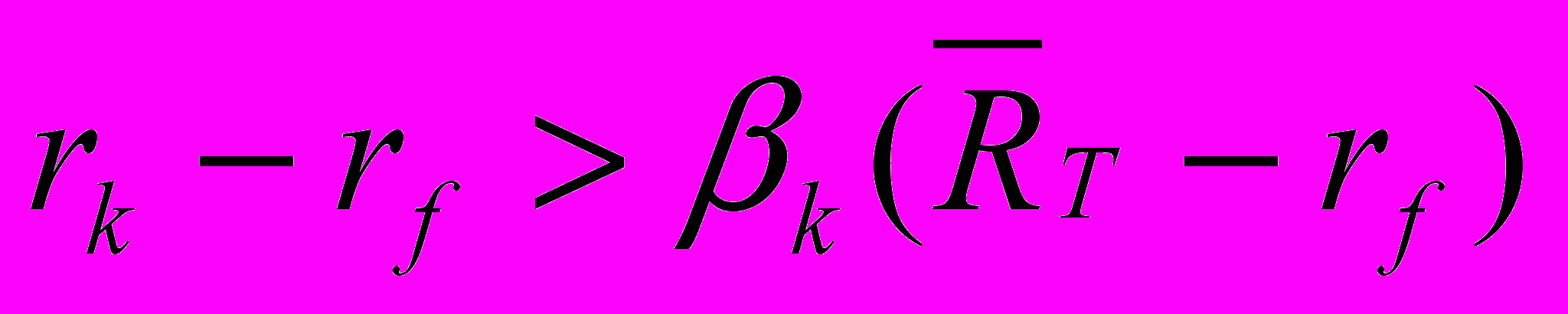 (5.6)
(5.6) Для малого m, добавление акции k к портфелю касания – финансируемому от положения отслеживающего портфеля с такой же предельной дисперсией, как и у акции k – не добавляет дисперсию портфелю Т, но из-за неравенства премии за риск (5.6), увеличивает среднюю.
Таким образом, если (5.6) верно, то добавление акции k, подобранной под равновеликую короткую позицию в отслеживающем портфеле (matched by an equal-sized short position in the tracking portfolio), приведет к новому портфелю, который доминирует над портфелем касания. Однако предположение о неравенстве премии за риск, выраженное в (5.6), не может быть верным, потому что по определению должен доминировать портфель касания.
Теперь предположим, что премия за риск от отслеживающего портфеля превышает ту же премию от акции k:
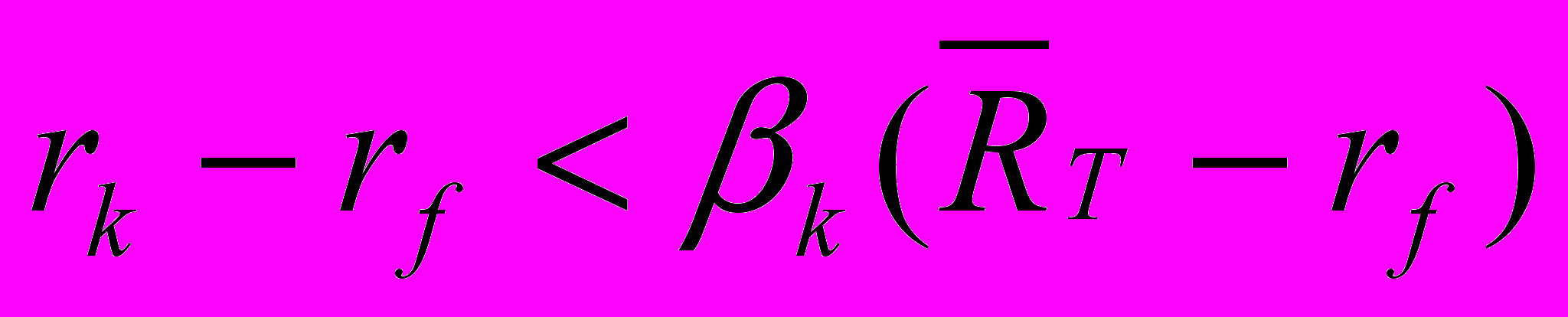 (5.7)
(5.7)Вычитание достаточно малого количества акции k из портфеля касания, уравновешенного равновеликой длинной позицией в отслеживающем портфеле с такой же предельной дисперсией (balanced by an equal-sized long position in the tracking portfolio with the same marginal variance), не добавляет дисперсии портфелю касания, но через (5.7) увеличивает среднюю. Таким образом, если (5.7) верно, то вычитание акции k, подобранной под обратную позицию отслеживающего портфеля (matched by an opposed tracking portfolio position), как описано выше, доминирует над портфелем касания. Т.к. портфель касания должен быть доминирующим, то (5.7) неверно.
Если беты рассчитаны относительно портфеля касания, а это невозможно, как показано выше, то можно наблюдать следующее:
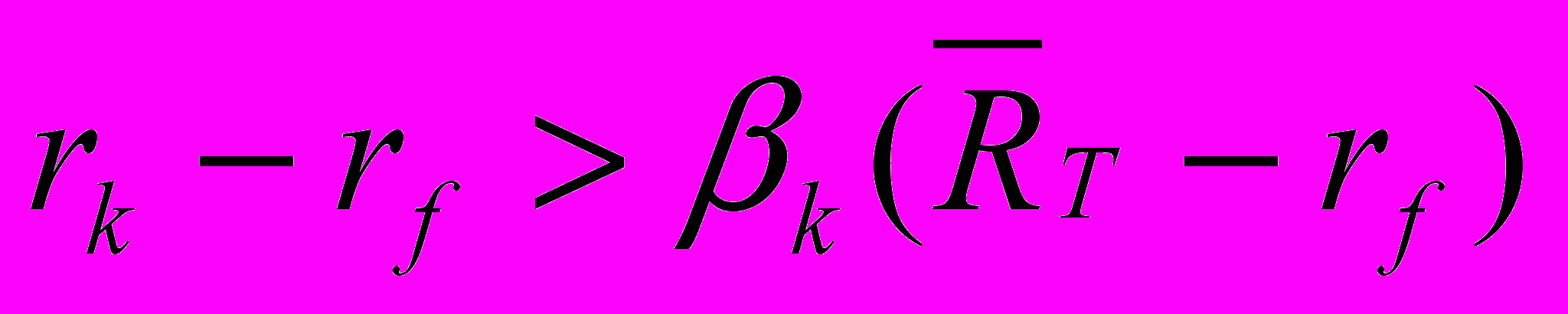 или
или 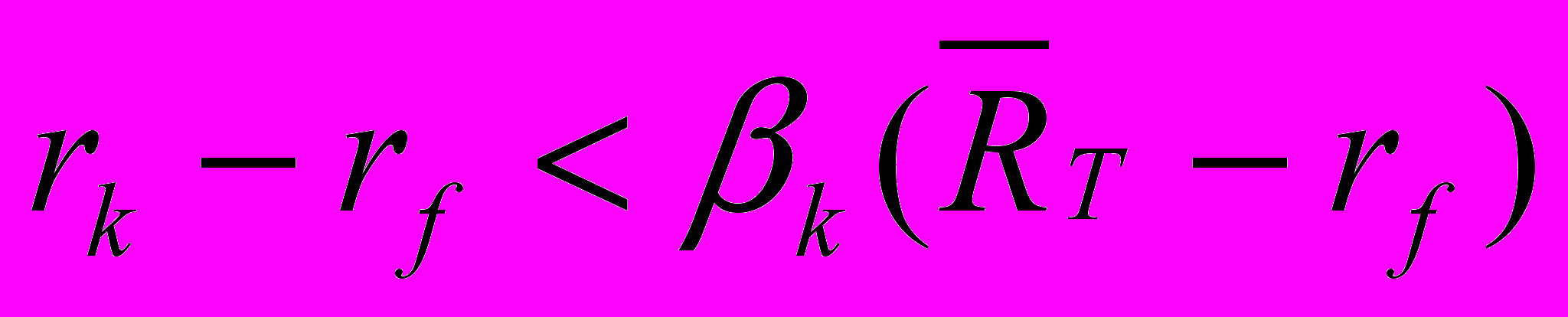 ,
,Единственный возможный вариант:
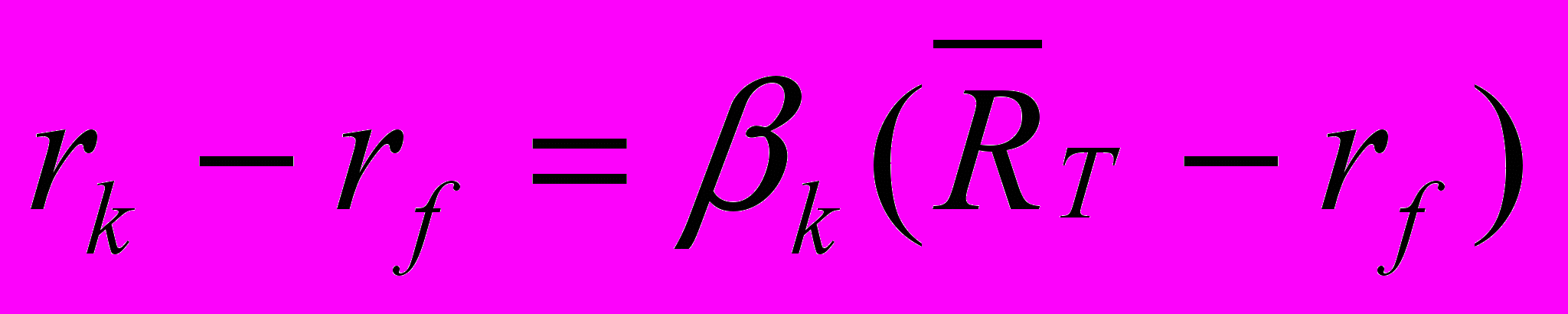
Это уравнение описывает ожидаемый риск и доход и определяет линейную зависимость ожидаемого дохода от бета.
Отслеживающие портфели в Управлении портфелями ценных бумаг и как способ для определения стоимости инвестиционного портфеля или ценной бумаги.
Последний раздел использует отслеживающие портфели, составленные из средних взвешенных из портфеля касания и безрискового актива, чтобы показать, почему уравнение, описывающее ожидаемый риск и доход, уместно. Однако понятие отслеживающего портфеля намного более широко, чем это представлено ранее. Например, профессиональные инвесторы используют отслеживающие портфели, отличающиеся от тех, которые были в последнем разделе тем, что ставят своей целью управление фондом (фонд, доходность которого поддерживается на одном уровне с определенным индексом ценных бумаг (index fund)) по низким транзакционным издержкам. Кроме того, этот текст обобщает понятие отслеживающего портфеля, чтобы развить оценочные модели (valuation models). Этот раздел обсуждает эти обобщения понятия отслеживающего портфеля.
Использование отслеживающих портфелей в инвестиционном менеджменте. Профессиональные инвесторы часто должны отслеживать, т.е. воспроизводить доходные характеристики больших портфелей, используя сравнительно малое число акций. Например, нескольких менеджеров попросили создать портфели, которые отслеживают индекс S&P 500 в надежде повысить его. Из чего следует, что иногда важно различать совершенное и несовершенное отслеживание.
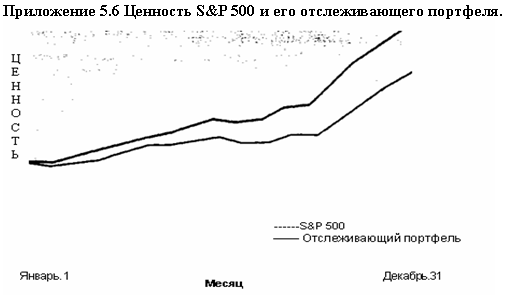
Портфель А в полной мере отслеживает портфель Б, если разница доходов от них постоянна.
Приложение 5.6 иллюстрирует ценность S&P 500 и отслеживающего портфеля, доход от которого выше, в 1995 году.
В стандартной стратегии отслеживания профессиональные инвесторы выбирают приблизительно 50 акций, которые он или она считают недооцененными, затем определяют вес каждой из недооцененных акций в портфеле с целью минимизировать дисперсию разницы между доходом от управляемого портфеля и доходом от S&P 500. Как мы видим, отслеживающие стратегии могут вести к пониманию уравнения ожидаемого риска и дохода.
Другие виды использования отслеживающих портфелей в этой теме (in this text). Одна из основных мыслей этого текста заключается в том, что возможно думать об отслеживании почти любой инвестиции. Можно отслеживать частные акции, материальный фонд, такой как фабрика, или индекс ценных бумаг, такой как S&P 500. В отличие от почти совершенного отслеживания всеобъемлющих портфелей, таких как S&P 500 или производных (которые имеют завершенные отслеживающие стратегии), отслеживание частных акций или материального фонда обычно вызывают существенную ошибку отслеживания. В таких случаях наилучшим отслеживающим портфелем является тот, который ближе всего находится к совпадению со сведениями (the returns) об отслеживаемых инвестициях. Этот вид отслеживающего портфеля минимизирует дисперсию ошибки отслеживания.
В этой главе, где акция k отслеживается портфелем безрискового актива, имеющего вес 1-b, и портфелем касания с весом b, лучшим отслеживающим портфелем является один из тех, которые отслеживают вес, b, также как бета акций, т.е.
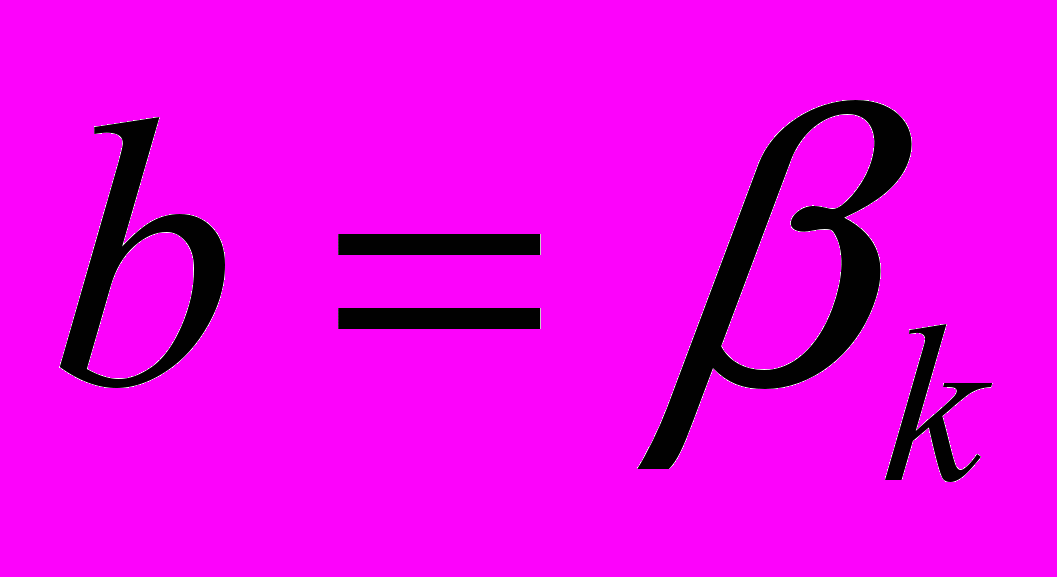
Отслеживающий портфель, созданный с использованием «лучшего» отслеживающего веса имеет такую же предельную дисперсию, что и акция k. Основная суть лучшего отслеживающего портфеля отражена в Результате 5.5.
Результат 5.5.
Если акция k и ее отслеживающий портфель имеют одинаковые предельные дисперсии относительно портфеля касания, тогда акция и ее отслеживающий портфель должны иметь такой же ожидаемый доход. Это применяется только тогда, когда предельная дисперсия рассчитана относительно эффективного портфеля. Предельные дисперсии, рассчитанные относительно недоминирующих портфелей не оказывают влияния на ожидаемый доход.
5.8 Модель оценки финансовых активов (CAPM)
Обеспечение зависимости ожидаемого дохода и риска требует наблюдения за портфелем касания. Однако невозможно получить портфель касания, просто наблюдая за историей доходов большого количества активов. Для начала такое применение является чрезвычайно комплексным и неточным, требующим тысяч ковариационных оценок. Кроме того, использование средних за период доходов для определения средних, и использование данных о доходах за длительный период времени для оценки ковариаций и дисперсий только создало бы потенциальный портфель касания, который был бы бесполезен для предсказания средних доходов. Требуемая норма прибыли, полученная из зависимости дохода с учетом риска, основанного на бетах, относительно которых портфель касания был бы просто средней норм прибыли за период, используется для нахождения портфеля касания. В случае Dell этот метод создал бы больший средний доход за период, чем его ожидаемый доход, который, как предполагалось ранее, оценен хуже. Очевидно, требуются другие методы для определения портфеля касания.
Чтобы внести немного экономического содержания в зависимость ожидаемого дохода и риска, описанную уравнением (5.4), необходимо развить теорию, которая определяет портфель касания среди устных теоретических предположений. Этот раздел развивает одну из таких теорий, обычно ссылающихся на Модель Оценки Финансовых Активов (CAPM), которая, как отмечено ранее, является моделью отношения риска и ожидаемого дохода.
Главное понимание CAPM заключается в том, что колебание отдельной акции – неглавный определяющий фактор ожидаемого дохода от акции. Что по-настоящему является важным, так это рыночная бета акции, которая измеряет ковариацию дохода от акции с рыночным индексом, вычисленную с помощью того же индекса.
Предположения CAPM
Как было отмечено ранее, два предположения об анализе средней дисперсии следующие:
Инвесторы заботятся только о средней и дисперсии своих портфельных доходов.
- Рынки свободны от трений и разногласий.
Чтобы развить CAPM, нужно дополнительное предположение:
- Инвесторы имеют однородные убеждения, что означает, что все инвесторы склонны к одинаковым выводам о средних и стандартных отклонениях всех возможных портфелей.
Предположение об одинаковых убеждениях подразумевает, что инвесторы не будут пытаться перехитрить друг друга вытолкнуть друг друга с рынка путем деятельного управления своими портфелями. Научное исследование средних, дисперсий и ковариаций все еще может быть использовано, но почти каждый человек делает те же заключения о среднем и стандартном отклонении от каждого возможного портфельного дохода после своих собственных научных исследований.
Заключение CAPM
Из этих трех предположений теоретики были способны развить модель оценки финансовых активов, которая делает вывод, что портфель касания (tangency portfolio) должен быть рыночным портфелем (market portfolio). Следующий раздел поясняет понятие «рыночный портфель» и как профессионалы используют его в модели оценки финансовых активов (CAPM).
Рыночный портфель
Рыночный портфель – это портфель, где вес каждого актива является рыночной стоимостью (так же называется рыночной капитализацией) этого актива, деленной на рыночную стоимость всех рискованных активов.
