Анализ среднего дисперсии и модель оценки финансовых активов
| Вид материала | Анализ |
- Нка финансовых активов» является составной частью комплексного обучения специальности, 11.88kb.
- Тестирование методов оценки финансовых активов на российском рынке, 697.91kb.
- Примерная тематика рефератов по курсу, 16.99kb.
- Анализ и планирование безубыточности производства, расчет производственного и финансового, 210.52kb.
- 2. Анализ финансовых результатов коммерческой организации Модель формирования показателей, 38.32kb.
- Вопрос 4 Дисконтирование. Ставки дисконта. Метод калькулятивного построения. Оценка, 68.83kb.
- Встатье рассматривается принцип усовершенствования оценки нематериальных активов, 95.39kb.
- Конспект тема : Основные производственные фонды ( опф), 205.4kb.
- Темы курсовых работ по дисциплине «Анализ и диагностика финансово-хозяйственной деятельности, 58.19kb.
- Решение задач описательной статистики средствами ms excel содержание, 164.81kb.
Пример 5.9: Вычисление весов рыночного портфеля
Рассмотрим экономику только с тремя инвестициями: акции HP (Hewlett Packard), IBM и DEC (Digital Equipment). К концу 1995 года приблизительная цена за одну акцию каждой из этих компаний составляет: HP = $83.75, IBM = $90.00 и DEC = $62.60. Приблизительное число акций этих компаний, выпущенных в обращение, составляет 513,43 миллиона (HP), 566,67 миллиона (IBM) 159,74 миллиона (DEC). Каковы же портфельные веса рыночного портфеля?
Ответ: Рыночная капитализация акций следующая:
HP = $83.75 x 513.43 млн. = $ 43 млрд.
IBM = $90.00 x 566.67 млн. = $ 51 млрд.
DEC = $62.60 x 159.74 млн. = $ 10 млрд.
Полная рыночная капитализация = $1 04 billion
Веса рыночного портфеля (с десятичными приближениями) на эти три акции следующие:
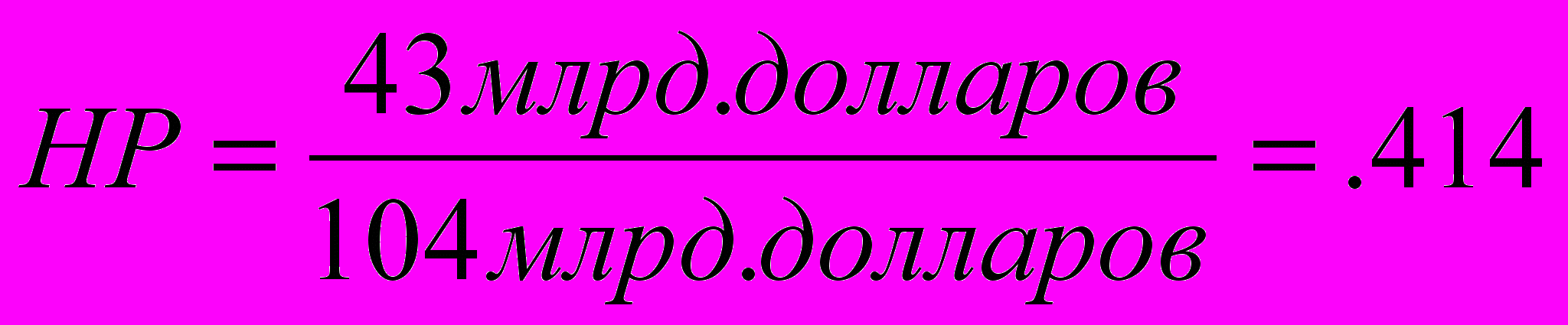
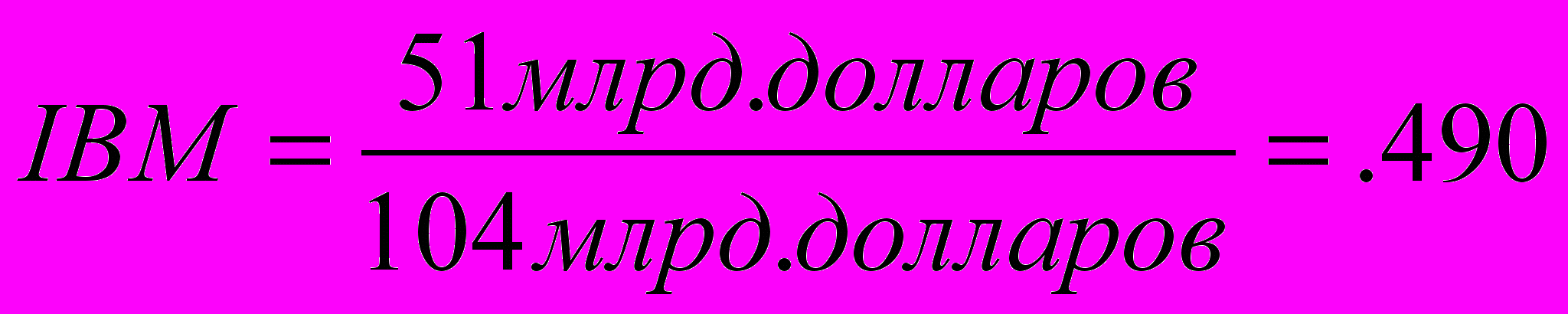
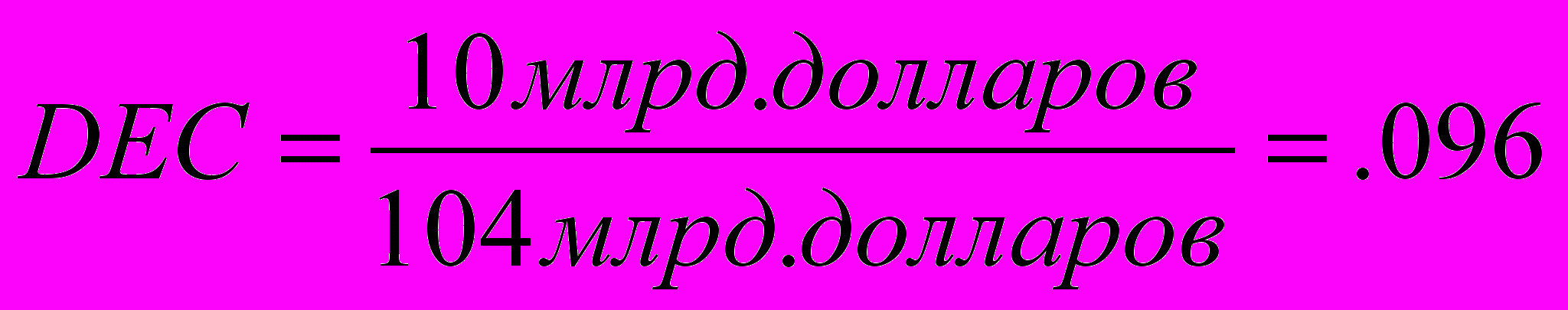
В Примере 5.9 доход от рыночного портфеля,
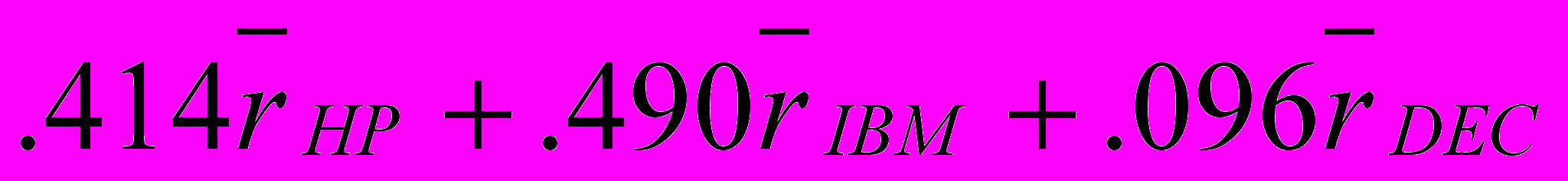, является важным доходом, с помощью которого вычисляют беты этих трех акций, если CAPM верен. Беты определяют ожидаемые доходы этих трех акций. Конечно, в мире множество инвестиционных активов, не только 3 акции, подразумевается, что реальный рыночный портфель имеет вес на каждый актив в мире.Задача вычисления рыночного портфеля со всеми всемирными активами очевидно непрактична. Как требуют материальные фонды корпораций, все акции и корпоративные облигации внесены в списки всех мировых бирж и те торгуются без рецепта, должны быть включены наряду со всем недвижимым имуществом (and those traded over the counter would have to be included along with all real estate).
Так как многими из этих инвестиций достаточно часто не торгуют, чтобы повысить их цену, то нужно использовать возможности (proxy - полномочия) рыночного портфеля. Часто используемая возможность - S&P 500, взвешивающий стоимость портфель, это значит, что этот портфель взвешивает каждую из 500 типично больших рыночных капитализаций акций – торгующихся на Нью-йоркской Фондовой бирже (NYSE), Американской Фондовой бирже (AMEX) и NASDAQ внебиржевом рынке – пропорционально рыночной стоимости той акции. Другая обычно используемая возможность – это портфель, взвешивающий стоимости всех акций, занесенных в списки Нью-йоркской Фондовой биржи и Американской Фондовой биржи. Однако громадными рынками (например, рынок жилой недвижимости, Токийская Фондовая биржа и Токийский рынок недвижимости) игнорируют эти возможности, делая их плохими заменителями настоящего рыночного портфеля.
Почему рыночный портфель является портфелем касания
Пример 5.9 рассматривал гипотетический мир, в котором было всего три рисковых инвестиции: акции HP (Hewlett Packard), IBM и DEC (Digital Equipment). Предположим, что также в мире существуют безрисковый актив, доступный для инвестиций, и только два инвестора: Джек и Джил.
Какой портфель выберет Джек? Анализ средней дисперсии подразумевает, что Джек проведет свой портфель касания вдоль или длинной или короткой позиции безрисковой инвестиции (will hold the tangency portfolio along with either a long or a short position in the risk-free investment). Доля его портфеля в безрисковой инвестиции зависит от отношения (дословно «отвращения») Джека к риску. Джил тоже хочет инвестировать в некую комбинацию портфеля касания и безрисковой инвестиции.
В Примере 5.9 рыночные стоимости всех акций HP, IBM и DEC составили соответственно $43 млрд., $51 млрд. и $10 миллиардов. Так как Джек и Джил – единственные два инвестора в мире, то их совместные вклады в HP, IBM и DEC также должны в сумме составлять $43 млрд., $51 млрд. и $10 млрд. Должно быть очевидным, что портфель касания должен содержать часть некоторую часть HP. Иначе ни Джек, ни Джил не будут держать акции, подразумевается, что предложение акций HP ($43 млрд.) не равнялось бы спросу на них ($0).
Если предложение равно спросу, Джек и Джил вдвоем держат портфель касания, Джек должен иметь такую же долю от всех выпущенных в обращение акций трех активов. То есть, если Джек держит половину от 513,43 миллиона акций HP, он должен также владеть половиной от 566,67 миллиона акций IBM и половиной от 159,74 миллиона акций DEC. В этом случае Джил владела бы половиной всех акций трех активов. Соответствующие пропорции их общих инвестиций, потраченных на каждую из этих трех видов акций, будут, таким образом, пропорциями рыночного портфеля; т.е., приблизительно, .414.490 и .096. (см. Пример 5.9)
Чтобы понять, почему это должно быть правдой, рассмотрим случай, когда Джек владеет половиной акций HP, но лишь 1/3 акций IBM. В этом случае отношение портфельного веса Джека по HP к его весу по IBM превысило бы .414/.490 - отношение их весов в рыночном портфеле. Это подразумевает, что Джил держала бы половину акций HP и 2/3 акций IBM при условии равенства спроса и предложения. Но тогда у Джил отношение веса HP к весу IBM, являющееся меньше .414/.490 – отношение рыночного портфеля, отличалось бы от Джека, что подразумевает, что Джек и Джил не могли вдвоем находиться на кривой рынка ценных бумаг (capital market line (CML)).
Короче говоря, поскольку Джек и Джил держать портфель касания, они владеют рискованными инвестициями в абсолютно равных пропорциях. Так как их владение рискованными акциями составляет предложение рискованных акций в экономике, то рыночный портфель также должен состоять из рискованных инвестиций, размещенных в тех же пропорциях. Из этого следует, что рыночный портфель является портфелем касания. То же самое заключение, что и сделанное в Результатах 5.6, достигнуто, если есть 2 инвестора в мире или миллиарды.
Результат 5.6 Согласно предположениям о CAPM и, если существует безрисковый актив, то рыночный портфель является портфелем касания, и ожидаемый доход от активов определяется уравнением (5.4):
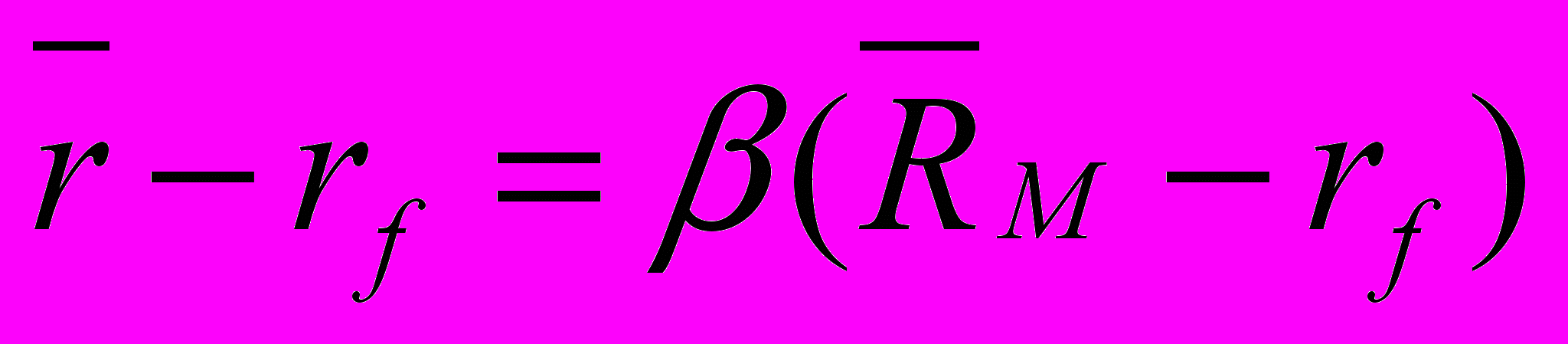(5.8)где
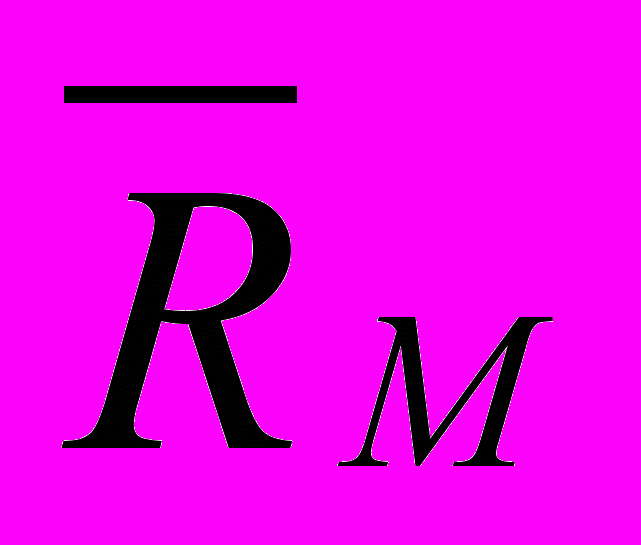- средний доход рыночного портфеля, 
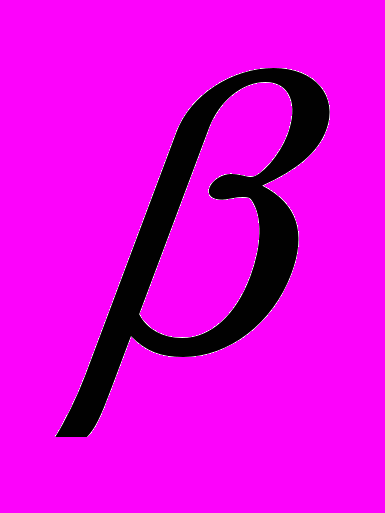- бета, вычисленная в отношении дохода рыночного портфеля.Уравнение (5.8) – частный случай уравнения (5.4) с рыночным портфелем, используемым как портфель касания. Определяя портфель касания, CAPM отношение риск-доход не только возможным для осуществления (implementable), но и осуществимым на практике.
Средства для оптимальных инвестиций
В добавление к возможной для осуществления (implementable) зависимости между риском и ожидаемым доходом, описанной Уравнением (5.8), CAPM также заключает в себе правило для оптимальной инвестиции:
Результат 5.7 Согласно допущениям (assumption) в CAPM, если существует безрисковый актив, то каждый инвестор должен оптимально владеть комбинацией рыночного портфеля и безрискового актива.
Согласно CAPM, главное различие между портфелями Джека и Джил полностью вытекает из их различия весов свободного от риска актива. Это продемонстрировано в Примере 5.10.
Пример 5.10 Портфельные веса, которые включают безрисковый актив.
Рассмотрим одномесячные американские казначейские векселя в качестве безрискового актива. Выпущен 1 миллион казначейских векселей по 9,900$ каждый. Джек владеет 400,000 казначейских векселей, а Джил – 600,000. Если у Джека есть 60 млрд. долл., что является портфельными весами Джека и Джил исходные данные из предыдущего примера, который определил, что богатство, вложенное в рискованные активы, составляет 104 млрд. долларов?
Ответ: Общее богатство в мире – ценность рискованных активов, 104 млрд. долларов плюс ценность казначейских векселей, 9,9 млрд. долл., которые в сумме дают 113,9 млрд. долл. Таким образом, если у Джека 60млрд. долл., то у Джил – 53,9 млрд. долларов. Джек тратит 3,96 млрд. долларов на казначейские векселя, делая его портфельный вес казначейских векселей $3,96 млрд./$60млрд.=.066. Джил тратит 5,94 млрд. долларов на казначейские векселя, делая ее портфельный вес казначейских векселей приблизительно .1102. Таким образом, Джек владеет $56,04млрд./$104млрд. от акций трех рисковых активов, а Джил владеет $47,96млрд./$104млрд. После некоторых подсчетов, 4 портфельных веса (в указанном порядке, безрисковый актив, HP, IBM и DEC) для Джека соответственно (.066, .387, .458, .090) и вес для Джил (.110, .368, .436, .085).
Обратите внимание, в Примере 5.10 последние 3 веса в портфелях Джека и Джил, т.е веса .387, .458, .090 (Джек) и .368, .436, .085 (Джил) по HP, IBM и DEC, соответственно, являются весами рыночного портфеля, если их пересчитать, чтобы суммировать в 1. Очевидно, что этот результат следует и от портфеля Джека, и от портфеля Джил, являющихся комбинациями (рыночного) портфеля касания и безрискового актива.
Чтобы понять важность Результата 5.7, снова вернемся ко вкладам (inputs), необходимым для нахождения портфеля касания. С тысячами ценных бумаг на выбор инвестору придется считать не только тысячи средних доходов, а еще и миллионы ковариаций. Такая устрашающая задача, конечно, требовала бы профессионального портфельного менеджера. Однако CAPM говорит о том, что ничего из этого не нужно, инвесторы могут делать точно также, вкладывая капитал в рыночный портфель.
1970-ые, 1980-ые и 1990-ые колоссальный рост использования пассивно управляемых индексных портфелей как средство передачи инвестиций в пенсионный фонд, взаимный фонд и в индустрии страхования жизни. Эти портфели пытались подражать взвешивающим ценность портфелям, таким как S&P 500. Одной из главных причин этого направления была CAPM, которая предложила, что среднее стандартное отклонение обмена инвестициями не может быть улучшено в рыночном портфеле.
5.9 Обобщение модели оценки финансовых активов
В этой главе рассматривается множество общих правил CAPM. Большинство из них сосредотачивается на отсутствии безрискового актива или наложении некоторых противоречий, включаючая рисковые или безрисковые активы, включая отсутствие продаж в короткую позицию рисковых активов, отсутствие безрисковых кредитов и различие между ставкой процента по безрисковым займам и ставкой процента по безрисковым кредитам. В этой главе также рассматривает важное многоэтапное расширение CAPM.
Что, если продажа в короткую позицию рискованных активов запрещена?
Наше первое рассуждение состоит в том, изменится ли заключение о том, что рыночный портфель имеет самую высокую ожидаемую доходность при данной дисперсии, если ограничить продажу за неимением (например, делая ее более дорогой). Ясно, что ограничение на продажу в короткую позицию затрагивают набор существующих портфелей. Все портфели с отрицательными знаками теперь должны быть исключены из анализа. Однако, рыночный портфель имеет положительный знак и все еще является выполнимым. Следовательно, если в отсутствие ограничений на продажу за неимением рыночный портфель имел самую высокую ожидаемую доходность при данной дисперсии, то он и должен таким остаться. Подводя итог, можно сделать вывод, что вышеупомянутое заключение не изменяется под влиянием ограничения продаж в короткую позицию и таким образом, связь отдачи и ожидаемого риска также не изменится.
Местоположение среднего и среднего квадратического отклонения рыночного портфеля если нет безрискового актива.
Ранее, в этой главе приводились аргументы против существования безрискового актива.
Даже если нет безрисковых активов, заключение о том, что рыночный портфель имеет самую высокую ожидаемую доходность при данной дисперсии, остается неизменным. В части 5.7 рассказывается о портфелях Джека и Джилла, которые расположены на эффективной границе. Рыночный портфель это средняя арифметическая взвешенная этих двух портфелей по доходности. Например, если
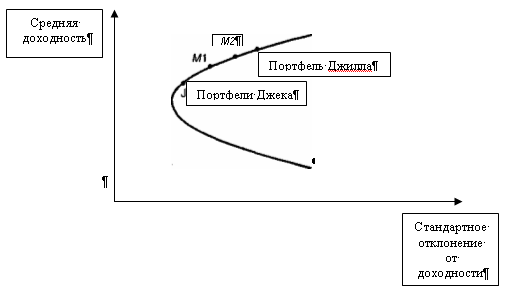
Джилл и Джек каждый имеет по $180 млн., то в рыночный портфель с равными весами войдут оба портфеля, и он будет лежать по середине между ними, в точке М1.
Если Джилл имеет $300 млн. а всего богатства на $360 млн. (т.е. у Джека $60 млн.), то в рыночный портфель они входят с долями 5/6 (т.е 300/360) от портфеля Джилла и 1/6 (60/360) от портфеля Джека, таким образом, рыночный портфель будет лежать между этими двумя портфелями, в соответствии с весами, с которыми и они в него входят и это будет точка М2.
Таким образом, разделение денежных средств на две части, показывает, что если эти два портфеля лежат на эффективной границе, то их средняя арифметическая взвешенная по доходности тоже будет лежать на эффективной границе (сравните приложение 5.7 и 5.2).
Приложение 5.7 Рыночный портфель при отсутствии безрискового актива.
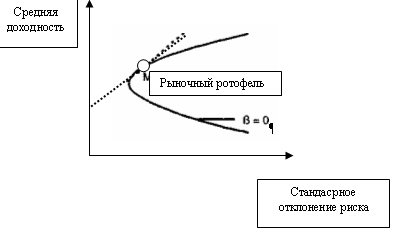
Уравнение риск-доходность, где рыночный портфель имеет самую высокую ожидаемую доходность, при данной дисперсии и когда нет безрискового актива, является фактически тем же самым, что и соответствующее уравнение, которое получается когда безрисковый актив существует. Единственное различие в том, что необходимо заменить отдачу от несуществующего безрискового актива другой величиной. Эта величина, Rz, которая получилась в результате пересечения касательной проведенной к эффективной границе в точке, где находится рыночный портфель (пунктирная линия в приложении 5.8) и осью отдачи.
Это представляет собой среднюю доходность портфеля, который является независимым от колебаний рыночного портфеля.
Почему - это так?
Вспомните, что ковариация относительно рыночного портфеля, что тоже самое, что и - это мера, которая показывает, как колеблется актив относительно рыночного портфеля. График (5.8) показывает, что все рисковые активы с равной нулю имеют ожидаемую доходность такую же, как и безрисковый актив (если он существует). Таким образом, если есть безрискокый актив, все рисковые активы с равной нулю лежат на одной линии (приложение 5.8), которая графически показывает, что у таких активов ожидаемый доход, такой же, как и у безрискового. Кроме того, можно легко заменить ожидаемый доход от актива с равной нулю, Rz, на идентичный доход от безрискового актива в уравнении (5.8).
Если убрать безрисковый актив с графика, то едва ли что-нибудь изменится для портфелей лежащих на прямой β=0, в приложении 5.8. Все эти портфели, по-прежнему имеют ту же самую ожидаемую доходность и тоже самое , равное нулю, относительно рыночного портфеля. Кроме того, все остальные активы тоже сохранили свою ожидаемую доходность и туже , относительно рыночного портфеля. Следовательно, уравнение ожидаемого риска и доходности остается тем же самым за исключением того, что ожидаемая доходность от актива с равной нулю заменяет доходность от безрискового актива. Единственное, что изменилось в этой диаграмме, после того как убрали безрисковый актив, это то, что все точки левее от гиперболической границы, включая пунктирную линию, больше не доступны для инвестиций.
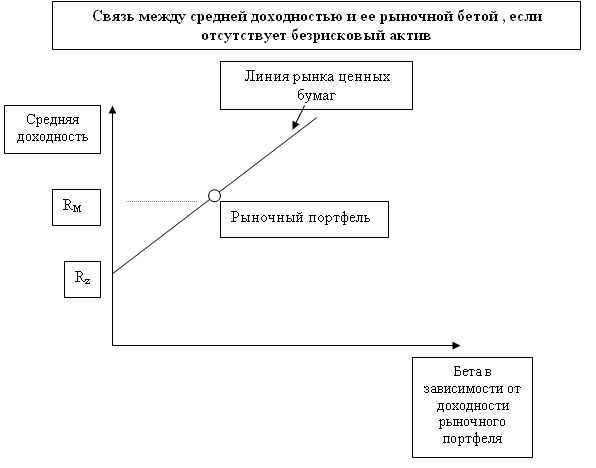
Приложение 5.9 показывает уравнение ожидаемого риска и доходности при отсутствии безрискового актива. Этот график идентичен тому, который был получен при условии существования безрисковоро актива за исключением того, что точка пересечения "линии рынка ценных бумаг" с Rz – это фактически ожидаемая доходность от актива с равной нулю, а не доходность от безрискового актива.
Модель, в которой отсутствует безрисковый актив, была разработана Блэком в 1972 году и называется модель нулевой (zero-beta model).
Приложение 5.8. Нахождение доходности в модели zero-beta
Приложение 5.9
Другие общие правила СAPM.
Несколько других предположений относительно CAPM тоже очень важны. Тот же самый результат ценообразования при нулевой влияет на все, приведенные выше, общие правила CAPM, несмотря на то, что во многих случаях нельзя использовать доходность от безрискового актива вместо доходности от актива с равной нулю.
Это включает в себя модель развитая Блэком, в которой длинные позиции (то есть, кредитование) допустимо для безрискоого актива, а продажа в короткую (т.е. безрисковый займ) нет. Бреннан в 1971 году представил модель, в которой ставка процента по безрисковым займам больше чем ставка процента по безрисковым кредитам. И так же есть модели, которые запрещают (в которых отсутствуют) продажи в короткую всех активов.
Модели оценки финансовых активов при равной нулю.
Все эти ограничения ведут к тому же ценообразующему результату, такому как уравнение (5.8) с rf замененным ожидаемой доходностью от портфеля с нулевой .
Однако, в этих моделях любой портфель, который включает безрисковый актив, уже не лежит на линии рынка ценных бумаг. Чтобы вычислять ожидаемую доходность прогнозируемую по CAPM для такого портфеля, его необходимо разделить на две части. Первая часть это ожидаемая отдача от чисто рисковой части портфеля полученной из CAPM (при нулевой ). А средняя взвешенная от этой ожидаемой доходности и доходности от безрискового актива – со взвешенной доходностью от безрискового актива, которая является весом безрискового актива - порождает вторую часть - ожидаемую отдачу от всего портфеля.
Многоэтапная модель оценки финансовых активов.
Другие расширения модели оценки финансовых активов влияют на торговлю на бирже в многопериодных условиях. В многорепиодной модели Мертонсона (1973 год), например торговля на бирже постоянно имеет место. В одном особом случае этой модели, уравнение ожидаемого риска и доходности для CAPM (уравнение 5.8) выглядит также, за исключением того, что все доходности и беты подсчитываются быстрее, чем, через конечный участок. В другом особом случае этой модели, средние и ковариации доходностей от активов определяются случайной переменной s (t), которая развивалась в течение долгого времени, и которая определяет выполнимый портфель в будущем. Здесь чувствительность отдачи актива от отдачи рыночного портфеля или , это не один фактор, определяющий ожидаемую доходность от актива в определенный момент времени. В дополнение, чувствительность доходности от портфеля который имеет максимальную корреляцию с s (t), также определяет ожидаемую доходность от актива.
5.10 Оценка , доходности от безрискового актива, премии за риск и рыночный портфель.
Чтобы применять зависимость ожидаемого риска и отдачи в модели оценки финансовых активов, необходимо оценить ее параметры. Такие как доходность от безрискового актива, , рыночная премия за риск и сам рыночный портфель.
Доходность от безрискового актива или доходность от актива с нулевой .
В большинстве академических исследований CAPM, использовалась доходность от краткосрочного Казначейского векселя, как заменитель отдачи от безрискового актива.
Однако, Блэк, Джансен и Шулес (1972), среди других, заметили, что этот показатель кажется слишком низким, таким же, как и доходность от актива с нулевой . Альтернативой является использование оценки ожидаемой доходности от актива с нулевой , которая получается из решения уравнения ожидаемого риска и доходности. Интересно, что ставка безрискового актива использовалась в смежных моделях с моделю оценки стоимости ценных бумаг, такой как межбанковские ставки процента предлогаемые в Лондоне (LIBOR), который является наиболее приближенным к нужному числу.
Оценка и сокращение .
Бета, как уже было сказано, является обозначением ковариации деленной на дисперсию, это соотношение является коэффициентом наклона регрессии. На практике нельзя получить точную , но легко можно получить ее оценку. Оценка данных за длительный период времени становится проще, если знать, что ковариация, деленная на дисперсию - это коэффициент наклона, который можно получить из уравнения линейной регрессии.
Левая переменная в регрессии это доходность от актива, по которому оценивается ; правая сторона представляет собой доходность от рыночного актива.
Много пакеты программ и калькуляторы имеют встроенные программы регрессии, которые используя данные определяют , как коэффициент наклона.
Улучшение , оцененной по регрессии.
Оценки имеют погрешности. Первая причина появления погрешности оценки, появляется просто по тому, что доходности ценных бумаг изменчивы, по этому, оценки, основанные на подобных доходностях неточны. Второй причиной появления погрешности является то, что изменения в цене одних ценных бумаг (обычно это ценные бумаги с малой капитализацией), отстают от изменений других, либо по причине того, что акции больше не участвуют в биржевых торгах, либо из-за просроченных лимитных ордеров, т.е. эти ордера были исполнены раньше того, как инвестор скорректировал их, относительно новой появившейся информации о ценных бумагах. (Лимитный ордер – приказ брокеру купить ценные бумаги по цене не выше указанной в приказе или продать по цене, не ниже указанной).
Чтобы понять важность погрешности оценки, рассмотрим случай, где прошлогодние отдачи были использованы, чтобы оценить четырех очень похожих фирм, обозначенных, как A, B, C и D. Полученные : A=1,4; B=0,8; C=0,6 и D=1,2. Так как это оцененные , они имеют погрешность в оценке. Истинные значения , вероятно, не разбросаны так сильно, как данные. Учитывая эти оценки, видно, что актив фирмы А имеет самую высокую и актив С самую низкую. Наше предположение, что актива А переоценена, а актива С недооценена.