Автореферат диссертации на соискание ученой степени кандидата
| Вид материала | Автореферат диссертации |
| В четвертой главе «Методика построения зависимостей «структура – функциональные свойства» В пятой главе «Исследование топологических индексов связанности на примере фрагментов ряда полимеров» |
- Акинфиев Сергей Николаевич автореферат диссертации, 1335.17kb.
- L. в экосистемах баренцева моря >03. 02. 04 зоология 03. 02. 08 экология Автореферат, 302.63kb.
- Автореферат диссертации на соискание ученой степени, 331.91kb.
- Автореферат диссертации на соискание ученой степени, 378.33kb.
- Автореферат диссертации на соискание ученой степени кандидата, 1242.08kb.
- Автореферат диссертации на соискание ученой степени кандидата искусствоведения, 484.62kb.
- Автореферат диссертации на соискание учёной степени, 846.35kb.
- «Тобольская государственная социально-педагогическая академия им. Д. И. Менделеева», 345.4kb.
- Эволюция лирического героя в поэзии м. Турсун -заде, 1088.86kb.
- Автореферат диссертации на соискание ученой степени кандидата политических наук, 643.82kb.
В четвертой главе «Методика построения зависимостей «структура – функциональные свойства» обсуждается алгоритм исследования взаимосвязи «структура-свойство» в теоретико-графовом подходе, который основан на предположении, что структура молекулы может быть представлена в виде графа и точно охарактеризована с помощью некоторых численных параметров (инвариантов графа). В математической химии инварианты молекулярных графов называются топологическими индексами. Эти топологические индексы могут быть скоррелированны с экспериментально найденными свойствами молекул.
Рассматривается история развития теоретико-графового подхода, а именно, использование топологических индексов, которая начинается с 70-80-х годов. В этот период появилось много работ, посвященных использованию теории графов в установлении корреляций между структурой соединения и его свойством. В основу разработки теоретико-графового описания молекул легли работы авторов: У. Платт, Н. Винер, М. Рандич. В работе обсуждаются проблемы, связанные с конструированием и дизайном топологических индексов, с проблемами мотивированного выбора топологических индексов. Отдельным вопросом является проблема инверсии (реконструировании) молекулярных графов из топологических индексов.
Как показывает обзор последних публикаций, топологические индексы достаточно широко применяются в исследовании взаимосвязи «структура – свойство» как самостоятельно, так и в комбинации с другими молекулярными дескрипторами. К числу достоинств топологических индексов относится простота и быстрота их вычисления, а также использование их при оценке свойств гипотетических структур, для которых нет никаких экспериментальных данных.
Теоретико-графовый подход включает в себя несколько принципиальных условий.
Важнейшим из них является выбор объектов исследования. Обучающая выборка должна включать объекты с известной структурой и свойствами. С точки зрения статистики число рассматриваемых соединений должно превышать число используемых топологических индексов.
При топологическом описании структурная формула соединения представляется в виде взвешенного графа G, вершинам которого соответствуют атомы, а ребрам - химические связи. При этом обычно рассматривают только скелетные атомы и связи между ними. Номенклатура теории графов не стандартизирована: вершины могут называться точками и узлами, а ребра – линиями, дугами и ветвями. Две вершины соединенные одним ребром, или два ребра, имеющие общую вершину, называются смежными. Степень вершины ri равна числу ребер, исходящих из нее, и непосредственно связана с валентностью i – того атома. Валентность химических элементов накладывает на степени вершин определенные ограничения.
Граф может быть представлен в матричном виде. Наиболее часто применяется матрица смежности А и матрица расстояния D. Элементы матрицы смежности aij равны или 1 или 0 в зависимости от того, связана ли ребром вершина i-графа G с вершиной j или не связана. При этом число единиц в i– й строке или j – м столбце матрицы равно степени вершины. Например: для графа, изображенного на рис.11 матрица выглядит следующим образом:
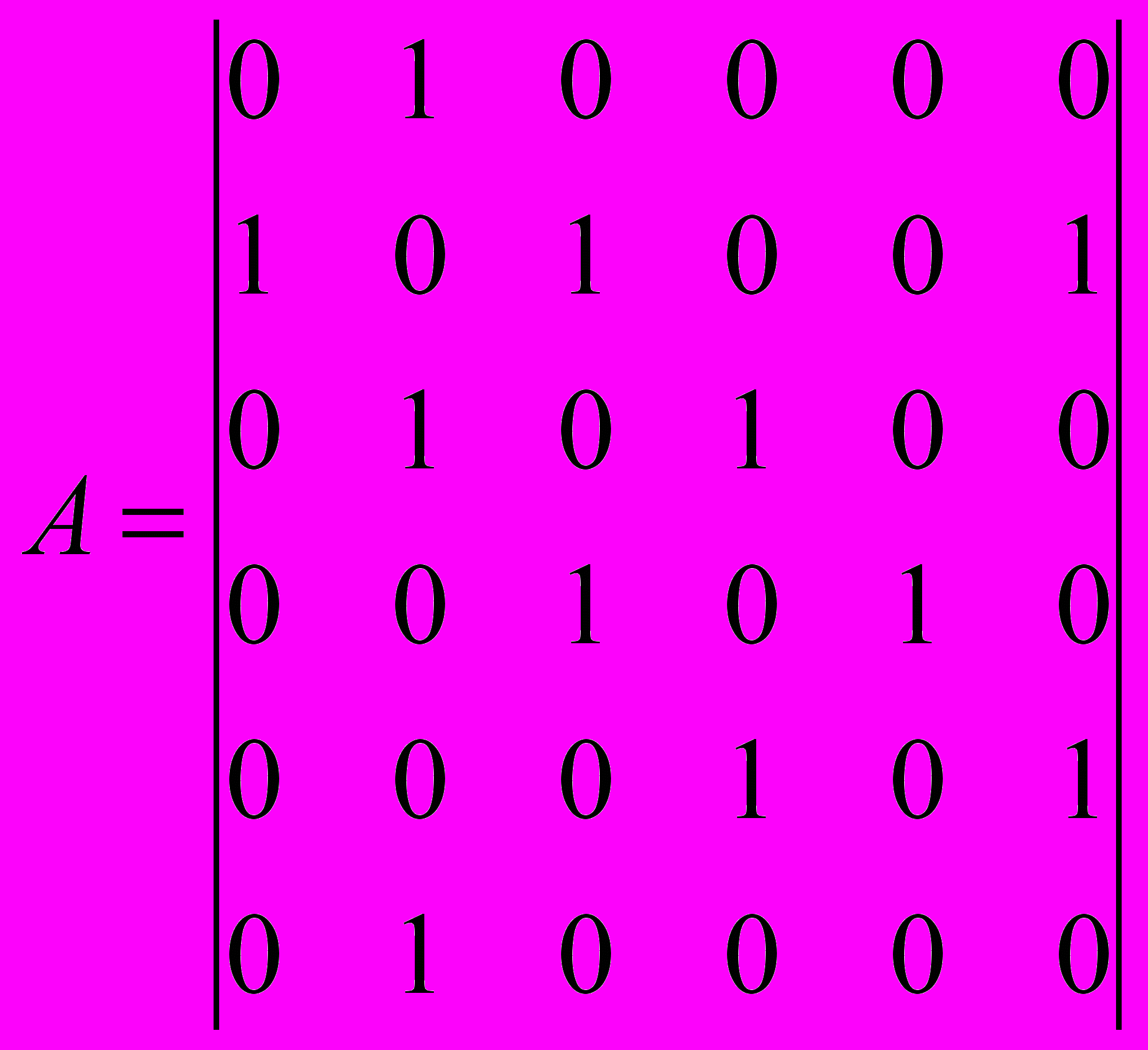
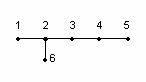
Рис.11. Молекулярный граф.
Топологические индексы – это инварианты графа, определяемые по его матрицам и не зависящие от способа нумерации вершин или ребер графа. Существуют разные схемы вычисления топологических индексов по данной матрице. В работе рассматриваются различные схемы построения топологических индексов.
Еще одной важной особенностью теоретико-графового описания молекул является выбор топологических индексов. В работе обсуждаются проблемы такого выбора. Как правило, при выборе топологического индекса необходимо учитывать две важные характеристики:
- дискриминирующая способность (способность однозначно описывать структуру);
- корреляционные зависимости.
Точность полученных моделей в теоретико-графовом подходе можно оценить с помощью статистических характеристик – коэффициента корреляции, стандартного отклонения, среднего отклонения, максимального отклонения и др. В QSPR/QSAR чаще всего используют две первых характеристики – коэффициент корреляции r (или r2) и стандартное отклонение S.
В пятой главе «Исследование топологических индексов связанности на примере фрагментов ряда полимеров» обсуждаются алгоритмы расчета топологических индексов связанности (по методу Бицерано) для отдельных молекул, виниловых полимеров, биополимеров.
Виниловые полимеры использовались в работе в качестве модельных систем, т.к. по составу и структуре они близки к биополимерам. На модельных фрагментах полимеров отрабатывался модифицированный метод Бицерано.
Семейство виниловых полимеров получают полимеризацией некоторых замещенных соединений ряда этилена. Замещенным является только один из атомов водорода на другой атом или группу атомов, например, таких, как ацетатная группа в случае винилацетата. Ацетатная группа служит своего рода внутренним пластификатором. Замещение приводит в целом к повышению физико-механических свойств полимеров.
В широком смысле термин “виниловые полимеры” включает в себя и такие материалы, как полистирол. Но чаще термин применяют к поливинилхлориду, его сополимерам с винилацетатом, сополимерам винилиденхлорида и винилхлорида. Поливинилацетат также является обычным виниловым полимером, но его используют только в дисперсной форме как клей или как основу для некоторых эмульсионных красок.
Одним из методов расчета свойств различных молекул, а также полимеров является топологический метод, разработанный Бицерано, который основан на использовании некоторых упрощений, связанных с введением индексов связанности. Индексы связанности широко распространены и применяемы для простых молекул. Индексы связанности строятся исходя из следующих начальных условий:
- количество атомов в структуре;
- число атомов водорода, связанных с рассматриваемым атомом;
- число валентных электронов атома.
Первые два индекса (δ, δV) описывают электронную среду и конфигурацию связей в каждом не водородном атоме. Значение данных индексов для некоторых атомов представлено в таблице1:
Таблица 1 : Рассчитанные δ, δV для атомов С, N, O, F
| Атом | Hyb | NH | δ | δV |
| C | sp3 sp2 sp | 3 2 1 0 2 1 0 1 0 | 1 2 3 4 1 2 3 1 2 | 1 2 3 4 2 3 4 3 4 |
| N | sp3 sp2 sp | 2 1 0 1 0 0 | 1 2 3 1 2 1 | 3 4 5 4 5 5 |
| O | sp3 sp2 | 1 0 0 | 1 2 1 | 5 6 6 |
| F | -- | 0 | 1 | 7 |
Первый атомный индекс δ - простой соединительный индекс. Он равен числу не водородных атомов, которые определяются числом не водородных связей.
Второй атомный индекс – валентный соединительный индекс δV. Его значения рассчитываются по формуле:
 , где , где | (1) |
ZV – число валентных электронов атома;
NH – число водородных атомов, связанных с ним;
Z=Zv+ N, где N - число электронов на внутреннем электронном уровне.
Такие атомы как C, N, O и F имеют только два электронных уровня. Следовательно, для них δV рассчитывается по этой формуле, где в знаменателе будет находиться выражение: ( Z=ZV-1)=[(ZV+2)-ZV-1]=1. Исключение составляет атом азота в нитрогруппе (-NO2), который будет иметь значение δV равное 6.
Другой парой индексов являются индексы связей, которые обозначаются β и βV. Они рассчитываются для каждой связи, кроме связей с атомами водорода. Тогда формулы для их нахождения выглядят следующим образом:
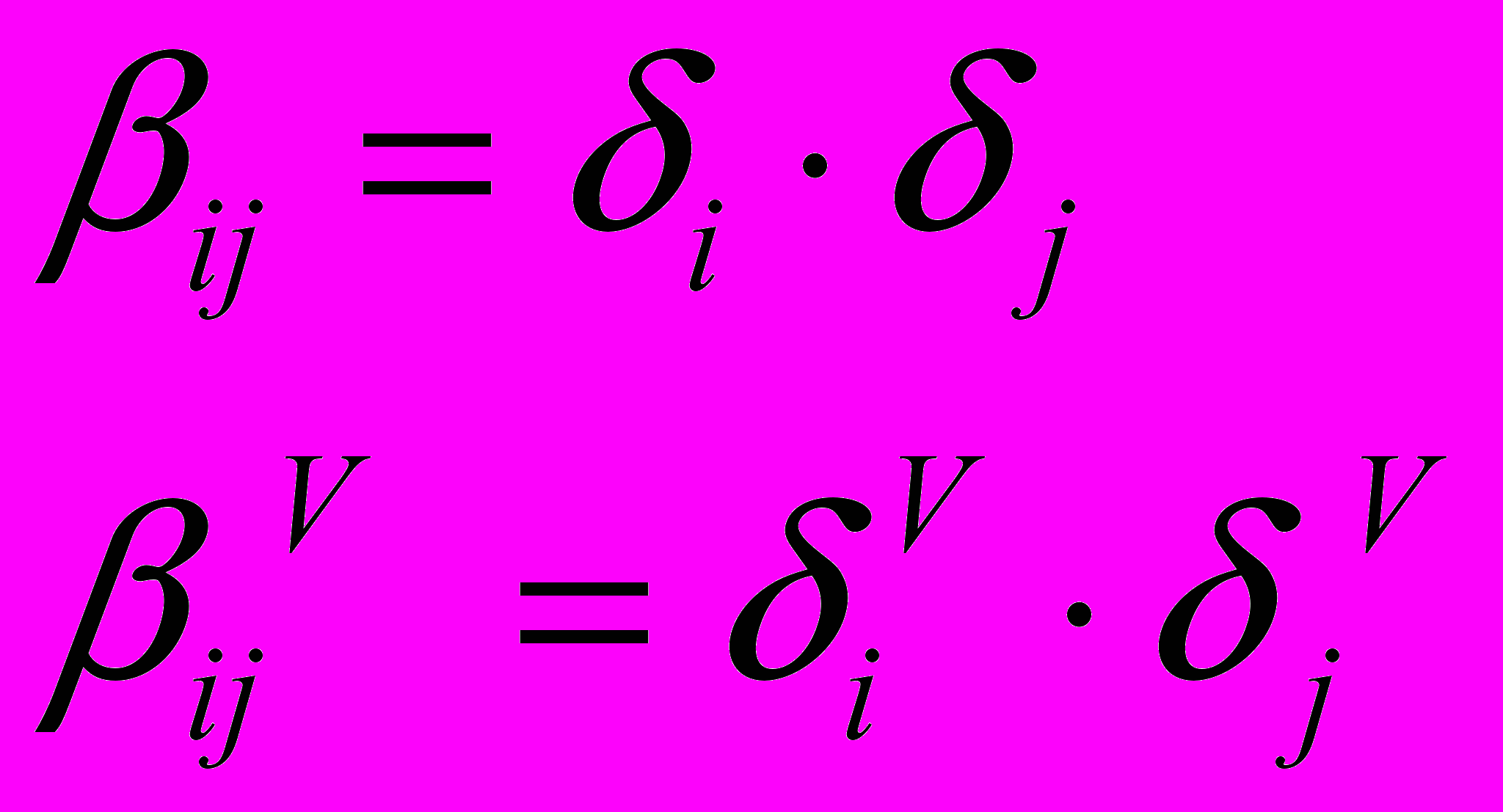 | (2) |
Следующая пара индексов называется индексами атомарной связанности молекулы нулевого порядка, которые обозначаются как 0χ, 0χV. Данные индексы рассчитываются по формулам:
 | (3) |
Следующей парой индексов являются индексы первого порядка 1χ, 1χV, которые рассчитываются по формулам:
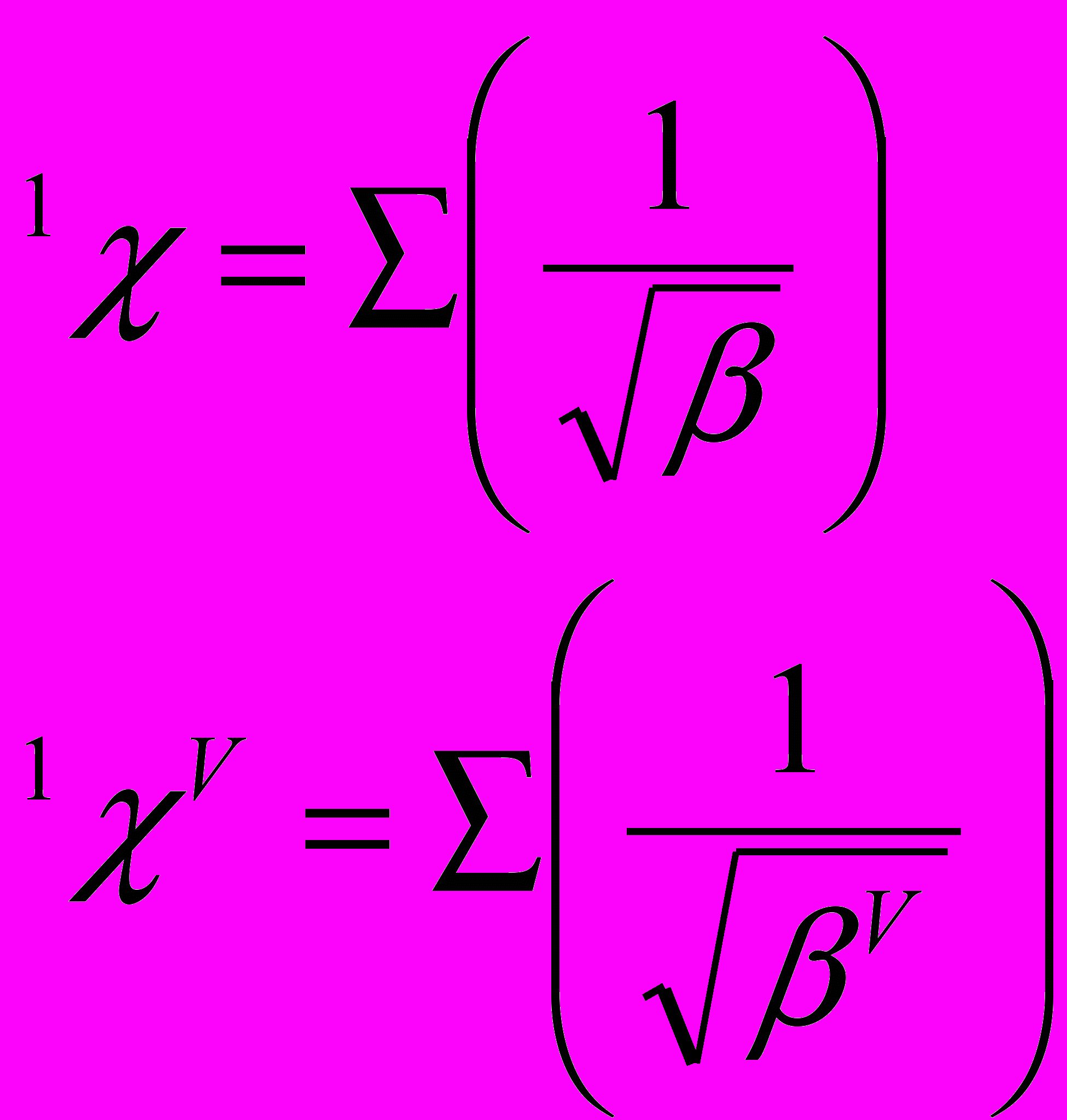 | (4) |
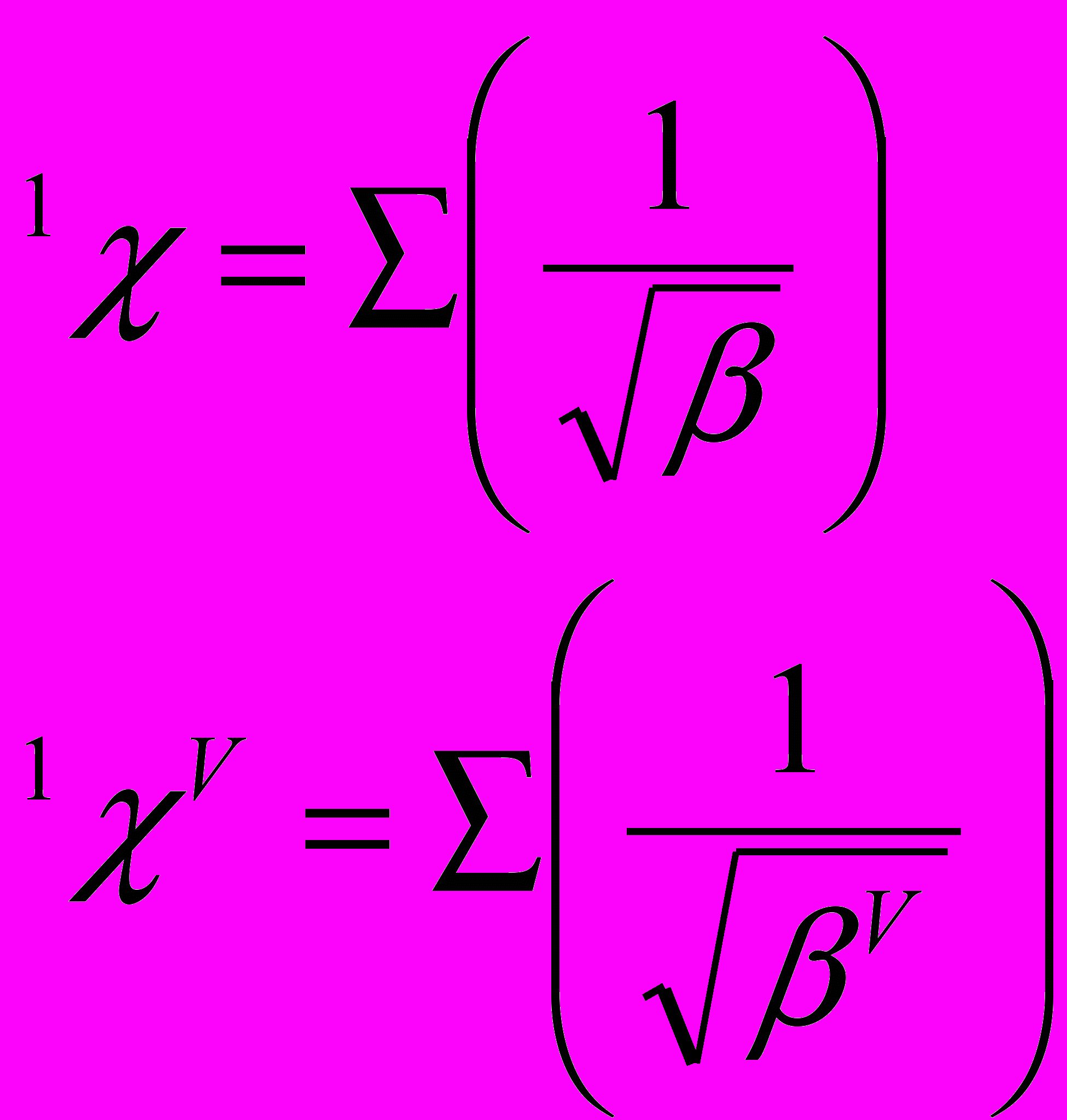 | (5) |
В качестве примера ниже приведены схемы расчета индексов первого и второго порядков для монофторэтилена.
 2 2 1 2 2 1 1 2 1 2(а) | 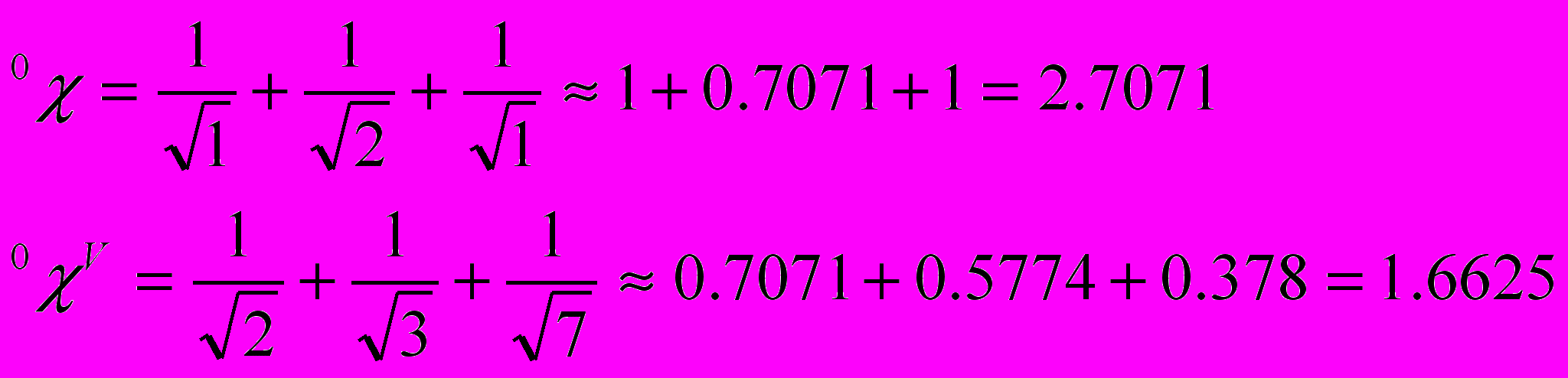 |
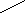 6 21 7 6 21 7 2 3 2 3 (б) |  |
Рис.12. Пример расчета 1, 1V для монофторэтилена.
Под пунктом (а) приведена структура графа монофторэтилена, где цифрами указаны значения индексов δ, β. Под пунктом (б) – значения индексов δV, βV. Величины δ и δV были взяты из таблицы 1, а значения индексов β и βV определяются по формулам (1).
Как правило, для расчёта основных физико-химических свойств достаточно корреляционных уравнений первой степени (линейная регрессия). Серьёзная практическая задача - определение числовых коэффициентов для этих корреляций.
При использовании топологических индексов связанности необходимо учитывать следующие условия:
- дискриминирующая способность;
- стандартное отклонение.
Дискриминирующая способность топологических индексов связанности определяется электронной структурой атома, т.е. количеством валентных электронов, числом энергетических уровней, количеством связей с водородом, общим числом электронов.
Для расчета свойств полимеров по методу Бицерано используются топологические индексы связанности нескольких порядков, 0χ, 0χV, 1, 1V. На графиках (рис.12) показана дискриминирующая способность топологических индексов и стандартное отклонение:
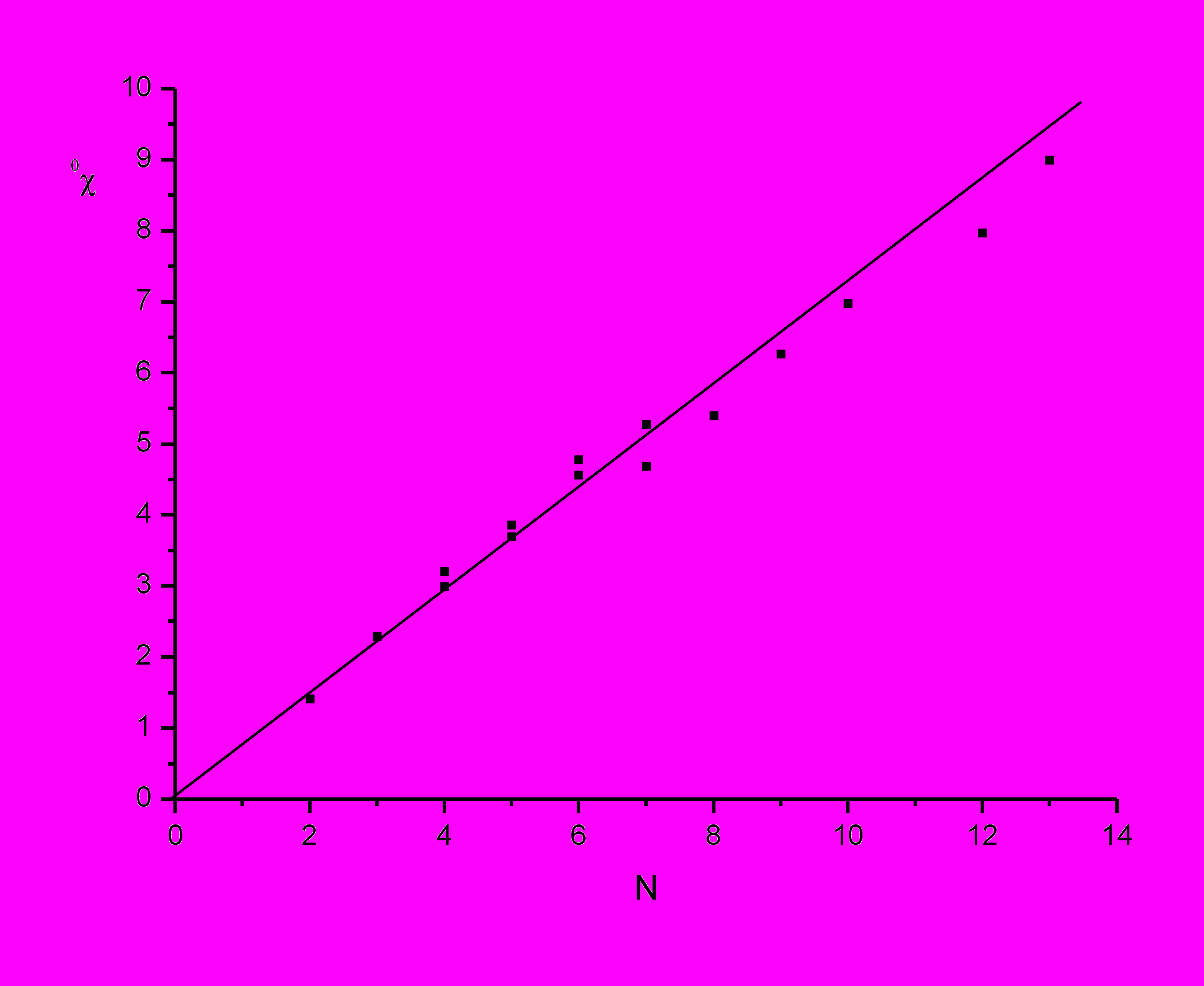
а
б

Рис. 13. Корреляционные зависимости N (число вершин графа) и индексов 0χ, 0χV. Стандартное отклонение: а – 5,9%, б – 15,5%
Дискриминирующая способность 0χ определяется общим числом электронов, а 0χV количеством валентных электронов, числом энергетических уровней в атоме, количеством связей с водородом. В первом случае дискриминирующая способность 0χ хуже, чем у 0χV, однако стандартное отклонение у 0χ лучше. Соответственно, можно сделать вывод о том, что чем больше параметров входит в описание топологических индексов, тем лучше их дискриминирующая способность, но стандартное отклонение становится больше. Однако такая картина наблюдается для полимеров с простым радикалом, например, винилхлорид (рис.13). Для полимеров со сложным строением дискриминирующая способность ухудшается. В связи с этим в методе Бицерано вводится новый индекс, дискриминирующая способность которого определяется общим числом электронов, количеством валентных электронов, числом энергетических уровней в атоме, количеством связей с водородом, т.е. возрастает порядок индекса. В итоге получается зависимость:
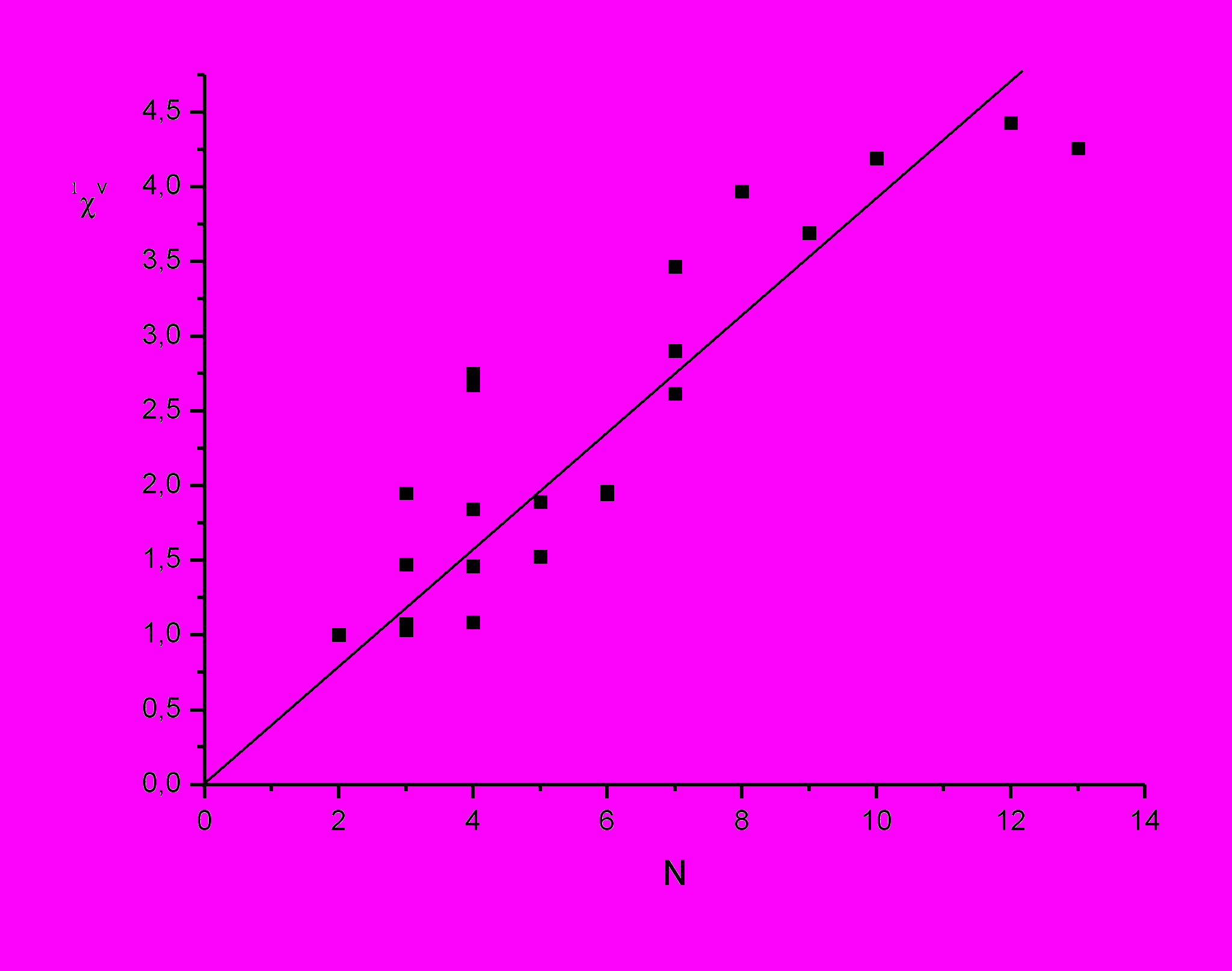
Рис. 14. Корреляция топологического индекса 1V с N, стандартное отклонение 24,4%.
Из графика видно, что дискриминирующая способность индекса 1V возрастает, как и возрастает стандартное отклонение.
Для расчета физико-химических свойств по методу Бицерано используются индексы связанности 0-го и 1-го порядков. Данные индексы однозначно описывают структуру соединения тогда, когда радикал состоит из одного или нескольких атомов. Если же радикал обладает более разветвленной структурой, то для её описания необходимо рассчитывать индексы связанности более высоких порядков.
В настоящей работе предполагается следующая модификация метода Бицерано для расчета свойств полимеров со сложным строением (Таблица 2).
Таблица 2. Схема расчета индексов связанности второго порядка.
 | 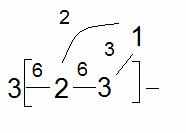 |
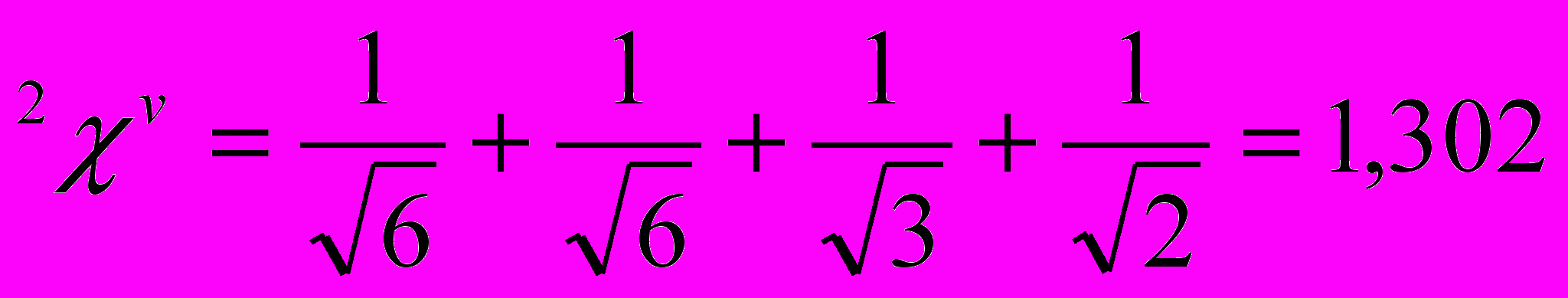 | |
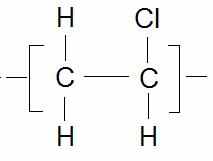 | 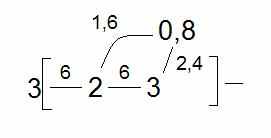 |
 | |
 | 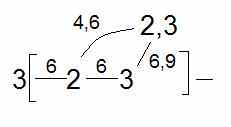 |
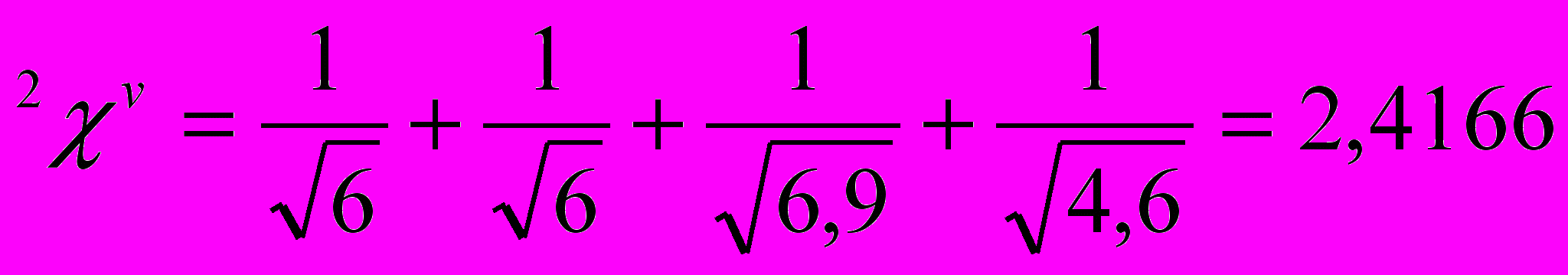 | |
Таблица 3. Индексы связанности различных порядков.
| полимер | 0χ | 0χV | 1 | 1V | 2V |
| поливинилфторид | 2,2845 | 1,6624 | 1,3938 | 1,0347 | 1,3021 |
| поливинихлорид | 2,2845 | 2,4183 | 1,3938 | 1,4711 | 2,2524 |
| поливинилбромид | 2,2845 | 3,2484 | 1,3938 | 1,9504 | 2,6633 |
| поливиниловый спирт | 2,2845 | 1,7317 | 1,3938 | 1,0747 | 1,3911 |
| поливинилиденфторид | 3,2071 | 1,9630 | 1,7071 | 1,0851 | 0,5153 |
| поливинилиденхлорид | 3,2071 | 3,4749 | 1,7071 | 1,8410 | 0,7319 |
| поливинилиденбромид | 3,2071 | 5,1350 | 1,7071 | 2,6711 | 1,2903 |
Таким образом, индексы связанности более высоких порядков более полно описывают соединение, имеют высокую дискриминирующую способность.
Было выявлено, что топологические индексы атомов, входящих в состав полимера коррелируют не только с ковалентными радиусами атомов, но и с электроотрицательностью атомов, молярной энергией когезии.
Таблица 4. Корреляции индексов связанности 1V, 2V с ковалентными радиусами атомов.
| |  |  |  |
| 1V | 1,0347 | 1,4711 | 1,9504 |
| 2V | 1,3021 | 2,2524 | 2,6633 |
| RA | 0,72 | 0,98 | 1,14 |
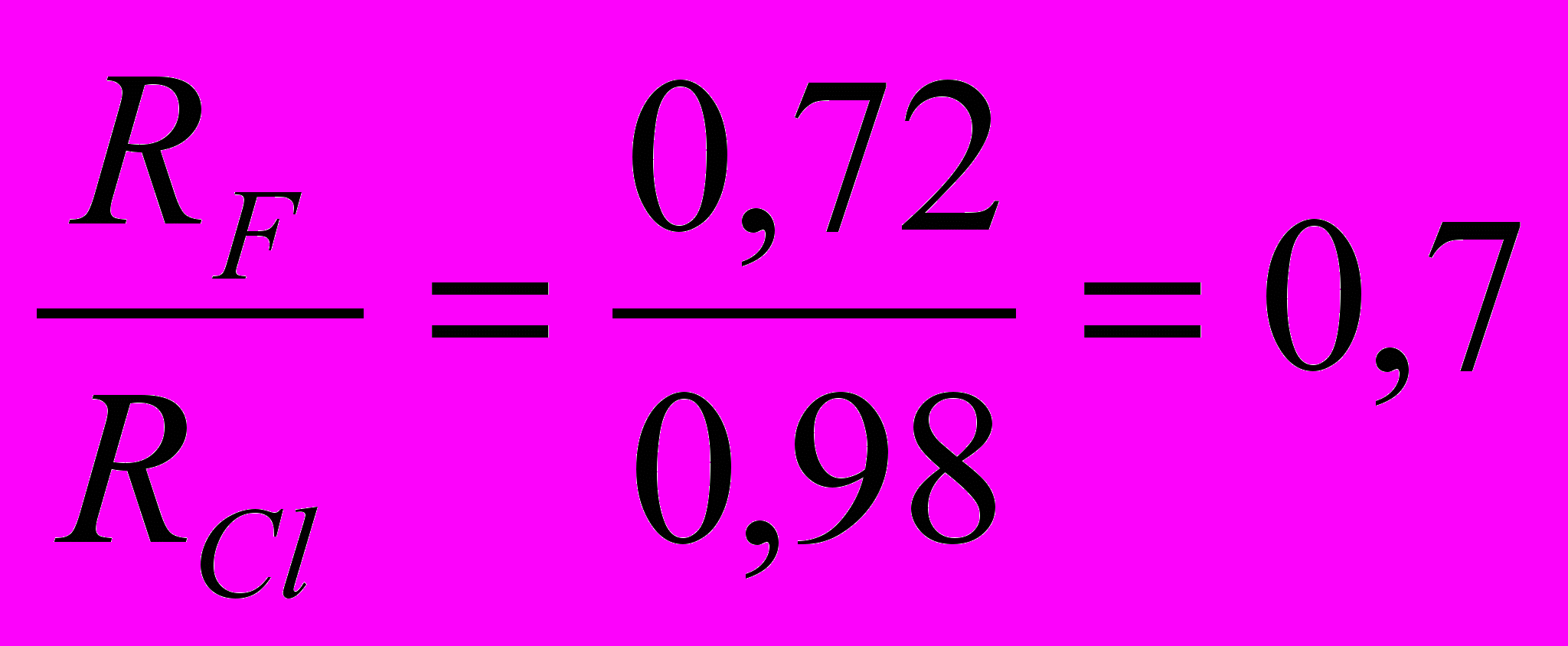
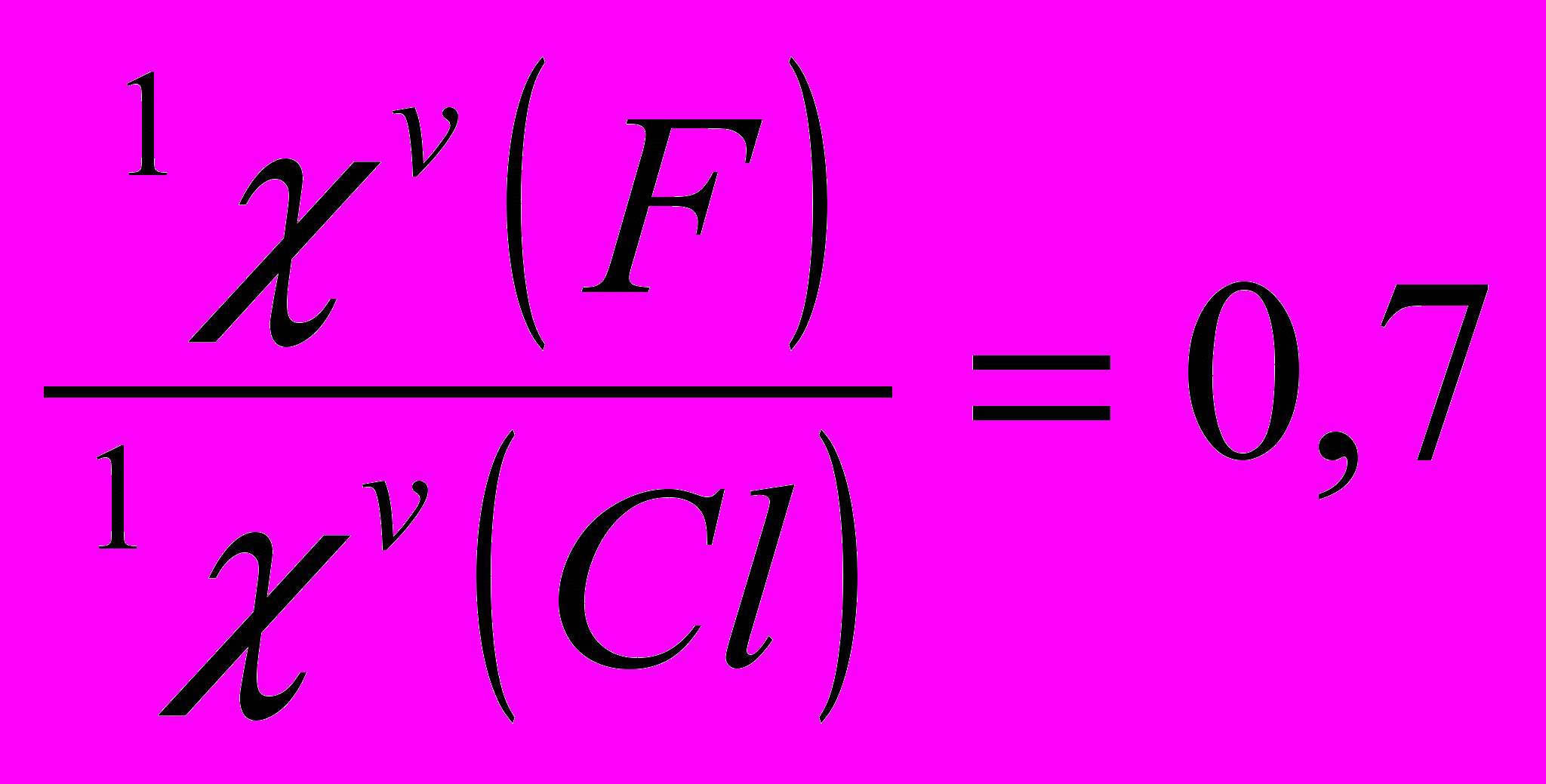
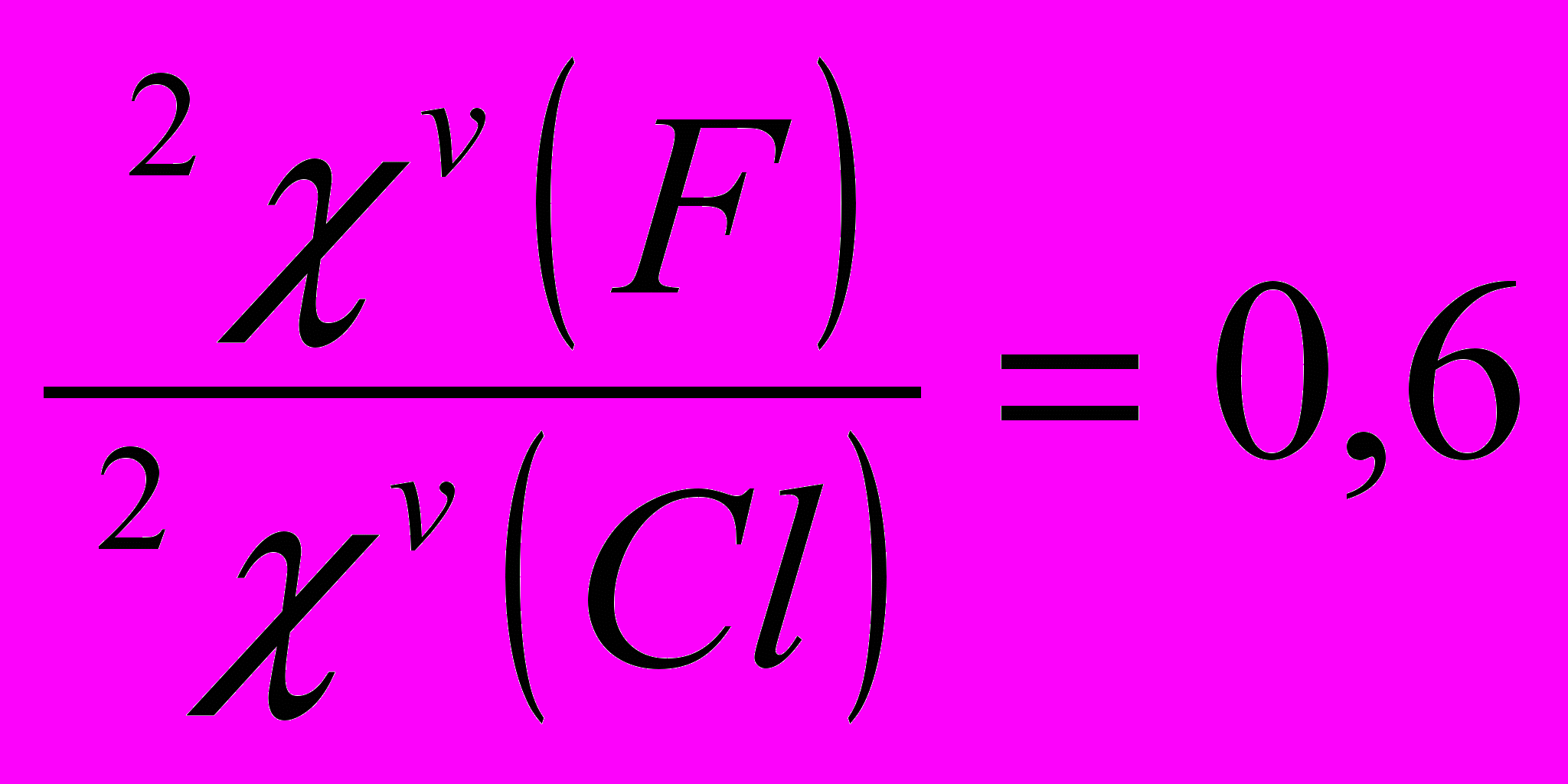
Данная зависимость характерна для всех полимеров винилового ряда.
