Методические указания к курсовому проектированию по учебной дисциплине

Вид материала

Методические указания

Содержание 2.4. Проектная часть 2.4.2. Разработка модели решения задачи. Рассмотрим основные этапы построения модели 2.4.4. Выбор экономико-математического аппарата, используемого для решения данной задачи.

Подобный материал:

• Методические указания к курсовому проектированию по учебной дисциплине «инновационный, 378.33kb.
• Методические указания к курсовому проектированию по учебной дисциплине «Управленческие, 1355.04kb.
• Методические указания по курсовому проектированию по дисциплине «страхование» для студентов, 1442.66kb.
• Методические указания по курсовому проектированию по дисциплине «страхование» для студентов, 1282.26kb.
• Методические указания к курсовому проектированию по дисциплине "антикризисное управление", 137.98kb.
• Методические указания к курсовому проектированию по дисциплине «экономика организации», 560.98kb.
• М. А. Бонч-Бруевича Методические указания к курсовому проектированию предварительных, 789.79kb.
• Методические указания к курсовому проектированию по дисциплине «Прикладное программирование», 474.71kb.
• Методические указания к курсовому проектированию по дисциплине: «Организация эвм, комплексов, 486.74kb.
• Методические указания введение Методические указания к курсовому проектированию разрабо­таны, 401.72kb.

2.4. ПРОЕКТНАЯ ЧАСТЬ

В этой части курсового проекта разрабатывается управленческое решение по той конкретной задаче, которая была выбрана в аналитической части проекта.

Прежде всего, должна быть четко сформулирована решаемая задача, например:

• разработать модель решения задачи формирования производственной программы вновь созданного механо-сборочного цеха;
  
• выбрать оптимальный вариант капиталовложений в реконструкцию организации;
  
• разработать эффективную модель оценки профес­сиональной пригодности персонала организации для включения работников во временные трудовые коллективы, работающие над созданием крупных инновационных (инвестиционных) проектов;
  
• построить график освоения производства нового изделия;
  
• минимизировать время разработки проекта освоения новой технологии сборки изделия;
  
• сформировать оптимальный график выполнения НИОКР в НИИ «Полет» и т.п.
  

От правильности фор­мулировки задачи зависит эффективность разработанного управленческого решения.

Далее по сформулированной задаче необходимо выполнить следующие процедуры:

1. Раскрыть ее организационно-экономическую сущность.
   
2. Разработать модель ее решения.
   
3. Построить дерево решений - альтернативных вариантов реализации модели на его основе выбрать наиболее предпочтительный для организации вариант, руководствуясь методикой, изложенной в научно-методической части данных «Методических указаний…».^*
   
4. Разработать алгоритм решения задачи на базе пунктов 2 и 3.
   

Рассмотрим подробнее состав и содержание каждой из процедур, перечисленных выше.

2.4.1. Организационно-экономическая сущность задачи. Организационно-экономическая сущность задачи включает:

1) формулирование цели решения задачи – определение конечного результата реализации управленческого решения, принимаемого по данной задаче. Например, для задачи разработки графика освоения производства нового изделия целью будет построение такого графика, который обеспечит минимальный цикл освоения нового изделия за счет оптимальной очередности обработки в производстве деталей и узлов изделия, или (и) при максимальной загрузке оборудования, или (и) при минимальном уровне оборотных заделов и т.п.

2) определение объекта (круга объектов), для которого решается задача (разрабатывается данное управленческое решение).


_____________________

^* Примечание: если методы решения поставленной конкретной задачи были выбраны в научно-методической части КП, то в проектной части эта работа не выполняется.


Например:

• собственное производство - для задачи разработки графика освоения производства нового изделия;
  
• профессиональные качества работника организации – для задачи разработки эффективной модели оценки профессиональной пригодности персонала организации и т.п.
  

3) определение места этой задачи в системе управления организацией, которое можно характеризовать либо с помощью схемы, отражающей организационно-экономические связи (функциональные, информационные, методические и др.), либо в текстовом изложении;

4) определение круга объектов, для которых предназначены результаты разрабатываемого управ­ленческого решения;

5) определение особенностей решения задачи: тип решаемой задачи – вариантная оптимизационная или прямого счета, одно- или многокритериальная; частота решения задачи; ограничительные, дополнительные условия и т.п. При этом следует иметь в виду, что чем более подробно и всесторонне характеризованы особенности решаемой задачи, тем легче будет построить модель и выбрать необходимый для ее решения инструментарий (используемые методы, приемы, процедуры и т.п.);

6) общая характеристика методов, методик или их элементов, используемых для разработки управленческого решения по данной задаче. В случае, когда сравнительный анализ и выбор методов решения задачи был уже сделан в научно-методической части, то в организационно-экономической следует только упомянуть особенности выбранных методов решения, чтобы в полной мере это учесть при разработке управленческого решения; в противном случае в этом пункте организационно-экономической сущности задачи должна быть выполнена сравнительная оценка методов в полном объеме;

7) характеристика или описание информационного обеспечения - входной и выходной информации. При этом особое внимание следует уделить описанию способов организа­ции сбора, передачи, накопления и обработки данных, проверке их достоверности, форм представления и используемых коммуникаций;

8) временные ограничения на разработку управленческого решения и выдачу выход­ных данных;

9) организация разработки управленческого решения: управленческое решение может разрабатываться как одним лицом, принимающим решение (ЛПР), так и целым коллективом. Существенное значение при проработке этого элемента имеет описание разделения работ по отдельным исполнителям, в частности, подготовка исходных данных, выработка альтернативных вариантов решения, условия приня­тия управленческого решения, построение модели, разработка алгоритма и т.п.

Качественное описание организационно-экономической сущности задачи играет важную роль в разработке управленческого решения. В качестве аргументации этого положения рассмотрим следующий пример. Необходимо решить две задачи:

1. проанализировать использование рабочего времени персоналом организации;
   

2) определить величину потерь рабочего времени персонала.

Отметим, что объект анализа в обоих случаях один - табели отработанного времени, служебные записки и т.д. Однако ме­тоды и цели анализа различны, а, следовательно, будут различны и результаты. Небрежность описания организационно-экономической сущности решаемой задачи может привести к разработке неверного управленческого решения, реализация которого может обусловить существенные потери.


2.4.2. Разработка модели решения задачи.

Построение экономико-математической модели, не зависимо от класса решаемой задачи, является обязательным в курсовом проекте по учебной дисциплине «Управленческие решения». Класс решаемой задачи будет оказывать влияние только на состав элементов модели и их взаимосвязи.

При разработке управленческого решения, прежде всего, необходимо определить, к какому классу относится решаемая задача: прямого счета, вариантная, оптимизационная. Если задача оптимизационная, необходимо установить, нужен выход на чистый математический оптимум или достаточно получить допустимое решение. Следует также иметь в виду, что для решения ряда задач в арсенале математического программирования и другого специального инструментария уже есть готовые модели. Поэтому нет необходимости разрабатывать новую модель, нужно выбрать наиболее подходящую и адаптировать ее к своей задаче. Например, решение задач, связанных с разработкой оптимальных графиков НИОКР; с разработкой производственных программ для вновь созданных производственных подразделений на определенные периоды времени, при этом программы формируются по критерию максимизации (минимизации) заданного показателя – объема выполняемых работ, количества (стоимости) выпускаемой продукции, величины издержек, используемых материальных ресурсов, численности персонала, затрат на подготовку и переподготовку кадров и т.п.

Пусть требуется максимизировать (минимизировать) функцию

F (x)  max (min)

F (x)  (a₁*x₁ + a₂*x₂ + …+a_i*x_i +… + a_n*x_n)  max (min),


где a₁, a₂, …, a_n – удельные призначные характеристики (показатели)

i – х элементов, формирующих величину функции (П_i).

Представим исходную функцию в следующем общем виде:




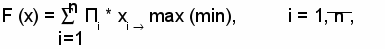
где П_i – призначная характеристика i –ой номенклатурной позиции (элемента);

х_i – искомая переменная величина (количество) i –ой позиции.

Такая запись представляет собой критериальную функцию решения задачи. Ограничительными условиями могут выступать имеющиеся ресурсы (трудовые, материальные, финансовые и другие), а также ограничения на величину самой функции



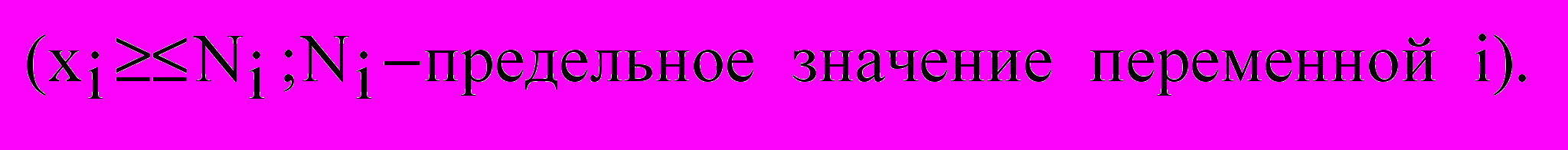
В общем виде ограничения могут быть записаны следующим образом:




При решении задачи переменные х_i не должны быть отрицательными: х_i ≥ 0.

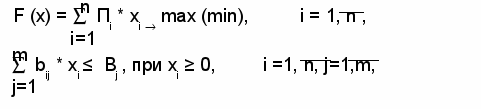Совокупность критериальной функции и ограничительных условий позволяет использовать классическую модель линейного программирования:


х_i ≥ 0



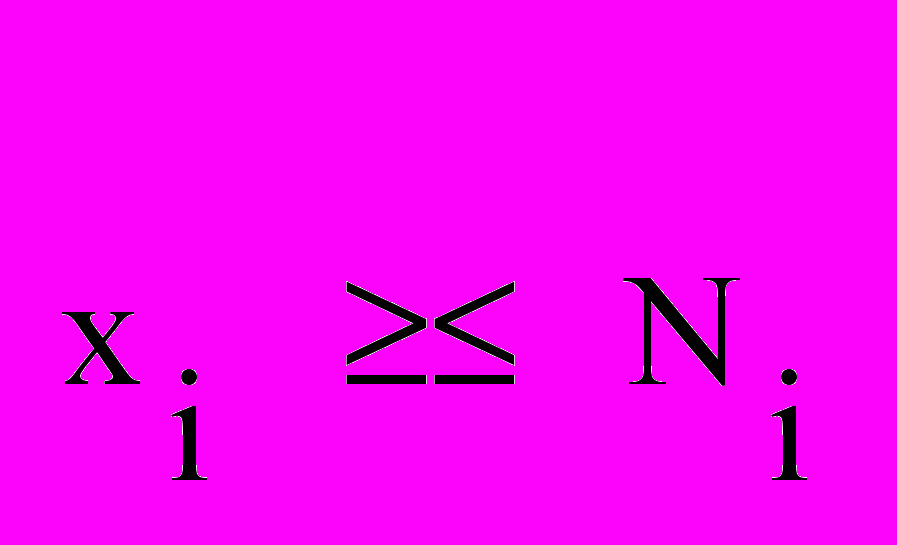
х_i – искомая переменная величина (количество) i –ой позиции;


b_ij – удельная величина j-го ограничения по i-ой переменной (позиции);

B_j – суммарная величина j-го ограничения;







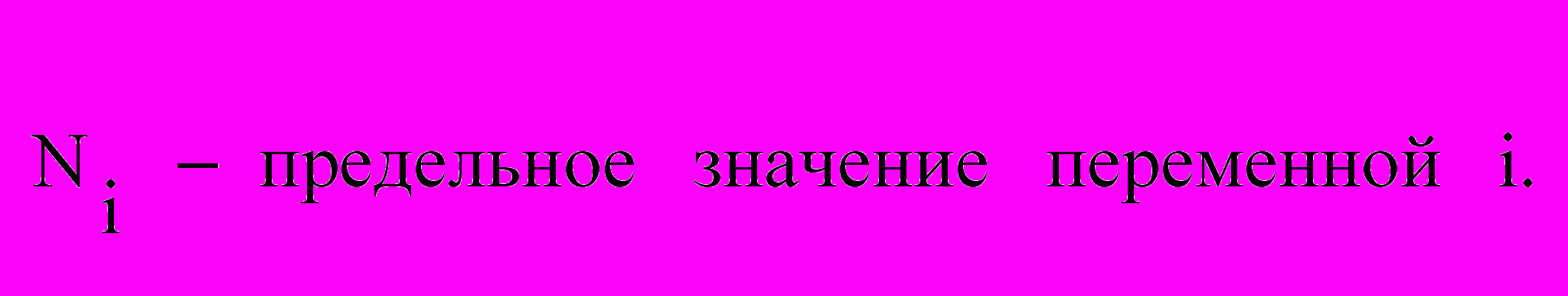
Таким образом, рассматриваемая ситуация вписывается в уже известные модели, и проектанту (студенту) нет необходимости самостоятельно разрабатывать такого рода модель.

Рассмотрим следующую ситуацию: выбрать претендента (кандидатуру) на включение в состав временного трудового коллектива для разработки крупного инновационного проекта, который бы в наибольшей степени соответствовал требованиям, предъявляемым организацией к претенденту. Готовой модели для решения этой задачи нет, поэтому студент вынужден самостоятельно ее разрабатывать.

Рассмотрим основные этапы построения модели.

1 этап. Формулирование решаемой задачи.

2 этап. Определение объекта моделирования. В качестве такого объекта может выступать процесс работы над инновационным проектом, претендент (кандидат) на включение в коллектив, выполняемая научно-исследовательская работа, формируемый график выпуска продукции, поиск вариантов сокращения транспортного маршрута для снижения величины транспортных расходов и т.п.

3 этап. Выявление элементов моделируемого объекта и их характеристика.

4 этап. Отбор из числа этих элементов наиболее существенных для решения данной конкретной задачи.

5 этап. Формирование набора показателей, характеризующих каждый из выбранных в пункте 4 элементов объекта.

6 этап. Описание в общем виде объекта моделирования с позиции решаемой задачи.

Этот этап можно реализовать в два приёма:

1) с помощью математических символов в неявном виде описываются взаимосвязи и взаимозависимости выбранных элементов объекта, то есть формируется набор показателей x₁, x₂,…,x_n (где x₁, x₂,…,x_n — показатели, характеризующие наиболее существенные элементы объекта), затем следует представить расчетные формулы этих показателей. Источником получения формул может быть прежде всего специальная литература. Если готовых формул найти не удается, то проектант может вывести их самостоятельно, комбинируя информацию из литературных источников, применяя специальные приемы и методы математической статистики, теории вероятностей и т.д., а также используя свои знания и навыки в области моделирования.

2) С учетом постановки задачи описать объект моделирования, увязав указанные выше показатели с помощью выявленных расчётных формул.

2.4.3. Реализация этапов построения модели.

Исходя из рассмотренной выше ситуации, сформулируем решаемую задачу: необходимо выбрать для включения во временный трудовой коллектив претендента – кандидата, у которого показатель его пригодности минимально отклонялся бы от заданного уровня. Показатель пригодности может характеризовать соответствие претендента 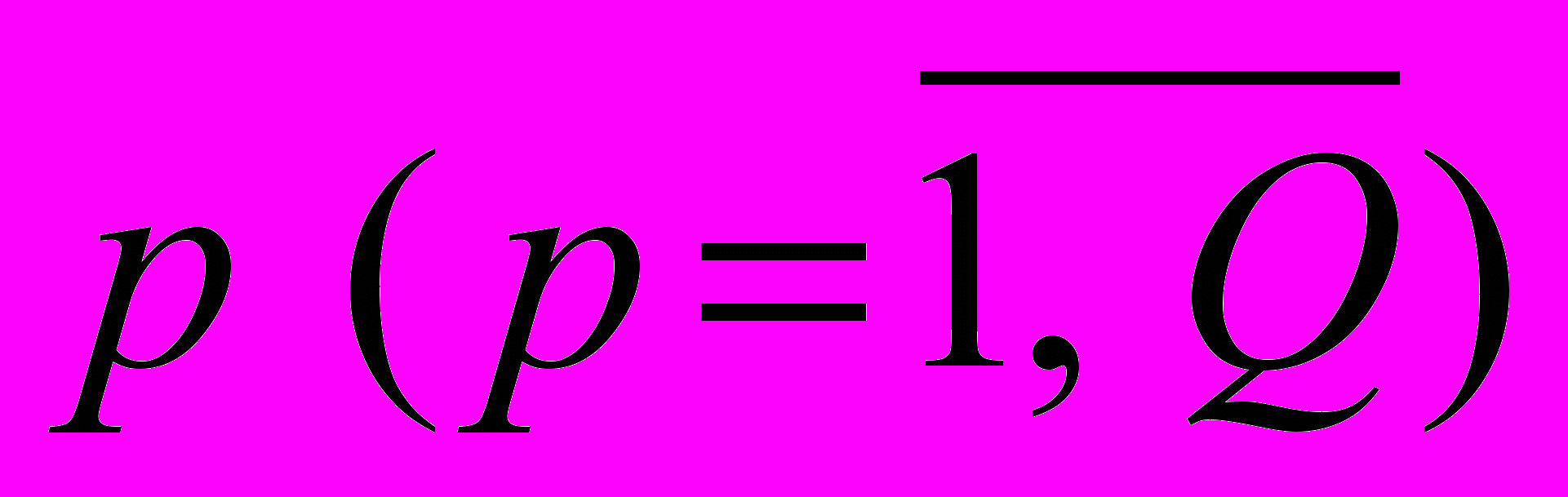требованиям организации, касающимся уровня его образования, практического опыта работы, коммуникабельности, восприятия инноваций и т.п., то есть его соответствие системе признаков 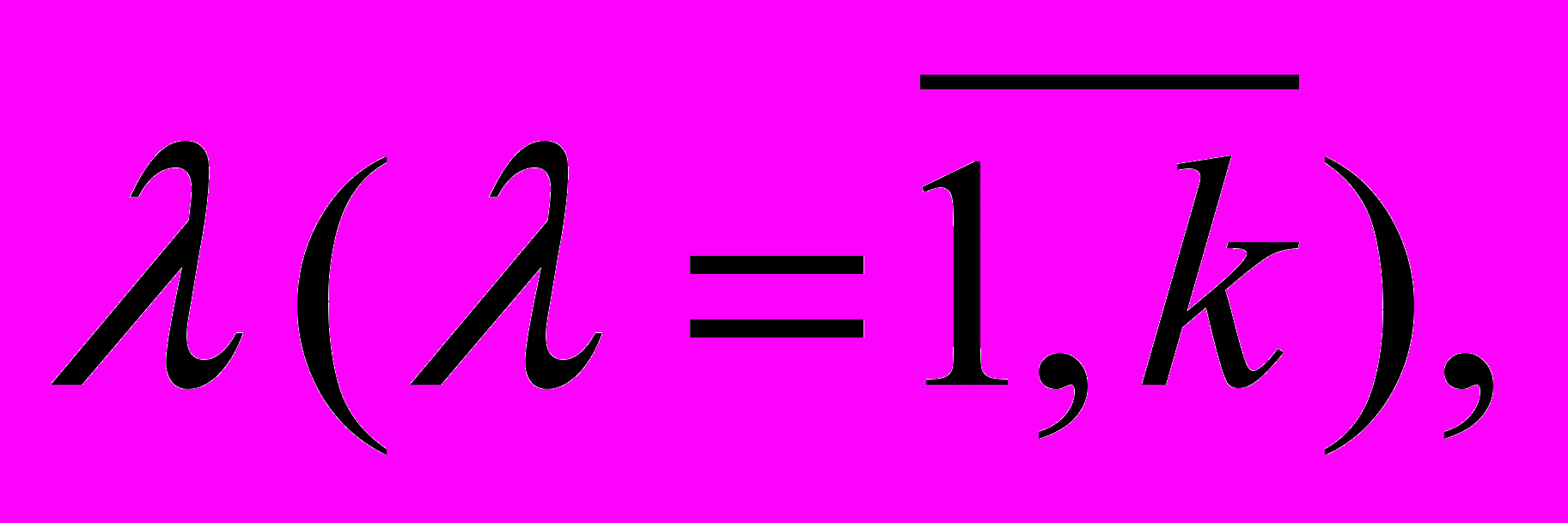которыми, по мнению организации – работодателя, должен обладать претендент на j – ю вакантную должность (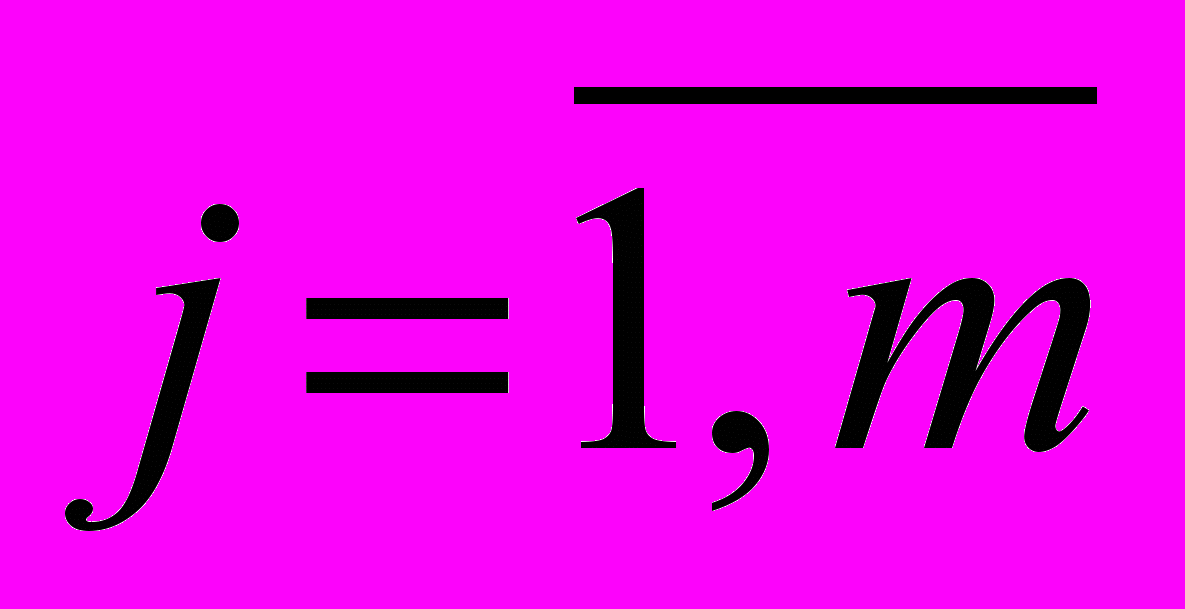). Примером таких признаков могут быть, например, возраст, образование, стаж работы, семейное положение и т.п. Каждый признак λ имеет широкий спектр характеризующих его величин (показателей), например, стаж работы от 0 до 45 лет, возраст, от 18 до 80 лет и т.п. Претендент на вакантную должность может обладать каким-либо одним из этих значений, не обладая другими, т.е. иметь возраст, например, или 20 лет, или 40, или 63 года и т.п. Следовательно, организация – работодатель, исходя из своей заинтересованности в наличии у претендента 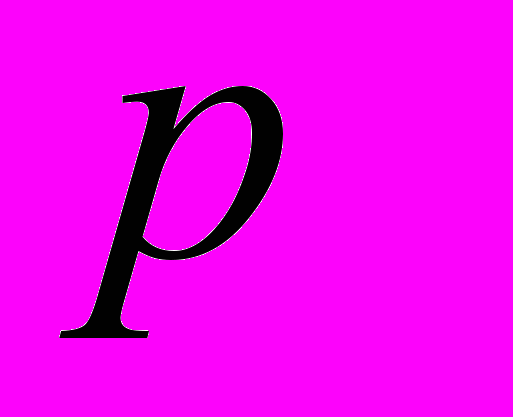на вакантную должность j тех или иных значений показателей – признаков (показателей – характеристик), устанавливает определённые границы (интервалы) значений этих признаков: 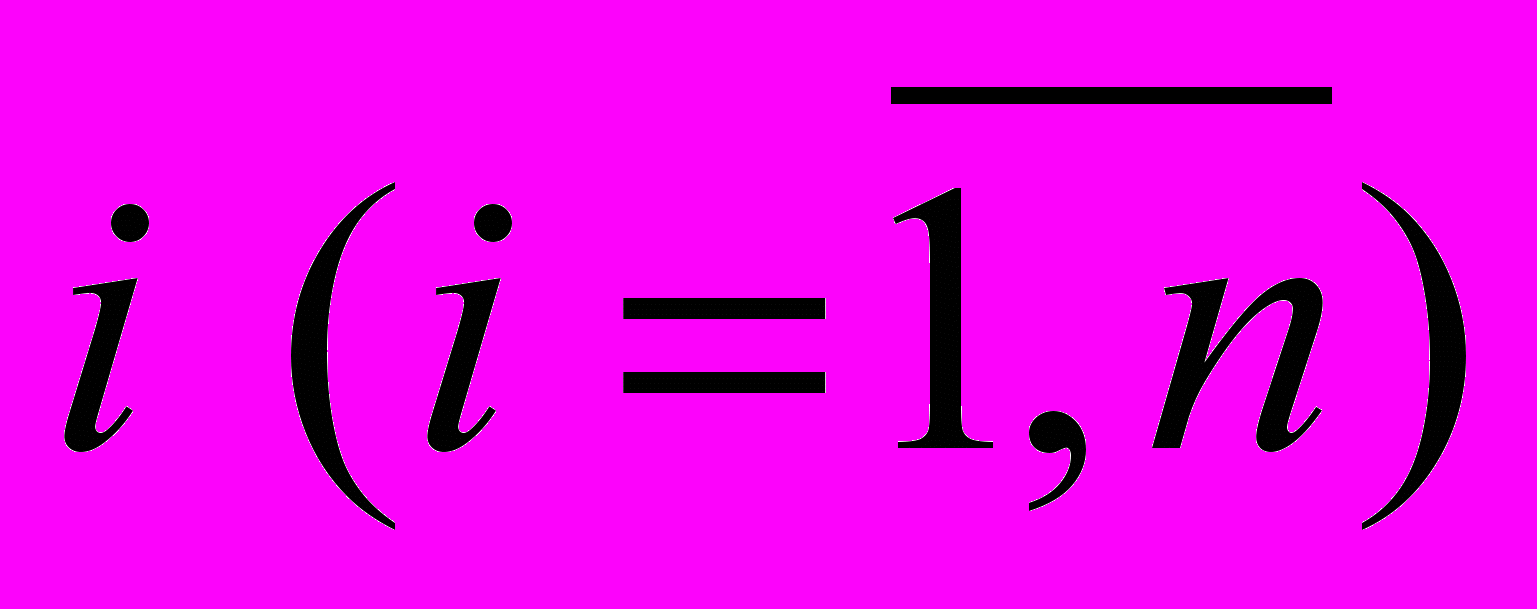. Каждому из этих интервалов присваиваются конкретные величины показателей – характеристик в привязке к конкретной вакансии - Наиболее предпочтительной величине таких показателей – характеристик по 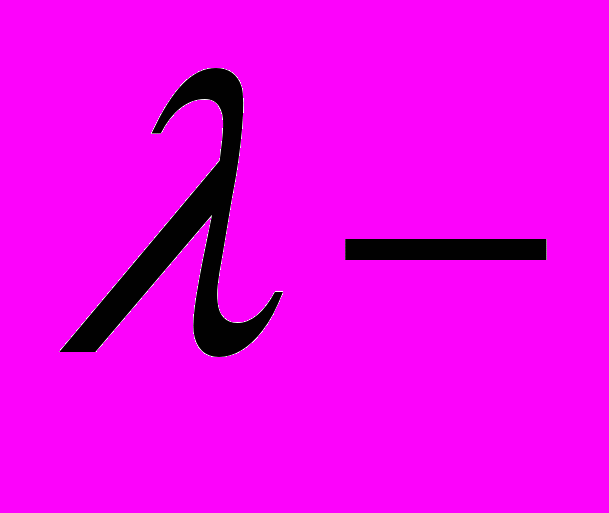му признаку 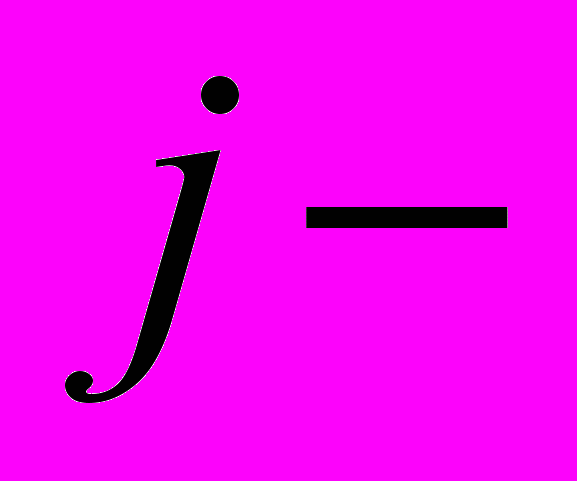ой вакансии дается статус нормативной – .

З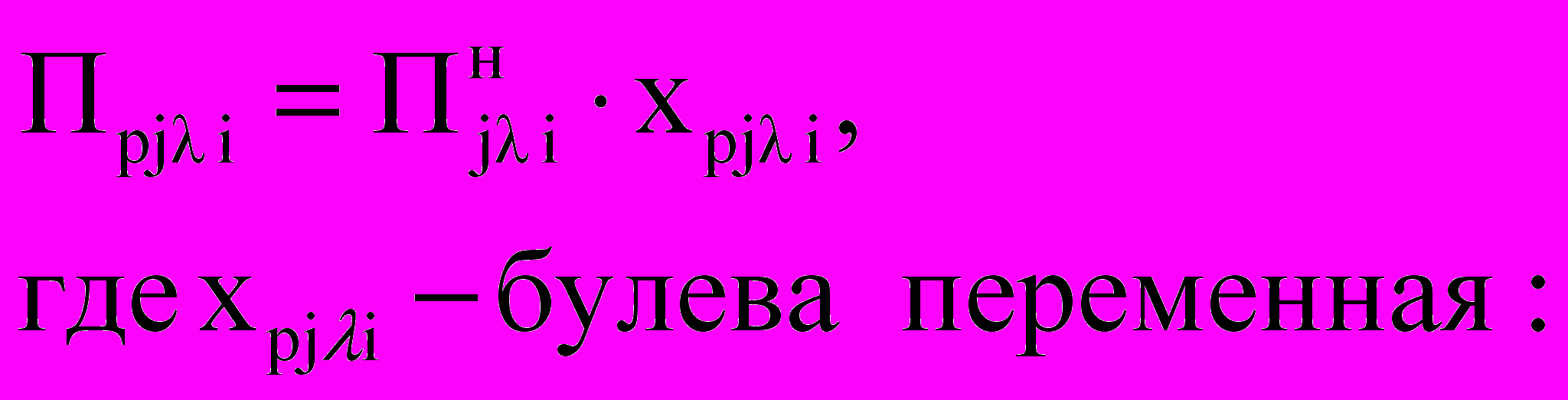начение признака, которое может быть у претендента, определяется следующим образом:





Величина всегда будет неотрицательной: .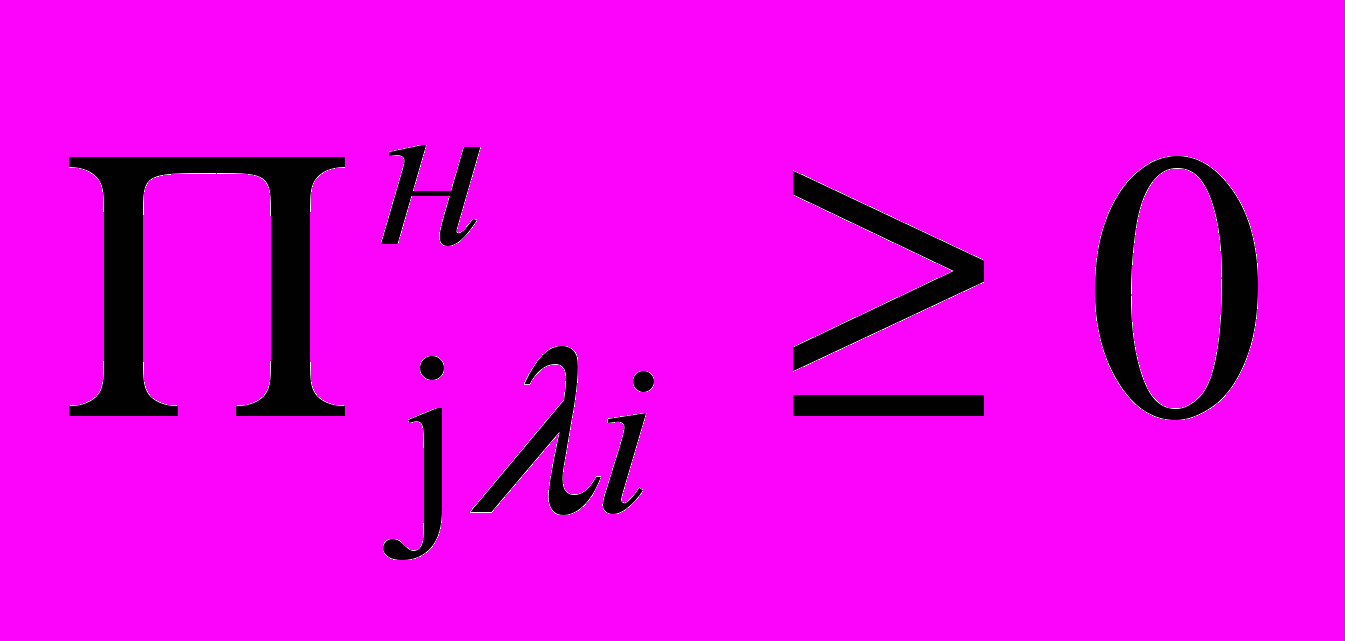


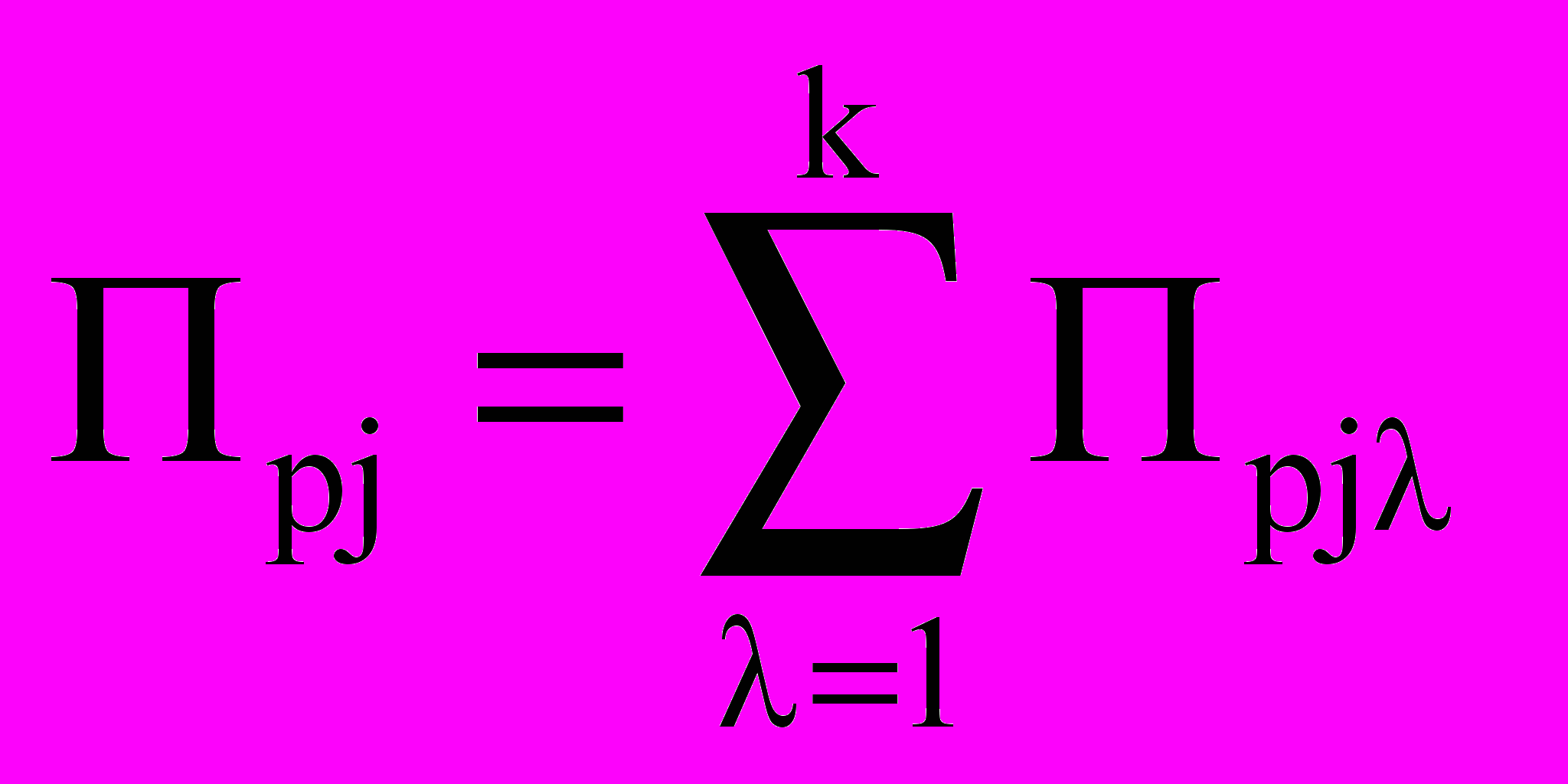Сумма всех значений показателей признаков (λ) р-го претендента на j-ю вакантную должность


Условием отбора р–го претендента, выбранного на 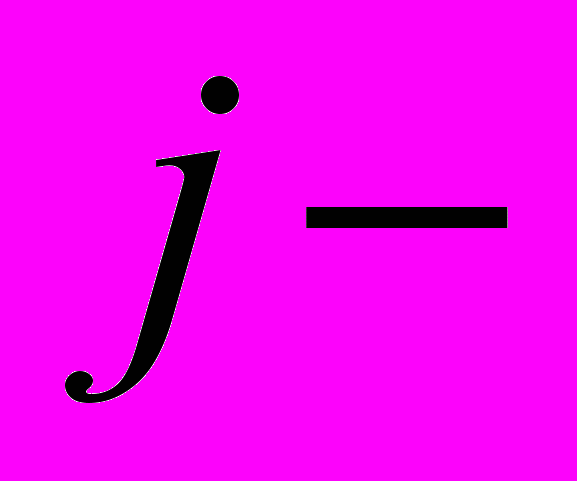ую вакантную должность, может быть одно из заданных условий:

1. наиболее высокая среди всех претендентов суммарная (итоговая) оценка по всем признакам λ:
   

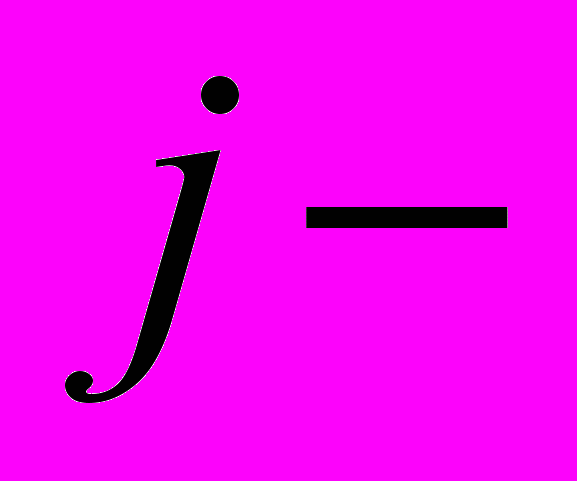где - суммарная оценка р-го претендента, выбранного на ую вакантную должность;

2. минимальное отклонение суммарной оценки у выбранного р-го претендента () от заданного организацией – работодателем по j-ой вакансии (). Организация-работодатель хотела бы, чтобы р-й претендент на j-ю должность обладал определённым i-ым уровнем значения -го признака. Это значение можно характеризовать как критическое – . Тогда в формализованном виде это условие отбора претендента на вакантную должность можно представить следующим образом:
   

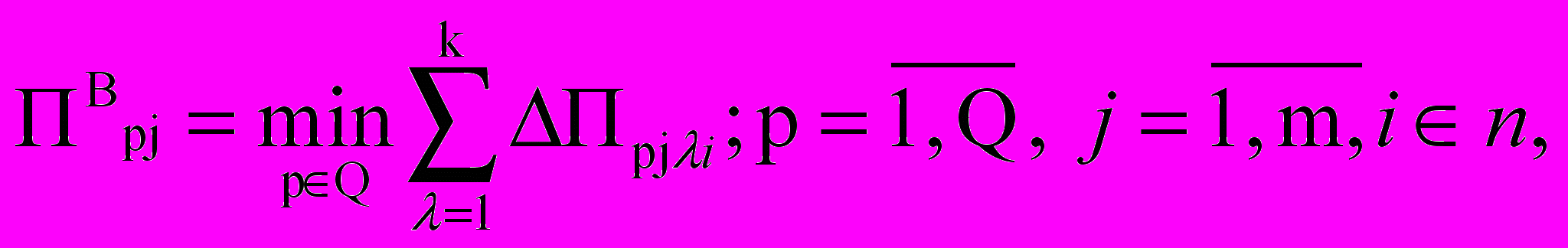
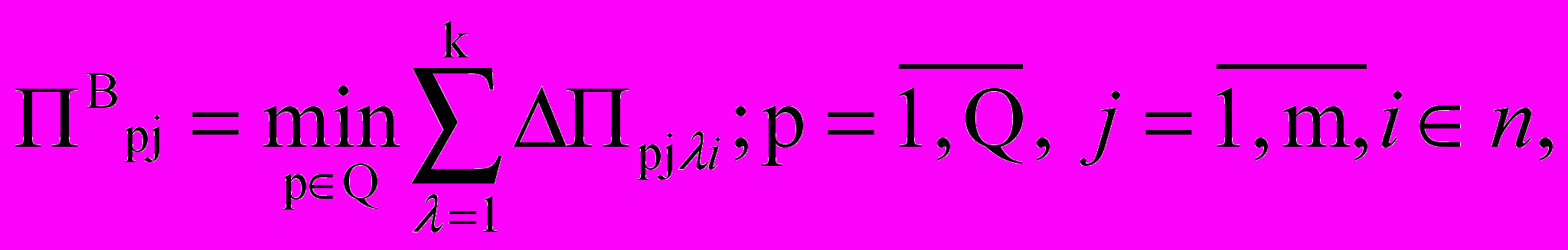
г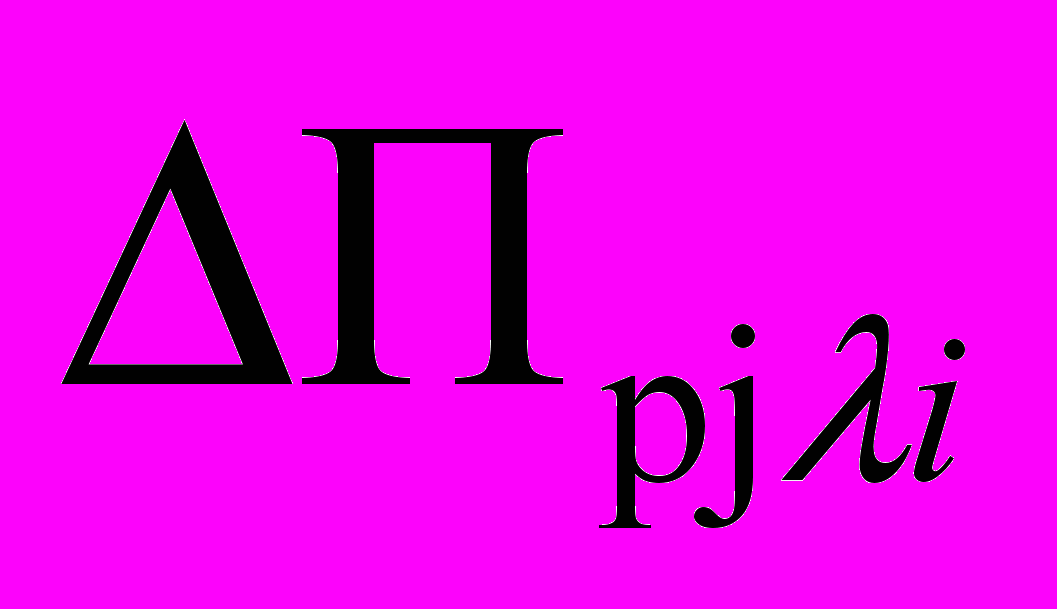де - отклонение значения -го признака по р-му претенденту


от критического значения.

Отклонение суммарной оценки, характеризующей р-го претендента (П_рj) можно рассчитать и следующим образом: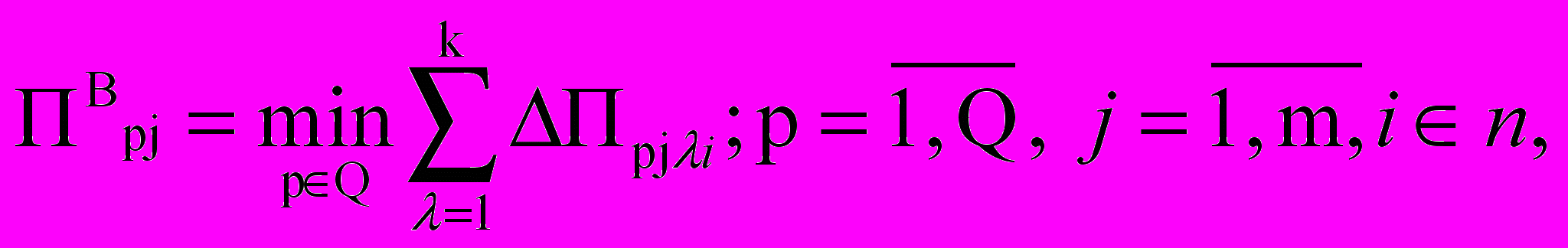





Претенденты, имеющие значения этих признаков соответственно выше или ниже критических, не устраивают организацию – работодателя. Тогда -й показатель – характеристика р-го претендента на j-ю должность должен отвечать определенным ограничениям:







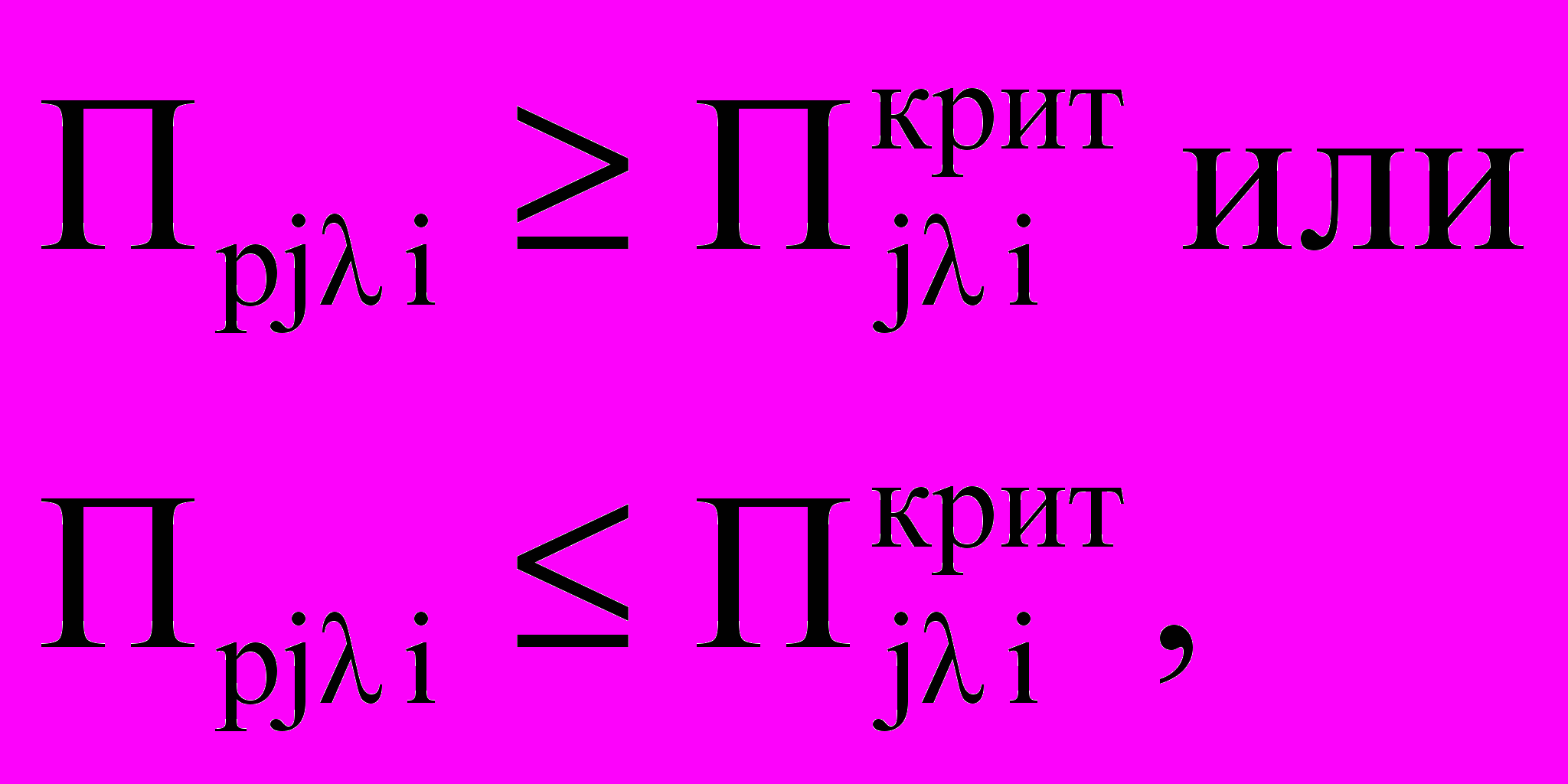
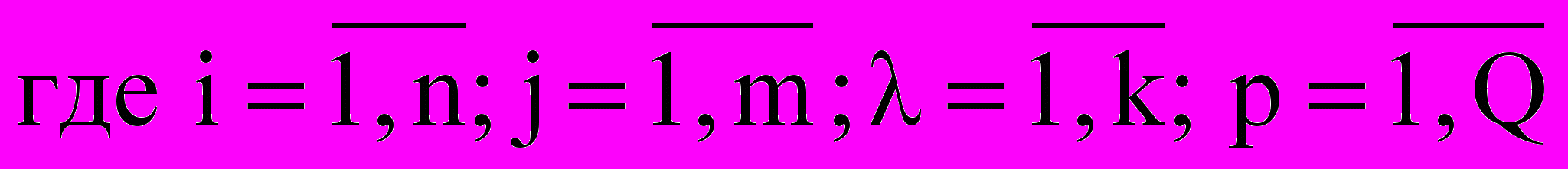
Таким образом, выполнены 1-5 этапы подготовки к построению модели. Далее можем сформировать модель по второму условию выбора претендента:

Критериальная функция:



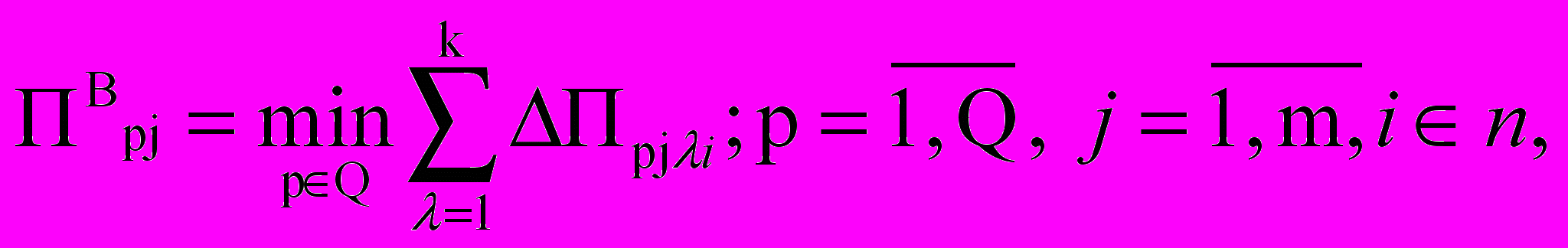
Ограничения:















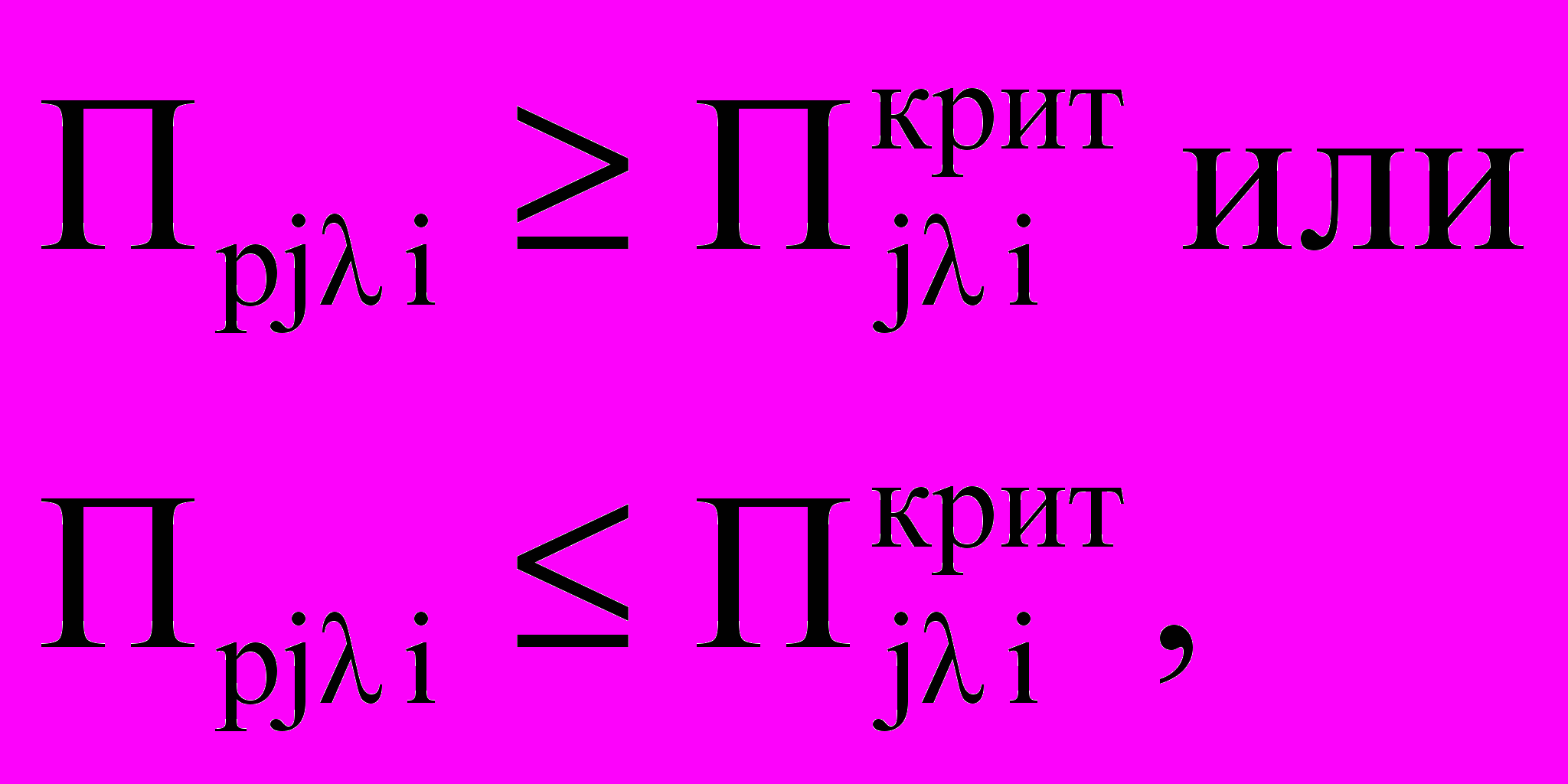
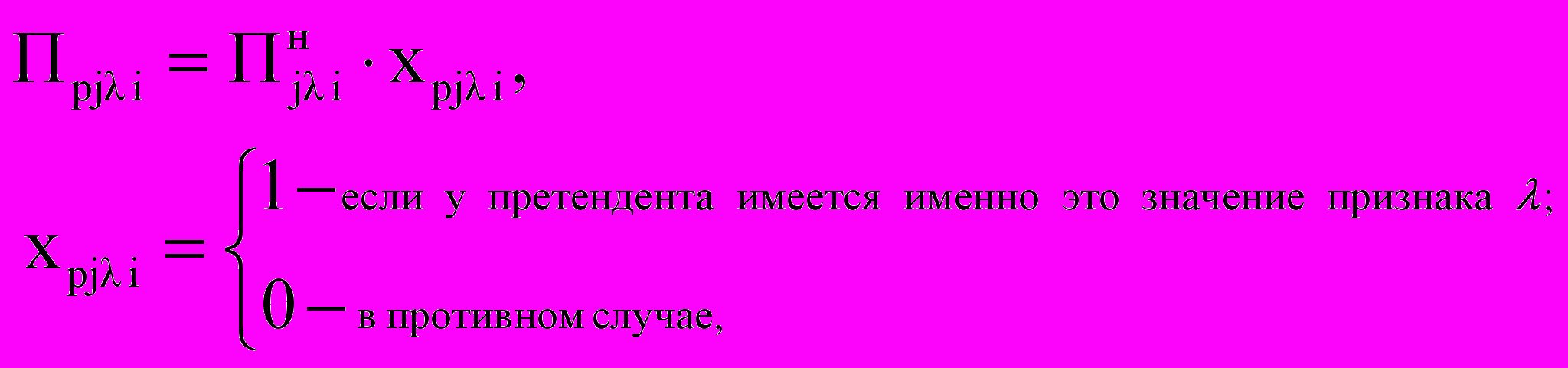
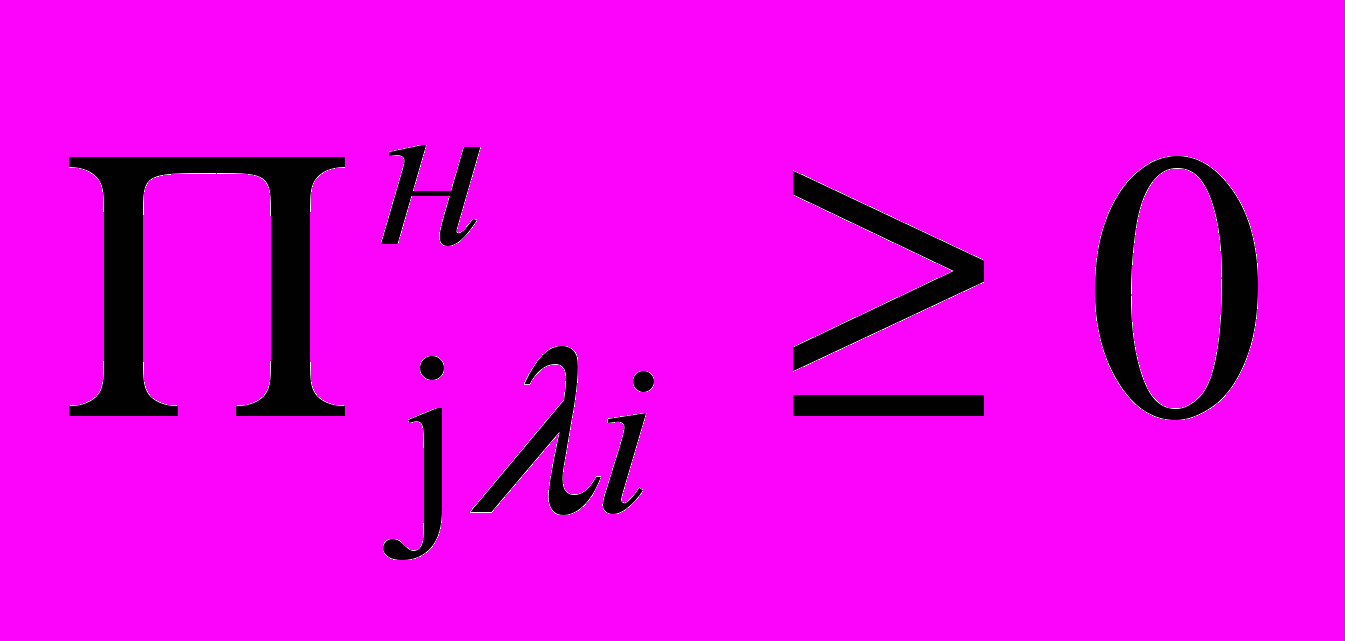
При построении экономико-математической модели объекта или системы, для которого разраба­тывается управленческое решение, особое внимание следует уделять четкости описания используемых признаков – характеристик, а также их условным обозначениям. Это облегчит реализацию процедур построения модели.


2.4.4. Выбор экономико-математического аппарата, используемого для решения данной задачи.

Этот выбор может осуществляться с помощью методов логического анализа, расчетно-аналитических методов, экспертных оценок и др.

Процедура оценки подробно рассмотрена в научно-методической части данных методических указаний.

Прежде всего, формируются признаки или критерии, по которым будет осуществлять­ся оценка методов. Каждому из признаков дается качественная оценка, которая лицом, разра­батывающим управленческое решение, трансформируется в количественную оценку. Следо­вательно, переход от качественной к количественной оценке - это субъективный процесс, ко­торый полностью зависит от лица, разрабатывающего управленческое решение. Инструмента­рием такого перевода являются, например, балльные оценки, сравнительный анализ, на основе которого устанавливается предпочтительность каждого метода. При этом может использоваться также и прогрессивная балльная шкала.

Выбранные альтернативные методы разработки управленческого решения рассматриваются с точки зрения рисковости их применения.

Далее в таблице 13 в качестве примера приведены различные варианты формирования рисковых ситуаций и их оценки на примере двух альтернативных методов решения транспортной задачи, выбранных в научно-методической части данных методических указаний.

Достоинства и недостатки этих методов приведены в таблице 14.

Основываясь на рассмотренных рисковых ситуациях, можно сделать вывод, что наиболее предпочтительным методом является метод линейного программирования, поскольку при автоматизации процесса риски могут проявиться лишь однажды (при внедрении системы), а после ее отладки и доводки возможно получение универсального средства для расчета оптимальных маршрутов, независимо от количества потребителей, размеров их заказов и расположения. Кроме того, после внедрения предлагаемой системы трудоемкость процесса определения оптимального маршрута резко сокращается.

Примечание: таблицы 13 и 14 можно посмотреть в «Методических указаниях к КП… » стр. 37;

2.4.5. Разработка алгоритма.

А. Последовательность процедур разработки алгоритма решения задачи управления.

• Формулирование решаемой задачи (по которой разрабатывается управленческое решение), для проработки информационного и методического обеспечения ее решения.
  
• Формирование информационного обеспечения решения задачи.
  
• Формирование на базе разработанной модели основных расчетных процедур решения задачи.
  
• Определение логической последовательности выполнения расчетных процедур: очередности выполнения процедур, связей между ними, расчетных циклов.
  
• Построение алгоритма (в пошаговом, блочном, модульном и др. исполнении).
  

Б. Особенности разработки алгоритма

• Отсутствие какой бы-то ни было неопределенности - информационной, методической, организационной.
  
• Полная проработанность каждого из элементов (шагов) алгоритма, позволяющая выполнить без дополнительных пояснений любой из его шагов (блоков, модулей).
  

В. Пример разработки алгоритма (по представленной схеме).

В. 1. Методическое и информационное обеспечение

• Формулировка решаемой задачи: Расчет ранних параметров сетевого графа.
  
• Формирование информационного обеспечения решения задачи:
  

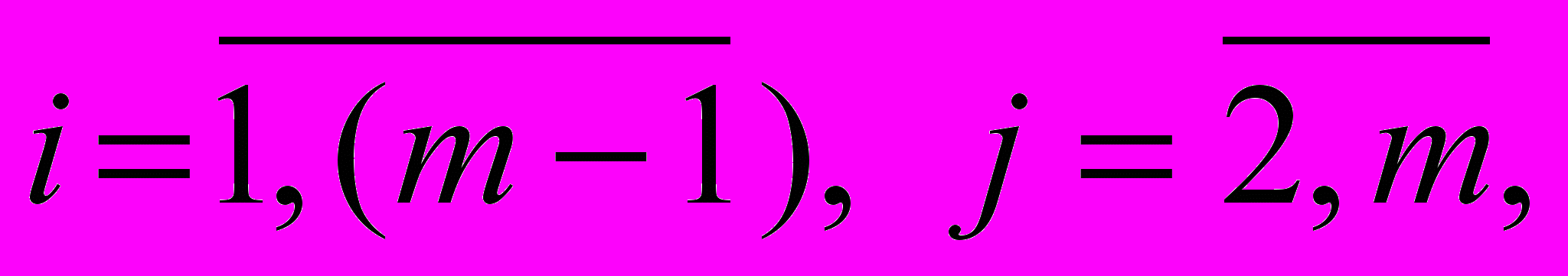
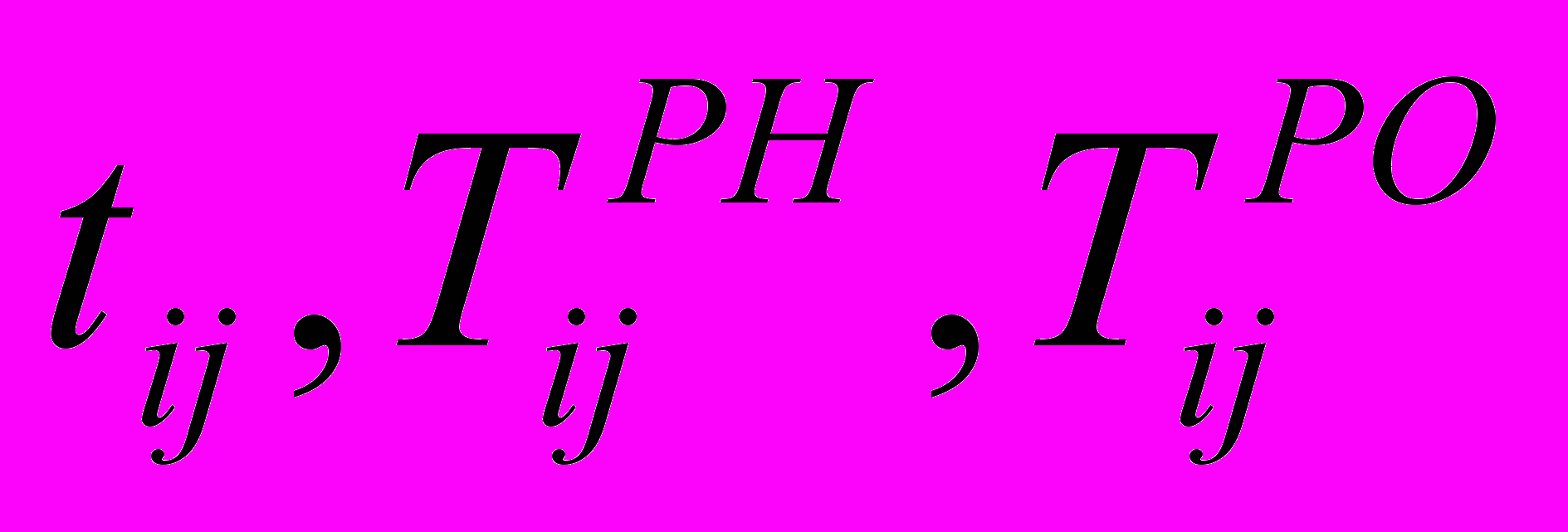
• Формирование на базе разработанной модели основных расчетных процедур решения задачи:
  

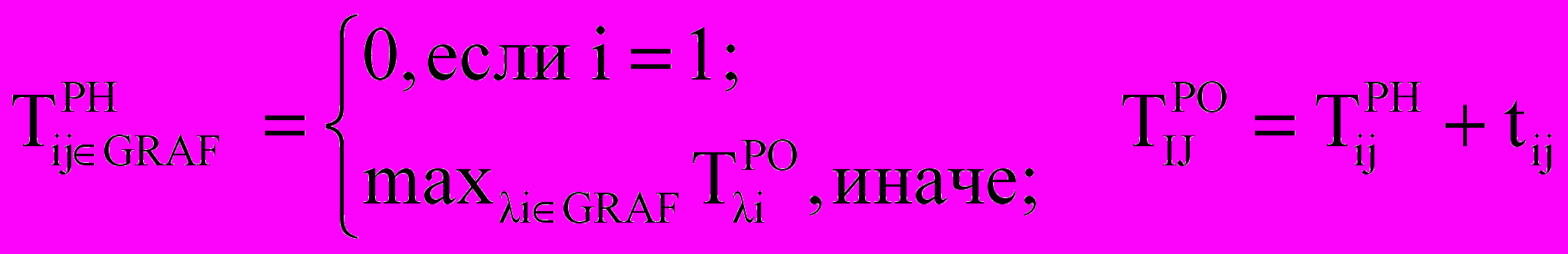
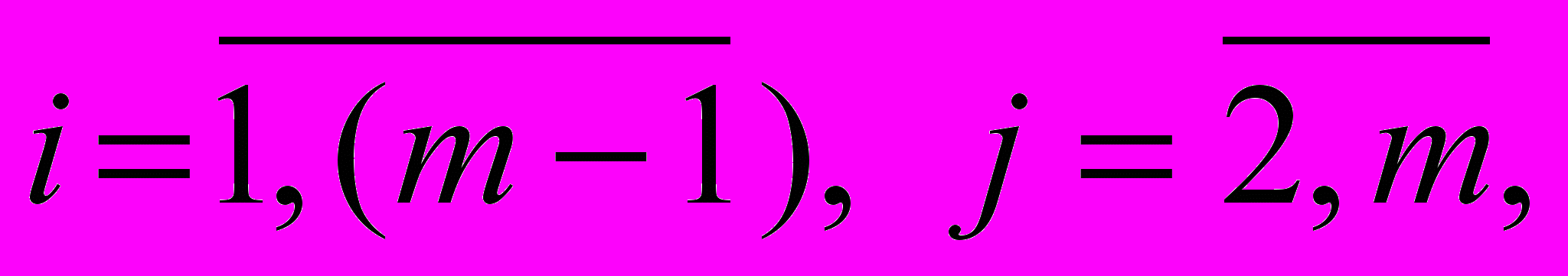
• Определение логической последовательности выполнения расчетных процедур:
  

1
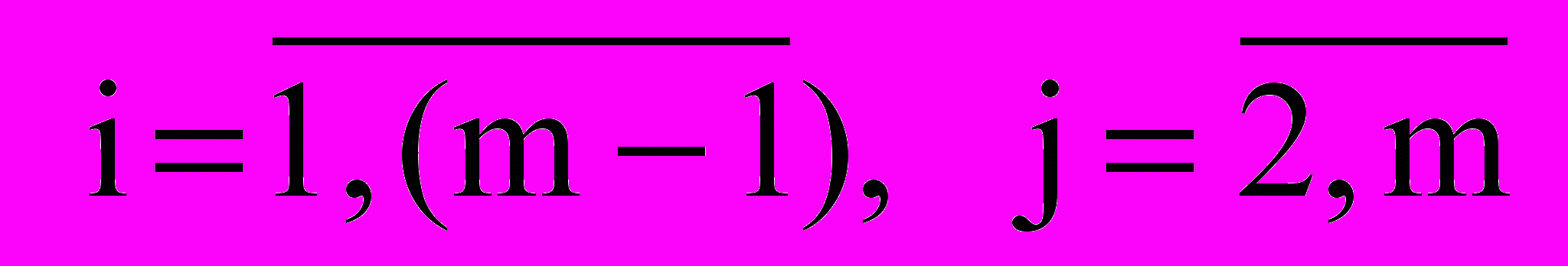
) последовательный перебор работ графа в порядке возрастания их кодов -

2)

• Построение алгоритма (в пошаговом исполнении).
  

В. 2. Разработка алгоритма

1. Сформировать данные по работам сетевого графа:

.

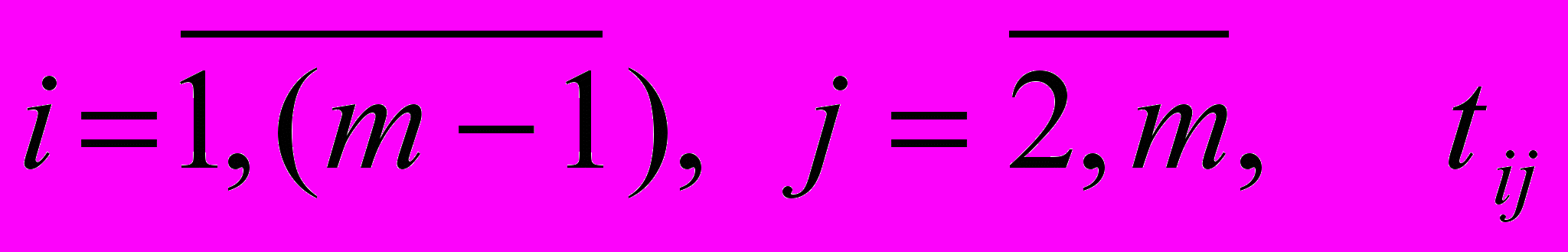2. Выбрать первую из непросмотренных работ, принадлежащую графу.

3.Проверить, является ли данная работа начальной.

Если да, то шаг 4, иначе 7.

4.

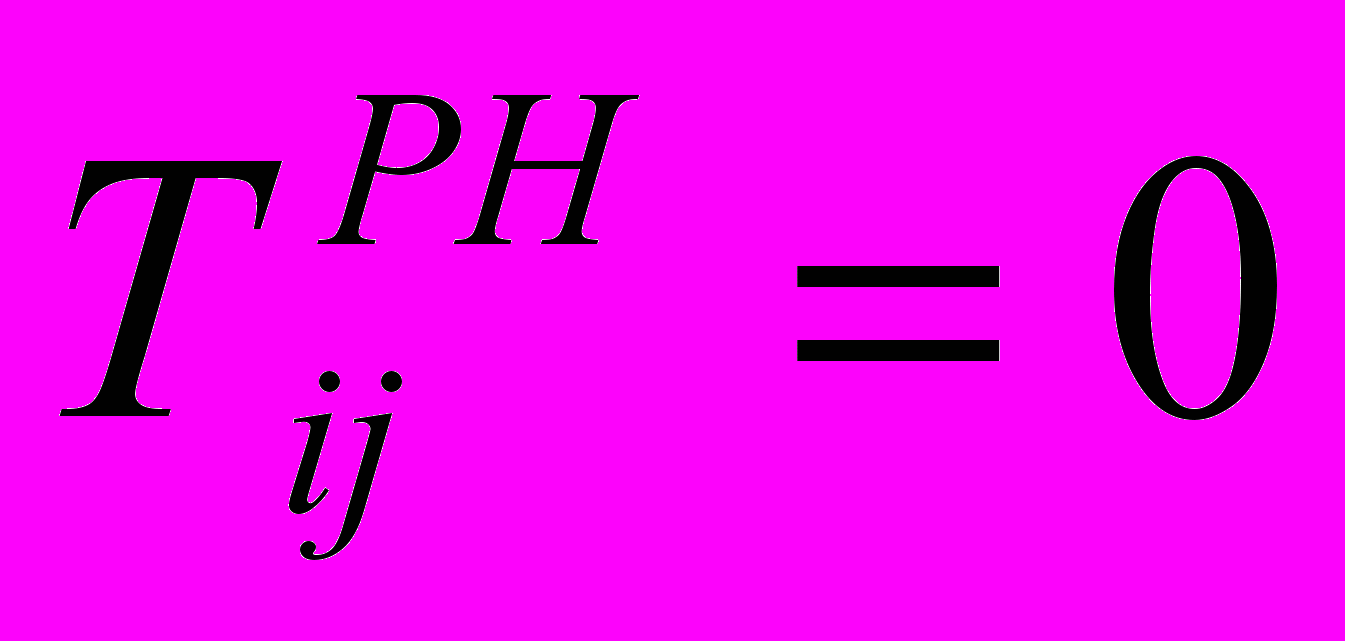
6
. Проверить наличие непросмотренных работ сетевого графа.

Если есть, то шаг 2, иначе - шаг 11.

7. Выбрать работы, непосредственно предшествующие ij-ой: .

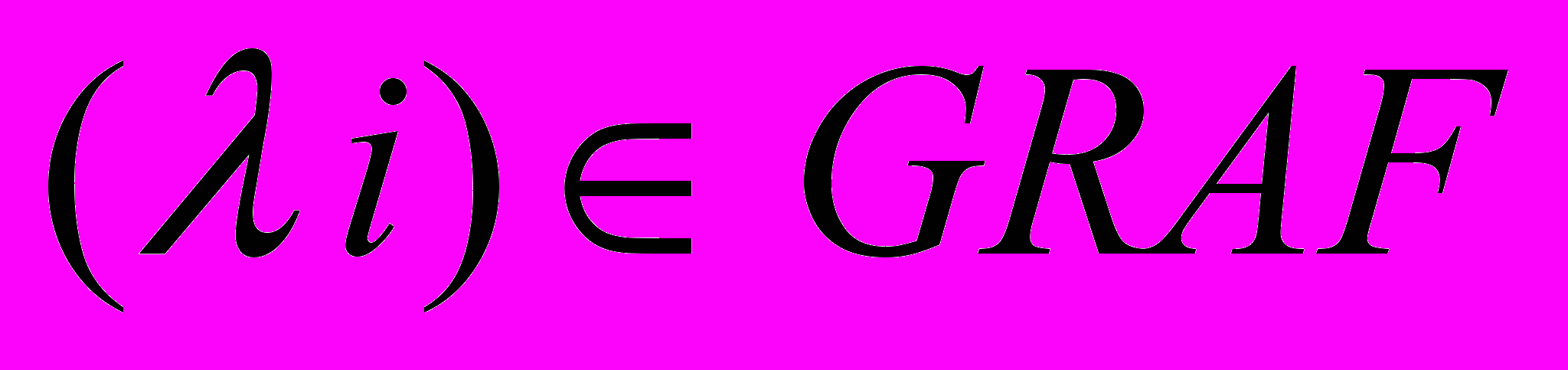8
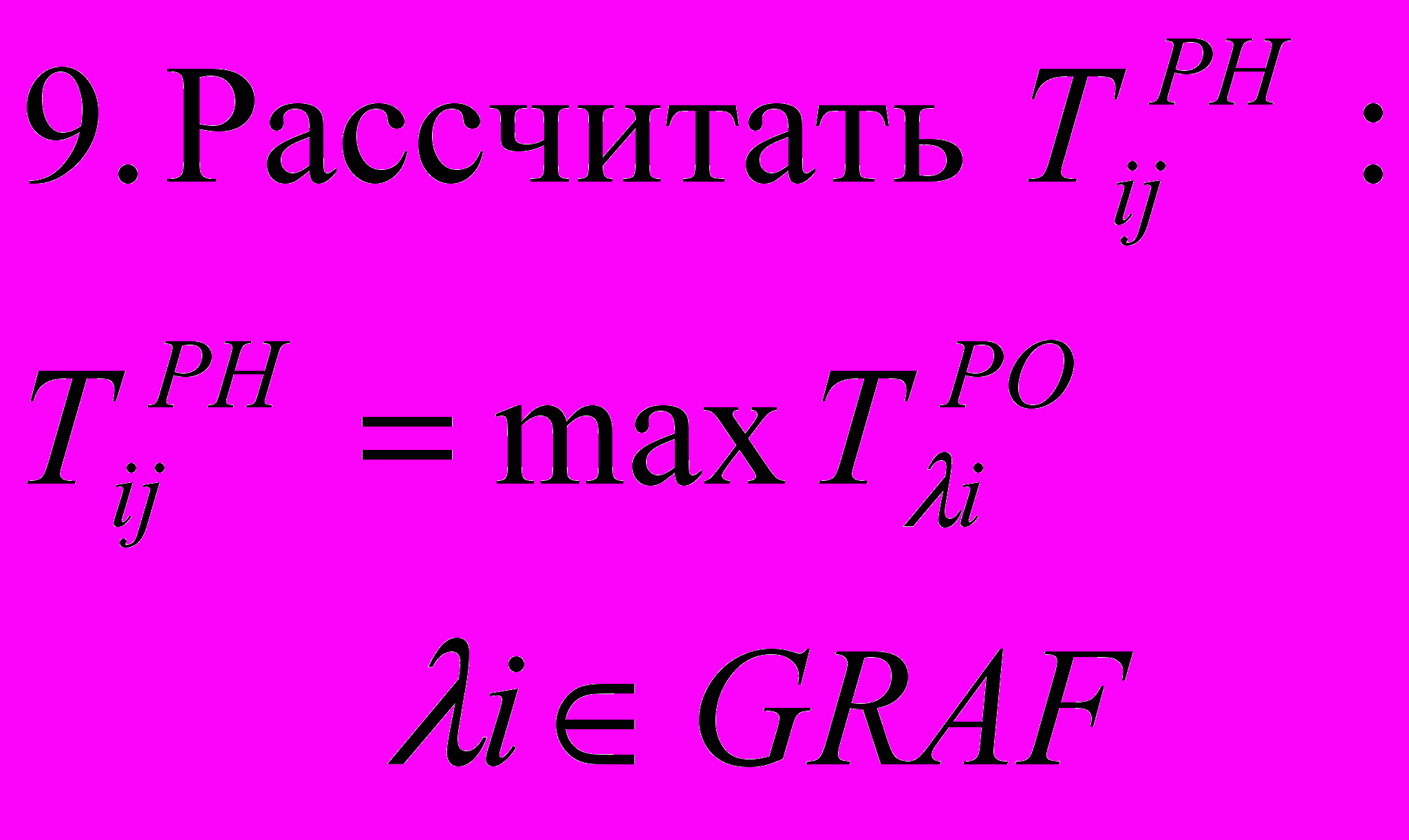
. Проверить наличие нескольких таких работ. Если да, то шаг 9, иначе шаг 10.

Перейти к шагу 5

П
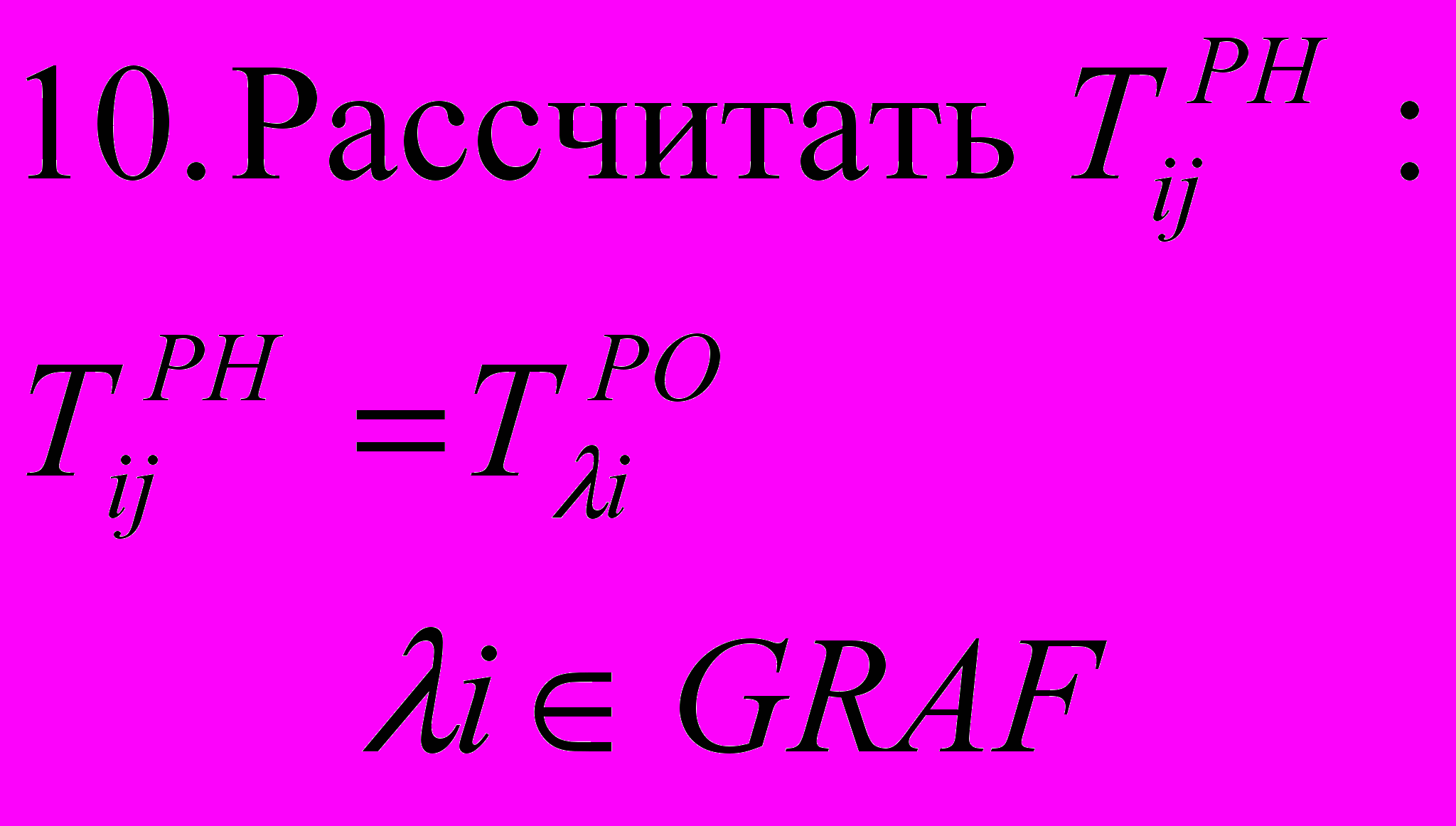
ерейти к шагу 5

11.Все расчеты выполнены, сформировать выходные данные решения задачи.

В ряде случаев в условиях большой размерности решаемой задачи можно рекомендо­вать построение укрупненной блок-схемы разработки управленческого решения или при малой размерности задачи разрабаты­вать не алгоритм, а блок-схему ее решения. Блок-схема представляет собой набор взаимосвязанных специальных символов, определяющих процедурность (технологию) разработки управленческого решения с выделением циклов, реализуемых в процессе расчетов, а также с условным предоставлением процедур расчетов в виде стандартных символов.

В проектной части также проектируются элементы информационного и организационного обеспечения разработки управленческого решения. Определяются состав и способы получения данных – номенклатура, носители, каналы передачи информации и т.п.; возможность и целесообразность использования ЭВМ; положения или инструкции по обеспечению реализации проектных разработок, контроль хода их выполнения; стимулирование качества разработанных управленческих решений.

Эти работы могут быть выполнены также в расчетной части, если проектная часть курсового проекта окажется слишком перегруженной, то есть большой по объему.