Аннотации к программам дисциплин (модулей)

Вид материала

Подобный материал:

1 2 3 4 5 6

2. Место дисциплины в модульной структуре ООП.

Дисциплина «Интегральные преобразования» является самостоятельным модулем.

3. Цель изучения дисциплины.

Целью освоения учебной дисциплины «Интегральные преобразования» является приобретение знаний и умений по теории функциональных пространств и теории обобщенных функций, теории преобразований Фурье, Лапласа, Шварца , приложения этих преобразований к исследованию обыкновенных дифференциальных уравнений и уравнений в частных производных, возможности приложения теории интегральных преобразований к исследованиям прикладного характера, формирование общекультурных и профессиональных компетенций, необходимых для осуществления научно-исследовательской деятельности.

4. Структура дисциплины.

Преобразования Фурье, Лапласа, Шварца, Меллина, Гильберта и др. Приложение интегральных преобразований.

5. Основные образовательные технологии.

В качестве ведущих форм организации педагогического процесса используются традиционные (лекции, практические, семинарские и т.д.), а также активные и интерактивные технологии (проблемное обучение и т.д.)

6. Требования к результатам освоения дисциплины.

Процесс изучения дисциплины направлен на формирование следующих общекультурных и профессиональных компетенций:

- культура мышления, способность к обобщению, анализу, восприятию информации, постановке цели и выбору путей её достижения (ОК-1);

- готовность к кооперации с коллегами, работе в коллективе, способность работать в команде и самостоятельно, а также быть коммуникативным, толерантным и честным; способность проявлять организованность, трудолюбие, исполнительскую дисциплину (ОК-3);

- способность находить организационно-управленческие решения в нестандартных ситуациях, самостоятельно принимать решения и готовность нести за них ответственность (ОК-4);

- готовность работать с технической документацией, необходимой для профессиональной деятельности (ПК-12);

- готовность анализировать, оценивать и разрабатывать стратегии организации (ПК-14);

- способность участвовать в разработке инновационных методов, средств и технологий в области профессиональной деятельности (ПК-17);

- готовность участвовать в реализации проектов в области профессиональной деятельности (ПК-19).

В результате изучения дисциплины студент должен:

- знать определение и свойства функциональных пространств и пространств обобщенных функций, определение и свойства основных интегральных преобразований, таблицы образов и прообразов этих преобразований, теоремы о свертке и мультипликаторах;

- уметь с помощью интегральных преобразований свести решение обыкновенных дифференциальных уравнений к решению алгебраических уравнений и решение уравнений в частных производных свести к решению обыкновенных дифференциальных уравнений, определить пару функциональных пространств в которых действуют основные интегральные преобразования;

- владеть (быть в состоянии продемонстрировать) методами решения обыкновенных дифференциальных уравнений и уравнений в частных производных, техникой дифференцирования и интегрирования функций комплексного переменного, способами решения алгебраических уравнений.

7. Общая трудоемкость дисциплины.

3 зачетных единиц (108 академических часов)

8. Формы контроля.

Промежуточная аттестация – зачет (8 семестр).

9. Составитель.

Смирницкий Юрий Алексеевич, кандидат физико-математических наук, доцент кафедры математического анализа и прикладной математики КГУ.

Аннотация к рабочей программе

дисциплины «Дискретные вейвлет преобразования»

1. Место дисциплины в структуре основной образовательной программы (ООП).

Дисциплина включена в вариативную часть профессионального цикла ООП.

К исходным требованиям, необходимым для изучения дисциплины «Дискретные вейвлет преобразования», относятся знания, умения и виды деятельности, сформированные в процессе изучения дисциплин: «Математический анализ» и «Алгебра», «Комплексный анализ (теория функций комплексного переменного)», «Функциональный анализ» а также знания , приобретенные в процессе написания курсовых работ по этим дисциплинам.

Дисциплина «Дискретные вейвлет преобразования» является основой для изучения дисциплин: «Уравнения в частных производных», для последующего изучения других дисциплин вариативной части профессионального цикла, а также для прохождения производственной практики.

2. Место дисциплины в модульной структуре ООП.

Дисциплина «Дискретные вейвлет преобразования» является самостоятельным модулем.

3. Цель изучения дисциплины.

Целью освоения учебной дисциплины «Дискретные вейвлет преобразования» является приобретение знаний и умений по теории функциональных пространств и теории обобщенных функций, теории преобразований Фурье и вейвлет преобразований, приложения этих преобразований к исследованию уравнений в частных производных, возможности приложения теории интегральных преобразований к исследованиям прикладного инженерного характера, формирование общекультурных и профессиональных компетенций, необходимых для осуществления научно-исследовательской деятельности.

4. Структура дисциплины.

Преобразования Фурье. Основы теории всплесков. Дискретные вейвлет преобразования.

5. Основные образовательные технологии.

В качестве ведущих форм организации педагогического процесса используются традиционные (лекции, практические, семинарские и т.д.), а также активные и интерактивные технологии (проблемное обучение и т.д.)

6. Требования к результатам освоения дисциплины.

Процесс изучения дисциплины направлен на формирование следующих общекультурных и профессиональных компетенций:

- культура мышления, способность к обобщению, анализу, восприятию информации, постановке цели и выбору путей её достижения (ОК-1);

- готовность к кооперации с коллегами, работе в коллективе, способность работать в команде и самостоятельно, а также быть коммуникативным, толерантным и честным; способность проявлять организованность, трудолюбие, исполнительскую дисциплину (ОК-3);

- способность находить организационно-управленческие решения в нестандартных ситуациях, самостоятельно принимать решения и готовность нести за них ответственность (ОК-4);

- готовность работать с технической документацией, необходимой для профессиональной деятельности (ПК-12);

- готовность анализировать, оценивать и разрабатывать стратегии организации (ПК-14);

- способность участвовать в разработке инновационных методов, средств и технологий в области профессиональной деятельности (ПК-17);

- готовность участвовать в реализации проектов в области профессиональной деятельности (ПК-19).

В результате изучения дисциплины студент должен:

- знать определение и свойства функциональных пространств и пространств обобщенных функций, определение и свойства основных интегральных преобразований, таблицы образов и прообразов этих преобразований, теоремы о свертке и мультипликаторах;

- уметь с помощью интегральных преобразований свести решение обыкновенных дифференциальных уравнений к решению алгебраических уравнений и решение уравнений в частных производных свести к решению обыкновенных дифференциальных уравнений, определить пару функциональных пространств в которых действуют основные интегральные преобразования;

- владеть (быть в состоянии продемонстрировать) методами решения обыкновенных дифференциальных уравнений и уравнений в частных производных, техникой дифференцирования и интегрирования функций комплексного переменного, способами решения алгебраических уравнений.

7. Общая трудоемкость дисциплины.

3 зачетных единиц (108 академических часов)

8. Формы контроля.

Промежуточная аттестация – зачет 8 семестр

9. Составитель.

Смирницкий Юрий Алексеевич, кандидат физико-математических наук, доцент кафедры математического анализа и прикладной математики КГУ.

Аннотация к рабочей программе

дисциплины «Интерполяционные пространства»

1. Место дисциплины в структуре основной образовательной программы (ООП).

Дисциплина является дисциплиной по выбору профессионального цикла ООП.

К исходным требованиям, необходимым для изучения дисциплины «Интерполяционные пространства», относятся знания, умения и виды деятельности, сформированные в процессе изучения дисциплин: «Математический анализ» и «Алгебра», «Комплексный анализ», «Функциональный анализ» а также знания , приобретенные в процессе написания курсовых работ по этим дисциплинам.

Дисциплина «Интерполяционные пространства» в некоторой степени, является обобщением выше названных дисциплин и позволяет студенту приблизиться к «переднему» краю науки. Ее изучение позволяет студенту в целом осознать и понять одно из современных направлений математической науки. Она является основой для более глубокого понимания дисциплин: «Уравнения в частных производных», «Вариационного исчисление и оптимального управление» для последующего изучения других дисциплин вариативной части профессионального цикла, а также для прохождения производственной практики.

2. Место дисциплины в модульной структуре ООП.

Дисциплина «Интерполяционные пространства» является самостоятельным модулем.

3. Цель изучения дисциплины.

Целью освоения учебной дисциплины «Интерполяционные пространства» является приобретение знаний и умений по теории функциональных пространств и теории интерполяции линейных операторов, а также приложения теории к исследованиям теоретического и прикладного характера, формирование общекультурных и профессиональных компетенций, необходимых для осуществления научно-исследовательской деятельности.

4. Структура дисциплины.

Интерполяция в конечномерных пространствах. Теорема Рисса-Торина и Марцинкевича. К- и J-функционалы. Вещественная интерполяция. Интерполяция пространств интегрируемых функций.

5. Основные образовательные технологии.

В качестве ведущих форм организации педагогического процесса используются традиционные (лекции, практические, семинарские и т.д.), а также активные и интерактивные технологии (проблемное обучение и т.д.)

6. Требования к результатам освоения дисциплины.

Процесс изучения дисциплины направлен на формирование следующих общекультурных и профессиональных компетенций:

- исследовательские навыки (ОК-7);

- способность приобретать новые знания, используя современные и образовательные технологии (ОК-8);

- способность к письменной и устной речи на русском языке(ОК-15)

- способность к анализу и синтезу (ОК-14);

-- умение формулировать результат (ПК-3);

- умение строго доказать утверждение (ПК-4);

- умение грамотно пользоваться языком предметной области (ПК-7);

- умение ориентироваться в постановках задач (ПК-8);

- знание корректных постановок классических задач (ПК-9);

- понимание корректности постановок задач (ПК-10);

- выделением главных смысловых аспектов в доказательствах (ПК-16);

- владения методами математического и алгоритмического моделирования при анализе теоретических проблем и задач (ПК-21);

- умение самостоятельно математически корректно ставить естественно-научные и инженерно-физические задачи (ПК-25);

В результате изучения дисциплины студент должен:

- иметь базовые знания основных принципов, функций, объектов, средств и методов функционального анализа и теории линейных и нелинейных операторов;

- уметь формулировать и доказывать теоремы и свойства, самостоятельно решать классические и составленные самостоятельно задачи функционального анализа;

- владеть навыками практического использования методов функционального анализа при решении различных задач (интегральных уравнений, уравнений в частных производных, задач методов оптимизации).

7. Общая трудоемкость дисциплины.

5 зачетных единиц (180 академических часов)

8. Формы контроля.

Промежуточная аттестация – зачет (8 семестр).

9. Составитель.

Кабанко Михаил Владимирович, кандидат физико-математических наук, заведующий кафедрой математического анализа и прикладной математики КГУ.

Аннотация к рабочей программе

дисциплины «Операторные алгебры»

1. Место дисциплины в структуре основной образовательной программы (ООП).

Дисциплина является дисциплиной по выбору профессионального цикла ООП.

К исходным требованиям, необходимым для изучения дисциплины «Операторные алгебры», относятся знания, умения и виды деятельности, сформированные в процессе изучения дисциплин: «Математический анализ» и «Алгебра», «Комплексный анализ», «Функциональный анализ» а также знания , приобретенные в процессе написания курсовых работ по этим дисциплинам.

Дисциплина «Операторные алгебры», в некоторой степени, является обобщением выше названных дисциплин и позволяет студенту приблизиться к «переднему» краю науки. Ее изучение позволяет студенту в целом осознать и понять одно из современных направлений математической науки. Она является основой для более глубокого понимания дисциплин: «Функциональный анализ» «Уравнения в частных производных», «Вариационного исчисление и оптимального управление», «Теоретическая физика» (квантовой механики), а также для прохождения производственной практики.

2. Место дисциплины в модульной структуре ООП.

Дисциплина «Операторные алгебры», является самостоятельным модулем.

3. Цель изучения дисциплины.

Целью освоения учебной дисциплины «Операторные алгебры», является приобретение знаний и умений по теории операторных пространств и алгебр, а также приложения теории к исследованиям теоретического и прикладного характера в квантовой механики, построения квантово-механических моделей, необходимых для осуществления научно-исследовательской деятельности.

4. Структура дисциплины.

Коммутативные банаховы алгебры. *- и С*-алгебры. ГНС- конструкция. Элементы теории представлений.

5. Основные образовательные технологии.

В качестве ведущих форм организации педагогического процесса используются традиционные (лекции, практические, семинарские и т.д.), а также активные и интерактивные технологии (проблемное обучение и т.д.)

4. Требования к результатам освоения дисциплины.

Процесс изучения дисциплины направлен на формирование следующих общекультурных и профессиональных компетенций:

- исследовательские навыки (ОК-7);

- способность приобретать новые знания, используя современные и образовательные технологии (ОК-8);

- способность к анализу и синтезу (ОК-14);

-- умение формулировать результат (ПК-3);

- умение строго доказать утверждение (ПК-4);

- умение грамотно пользоваться языком предметной области (ПК-7);

- умение ориентироваться в постановках задач (ПК-8);

- знание корректных постановок классических задач (ПК-9);

- понимание корректности постановок задач (ПК-10);

- выделением главных смысловых аспектов в доказательствах (ПК-16);

- владения методами математического и алгоритмического моделирования при анализе теоретических проблем и задач (ПК-21);

- умение самостоятельно математически корректно ставить естественно-научные и инженерно-физические задачи (ПК-25);

В результате изучения дисциплины студент должен:

- иметь базовые знания основных принципов, функций, объектов, средств и методов теории банаховых алгебр;

- уметь формулировать и доказывать теоремы и свойства, самостоятельно решать классические и составленные самостоятельно задачи теории операторных алгебр;

- владеть навыками практического использования методов функционального анализа при решении различных задач (интегральных уравнений, уравнений в частных производных, задач методов оптимизации, задач квантовой механики).

5. Общая трудоемкость дисциплины.

5 зачетных единиц (180 академических часов)

6. Формы контроля.

Промежуточная аттестация – зачет (8 семестр).

7. Составитель.

Кабанко Михаил Владимирович, кандидат физико-математических наук, заведующий кафедрой математического анализа и прикладной математики КГУ.

Аннотация к рабочей программе

дисциплины «Глобальный анализ в задачах математической физики»

1.Место дисциплины в структуре основной образовательной программы (ООП).

Дисциплина включена в вариативную часть профессионального цикла ООП.

К исходным требованиям, необходимым для изучения дисциплины « Глобальный анализ», относятся знания, умения и виды деятельности, сформированные в процессе изучения дисциплин: «Аналитическая геометрия », «Алгебра», «Математический анализ»,.

2. Место дисциплины в модульной структуре ООП.

Дисциплина «Глобальный анализ» является курсом по выбору.

3. Цель изучения дисциплины.

Целью освоения учебной дисциплины «Глобальный анализ» изучение и применение основных понятий, идей и методов Глобального анализа для изучения других естественнонаучных дисциплин, а также для решения базовых задач и математических проблем, возникающих при проведении научных и прикладных исследований.

4. Требования к результатам освоения дисциплины.

Процесс изучения дисциплины «Глобальный анализ» направлен на формирование следующих общекультурных и профессиональных компетенций:

фундаментальной подготовкой по основам профессиональных знаний и готовностью к использованию их в профессиональной деятельности (ОК-11);

- умение понять поставленную задачу (ПК-2);

- умение формулировать результат (ПК-3);

- умение строго доказать утверждение (ПК-4).

- умение грамотно пользоваться языком предметной области (ПК-7);

- выделение главных аспектов при доказательстве теорем (ПК-16)

В результате изучения дисциплины студент должен

знать:

- основы глобального анализа;

- способы применения глобального анализа в различных областях математики и физики;

- уметь формулировать и доказывать теоремы глобального анализа, самостоятельно решать классические задачи глобального анализа;

владеть (быть в состоянии продемонстрировать) навыками: практического использования методов глобального анализа при решениие различных задач.

5. Структура дисциплины.

Многообразия. Тензоры и дифференциальные формы. Связности Обыкновенные дифференциальные уравнения Начала теории многозначных отображений.

6. Основные образовательные технологии.

В качестве ведущих форм организации педагогического процесса используются традиционные (лекции, практические, семинарские и т.д.), а также активные и интерактивные технологии (проблемное обучение и т.д.)

7. Общая трудоемкость дисциплины.

2 зачетных единицы (72 академических часа)

8. Формы контроля.

Зачет – 8 семестр.

9. Составитель.

Зыков Пётр Сергеевич, кандидат физико-математических наук, доцент кафедры алгебры, геометрии и ТОМ КГУ.

Аннотация к рабочей программе

дисциплины «Анализ на многообразиях»

1. Место дисциплины в структуре основной образовательной программы (ООП).

Дисциплина включена в вариативную часть профессионального цикла ООП.

К исходным требованиям, необходимым для изучения дисциплины «Анализ на многообразиях», относятся знания, умения и виды деятельности, сформированные в процессе изучения дисциплин: «Аналитическая геометрия», «Алгебра», «Математический анализ.

2. Место дисциплины в модульной структуре ООП.

Дисциплина «Анализ на многообразиях» является самостоятельным модулем.

3. Цель изучения дисциплины.

Целью освоения учебной дисциплины «Анализ на многообразиях» изучение и применение основных понятий, идей и методов Дифференциальной геометрии для изучения других естественнонаучных дисциплин, а также для решения базовых задач и математических проблем, возникающих при проведении научных и прикладных исследований.

4. Требования к результатам освоения дисциплины.

Процесс изучения дисциплины «Анализ на многообразиях» направлен на формирование следующих общекультурных и профессиональных компетенций:

- фундаментальной подготовкой по основам профессиональных знаний и готовностью к использованию их в профессиональной деятельности (ОК-11);

- умение понять поставленную задачу (ПК-2);

- умение формулировать результат (ПК-3);

- умение строго доказать утверждение (ПК-4).

- умение грамотно пользоваться языком предметной области (ПК-7);

- выделение главных аспектов при доказательстве теорем (ПК-16)

В результате изучения дисциплины студент должен

знать:

- основы дифференциальной геометрии и тензорного анализа;

- способы применения дифференциальной геометрии в различных областях математики и физики;

- уметь формулировать и доказывать теоремы дифференциальной геометрии, самостоятельно решать классические задачи дифференциальной геометрии;

владеть (быть в состоянии продемонстрировать) навыками: практического использования методов дифференциальной геометрии при решении математических и физических задач.

5. Структура дисциплины.

Многообразия. Касательные векторы, касательные расслоения и векторные поля. Кокасательные расслоения и ковекторные поля. Римановы метрики. Ковариантная производная. Геодезические.

6. Основные образовательные технологии.

В качестве ведущих форм организации педагогического процесса используются традиционные (лекции, практические, семинарские и т.д.), а также активные и интерактивные технологии (проблемное обучение и т.д.)

7. Общая трудоемкость дисциплины.

2 зачетных единицы (72 академических часа)

8. Формы контроля.

Зачет – 8 семестр.

9. Составитель.

Зыков Пётр Сергеевич, кандидат физико-математических наук, доцент кафедры алгебры, геометрии и ТОМ КГУ.

Аннотация к рабочей программе

дисциплины «Функции и их графики»

1. Место дисциплины в структуре основной образовательной программы (ООП).

Дисциплина является одной из дисциплин по выбору в вариативной части профессионального цикла ООП.

К исходным требованиям, необходимым для изучения дисциплины «Функции и их графики», относятся знания, умения и виды деятельности, сформированные в школьном курсе математики.

Дисциплина «Функции и их графики» является основой для изучения дисциплин «Численные методы», «Теоретическая механика», «Математический анализ», «Аналитическая геометрия», «Дифференциальные уравнения», «Комплексный анализ», «Функциональный анализ», «Дифференциальная геометрия и топология», «Теория вероятностей и случайные процессы», входящих в базовую часть математического и естественнонаучного и профессионального циклов, а также для последующего изучения других дисциплин вариативной части профессионального цикла.

2. Место дисциплины в модульной структуре ООП.

Дисциплина «Функции и их графики» является самостоятельным модулем.

3. Цель изучения дисциплины.

Целью освоения учебной дисциплины «Функции и их графики» является приобретение знаний и умений по изучению элементарных функций, изучению их свойств и построению их графиков различными методами. Другой важной целью является приобретение обратных навыков - зная вид графика функции, уметь определить свойства процессов, описываемых этой функцией.

4. Структура дисциплины.

Определения основных элементарных функций. Построение графиков. Преобразования функций и их графиков.

5. Основные образовательные технологии.

В качестве ведущих форм организации педагогического процесса используются традиционные (лекции, практические, семинарские и т.д.), а также активные и интерактивные технологии (проблемное обучение и т.д.)

6. Требования к результатам освоения дисциплины.

Процесс изучения дисциплины направлен на формирование следующих общекультурных и профессиональных компетенций:

- способности применять знания на практике (ОК-6);

- исследовательских навыков (ОК-7);

- умение находить, анализировать и контекстно обрабатывать научно-техническую информацию (ОК-10);

- фундаментальной подготовки по основам профессиональных знаний и готовности к использованию их в профессиональной деятельности (ОК-11);

- определение общих форм, закономерностей ти инструментальных средств отдельной предметной области (ПК-1);

- умение понять поставленную задачу (ПК-2);

- умение формулировать результат (ПК-3);

- умение на основе анализа увидеть и корректно формулировать результат (ПК-5);

- умение самостоятельно увидеть следствия сформулированного результата (ПК-6);

- умение грамотно пользоваться языком предметной области (ПК-7);

- умением ориентироваться в поставленных задачах (ПК-8);

- самостоятельным построением алгоритма и его анализом (ПК-11);

- контекстной обработкой информации (ПК-14);

- умением публично представлять собственные и известные научные результаты (ПК-18);

- обретением опыта самостоятельного различения типов знания (ПК-26);

В результате изучения дисциплины студент должен:

- иметь базовые знания в области прикладной и фундаментальной математики;

- уметь самостоятельно решать классические задачи математики;

- владеть навыками практического использования математических методов при анализе различных задач.

7. Общая трудоемкость дисциплины.

4 зачетных единиц (144 академических часов)

8. Формы контроля.

Изучение дисциплины заканчивается зачетом (1 семестр).

9. Составитель.

Власов Эдуард Вячеславович, кандидат физико-математических наук, доцент кафедры «Математического анализа и прикладной математики» ГОУ ВПО «КГУ».

Аннотация к рабочей программе дисциплины

«Элементарная математика»

1. Место дисциплины в структуре основной образовательной программы, в модульной структуре ООП

Данная учебная дисциплина включена в вариативную часть профессионального цикла цикла ООП и является курсом по выбору.

Для изучения дисциплины необходимы компетенции, сформированные у выпускников средней (полной) общеобразовательной школы. «Элементарная математика» базируется на понятиях и утверждениях ранее изучаемой дисциплины «Вводный курс математики».

Знания и умения, сформированные у обучающихся в результате изучения дисциплины «Элементарная математика» будут использоваться при изучении дисциплин естественнонаучного и профессионального циклов, при прохождении производственной практики.

2. Цель изучения дисциплины

Целью изучения дисциплины «Элементарная математика» является содействие становлению профессиональной компетентности бакалавра педагогического образования на основе овладения содержанием дисциплины.

Задачи по обеспечению достижения цели:

формирование представлений о математике как универсальном языке науки;
формирование математической культуры и развитие логического мышления;
формирование навыков проведения доказательных рассуждений, логического обоснования выводов;
совершенствование опыта поисковой и творческой деятельности при решении задач повышенной сложности и нетиповых задач;
овладение знаниями по разделам курса;
овладение методами решения математических задач дисциплины;

– формирование навыков самостоятельной работы с источниками информации, анализа, обобщения и систематизации полученной информации, приобретение знаний и умений, позволяющих в дальнейшем заниматься педагогической деятельностью, формирование общекультурных компетенций.

3. Структура дисциплины

Классы функций: ограниченные функции, достижение функций своего наибольшего и наименьшего значения, четные и нечетные функции и их свойства, монотонные функции и их свойства, периодические функции и их свойства. Правила построения графиков функций с помощью преобразований координатной плоскости. Понятие уравнения, неравенства, системы и совокупности. Понятие равносильных переходов и переходов к следствию для уравнений, неравенств, систем и совокупностей с одной и той же переменной. Основные равносильности и следствия для уравнений, неравенств, систем и совокупностей с одной и той же переменной. Метод промежутков и его использование при построении графиков функций, неравенств, систем и совокупностей. Числовые и буквенные выражения и связанные с ними понятия.

Степень с натуральным показателем и ее основные свойства. Степенная функция с натуральным основанием. Линейные функции, уравнения и неравенства. Квадратичная функция, квадратные уравнения и неравенства, их основные свойства. Дробно-линейная функция, квадратные уравнения и неравенства, их основные свойства. Степень и степенная функция с целым показателем. Радикалы: определение и основные свойства. Функция

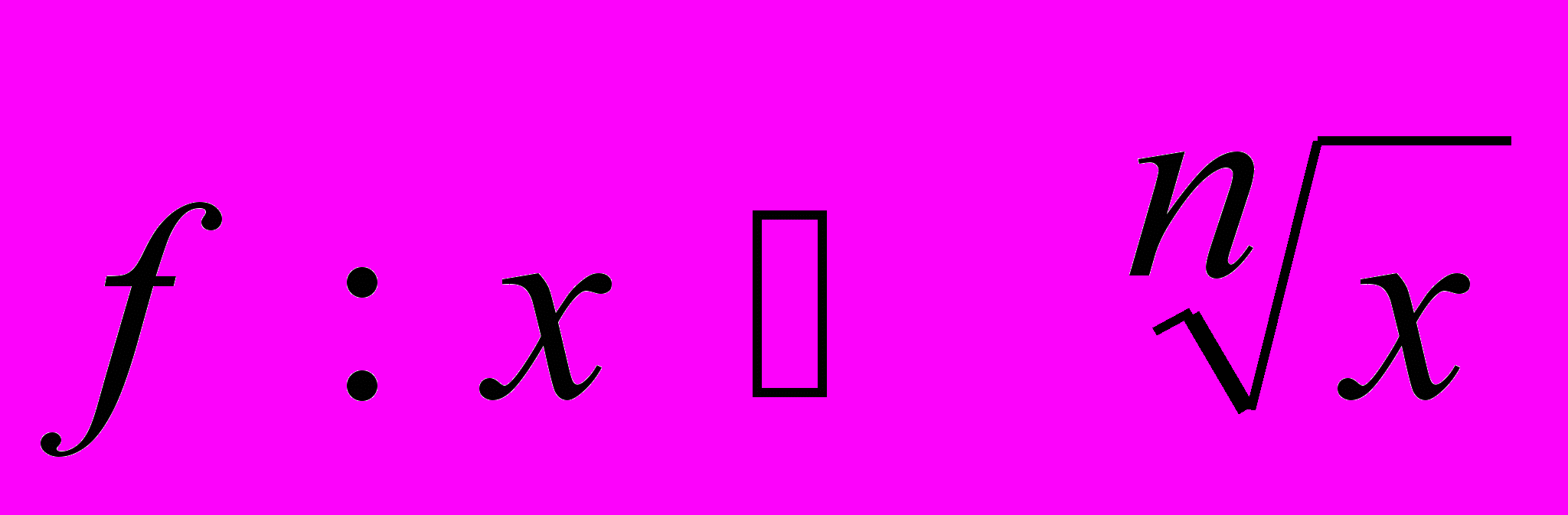. Степенная функция с рациональным показателем и ее основные свойства. Иррациональные уравнения и неравенства. Тождественные преобразования алгебраических выражений. Степень с действительным показателем: определение и основные свойства. Показательные и логарифмические функции: определение и основные свойства. Показательные и логарифмические уравнения и неравенства. Основные тригонометрические функции: определение и основные свойства. Тригонометрические тождества. Формулы приведения для основных тригонометрических функций. Свойства и графики тригонометрических функций. Тождественные преобразования выражений. Тригонометрические уравнения и неравенства. Обратные тригонометрические функции.

4. Основные образовательные технологии

В процессе изучения дисциплины используются лекции, практические и самостоятельные работы, мультимедийные лекции.

5. Требования к результатам освоения дисциплины

Процесс изучения дисциплины направлен на формирование следующих общекультурных и профессиональных компетенций:

- фундаментальной подготовкой по основам профессиональных знаний и готовностью к использованию их в профессиональной деятельности (ОК-11);

- умение понять поставленную задачу (ПК-2);

- умение формулировать результат (ПК-3);

- умение строго доказать утверждение (ПК-4).

- умение грамотно пользоваться языком предметной области (ПК-7);

- выделение главных аспектов при доказательстве теорем (ПК-16)

В результате изучения дисциплины студенты должны:

– иметь представление о математике как универсальном языке науки;

– знать способы и методы решения рациональных, иррациональных, показательных, логарифмических и тригонометрических уравнений и неравенств;

– уметь исследовать функции на ограниченность, монотонность, четность и нечетность, периодичность; выбирать методы и способы решения задач, точно и ясно выражать свои мысли в устной и письменной речи;

– иметь навыки проведения доказательных рассуждений, логического обоснования выводов, самостоятельной работы с источниками информации, анализа, обобщения и систематизации полученной информации, поисковой и творческой деятельности.

6. Общая трудоемкость дисциплины

4 зачетных единицы (144 академических часа)

7. Формы контроля

Зачет – 1 семестр.

8. Составитель

Бородина Марина Валентиновна, старший преподаватель кафедры алгебры, геометрии и ТОМ КГУ.

Аннотация к рабочей программе

дисциплины «Элементы проективной геометрии»

1. Место дисциплины в структуре основной образовательной программы (ООП).

Дисциплина включена в вариативную часть профессионального цикла ООП. К исходным требованиям, необходимым для изучения дисциплины «Элементы проективной геометрии» относятся знания, умения, виды деятельности и компетенции, сформированные в процессе изучения дисциплины «Аналитическая геометрия». Дисциплина «Элементы проективной геометрии» является важной составляющей подготовки бакалавра математики.

2. Место дисциплины в модульной структуре ООП.

Дисциплина «Элементы проективной геометрии» является курсом по выбору.

3. Цель изучения дисциплины.

Целью освоения учебной дисциплины «Элементы проективной геометрии» является формирование компетенций, необходимых для осуществления профессиональной деятельности, требующей углубленной фундаментальной и профессиональной подготовки в области математики.

4. Требования к результатам освоения дисциплины.

Процесс изучения дисциплины направлен на формирование следующих общекультурных и профессиональных компетенций:

- фундаментальной подготовкой по основам профессиональных знаний и готовностью к использованию их в профессиональной деятельности (ОК-11);

- умение понять поставленную задачу (ПК-2);

- умение формулировать результат (ПК-3);

- умение строго доказать утверждение (ПК-4).

- умение грамотно пользоваться языком предметной области (ПК-7);

- выделение главных аспектов при доказательстве теорем (ПК-16)

- понимание того, что фундаментальные знания являются основой компьютерных наук (ПК-12);

В результате изучения дисциплины студент должен:

- знать основные определения и теоремы проективной геометрии, место проективной геометрии среди других математических дисциплин;

- уметь формулировать и доказывать теоремы проективной геометрии, самостоятельно решать классические задачи проективной геометрии;

- владеть (быть в состоянии продемонстрировать) навыками: практического использования математических методов при анализе различных задач

5. Структура дисциплины.

Проективная прямая. Координаты на проективной прямой. Проективная плоскость. Координаты на проективной плоскости.

6. Основные образовательные технологии.

В качестве ведущих форм организации педагогического процесса используются традиционные (лекции, практические, семинарские и т.д.), а также активные и интерактивные технологии (проблемное обучение и т.д.)

7. Общая трудоемкость дисциплины.

3 зачетных единицы (108 академических часов).

8. Формы контроля.

Промежуточная аттестация – зачёт (2 семестр).

9. Составитель.

Зыков Пётр Сергеевич, кандидат физико-математических наук, доцент кафедры алгебры, геометрии и теории обучения математике КГУ.

Аннотация к рабочей программе

дисциплины «Элементы многомерной геометрии»

1. Место дисциплины в структуре основной образовательной программы (ООП).

Дисциплина включена в вариативную часть профессионального цикла ООП. К исходным требованиям, необходимым для изучения дисциплины «Элементы многомерной геометрии» относятся знания, умения, виды деятельности и компетенции, сформированные в процессе изучения дисциплины «Аналитическая геометрия». Дисциплина «Элементы проективной геометрии» является важной составляющей подготовки бакалавра математики.

2. Место дисциплины в модульной структуре ООП.

Дисциплина «Элементы многомерной геометрии» является курсом по выбору.

3. Цель изучения дисциплины.

Целью освоения учебной дисциплины «Элементы многомерной геометрии» является формирование компетенций, необходимых для осуществления профессиональной деятельности, требующей углубленной фундаментальной и профессиональной подготовки в области математики.

4. Требования к результатам освоения дисциплины.

Процесс изучения дисциплины направлен на формирование следующих общекультурных и профессиональных компетенций:

- фундаментальной подготовкой по основам профессиональных знаний и готовностью к использованию их в профессиональной деятельности (ОК-11);

- умение понять поставленную задачу (ПК-2);

- умение формулировать результат (ПК-3);

- умение строго доказать утверждение (ПК-4).

- умение грамотно пользоваться языком предметной области (ПК-7);

- выделение главных аспектов при доказательстве теорем (ПК-16)

- понимание того, что фундаментальные знания являются основой компьютерных наук (ПК-12);

В результате изучения дисциплины студент должен:

- знать основные определения и теоремы многомерной геометрии, место многомерной геометрии среди других математических дисциплин;

- уметь формулировать и доказывать теоремы многомерной геометрии, самостоятельно решать классические задачи многомерной геометрии;

- владеть (быть в состоянии продемонстрировать) навыками: практического использования математических методов при анализе различных задач

5. Структура дисциплины.

Элементы общей теории многомерных пространств. Понятие векторного многомерного пространства на основе аксиоматики Вейля. Евклидово векторное пространство. Четырёхмерное пространство, его определение и исследование. Применение многомерной геометрии.

6. Основные образовательные технологии.

В качестве ведущих форм организации педагогического процесса используются традиционные (лекции, практические, семинарские и т.д.), а также активные и интерактивные технологии (проблемное обучение и т.д.)

7. Общая трудоемкость дисциплины.

3 зачетных единицы (108 академических часов).

8. Формы контроля.

Промежуточная аттестация – зачёт (2 семестр).

9. Составитель.

Зыков Пётр Сергеевич, кандидат физико-математических наук, доцент кафедры алгебры, геометрии и теории обучения математике КГУ.

Аннотация к рабочей программе

дисциплины «Системы управления базами данных»

1. Место дисциплины в структуре основной образовательной программы (ООП).

Место дисциплины в ООП – Профессиональный цикл. Дисциплины по выбору (Б.3.ДВ7).

2. Место дисциплины в модульной структуре ООП.

Изучение дисциплины предполагает знание студентами основ информатики и практическое умение работы на персональном компьютере (ПК).

3. Цель изучения дисциплины.

Целью освоения учебной дисциплины «Системы управления базами данных» является формирование у учащихся теоретических знаний о принципах и основах построения современных систем управления базами данных (СУБД), навыков проведения научно-исследовательской работы, а также практических умений и навыков по моделированию, созданию и манипулированию СУБД.

4. Требования к результатам освоения дисциплины.

Процесс изучения дисциплины направлен на формирование следующих общекультурных и профессиональных компетенций:

навыками работы на компьютере (ОК-12);
базовыми знаниями в областях информатики и современных информационных технологий, навыками использования программных средств и навыками работы в компьютерных сетях, умение создавать базы данных и использовать ресурсы Интернет (ОК-13);
умением извлекать полезную научно-техническую информацию из электронных библиотек, реферативных журналов, сети Интернет (ПК-17);

В результате изучения дисциплины студент должен:

знать:

проблематику курса «Системы управления базами данных» и его основных разделов, базовые понятия и определения;
уровни представления данных в системах обработки информации, модели и методы обработки моделей представления данных;
операции реляционной алгебры и исчисления; нормальные формы схем отношений;
команды языка запросов SQL;

уметь:

ориентироваться в системах управления базами данных, пользоваться специальной литературой в изучаемой предметной области;
разрабатывать базы данных и анализировать существующие;
обрабатывать данные с помощью языка запросов SQL;
обосновывать выбор средств для решения конкретных задач учебного назначения;
ориентироваться в системах управления базами данных, их структурах, возможностях, перспективах развития;

владеть (быть в состоянии продемонстрировать) навыками:

проектирования баз данных;
оформления проектной документации;
описания и отладке схем и подсхем;
общения с базой данных.

навыками работы на компьютере (ОК-12);
базовыми знаниями в областях информатики и современных информационных технологий, навыками использования программных средств и навыками работы в компьютерных сетях, умение создавать базы данных и использовать ресурсы Интернет (ОК-13);
умением извлекать полезную научно-техническую информацию из электронных библиотек, реферативных журналов, сети Интернет (ПК-17);

В результате изучения дисциплины студент должен:

знать принципы построения, назначение, структуру, функции и основы электронного бизнеса, сущность и содержание электронной коммерции, классификацию электронных предприятий, модели электронного бизнеса инструментальные средства создания электронного бизнеса, особенности продажи товаров и предоставления услуг по категориям товаров и услуг, сущность и содержание электронных платежей, теоретические основы информационной безопасности электронного бизнеса
уметь выбирать рациональные ИС и ИКТ-решения для управления бизнесом, управлять контентом предприятия и Интернет-ресурсов, управлять процессами создания и использования информационных сервисов (контент-сервисов), использовать современные стандарты и методики, разрабатывать регламенты для организации управления процессами жизненного цикла ИТ- инфраструктуры предприятий, позиционировать электронное предприятие на глобальном рынке; формировать потребительскую аудиторию и осуществлять взаимодействие с потребителями, организовывать продажи в среде Интернет, проектировать и внедрять компоненты ИТ-инфраструктуры предприятия, обеспечивающие достижение стратегических целей и поддержку бизнес-процессов, проектировать архитектуру электронного предприятия, разрабатывать контент и ИТ-сервисы предприятия и Интернет-ресурсов, работать с различными платежными системами.
владеть (быть в состоянии продемонстрировать) навыками выбора инструментальных решений для управления бизнесом, управления процессами создания и использования информационных сервисов на основе современных стандартов и методик, взаимодействия с потребителем, организации продаж в среде Интернет, проектирования электронного предприятия, работы с различными платежными системами.

5. Общая трудоемкость дисциплины.

6 зачетных единиц (216 академических часов)

6. Формы контроля.

Промежуточная аттестация, зачет (4 семестр).

7. Составитель.

Травкин Евгений Иванович, к.п.н, доцент кафедры методики преподавания информатики и информационных технологий КГУ.

Аннотация к рабочей программе дисциплины «Мультимедиа-и интернет технологии»

1. Место дисциплины в структуре основной образовательной программы, в модульной структуре ООП.

Дисциплина «Мультимедиа и интернет технологии» включена в вариативную часть профессионального цикла ООП. К исходным требованиям, необходимым для изучения дисциплины «Мультимедиа и интернет технологии», относятся знания, умения и виды деятельности, сформированные в процессе изучения дисциплин «Технологии программирования на ЭВМ».

Дисциплина «Мультимедиа и интернет технологии» является основой для изучения дисциплин: «Web дизайн» и для последующего изучения других дисциплин вариативной части профессионального цикла, а также для прохождения производственной практики.

2. Цель изучения дисциплины

Целью изучения учебной дисциплины «Мультимедиа и интернет технологии» является приобретение знаний и умений по проектированию, разработке профессиональных мультимедиа материалов, необходимых для успешной профессиональной деятельности и организации работы с ними с помощью интернет технологий.

3. Структура дисциплины

Восприятие звуковой и видеоинформации человеком. Аппаратные средства мультимедиа. Инструментальные интегрированные программные среды разработчика мультимедиа. Форматы и стандарты мультимедиа. Сжатие звуковой информации. Программные и аппаратные средства обработки звука. Сжатие видеоинформации. Программные и аппаратные средства обработки видео. Мультипликация. Flash технологии. Каскадные таблицы стилей. Программирование на стороне клиента. Программирование на стороне сервера. Серверные языки программирования. MYSQL. Фреймворки. Системы управления контентом.

4. Основные образовательные технологии

В процессе изучения дисциплины используются не только традиционные, но и инновационные технологии, активные и интерактивные методы и формы обучения: лекции, практические занятия, деловые игры, элементы научного исследования и др.

5. Требования к результатам освоения дисциплины.

Процесс изучения дисциплины «Мультимедиа-технологии» направлен на формирование следующих общекультурных и профессиональных компетенций:

Способность применять знания на практике (ОК-6);
Исследовательскими навыками (ОК-7);
Способность приобретать новые знания, используя современные образовательные и информационные технологии (ОК-8);
Способность понимать сущность и значение информации в развитии современного общества, соблюдением основных требований информационной безопасности, в том числе защиты государственных интересов и приоритетов (ОК-9);
Умением находить, анализировать и контекстно обрабатывать научно-техническую информацию (ОК-10);
фундаментальной подготовкой по основам профессиональных знаний и готовностью к использованию их в профессиональной деятельности(ОК-11);
навыками работы с компьютером (ОК-12)
базовыми знаниями в областях информатики и современных информационных технологий, навыки использования программных средств и навыки работы в компьютерных сетях, умение создавать базы данных и использовать ресурсы Интернет (ОК-13);
определение общих форм, закономерностей и инструментальных средств отдельной предметной области (ПК-1);
умением понять поставленную задачу (ПК-2);
умением формулировать результат (ПК-3);
умением грамотно пользоваться языком предметной области (ПК-7);
умением ориентироваться в постановках задач (ПК-8);
Самостоятельным построением алгоритма и его анализ (ПК-11);
Пониманием того, что фундаментальное знание является основой компьютерных наук (ПК-12);
Контекстной обработкой информации (ПК-14);
Умением извлекать полезную научно-техническую информацию из электронных библиотек, реферативных журналов, сети Интернет (ПК-17);

В результате изучения дисциплины обучающийся должен:

знать: различные типы мультимедиа-информации; программные комплексы по созданию и редактированию мультимедиа-информации; принципы разработки мультимедиа-материалов; языки программирования на стороне сервера; языки программирования на стороне клиента; framework для разработки web-приложений и информационных ресурсов; принципы и способы проектирования и создания web-приложений; принципы создания и функционирования систем управления контентом.
уметь: работать в современных программных комплексах по созданию и редактированию мультимедиа-информации; проектировать и разрабатывать профессиональные мультимедиа-материалы; проектировать и разрабатывать web-приложения и информационные ресурсы.
владеть (быть в состоянии продемонстрировать): навыками использования программ для создания и редактирования мультимедиа-информации; навыками разработки профессиональных мультимедиа материалов; навыками проектирования и разработки web-приложений и информационных ресурсов.

6. Общая трудоемкость дисциплины.

4 зачетных единиц (144 академических часов)

7. Формы контроля.

Промежуточная аттестация – зачет.

8. Составитель.

Телегин Антон Александрович, кандидат педагогических наук, доцент кафедры методики преподавания информатики и информационных технологий.

Аннотация к рабочей программе

дисциплины «Web-дизайн»

1. Место дисциплины в структуре основной образовательной программы (ООП).

Дисциплина «Web-дизайн» включена в вариативную часть профессионального цикла ООП. К исходным требованиям, необходимым для изучения дисциплины «Web-дизайн», относятся знания, умения и виды деятельности, сформированные в процессе изучения дисциплин «Технологии программирования на ЭВМ», «Мультимедиа и интернет технологии».

Дисциплина «Web дизайн» является основой для последующего изучения других дисциплин вариативной части профессионального цикла, а также для прохождения производственной практики.

2. Цель изучения дисциплины.

Целью изучения учебной дисциплины «Web-дизайн» является приобретение знаний и умений по проектированию, разработке использованию и поддержке информационных ресурсов, применяемых в профессиональной деятельности.

3. Структура дисциплины

Определение проекта. Разработка структуры. Работа с контентом. Разработка визуального (графического) оформления. Проектирование usability. Кодирование и контроль качества. Запуск и сопровождение.

4. Основные образовательные технологии

В процессе изучения дисциплины используются не только традиционные, но и инновационные технологии, активные и интерактивные методы и формы обучения: видео лекции, практические занятия, деловые игры, дискуссионные методы, тренинги.

5. Требования к результатам освоения дисциплины

Процесс изучения дисциплины «Web-дизайн» направлен на формирование следующих профессиональных и профессиональных компетенций:

Способность применять знания на практике (ОК-6);
Исследовательскими навыками (ОК-7);
Способность приобретать новые знания, используя современные образовательные и информационные технологии (ОК-8);
Способность понимать сущность и значение информации в развитии современного общества, соблюдением основных требований информационной безопасности, в том числе защиты государственных интересов и приоритетов (ОК-9);
Умением находить, анализировать и контекстно обрабатывать научно-техническую информацию (ОК-10);
фундаментальной подготовкой по основам профессиональных знаний и готовностью к использованию их в профессиональной деятельности(ОК-11);
навыками работы с компьютером (ОК-12)
базовыми знаниями в областях информатики и современных информационных технологий, навыки использования программных средств и навыки работы в компьютерных сетях, умение создавать базы данных и использовать ресурсы Интернет (ОК-13);
определение общих форм, закономерностей и инструментальных средств отдельной предметной области (ПК-1);
умением понять поставленную задачу (ПК-2);
умением формулировать результат (ПК-3);
умением грамотно пользоваться языком предметной области (ПК-7);
умением ориентироваться в постановках задач (ПК-8);
Самостоятельным построением алгоритма и его анализ (ПК-11);
Пониманием того, что фундаментальное знание является основой компьютерных наук (ПК-12);
Контекстной обработкой информации (ПК-14);
Умением извлекать полезную научно-техническую информацию из электронных библиотек, реферативных журналов, сети Интернет (ПК-17);

В результате изучения дисциплины должен:

знать язык разметки html; каскадные таблицы стилей css; принципы проектирования сайта; алгоритмы проектирования структуры сайта; принципы создания графического дизайна; принципы совершенствования usability сайта; принципы работы в системах управления контентом.
уметь проектировать структуру сайта; разрабатывать графический дизайн сайта; верстать html-страницы с помощью разных типов верстки; устанавливать, настраивать и работать в различных системах управления контентом; проводить анализ качества сайта.
владеть (быть в состоянии продемонстрировать): навыками html-верстки; навыками разработки графического дизайна сайта; навыками повышения usability сайта; установки, настройки и использования систем управления контентом; навыками проектирования и разработки сайтов.

6. Общая трудоемкость дисциплины.

4 зачетных единицы (144 академических часов)

7. Форма(-ы) контроля.

Промежуточная аттестация – зачет.

8. Составитель.

Телегин Антон Александрович, кандидат педагогических наук, доцент кафедры методики преподавания информатики и информационных технологий.

Blog

Аннотации к программам дисциплин (модулей)