Теоретические и экспериментальные исследования магнитных полей дефектов конечных размеров и создание специализированных сканеров для дефектоскопии трубопроводов

Вид материала

Автореферат

Содержание Глава 3. Теоретическое исследование распределения магнитного поля рассеяния дефектов конечных размеров для внутритрубной дефекто Рис.10. Поверхностные трещины В главе разработан новый подход к решению задачи распределения магнитного поля рассеяния над дефектом типа трещина.

Подобный материал:

• Методы дефектоскопии трубопроводов нефтеперерабатывающих заводов, 49.38kb.
• Возможности формирования магнитных полей с заданным распределением индукции на центральной, 9.53kb.
• Лабораторная работа по физике №2-24. Экспериментальные исследования электростатических, 311.12kb.
• Магнитное поле в вакууме, 56.29kb.
• Первоначальные сведения о магнетизме, 53.52kb.
• Устойчивость состояний тонкопленочных слоев магнитных носителей к внешним импульсным, 96.67kb.
• Рабочая программа учебной дисциплины (модуля) Метод конечных элементов и программы, 141.68kb.
• Луцький национальный технический университет, 95.19kb.
• Теоретические и экспериментальные Исследования распространения упругих волн в поврежденных, 277.14kb.
• Метод эпр для измерения магнитной индукции переменных полей, 65.24kb.

Глава 3. Теоретическое исследование распределения магнитного поля рассеяния дефектов конечных размеров для внутритрубной дефектоскопии

Б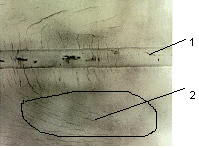ольшинство реальных трещин являются трещинами конечных размеров и распространяются вглубь металла не перпендикулярно поверхности, а под некоторым углом к ней (рис.10,11).

Рис.10. Поверхностные трещины 1- продольный сварной шов; 2- стресс-коррозионные трещины.

Рис.11. Поперечный шлиф стенки трубы с дефектом типа "трещина". 1-стенка трубы; 2-трещина.

В главе разработан новый подход к решению задачи распределения магнитного поля рассеяния над дефектом типа трещина.

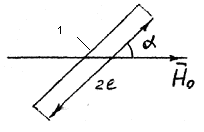
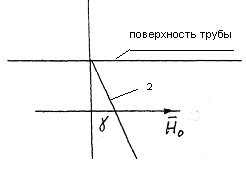а в




Рис.12. Варианты расположения трещин: а-трещина 1 расположенная под

углом к направлению намагничивающего поля H₀; в- трещина 2 расположенная под углом 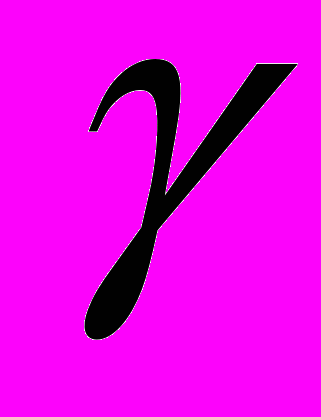поверхности трубы.


В качестве модели дефекта предлагается модель магнитного поля рассеяния дефекта типа «трещина» конечных размеров на внутренней и внешней сторонах трубопровода в виде двух бесконечно тонких витков прямоугольного сечения длиной, равной длине дефекта, высотой, равной глубине дефекта, по которым протекает ток I, плотностью , пропорциональной нормальной составляющей намагниченности J_п ферромагнетика, в котором находится данный дефект (рис.13).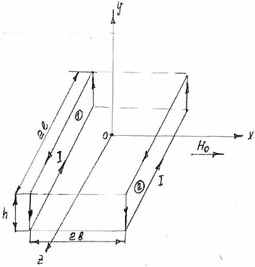





Рис.13. Токовая модель поверхностного дефекта конечной протяженности.

2l –длина, 2b-ширина, h-глубина трещины, 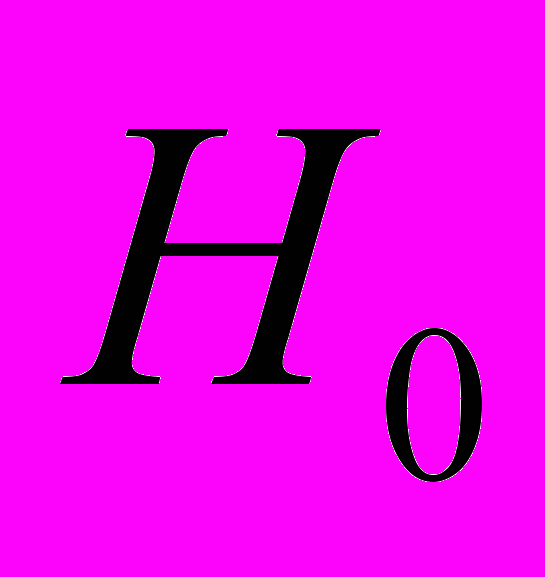-напряженность намагничивающего магнитного поля, 1,2-витки с током.


Получены формулы для определения нормальной и тангенциальной составляющих магнитного поля рассеяния дефектов типа трещина конечных размеров на внутренней и внешней сторонах трубопровода, расположенных под углом к направлению намагничивающего поля и под углом 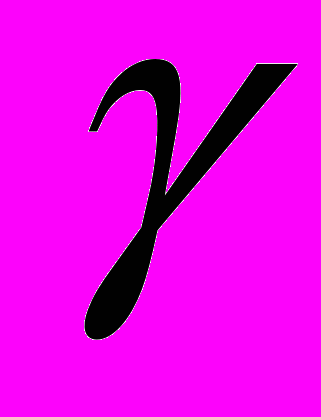поверхности трубы.

Ниже приведены формулы для тангенциальной составляющей магнитного поля рассеяния дефектов трещины конечных размеров на внутренней поверхности трубопровода (угол и угол 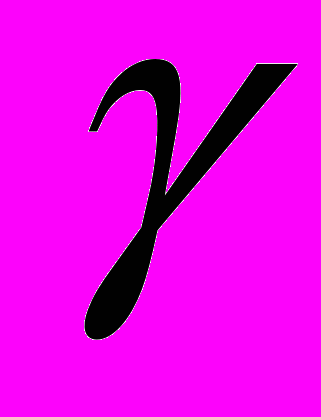равны нулю)

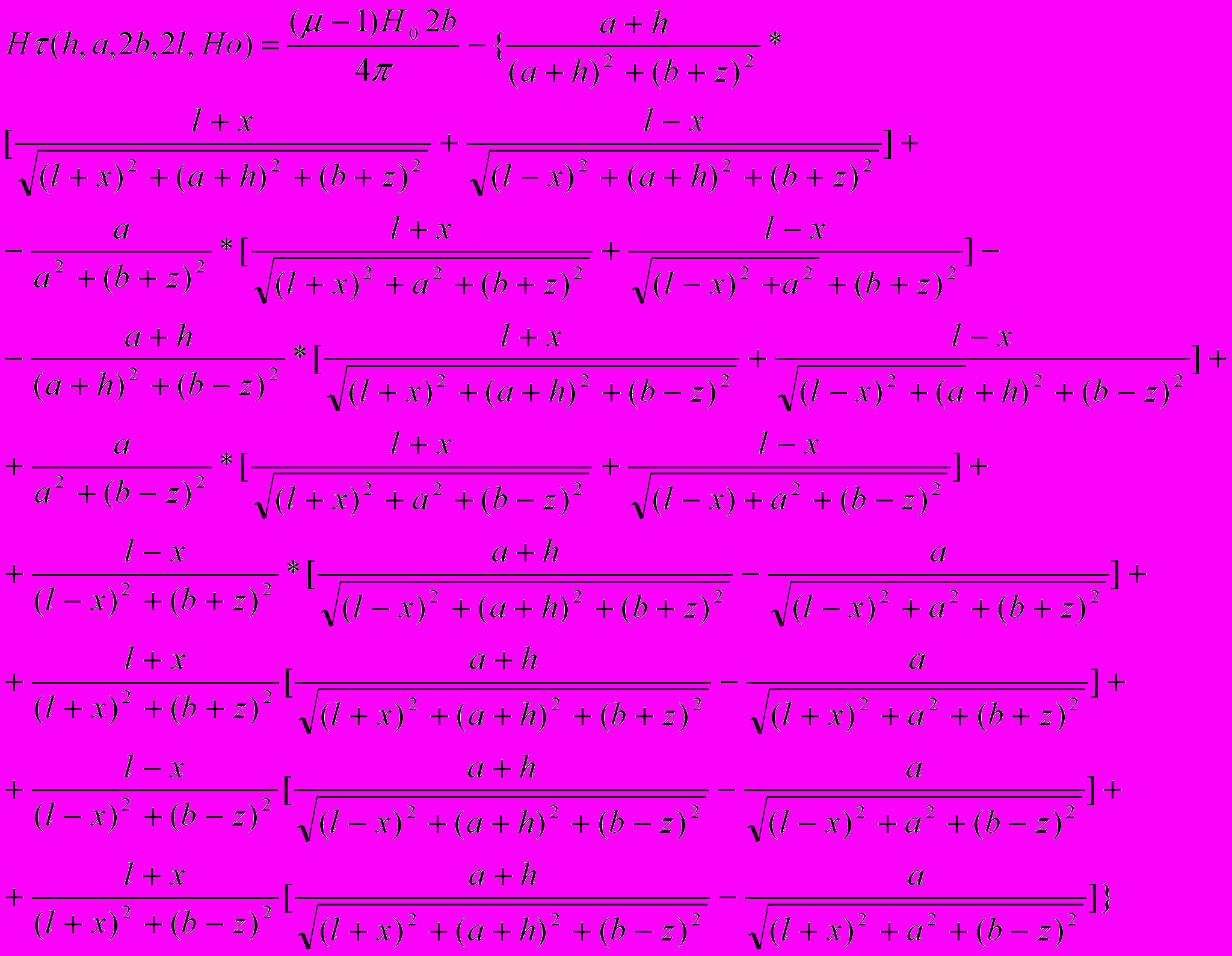(2)


и на внешней стороне трубопровода


(3)




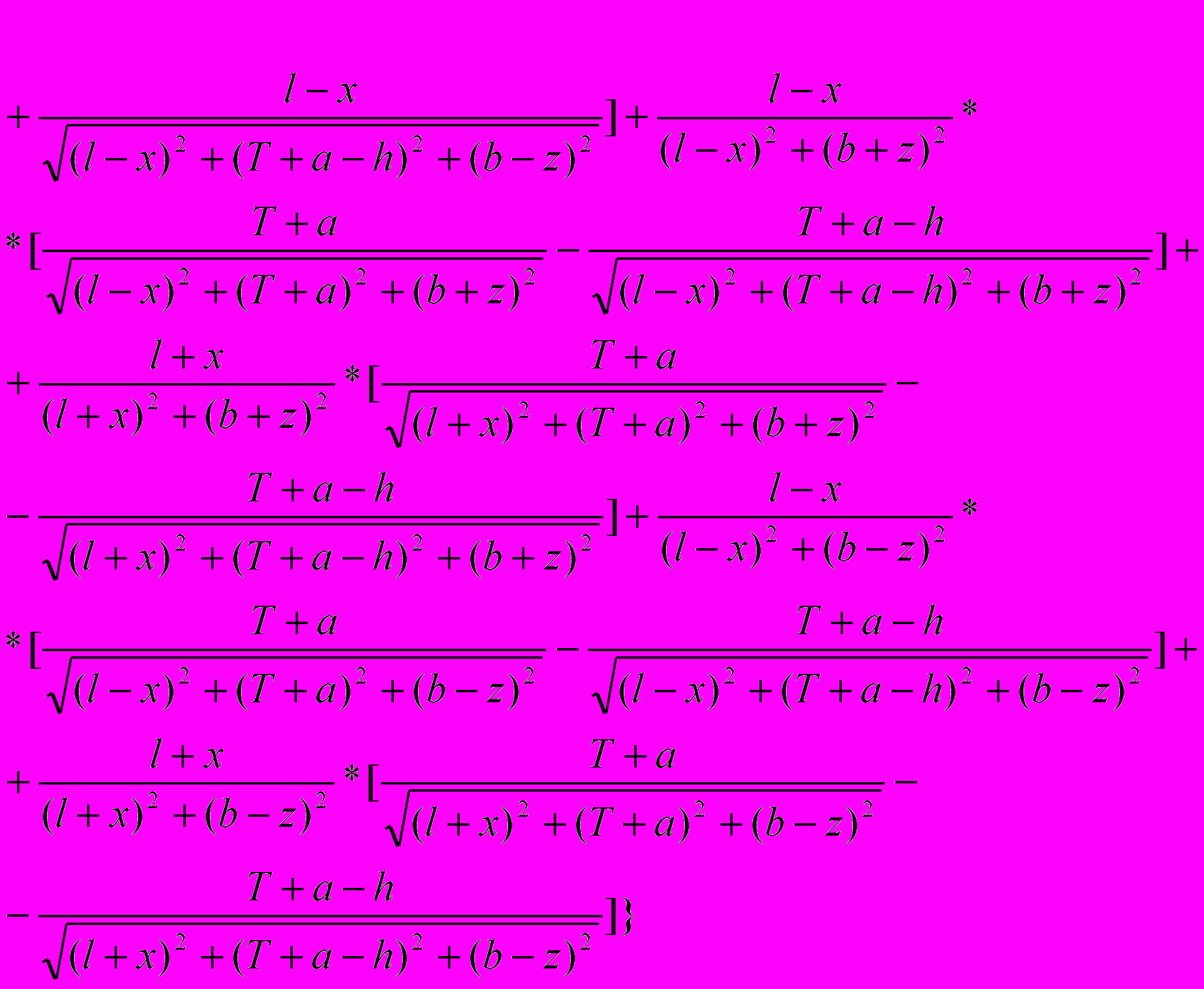
Здесь T-толщина стенки трубопровода.

Остальные формулы не приводятся из-за их громоздкости.


На рис.14.,15. (длина дефекта равна 40мм) приведены распределения магнитных полей рассеяния дефектов типа внутренняя и наружная трещины, рассчитанные по формулам, полученным в работе

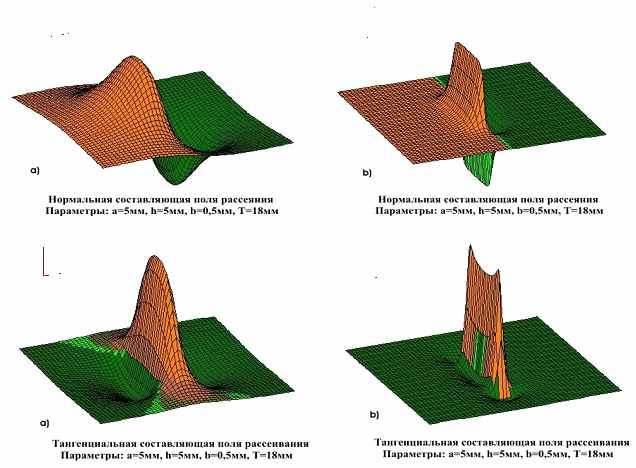
Рис.14. Распределение нормальной составляющей магнитного поля рассеяния над трещиной с параметрами: а=5мм, h=5мм, b=0,5мм, толщина стенки трубопровода T=18мм; a на внешней стороне трубопровода b- на внутренней стороне трубопровода.





Рис.15. Распределение тангенциальной составляющей магнитного поля рассеяния над трещиной с параметрами: а=5мм, h=5мм, b=0,5мм, толщина стенки трубопровода T=18мм; a-на внешней стороне трубопровода b- на внутренней стороне трубопровода.


Разработан математический аппарат решения задачи распределения магнитного поля рассеяния от сварного шва и дефекта типа пора в сварном шве. Получена формула (4) для расчета распределения тангенциальная составляющая магнитного поля рассеяния Н_, в зоне бездефектного сварного шва для расчетной модели, приведенной на рис.16.


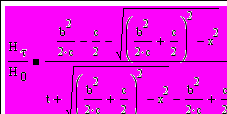(4)



где 2b - ширина валика усиления сварного шва,

с - высота валика усиления сварного шва,

t – толщина стенки трубы,

 - высота точки наблюдения.



Рис.16. Расчетная модель для бездефектного сварного шва.


Для исследования влияния дефекта типа пора в сварном шве на распределение магнитного поля выбрана расчетная модель, представленная на рис.17.



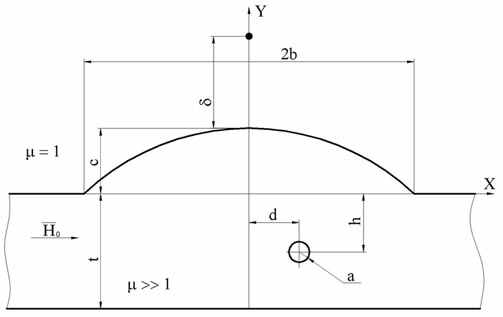
Рис.17. Расчетная модель с дефектом типа пора в сварном шве

где 2b - ширина валика усиления сварного шва,

с - высота валика усиления сварного шва,

t – толщина стенки трубы,

 - высота точки наблюдения,

d – расстояние от поры до оси шва,

a – радиус поры,

h – глубина залегания поры.


Получена формула для определения зависимости и распределения тангенциальной составляющей магнитного поля Н_d/Н₀ для дефекта типа «пора» в толще шва с учетом неоднородности распределения магнитного поля в сварном шве:



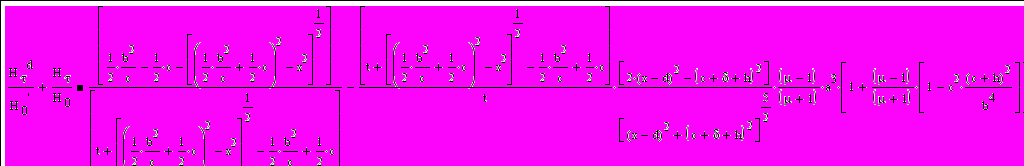
(5)


где, H_^d – тангенциальная составляющая поля от дефекта на поверхности;

H₀^` - значение поля в сварном шве;

d – смещение поры от центральной оси Y в направлении оси X;


Приведен расчет распределения магнитного поля рассеяния над дефектом типа «пора», расположенной внутри сварного шва. При смещении «поры» от центральной оси Y распределение тангенциальной составляющей магнитного поля выглядит следующим образом (рис.18):





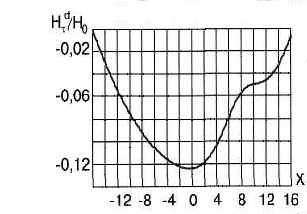
Рис.18. Зависимость H_^d /Н₀ от Х [мм], для d=6мм, h=5мм, a=1.5мм.


Проведена адаптация теоретических решений распределения магнитного поля над дефектом типа трещина к внутритрубному контролю. Важную роль при определении остаточного ресурса играет точность измерения параметров дефектов: длины и глубины. Особенно глубины, так как. она напрямую связана с точностью определения Hmax. В современных дефектоскопах информация о распределении магнитного поля рассеяния дефекта представлена в дискретном виде как вдоль трубопровода, так и поперек него.

На примере дискретного распределения магнитного поля над дефектом типа трещина (рис. 19) показан путь определения Hmax при проведении внутритрубного контроля с шагом записи распределения магнитного поля над поверхностью трубы равном «с»( продольное намагничивание), для поперечного намагничивания «с» равно расстоянию между датчиками.




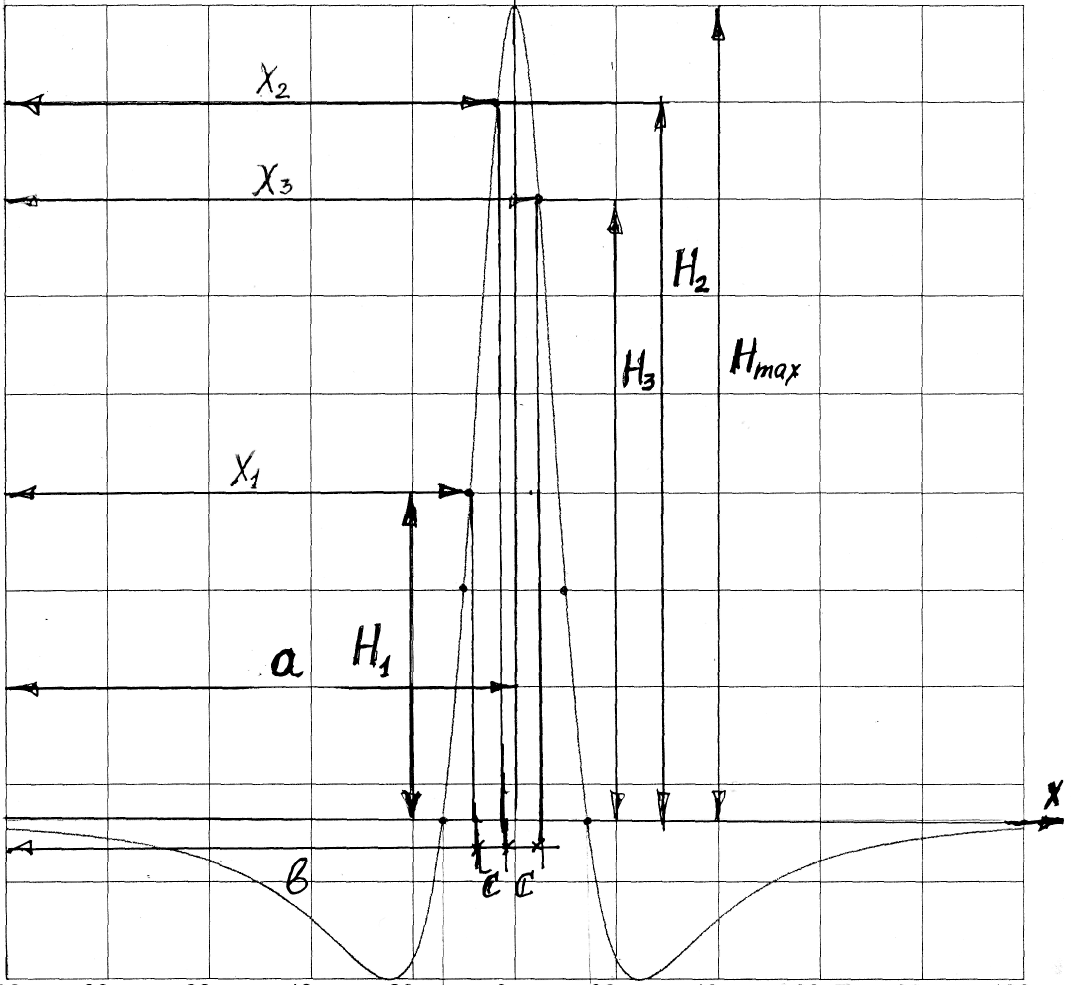
Н (А/м)


Рис 19. Дискретное распределения магнитного поля над дефектом типа трещина:

-расстояние от точки отсчета до кривой распределения магнитного поля над дефектом типа трещина Hmax;

Х₁-расстояние от точки отсчета до кривой распределения магнитного поля над дефектом типа трещина;

H₁-значение магнитного поля в точке Х=Х₁;

Х₂-расстояние от точки отсчета до кривой распределения магнитного поля над дефектом типа трещина;

H₂- значение магнитного поля в точке Х=Х₂;

Х₃-расстояние от точки отсчета до кривой распределения магнитного поля над дефектом типа трещина;

H₃- значение магнитного поля в точке Х=Х₃;

С-расстояние между датчиками (в случае продольного намагничивания расстояние между точками отсчета).

Здесь значения Х₁, Х₂, Х₃, и H₁, H₂, H₃-это значения измеренные дефектоскопом, необходимо найти Hmax.

Для этого воспользуемся формулой

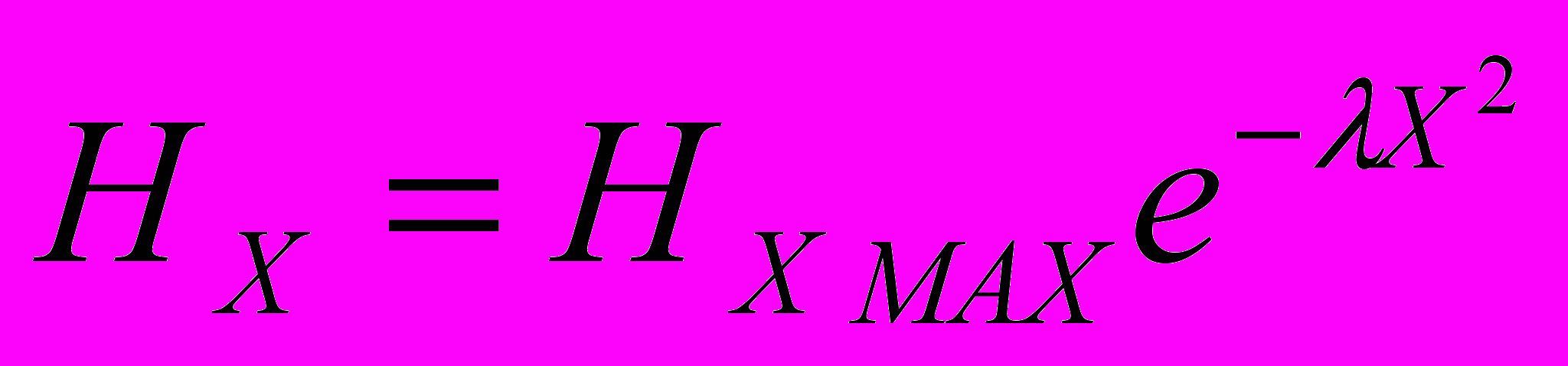(6)

После подстановки известных значений Х₁, Х₂, Х₃, и H₁, H₂, H₃ в эту формулу (6) и решения системы уравнений:



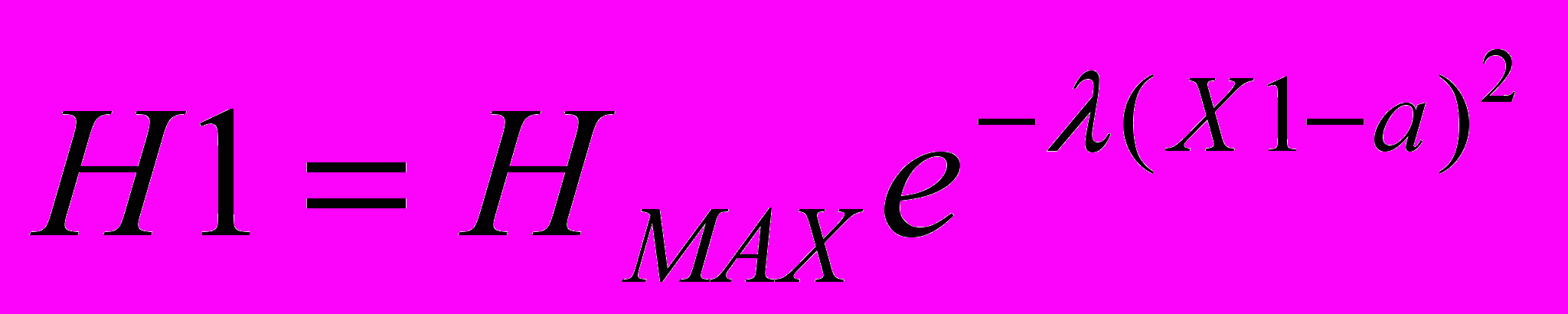
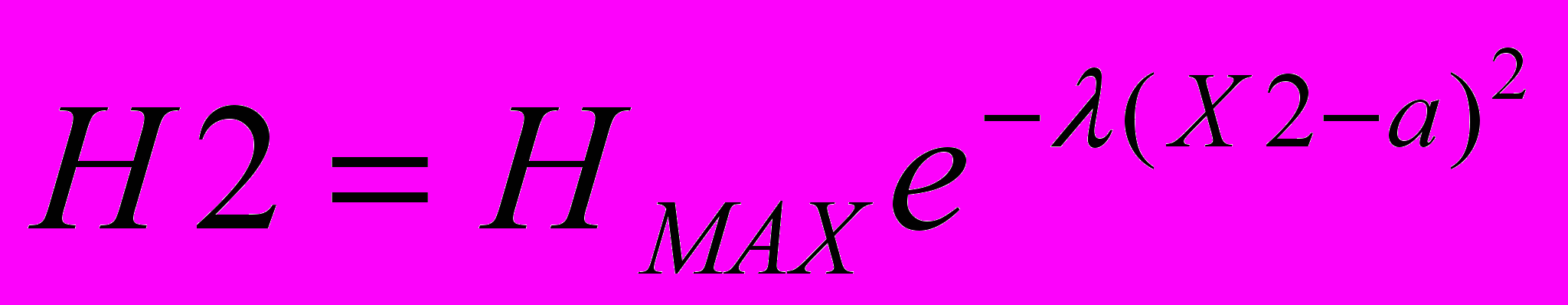(7)



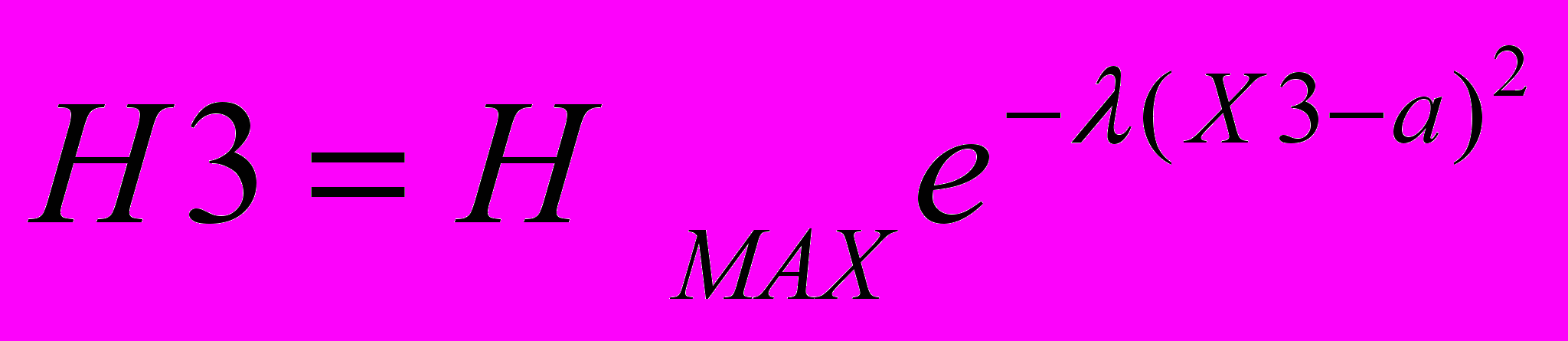
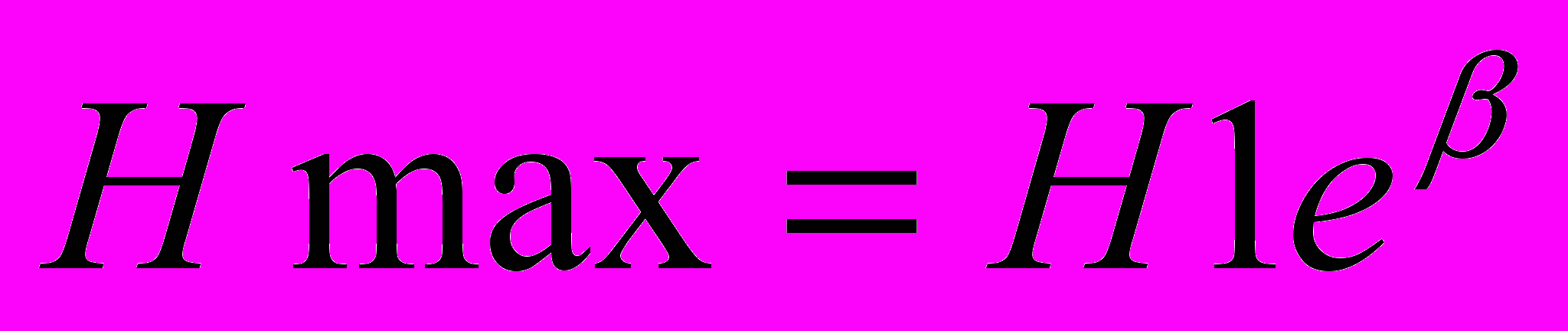
получим: где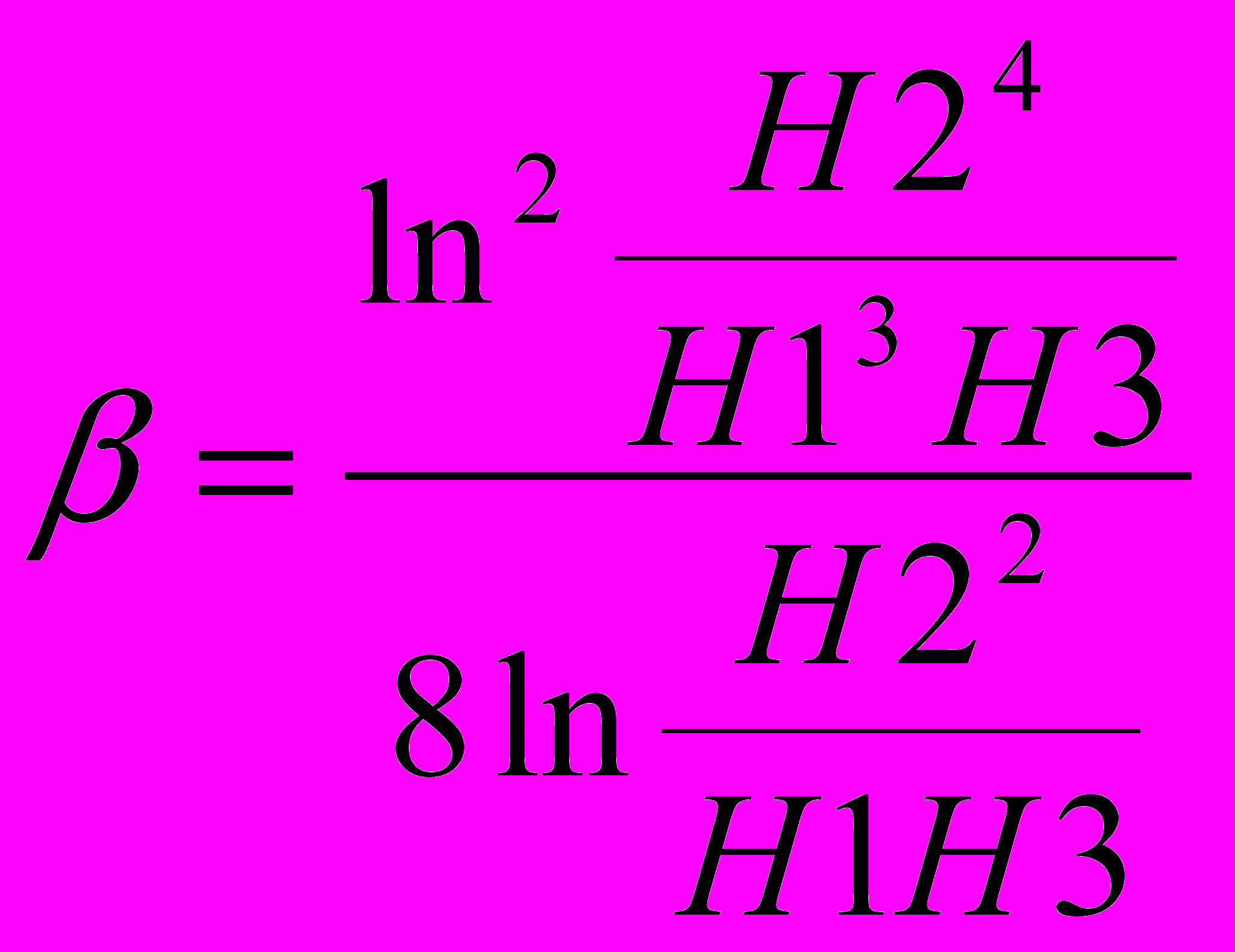

Разработана и исследована математическая модель распределения магнитного поля рассеяния дефектов типа «расслоение в стенке трубопровода. Показано, что максимальная ошибка между теоретически и экспериментально полученными распределениями магнитного поля рассеяния дефектов типа «расслоение в стенке трубопровода, составляет примерно 20%

Проведена оптимизация технологии магнитного контроля трубопроводов. Предложена методика определения необходимого и достаточного количества сенсоров для решения обратной задачи дефектоскопии (определение параметров дефекта по виду распределения магнитного поля рассеяния от него) на примере распределения тангенциальной составляющей магнитного поля рассеяния дефекта типа трещина. Для построения магнитных образов дефектов и градуировочных кривых разработан специальный стенд эталонных дефектов, где магнитное поле рассеяния снимается с помощью специального магнитного сканера. По величине поля над бездефектным участком трубы определяется значение приложенного поля в стенке трубопровода (H₀). Сканер производит контроль поверхности трубопровода с шагом 1 х 2,25 мм, что позволяет получить развертку магнитного поля над контролируемой поверхностью с цветовой градацией по величине поля рассеивания. Вид дефекта, его длина и ширина определяется по топологии распределения поля над дефектом по алгоритмам, в которых использованы полученные выше формулы распределения магнитного поля рассеяния над дефектами. По градуировочной кривой распределения магнитного поля рассеяния над дефектом определяется его глубина. Максимальная ошибка между теоретически и экспериментально полученными распределениями магнитного поля рассеяния дефектов в стенке трубопровода, составляет примерно 20%-25%