Методика формирования у старшеклассников логических приемов мышления при решении уравнений и неравенств 13. 00. 02 теория и методика обучения и воспитания (математика, уровень общего образования)
| Вид материала | Автореферат |
- Методика дифференцированного обучения решению математических задач с использованием, 253.93kb.
- Задачи как средство развития креативности мышления у младших школьников специальность, 351.93kb.
- Методика обучения решению математических задач учащихся основной школы в условиях дифференциации, 489.79kb.
- Методика создания и использования системы повторительных математических диктантов как, 452.55kb.
- Развитие интереса учащихся к математике через эстетический потенциал исторических задач, 468.64kb.
- Методика формирования исследовательской компетентности школьников в области приложений, 378.99kb.
- Методика преподавания математики в средней школе. Частная методика. А. Я. Блох, 18.34kb.
- Подготовка студентов математических специальностей педвузов к обучению учащихся общеобразовательных, 355.06kb.
- Программа-минимум кандидатского экзамена по специальности 13. 00. 02 «Теория и методика, 154.39kb.
- Повышение качества математической подготовки студентов технического вуза с помощью, 352.42kb.
ОСНОВНОЕ СОДЕРЖАНИЕ ДИССЕРТАЦИИ
Во введении обосновывается актуальность темы, определяются проблема, цель, задачи, предмет и гипотеза исследования, показаны научная новизна, теоретическая значимость и практическая ценность работы.
В первой главе «Психолого-дидактические основы формирования у старшеклассников логических приемов мышления» на основе анализа психолого-дидактической и научно-методической литературы выявлены сущностные характеристики логических приемов мышления, приемов учебной работы, на их основе — взаимосвязь между этими понятиями; разработана этапная модель формирования у старшеклассников логических приемов мышления; представлены критерии и уровни сформированности логических приемов мышления у старшеклассников.
Построение модели формирования логических приемов мышления осуществляется нами в рамках деятельностного подхода.
Логический прием мышления – способ, которым учащиеся осуществляют умственную деятельность. Поскольку умственная деятельность есть «внутренний» процесс, то о сформированности логического приема мышления можно судить только по внешним проявлениям, формой которых является прием учебной работы. Под приемами учебной работы будем понимать последовательность действий, служащих для выполнения логических приемов мышления, которая задается через алгоритмические предписания. Каждый логический прием мышления реализуется через приемы учебной работы, организованные в алгоритмические предписания действий.
В психологии при формировании умственных действий выделяют полные и неполные ориентировочные основы. В качестве полных ориентировочных основ могут выступать предписания алгоритмического типа. А поскольку логический прием мышления определяется нами, вслед за А.Н. Леонтьевым, Е.Н. Кабановой-Меллер и др., через умственную деятельность, то для формирования его используются полные ориентировочные основы действия (П.Я. Гальперин, Н.Ф. Талызина), которые содержат не только образцы действия, но и все указания на то, как правильно выполнять действие с новым материалом. При этом учащийся приобретает определенное умение анализировать материал с точки зрения предстоящего действия. В рамках нашего исследования полные ориентировочные основы действий реализованы в виде приемов учебной работы, которые представляют собой алгоритмические предписания для учащихся по выполнению конкретного логического приема мышления.
Анализ научно-методической литературы (Ю.М. Колягин, Н.В. Метельский, Д. Пойа, В.И. Крупич, Г.И. Саранцев, Л.М. Фридман, К.Н. Лунгу, М.И. Махмутов) показал, что мышление формируется и изучается исследователями в методике преподавания математики в процессе решения математических задач. Решение задачи включает поиск способа, необходимого для достижения поставленной цели, а так же выполнение действия, определяемого этой целью. Процесс решения задачи реализуется через приемы учебной работы. Успешность решения задач, по К.Н. Лунгу, во многом определяется тем, насколько адекватны содержанию задачи приемы и компоненты мышления. В разных задачах могут понадобиться различные компоненты (логические приемы) мышления и их соотношения.
В соответствии с сущностными характеристиками понятия «логический прием мышления» и его взаимосвязью с приемом учебной работы нами выделены три уровня и три критерия сформированности логического приема мышления (табл. 1). Процентное соотношение количества выполненных заданий рассчитано нами с опорой на экспериментально проверенную методику перевода первичных баллов ЕГЭ в тестовые и школьные отметки из расчета соответствия отметки 3 первому уровню сформированности, 4 – второму, 5 – третьему.
Теоретический анализ научно-методической литературы и диагностирование старшеклассников позволили выявить у них три уровня сформированности логических приемов мышления, которые мы назовем с опорой на характеристики соответствующих типов мышления: репродуктивный, продуктивный эмпирический и продуктивный теоретический.
В ходе исследования разработана модель процесса формирования логических приемов мышления, которая содержит 4 этапа.
- Подготовительный этап. Цель: знакомство учащихся с определениями и схемой выполнения логических приемов мышления.
Действия учителя: инструктаж учащихся (формулирование определений, структур выполнения логических приемов мышления — приемов учебной работы).
Действия учащихся: запись и прочтение определений, запись алгоритмических предписаний выполнения логических приемов (создание словаря).
Результат этапа: воспроизведение определения конкретного логического приема мышления и умение сформулировать последовательность действий его выполнения (осмысливание действий учащимися).
- Обучающий этап. Цель: запоминание структуры приемов; формирование умений выполнять приемы по схеме.
Действия учителя: обучение логическим приемам мышления на математическом материале (работа по образцу). Оперативный контроль и коррекция процесса выполнения приемов учебной работы.
Действия учащихся: а) выполнение логических приемов мышления по образцу (по алгоритмическим предписаниям и определениям); б) самостоятельное пошаговое выполнение логических приемов мышления; в) выполнение логических приемов мышления при решении задач. Проговаривание этапов схемы выполнения приемов.
Результат этапа: осознанное выполнение приемов учебной работы, сформированность умения выполнять логические приемы мышления по схеме.
- Закрепляющий этап. Цель: формирование навыка выполнения логических приемов мышления в стандартной ситуации (без использования схемы).
Таблица 1
| Критерии Уровни | Способность учащегося дать определение конкретного логического приема мышления и сформулировать последовательность действий (приемов учебной работы) его выполнения | Выполнение приемов учебной работы, соответствующих логическому приему мышления (количество верно выполненных заданий в % от общего количества заданий) | Умение перенести логический прием мышления в новую ситуацию |
| 1-й Репродуктивный | Учащийся не способен дать определение логического приема мышления и сформулировать последовательность действия (приемы учебной работы) его выполнения | Учащийся выполняет приемы учебной работы с помощью учителя и по алгоритмическим предписаниям действий (верное выполнение 1 — 19% от числа предложенных задач) | Учащийся умеет выполнять логический прием по схеме в стандартной ситуации |
| 2-й Продуктивный эмпирический | Учащийся имеет представление о логическом приеме мышления и последовательности действий его выполнения, может сформулировать своими словами определение логического приема и схему его выполнения | Учащийся выполняет приемы учебной работы без помощи учителя и алгоритмических предписаний действий (верное выполнение 20—50% от числа предложенных задач) | Учащийся умеет выполнять прием без обращения к схеме в стандартной ситуации |
| 3-й Продуктивный теоретический | Учащийся способен дать определение конкретного логического приема мышления и сформулировать последовательность действий его выполнения | Учащийся осознанно выполняет приемы учебной работы (верное выполнение 51—100% от числа предложенных задач) | Учащийся умеет выполнять прием без обращения к схеме в нестандартной ситуации |
Действия учителя: обучение выполнению приемов учебной работы в стандартной ситуации.
Действия учащихся: пошаговое выполнение приемов без обращения к алгоритмическим предписаниям; воспроизведение схем выполнения приемов без обращения к словарю.
Результат этапа: сформированность навыка выполнения логических приемов; умение выполнять приемы в стандартной ситуации.
- Практический этап. Цель: перенос логических приемов мышления в новые ситуации.
Действия учителя: обучение умению выбирать тот или иной логический прием мышления в зависимости от содержания изучаемого материала либо задачи; организация работы по применению логических приемов мышления при изучении алгебраических темах, отличных от тем обучающего и закрепляющего этапов, то есть обучение переносу в новую ситуацию.
Действия учащихся: пошаговое выполнение приемов при решении задач без обращения к алгоритмическому предписанию; решение предложенных задач по определенным правилам; применение усвоенных логических приемов мышления; перенос умения выполнять логические приемы мышления в новые ситуации.
Результат этапа: умение выполнять приемы в нестандартной ситуации.
Во второй главе «Процесс формирования у старшеклассников логических приемов мышления при решении уравнений и неравенств» представлены методика поэтапного формирования у старшеклассников логических приемов мышления (анализ, синтез, обобщение, абстракция и конкретизация) при решении уравнений и неравенств и описание результатов экспериментальной работы.
Формирование приемов осуществляется при изучении курса алгебры и начал анализа в 10—11-х классах при изучении содержательно-методической линии «Уравнения и неравенства» (16 ч). В общей сложности на целенаправленное обучение логическим приемам отводится 16 ч: 1 и 2-й этапы формирования логических приемов мышления — при изучении тем «Иррациональные уравнения и неравенства» (4 ч), «Показательные уравнения и неравенства» (4 ч); 3 и 4-й этапы – при изучении тем «Решение логарифмических уравнений и неравенств» (4 ч), «Уравнения и неравенства с модулем» (4 ч). Формирование логических приемов осуществляется непрерывно при изучении всего курса алгебры и начал анализа, начиная с иррациональных уравнений.
Разработанная нами методика на основе модели формирования логических приемов мышления построена в соответствии с психологическим механизмом формирования, заключающимся в прохождении нескольких этапов, на каждом из которых определены компоненты (мотивационный, операционно-исполнительский и контрольно-оценочный).
Для реализации подготовительного этапа необходимо, чтобы учащиеся имели возможность постоянно обращаться к определению приема и алгоритму его выполнения. С этой целью каждому учащемуся требуется записать информацию в отдельную тетрадь (создать словарь, памятку).
В ходе эксперимента, исходя из теоретического анализа учебно-методической литературы, в качестве определений выбранных нами приемов и алгоритмических предписаний их выполнения (приемов учебной работы) при решении уравнений и неравенств были приняты следующие.
АНАЛИЗ — логический прием мышления, с помощью которого происходят мысленное разделение уравнения или неравенства на смысловые части в определенном порядке, исследование каждой части в отдельности (поиск пути решения).
Схема:
- Разделить уравнение или неравенство на смысловые части (выявить состав уравнения или неравенства; определить, какие алгебраические операции выполняются в уравнении или неравенстве; выявить, какие функции входят в уравнение или неравенство(определить степень уравнения или неравенства, либо степень неизвестного в уравнении или неравенстве) выявить логические структуры уравнения или неравенства).
- Исследовать отдельно каждую смысловую часть (при каких условиях имеет смысл выражение, входящее в уравнение или неравенство; какие следствия можно получить из данного уравнения или неравенства).
- Если нужно, включить уравнение или неравенство в связи и отношения с другими уравнениями или неравенствами или их системами, с известными теоремами (теоремы равносильности, уравнения-следствия).
Например, выполнить по схеме анализ уравнения
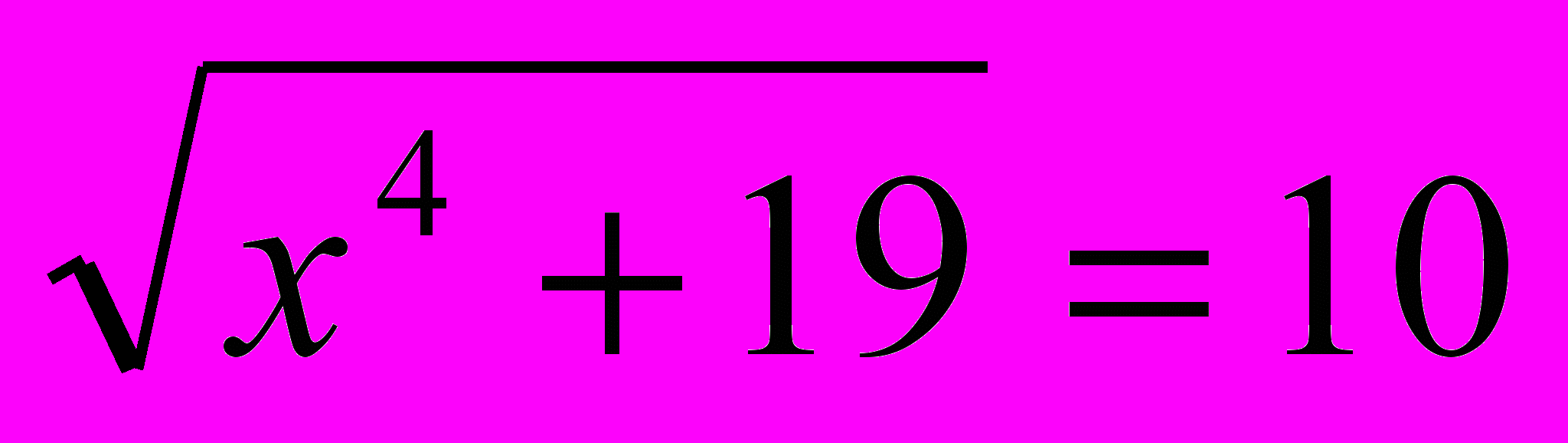 .
.Анализ:
- уравнение содержит неизвестную под знаком радикала, следовательно, задано иррациональное уравнение;
- неизвестное х в четвертой степени, следовательно, уравнение сводится к степенному уравнению;
- связи с определениями соответствующего вида уравнений:
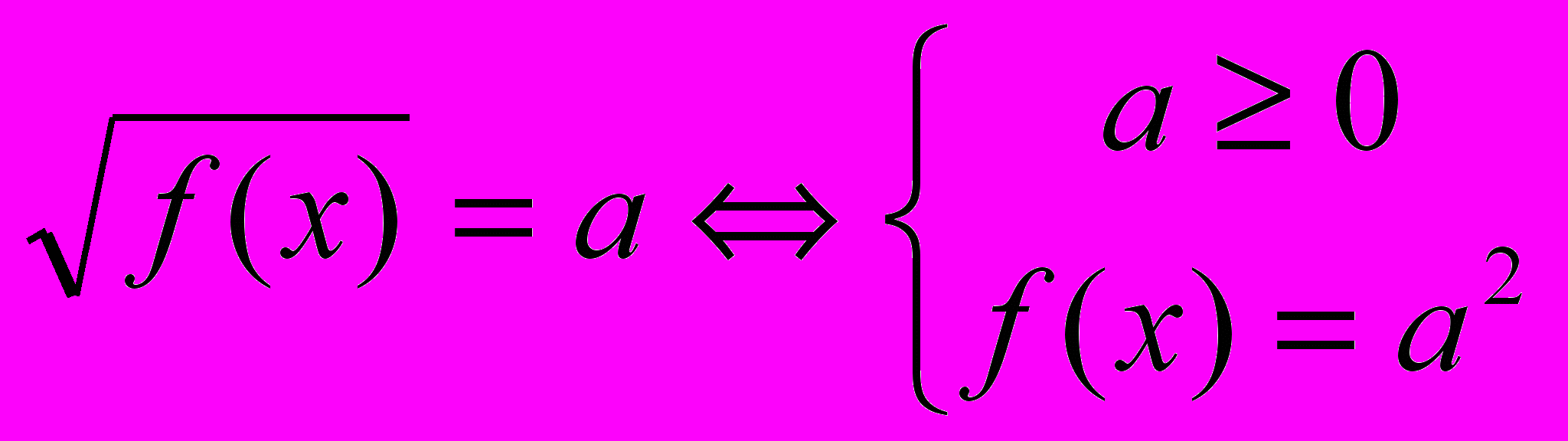 ;
; 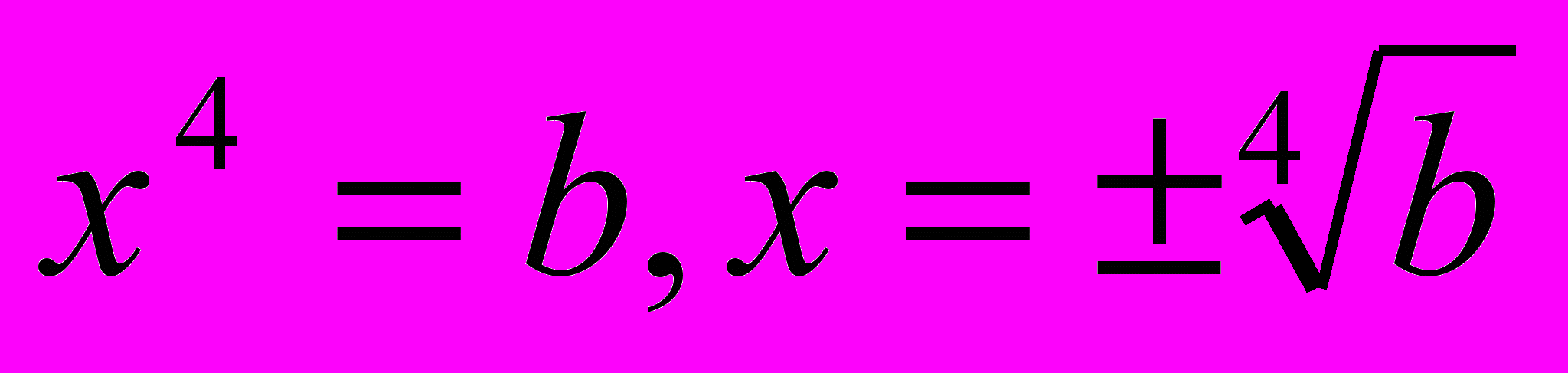 .
.
СИНТЕЗ — логический прием мышления, характеризующийся соединением результатов исследования смысловой части уравнения или неравенства в единое целое, решение уравнения или неравенства.
Схема:
- Решить уравнение или неравенство (по плану, полученному при анализе) или выполнить действия, решить уравнение или неравенство по известному алгоритму.
- Из предполагаемых корней выбрать те числа, которые удовлетворяют условиям существования выражений, входящих в исходное уравнение или неравенство (ОДЗ).
- Записать ответ.
Например, дано уравнение
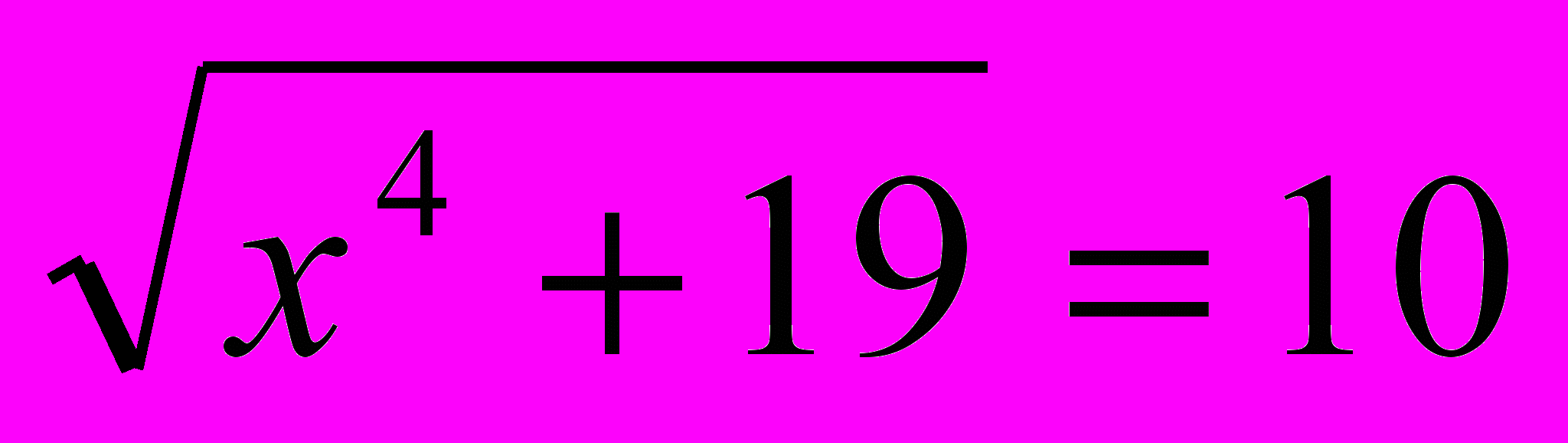 .
.Синтез:
1)
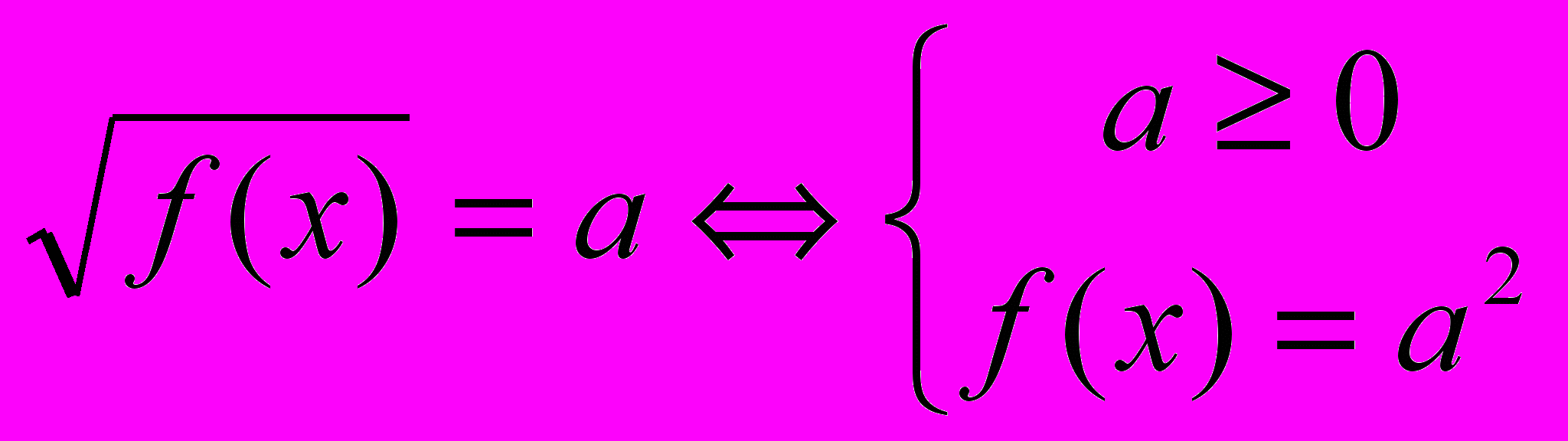 ; так как
; так как 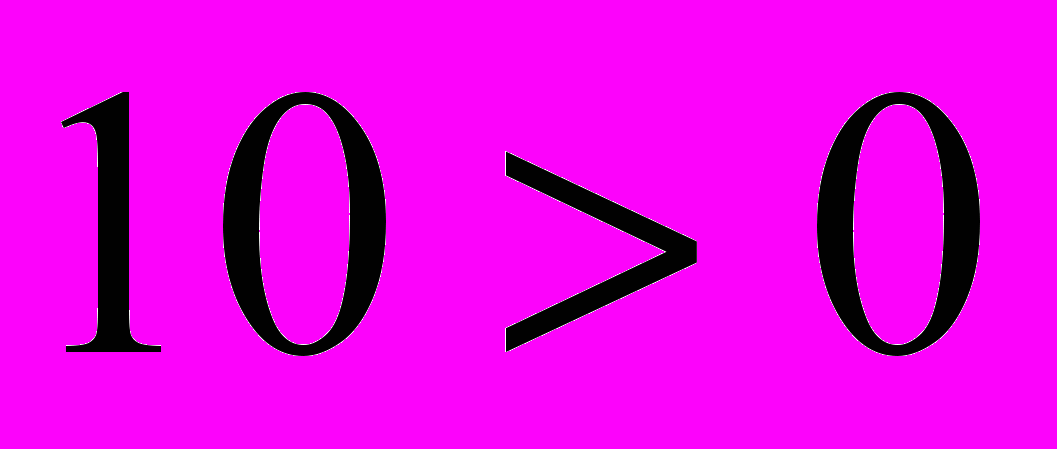 , то
, то  ;
;2)
 ,
, 



 ,
,  ;
;3) так как под знаком арифметического корня находится положительное число (
 ), то оба числа являются корнями уравнения.
), то оба числа являются корнями уравнения.Ответ: –3, 3.
ОБОБЩЕНИЕ — логический прием мышления, при котором мысленно выделяют (фиксируют) какое-либо общее для нескольких уравнений или неравенств свойство и включают уравнения и неравенства в один класс, обладающий выделенным свойством.
Схема:
- Проанализировать несколько уравнений или неравенств на предмет существования их общих свойств, сравнить, решить.
- Выделить какое-либо одно свойство.
- Объединить уравнения или неравенства, обладающие выделенным свойством, в один класс.
- Записать обобщенную формулу полученного класса уравнений и неравенств или обобщенную формулу процесса решения класса уравнений или неравенств.
Например, даны неравенства, запишите, если это возможно, обобщенную формулу их записи.
|
|
Обобщение:
- все заданные неравенства показательные; характер неравенства одинаков: «
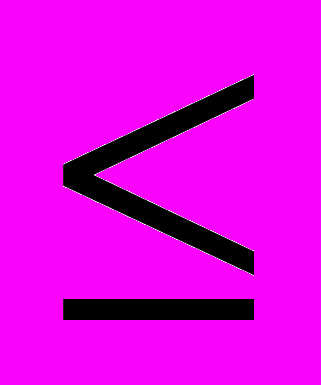 »; в каждом неравенстве содержится число меньшее единицы (дробь), следовательно, каждое неравенство можно привести к основанию
»; в каждом неравенстве содержится число меньшее единицы (дробь), следовательно, каждое неравенство можно привести к основанию 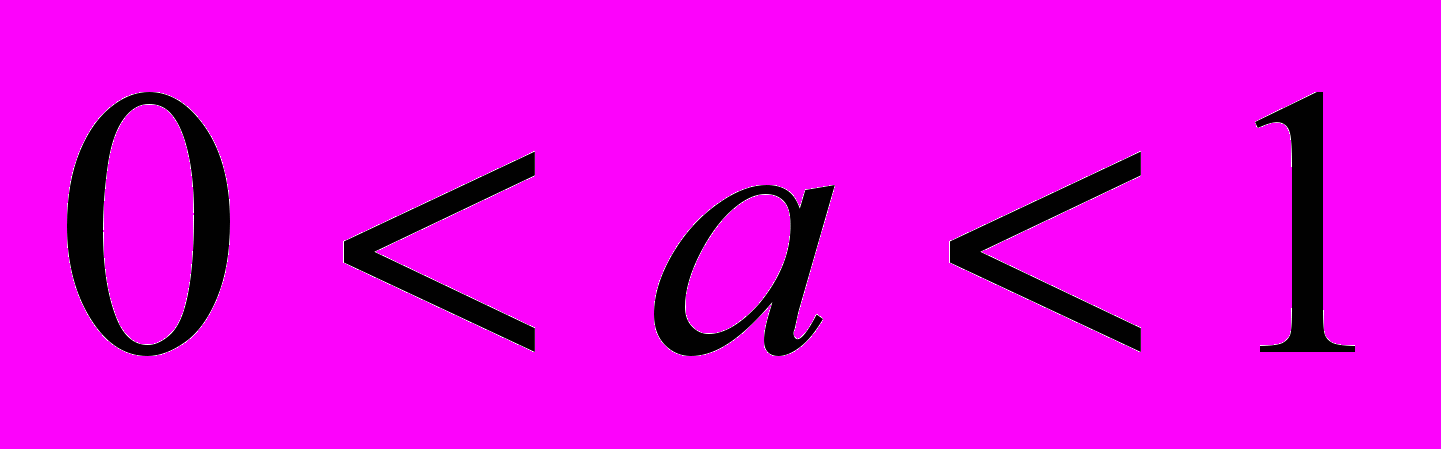 ;
;
- выделим свойство неравенств: показательное неравенство с основанием больше нуля, но меньше единицы, характер неравенства «
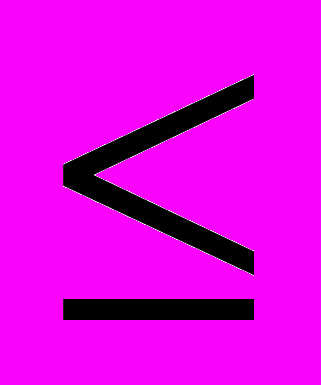 »;
»;
- выделенным свойством обладают неравенства под номерами 1, 2, 4, 5;
- обобщенная формула записи:
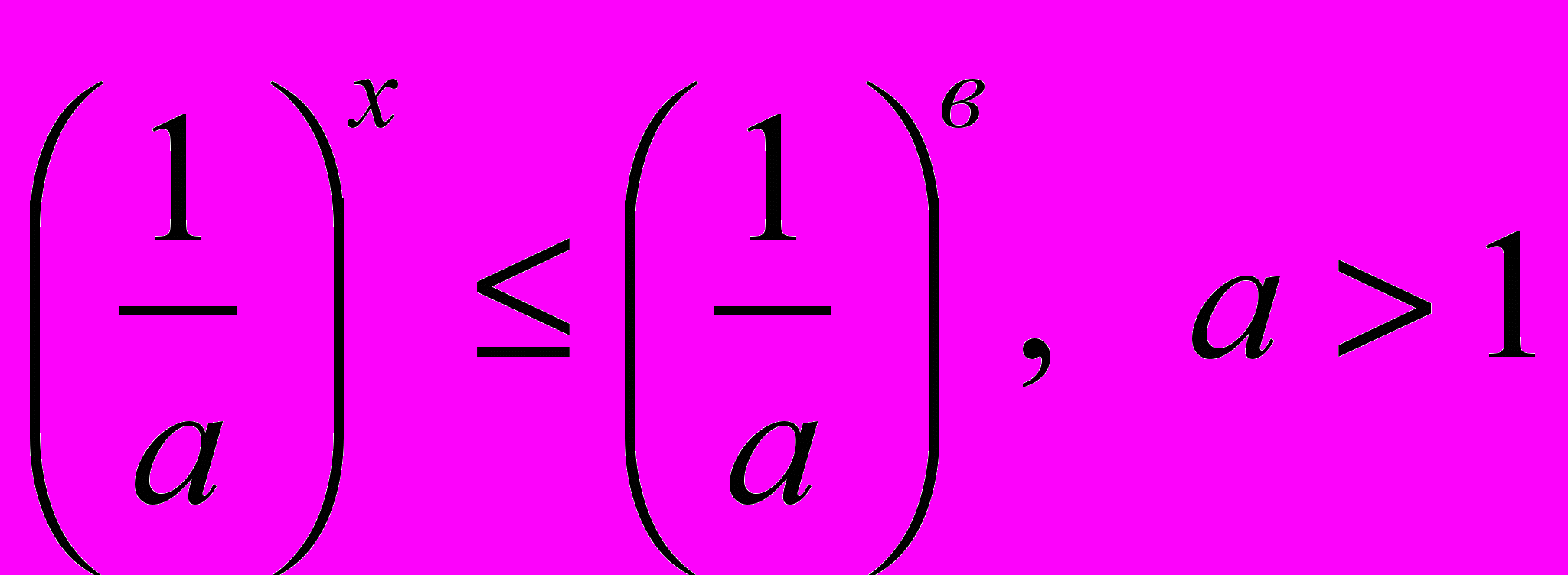 .
.
АБСТРАГИРОВАНИЕ — логический прием мышления, при котором выделяют один признак в уравнении, или неравенстве, или наборе уравнений или неравенств.
Схема:
- Зафиксировать какой-либо признак (существенное свойство) в уравнении или неравенстве.
- Не обращая внимания на остальные признаки в уравнении или неравенстве, расчленить уравнение или неравенство на элементы (смысловые части и пр.), решить уравнение или неравенство.
Например, используя схему выполнения логического приема «абстракция», предложите метод решения заданных неравенств
(1)
 ,
,(2)
 ,
,(3)
 .
.АБСТРАГИРОВАНИЕ
- В каждом из показательных неравенств есть два слагаемых, отличающихся показателями степеней, после преобразования (приведения к одному основанию выражений в степени) получаем неравенства, по структуре похожие на квадратные неравенства. Свойство, которое мы зафиксируем как основание абстракции, — схожесть структуры показательного неравенства с квадратным неравенством.
-
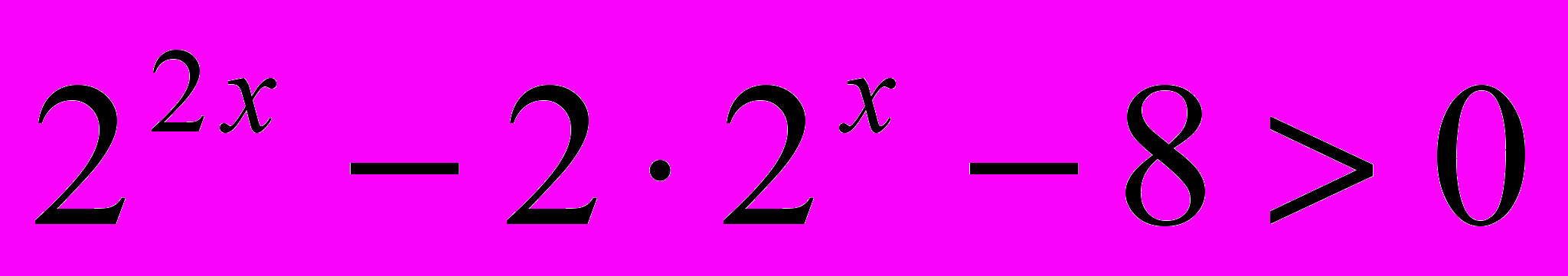 |  | 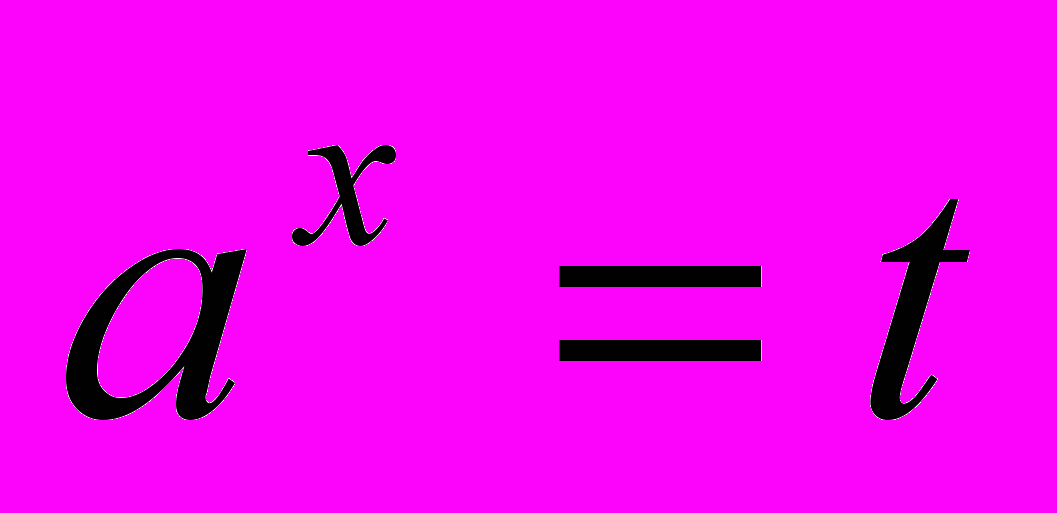 , , 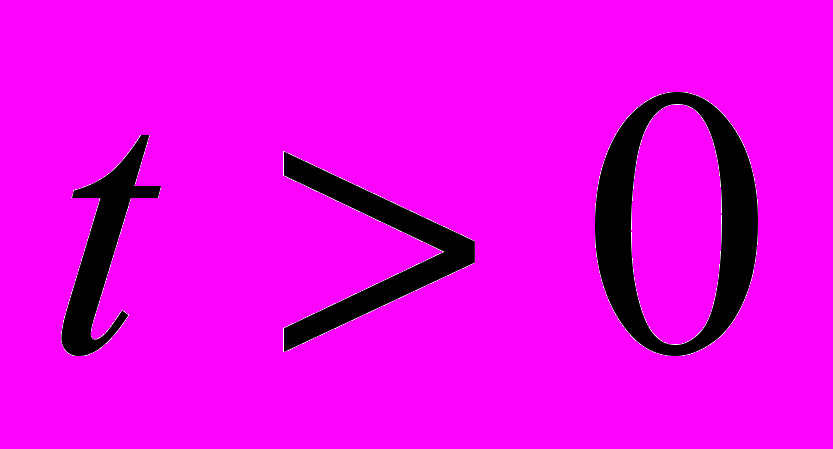 , , 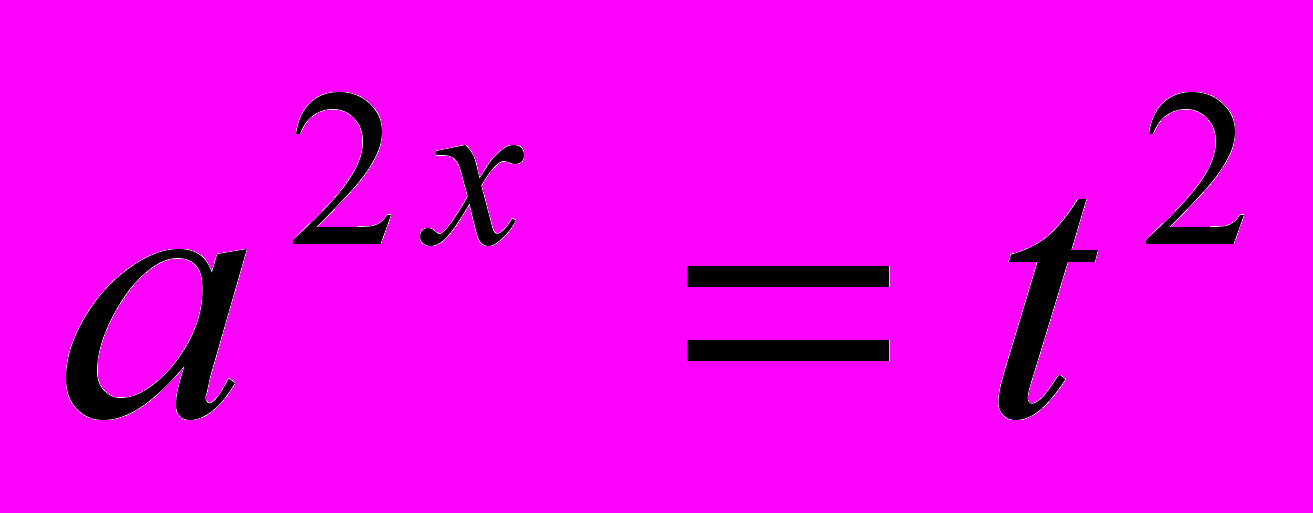 |  | 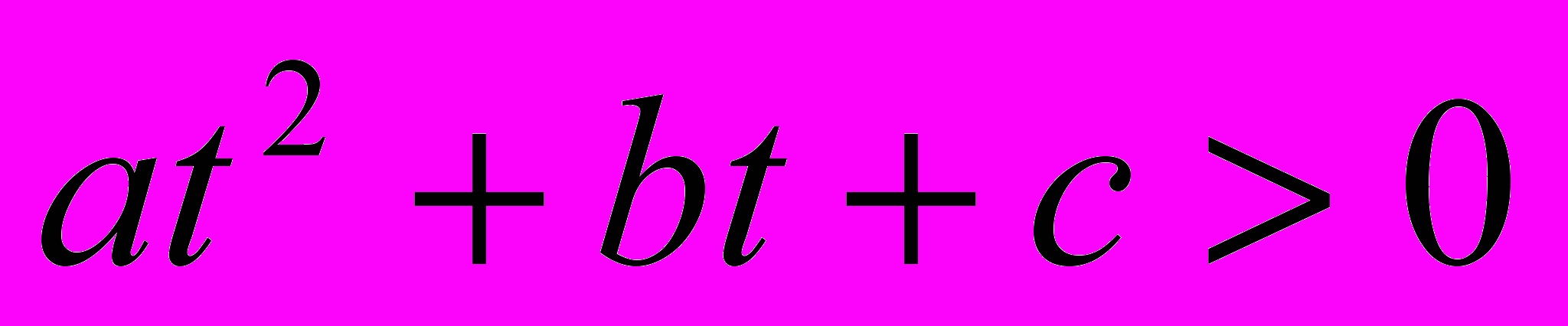 |
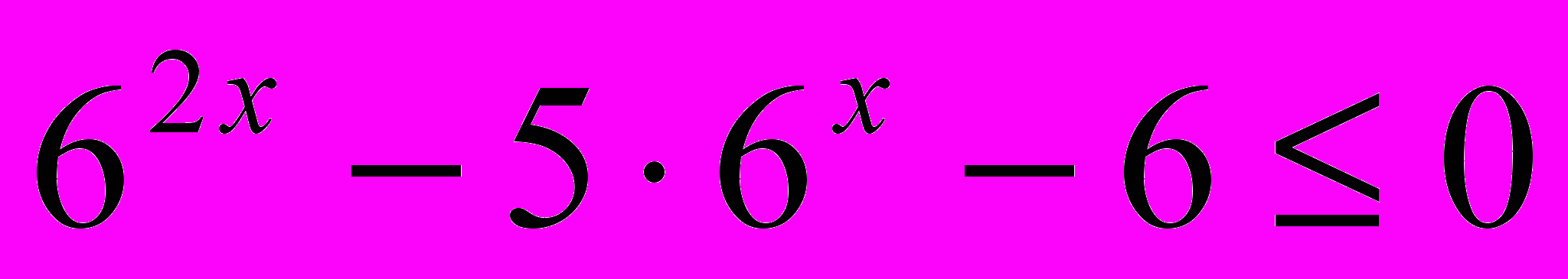 | ||||
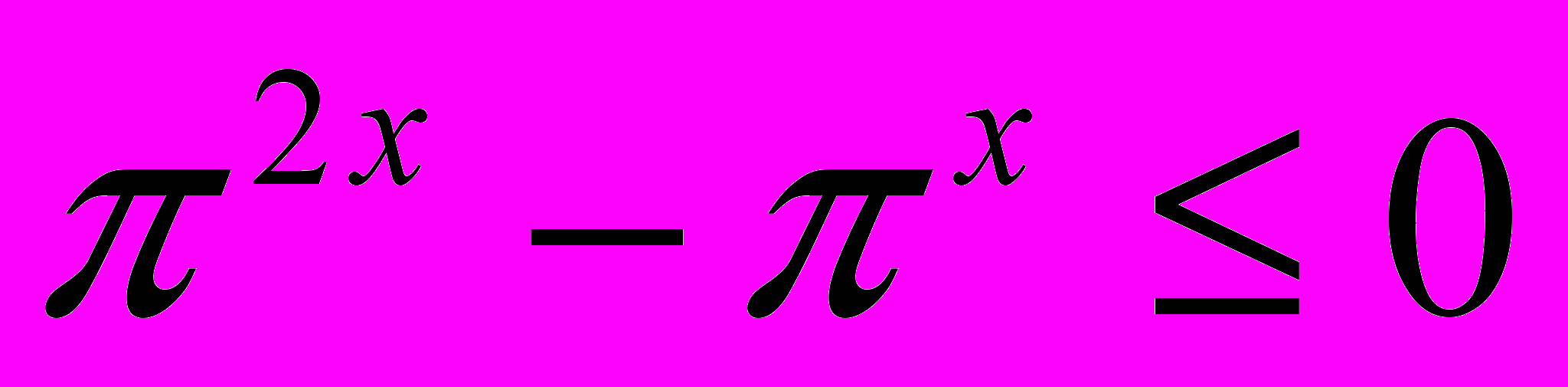 |
Конкретизирование — логический прием мышления, при котором происходит выделение серии уравнений или неравенств, решаемых одним способом, либо переход от более общего класса уравнений к менее общему, единичному виду уравнений или неравенств.
Схема:
- Выделить в серии уравнений или неравенств те, которые имеют общую структуру или общий способ решения;
- Выбрать за основание конкретизации одно из общих свойств;
- Выбрать уравнения или неравенства, обладающие выделенным свойством, в отдельный класс;
- Исследовать как отдельный класс на возможное частное решение.
Например, конкретизировать какой-либо класс неравенств из представленных:
(1)
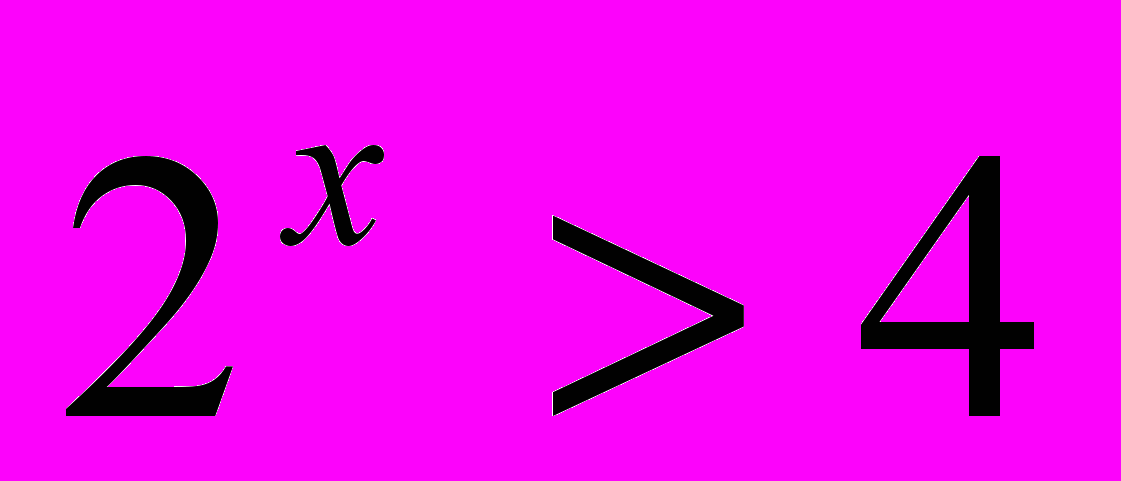 ; (4)
; (4) 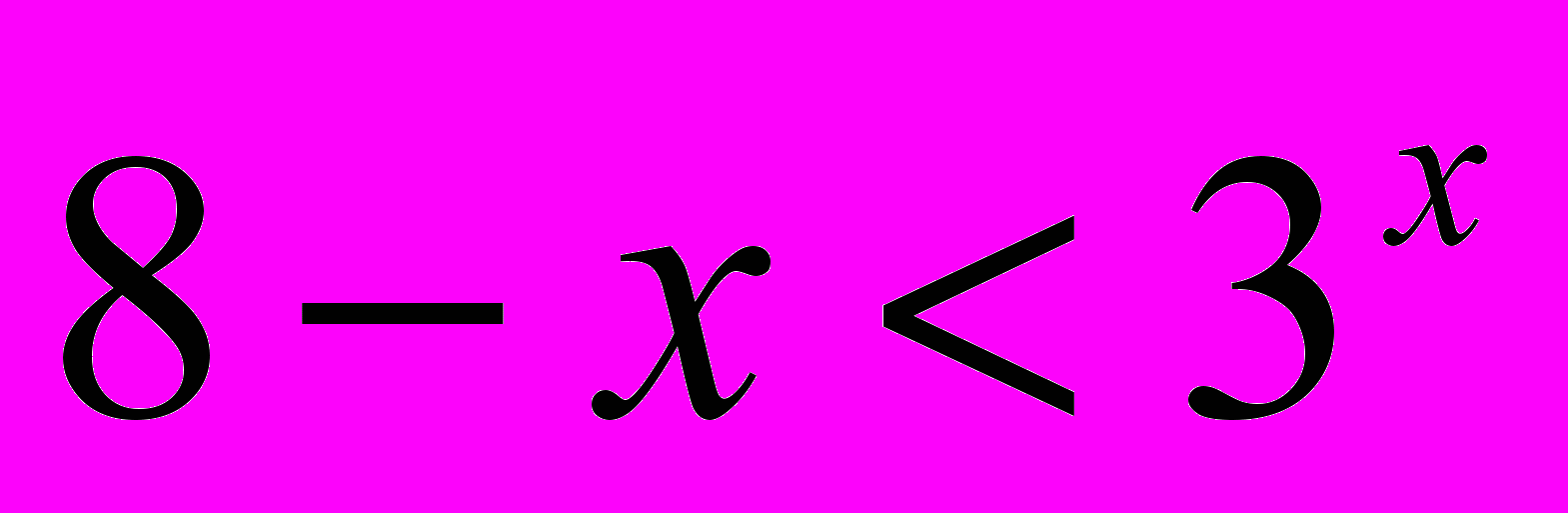 ;
;(2)
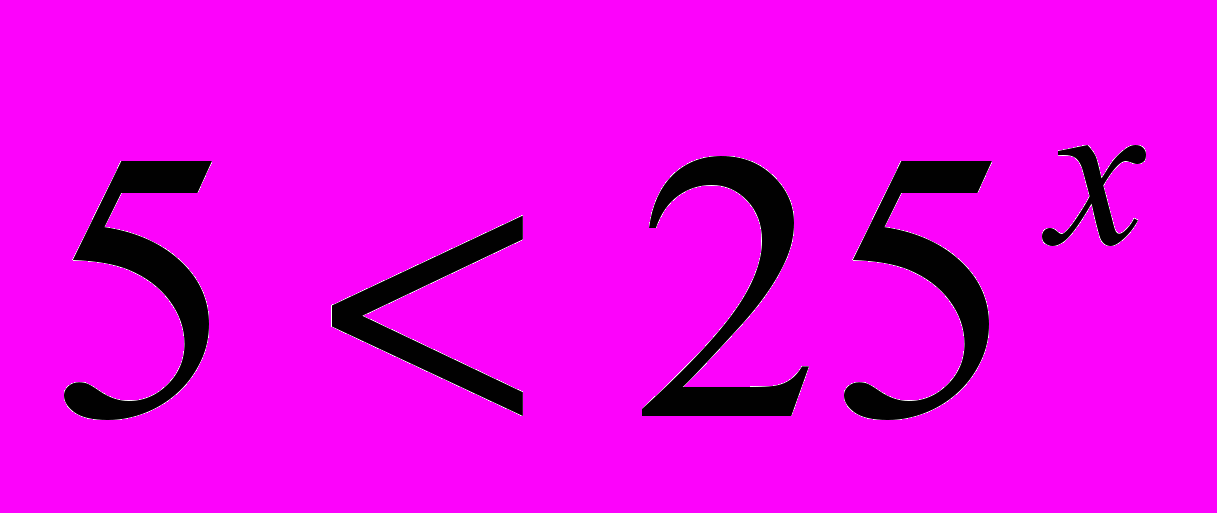 ; (5)
; (5) 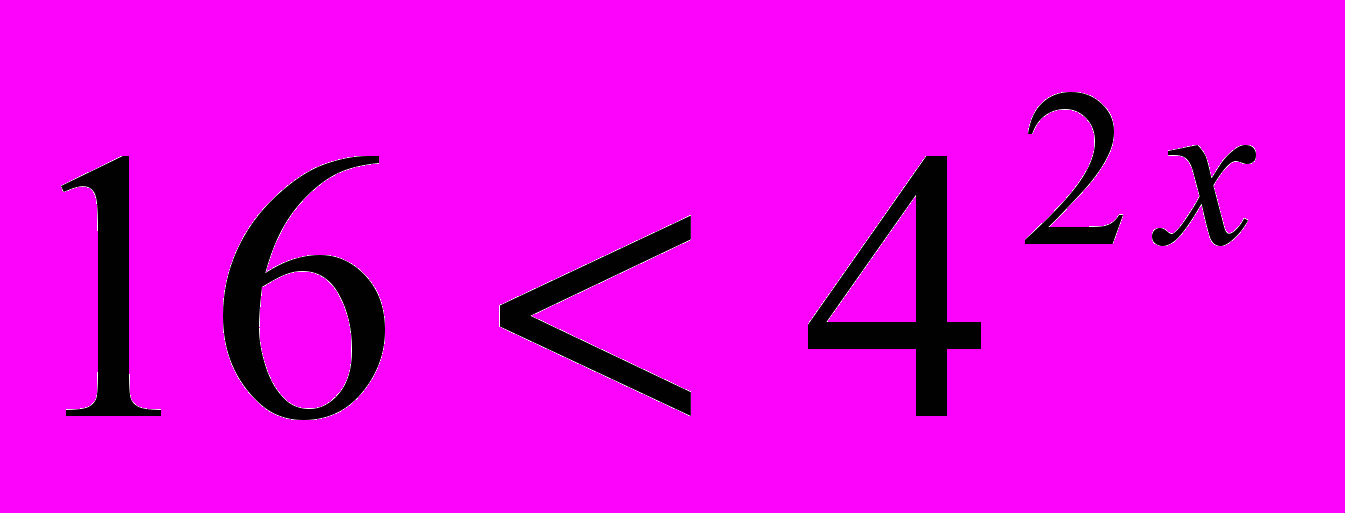 ;
;(3)
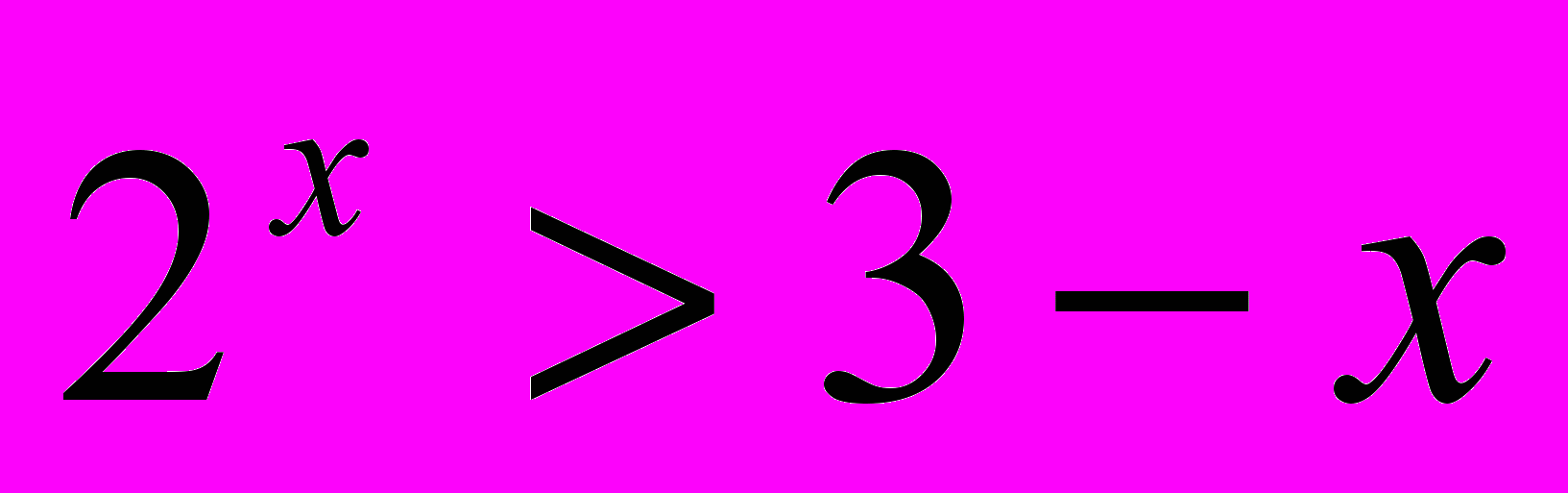 ; (6)
; (6) 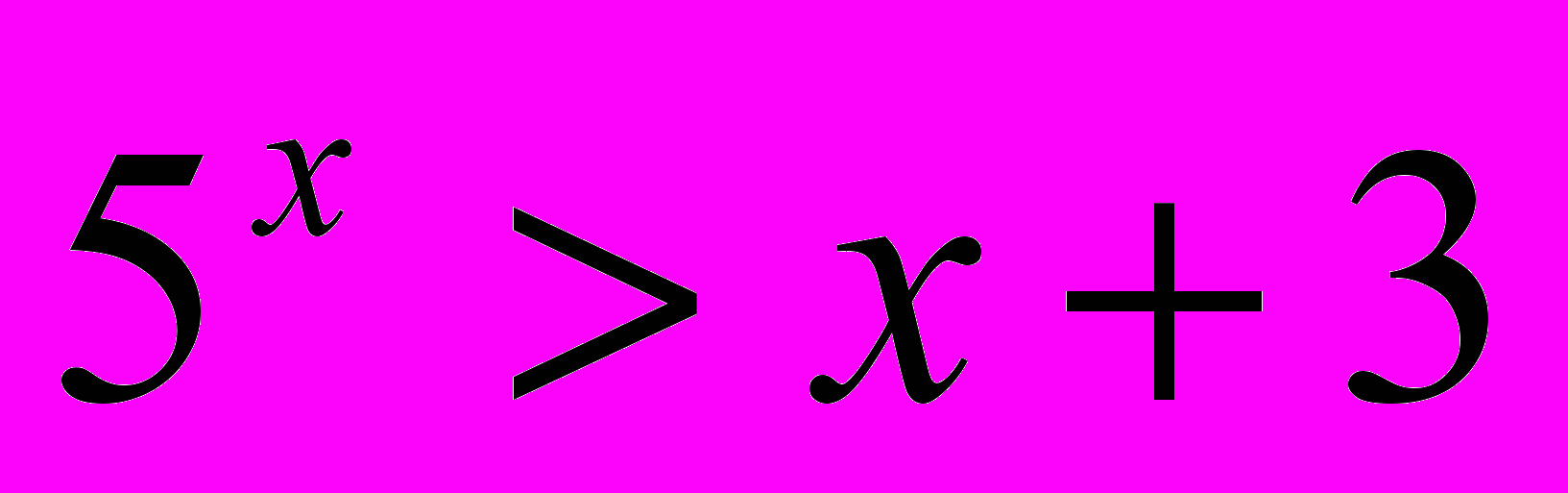 .
.КОНКРЕТИЗИРОВАНИЕ
- Все неравенства имеют похожую структуру:
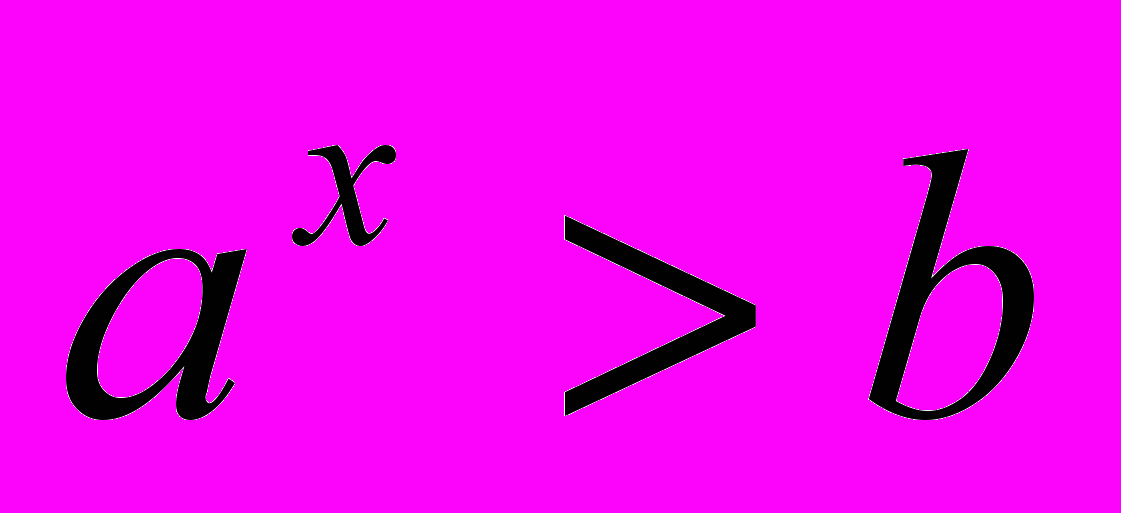 или
или 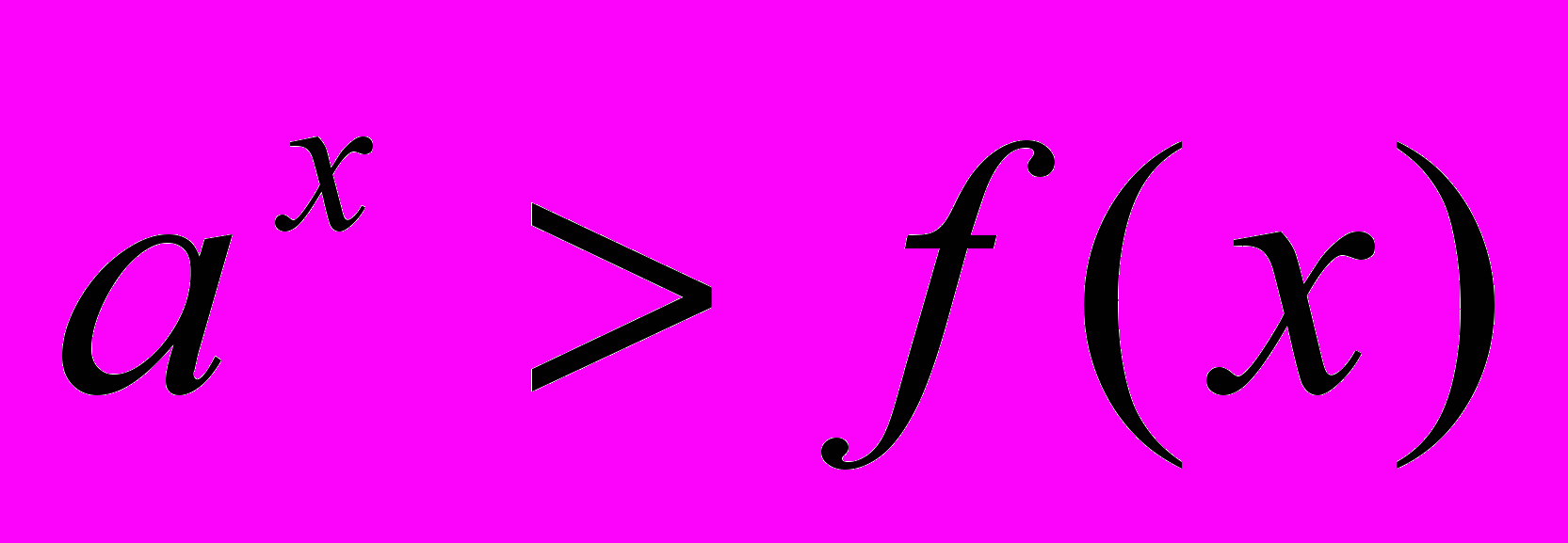 ; каждое из неравенств содержит показательную функцию; неравенства под номерами 1, 2, 5 имеют структуру
; каждое из неравенств содержит показательную функцию; неравенства под номерами 1, 2, 5 имеют структуру 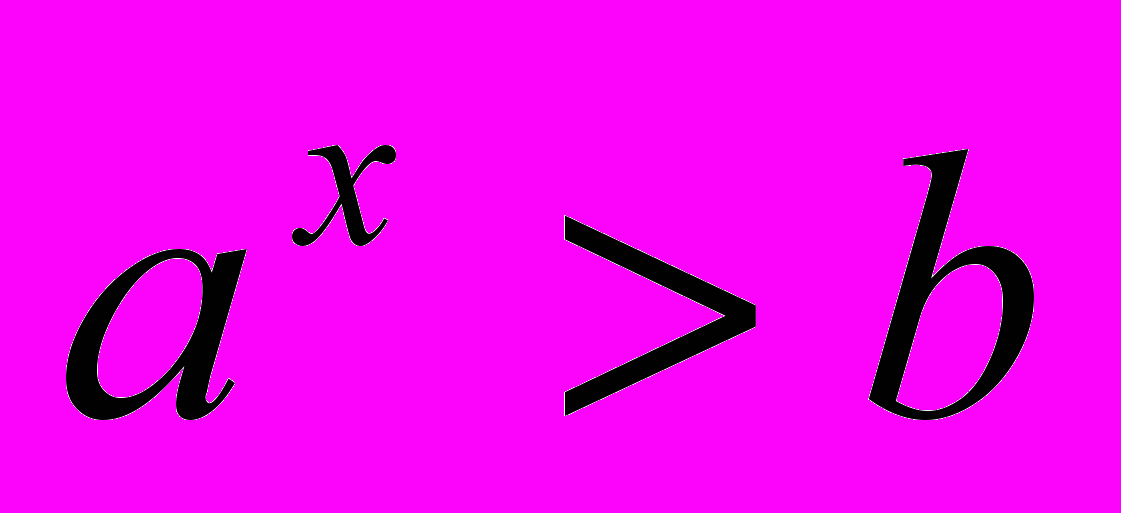 , то есть сравнивается показательная функция и константа; неравенства под номерами 3, 4, 6 имеют структуру
, то есть сравнивается показательная функция и константа; неравенства под номерами 3, 4, 6 имеют структуру 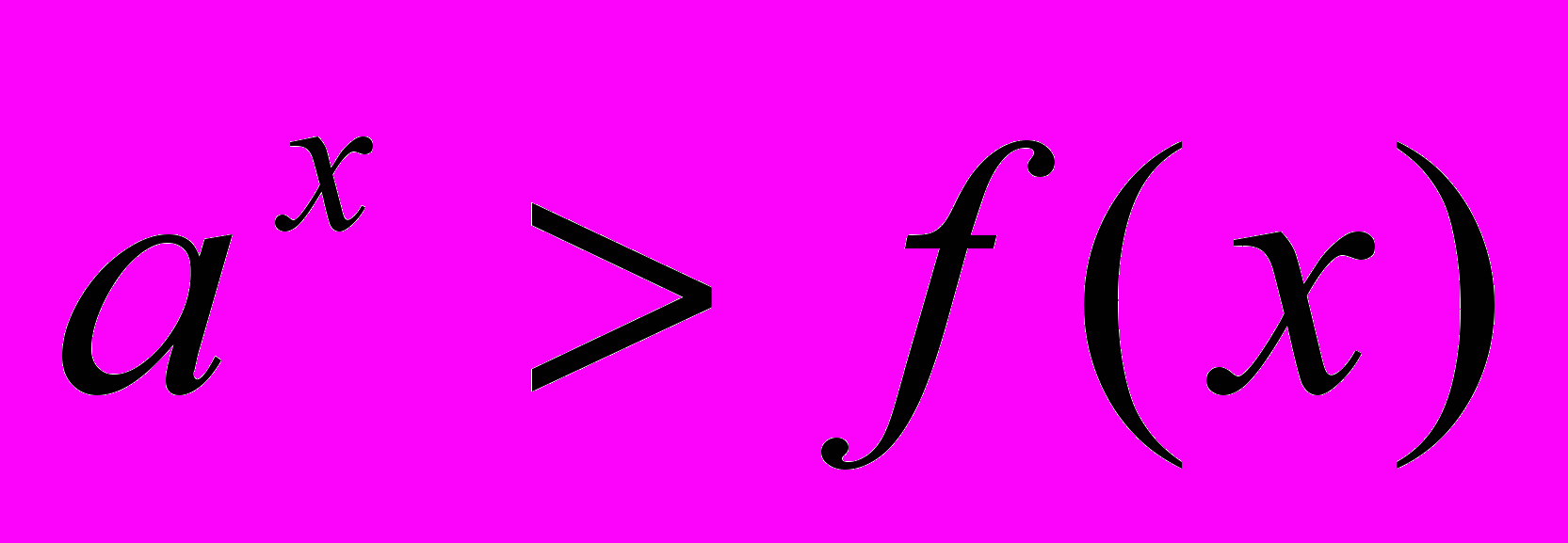 , то есть показательная функция сравнивается с другой функцией (в данном случае с линейной);
, то есть показательная функция сравнивается с другой функцией (в данном случае с линейной);
- выделим свойство: сравнивается показательная функция с линейной функцией;
- получаем класс неравенств под номерами 3, 4, 6; обобщим уравнения в общую запись:
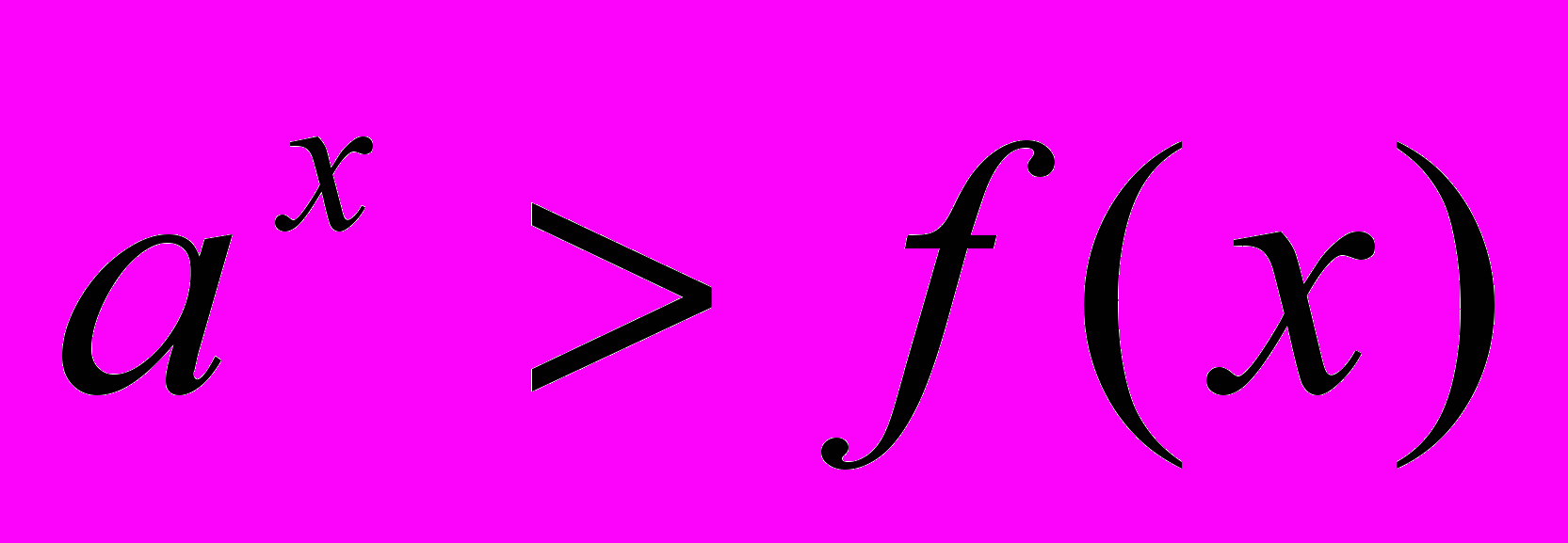 ;
;
- неравенства вида
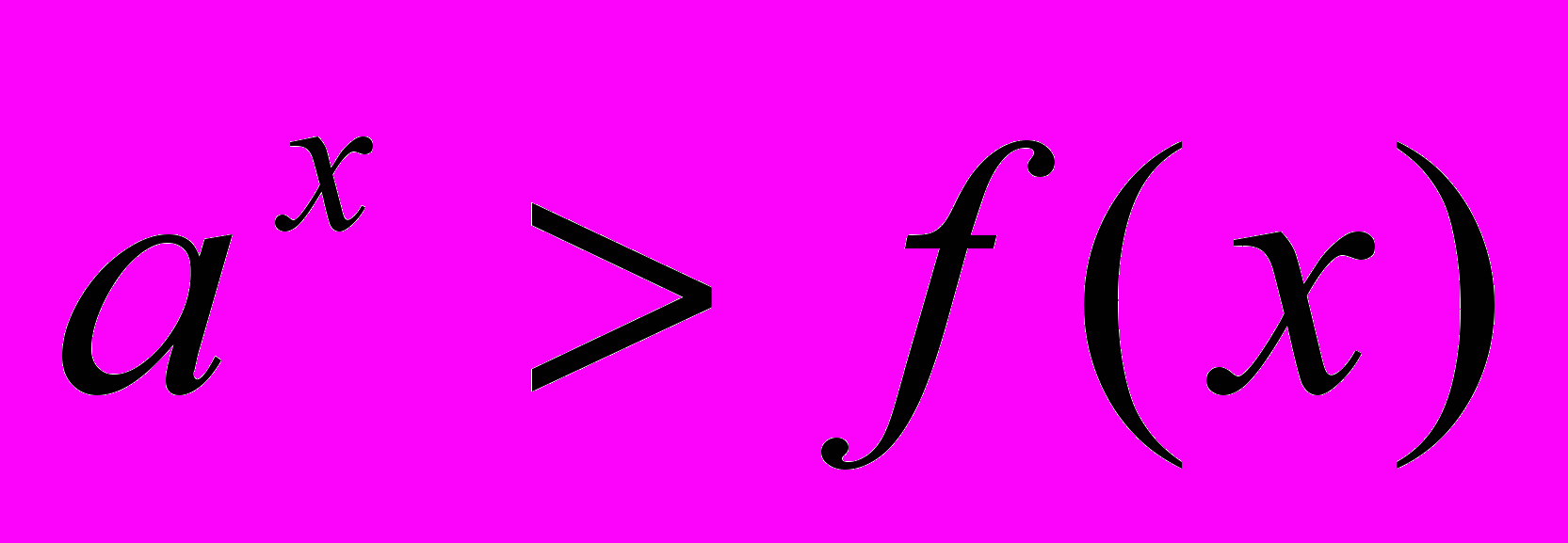 будут иметь частный метод решения– графический метод наиболее рациональный для этого случая, потому как невозможно выделить общее основание у заданных функций или свести их к одному виду.
будут иметь частный метод решения– графический метод наиболее рациональный для этого случая, потому как невозможно выделить общее основание у заданных функций или свести их к одному виду.
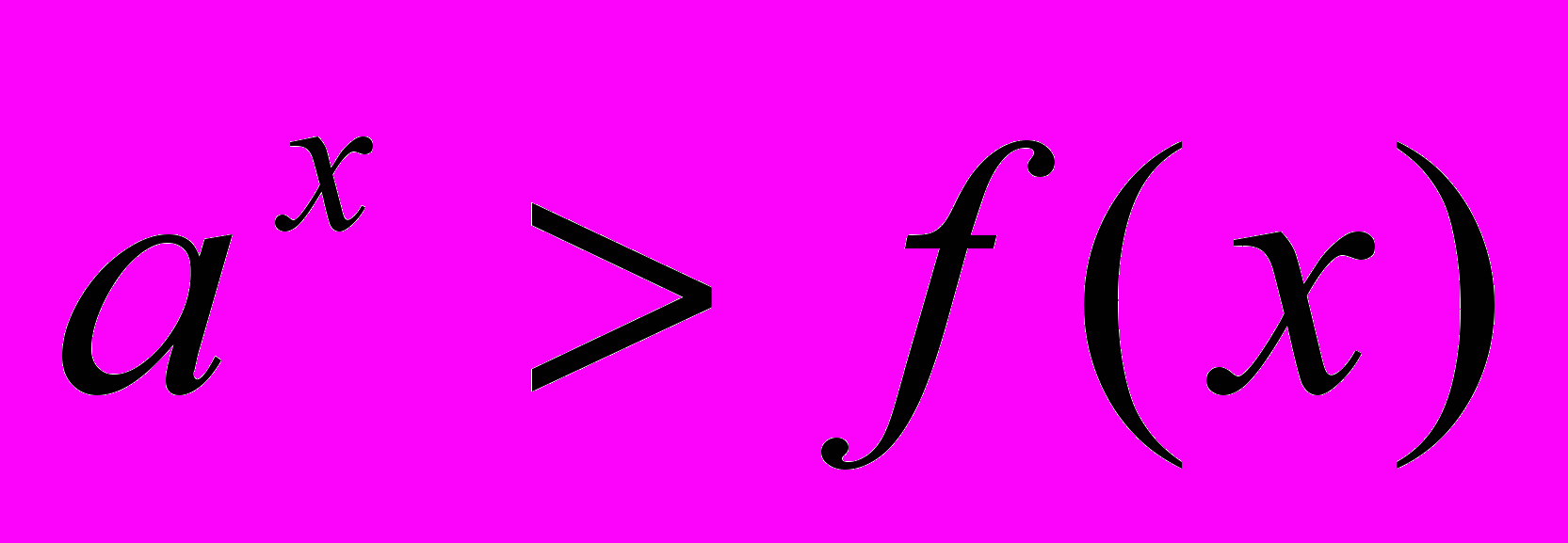 , где
, где 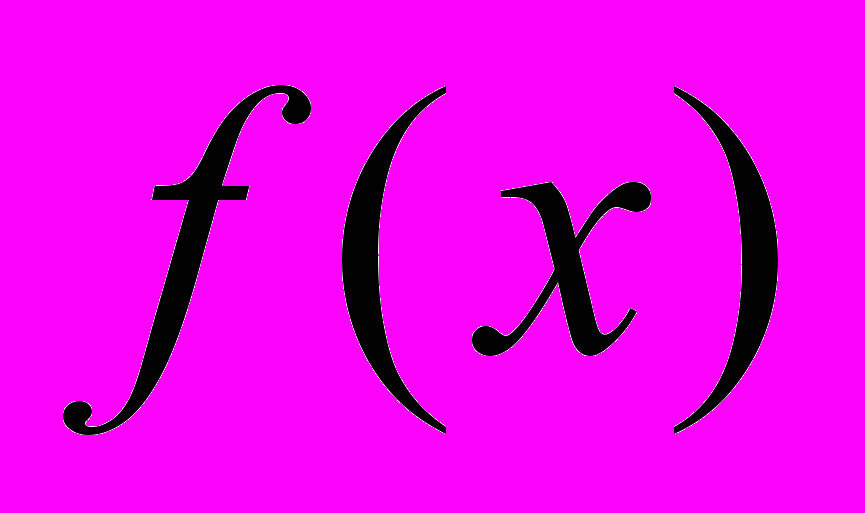 — любая функция, кроме
— любая функция, кроме 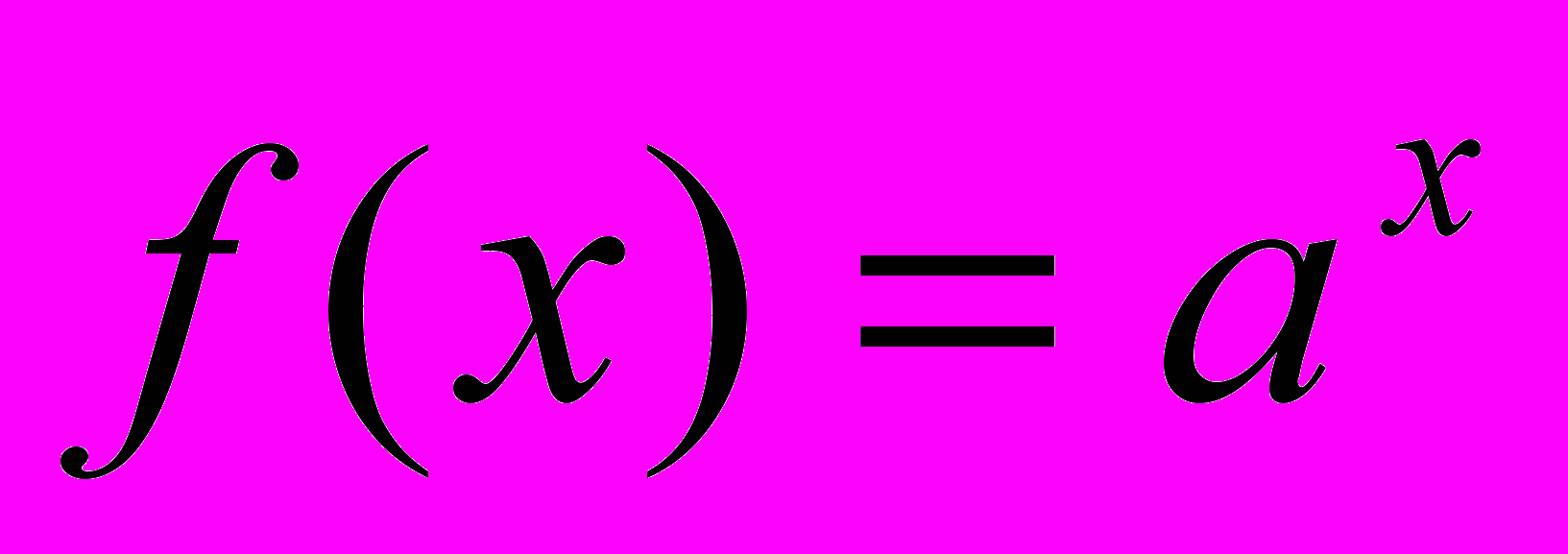
 графический метод решения.
графический метод решения.Обучающий и закрепляющий этапы предполагают обучение старшеклассников приемам учебной работы, составляющим алгоритмические предписания выполнения логических приемов мышления при решении уравнений и неравенств. Формирование логических приемов мышления проходит в рамках урока как основной формы обучения и в рамках программного материала. В ходе эксперимента было выявлено, что в качестве средства формирования используются специально составленные математические задачи. На каждый логический прием мышления требуется своя серия задач, которая в свою очередь может быть дифференцирована по уровню сложности либо содержать набор вопросов, отражающих свойства, необходимые для изучения предметного материала. Задачи составляются с учетом цели этапа формирования, определения логического приема мышления и схемы его выполнения.
Используются упражнения 1-го типа (обучающий этап) — для решения задачи (выполнения задания) требуется знание определения логического приема мышления и схемы выполнения приема. Задания могут быть следующего вида: определите, с помощью какого логического приема мышления выполнено задание; найдите ошибки при выполнении приема учебной работы; используя схему выполнения приема учебной работы, выполните анализ, синтез, обобщите и пр.; составьте план выполнения задания, зная схемы выполнения логических приемов мышления…; следуя схеме выполнения приема логического мышления, выполните…; заполните пропуски в выполнении приема учебной работы.
Пример: Задача. Определить какой логический прием мышления был использован при выполнении задания.
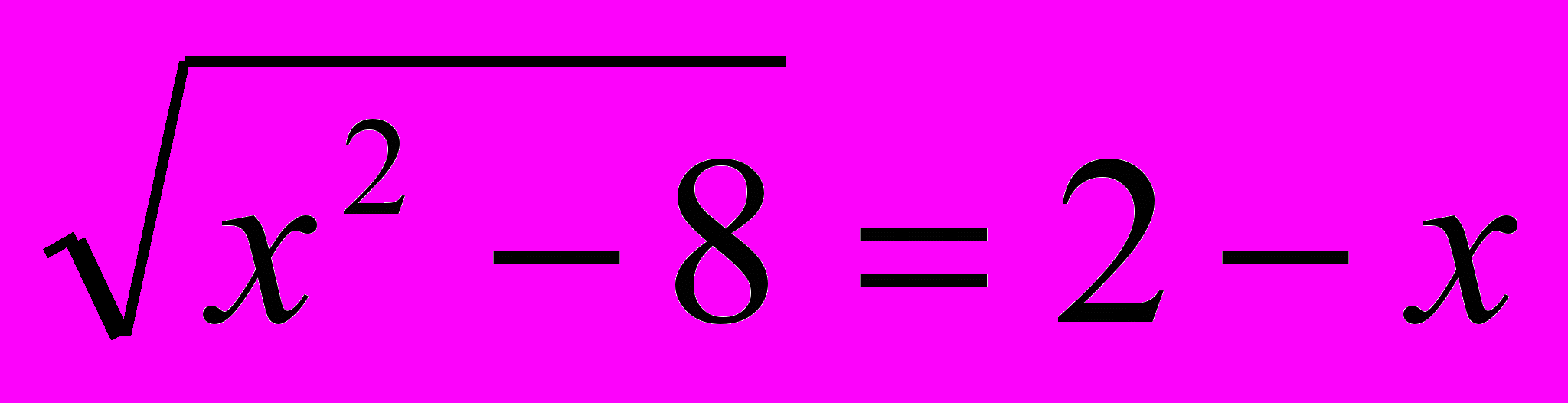 .
.Решение:
- Уравнение содержит неизвестную под знаком радикала, следовательно, задано иррациональное уравнение;
- результат извлечения арифметического квадратного корня должен быть неотрицательным числом, следовательно
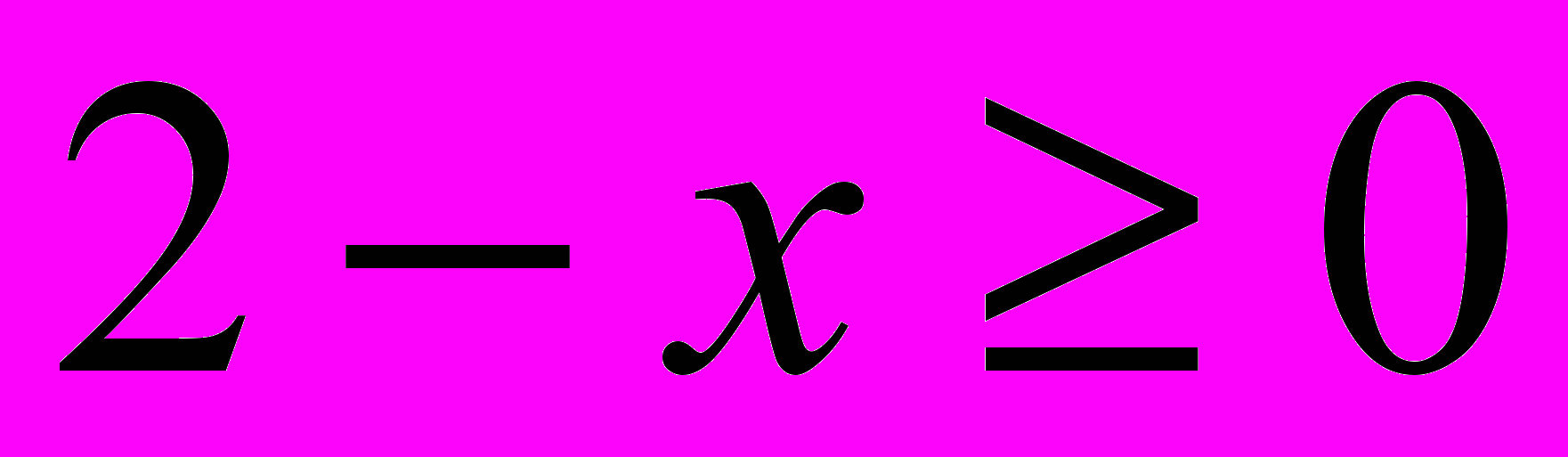 ;
;
- по определению арифметическим квадратным корнем из неотрицательного числа называется такое неотрицательное число, квадрат которого равен самому числу, значит, решение уравнения сводится к решению системы
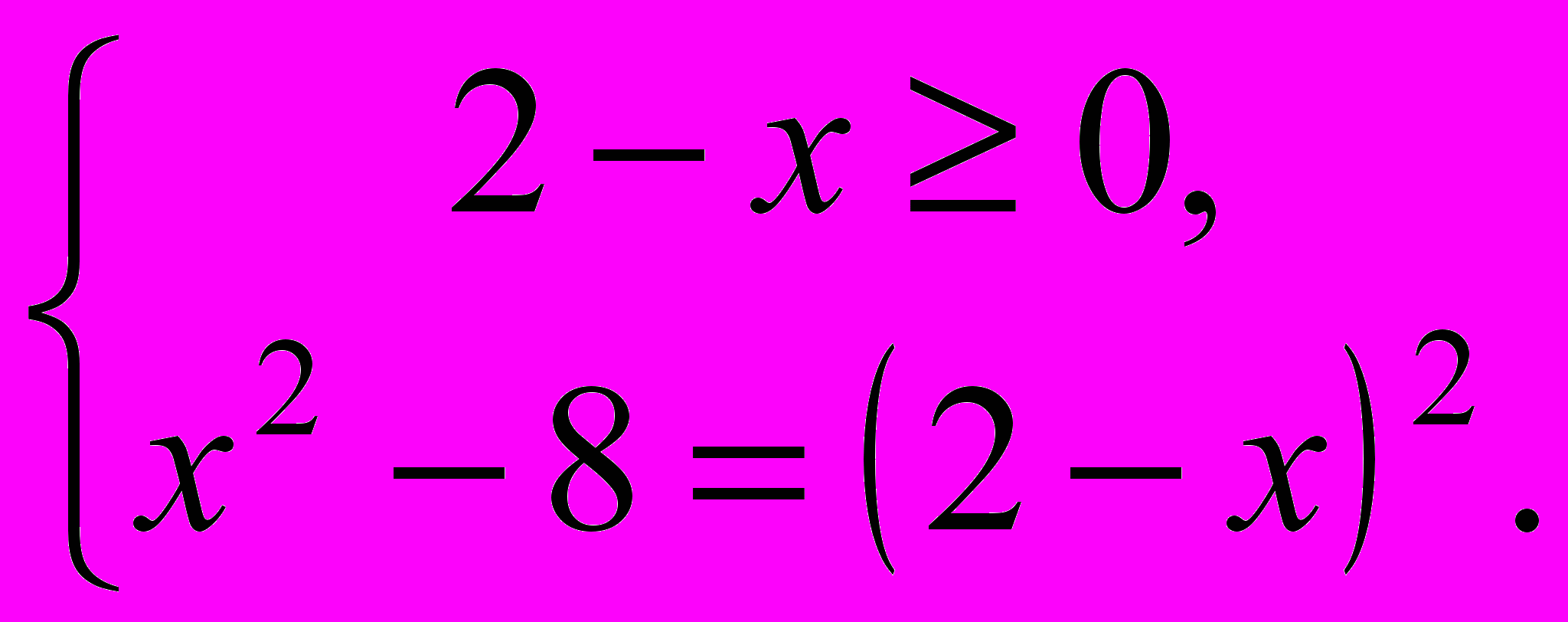 (Ответ: анализ).
(Ответ: анализ).
Применяются упражнения 2-го типа (закрепляющий этап), требующие выполнения конкретного приема: без помощи схемы выполните анализ (синтез, обобщение и пр.) для решения задачи …; укажите, какими логическими приемами вам необходимо воспользоваться при выполнении задания…; решите с помощью логического приема анализа (синтеза), обобщите, найдите конкретизацию данного типа уравнений, абстрагируясь от свойства уравнения, запишите в символах общий вид уравнения и пр.
Пример. Задача. Предложите какую-либо конкретизацию уравнения
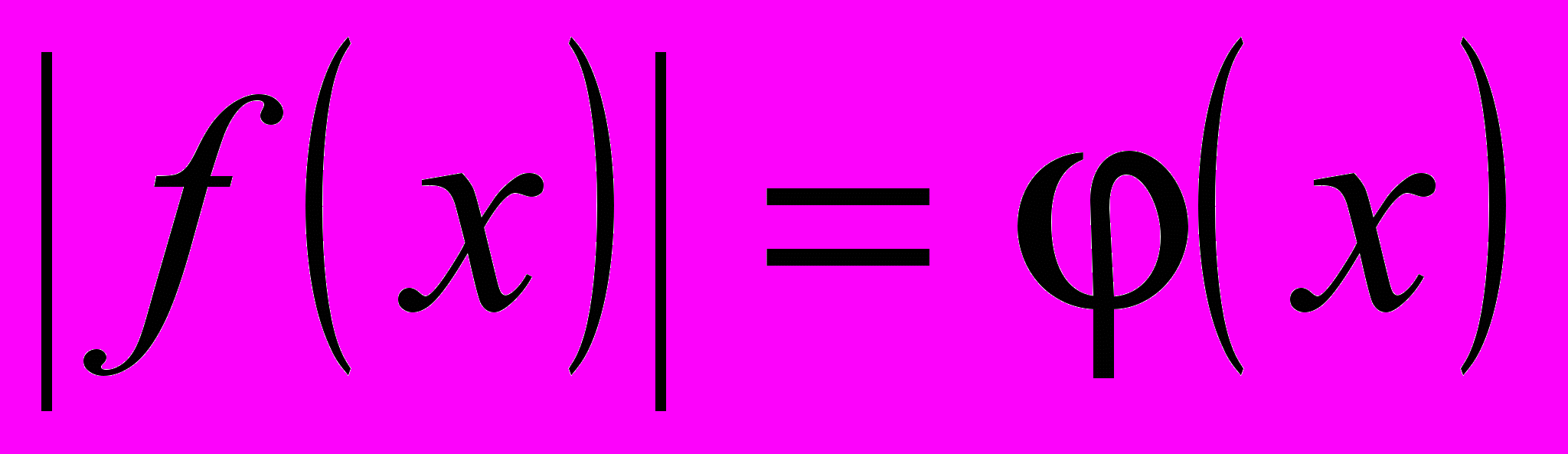 , задав такие условия для
, задав такие условия для 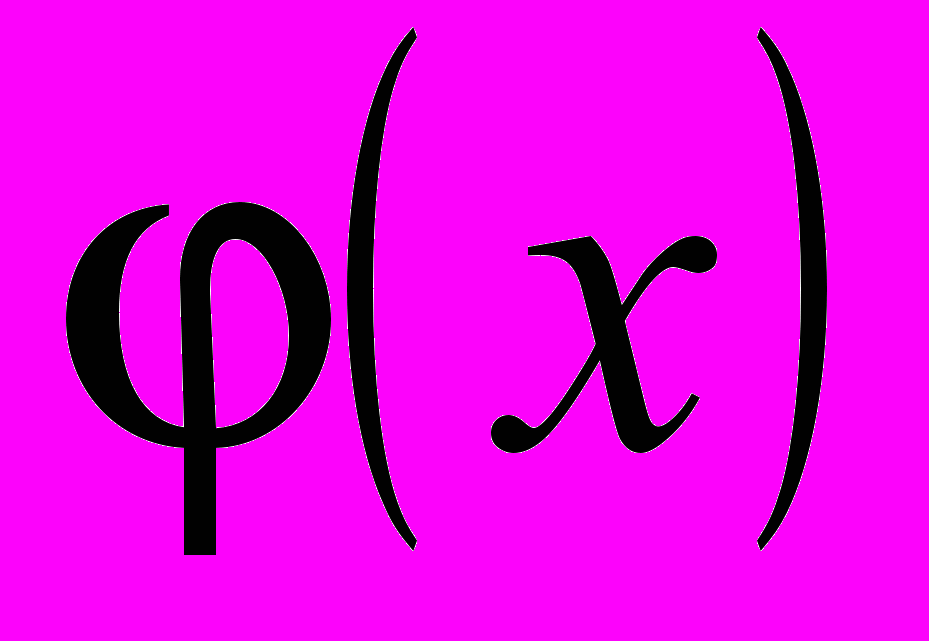 , чтобы получить отдельный тип уравнений с модулем, которые имеют свой способ решения, отличный от общего (по определению). Предложите возможный способ решения.
, чтобы получить отдельный тип уравнений с модулем, которые имеют свой способ решения, отличный от общего (по определению). Предложите возможный способ решения.Например,
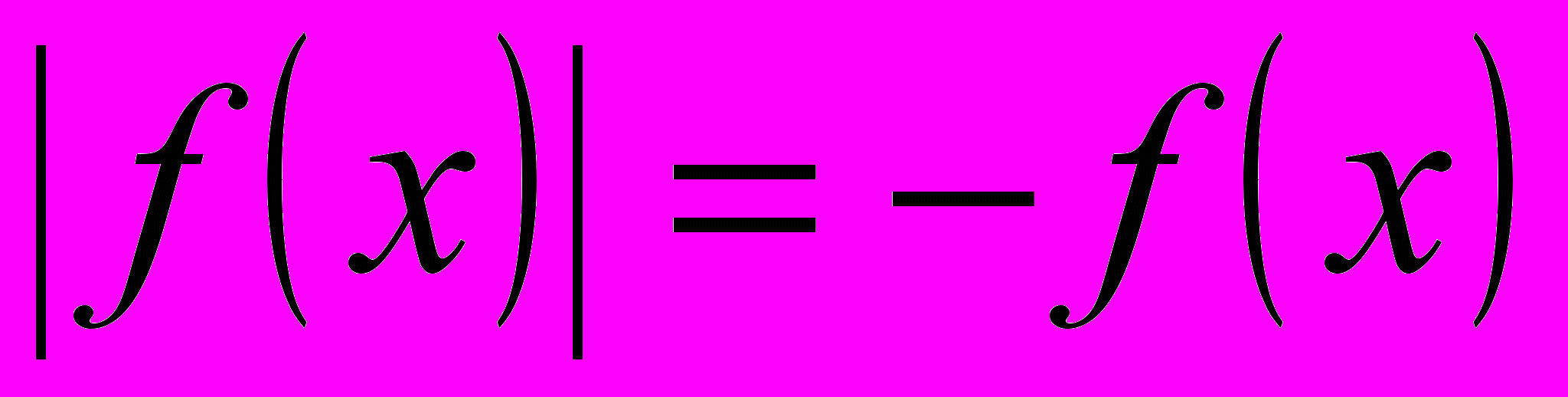 , то есть
, то есть 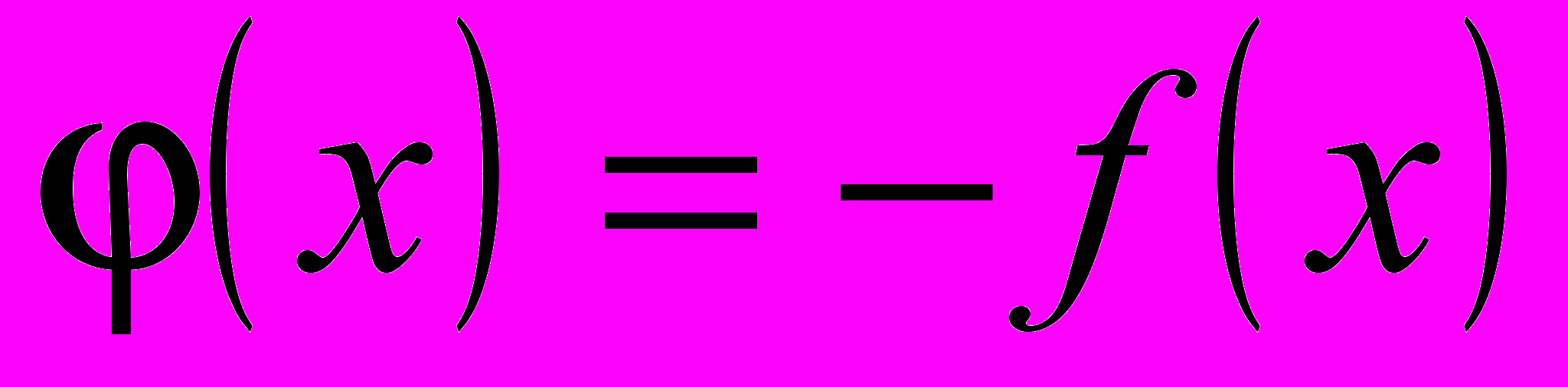 . Тогда решение
. Тогда решение 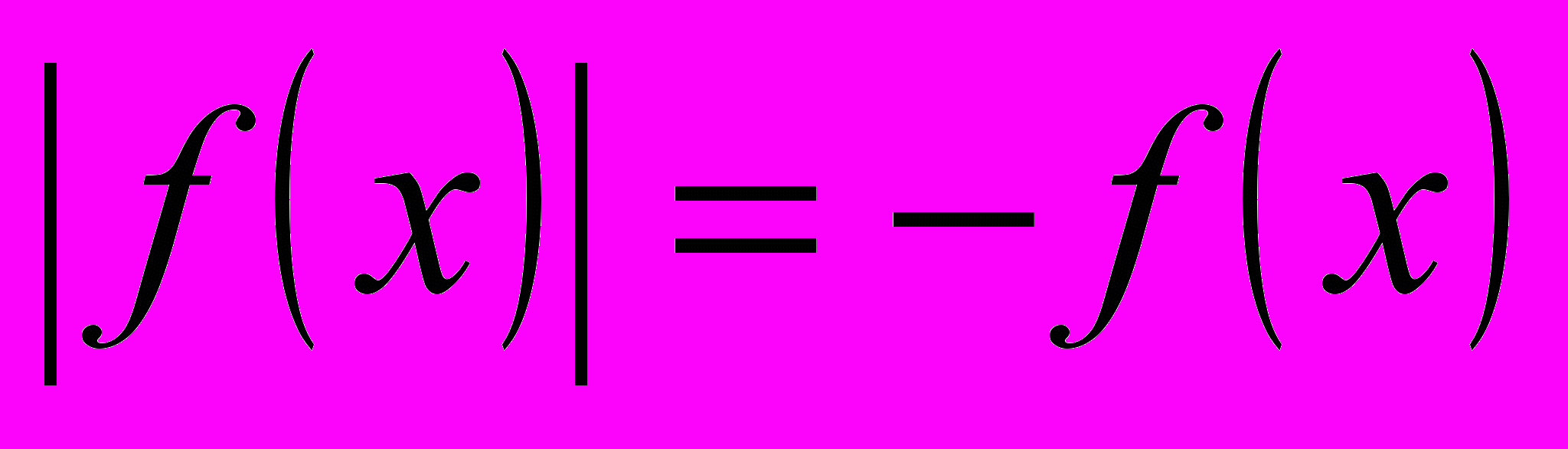

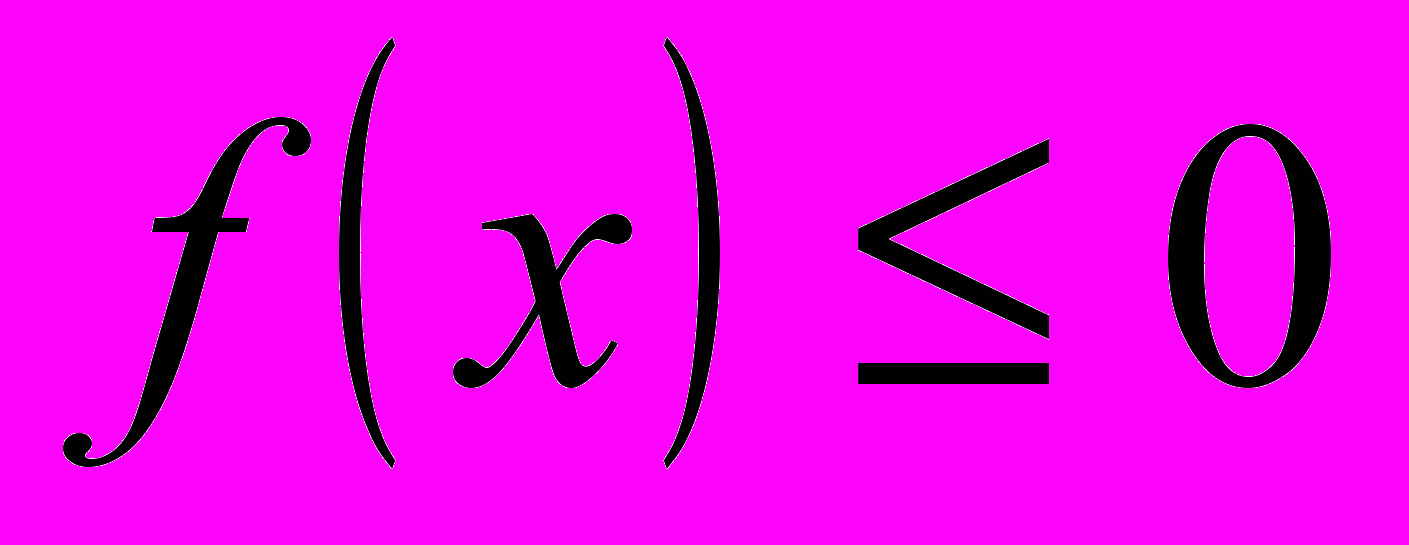 .
.Практический этап предполагает применение усвоенных логических приемов мышления на специально подобранных задачах, а так же на задачах учебника. При этом предлагаются задачи не только на решение уравнений и неравенств.
На практическом этапе используются упражнения 3-го типа, требующие применения логических приемов без указания на схему выполнения или их переноса на другой материал. Формулировки задач не содержат указания на логические приемы мышления.
Пример. Задача

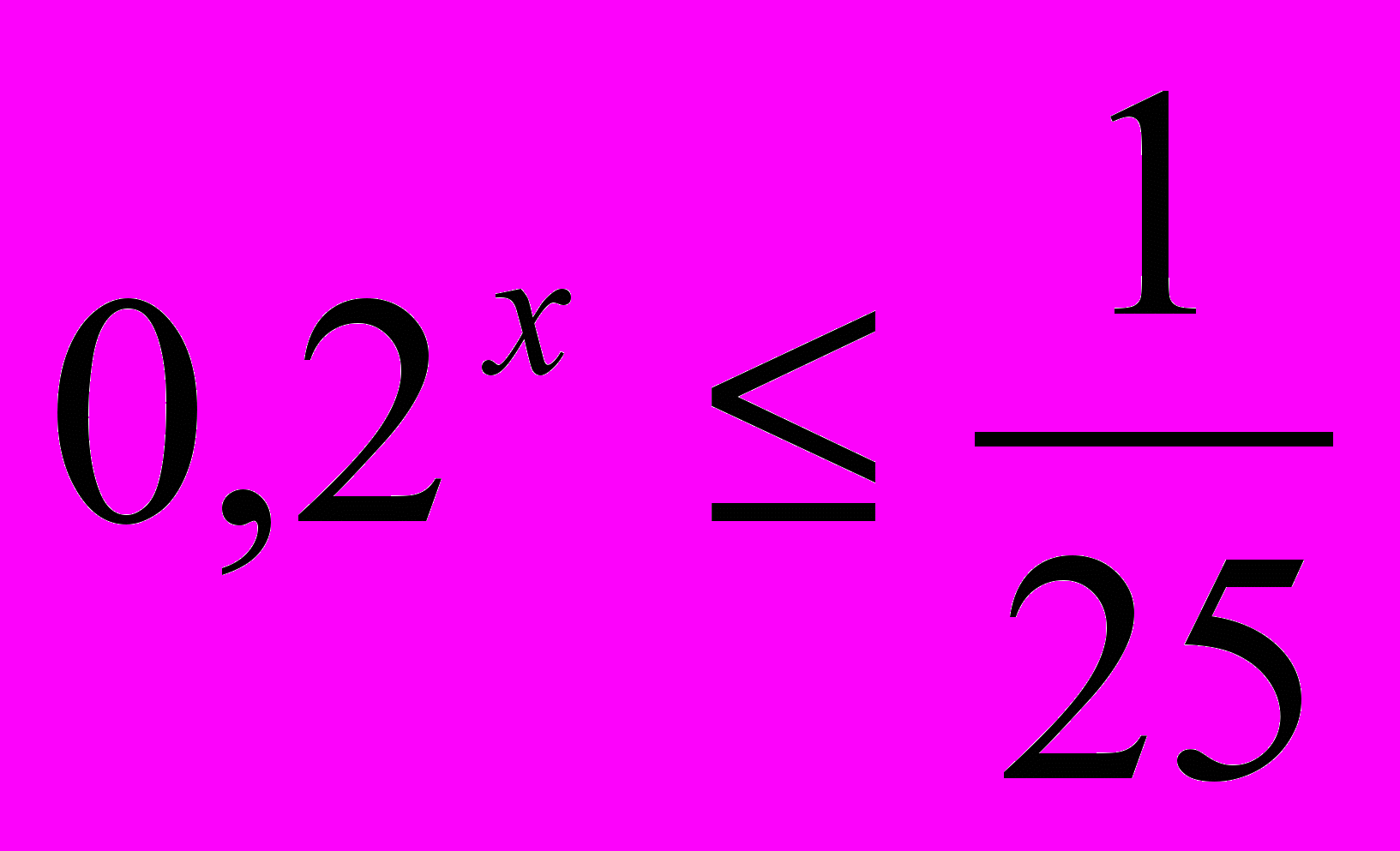 ;
;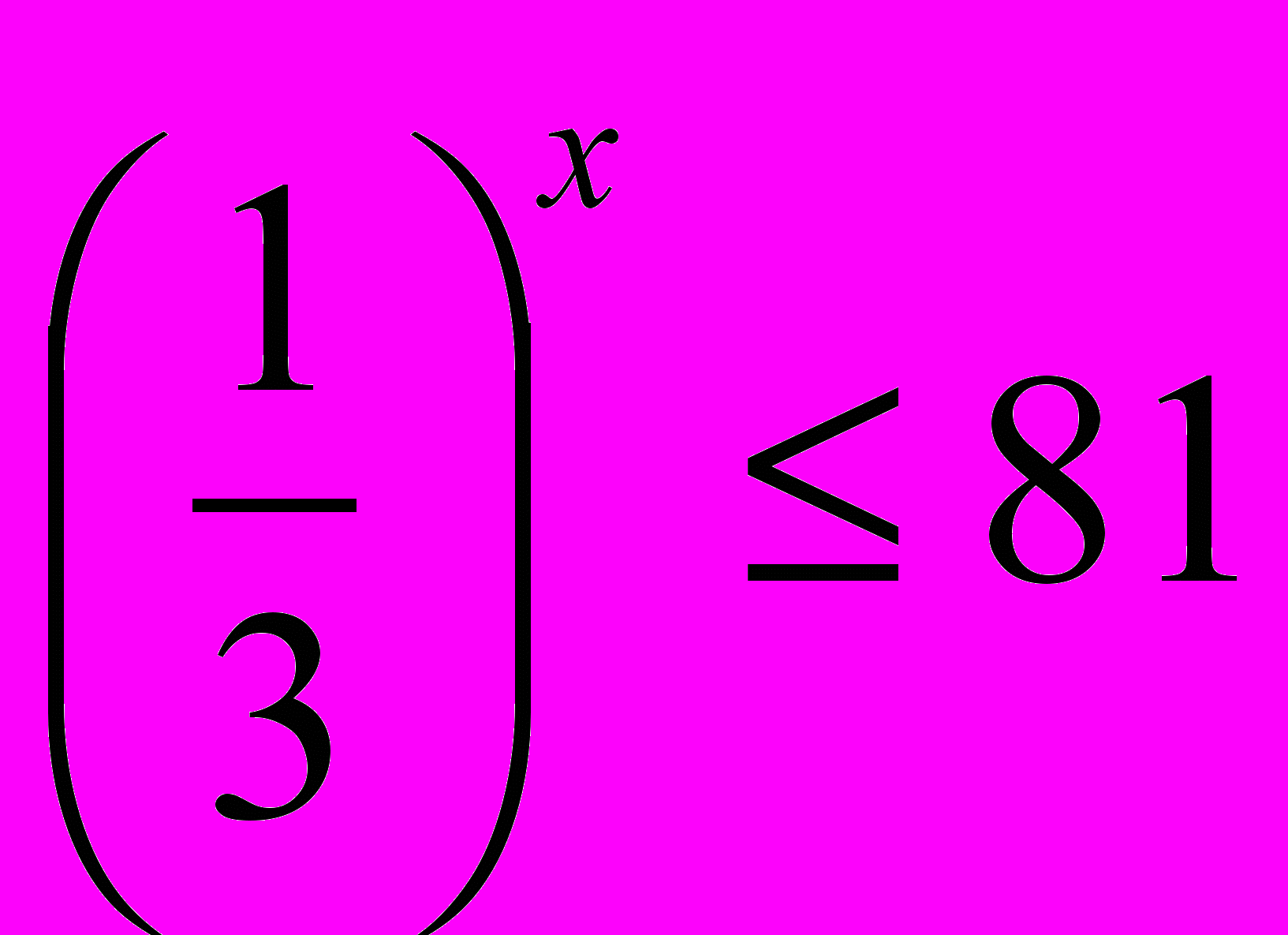 ;
;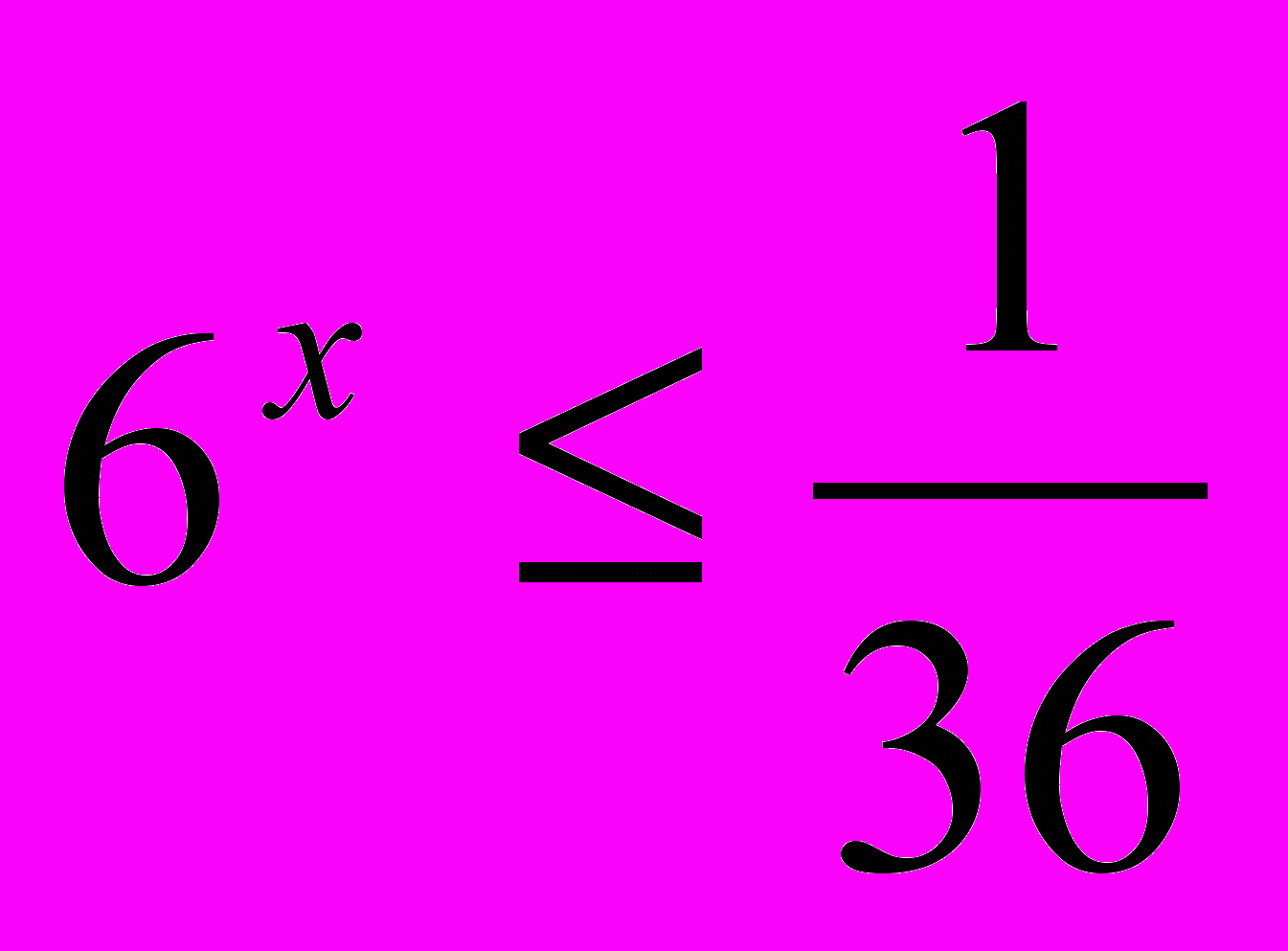 ;
;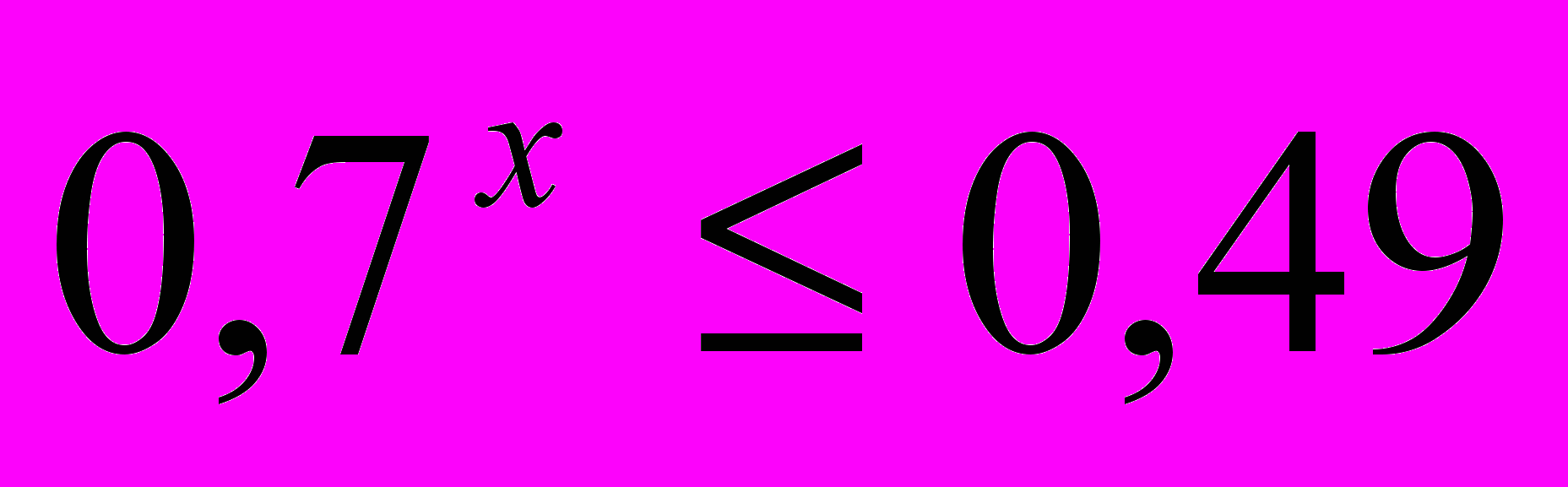 ;
;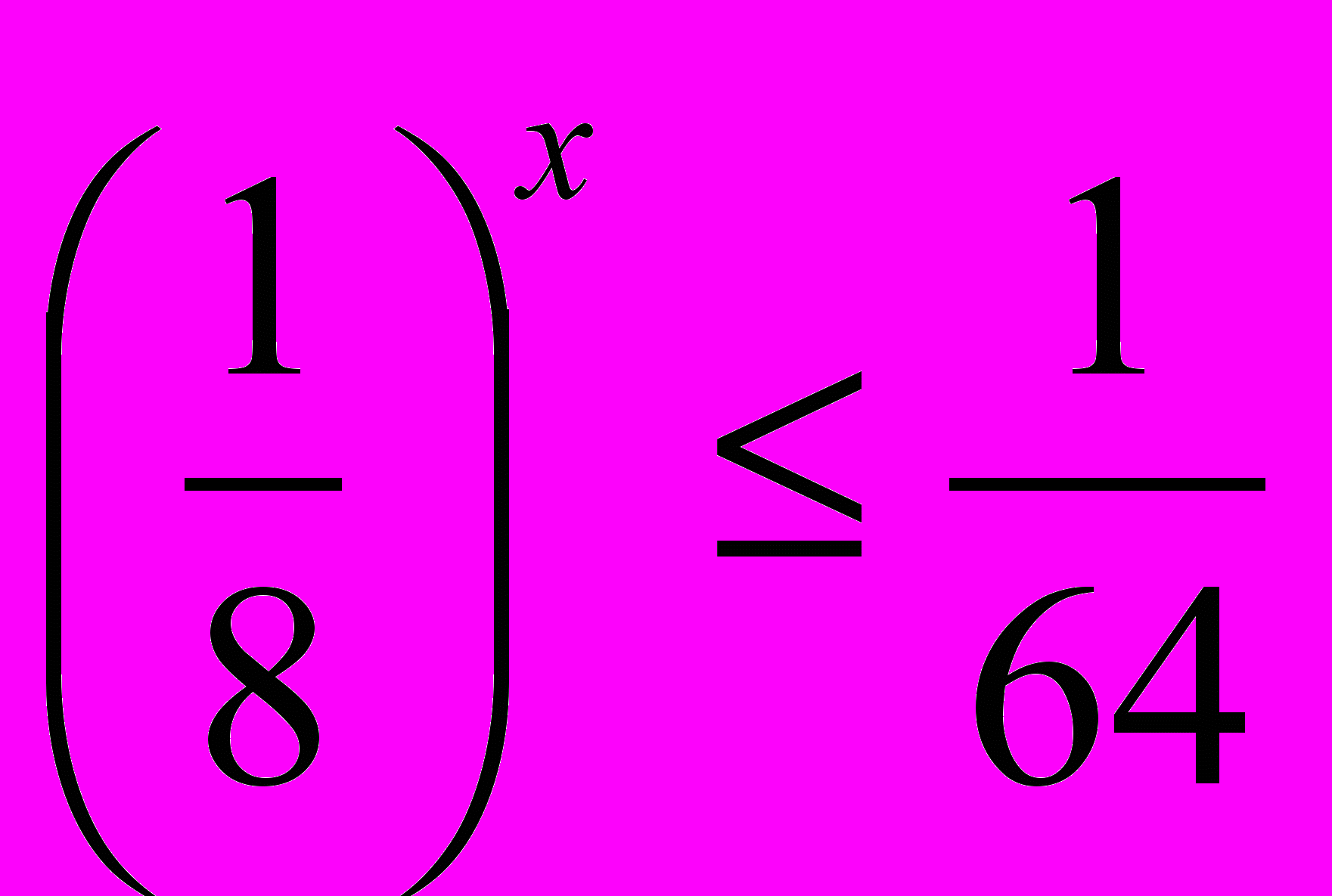 .
.