Методика дифференцированного обучения решению математических задач с использованием инфокоммуникационных технологий 13. 00. 02- теория и методика обучения и воспитания (математика, уровень общего образования)

Вид материала

Содержание

Бакмаев Ширвани Абдулатипович
Кучугурова Нина Дмитриевна
Ведущая организация
Общая характеристика работы
Основное содержание диссертации
Пример: (Шарыгин И.Ф. 7-9 кл)
Таблица 3 Уровни умения учеников решать задачи
Таблица 4 Результаты итоговой контрольной работы
Диаграмма результатов итоговой контрольной работы
Таблица 5 Показатели дисперсионного анализа
Основные выводы исследования
Основное содержание диссертационной работы отражено в следующих публикациях

Подобный материал:

На правах рукописи

Магомедова Рабият Магомедовна

МЕТОДИКА ДИФФЕРЕНЦИРОВАННОГО ОБУЧЕНИЯ РЕШЕНИЮ МАТЕМАТИЧЕСКИХ ЗАДАЧ С ИСПОЛЬЗОВАНИЕМ ИНФОКОММУНИКАЦИОННЫХ ТЕХНОЛОГИЙ

13.00.02— теория и методика обучения и воспитания

(математика, уровень общего образования)

Автореферат

на соискание ученой степени

кандидата педагогических наук

Астрахань-2010

Работа выполнена в ГОУ ВПО «Дагестанский государственный педагогический университет»

Научный Руководитель:	кандидат педагогических наук, профессор Бакмаев Ширвани Абдулатипович
Официальные оппоненты:	доктор педагогических наук, профессор Кучугурова Нина Дмитриевна
Официальные оппоненты:	доктор педагогических наук, профессор Мехтиев Мурадхан Гаджиханович
Ведущая организация:	ГОУ ВПО «Орловский государственный университет»

Защита диссертации состоится «26»февраля 2010 года в 16 часов на заседании диссертационного совета ДМ 212.009.05 в ГОУ ВПО «Астраханский государственный университет» по адресу: 414 000, г.Астрахань, пл.Шаумяна1, Естественный институт.

С диссертацией можно ознакомиться в библиотеке ГОУ ВПО «Астраханский государственный университет»

Автореферат выставлен на официальном сайте Астраханского государственного университета: www.aspu.ru.

Автореферат разослан «20» января 2010 года

Ученый секретарь

диссертационного совета

кандидат педагогических наук С.З. Кенжалиева

ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ

Актуальность исследования

Одной из ведущих тенденций развития современного образования является личностно-ориентированный подход к обучению. Ориентация на ученика как субъекта образовательного процесса привела к пересмотру принципов реформирования системы образования, традиционных методов обучения. Личностно-ориентированное образование предполагает, в первую очередь, максимальный учет неповторимой индивидуальности учащегося посредством дифференциации обучения.

Проблема дифференцированного подхода к обучению не является новой для отечественной школы. Исследованию этой проблемы с психологических и педагогических позиций посвящены работы Ю.К. Бабанского, А.А. Бударного, И.Д. Бутузова, В.А Гусева, З.И. Калмыковой, А.Н. Капиносова, А.А. Кирсанова, В.А. Крутецкого, В.В. Куприяновича, А.Н. Леонтьева, И.Я. Лернера, Н.И. Мурачковского, Е.С. Рабунского, М.Н. Скаткина, И.Э. Унт, Р.А. Утеевой И.С. Якиманской и др, в которых представлены системы обучения, отвечающие склонностям учащихся.

Особую роль дифференциация играет в обучении математике, так как она объективно является одной из самых сложных школьных дисциплин и вызывает субъективные трудности у многих учащихся, в то же время многие из них имеют явно выраженные способности к этому предмету, и разрыв в возможностях восприятия курса учащимися весьма велик; причем наибольшие расхождения в темпе усвоения материала наблюдаются у учеников в процессе решения математических задач.

Проблема дифференциации обучения с позиции решения задач и методики обучения математике рассматривается в работах Ш.А. Бакмаева, В.А.Гусева, Г.В. Дорофеева, Л.О. Денищевой, Т.Б. Захаровой, В.И. Крупича, Л.В. Кузнецовой, М.Б. Миндюк, В.М. Монахова, В.А. Орлова, И.Э. Унт, В.В. Фирсова, и др.

Необходимость реализации дифференцированного подхода при обучении решению математических задач связанна с объективными противоречиями между общими для всех обучающихся в том или ином классе целями, содержанием обучения и индивидуальными возможностями каждого ребенка, между коллективной формой учебного процесса и индивидуальным характером усвоения учебного материала и развития детей.

Несмотря на наличие, многочисленных исследований, посвященных проблеме дифференциации и индивидуализации обучения, в том числе при обучении решению математических задач, и богатого многолетнего опыта исследовательской и практической работы по этим проблемам, существует ряд проблем значительно снижающих эффективность дифференцированного обучения решению математических задач:

1) отсутствие возможности проведения контроля (слежения) за ходом деятельности каждого ученика непрерывно в процессе решения учеником задачи, и оперативной коррекции в этом же процессе;

2) отсутствие у ученика возможности видеть результат своей деятельности;

3) трудности оказания своевременной методической помощи непосредственно при решении учеником задачи.

Решение вышеизложенных проблем - задача трудновыполнимая по традиционной методике, которая становится реальной при использовании новых инфокоммуникационных технологий в качестве средства обучения. В связи с чем, актуальной становится проблема совершенствования методики дифференцированного обучения учащихся решению математических задач в условиях компьютеризации образования, в нашем случае с использованием инфокоммуникационных технологий в качестве средства обучения.

Проблема исследования состоит в выявлении эффективных методов и средств дифференцированного обучения решению математических задач с использованием инфокоммуникационных технологий.

Объектом исследования является обучение учащихся решению математических задач.

Предметом исследования являются способы дифференциации процесса обучения решению математических задач средствами инфокоммуникационных технологий.

Цель исследования: разработка методики дифференцированного обучения решению математических задач с помощью инфокоммуникационных технологий.

В основу исследования положена гипотеза: если разработать методику дифференцированного обучения решению математических задач включающую:

- систему задач, предназначаемую для реализации дифференцированного обучения их решению с использованием инфокоммуникационных технологий;

- программное приложение, выполняющее функции сетевой методической обучающей среды (СМОС) и реализующее методику дифференцированного обучения решению математических задач;

то, это будет способствовать формированию осознанности реализации приемов решения задач, и повышению качества знаний учащихся.

Цель, предмет и гипотеза исследования определили его задачи:

Изучить состояние проблемы исследования в научной, педагогической и методической литературе с целью выявления концептуальных положений дифференцированного и индивидуального подхода к обучению и определения возможностей их реализации в процессе обучения решению математических задач;
Разработать методику организации дифференцированного обучения решению задач с использованием инфокоммуникационных технологий;
Разработать систему задач, предназначенную для реализации дифференцированного обучения их решению с использованием инфокоммуникационных технологий;
Разработать программное приложение, выполняющее функции сетевой методической обучающей среды и реализующее методику дифференцированного обучения решению математических задач;
Экспериментально проверить эффективность предложенной методики.

Теоретико - методологические основы исследования: исследование опиралось на основные положения:

- концепции дифференцированного и индивидуального подхода к обучению (В.А. Гусев, Г.В. Дорофеев, В.В. Фирсов, И.Э Унт. и др);

- теорию деятельностного подхода и поэтапного формирования умственных действий (П. Я. Гальперин А.Н. Леонтьев, Н. Ф. Талызина, Л.М.Фридман);

- теорию учебных задач (Ш.А. Бакмаев, Г.А. Балл, Ю.М. Колягин, Н.Д. Кучугурова, Д. Пойа, Л.М. Фридман);

- концепцию компьютеризации образования и программированного обучения (В.П. Беспалько, Ю.С. Брановский, Т.Г. Везиров, Е.А. Машбиц, М.Г.Мехтиев, В. М.Монахов, И.В. Роберт. и др.)

Для решения поставленных задач использовались следующие методы исследования:

Изучение и анализ психолого-педагогической и научно-методической литературы, связанной с дифференцированным подходом к обучению решению математических задач, систематизацией математических знаний у учащихся, алгоритмизацией и программированием обучающих сред;
Эмпирические методы: обсервационные (педагогическое наблюдение явлений и процессов), диагностические (анкетирование учителей и студентов; анализ уроков, беседы с учителями и учащимися) и др.;
Математические методы, основанные на теории вероятностей и математической статистике для обработки данных и оценки качества методической системы.
Проведение педагогического эксперимента.

Научная новизна исследования заключается в том, что

- выявлена возможность осуществления контроля и коррекции знаний при дифференцированном подходе непосредственно в процессе решения учеником задач на базе специально разработанной системы задач, реализация которой становится возможной с использованием инфокоммуникационных технологий;

- разработана методика дифференцированного обучения решению математических задач с использованием инфокоммуникационных технологий;

- разработана сетевая методическая обучающая среда, предназначенная для организации дифференцированного обучения решению математических задач.

Теоретическая значимость исследования состоит в том, что разработана методика дифференцированного обучения решению математических задач, реализуемая средствами инфокоммуникационных технологий.

Практическая значимость исследования состоит в том, что, разработанная нами СМОС содержит в себе систему заданий, включающую специальным образом разработанные тесты, упражнения, задачи и «систему ориентиров», которая может быть использована учителями математики при дифференцированном обучении решению задач.

Обоснованность и достоверность полученных результатов обеспечена опорой на методологические основы теории и методики обучения математике с учетом современных положений психологии обучения; положительной оценкой учителями и методистами разработанных учебных материалов и методики их использования; подтверждается опытно-экспериментальной проверкой основных положений и рекомендаций; результатами внедрения в практику обучения разработанной системы заданий, обучающей программы и методических рекомендаций.

Этапы исследования

Экспериментальное исследование проводилось с 2005 по 2009 гг., и включало ряд этапов: констатирующий, поисковый и обучающий эксперимент.

Цель первого этапа (2005-2006гг.) состояла в сборе данных, которые позволили установить проводится ли в школе целенаправленная работа по реализации дифференцированного обучения решению математических задач, методах, средствах и проблемах ее организации. Эти данные, результаты анализа психолого-педагогической и методической литературы послужили основой для выдвижения гипотезы исследования.

На втором этапе (2006-2007гг.) осуществлялась разработка методики дифференцированного обучения решению математических задач с использованием инфокоммуникационных технологий, которая позволит правильно подбирать оптимальные условия для индивидуальной работы каждого учащегося; а также реализует возможность осуществления контроля и коррекции непосредственно в процессе решения задачи.

Были разработаны система заданий раздела «Четырехугольники» и сетевая методическая обучающая среда «Математика», реализующая названные цели.

Третий этап работы (2007-2009гг.) состоял в проверке гипотезы. Выяснялось, действительно ли разработанная нами методика дифференцированного обучения решению задач с использованием инфокоммуникационных технологий будет способствовать повышению качества знаний учащихся.

Апробация работы и внедрение результатов проводились в процессе проведения занятий по геометрии в 7-9 классах МОУ СОШ №8 и №48 города Махачкалы. Основные результаты исследования докладывались на заседаниях кафедры методики преподавания математики и информатики Дагестанского государственного педагогического университета с 2005 по 2009 годы; получили отражение на ряде конференций и семинаров Межрегиональной научно-практической конференции «Современные проблемы обучения математике и информатике в школе и вузе» (Махачкала 2008); Всероссийской научно-практической конференции «Российское образование в XXI веке: проблемы и перспективы» (Пенза 2008); Всероссийской научно-практической конференции «Современные информационные технологии в науке, образовании и практике» (Оренбург 2008); Всероссийской научно-практической конференции «Проблемы преподавания математики и информатики в школе и вузе» (Махачкала 2008); Международной научно-практической конференции conference “Problems of cybernetcs and informatics”(2008. Baku)

На защиту выносятся следующие положения:

Теоретическое обоснование методики дифференцированного обучения решению математических задач с использованием инфокоммуникационных технологий.
Система задач, предназначенная для реализации дифференцированного обучения их решению с использованием инфокоммуникационных технологий;
Авторская компьютерная программа, выполняющая функции сетевой методической обучающей среды и реализующая методику дифференцированного обучения решению математических задач;

Структура диссертации. Диссертация состоит из введения, двух глав, заключения, списка литературы из 234 наименований и двух приложений. Общий объем диссертации составляет 161 страницу. Приложения: 53 страницы - система задач в приложении №1, 167 страниц - программа на языке Delphi в приложении №2.

ОСНОВНОЕ СОДЕРЖАНИЕ ДИССЕРТАЦИИ

Во введении обоснована актуальность темы исследования, определены его объект и предмет, цели и гипотеза, задачи и методы. Раскрыты научная новизна, теоретическая и практическая значимость, положения, выносимые на защиту. Приведены сведения об апробации диссертационного исследования.

В первой главе «Теоретические основы дифференцированного обучения решению математических задач с использованием инфокоммуникационных технологий» раскрывается сущность, основные положения и пути реализации дифференцированного подхода к обучению решению математических задач; обосновывается выбор средств инфокоммуникационных технологий для организации дифференцированного обучения, подкрепленный современными психолого-педагогическими положениями возможностей такого обучения с использованием средств ИКТ.

Под дифференциацией мы понимаем способ организации вариативного учебного процесса, при котором учитываются индивидуальные особенности, присущие группам учеников. Индивидуализация в нашем случае это предельный вариант дифференциации, когда учебный процесс строится с учетом особенностей не групп, а каждого отдельно взятого ученика. При этом уровневая дифференциация в обучении математике основывается на планировании результатов обучения: явном выделении уровня обязательной подготовки, задаваемого стандартом математического образования и формировании на этой основе повышенных уровней овладения материалом.

Если рассматривать процесс дифференцированного обучения решению задач с позиции деятельностного подхода и поэтапного формирования умственных действий (П. Я. Гальперин, Н. Ф. Талызина, Л.М.Фридман), то ее осуществление мы видим в возможности проведения контроля (слежения) за ходом деятельности каждого ученика непосредственно в процессе решения учеником системы задач и оперативной коррекции в этом же процессе. С этой целью мы объединили исполнительный и коррекционный этапы, не меняя их сущности, выделив, в организации дифференцированного обучения два этапа: диагностико-ориентировочный, исполнительно-коррекционный. При этом контролирующая функция, как неотъемлемая часть обучения присутствует на обоих этапах организации дифференцированного обучения, и в зависимости от этапа осуществляет определенный вид контроля: предварительный, текущий и итоговый.(Рис1)

Поиск путей и средств организации дифференцированного обучения решению математических задач привел нас к возможности и необходимости использования инфокоммуникационных технологий в качестве средства обучения. Применение средств ИКТ позволяет организовать процесс обучения решению задач с учетом индивидуальных особенностей каждого ученика, делая процесс обучения более наглядным и интересным для ученика.

Рис 1. Общая психолого-педагогическая структура обучения решению математических задач применительно к дифференцированному подходу.

Для организации дифференцированного процесса обучения решению задач мы пришли к необходимости составления цикла взаимосвязанных и организованных в систему задач, удовлетворяющих следующим требованиям:

Система задач должна быть взаимосвязанной;
Система задач должна быть единой для всех учащихся, с возможностью выбора индивидуальной последовательности задач;
Все задачи (за исключением нестандартных задач) по определенной теме классифицируются на основе элементов знаний, использованных при их решении, т.е. в одну подсистему должны попасть задачи, в процессе решения которых используется один и тот же набор базовых знаний;
Задачи в подсистемах (названные в требовании 3) должны находиться в некоторой последовательности друг за другом, где предыдущие задачи подсистемы могут содержаться в последующих, в качестве подзадач;
Система задач должна обеспечивать постепенное нарастание сложности задач на базе их внутренней структуры;
Системообразующим элементом каждой подсистемы задач должны являться конструкции геометрических фигур или математические модели и набор базовых знаний;
Группа задач в системе, рассчитанная на оценку «3», должна удовлетворять стандартам обязательной общеобразовательной подготовки.

На основе описанных выше требований к составлению системы задач, и с учетом общей психолого-педагогической структуры обучения применительно к дифференцированному подходу, реализуемому средствами ИКТ, мы проиллюстрируем схему организации дифференцированного обучения решению математических задач на примере группы учеников, начавших свое движение, по итогам диагностического этапа, с задачи А₁₃. (рис 2)

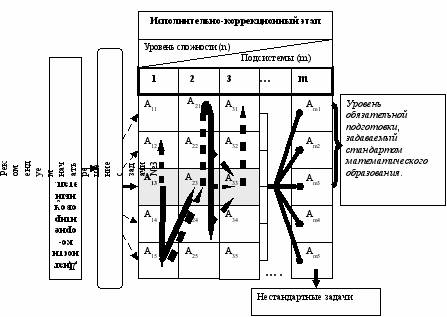
Рис 2. Схема организации дифференцированного обучения решению математических задач с использованием ИКТ

Сплошными стрелками на схеме показано движение ученика, в случае, если задача решена; аналогично пунктирными стрелками показано движение ученика, не решившего задачу. Решение задач начинается с подсистемы 1, и уровня сложности n рекомендуемого по результатам диагностического этапа. Движение внутри подсистемы происходит от n к n+1 номеру по нарастающей степени сложности задач данной подсистемы. Решение задач следующей подсистемы ученик начинает с того же номера n, что и в предыдущей подсистеме. В случае если задача номера n не решена, движение внутри подсистемы происходит от n к n-1 номеру.

В качестве примера мы рассматриваем геометрические задачи раздела «Четырехугольники». Хотя выбор темы не является принципиальным, мы мотивировали его тем, что планиметрические задачи являются не только одними из наиболее распространенных, но и базовыми в школьном курсе геометрии.

Анализ педагогических программных средств используемых при обучении математике привел нас к выводу, что имеющиеся программные средства не позволяют реализовать вышеописанную схему организации дифференцированного обучения решению математических задач, это привело нас к необходимости создания соответствующего программного приложения.

Во второй главе «Методика дифференцированного обучения решению математических задач с использованием СМОС «Математика»» раскрывается идея использования инфокоммуникационных технологий как средства дифференцированного обучения решению математических задач и описана методика такого обучения. Также в данной главе описан педагогический эксперимент.

При использовании программного приложения в качестве средства дифференцированного обучения решению математических задач мы предполагаем создание информационно-образовательной среды (ИОС) в классе, а соответственно и решения комплекса задач: образовательная задача; управление образовательным процессом; обеспечение коммуникации, налагаемых на ИОС в этом процессе. Если в подобную среду встраивается определенная методика или методики обучения, то среда носит название методической обучающей среды. Для реализации нашей методики дифференцированного обучения решению математических задач мы разработали сетевую методическую обучающую среду (СМОС) «Математика».

СМОС «Математика» представляет собой программное приложение архитектуры клиент-сервер. В качестве платформы для разработки был использован язык Borland Delphi 7, СУБД - локальная с использованием библиотеки Firebird - gds32.dll. Клиентская часть программы предназначена для ученика. Соответственно сервер базы данных - для учителя.

Мы разбили организацию дифференцированного обучения решению задач с использованием СМОС «Математика» на вышеописанные этапы. Диагностико-ориентировочный этап включает в себя 2 тура: теоретический тест - опрос, который состоит из 10 теоретических тестов, общих для всей системы задач, и 10 упражнений, которые представляют собой устные задачи в одно – два действие, решение которых занимает 2-3 мин. Исполнительно-коррекционный этап включает в себя разработанную нами систему задач раздела «Четырехугольники» и реализовывается по описанной выше схеме.

В случае, когда ученику оказывается недоступна самостоятельная поисковая деятельность, наиболее оптимальной здесь является деятельность по заданной учителем «системе ориентиров» (она указана в алгоритме), которая включает в себя:

- теоретический материал, на которое опиралось решение задачи;

- чертеж к задаче;

- указание к задаче;

- решенную задачу, с помощью которой учащимся демонстрируются приемы поиска решений задач данного типа (подсистемы), и не входящей в число задач, которые ученику необходимо решить в данной подсистеме, а является аналогичной ей;

- динамические чертежи, которые в нашем исследовании представляют собой чертежи с проблемными вопросами и раскрывают построение или ход решения задачи шаг за шагом. Такие чертежи помогают анализировать задачу, находить связи между элементами, и сопровождают их текстовыми комментариями, которые носят обучающий характер, создавая проблемные ситуации. Особенность проблемных методов состоит в обучении учащихся видению взаимосвязей между видами знаний.

Поясним все выше сказанное на примере.

Пример: (Шарыгин И.Ф. 7-9 кл) Около окружности описана трапеция, с углом при основании в 30 градусов, а в окружность вписан прямоугольник, стороны которого удалены от центра окружности на 3 и 4 см. Найти боковую сторону трапеции, прилежащую к углу в 30 градусов. (рис 3)

Рис 3 Пример динамических чертежей при решении задачи

Серверное приложение СМОС «Математика» выполняет следующие функции:

- создание и редактирование списка учеников класса;

- наличие СУБД, в которой учитель может менять систему заданий;

- настройка таймеров на каждую задачу;

- наличие страницы отчетов, благодаря которой учитель получает возможность следить за ходом выполнения учеником системы задач в течение урока, получая отчеты в виде номера задачи, решением которой ученик занимается в данное время;

- фиксирование в отдельном списке в отчете номеров задач, которые вызывают наибольшее затруднение у учеников.

Также во второй главе приводятся результаты экспериментального исследования.

Исследование проводилось школах № 8, 48 г. Махачкалы.

Достижение цели третьего этапа предполагало проверить:

- осознанность реализации приемов решения задач;

- повышение качества знаний учащихся.

Говоря о критериях осознанности реализации приемов решения задачи напомним, что решение любой математической задачи осуществляется с помощью ряда приемов. Каждый прием, как правило, предполагает использование учеником имеющихся знаний, в том числе – сформированных (известных) приемов. Если ученик может выбрать нужные для выполнения конкретного приема знания, установить последовательность их использования (что обусловлено видением взаимосвязей между знаниями), то это приводит к реализации приема, а значит к решению данной задачи. Следовательно, информация о том, что данный прием применен для решения предложенной задачи правильно, косвенно может свидетельствовать, с одной стороны, об умении выбрать из системы соответствующих знаний нужный блок, а с другой, - о наличии связей между знаниями, составляющими основу конкретного приема. Если же правильно применены несколько приемов решения задач конкретного типа, то это дает обоснование для вывода о наличии действенных взаимосвязей между знаниями и об умении их реализовывать. При этом выбор одного и того же приема при решении задач определенного типа, его видение и реализация в различных задачных ситуациях, как правило, происходит в том случае, если установление связей между видами знаний происходит осознанно. Поэтому в качестве критерия осознанности мы рассматривали умение учащихся устанавливать взаимосвязи между знаниями, используемыми в процессе решения задач определенного типа.

В нашем исследовании для проверки осознанности реализации приемов решения задач мы провели контрольную работу, в которой задачи были сгруппированы на основе одного и того же набора знаний, использованных при их решении. Контрольная работа состояла из 4-х задач находящихся в определенной последовательности, где предыдущие задачи содержатся в последующих в качестве подзадач, обеспечивая тем самым постепенное нарастание сложности на базе их внутренней структуры. Выполнение задач различных уровней сложности было связано с применением одного и того же «базисного» приема решения и набора знаний, но для различных геометрических конструкций.

В ходе выполнения данной контрольной работы возможна ситуация когда часть учеников правильно реализует отдельные приемы решения задач с помощью случайного подбора необходимых знаний. В этом случае необходимо определить количество приемов, правильная реализация которых свидетельствовала бы о наличии умений устанавливать взаимосвязи между знаниями. Причем делать вывод об осознанности реализации этих приемов можно лишь в случае правильного решения всех задач. В случае частичного выполнения контрольной работы необходимо учитывать уровни умения учеников решать задачи.

Результаты контрольной работы отражены в таблицах 1,2.

Для получения информации об осознанности реализации приемов решения задач мы рассматривали задачи № 2,3,4 Базисные приемы решения прямоугольного треугольника, при этом, выражаются в системе операций, выделенной в таблице 1. В задаче №2 прием состоит из двух операций (1,2), в задаче 3 из тех операций (2,3,4), в задаче 4 также из трех операций (3,4,5). Говорить об осознанности реализации приемов решения задач можно в случае правильной реализации базисных приемов во всех трех задачах.

В таблице 1 указано выполнение каждой операции в процентном отношении от общего числа учеников. При подобном подходе к количественному анализу легко подсчитать количество учащихся выполнивших базисные приемы решения задач, вычислив среднее арифметическое данных таблицы 1 в указанных выше операциях для каждой задачи. Результаты такого подсчета отражены в таблице 2.

В случае частичного выполнения контрольной работы мы обратились к уровням умения учеников решать задачи. В таблице 3 приведены результаты количественного анализа: оценки и распределение по уровням контрольной и экспериментальной групп.

Данные таблиц 1, 2, 3 позволяют сделать вывод о том, что в экспериментальных классах число учащихся находящихся на опорном и повышенном уровнях, и, соответственно, правильно реализующих приемы решения задач увеличивается по сравнению с классами контрольной группы. Указанное увеличение позволяет говорить о сформированности осознанности приемов решения задач.

С целью проверки изменения качества знаний учащихся за время текущего этапа эксперимента была проведена итоговая контрольная работа. Результаты ее выполнения отражены в таблице 4.

Таблица 3 Уровни умения учеников решать задачи

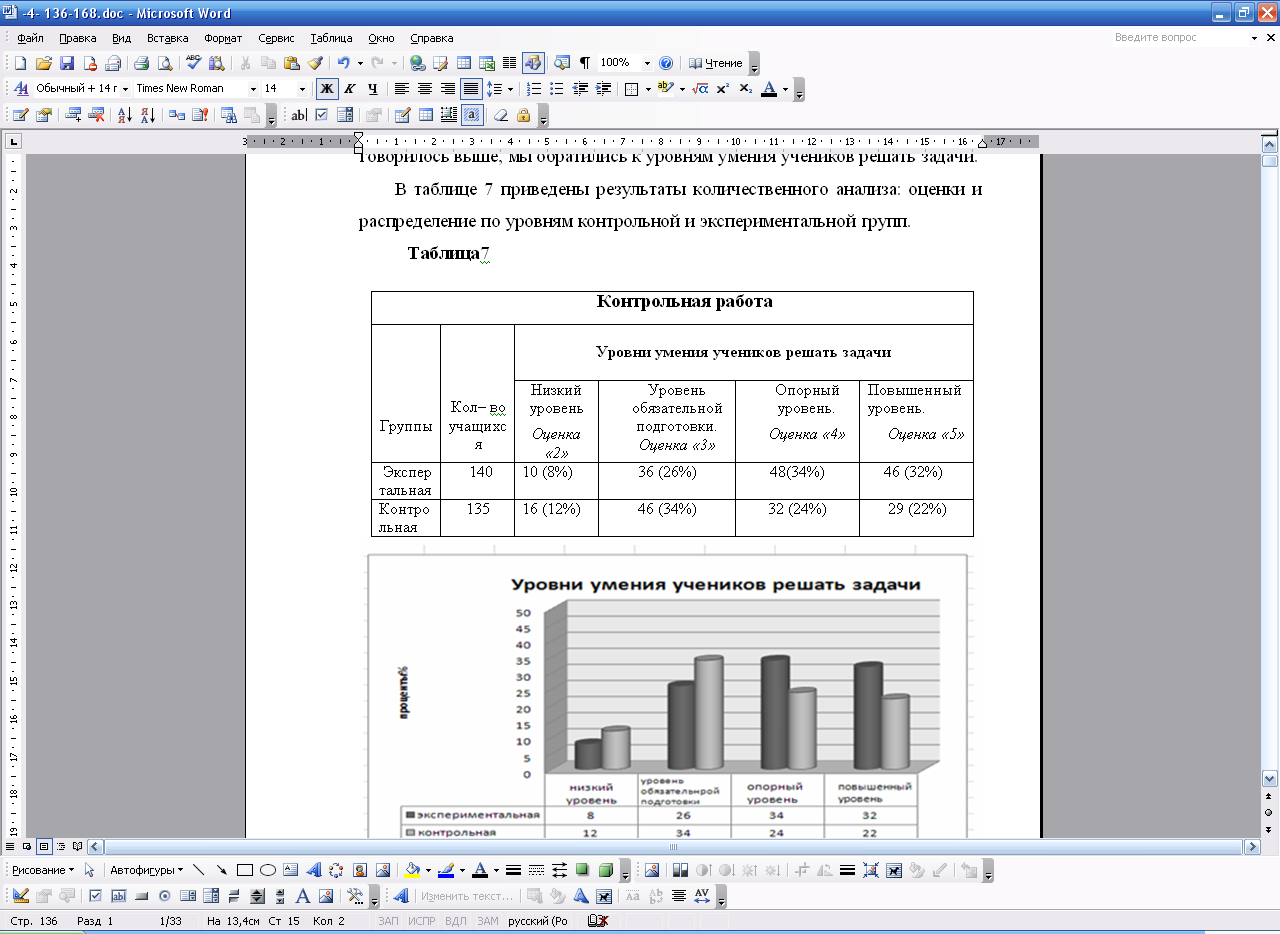
Рис 4 Диаграмма уровня умения учеников решать задачи

Таблица 4 Результаты итоговой контрольной работы

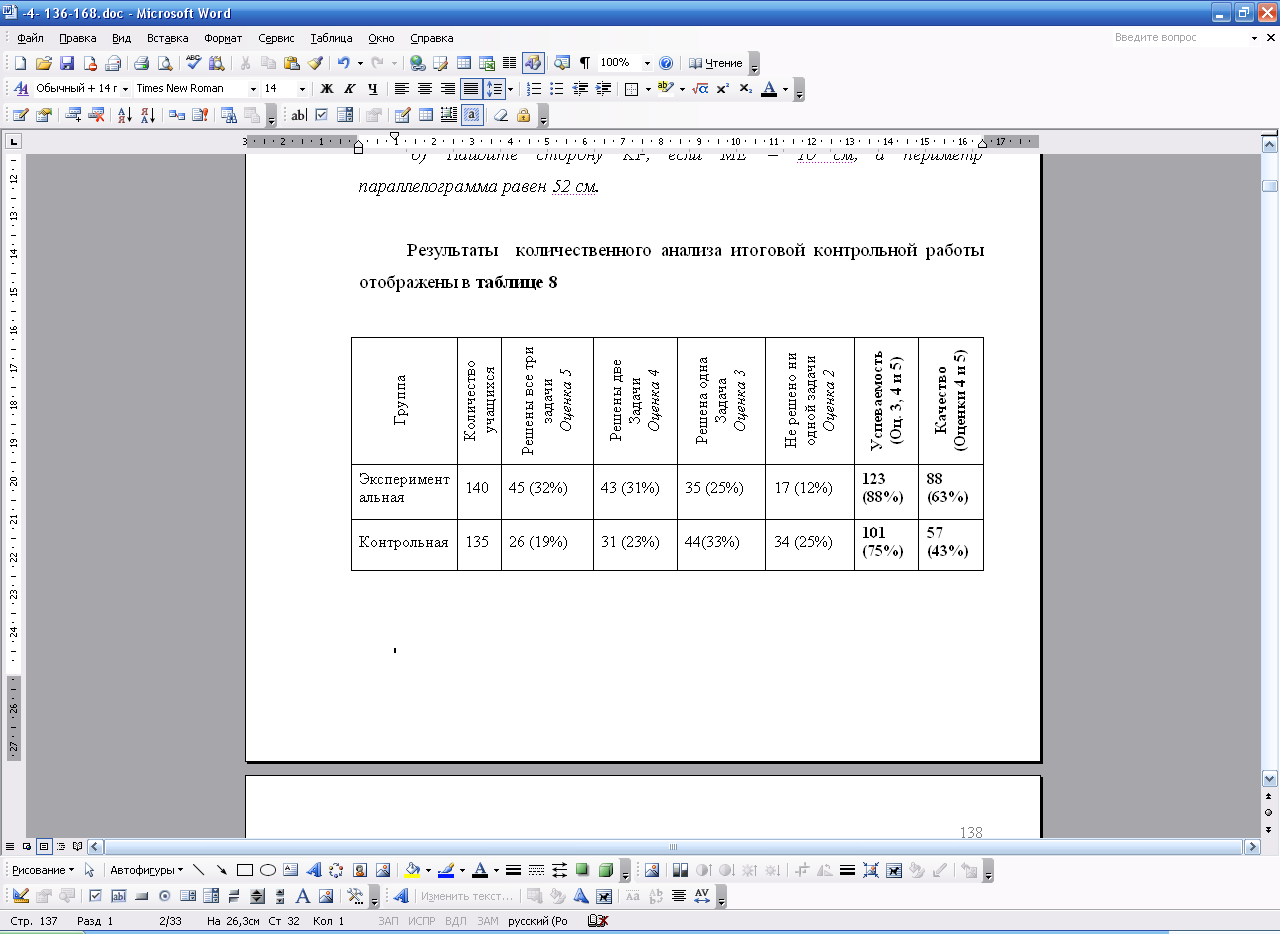
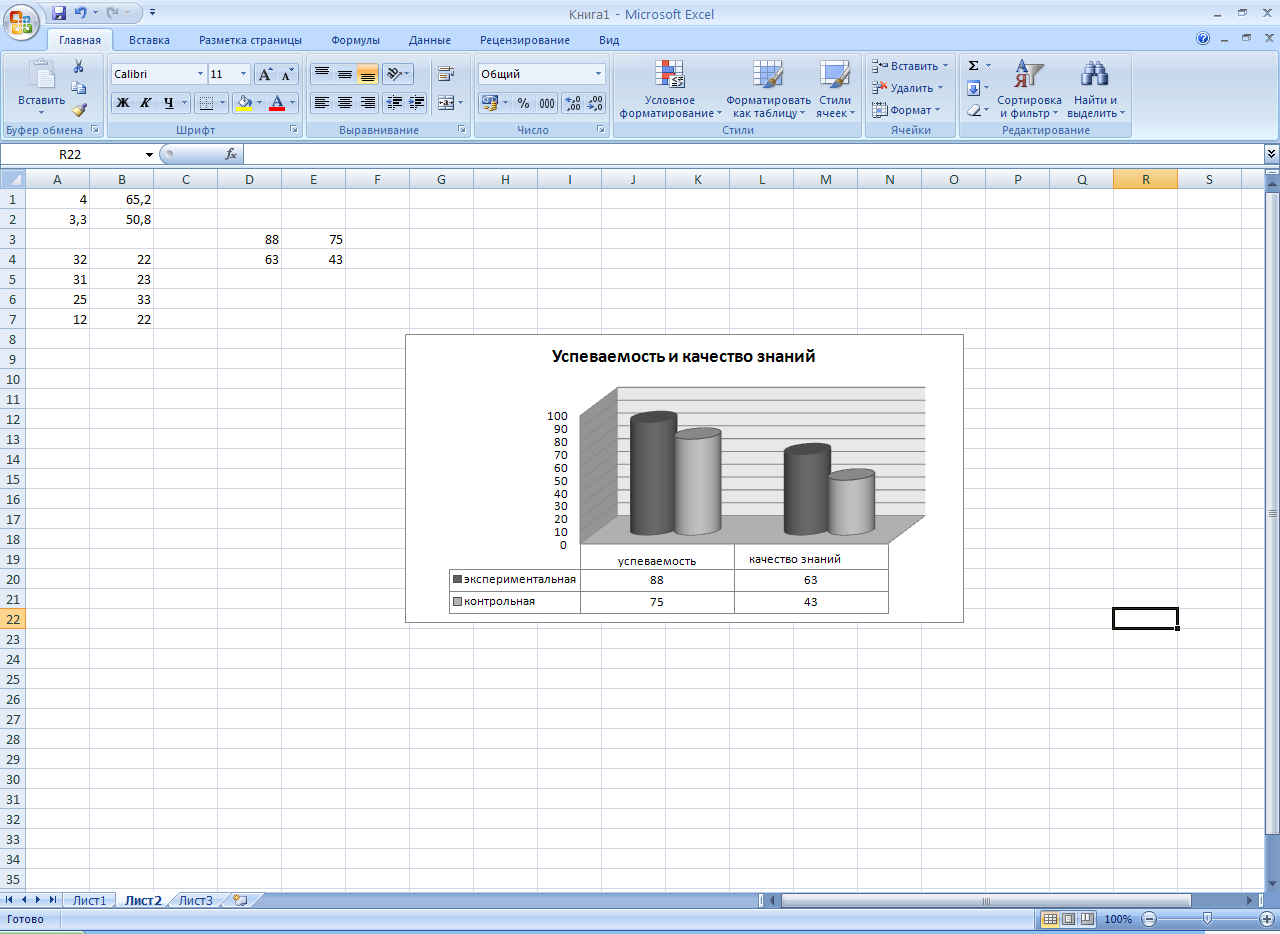
Рис 5 Диаграмма результатов итоговой контрольной работы

Как известно, для определения качества знаний учащихся существуют несколько подходов:

1. Вычисление средней арифметической всех оценок, полученных учащимися в каждой группе.

2. Определение качества знаний на основании метода академика Б.П. Смирнова:

СО =

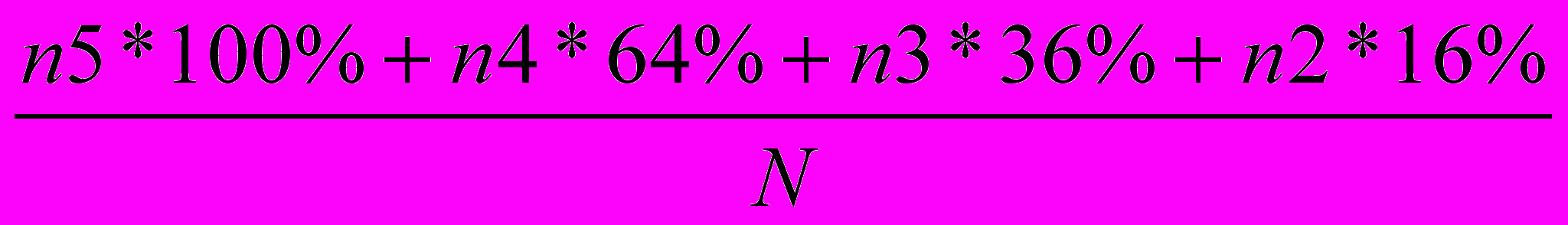
Где N – количество испытуемых, n5 – количество пятерок, n4 – количество четверок, n3 – количество троек, n2 – количество двоек.

3. Использование метода однофакторного дисперсионного анализа, который позволяет выяснить, какую долю изменчивости результатирующего признака можно объяснить действием факториального признака.

Наиболее распространенным является определение качества знаний как средней арифметической всех оценок, полученных учащимися в каждой группе по пятибалльной шкале.

Для этого воспользуемся данными таблицы 4.

∑_ср эксп. =

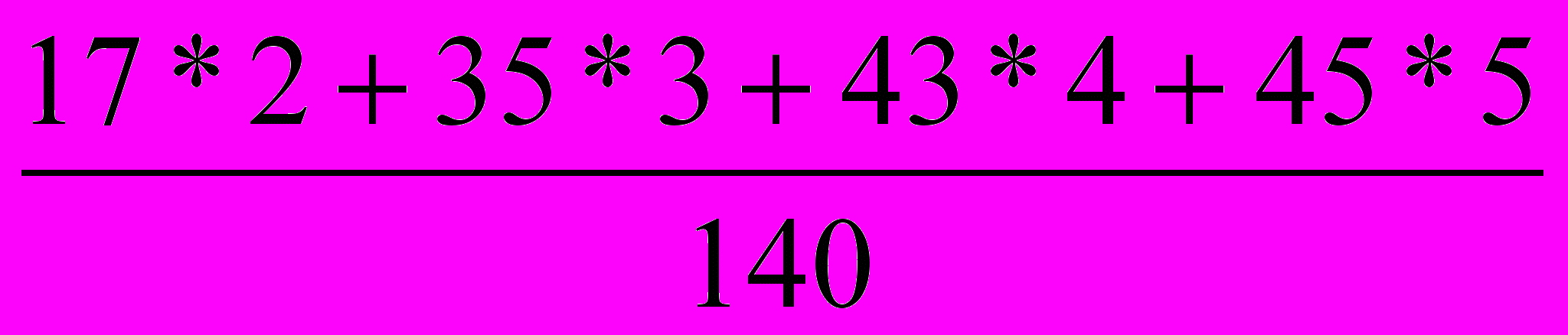≈ 3,82≈3,8

∑_ср конт.=

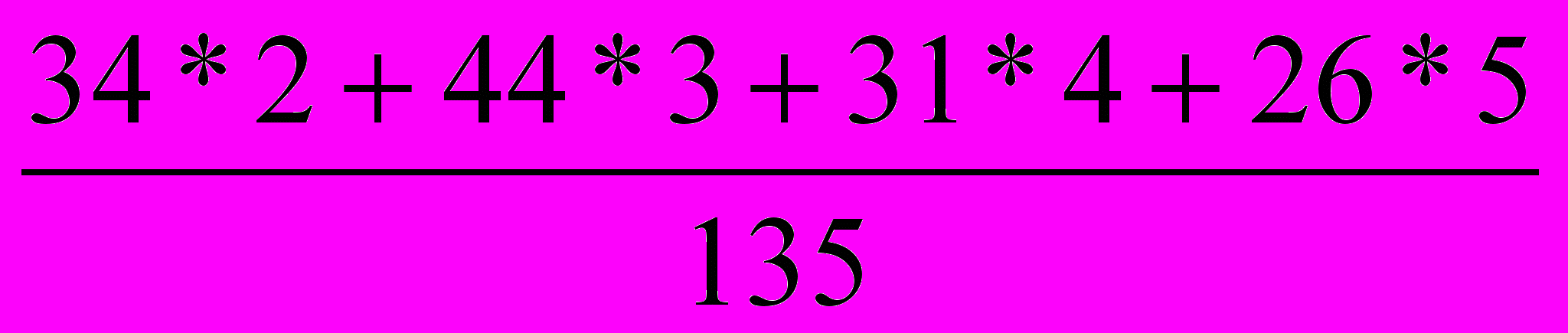≈ 3,36≈3,4

Результаты контрольной работы показали следующие результаты. В контрольной группе уровень умения учеников решать задачи составил 3,4 балла, а в экспериментальной группе 3,8 баллов.

Второй вариант определения качества знаний основанный на методе академика Б.П. Смирнова.

СО_экс =

= 63,7 %

СО_кон.=

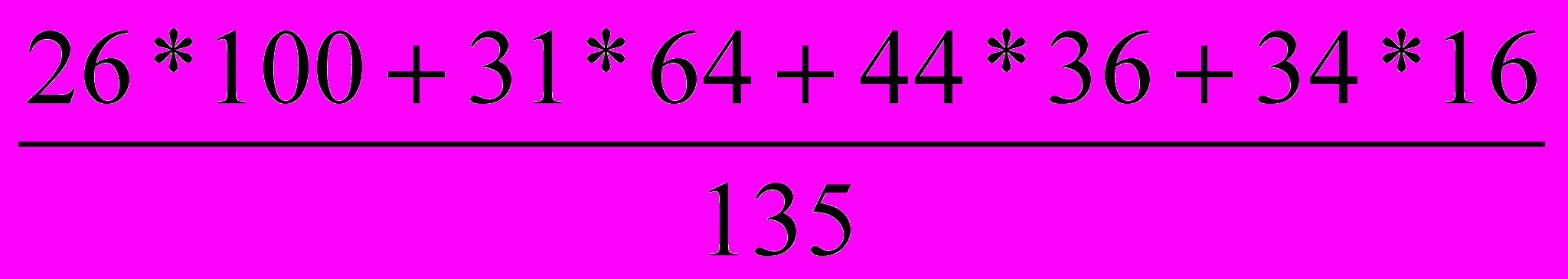= 49,7 %

3. Приведем показатели дисперсионного анализа.

Таблица 5 Показатели дисперсионного анализа

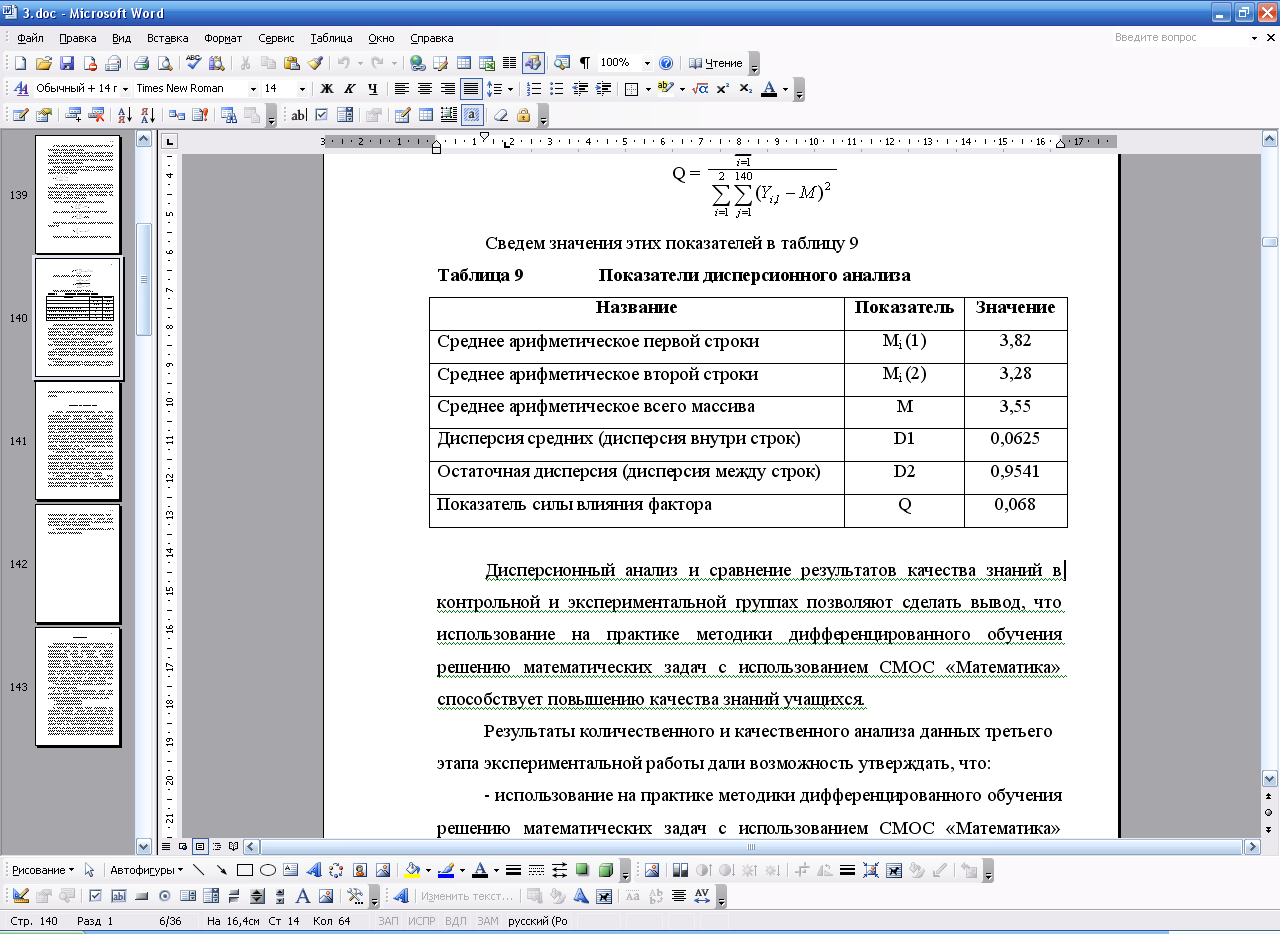
Чем меньше рассеивание внутри каждой строки, и чем больше расстояние между строками, тем более существенно влияние фактора на изменчивость изучаемой переменной.

Результаты количественного и качественного анализа данных третьего этапа экспериментальной работы дали возможность утверждать, что использование на практике методики дифференцированного обучения решению математических задач с использованием СМОС «Математика» приводит к увеличению числа учащихся осознанно реализующих приемы решения задач, а также способствует повышению качества знаний учащихся, что полностью подтверждает выдвинутую нами гипотезу.

ОСНОВНЫЕ ВЫВОДЫ ИССЛЕДОВАНИЯ

В ходе исследования решены все поставленные в диссертации задачи и получены следующие результаты:

1. На основе психолого-педагогического анализа теории деятельностного подхода и поэтапного формирования умственных действий в организации дифференцированного обучения мы выделяем два этапа: диагностико-ориентировочный; исполнительно-коррекционный. При этом контролирующая функция, как неотъемлемая часть обучения присутствует на обоих этапах/

2. Выявлены этапы процесса обучения учащихся решению математических задач: актуализация знаний используемых при решении задач; формирование системы базовых блоков знаний; индивидуализация и дифференциация обучения решению задач. Обучение взаимосвязям между знаниями происходит на всех вышеперечисленных этапах. Разработана «система ориентиров», необходимая в случае, когда ученику оказывается недоступна самостоятельная поисковая деятельность, которая включает в себя: теоретический материал, чертеж к задаче, указание к задаче, решенную задачу, динамические чертежи.

3. Разработана система задач, предназначенную для реализации дифференцированного обучения их решению с использованием инфокоммуникационных технологий

4. Разработана сетевая методическая обучающая среда, предназначенная для реализации методики дифференцированного обучения решению математических задач.

Проведенные экспериментальные исследования подтвердили методическую обоснованность и эффективность разработанной методики дифференцированного обучения решению математических задач с использованием инфокоммуникационных технологий.

Направление дальнейшего исследования проблемы выявления эффективных методов и средств дифференцированного обучения учащихся решению математических задач с использованием инфокоммуникационных технологий мы видим возможности непрерывного слежения за процессом решения задачи каждого ученика, т.е. в присоединении к СМОС «Математика» интерактивных планшетов (мини интерактивных досок с рабочей поверхностью А5), обеспечивающих бесклавиатурный ввод графической и текстовой информации в компьютер.

Основное содержание диссертационной работы отражено в следующих публикациях:

Магомедова Р.М. Методика дифференцированного обучения решению математических задач с использованием инфокоммуникационных технологий [Текст]/ Р.М. Магомедова // Сибирский педагогический журнал -. № 15. – 2008. – С. 142-154. (1 п.л.) (входит в «Перечень…» рецензируемых изданий ВАК РФ)
Магомедова Р.М. Дифференцированное обучение школьников в сетевой методической обучающей среде. [Текст]/ Р.М. Магомедова // Педагогические науки. Известия южного федерального университета. -№1.- 2009. С. 95-103. (0,6 п.л.) (входит в «Перечень…» рецензируемых изданий ВАК РФ)
Магомедова Р.М. Методика формирования приемов решения геометрических задач. [Текст]/ Р.М. Магомедова // Актуальные проблемы математики, информатики и методик их преподавания. Материалы научно-практической конференции, посвященной 60-летию математического факультета ДГПУ.- Махачкала.- 2005. С.117-122.(0,4 п.л.)
Магомедова Р.М. Дифференцированное обучение решению математических задач с использованием инфокоммуникационных технологий. [Текст]/ Р.М. Магомедова, Ш.А Бакмаев. // Сборник научных трудов кафедры прикладной математики механики. Вып.1 – ГОУ ВПО «Московский Государственный Открытый Университет» Институт (филиал) в Махачкале – Махачкала 2007, С. 86-96. (0,6 п.л.)
Магомедова Р.М. Применение ИКТ в дифференцированном обучении решению геометрических задач. [Текст]/ Р.М. Магомедова // Инновационные технологии в обучении и воспитании младших школьников. Материалы второго республиканского научно-практического семинара учителей начальных классов – Карачаевск: КЧГУ, 2007 – С.264-267. (0,2 п.л.)
Магомедова Р.М. Психолого-педагогические аспекты дифференцированного и индивидуального обучения в процессе решения математических задач, с использованием ИКТ технологий. [Текст]/ Р.М. Магомедова, Г.С. Ахмедов// Современные проблемы обучения математики и информатики в школе и вузе: сборник материалов межрегиональной научно-практической конференции/ под редакцией А.А.Абдуллаева, Д.М.Нурмагомедова.- Махачкала: Издательство ДГПУ, 2008. С.28-30 (0,1 п.л.)
Магомедова Р.М Методика структурирования системы задач, как основа обучения учащихся приемам их решения. [Текст]/ Р.М. Магомедова // Современные проблемы обучения математики и информатики в школе и вузе: сборник материалов межрегиональной научно-практической конференции/ под редакцией А.А.Абдуллаева, Д.М.Нурмагомедова. - Махачкала: Издательство ДГПУ, 2008. С. 79-82 (0,2 п.л.)
Magomedova R.M. Methodic of the differentiated training organization for the decision of mathematical problems with use infocommunicative technologies // PCI’2008. The Second internationfl conference “Problems of cybernetcs and informatics” Dedicated to the 50 th Anniversary of the ICT in Azerbaijan. Volume I. September 10-12, 2008. Baku, Azerbaijan. P.27-30. (0,2 п.л.)
Магомедова Р.М. Использование компьютерных технологий при дифференцированном обучении решению математических задач. [Текст]/ Р.М. Магомедова, З.Г. Лахикова // Проблемы преподавания математики и информатики в школе и вузе: Материалы Всероссийской научно-практической конференции. Махачкала, 19-21 сентября 2008.- С.65-69 (0,2 п.л.)
Магомедова Р.М. Методическая компьютерная обучающая среда как средство организации дифференцированного обучения решению математических задач. [Текст]/ Р.М. Магомедова // Российское образование в XXI веке: проблемы и перспективы. Материалы всероссийской научно-практической конференции. // Пенза, ноябрь 2008. С. 74-75 (0,1 п.л.)
Магомедова Р.М. Инфокоммуникационые технологии как средство организации дифференцированного обучения решению математических задач. [Текст]/ Р.М. Магомедова // Современные информационные технологии в науке, образовании и практике: Материалы седьмой всероссийской научно-практической конференции. Оренбург, 27-28 ноября 2008. С. 485-488 (0,2 п.л.)
Магомедова Р.М. Психологические аспекты организации дифференцированного обучения средствами ИКТ. [Текст]/ Р.М. Магомедова // межвузовский сборник научных трудов «Вузовская наука и проблемы регионального образовательного пространства»// ГОУ ВПО «КГУ им. У.Д. Алиева», Карачаевск, 2008. С. 22-24 (0,2 п.л.)
Магомедова Р.М. Организация дифференцированного обучения решению математических задач средствами ИКТ [Текст]/ Р.М. Магомедова //Технологии совершенствования подготовки педагогических кадров: теория и практика. Межвузовский сборник научных трудов № 12 // Казань, 2008. С.185-187 (0,2 п.л.)
Магомедова Р.М. Динамические чертежи как средства обучения решению математических задач. [Текст]/ Р.М. Магомедова //материалы международной научно-практической конференции «Модернизация системы непрерывного образования». – Махачкала, 26 – 28 июня 2009. – 382-387 (0,3 п.л.)

Blog

Содержание